Cost-Benefit Analysis of a Standby Retrial System with an Unreliable Server and Switching Failure

Abstract

In many industries and plants, a stable power supply system with acceptable cost/benefit is essential. This paper investigates the cost-effectiveness of an unreliable retrial system that includes standby generators and experiences the switchover failures of standby generators. Four different standby retrial configurations are included, and each configuration includes various numbers of primary and standby generators. Upon arrival, a failed generator is repaired immediately if the server is available; otherwise, the failed generator will enter into orbit. The server is subject to breakdown even when the server is idle. The explicit expressions of the mean time-to-failure and steady-state availability for each configuration are derived and compared. We also compare the cost/benefit ratio among four configurations. The developed results can provide managers with decision reference for stable power supply system and cost reduction.

1. Introduction

A robust power supply system with acceptable cost/benefit is a fundamental part for high-tech fabrication plants (called fabs), which plays an important role in modern industries, such as packaging and testing, IC design, and wafer foundry. For fabs, a stable power supply system is essential for maintaining the competition. Liu et al. [1] applied a retrial system with standby switching failure to model the power supply system for a fab. In their work, the repair server is assumed to be reliable. They applied the supplementary variables techniques to obtain the explicit expressions of the steady-state availability. However, in real world application, the repair server may be malfunctioned, but can be repaired. To address this issue, in this paper, we extend the work of Liu et al. [1] to the case of a unreliable repair server. As we know, the more system features we take into consideration simultaneously, the more difficulty we have in modelling the system and deriving the equations. Hence, the investigated model has not been studied in the literature so far. In addition, we derive the explicit expressions of the mean time-to-failure and steady-state availability for each configuration. Four different standby retrial configurations are included, and each configuration includes various numbers of primary and standby generators. Except for obtaining the explicit expressions of steady-state availability for each configuration, we also obtain the explicit expressions of the mean time-to-failure for each configuration and make a comparison.

Due to the practical applicability of the retrial queues, more and more researchers have attracted attention to retrial systems. For existing works related to retrial systems, interested readers can refer to Falin and Templeton [2], Artalejo [3], Artalejo and Gomez-Corral [4], Yang and Chang [5], Chen [6], Chen and Wang [7], Yang and Tsao [8], Phung-Duc [9], and the references therein. Recently, Yen, Wang, and Wu [10] investigated the system availability and sensitivity analysis of a retrial queue with working breakdowns operating under the F-policy. Yen and Wang [11] investigated the reliability and availability of four retrial systems with imperfect coverage and compared the cost/benefit among these four retrial systems. Gao and Wang [12] studied a retrial unreliable machine system with mixed standbys and optimized the cost-effectiveness ratio. Wu and Yang [13] constructed a repairable system with warm standbys and imperfect switchovers and evaluated its availability and reliability. Hirata et al. [14] presented an evaluation method for the variance of failure times in the two-component priority standby redundant system by expanding the idea by evaluating mean time-to-failure proposed in the previous research. They proposed a procedure for deriving the reliability function in the system based on the maximum entropy principle by utilizing mean time-to-failure and variance of failure times. Liu et al. [15] studied a K-out-of-N retrial system with mixed standby components and a single repair server under Bernoulli vacation schedule. They used vector Markov process and Laplace transform theory to derive the steady-state availability, reliability function, and mean time-to-failure.

The process of switching over standbys in the actual repairable standby system may not be perfect, as described by Lewis [16]. Kuo and Ke [17] constructed three standby unreliable systems with switching failure and compared the cost/benefit ratio and availability among the three systems. Ke et al. [18] modeled a machine repairing system incorporating standby switching failure, in which the general repair times are considered, and constructed a cost function to search the optimal system parameters. Utilizing supplementary variables, Lee [19] studied the availability analysis of a redundancy model with general repair times, switching failure, and interrupted repairs. Other research works along this line includes Shekhar et al. [20], Ke et al. [21], Jain and Gupta [22], and Liu et al. [23].

The contents of this work are managed in the following sections. The model description is given in Section 2. The four different unreliable retrial systems are introduced in Section 3. For each configuration, the explicit expressions for mean time-to-failure (MTTF) and steady-state availability (Av) are derived by the matrix-analytic method. The numerical results are presented in Section 4. We also rank four configurations according to MTTF, Av, and the cost/benefit ratio. Section 5 is devoted to the summary and conclusions.

2. System Description

By referring to Liu et al. [1], we consider that a system requires 24 megawatts (MW) power and assume that the power generating capacity of a generator is available in units of 24 MW, 12 MW, and 8 MW. In this system, the energy generator that is supplying electricity is called the primary generator, and the energy generator that is online but does not provide power is called the standby generator. Both the primary and standby energy generators may fail and can be repaired. The failure times of primary and standby generators obey an exponential distribution with rate λ and α (0 < α < λ), respectively. We assume that the switching device has a failure probability q. In the repair facility, only one server is responsible for repairing a failed generator and there is no waiting space in front of the server. Hence, a failed generator finding that the server is free is repaired immediately; otherwise, it will enter orbit. The retrial time obeys exponential distribution with the rate γ. The failed generators will continue to retry until it gets the required repair. The repair times of a failed generator obey exponentially distributed with rate µ. Additionally, the server may fail at any time even if it is idle. The server fails with an exponential breakdown rate of η. The repair time for the server obeys exponentially distributed with mean β⁻¹.

Four configurations are considered as follows: configuration 1 consists of one 24 MW primary generator and one 24 MW standby generator. Configuration 2 includes two 12 MW primary generator s and one 12 MW standby generator. Configuration 3 contains two 12 MW primary generators and two 12 MW standby generators. Configuration 4 contains three 8 MW primary generators and two 8 MW standby generators.

3. Systematic Methodology

We first draw the transition-rate diagram for each configuration. According to the diagram, we develop the differential-difference equations. Finally, we utilize the matrix-analytic method to obtain the explicit expressions of MTTF and Av. We define the following probabilities throughout the paper.

$$\begin{gathered} P_{0,n}\left(t\right)=Pr\left(W\left(t\right)=n, J\left(t\right)=0\right), \\ {P}_{1,n}\left(t\right)=Pr\left(W\left(t\right)=n, J\left(t\right)=1\right), \\ {P}_{2,n}\left(t\right)=Pr\left(W\left(t\right)=n, J\left(t\right)=2\right), \\ {P}_{3,n}\left(t\right)=Pr\left(W\left(t\right)=n, J\left(t\right)=3\right), \end{gathered}$$

where $W\left(t\right)$ represents the number of failed generators in orbit at time t, and $J\left(t\right)$ denotes the states of the server at time t, and

$$J\left(t\right)=\{\begin{array}{c}0,\mathrm{the}\mathrm{server}\mathrm{is}\mathrm{free},\hfill \\ 1,\mathrm{the}\mathrm{server}\mathrm{is}\mathrm{busy},\hfill \\ 2,\mathrm{the}\mathrm{free}\mathrm{server}\mathrm{is}\mathrm{under}\mathrm{repair},\hfill \\ 3,\mathrm{the}\mathrm{busy}\mathrm{server}\mathrm{is}\mathrm{under}\mathrm{repair}.\hfill \end{array}$$

3.1. Configuration 1

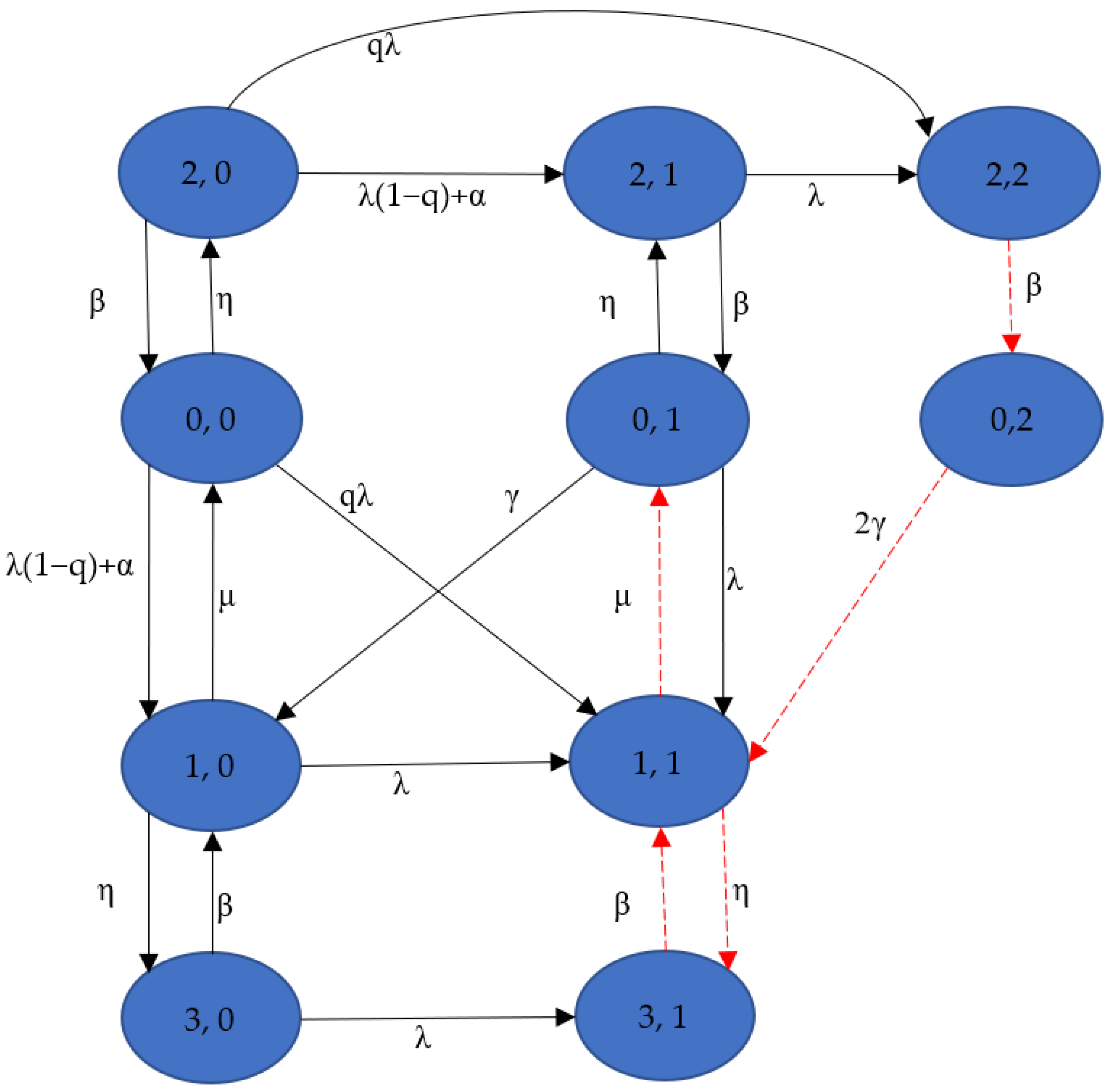
For the reliability case, the state-transition-rate diagram of configuration 1 is provided in Figure 1. It is assumed that the system is characterized as a failure as soon as the remaining electricity generation capacity is less than 24 MW. So, if the system cannot be resumed, the states (0, 2), (1, 1), (2, 2), and (3, 1) are absorbing states. Based on the Figure 1, the differential-difference equations can be written as the following matrix form:

$$\frac{d}{dt}{\mathit{P}}_1\left(t\right)={\mathit{Q}}_1{\mathit{P}}_1\left(t\right),$$

(1)

where

$$\begin{gathered} {\mathit{Q}}_1=\left[\begin{array}{cccccccccc}-{\mathsf{\Delta }}_{10}& 0& 0& \mu & 0& \beta & 0& 0& 0& 0\\ 0& -{\mathsf{\Delta }}_{11}& 0& 0& 0& 0& \beta & 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ x_{11}& \gamma & 0& -{\mathsf{\Delta }}_{12}& 0& 0& 0& 0& \beta & 0\\ \lambda q& \lambda & 0& \lambda & 0& 0& 0& 0& 0& 0\\ \eta & 0& 0& 0& 0& -{\mathsf{\Delta }}_{13}& 0& 0& 0& 0\\ 0& \eta & 0& 0& 0& x_{11}& -\left(\lambda +\beta \right)& 0& 0& 0\\ 0& 0& 0& 0& 0& \lambda q& \lambda & 0& 0& 0\\ 0& 0& 0& \eta & 0& 0& 0& 0& -\left(\lambda +\beta \right)& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& \lambda & 0\end{array}\right], \\ {\mathit{P}}_1\left(t\right)={\left[P_{0,0}\left(t\right),P_{0,1}\left(t\right),P_{0,2}\left(t\right), P_{1,0}\left(t\right),P_{1,1}\left(t\right),P_{2,0}\left(t\right),P_{2,1}\left(t\right), P_{2,2}\left(t\right),P_{3,0}\left(t\right),P_{3,1}\left(t\right)\right]}^T, \\ {\mathsf{\Delta }}_{10}=\lambda +\alpha +\eta ,{\mathsf{\Delta }}_{11}=\lambda +\gamma +\eta ,{\mathsf{\Delta }}_{12}=\lambda +\mu +\eta ,{\mathsf{\Delta }}_{13}=\lambda +\alpha +\beta ,x_{11}=\lambda \left(1-q\right)+\alpha . \end{gathered}$$

To evaluate MTTF₁, we define A₁ as the transpose matrix of Q₁ omitting the row and column for the absorbing states. First, 1 represents a column vector with all elements equal to 1, and the initial condition is

$$\mathit{P}\left(0\right)={\left[P_{0,0}\left(0\right),P_{0,1}\left(0\right),P_{1,0}\left(0\right),P_{2,0}\left(0\right),P_{2,1}\left(0\right), P_{3,0}\left(0\right)\right]}^T={\left[1,0,0,0,0, 0\right]}^T.$$

Then, we can obtain

$$E\left[T_{0\to absorbing}\right]={\mathit{P}}_1{\left(0\right)}^{\mathit{T}}\left(-A_1^{-1}\right)1,$$

(2)

where

$$A_1=\left[\begin{array}{cccccc}-{\mathsf{\Delta }}_{10}& 0& x_{11}& \eta & 0& 0\\ 0& -{\mathsf{\Delta }}_{11}& \gamma & 0& \eta & 0\\ \mu & 0& -{\mathsf{\Delta }}_{12}& 0& 0& \eta \\ \beta & 0& 0& -{\mathsf{\Delta }}_{13}& x_{11}& 0\\ 0& \beta & 0& 0& -\left(\lambda +\beta \right)& 0\\ 0& 0& \beta & 0& 0& -\left(\lambda +\beta \right)\end{array}\right].$$

MTTF₁ can be expressed as

$$E\left[T_{0\to absorbing}\right]=MTT{F}_1.$$

(3)

Due to the complexity of the explicit expression for MTTF₁, this formula is difficult to display here. However, by using a suitable computer program, it can be evaluated numerically.

To discuss the availability of this configuration, we need the process below to obtain the steady-state availability. In steady-state, we let the derivatives of the state probabilities be zero. Then, we have

$$\left[\begin{array}{cccccccccc}-{\mathsf{\Delta }}_{10}& 0& 0& \mu & 0& \beta & 0& 0& 0& 0\\ 0& -{\mathsf{\Delta }}_{11}& 0& 0& \mu & 0& \beta & 0& 0& 0\\ 0& 0& -2\gamma & 0& 0& 0& 0& \beta & 0& 0\\ x_{11}& \gamma & 0& -{\mathsf{\Delta }}_{12}& 0& 0& 0& 0& \beta & 0\\ \lambda q& \lambda & 2\gamma & \lambda & -\left(\mu +\eta \right)& 0& 0& 0& 0& \beta \\ \eta & 0& 0& 0& 0& -{\mathsf{\Delta }}_{13}& 0& 0& 0& 0\\ 0& \eta & 0& 0& 0& x_{11}& -\left(\lambda +\beta \right)& 0& 0& 0\\ 0& 0& 0& 0& 0& \lambda q& \lambda & -\beta & 0& 0\\ 0& 0& 0& \eta & 0& 0& 0& 0& -\left(\lambda +\beta \right)& 0\\ 0& 0& 0& 0& \eta & 0& 0& 0& \lambda & -\beta \end{array}\right]\left[\begin{array}{c}{P}_{0,0}(\infty )\\ P_{0,1}(\infty )\\ P_{0,2}(\infty )\\ P_{1,0}(\infty )\\ P_{1,1}(\infty )\\ P_{2,0}(\infty )\\ P_{2,1}(\infty )\\ P_{2,2}(\infty )\\ P_{3,0}(\infty )\\ P_{3,1}(\infty )\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right]$$

(4)

By partitioning the probability vector as ${\Pi }_1={\left[{\pi }_1\left(0\right),{\pi }_1\left(1\right),{\pi }_1\left(2\right),{\pi }_1\left(3\right)\right]}^T$, where ${\pi }_1\left(i\right)={\lceil P_{i,0}(\infty ),P_{i,1}(\infty )\rceil }^T\left(i=1,3\right)$ and ${\pi }_1\left(i\right)={\lceil P_{i,0}(\infty ),P_{i,1}(\infty ),P_{i,2}(\infty )\rceil }^T\left(i=0,2\right)$, then Equation (4) can be rewritten as

$$\left[\begin{array}{cccc}{F}_{11}& F_{12}& F_{13}& \\ F_{21}& F_{22}& & F_{24}\\ F_{31}& & F_{33}& \\ & F_{42}& & F_{44}\end{array}\right]\left[\begin{array}{c}{\pi }_1\left(0\right)\\ {\pi }_1\left(1\right)\\ {\pi }_1\left(2\right)\\ {\pi }_1\left(3\right)\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right],$$

(5)

where

$$\begin{gathered} F_{11}=\left[\begin{array}{ccc}-{\mathsf{\Delta }}_{10}& 0& 0\\ 0& -{\mathsf{\Delta }}_{11}& 0\\ 0& 0& -2\gamma \end{array}\right],F_{12}=\left[\begin{array}{cc}\mu & 0\\ 0& \mu \\ 0& 0\end{array}\right],F_{13}=\left[\begin{array}{ccc}\beta & 0& 0\\ 0& \beta & 0\\ 0& 0& \beta \end{array}\right], \\ {F}_{21}=\left[\begin{array}{ccc}\lambda \left(1-q\right)+\alpha & \gamma & 0\\ \lambda q& \lambda & 2\gamma \end{array}\right],F_{22}=\left[\begin{array}{cc}-{\mathsf{\Delta }}_{12}& 0\\ \lambda & -\left(\mu +\eta \right)\end{array}\right],F_{24}=\left[\begin{array}{cc}\beta & 0\\ 0& \beta \end{array}\right], \\ {F}_{31}=\left[\begin{array}{ccc}\eta & 0& 0\\ 0& \eta & 0\\ 0& 0& 0\end{array}\right],F_{33}=\left[\begin{array}{ccc}-{\mathsf{\Delta }}_{13}& 0& 0\\ \lambda \left(1-q\right)+\alpha & -\left(\lambda +\beta \right)& 0\\ \lambda q& \lambda & -\beta \end{array}\right], \\ {F}_{42}=\left[\begin{array}{cc}\eta & 0\\ 0& \eta \end{array}\right],F_{44}=\left[\begin{array}{cc}-\left(\lambda +\beta \right)& 0\\ \lambda & -\beta \end{array}\right], \end{gathered}$$

and 0 is a zero matrix with the appropriate dimension.

By solving Equation (5) and after some routine substitutions, we have

$${\pi }_1\left(0\right)=-{\left(F_{21}\right)}^{-1}\left(F_{22}+F_{24}{\Psi }_3\right){\pi }_1\left(1\right)={\Psi }_0{\pi }_1\left(1\right),$$

(6)

$${\pi }_1\left(2\right)=-{\left(F_{33}\right)}^{-1}{F}_{31}{\pi }_1\left(0\right)={\Psi }_2{\pi }_1\left(1\right),$$

(7)

$${\pi }_1\left(3\right)=-{\left(F_{44}\right)}^{-1}{F}_{42}{\pi }_1\left(1\right)={\Psi }_3{\pi }_1\left(1\right),$$

(8)

$$\left(F_{11}{\Psi }_0+F_{12}+F_{13}{\Psi }_2\right){\pi }_1\left(1\right)=0.$$

(9)

Hence, we can calculate ${\pi }_1\left(1\right)$ by solving Equation (9) and the normalizing condition ${\displaystyle \sum }_{j=0}^2{P}_{0,j}(\infty )+{\displaystyle \sum }_{j=0}^1{P}_{1,j}(\infty )+{\displaystyle \sum }_{j=0}^2{P}_{2,j}(\infty )+{\displaystyle \sum }_{j=0}^1{P}_{3,j}(\infty )=1$. Thus, the steady-state availability of configuration, $A{v}_1=1-P_{0,2}(\infty )-P_{1,1}(\infty )-P_{2,2}(\infty )-P_{3,1}(\infty )$, can be computed once the steady-state probabilities are obtained.

3.2. Configuration 2

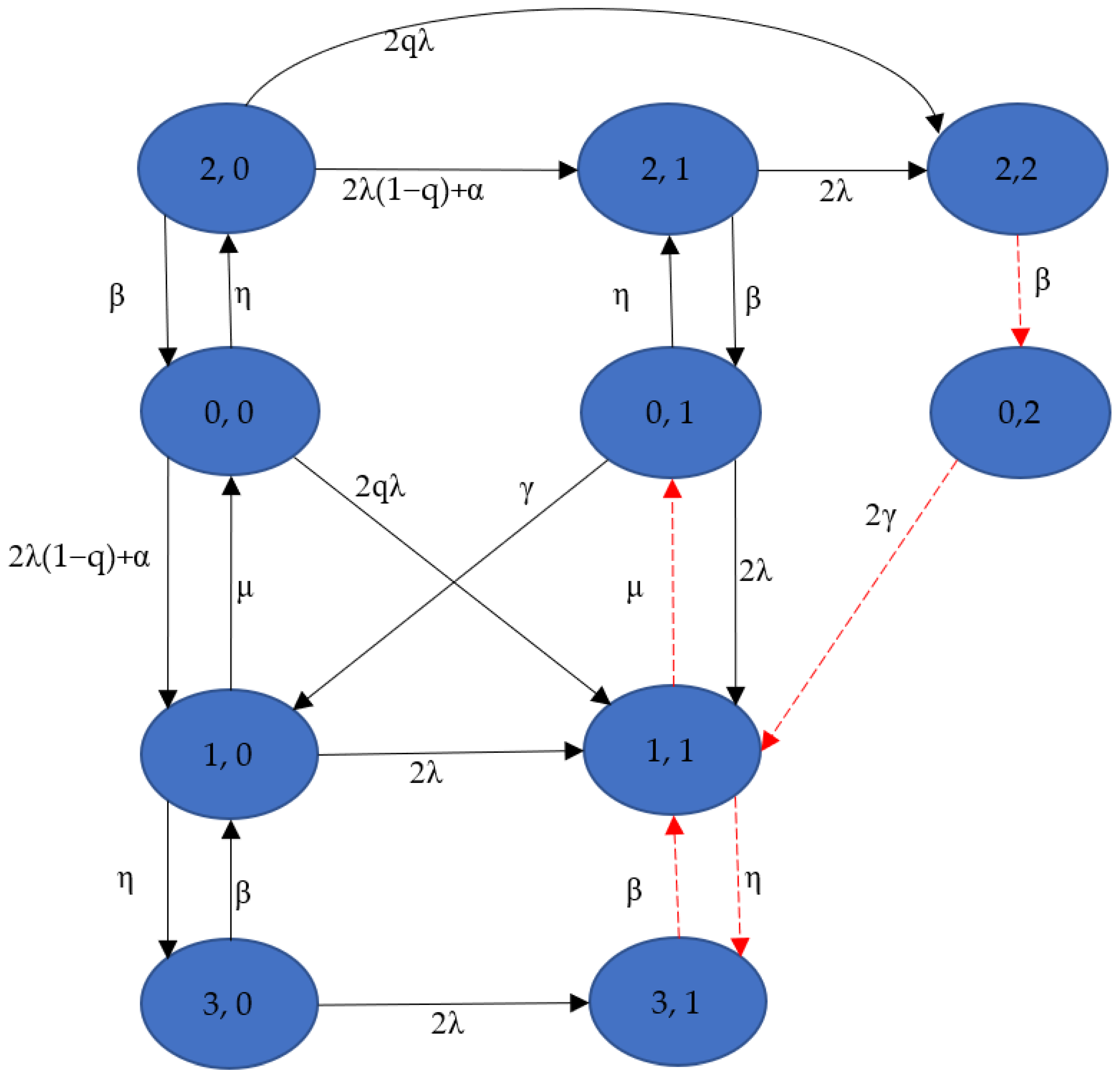
Figure 2 presents the state-transition-rate diagram of configuration 2. Similarly, the transition from (2, 2) to (0, 2), the transition from (0, 2) to (1, 1), the transition from state (1, 1) to (0, 1) and (3, 1), and the transition from (3, 1) to (1, 1) are ignored when investigating the system MTTF. The associated probability vector for this configuration is defined as:

$$\mathit{P}\left(t\right)={\left[P_{0,0}\left(t\right),P_{0,1}\left(t\right),P_{0,2}\left(t\right),P_{1,0}\left(t\right),P_{1,1}\left(t\right),P_{2,0}\left(t\right),P_{2,1}\left(t\right),P_{2,2}\left(t\right),P_{3,0}\left(t\right),P_{3,1}\left(t\right)\right]}^T.$$

We can write the differential-difference equations of configuration 2 as the following matrix form:

$$\frac{d}{dt}{\mathit{P}}_2\left(t\right)={\mathit{Q}}_2{\mathit{P}}_2\left(t\right),$$

(10)

where

$$\begin{gathered} {\mathit{Q}}_2=\left[\begin{array}{cccccccccc}-{\mathsf{\Delta }}_{20}& 0& 0& \mu & 0& \beta & 0& 0& 0& 0\\ 0& -{\mathsf{\Delta }}_{21}& 0& 0& 0& 0& \beta & 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ x_{21}& \gamma & 0& -{\mathsf{\Delta }}_{22}& 0& 0& 0& 0& \beta & 0\\ 2\lambda q& 2\lambda & 0& 2\lambda & 0& 0& 0& 0& 0& 0\\ \eta & 0& 0& 0& 0& -{\mathsf{\Delta }}_{23}& 0& 0& 0& 0\\ 0& \eta & 0& 0& 0& x_{21}& -\left(2\lambda +\beta \right)& 0& 0& 0\\ 0& 0& 0& 0& 0& 2\lambda q& 2\lambda & 0& 0& 0\\ 0& 0& 0& \eta & 0& 0& 0& 0& -\left(2\lambda +\beta \right)& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 2\lambda & 0\end{array}\right], \\ {\mathsf{\Delta }}_{20}=2\lambda +\alpha +\eta ,{\mathsf{\Delta }}_{21}=2\lambda +\gamma +\eta ,{\mathsf{\Delta }}_{22}=2\lambda +\mu +\eta ,{\mathsf{\Delta }}_{23}=2\lambda +\alpha +\beta ,x_{21}=2\lambda \left(1-q\right)+\alpha . \end{gathered}$$

We define A₂ as the transpose matrix of Q₂ omitting the row and column for the absorbing state. Let

$${\mathit{P}}_2\left(0\right)={\left[P_{0,0}\left(0\right),P_{0,1}\left(0\right),P_{1,0}\left(0\right),P_{2,0}\left(0\right),P_{2,1}\left(0\right),P_{3,0}\left(0\right)\right]}^T={\left[1,0,0,0,0,0\right]}^T$$

represent the initial condition. We can obtain

$$E\left[T_{0\to absorbing}\right]={\mathit{P}}_2{\left(0\right)}^T\left(-A_2^{-1}\right)1,$$

(11)

where

$$A_2=\left[\begin{array}{cccccc}-{\mathsf{\Delta }}_{20}& 0& x_{21}& \eta & 0& 0\\ 0& -{\mathsf{\Delta }}_{21}& \gamma & 0& \eta & 0\\ \mu & 0& -{\mathsf{\Delta }}_{22}& 0& 0& \eta \\ \beta & 0& 0& -{\mathsf{\Delta }}_{23}& x_{21}& 0\\ 0& \beta & 0& 0& -\left(2\lambda +\beta \right)& 0\\ 0& 0& \beta & 0& 0& -\left(2\lambda +\beta \right)\end{array}\right].$$

For this configuration, MTTF₂ can be expressed as

$$E\left[T_{0\to absorbing}\right]=MTT{F}_2.$$

(12)

As mentioned earlier, the explicit expression of MTTF₂ is not shown here due to its complexity. We compare the four configurations in Section 4 based on the calculated numerical results. We utilize the same process in the prior subsection to get the steady-state availability. In steady-state, we let the derivatives of the state probabilities be zero, then

$$\left[\begin{array}{cccccccccc}-{\mathsf{\Delta }}_{20}& 0& 0& \mu & 0& \beta & 0& 0& 0& 0\\ 0& -{\mathsf{\Delta }}_{21}& 0& 0& \mu & 0& \beta & 0& 0& 0\\ 0& 0& -2\gamma & 0& 0& 0& 0& \beta & 0& 0\\ x_{21}& \gamma & 0& -{\mathsf{\Delta }}_{22}& 0& 0& 0& 0& \beta & 0\\ 2\lambda q& 2\lambda & 2\gamma & 2\lambda & -\left(\mu +\eta \right)& 0& 0& 0& 0& \beta \\ \eta & 0& 0& 0& 0& -{\mathsf{\Delta }}_{23}& 0& 0& 0& 0\\ 0& \eta & 0& 0& 0& x_{21}& -\left(2\lambda +\beta \right)& 0& 0& 0\\ 0& 0& 0& 0& 0& 2\lambda q& 2\lambda & -\beta & 0& 0\\ 0& 0& 0& \eta & 0& 0& 0& 0& -\left(2\lambda +\beta \right)& 0\\ 0& 0& 0& 0& \eta & 0& 0& 0& 2\lambda & -\beta \end{array}\right]\left[\begin{array}{c}{P}_{0,0}(\infty )\\ P_{0,1}(\infty )\\ P_{0,2}(\infty )\\ P_{1,0}(\infty )\\ P_{1,1}(\infty )\\ P_{2,0}(\infty )\\ P_{2,1}(\infty )\\ P_{2,2}(\infty )\\ P_{3,0}(\infty )\\ P_{3,1}(\infty )\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right]$$

(13)

Solving the above equation and using the normalizing condition ${\displaystyle \sum }_{j=0}^2{P}_{0,j}(\infty )+{\displaystyle \sum }_{j=0}^1{P}_{1,j}(\infty )+{\displaystyle \sum }_{j=0}^2{P}_{2,j}(\infty )+{\displaystyle \sum }_{j=0}^1{P}_{3,j}(\infty )=1$, we can obtain the steady-state probabilities. Once the steady-state probabilities are obtained, the availability of configuration 2, $A{v}_2=1-P_{0,2}(\infty )-P_{1,1}(\infty )-P_{2,2}(\infty )-P_{3,1}(\infty )$, can be computed.

3.3. Configuration 3

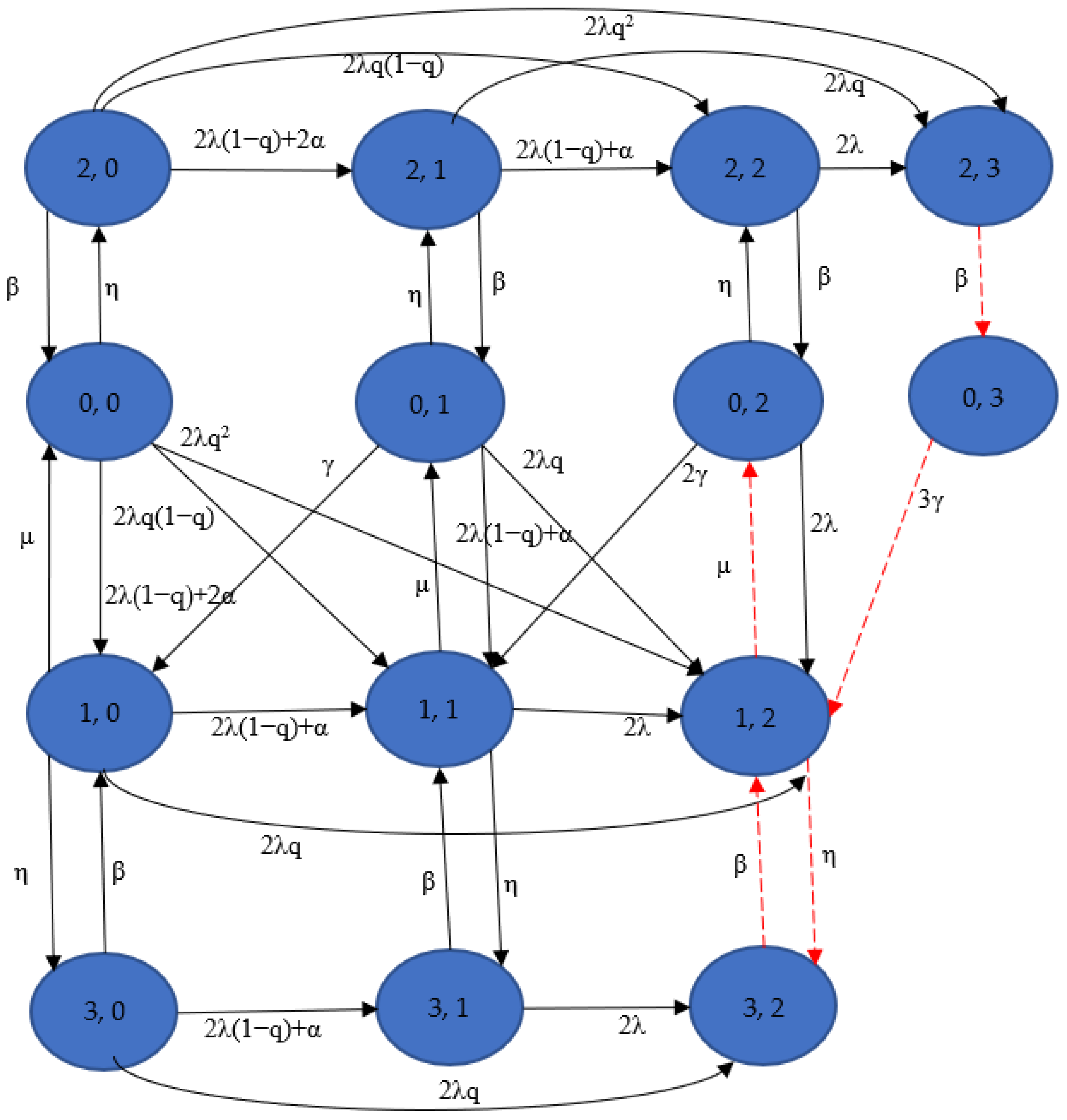
Figure 3 presents the state-transition-rate diagram of configuration 3. When deriving the system MTTF, the transition from state (2, 3) to (0, 3), transition (0, 3) to (1, 2), transition from state (1, 2) to states (0, 2) and (3, 2), and transition from state (3, 2) to (1, 2) should be deleted. Let

$$\begin{gathered} {\mathit{P}}_3\left(0\right)=[P_{0,0}\left(0\right),P_{0,1}\left(0\right),P_{0,2}\left(0\right), P_{1,0}\left(0\right),P_{1,1}\left(0\right), \\ {P_{2,0}\left(0\right),P_{2,1}\left(0\right),P_{2,2}\left(0\right), P_{3,0}\left(0\right),P_{3,1}\left(0\right)]}^T \\ ={\left[1,0,0,0,0,0,0,0,0,0\right]}^T \end{gathered}$$

represent the initial condition. We can write the differential-difference equations of this configuration as the following matrix form:

$$\frac{d}{dt}{\mathit{P}}_3\left(t\right)={\mathit{Q}}_3{\mathit{P}}_3\left(t\right),$$

(14)

where

$$\begin{gathered} {\mathit{Q}}_3=\left[\begin{array}{cccccccccccccc}-{\mathsf{\Delta }}_{30}& 0& 0& 0& \mu & 0& 0& \beta & 0& 0& 0& 0& 0& 0\\ 0& -{\mathsf{\Delta }}_{31}& 0& 0& 0& \mu & 0& 0& \beta & 0& 0& 0& 0& 0\\ 0& 0& -{\mathsf{\Delta }}_{32}& 0& 0& 0& 0& 0& 0& \beta & 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ x_{32}& \gamma & 0& 0& -{\mathsf{\Delta }}_{33}& 0& 0& 0& 0& 0& 0& \beta & 0& 0\\ x_{33}& x_{31}& 2\gamma & 0& x_{31}& -{\mathsf{\Delta }}_{34}& 0& 0& 0& 0& 0& 0& \beta & 0\\ 2\lambda q^2& 2\lambda q& 2\lambda & 0& 2\lambda q& 2\lambda & 0& 0& 0& 0& 0& 0& 0& 0\\ \eta & 0& 0& 0& 0& 0& 0& -{\mathsf{\Delta }}_{35}& 0& 0& 0& 0& 0& 0\\ 0& \eta & 0& 0& 0& 0& 0& x_{32}& -{\mathsf{\Delta }}_{36}& 0& 0& 0& 0& 0\\ 0& 0& \eta & 0& 0& 0& 0& x_{33}& x_{31}& -\left(2\lambda +\beta \right)& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 2\lambda q^2& 2\lambda q& 2\lambda & 0& 0& 0& 0\\ 0& 0& 0& 0& \eta & 0& 0& 0& 0& 0& 0& -{\mathsf{\Delta }}_{37}& 0& 0\\ 0& 0& 0& 0& 0& \eta & 0& 0& 0& 0& 0& x_{31}& -\left(2\lambda +\beta \right)& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 2\lambda q& 2\lambda & 0\end{array}\right], \\ {\mathsf{\Delta }}_{30}=2\lambda +2\alpha +\eta ,{\mathsf{\Delta }}_{31}=2\lambda +\alpha +\gamma +\eta ,{\mathsf{\Delta }}_{32}=2\lambda +2\gamma +\eta ,{\mathsf{\Delta }}_{33}=2\lambda +\mu +\eta , \\ {\mathsf{\Delta }}_{34}=2\lambda +\mu +\eta ,{\mathsf{\Delta }}_{35}=2\lambda +2\alpha +\beta ,{\mathsf{\Delta }}_{36}=2\lambda +\alpha +\beta ,{\mathsf{\Delta }}_{37}=2\lambda +\alpha +\beta , \\ {x}_{31}=2\lambda \left(1-q\right)+\alpha ,x_{32}=2\lambda \left(1-q\right)+2\alpha ,x_{33}=2\lambda q\left(1-q\right). \end{gathered}$$

We define A₃ as the transpose matrix of Q₃ omitting the row and column for the absorbing state. After the transpose operation, we have

$$A_3=\left[\begin{array}{cccccccccc}-{\mathsf{\Delta }}_{30}& 0& 0& x_{32}& x_{33}& \eta & 0& 0& 0& 0\\ 0& -{\mathsf{\Delta }}_{31}& 0& \gamma & x_{31}& 0& \eta & 0& 0& 0\\ 0& 0& -{\mathsf{\Delta }}_{32}& 0& 2\gamma & 0& 0& \eta & 0& 0\\ \mu & 0& 0& -{\mathsf{\Delta }}_{33}& x_{31}& 0& 0& 0& \eta & 0\\ 0& \mu & 0& 0& -{\mathsf{\Delta }}_{34}& 0& 0& 0& 0& \eta \\ \beta & 0& 0& 0& 0& -{\mathsf{\Delta }}_{35}& x_{32}& x_{33}& 0& 0\\ 0& \beta & 0& 0& 0& 0& -{\mathsf{\Delta }}_{36}& x_{31}& 0& 0\\ 0& 0& \beta & 0& 0& 0& 0& -\left(2\lambda +\beta \right)& 0& 0\\ 0& 0& 0& \beta & 0& 0& 0& 0& -{\mathsf{\Delta }}_{37}& x_{31}\\ 0& 0& 0& 0& \beta & 0& 0& 0& 0& -\left(2\lambda +\beta \right)\end{array}\right].$$

(15)

We can obtain the mean time-to-failure for configuration 3 as follows.

$$E\left[T_{0\to absorbing}\right]={\mathit{P}}_3{\left(0\right)}^T\left(-A_3^{-1}\right)1.$$

(16)

For the availability case of this configuration, we utilize the same process in the prior subsection to get the steady-state availability. In steady-state, we let the derivatives of the state probabilities be zero, then we have

$$\left[\begin{array}{cccc}{G}_{11}& G_{12}& G_{13}& \\ G_{21}& G_{22}& & G_{24}\\ G_{31}& & G_{33}& \\ & G_{42}& & G_{44}\end{array}\right]\left[\begin{array}{c}{\pi }_3\left(0\right)\\ {\pi }_3\left(1\right)\\ {\pi }_3\left(2\right)\\ {\pi }_3\left(3\right)\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right],$$

(17)

where

$$\begin{gathered} G_{11}=\left[\begin{array}{cccc}-{\mathsf{\Delta }}_{30}& 0& 0& 0\\ 0& -{\mathsf{\Delta }}_{31}& 0& 0\\ 0& 0& -{\mathsf{\Delta }}_{32}& 0\\ 0& 0& 0& -3\gamma \end{array}\right],G_{12}=\left[\begin{array}{ccc}\mu & 0& 0\\ 0& \mu & 0\\ 0& 0& \mu \\ 0& 0& 0\end{array}\right], \\ {G}_{13}=\left[\begin{array}{cccc}\beta & 0& 0& 0\\ 0& \beta & 0& 0\\ 0& 0& \beta & 0\\ 0& 0& 0& \beta \end{array}\right],G_{21}=\left[\begin{array}{cccc}{x}_{32}& \gamma & 0& 0\\ x_{33}& x_{31}& 2\gamma & 0\\ 2\lambda q^2& 2\lambda q& 2\lambda & 3\gamma \end{array}\right], \\ {G}_{22}=\left[\begin{array}{ccc}-{\mathsf{\Delta }}_{33}& 0& 0\\ x_{31}& -{\mathsf{\Delta }}_{34}& 0\\ 2\lambda q& 2\lambda & -\left(\mu +\eta \right)\end{array}\right],G_{24}=\left[\begin{array}{ccc}\beta & 0& 0\\ 0& \beta & 0\\ 0& 0& \beta \end{array}\right], \\ {G}_{31}=\left[\begin{array}{cccc}\eta & 0& 0& 0\\ 0& \eta & 0& 0\\ 0& 0& \eta & 0\\ 0& 0& 0& 0\end{array}\right],G_{33}=\left[\begin{array}{cccc}-{\mathsf{\Delta }}_{35}& 0& 0& 0\\ x_{32}& -{\mathsf{\Delta }}_{36}& 0& 0\\ x_{33}& x_{31}& -\left(2\lambda +\beta \right)& 0\\ 2\lambda q^2& 2\lambda q& 2\lambda & -\beta \end{array}\right], \\ {G}_{42}=\left[\begin{array}{ccc}\eta & 0& 0\\ 0& \eta & 0\\ 0& 0& \eta \end{array}\right],G_{44}=\left[\begin{array}{ccc}-{\mathsf{\Delta }}_{37}& 0& 0\\ x_{31}& -\left(2\lambda +\beta \right)& 0\\ 2\lambda q& 2\lambda & -\beta \end{array}\right], \\ {\pi }_3\left(i\right)=\left[\begin{array}{c}{P}_{i,0}(\infty )\\ P_{i,1}(\infty )\\ P_{i,2}(\infty )\end{array}\right](i=1,3),{\pi }_3\left(i\right)=\left[\begin{array}{c}{P}_{i,0}(\infty )\\ P_{i,1}(\infty )\\ P_{i,2}(\infty )\\ P_{i,3}(\infty )\end{array}\right]\left(i=0,2\right). \end{gathered}$$

Similarly, solving Equation (17) recursively with the normalizing condition ${\displaystyle \sum }_{j=0}^3{P}_{0,j}(\infty )+{\displaystyle \sum }_{j=0}^2{P}_{1,j}(\infty )+{\displaystyle \sum }_{j=0}^3{P}_{2,j}(\infty )+{\displaystyle \sum }_{j=0}^2{P}_{3,j}(\infty )=1$ can obtain the steady-state probabilities. Once the steady-state probabilities are obtained, then the availability of this configuration, $A{v}_3=1-P_{0,3}(\infty )-P_{1,2}(\infty )-P_{2,3}(\infty )-P_{3,2}(\infty )$ is computed.

3.4. Configuration 4

The state-transition-rate diagram of configuration 4 is shown in Figure 4. The associated probability vector is

$$\begin{gathered} \mathit{P}\left(t\right)=[P_{0,0}\left(t\right),P_{0,1}\left(t\right),P_{0,2}\left(t\right),P_{0,3}\left(t\right), P_{1,0}\left(t\right),P_{1,1}\left(t\right),P_{1,2}\left(t\right), \\ {P_{2,0}\left(t\right),P_{2,1}\left(t\right),P_{2,2}\left(t\right),P_{2,3}\left(t\right), P_{3,0}\left(t\right),P_{3,1}\left(t\right),P_{3,2}\left(t\right)]}^T. \end{gathered}$$

According to the Figure 4, the differential-difference equations of this configuration can be written as the following matrix form:

$$\frac{d}{dt}\mathit{P}\left(t\right)={\mathit{Q}}_4\mathit{P}\mathit{s}\left(t\right),$$

(18)

where

$$\begin{gathered} {\mathit{Q}}_4=\left[\begin{array}{cccccccccccccc}-{\mathsf{\Delta }}_{40}& 0& 0& 0& \mu & 0& 0& \beta & 0& 0& 0& 0& 0& 0\\ 0& -{\mathsf{\Delta }}_{41}& 0& 0& 0& \mu & 0& 0& \beta & 0& 0& 0& 0& 0\\ 0& 0& -{\mathsf{\Delta }}_{42}& 0& 0& 0& 0& 0& 0& \beta & 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ x_{42}& \gamma & 0& 0& -{\mathsf{\Delta }}_{43}& 0& 0& 0& 0& 0& 0& \beta & 0& 0\\ x_{43}& x_{41}& 2\gamma & 0& x_{41}& -{\mathsf{\Delta }}_{44}& 0& 0& 0& 0& 0& 0& \beta & 0\\ 3\lambda q^2& 3\lambda q& 3\lambda & 0& 3\lambda q& 3\lambda & 0& 0& 0& 0& 0& 0& 0& 0\\ \eta & 0& 0& 0& 0& 0& 0& -{\mathsf{\Delta }}_{45}& 0& 0& 0& 0& 0& 0\\ 0& \eta & 0& 0& 0& 0& 0& x_{42}& -{\mathsf{\Delta }}_{46}& 0& 0& 0& 0& 0\\ 0& 0& \eta & 0& 0& 0& 0& x_{43}& x_{41}& -\left(3\lambda +\beta \right)& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 3\lambda q^2& 3\lambda q& 3\lambda & 0& 0& 0& 0\\ 0& 0& 0& 0& \eta & 0& 0& 0& 0& 0& 0& -{\mathsf{\Delta }}_{47}& 0& 0\\ 0& 0& 0& 0& 0& \eta & 0& 0& 0& 0& 0& x_{41}& -\left(3\lambda +\beta \right)& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 3\lambda q& 3\lambda & 0\end{array}\right], \\ {\mathsf{\Delta }}_{40}=3\lambda +2\alpha +\eta ,{\mathsf{\Delta }}_{41}=3\lambda +\alpha +\gamma +\eta ,{\mathsf{\Delta }}_{42}=3\lambda +2\gamma +\eta ,{\mathsf{\Delta }}_{43}=3\lambda +\mu +\eta , \\ {\mathsf{\Delta }}_{44}=3\lambda +\mu +\eta ,{\mathsf{\Delta }}_{45}=3\lambda +2\alpha +\beta ,{\mathsf{\Delta }}_{46}=3\lambda +\alpha +\beta ,{\mathsf{\Delta }}_{47}=3\lambda +\alpha +\beta , \\ {x}_{41}=3\lambda \left(1-q\right)+\alpha ,x_{42}=3\lambda \left(1-q\right)+2\alpha ,x_{43}=3\lambda q\left(1-q\right). \end{gathered}$$

We define A₄ as the transpose matrix of Q₄ omitting the row and column for the absorbing state. Let

$$\begin{gathered} {\mathit{P}}_4\left(0\right)=[P_{0,0}\left(0\right),P_{0,1}\left(0\right),P_{0,2}\left(0\right),P_{1,0}\left(0\right),P_{1,1}\left(0\right), \\ {P_{2,0}\left(0\right),P_{2,1}\left(0\right),P_{2,2}\left(0\right),P_{3,0}\left(0\right),P_{3,1}\left(0\right)]}^T \\ ={\left[1,0,0,0,0,0,0,0,0,0\right]}^T \end{gathered}$$

represent the initial condition, we can obtain

$$E\left[T_{0\to absorbing}\right]={\mathit{P}}_4{\left(0\right)}^T\left(-A_4^{-1}\right)1,$$

(19)

where

$$A_4=\left[\begin{array}{cccccccccc}-{\mathsf{\Delta }}_{40}& 0& 0& x_{42}& x_{43}& \eta & 0& 0& 0& 0\\ 0& -{\mathsf{\Delta }}_{41}& 0& \gamma & x_{41}& 0& \eta & 0& 0& 0\\ 0& 0& -{\mathsf{\Delta }}_{42}& 0& 2\gamma & 0& 0& \eta & 0& 0\\ \mu & 0& 0& -{\mathsf{\Delta }}_{43}& x_{41}& 0& 0& 0& \eta & 0\\ 0& \mu & 0& 0& -{\mathsf{\Delta }}_{44}& 0& 0& 0& 0& \eta \\ \beta & 0& 0& 0& 0& -{\mathsf{\Delta }}_{45}& x_{42}& x_{43}& 0& 0\\ 0& \beta & 0& 0& 0& 0& -{\mathsf{\Delta }}_{46}& x_{41}& 0& 0\\ 0& 0& \beta & 0& 0& 0& 0& -\left(3\lambda +\beta \right)& 0& 0\\ 0& 0& 0& \beta & 0& 0& 0& 0& -{\mathsf{\Delta }}_{47}& x_{41}\\ 0& 0& 0& 0& \beta & 0& 0& 0& 0& -\left(3\lambda +\beta \right)\end{array}\right].$$

We utilize the same process in the prior subsection to get the steady-state availability. The steady-state probabilities can be obtained by solving

$$\left[\begin{array}{cccc}{H}_{11}& H_{12}& H_{13}& \\ H_{21}& H_{22}& & H_{24}\\ H_{31}& & H_{33}& \\ & H_{42}& & H_{44}\end{array}\right]\left[\begin{array}{c}{\pi }_4\left(0\right)\\ {\pi }_4\left(1\right)\\ {\pi }_4\left(2\right)\\ {\pi }_4\left(3\right)\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right],$$

(20)

with the normalizing condition ${\displaystyle \sum }_{j=0}^3{P}_{0,j}(\infty )+{\displaystyle \sum }_{j=0}^2{P}_{1,j}(\infty )+{\displaystyle \sum }_{j=0}^3{P}_{2,j}(\infty )+{\displaystyle \sum }_{j=0}^2{P}_{3,j}(\infty )=1$, where

$$\begin{gathered} H_{11}=\left[\begin{array}{cccc}-{\mathsf{\Delta }}_{40}& 0& 0& 0\\ 0& -{\mathsf{\Delta }}_{41}& 0& 0\\ 0& 0& -{\mathsf{\Delta }}_{42}& 0\\ 0& 0& 0& -3\gamma \end{array}\right],H_{12}=\left[\begin{array}{ccc}\mu & 0& 0\\ 0& \mu & 0\\ 0& 0& \mu \\ 0& 0& 0\end{array}\right], \\ {H}_{13}=\left[\begin{array}{cccc}\beta & 0& 0& 0\\ 0& \beta & 0& 0\\ 0& 0& \beta & 0\\ 0& 0& 0& \beta \end{array}\right],H_{21}=\left[\begin{array}{cccc}{x}_{42}& \gamma & 0& 0\\ x_{43}& x_{41}& 2\gamma & 0\\ 3\lambda q^2& 3\lambda q& 3\lambda & 3\gamma \end{array}\right], \\ {H}_{22}=\left[\begin{array}{ccc}-{\mathsf{\Delta }}_{43}& 0& 0\\ x_{41}& -{\mathsf{\Delta }}_{44}& 0\\ 3\lambda q& 3\lambda & -\left(\mu +\eta \right)\end{array}\right],H_{24}=\left[\begin{array}{ccc}\beta & 0& 0\\ 0& \beta & 0\\ 0& 0& \beta \end{array}\right], \\ {H}_{31}=\left[\begin{array}{cccc}\eta & 0& 0& 0\\ 0& \eta & 0& 0\\ 0& 0& \eta & 0\\ 0& 0& 0& 0\end{array}\right],H_{33}=\left[\begin{array}{cccc}-{\mathsf{\Delta }}_{45}& 0& 0& 0\\ x_{42}& -{\mathsf{\Delta }}_{46}& 0& 0\\ x_{43}& x_{41}& -\left(3\lambda +\beta \right)& 0\\ 3\lambda q^2& 3\lambda q& 3\lambda & -\beta \end{array}\right], \\ {H}_{42}=\left[\begin{array}{ccc}\eta & 0& 0\\ 0& \eta & 0\\ 0& 0& \eta \end{array}\right],H_{44}=\left[\begin{array}{ccc}-{\mathsf{\Delta }}_{47}& 0& 0\\ x_{41}& -\left(3\lambda +\beta \right)& 0\\ 3\lambda q& 3\lambda & -\beta \end{array}\right], \\ {\pi }_4\left(i\right)=\left[\begin{array}{c}{P}_{i,0}(\infty )\\ P_{i,1}(\infty )\\ P_{i,2}(\infty )\end{array}\right](i=1,3),{\pi }_4\left(i\right)=\left[\begin{array}{c}{P}_{i,0}(\infty )\\ P_{i,1}(\infty )\\ P_{i,2}(\infty )\\ P_{i,3}(\infty )\end{array}\right]\left(i=0,2\right). \end{gathered}$$

Once the steady-state probabilities are obtained, the availability of configuration 4, $A{v}_4=1-P_{0,3}(\infty )-P_{1,2}(\infty )-P_{2,3}(\infty )-P_{3,2}(\infty )$, is computed. In the following section, we compare these four configurations based on MTTF and the availability.

4. Comparative Results

4.1. Comparison of MTTF and Av

The cases listed below are provided in this section to compare four configurations according to their MTTF_i and Av_i (i = 1,2,3,4).

Case1.

Given $\mathsf{\alpha }=0.01$, $\mathsf{\mu }=2$, $q=0.2$, $\mathsf{\gamma }=3$, $\mathsf{\eta }=0.05$, $\mathsf{\beta }=0.5$, and change the values of $\mathsf{\lambda }$.

Case2.

Given $\mathsf{\lambda }=0.5$, $\mathsf{\alpha }=0.01$, $q=0.2$, $\mathsf{\gamma }=3$, $\mathsf{\eta }=0.05$, $\mathsf{\beta }=0.5$, and change the values of $\mathsf{\mu }$.

Case3.

Given $\mathsf{\lambda }=0.5$, $\mathsf{\alpha }=0.01$, $\mathsf{\mu }=2$, $\mathsf{\gamma }=3$, $\mathsf{\eta }=0.05$, $\mathsf{\beta }=0.5$, and change the values of $q$.

Case4.

Given $\mathsf{\lambda }=0.5$, $\mathsf{\alpha }=0.01$, $\mathsf{\mu }=2$, $q=0.2$, $\mathsf{\eta }=0.05$, $\mathsf{\beta }=0.5$, and change the values of $\mathsf{\gamma }$.

Case5.

Given $\mathsf{\lambda }=0.5$, $\mathsf{\alpha }=0.01$, $\mathsf{\mu }=2$, $q=0.2$, $\mathsf{\gamma }=3$, $\mathsf{\beta }=0.5$, and change the values of $\mathsf{\eta }$.

Case6.

Given $\mathsf{\lambda }=0.5$, $\mathsf{\alpha }=0.01$, $\mathsf{\mu }=2$, $q=0.2$, $\mathsf{\gamma }=3$, $\mathsf{\eta }=0.05$, and change the values of $\mathsf{\beta }$.

Table 1. Comparisons of configurations 1–4 for MTTF.

$\mathbf{Scope}\mathbf{of}\mathit{\lambda }$	Results
$0.01<\mathsf{\lambda }<0.0542$	$MTT{F}_2<MTT{F}_1<MTT{F}_4<MTT{F}_3$
$0.0542<\mathsf{\lambda }<0.2731$	$MTT{F}_2<MTT{F}_4<MTT{F}_1<MTT{F}_3$
$0.2731<\mathsf{\lambda }<0.5$	$MTT{F}_2<MTT{F}_4<MTT{F}_3<MTT{F}_1$
Scope of $\mathsf{\mu }$	Results
$0.5<\mathsf{\mu }<0.9834$	$MTT{F}_4<MTT{F}_2<MTT{F}_3<MTT{F}_1$
$0.9834<\mathsf{\mu }<2$	$MTT{F}_2<MTT{F}_4<MTT{F}_3<MTT{F}_1$
Scope of q	Results
$0<q<0.3981$	$MTT{F}_2<MTT{F}_4<MTT{F}_3<MTT{F}_1$
$0.3981<q<1$	$MTT{F}_4<MTT{F}_2<MTT{F}_3<MTT{F}_1$
Scope of $\mathsf{\gamma }$	Results
$0.5<\mathsf{\gamma }<6$	$MTT{F}_2<MTT{F}_4<MTT{F}_3<MTT{F}_1$
Scope of $\mathsf{\eta }$	Results
$0.01<\mathsf{\eta }<0.5$	$MTT{F}_2<MTT{F}_4<MTT{F}_3<MTT{F}_1$
Scope of $\mathsf{\beta }$	Results
$0.01<\mathsf{\beta }<1$	$MTT{F}_2<MTT{F}_4<MTT{F}_3<MTT{F}_1$

and

Table 2. Comparisons of configurations 1–4 for $Av$.

$\mathbf{Scope}\mathbf{of}\mathit{\lambda }$	Results
$0.01<\mathsf{\lambda }<0.0265$	$A{v}_2<A{v}_3<A{v}_1<A{v}_4$
$0.0265<\mathsf{\lambda }<0.1390$	$A{v}_2<A{v}_3<A{v}_4<A{v}_1$
$0.1390<\mathsf{\lambda }<0.2420$	$A{v}_2<A{v}_4<A{v}_3<A{v}_1$
$0.2420<\mathsf{\lambda }<0.5$	$A{v}_4<A{v}_2<A{v}_3<A{v}_1$
Scope of $\mathsf{\mu }$	Results
$0.5<\mathsf{\mu }<2$	$A{v}_4<A{v}_2<A{v}_3<A{v}_1$
Scope of q	Results
$0<q<1$	$A{v}_4<A{v}_2<A{v}_3<A{v}_1$
Scope of $\mathsf{\gamma }$	Results
$0.5<\mathsf{\gamma }<6$	$A{v}_4<A{v}_2<A{v}_3<A{v}_1$
Scope of $\mathsf{\eta }$	Results
$0.01<\mathsf{\eta }<0.5$	$A{v}_4<A{v}_2<A{v}_3<A{v}_1$
Scope of $\mathsf{\beta }$	Results
$0.01<\mathsf{\beta }<2$	$A{v}_4<A{v}_2<A{v}_3<A{v}_1$

show the results of MTTF and Av for each configuration. From Table 1, the MTTF of configuration 3 is larger than that of configurations 1, 2, and 4 if $0.01<\mathsf{\lambda }<0.2731$, but the MTTF₁ is larger than that of the other configurations if $0.2731<\mathsf{\lambda }<0.5$. From Table 2, one can find that based on the comparison of $Av$, configuration 3 may be the best configuration as $0.01<\mathsf{\lambda }<0.1390$, but as $0.1390<\mathsf{\lambda }<0.5$, the best configuration may be configuration 1. In addition, no matter how we vary the values of $\mathsf{\mu }$, $q$, $\mathsf{\gamma }$, $\mathsf{\eta }$ and $\mathsf{\beta }$, the best configuration is always configuration 1 whether it is based on MTTF comparisons or $Av$ comparisons. From Table 2, one can find that in most cases, configuration 1 has the highest steady-state availability, while configuration 4 performs the worst among the four configurations, only outperforming configuration 2 in some cases. As a standard for comparing these four configurations, the cost/benefit ratio may be equitable to the benefit, since each configuration spends different costs during the construction process.

4.2. Comparison Based on Their Cost/Benefit Ratio

We consider a situation where different configurations may have different costs. To compare different configurations fairly, these costs should be considered. We list the costs (C_i) for each configuration i (i = 1,2,3,4) as shown below.

$$C_1=\$18\times {10}^6,C_2=\$15\times {10}^6,C_3=\$18\times {10}^6,C_4=\$16\times {10}^6.$$

Considering the same cases as in the previous subsection, we compare the $cost/benefit$ ratio for each configuration i (i = 1,2,3,4), i.e., $cost/MTTF$ and $cost/Av$. The results depicted in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 indicate that when $\mathsf{\lambda }$, $q$, or $\mathsf{\eta }$ increase, $cost/MTTF$ and $cost/Av$ increase for any configuration, but $cost/MTTF$ and $cost/Av$ decrease as $\mathsf{\mu }$, $\mathsf{\gamma }$ or $\mathsf{\beta }$ increase for any configuration. Figure 5 displays that configuration 2 has minimum $cost/Av$ for different ranges of $\mathsf{\lambda }$. The best configuration of $cost/benefit$ ratio is $cos{t}_3/MTT{F}_3$ if $0.01<\mathsf{\lambda }<0.2731$. Otherwise, the best configuration of $cost/benefit$ ratio is $cos{t}_1/MTT{F}_1$. The worst configuration of $cost/MTTF$ ratio is $cos{t}_2/MTT{F}_2$.

From Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, the optimum configuration based on the $cost/Av$ is dependent on $\mathsf{\mu }$, $q$, $\mathsf{\gamma }$, $\mathsf{\eta }$, and $\mathsf{\beta }$. With the $cost/Av$ ratio, the worst configuration is configuration 4 for different ranges of $\mathsf{\mu }$, $q$, $\mathsf{\gamma }$, $\mathsf{\eta }$, and $\mathsf{\beta }$. $C_2/A{v}_2$ has the minimum $cost/availability$ ratio if $\mathsf{\mu }>1.8495$, $q<0.4514$, $\mathsf{\gamma }>1.6048$ or $\mathsf{\eta }<0.0780$. Otherwise, the best configuration of the $cost/availability$ is $C_1/A{v}_1$. In addition, they also show that the optimum configuration based on the $cost/MTTF$ will not change as $\mathsf{\mu }$, $q$, $\mathsf{\gamma }$, $\mathsf{\eta },$ and $\mathsf{\beta }$ vary. $C_2/MTT{F}_2$ has the minimum $cost/MTTF$ ratio. The worst configuration of $cost/benefit$ ratio is $C_2/MTT{F}_2$ for all ranges of $\mathsf{\beta }$. The worst configuration is $C_2/MTT{F}_2$ if $\mathsf{\gamma }>2.1352$, $q<0.2352$, $\mathsf{\eta }>0.1245$ or $\mathsf{\mu }>1.8469$. Otherwise, the worst configuration is configuration 4.

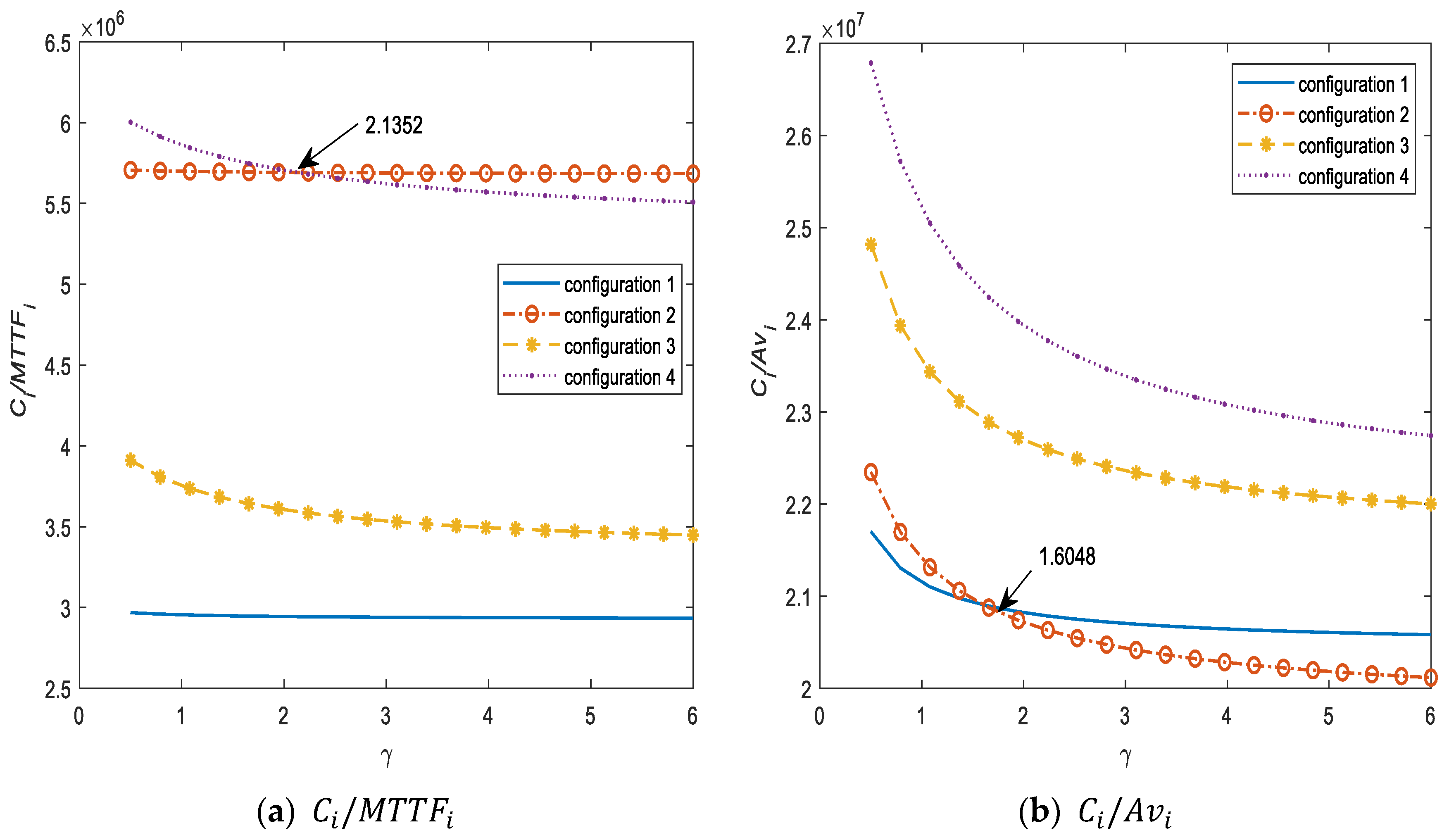
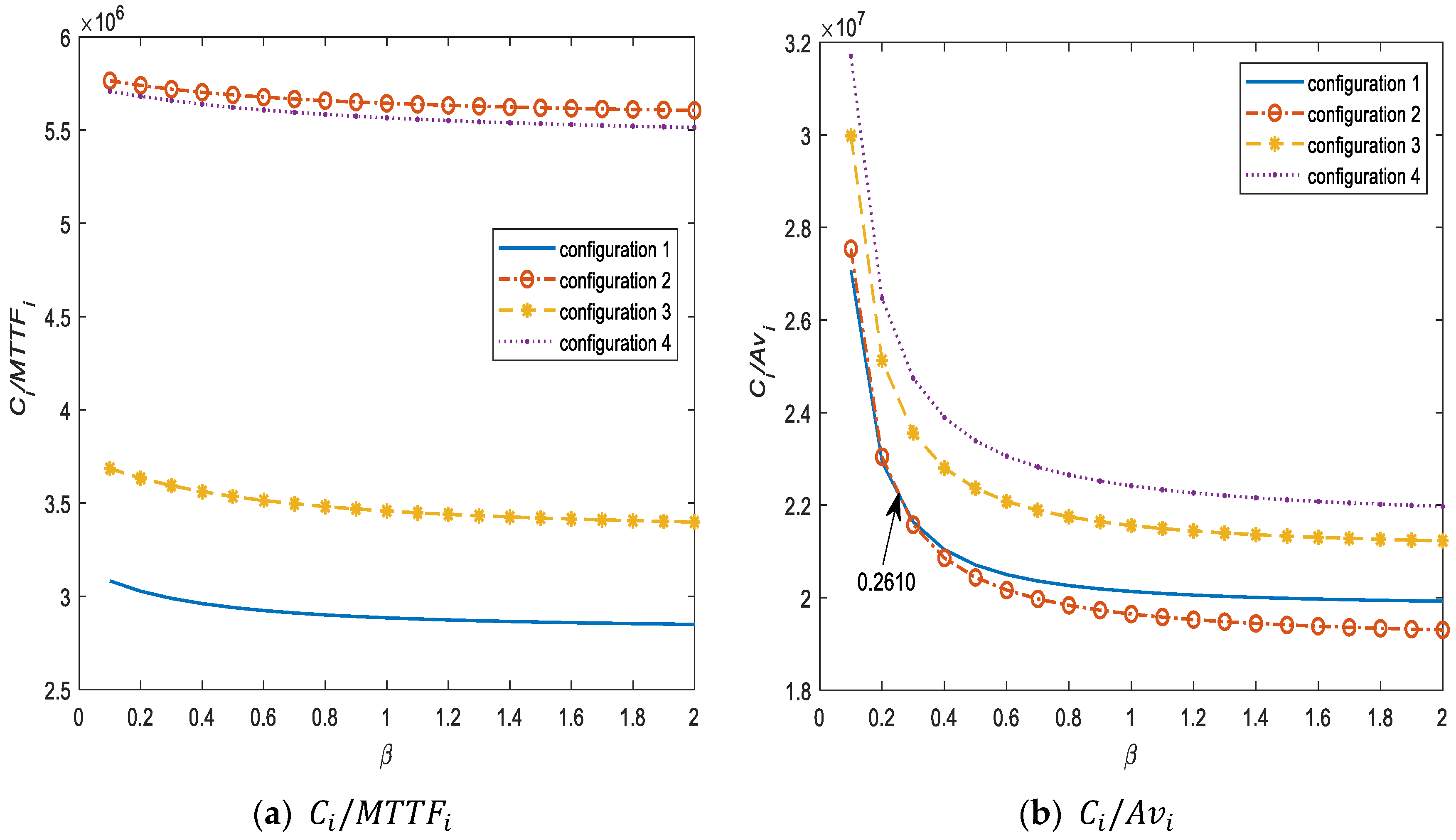
5. Conclusions

This work evaluated the cost-benefit of four standby unreliable retrial configurations with standby switching failure. The explicit and computationally tractable expressions for MTTF_i and $A{v}_i$ ($i=1,2,3,4$) were derived for each configuration. A Matlab computer program is utilized to carry out the proposed approach. We ranked four configurations based on $MTTF$, $Av$ and the cost/benefit ratio. According to our numerical results, the system with configuration 1 displayed the highest performance in most cases. Therefore, the procedure proposed in this paper can provide managers with a valuable tool to select the configuration with greatest benefit in terms of MTTF or availability. For future research, we may consider the general repair times of failed generators and the server. Moreover, we may also design the optimal management system.