Abstract
Full-potential linearized augmented plane wave (LAPW) and APW plus local orbital (APW+) codes differ widely in both their user interfaces and in capabilities for calculations and analysis beyond their common central task of all-electron solution of the Kohn–Sham equations. However, that common central task opens a possible route to performance enhancement, namely to offload the basic LAPW/APW+ algorithms to a library optimized purely for that purpose. To explore that opportunity, we have interfaced the Exciting-Plus (“EP”) LAPW/APW+ DFT code with the highly optimized SIRIUS multi-functional DFT package. This simplest realization of the separation of concerns approach yields substantial performance over the base EP code via additional task parallelism without significant change in the EP source code or user interface. We provide benchmarks of the interfaced code against the original EP using small bulk systems, and demonstrate performance on a spin-crossover molecule and magnetic molecule that are of size and complexity at the margins of the capability of the EP code itself.
1. Dedication
Much credit for the widespread use of full-potential linearized augmented plane wave (LAPW) methodology to solve the Kohn–Sham (KS) [1] equation for solids goes to Karlheinz Schwarz. The history of that contribution is related in Section 3 of Ref. [2]. It suffices to say here that Heinz started using the original APW in his thesis work, then came to Gainesville and Quantum Theory Project (QTP) in 1969 to work with Prof. J.C. Slater, the inventor of the APW method. That is how the last author of this paper became a collaborator with Heinz and a friend.
Years later, when linearized methods removed the explicit energy dependence difficulty in the APW basis, Heinz undertook development of the code that became WIEN [3]. Again there was a collaboration involving QTP, University of Florida, and the last author. Apparently that was the first publicly available FLAPW code. By now, it has evolved to WIEN2k [2,4]. During that evolutionary period, methodological developments led to revival of the APW scheme via the APW plus local orbitals (APW+) combination (summarized below). That has been instantiated in several other codes as well as WIEN2k, e.g., ELK [5], FlEUR [6], exciting [7], and Exciting-plus [8]. Here, we are pleased to contribute to the further advance of this important methodology and particularly pleased to be able to do so in honor of Heinz’ birthday.
2. Motivating Physical Systems
The materials physics problem class driving our effort is molecular magnetism, in particular, the contriving of condensed aggregates of molecular magnets into materials of relevance to quantum information systems, notably, quantum computing [9,10]. The computational challenge is to predict promising molecular magnets [11,12], and promising aggregates of them as well as parametrizing spin Hamiltonians and aiding interpretation of experimental data. The molecules themselves are large and complicated.
A pertinent example is the molecular magnet -, dichloro-tetrakis-thourea-nickel, commonly called “DTN” and its Co analogue, DTC [13]. DTN is important in this context because of its multi-ferroicity, the coexistence of ferromagnetism and ferroelectricity [14], in contrast with the absence of multi-ferroicity in DTC. The DTN cubic molecular crystal structure has two Ni atoms as magnetic centers in the unit cell. Each Ni has four S atoms and two Cl atoms as nearest neighbors, forming an octahedral structure (like the octahedra in perovskites). The unit cell has 70 atoms and 444 electrons,
Spin-crossover systems are a closely related, highly relevant class, as they are candidate linkers for quantum information systems [15,16,17]. The electronic structure challenge is to calculate the low-spin, high-spin energy difference and provide the potential surface to calculate the vibrational entropic contributions. A particular significant example is the so-called [Mn(taa)] molecule ([]), a meridional pseudo-octahedral chelate complex of a single Mn as the magnetic center and the hexadentate tris[(E)-1-(2-azolyl)-2-azabut-1-en-4-yl]amine ligand. It has 53 atoms and 224 electrons. Calculating its spin-crossover energy with low-computational-cost, commonly used density functional methodology without user intervention and tuning has proven to be a formidable task [18].
While these two examples are convenient for the demonstration of capacity focus of this paper, they actually are a bit on the small side for the investigation of molecular magnetic materials in general. An illustration of that challenge is a molecule of current interest, the [MnO(OCPh)(HO)] complex [19,20]. It has spin from 176 atoms and 1210 electrons.
Essential computational issues are made evident by these examples. The individual molecules are structurally and electronically intricate. Typically they have complicated spin manifolds that are strongly structurally dependent. Their condensed aggregates are correspondingly complicated and demanding. Moreover, the presence of heavy nuclei and the importance of anisotropy both implicate the significance of relativistic effects, including spin-orbit coupling. In sum, predictive, materials-specific simulations of condensed magnetic molecule systems and spin-crossover systems are extremely challenging tasks.
In the remainder of this paper, we describe the context and need for all-electron computational methods with emphasis on LAPW and APW+ methodology, then discuss impediments to use of existing codes on the physical systems of interest, introduce separation of concerns as identifying and off-loading algorithmic elements common to any LAPW/APW+ code, and the SIRIUS package used as a library for that off-loading, show how interfacing between the Exciting-Plus code and SIRIUS can be achieved, and give numerical examples and timings for the combination.
3. Predictive Computational Approaches
Balance of computational cost-effectiveness and accuracy in treatment of electronic structure of challengingly complicated systems is the pragmatic reason for prevalent use of density functional theory (DFT) [21] in its KS variational form [21,22,23,24]. In the context motivating this work, accuracy is crucial for predicting both structural properties and characterizing spin manifolds. The primary choices regarding accuracy are the selection of an exchange-correlation () approximation and selection of a method for solving the resulting KS equations. We address the second. The first is an arena of intense effort that has provided many options.
Most “electronic structure methods” come down to the choice of a basis set (and its truncation) by which to reduce the KS equation to a linear algebra problem. The obvious, naïve basis for periodic systems is plane waves. It provides systematic enrichment and is unbiased with respect to ionic charge. The long-known limitation is that the basis becomes unmanageably large if the oscillations of near-nucleus orbitals caused by the bare Coulomb potential are included [25]. This burden is removed by use of a pseudo-potential instead [26] or, more recently, use of projector augmented waves (PAWs) [27]. Widely used examples of such “plane-wave pseudo-potential-PAW” (PW-PP-PAW) codes include VASP [28], QuantumEspresso [29], and ABINIT [30,31,32].
Such calculations intrinsically are not truly all-electron. Pseudo-potentials eliminate core states, while PAWs reconstruct them. There is a need therefore to test and cross-check plane-wave pseudo-potential calculations against truly all-electron calculations. For only three examples of many, see Refs. [33,34,35]. Another example is a comparatively early use of all-electron calculations for materials-by-design [36]. That was a study of Li-ion battery formulations with the WIEN2k code. Though nontrivial (especially at the time), at 14 atoms per cell with 170–178 electrons, those systems were smaller than the motivating examples discussed above. Cross-validation is particularly important in the context of molecular magnetic quantum materials because of core contributions to spin manifolds and spin-orbit interaction effects.
The all-electron methodology of choice is the LAPW method or its close kin, APW+ [37]. Basis set construction is by use of the “muffin-tin” potential, the spherical average of the KS potential in non-overlapping, nuclear-centered spheres and a constant average elsewhere (the “interstitial” region). “Full-potential” denotes use of the whole KS crystalline potential, not just the so-called muffin-tin (MT) part. Historically that was an important distinction but today the MT potential is used only for basis set construction. Both LAPW and APW+ are rooted in Slater’s original APW scheme [38,39,40,41,42,43]. Within the MT spheres, all three sets have basis functions that are atomic-like solutions of spherical potentials. Those are matched with plane waves in the interstitial region.
Original LAPW literature is extensive, see Refs. [44,45,46,47,48,49,50,51,52,53,54,55,56,57,58]. Subsequently there was a particular kind of local orbital (“LO”, not “”) added [59], and then the closely related APW+ scheme [60]. These are covered in at least two other books [37,61] as well as various review chapters (e.g., Refs. [2,62]). Therefore here we display only those equations directly relevant to our discussion of codes and algorithmic libraries.
The original APW basis function for Bloch wave-vector and plane-wave vector is
Here is the solution of the (energy-dependent, ) radial Schrodinger equation in the MT sphere labeled , that is regular at the origin with principle quantum number , are spherical harmonics, are the coefficients for matching with the interstitial plane wave, ℓ and m are the azimuthal and magnetic quantum numbers in a particular sphere. (The APW basis does not have continuous radial first derivatives at the sphere surfaces). Since the radial functions are -dependent, continuity at the sphere surface requires that energy to correspond to a KS eigenvalue. The APW secular equation thus is highly non-linear in the one-electron energies. That non-linearity induces both an important computational computational cost and difficult-to-manage singularities whenever a radial basis function has a node on a sphere surface.
The LAPW basis addresses those difficulties by using both the radial functions at reference energies and their energy derivatives
(The “dotted” notation for the energy derivative is conventional in LAPW literature). Thus the basis functions become
The coefficients follow from making each basis function continuous with continuous first radial derivative at each sphere boundary. Unlike the APW case, the KS secular equation in the LAPW basis is of the ordinary linear variational form. The only user-dependent choices are the reference energies and muffin-tin radii.
As the LAPW linearization is not unique, exploration of options eventually led [60] to the recognition that a more efficient linearization combines the original APW basis functions inside the sphere at fixed reference energies with a set of linearized (in energy) radial functions inside the sphere, each of which vanishes at the sphere surface. This “APW+” basis consists of Equation (1) enhanced with different local orbitals (“”),
These localized basis functions do not have continuous derivatives at the sphere boundary, so surface terms arise in the kinetic energy and in any gradient-dependent exchange correlation functional.
The LAPW and APW+ basis sets can be used together with suitable reference energy choices and consideration of the atomic structure differences among spheres. Observe that both basis sets are adaptive in that the radial functions evolve as the KS potential evolves from SCF iteration to iteration.
The forms of the electron number density and the KS effective potential matrix elements in these basis sets are given in Appendix A for completeness.
4. Codes and Libraries
4.1. Base Code
The present work focuses on the Exciting-Plus code, hereafter “EP” for brevity [8]. EP was developed from an early version of the ELK/exciting code, that was branched at the time when independent evolution of exciting and ELK had just begun. EP was developed with emphasis on post-ground-state calculations such as for the density response function [63] and RPA [8] and GW [64] calculations. Ground state KS calculations are done in EP with k-point task distribution and LAPACK [65] diagonalization support. EP also implemented a convenient mpi-grid task parallelization in several independent variable dimensions, e.g., k-points, i-j index pairs of KS states, and q points in the calculation of the KS density response function.
EP was constructed conscientiously in terms of coding practices. However, its design did not focus on high performance for multi-atom unit cells. Our context makes that important. Our goal is to retain the features and capabilities of EP while making it fast enough for routine all-electron DFT calculations to be feasible for large, complicated systems such as the magnetic molecules, spin-crossover molecules, and aggregates discussed at the outset.
4.2. Separation of Concerns and the SIRIUS Package
LAPW/APW+ codes evidently share their central formalism. Because their basis sets start from plane waves, those codes also share significant procedural elements with PW-PP-PAW codes. Shared tasks include unit cell setup, atomic configurations, definition and generation of reciprocal lattice vectors , combinations with Bloch vectors , definition of basis functions on regular grids as Fourier expansion coefficients, construction of the plane wave contributions to the KS Hamiltonian matrix, generation of the charge density, effective potential, and magnetization on a regular grid, iteration-to-iteration mixing schemes for density and potential, and diagonalization of the secular equation. Compared to PW-PP-PAW codes, LAPW/APW+ codes additionally have spatially decomposed basis sets as outlined above.
These extensive commonalities constitute an opportunity for performance enhancement via separation of concerns. Computer scientists can bring their skills to bear on the shared algorithmic core of LAPW/APW+ methodology while computational materials physicists can focus on implementation of analysis, post-processing, better exchange-correlation functionals, etc.
With achievement of the benefits of this separation in mind, an optimized package, SIRIUS [66], was created by some of us. It has explicit, focused, highly refined implementation of LAPW/APW+ commonalities (and PW-PP-PAW to the extent of the broader commonality) as the goal. That is, abstracting and encapsulating objects common to LAPW and APW+ as the design objective for SIRIUS. By concept, it had both task parallelization and data parallelization. It has been optimized for multiple MPI levels as well as OpenMP parallelization and for GPU utilization.
SIRIUS can be used two ways, as a library or as a simple LAPW/APW+ code. Elsewhere, we will report on its use in the latter way [67]. In that case the compromise involved is to accept the functionality limits of SIRIUS in return for being able to handle very large systems by both task and data parallelism. Here we report on exploitation of SIRIUS purely as a DFT library by construction of an EP-SIRIUS interface using the SIRIUS API. The expected gain is speed-up while retaining the familiar user-interface and post-processing functionalities of EP. Figure 1 illustrates the scheme. The intrinsic limitation of separation of concerns is that the resulting package has limitations that, in essence, are the union of the limitations of the host code and of the library. We discuss that briefly at the end.
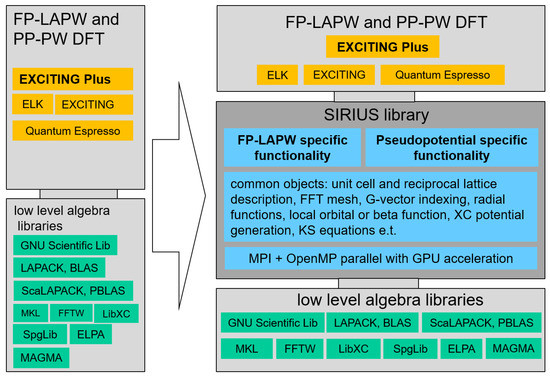
Figure 1.
General scheme for utilization of SIRIUS as a library to enhance performance of a host code.
4.3. SIRIUS Characteristics and Features
SIRIUS is written in C++ in combination with the CUDA [68] back-end to provide (1) low-level support (e.g., pointer arithmetic, type casting) as well as high-level abstractions (e.g., classes and template meta-programming); (2) easy interoperability between C++ and widely used Fortran90; (3) full support from the standard template library (STL) [69]; and (4) easy integration with the CUDA nvcc compiler [70]. The SIRIUS code provides dedicated API functions to interface to exciting and to QuantumEspresso [29,71,72].
Virtually all KS electronic structure calculations rely at minimum on two basic functionalities: distributed complex matrix-matrix multiplication (e.g., pzgemm in LAPACK) and a distributed generalized eigenvalue solver (e.g., pzhegvx also in LAPACK). SIRIUS handles these two major tasks with data distribution and multiple task distribution levels.
The eigenvalue solver deserves particular attention. Development of exciting led to significant code facilities to scale the calculation to larger numbers of distributed tasks than originally envisioned by making the code switchable from LAPACK to ScaLAPACK. This can be verified by comparing the task distribution and data distribution of the base ground state subroutine in recent versions of exciting (version Nitrogen for example) and ELK (version 5.2.14 or earlier for example). ELK development appears to have emphasized physics features and functionalities rather than adding ScaLAPACK support. The EP situation is similar. It has only LAPACK support and does not have data distribution of large arrays. Table 1 summarizes the diagonalization methods available in these codes.

Table 1.
Eigensolver options.
Eigenvalue solver performance depends strongly upon the algorithm type. Widely used linear algebra libraries (e.g., LAPACK, ScaLAPACK) implement robust full diagonalization. They can handle system size up to about . Unfortunately for LAPW/APW+ calculations on systems as large as 100+ atoms, the eigensystem often is several times larger. A Davidson-type iterative diagonalization algorithm is appropriate in that case because it typically suffices to solve for the lowest 10–20 percent of all occupied eigenvalues and associated eigenvectors up through and somewhat above the Fermi energy.
Davidson-type diagonalization algorithms are available in some APW+ and PW-PP-PAW codes, e.g., WIEN2k [73] and PWscf [74] respectively. They are not offered in standard linear algebra libraries however. At least in part that is because such algorithms repeatedly apply the Hamiltonian to a sub-space of the system. Therefore the algorithm depends upon details of the Hamiltonian matrix, hence upon the specific basis-set formalism. By virtue of focus on tasks central to LAPW/APW+ and PW-PP calculations, the SIRIUS package can provide an efficient implementation of Davidson-type diagonalization [75] for LAPW/APW+ and PW-PP-PAW codes.
4.4. Interfacing Exciting-Plus with SIRIUS
Despite its many attractive features, especially for important post-ground state calculations, EP has some significant limitations in regard to ground state calculations on large systems such as magnetic and spin-crossover molecules. Those limits include: (1) provision of only the LAPACK eigensolver; and (2) -point-only MPI parallelization. This second limit renders the code completely serial for single -point calculations, e.g., on an isolated molecule in a big cell.
We frame the task therefore as straight-forward interfacing to SIRIUS as an unaltered library with comparatively minimal modification of EP. This black-box approach is pure separation of concerns, since it is the simplest route an experienced EP user could take to try to gain advantage from SIRIUS without investing effort in learning its inner workings. A benefit is that the user interface to EP+SIRIUS is essentially unaltered EP, yet the combined system provides (a) ScaLAPACK support, (b) Davidson iterative eigensolver, (c) band MPI parallelization for one -point, and (d) thread-level OMP parallelization per k-point per band. It also exposes some oddities introduced by the black-box strategy.
Interface implementation benefits from the FORTRAN API functionalities provided by SIRIUS. Listing 1 displays the FORTRAN API function calls for parsing the atomic configuration, the APW and basis from EP, and passing them to SIRIUS.
| Listing 1: Setting up atomic configuration. |
|
The code segment in Listing 1 loops over the number of states of a single atom type atom (spnst: species’ number of states). For each state, the API call provides to SIRIUS the quantum numbers n, l and k for each state (spn, spl and spk), the occupation of that state (spocc), and whether that state is treated as a core state (spcore).
The first of the two double loops in the code chunk shown in Listing 2 goes over the APWs of one atom type and the ℓ-channels of each APW. For each ℓ-channel, the API call passes the following information to SIRIUS: principle quantum numbers n (apwpqn), value of ℓ (l), value of the initial linearization energy (apwe0), the order of energy derivative of that APW (apwdm), and whether the linearization energy is allowed to be adjusted automatically (autoenu). The second loop is over the total number of local orbitals (nlorb) of one atom type and the orders (lorbord) of each local orbital (i.e., number of or terms in that local orbital). The API call passes the following information to SIRIUS: quantum numbers n and l (lopqn and lorbl), initial linearization energy (lorbe0), order of energy derivative (lorbdm), and whether the linearization energy is allowed to be adjusted automatically (autoenu).
| Listing 2: Fortran API for basis description. |
|
General input parameters such as the plane-wave cutoff, ℓ cutoff for the APWs and for density and potential expansion, -points, lattice vectors and atom positions, etc., all are set as usual in the EP input file. Then they are passed to SIRIUS via its built-in import and set parameter functionalities. Other important parameters such as the fast Fourier transform grid, radial function grid inside each MT sphere, and number of first variational states [37] often are not set in EP input files but defaulted. For EP+SIRIUS, however, those also must be passed to SIRIUS in the initialization step to ensure that the Hamiltonian matrix and eigenvectors are precisely the same in EP and SIRIUS. Other information such as specification of core states, linearization energy values and MT radii defined in the so-called species files of EP is passed to SIRIUS at the beginning of the calculation to overwrite the corresponding SIRIUS default values. Consider Listing 3 therefore.
| Listing 3: Fortran API for setting inputs for SIRIUS. |
|
The code chunk shown in Listing 3 is an example of basic inputs that are added to EP in the initialization step, in the piece of code named init0.f90. Most of the meanings are explicit in the name. zora means zero-order relativistic approximation. ngrid is the FFT grid set up in EP and passed to SIRIUS. Plane wave cutoff and cutoff values are gmaxvr and gkmax in EP. The lmaxapw and lmaxvr are the angular momentum cutoff for APW and for charge density (and potential) inside the MT.
The inserted code shown in Listing 4 supplies SIRIUS with additional parameters for the Davidson method if it is used. After ensuring that the setup of input quantities is identical between the host code (EP) and SIRIUS, the ground state calculation is done solely by SIRIUS. The results, eigenvalues and eigenvectors, are passed back to EP for further calculation.
| Listing 4: Eigen-solver selection and Davidson solver parameter setup. |
|
Next we display, in Listing 5, a code segment with the typical API calls from EP to retrieve the resulting eigenvalues and eigenvectors. It is inserted in the ground state subroutine, the piece of code named gndstate.f90.
| Listing 5: Fortran API for retrieving eigenvalues and eigenvectors from SIRIUS. |
|
Care is needed in dealing with the MPI task schedules when interfacing to SIRIUS as a library because typically the host code will have an MPI implementation that differs from that in SIRIUS. For EP as the host, the task is simplified because EP has only k-point parallelization in the ground-state calculation. In the initialization step, we set the SIRIUS MPI communicator to be derived from the global MPI communicator (MPI_COMM_WORLD) of the host code so that all MPI ranks will be used by SIRIUS. Then the user needs to specify how SIRIUS will carry out the k-point distribution, how to plan further band parallelization within a k-point, and thread-level parallelization. The schedules of k-point parallelization and band parallelization are required additional inputs. Thread-level parallelization also has additional inputs which are specified in the run job script.
If band parallelization is used in SIRIUS, the eigenvalues and eigenvectors associated with a single k-point are distributed in multiple MPI tasks. It therefore is necessary to combine the band subset results before transmitting the eigenvalues and eigenvectors back to EP. Thus, after SIRIUS finishes the ground state calculation but before calling the API to return the eigenvalues and eigenvectors to EP, SIRIUS will do mpi_reduce in the MPI band dimension and prepare full eigenvalues and eigenvectors labeled by k-points and by the global band index at each k-point.
The last piece of the interface provides the additional inputs for the SIRIUS Davidson diagonalization algorithm. These are adjustable numerical parameters passed directly to SIRIUS by EP.
As anticipated, the MPI parallelization in the band degree of freedom is one major gain from interfacing EP to SIRIUS. We noted above that EP runs entirely in non-parallel mode for a single k-point calculation (often a “Gamma-point calculation” or “Balderschi-point calculation”), such as is typical for isolated molecule calculations. Hence the SIRIUS-enhanced-EP has the same scaling as SIRIUS alone in the case of single k-point calculations. This is an example of the antithesis of the union of limitations that is inherent in separation of concerns. Here, separation of concerns actually avoids a limitation of the host code.
To illustrate, Figure 2 displays the benchmark of band-parallelization on the DTN molecule (brief details about the molecule are below). It is placed in a Å cubic unit cell, with plane-wave cutoff (inverse Bohr radius) and angular momentum cutoff . All jobs were set to 16 multi-threads in one task in accord with the hardware configuration. The recorded time is for the first 100 SCF iterations using the Davidson diagonalization eigensolver. Note that the figure also shows that employment of EP as a front-end to SIRIUS does not introduce any significant overhead. The timings for EP+SIRIUS are almost identical to those for SIRIUS alone. Timings compared to PW-PP-PAW codes are in the next section.
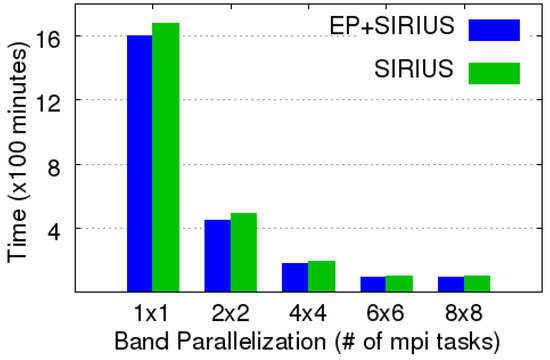
Figure 2.
Benchmark of band parallelization in single k-point jobs. ranks are used for one k-point.
5. EP+SIRIUS: Verification Tests on Small Solid State Systems
The EP+SIRIUS combination was bench-marked first against SIRIUS standalone on ground-state calculations of the total energy (and magnetization for magnetic systems) for the simple bulk materials Al, Ni, Fe, NiO, C, Si, Ge, and GaAs. For each system, identical input parameters were used for the SIRIUS and EP+SIRIUS runs. To be systematic, we adopted the experimental lattice parameters for all systems. The APW+ and LAPW bases were used. Both local density approximation (LDA) and generalized gradient approximation (GGA; PBE [76]) exchange-correlation functionals were used. In the interstitial potential and charge density expansions, the maximum length of the reciprocal lattice vector used as plane wave cut-off for the APW was set to for all systems. The angular momentum truncation was taken as for APW, with the same value used for the charge density, potential, and orbital inside the MT sphere. The linearization energy associated with each APW radial function was chosen at the center of the corresponding band with ℓ-like character for all systems. Sampling of the first Brillouin zone was by a dense k-mesh for all systems. All parameters were tested carefully to achieve total energy convergence (tolerance Hartree). For the EP+SIRIUS calculations, diagonalization always was done with the Davidson iterative eigensolver.
Table 2 summarizes the APW+ basis configuration, settings other than those already stated, and the converged total energy and magnetization of these small systems. Table 3 summarizes the same calculation setup with the LAPW basis. The good agreements in total energy and magnetization in these tests validate the assumption that the identical basis setup was invoked and that the constructed interface linked the SIRIUS calculation properly with the EP host code.

Table 2.
EP+SIRIUS vs. SIRIUS, using APW+.

Table 3.
EP+SIRIUS vs. SIRIUS, using LAPW.
6. EP+SIRIUS: Two Molecular Examples
6.1. [Mn(taa)] Molecule
As the first known example of a manganese(III) spin-crossover system [77], [Mn(taa)] is a system of long-standing interest. Experiment shows that the cation goes from a low-spin state (LS) to a high-spin state (HS) at a transition temperature of about 45 K. The [Mn(taa)] structure (see Figure 3) is sufficiently large that it has non-negligible intra-molecular dispersion interactions with significant HS-LS dependence. The HS ground state involves anti-bonding molecular orbital occupation, hence the octahedral HS complex tends to have weaker and therefore longer metal-ligand bonds than in the LS ground state.
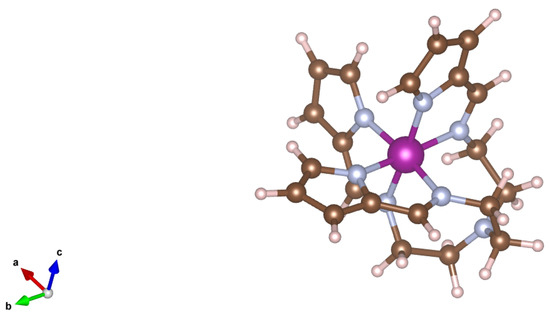
Figure 3.
[Mn(taa)] molecule.
This combination of spin- and structural dependence makes [Mn(taa)] a significant challenge to the computational determination of the two ground states. The purely molecular (non-thermal) is small compared to the total energies. Estimates are about 50 ± 30 meV but as high as a few hundred meV. Extensive details of studies with various codes are in Ref. [18]. Several factors can affect a DFT calculation of the molecular . For consistency with condensed phase calculations, it is appropriate to study the isolated molecule in a large, periodically bounded box. Appropriate accuracy necessitates a rather large plane wave cutoff, a need that is worsened by the amount of vacuum in the unit cell. (We remark that the self-interaction error of the usual GGA exchange-correlation functions (e.g., PBE) tends to cause the the LS state to be favored, hence cause overestimated values. That is not of concern here since what we are testing is algorithmic efficiency. Similarly we did not use Hubbard U).
For the test of EP + SIRIUS, we used the experimentally determined HS and LS [Mn(taa)] structures and did PBE calculations for a single molecule in a 10 × 10 × 10 Å box. Comparison data are from VASP calculations on optimized structures, also with PBE and without U. Notice, however, that the VASP calculations used a 20 × 20 × 20 Å box. Table 4 gives the parameters and results for the LS state. Its total energy is determined to be about 412meV below that of the HS state. In contrast, the VASP results are 458-497 mev (at the optimized geometry) with the variation arising from whether the Mn pseudo-potential has 7, 13, or 15 Mn valence electrons. This illustrates the kind of assessment that all-electron calculations facilitate. Regarding timing, observe that the EP + SIRIUS timing is for 16 (4 × 4) MPI tasks with 8 cores per task.

Table 4.
Parameters and results for the APW+ calculation of the [Mn(taa)] LS state, with comparison with VASP timings.
Table 5 compares timing for the EP only and EP+SIRIUS all-electron calculations and VASP PW-PP-PAW calculations. Evidently EP-only is not competitive but EP+SIRIUS is, at least on a per iteration basis.

Table 5.
For = 4, the average time (seconds) consumed per SCF iteration of EP-SIRIUS for single [Mn(taa)] in 10 × 10 × 10 Å box, single k-point calculation over 60 min of iterations. Comparison is to VASP for three different pseudo-potentials (see text) in a 20 × 20 × 20 Å box.
There is a difficulty hidden in these results however. The lesser aspect is that we cannot run EP alone at all in a 20 × 20 × 20 box. The appropriate cutoffs for such a large vacuum region cause out-of-memory problems with EP because of the way its arrays are structured. The more severe consequence is that we also cannot do a full EP+SIRIUS run, in the sense of returning solutions from SIRIUS to EP for post-processing, on that size box. In effect, EP+SIRIUS is limited in this situation to being an EP user interface for input and control of SIRIUS. The work goes to SIRIUS from EP but the results cannot be returned to EP. Examination of EP suggests that it would take some significant restructuring to remedy the problem, a task well outside the scope of this work or of the separation of concerns approach.
6.2. EP+SIRIUS: DTN Molecule
The challenges and opportunities posed by the DTN molecule were summarized in Section 2. In essence one has two transition metals in a complicated structure reminiscent of the perovskites such that the system is both ferromagnetic and ferroelectric. See Figure 4. Recall that the molecule has 70 atoms and 444 electrons.
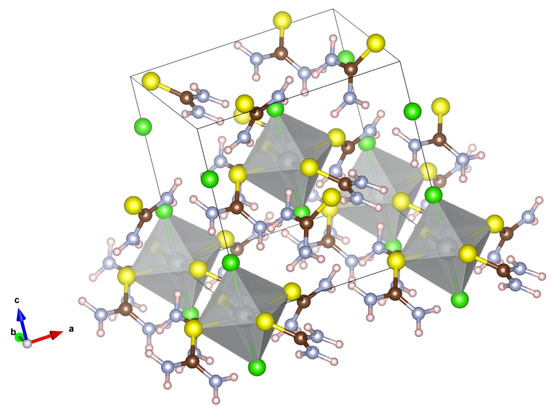
Figure 4.
DTN molecule crystal.
We used EP+SIRIUS to calculate the AFM ground state of DTN. We make no attempt at a thorough study, but simply use DTN to show the speed of an all-electron APW+ calculation done with EP+SIRIUS versus with the conventional implementation in EP. Table 6 shows the parameters used and the basic results.

Table 6.
Input parameters and outputs of DTN.
Table 7 shows the average time per scf iteration as a function of the longest expansion vector for the density and potential. Notice that the main gain from EP+SIRIUS over EP alone at the level of one MPI task per k-vector is that the iteration time is almost independent of that vector magnitude. The bigger gain comes from the multiple MPI tasks.

Table 7.
For the DTN MOF structure, with , the average time (seconds) consumed per SCF iteration as a function of longest expansion vector for the potential and density. k-points, run of 60 min.
7. Summary and Conclusions
To summarize, we have implemented a performance enhancement strategy for the Exciting-Plus LAPW/APW+ code by interfacing it with SIRIUS used as a library. We have explored the simplest possible approach to exploiting the separation-of-concerns design philosophy of SIRIUS, namely to interface to it as a black box. The interface outsources the central tasks of the ground-state KS problem from EP to SIRIUS. The objective is to embed a SIRIUS SCF loop inside EP. The implementation effort involved is moderate, benefiting from the similarity of the data structures between EP and the LAPW/LAPW+ elements of SIRIUS.
The EP+SIRIUS combination provides performance gains through diagonalization and parallelization improvements while retaining the user interface and post-processing functionalities of EP. The result is a major advance in capability for treating large, complex molecular aggregates. From the user perspective, only small modifications to the original EP input files are needed. A few lines to select use of SIRIUS and to specify the additional parameters for the Davidson eigensolver are the only changes.
This simplest separation of concerns implementation resolves the eigenvalue solver bottleneck in EP that comes from use of LAPACK full diagonalization. (It cannot handle Hamiltonian matrices larger than ≈). The hand-off to SIRIUS provides the option to use diverse diagonalization algorithms (Davidson, ScaLAPACK, or LAPACK). Use of Davidson-type diagonalization of the Hamiltonian in the self-consistent loop thus benefits from multiple level parallelization within k-points and bands. The eigenvalues and eigenvectors resulting from the SIRIUS calculation have the same structure as those of EP. The design intent therefore is to transfer them back to EP. However, the array structure design of EP inhibits this, as we found with [Mn(taa)]. We return to that below.
For testing and validation, we showed results from small bulk systems calculated in both the APW+ basis and the LAPW basis. The resulting total energy and magnetization show no meaningful deviation from the SIRIUS standalone runs. Two very much larger molecular systems were calculated using the APW+ basis using both EP alone and EP+SIRIUS. Good scaling in band parallelization for a single k-point is observed, The parallelization of the interfaced code works well on high-performance computers, and the computational time is drastically reduced in comparison with the original EP.
The main advantage of the interfaced code is the ease of its construction and the support from advanced eigensolvers. We expect similar interface construction can be done with the ELK or exciting codes without unreasonable effort.
Looking ahead, we have found that the non-distributed large arrays defined in EP have become the new bottleneck. That is especially the case when dealing with molecular systems containing more than ≈100 atoms in a large unit cell. The primary cause of the bottleneck is the high plane wave G cutoff for large systems, and the fact that some fundamental multi-dimensional arrays are defined with one dimension containing all indices of the G vector or vector. Examples of such fundamental quantities include the augmentation wave part ( part) of the APW basis and the so-called structure factor, the form . These basic quantities are used in many places in the host code. It is not an easy job to change them to be distributed data in all occurrences. Although that system-size limitation remains, calculations based on the current EP+SIRIUS can handle larger systems than the original Exciting-Plus and offer a significantly improved foundation for examining the validity of the results from calculations based on various pseudo-potentials.
Author Contributions
Conceptualization, T.S. and H.-P.C.; Formal analysis, A.K. and S.B.T.; Methodology, L.Z., A.K., T.S., H.-P.C. and S.B.T.; Resources, H.-P.C.; Software, L.Z., A.K. and T.S.; Supervision, H.-P.C. and S.B.T.; Validation, L.Z.; Writing—original draft, L.Z.; Writing—review & editing, S.B.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The work of L.Z., H.-P.C., and S.B.T. was supported as part of the Center for Molecular Magnetic Quantum Materials, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under Award No. DE-SC0019330. Computations were performed at the U.S. National Energy Research Supercomputer Center and the University of Florida Research Computer Center. SBT thanks Angel M. Albavera Mata for providing some [Mn(taa)] calculation timing data from VASP and a helpful remark.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Expressions for Number Density and KS Potential
In the LAPW and APW+ basis sets, the number density and KS potential obviously are adapted, through their matrix elements, to the MT subdivision of the unit cell. In the interstitial region they are expanded in plane waves and inside MT spheres in real spherical harmonics :
and
Here , , , and are expansion coefficients determined through the self-consistent solution of the KS equation.
References
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef] [Green Version]
- Blaha, P.; Schwarz, K.; Trickey, S. Electronic structure of solids with WIEN2k. Mol. Phys. 2010, 108, 3147–3166. [Google Scholar]
- Blaha, P.; Schwarz, K.; Sorantin, P.; Trickey, S. Full-potential, Linearized Augmented Plane Wave Programs for Crystalline Systems. Comput. Phys. Commun. 1990, 59, 399–415. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Tran, F.; Laskowski, R.; Madsen, G.; Marks, L. WIEN2k: An APW+lo program for calculating the properties of solids. J. Chem. Phys. 2020, 152, 074101. [Google Scholar] [CrossRef] [PubMed]
- The Elk Code. Available online: http://elk.sourceforge.net (accessed on 16 October 2020).
- The Fleur Code. Available online: http://www.flapw.de (accessed on 11 December 2020).
- Gulans, A.; Kontur, S.; Meisenbichler, C.; Nabok, D.; Pavone, P.; Rigamonti, S.; Sagmeister, S.; Werner, U.; Draxl, C. Exciting—A full-potential all-electron package implementing density-functional theory and many-body perturbation theory. J. Phys. Condens. Matter 2014, 26, 363202. [Google Scholar] [CrossRef] [PubMed]
- Kozhevnikov, A.; Eguiluz, A.G.; Schulthess, T.C. Toward First Principles Electronic Structure Simulations of Excited States and Strong Correlations in Nano- and Materials Science. In Proceedings of the 2010 ACM/IEEE International Conference for High Performance Computing, Networking, Storage and Analysis, New Orleans, LA, USA, 13–19 November 2010; pp. 1–10. [Google Scholar] [CrossRef]
- Wasielewski, M.R.; Forbes, M.D.E.; Frank, N.L.; Kowalski, K.; Scholes, G.D.; Yuen-Zhou, J.; Baldo, M.A.; Freedman, D.E.; Goldsmith, R.H.; Goodson, T., III; et al. Exploiting chemistry and molecular systems for quantum information science. Nat. Rev. Chem. 2020, 4, 490–504. [Google Scholar] [CrossRef]
- Gaita-Ari no, A.; Luis, F.; Hill, S.; Coronado, E. Molecular spins for quantum computation. Nat. Chem. 2019, 11, 301–309. [Google Scholar] [CrossRef] [PubMed]
- Castro, S.L.; Sun, Z.; Grant, C.M.; Bollinger, J.C.; Hendrickson, D.N.; Christou, G. Single-Molecule Magnets: Tetranuclear Vanadium(III) Complexes with a Butterfly Structure and an S = 3 Ground State. J. Am. Chem. Soc. 1998, 120, 2365–2375. [Google Scholar] [CrossRef]
- Bagai, R.; Christou, G. The Drosophila of single-molecule magnetism: [Mn12O12(O2CR)16(H2O)4]. Chem. Soc. Rev. 2009, 38, 1011–1026. [Google Scholar] [CrossRef]
- Mun, E.; Wilcox, J.; Manson, J.L.; Scott, B.; Tobash, P.; Zapf, V.S. The Origin and Coupling Mechanism of the Magnetoelectric Effect in TMCl2-4SC(NH2)2 (TM = Ni and Co). Adv. Condens. Matter Phys. 2014, 2014, 512621. [Google Scholar] [CrossRef] [Green Version]
- Jain, P.; Stroppa, A.; Nabok, D.; Marino, A.; Rubano, A.; Paparo, D.; Matsubara, M.; Nakotte, H.; Fiebig, M.; Picozzi, S.; et al. Switchable electric polarization and ferroelectric domains in a metal-organic-framework. NPJ Quantum Mater. 2016, 1, 16012. [Google Scholar] [CrossRef] [Green Version]
- Kepp, K.P. Consistent descriptions of metal–ligand bonds and spin-crossover in inorganic chemistry. Coord. Chem. Rev. 2013, 257, 196–209. [Google Scholar] [CrossRef]
- Shatruk, M.; Phan, H.; Chrisostomo, B.A.; Suleimenova, A. Symmetry-breaking structural phase transitions in spin crossover complexes. Coord. Chem. Rev. 2015, 289–290, 62. [Google Scholar] [CrossRef]
- Collet, E.; Guionneau, P. Structural analysis of spin-crossover materials: From molecules to materials-Etudes structurales des materiaux a conversion de spin: De la molecule aux materiaux. Comptes Rendu Chim. 2018, 21, 1133–1151. [Google Scholar] [CrossRef]
- Mejía-Rodríguez, D.; Albavera-Mata, A.; Fonseca, E.; Chen, D.T.; Chen, H.P.; Hennig, R.G.; Trickey, S. Barriers to Predictive High-throughput Screening for Spin-crossover. Comput. Mater. Phys. 2022, 206, 111161. [Google Scholar] [CrossRef]
- Caneschi, A.; Gatteschi, D.; Sessoli, R.; Barra, A.L.; Brunel, L.C.; Guillot, M. Alternating current susceptibility, high field magnetization, and millimeter band EPR evidence for a ground S = 10 state in [Mn12O12(Ch3COO)16(H2O)4]·2CH3COOH·4H2O. J. Am. Chem. Soc. 1991, 113, 5873–5874. [Google Scholar] [CrossRef]
- Sessoli, R.; Tsai, H.L.; Schake, A.R.; Wang, S.; Vincent, J.B.; Folting, K.; Gatteschi, D.; Christou, G.; Hendrickson, D.N. High-spin molecules: [Mn12O12(O2CR)16(H2O)4]. J. Am. Chem. Soc. 1993, 115, 1804–1816. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef] [Green Version]
- Parr, R.G.; Yang, R.G.P.W. Density-Functional Theory of Atoms and Molecules; Oxford University Press: Oxford UK, 1989. [Google Scholar]
- Dreizler, R.; Gross, E. Density Functional Theory: An Approach to the Quantum Many-Body Problem; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Engel, E.; Dreizler, R.M. Density Functional Theory; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Schlosser, H.; Marcus, P.M. Composite Wave Variational Method for Solution of the Energy-Band Problem in Solids. Phys. Rev. 1963, 131, 2529–2546. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Gonze, X.; Amadon, B.; Anglade, P.M.; Beuken, J.M.; Bottin, F.; Boulanger, P.; Bruneval, F.; Caliste, D.; Caracas, R.; Côté, M.; et al. ABINIT: First-principles approach to material and nanosystem properties. Comput. Phys. Commun. 2009, 180, 2582–2615. [Google Scholar] [CrossRef]
- Gonze, X.; Beuken, J.M.; Caracas, R.; Detraux, F.; Fuchs, M.; Rignanese, G.M.; Sindic, L.; Verstraete, M.; Zerah, G.; Jollet, F.; et al. First-principles computation of material properties: The ABINIT software project. Comput. Mater. Sci. 2002, 25, 478–492. [Google Scholar] [CrossRef]
- Torrent, M.; Jollet, F.; Bottin, F.; Zèrah, G.; Gonze, X. Implementation of the projector augmented-wave method in the ABINIT code: Application to the study of iron under pressure. Comput. Mater. Sci. 2008, 42, 337–351. [Google Scholar] [CrossRef]
- Paier, J.; Marsman, M.; Hummer, K.; Kresse, G.; Gerber, I.C.; Ángyán, J.G. Screened hybrid density functionals applied to solids. J. Chem. Phys. 2006, 124, 154709. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haas, P.; Tran, F.; Blaha, P. Calculation of the lattice constant of solids with semilocal functionals. Phys. Rev. B 2009, 79, 085104. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Singh, D. Applicability of the Strongly Constrained and Appropriately Normed Density Functional to Transition-Metal Magnetism. Phys. Rev. Lett. 2018, 121, 207201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eglitis, R.I.; Borstel, G. Towards a practical rechargeable 5 V Li ion battery. Phys. Status Solidi A 2005, 202, R13–R15. [Google Scholar] [CrossRef]
- Singh, D.J.; Nordstrom, L. Plane Waves, Pseudopotentials, and the LAPW Method, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Slater, J. Wave Functions in a Periodic Potential. Phys. Rev. 1937, 51, 846–851. [Google Scholar] [CrossRef]
- Slater, J. An Augmented Plane Wave Method for the Periodic Potential Problem. Phys. Rev. 1953, 92, 603–608. [Google Scholar] [CrossRef]
- Leigh, R.S. The Augmented Plane Wave and Related Methods for Crystal Eigenvalue Problems. Proc. Phys. Soc. A 1956, 69, 388–400. [Google Scholar] [CrossRef]
- Loucks, T. The Augmented Plane Wave Method; Benjamin: New York, NY, USA, 1967. [Google Scholar]
- Slater, J. Energy Bands and the Theory of Solids. In Methods of Computational Physics; Alder, B., Fernbach, S., Rotenberg, M., Eds.; Academic: New York, NY, USA, 1968; Volume 8, pp. 1–20. [Google Scholar]
- Mattheiss, L.; Wood, J.; Switendick, A. A Procedure for Calculating Electronic Energy Bands Using Symmetrized Augmented Plane Waves. In Methods of Computational Physics; Alder, B., Fernbach, S., Rotenberg, M., Eds.; Academic: New York, NY, USA, 1968; Volume 8, pp. 63–147. [Google Scholar]
- Marcus, P. Variational methods in the computation of energy bands. Int. J. Quantum Chem. 1967, 1, 567–588. [Google Scholar] [CrossRef]
- Koelling, D. Linearized form of the APW method. J. Phys. Chem. Solids 1972, 33, 1335–1338. [Google Scholar] [CrossRef]
- Andersen, O. Simple Approach to the Band-Structure Problem. Solid State Commun. 1973, 13, 133–136. [Google Scholar] [CrossRef]
- Andersen, O. Linear methods in band theory. Phys. Rev. B 1975, 12, 3060–3083. [Google Scholar] [CrossRef] [Green Version]
- Koelling, D.; Arbman, G. Use of energy derivative of the radial solution in an augmented plane wave method: Application to copper. J. Phys. F 1975, 5, 2041–2054. [Google Scholar] [CrossRef]
- Koelling, D.; Harmon, B. A technique for relativistic spin-polarised calculations. J. Phys. C 1977, 10, 3107–3114. [Google Scholar] [CrossRef]
- Wimmer, E.; Krakauer, H.; Weinert, M.; Freeman, A. Full-potential self-consistent linearized-augmented-plane-wave method for calculating the electronic structure of molecules and surfaces: O2 molecule. Phys. Rev. B 1981, 24, 864–875. [Google Scholar] [CrossRef]
- Weinert, M. Solution of Poisson’s equation: Beyond Ewald-type methods. J. Math. Phys. 1981, 22, 2433–2439. [Google Scholar] [CrossRef]
- Weinert, M.; Wimmer, E.; Freeman, A. Total-energy all-electron density functional method for bulk solids and surfaces. Phys. Rev. B 1982, 26, 4571–4578. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K. Electron densities and chemical bonding in TiC, TiN, and TiO derived from energy band calculations. Int. J. Quantum Chem. 1983, XXIII, 1535–1552. [Google Scholar] [CrossRef]
- Jansen, H.; Freeman, A. Total-energy full-potential linearized augmented-plane-wave method for bulk solids: Electronic and structural properties of tungsten. Phys. Rev. B 1984, 30, 561–569. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Herzig, P. First-Principles Calculation of the Electric Field Gradient of Li3N. Phys. Rev. Lett. 1985, 54, 1192–1195. [Google Scholar] [CrossRef]
- Wei, S.; Krakauer, H.; Weinert, M. Linearized augmented-plane-wave calculation of the electronic structure and total energy of tungsten. Phys. Rev. B 1985, 32, 7792–7797. [Google Scholar] [CrossRef] [PubMed]
- Mattheiss, L.; Hamann, D. Linear augmented-plane-wave calculation of the structural properties of bulk Cr, Mo, and W. Phys. Rev. B 1986, 33, 823–840. [Google Scholar] [CrossRef] [PubMed]
- Goedecker, S.; Maschke, K. Operator approach in the linearized augmented-plane-wave method: Efficient electronic-structure calculations including forces. Phys. Rev. B 1992, 45, 1597–1604. [Google Scholar] [CrossRef] [PubMed]
- Singh, D.J. Ground-state properties of lanthanum: Treatment of extended-core states. Phys. Rev. B 1991, 43, 6388–6392. [Google Scholar] [CrossRef] [PubMed]
- Sjöstedt, E.; Nordstrom, L.; Singh, D. An alternative way of linearizing the augmented plane-wave method. Solid State Commun. 2000, 114, 15–20. [Google Scholar] [CrossRef]
- Cottenier, S. Density Functional Theory and the Family of (L)APW-Methods: A Step-by-Step Introduction; Self-Published: Zwijnaarde, Belgium, 2013; ISBN 978-90-807215-1-7. [Google Scholar]
- Schwarz, K. Computation of Materials Properties at Atomic Scale. In Selected Topics in Applications of Quantum Mechanics; Pahlavani, M.R., Ed.; IntechOpen: London, UK, 2015; pp. 275–310. [Google Scholar] [CrossRef] [Green Version]
- Petersilka, M.; Gossmann, U.J.; Gross, E.K.U. Excitation Energies from Time-Dependent Density-Functional Theory. Phys. Rev. Lett. 1996, 76, 1212–1215. [Google Scholar] [CrossRef] [Green Version]
- Chu, I.H.; Trinastic, J.P.; Wang, Y.P.; Eguiluz, A.G.; Kozhevnikov, A.; Schulthess, T.C.; Cheng, H.P. All-electron self-consistent GW in the Matsubara-time domain: Implementation and benchmarks of semiconductors and insulators. Phys. Rev. B 2016, 93, 125210. [Google Scholar] [CrossRef] [Green Version]
- Anderson, E.; Bai, Z.; Bischof, C.; Blackford, S.; Demmel, J.; Dongarra, J.; Du Croz, J.; Greenbaum, A.; Hammarling, S.; McKenney, A.; et al. LAPACK Users’ Guide, 2rd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1999. [Google Scholar]
- Solcá, R.; Kozhevnikov, A.; Haidar, A.; Tomov, S.; Dongarra, J.; Schulthess, T.C. Efficient Implementation of Quantum Materials Simulations on Distributed CPU-GPU Systems. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, ser. SC’15, Austin, TX, USA, 15–20 November 2015; ACM: New York, NY, USA, 2015; pp. 1–12. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Kozhevnikov, A.; Schulthess, T.C.; Trickey, S.B.; Cheng, H.P. Large-scale All Electron APW+lo calculations using SIRIUS. 2022; unpublished. [Google Scholar]
- CUDA ToolKit Documentation. Version: v11.2.1. Available online: https://docs.nvidia.com/cuda/index.html (accessed on 16 February 2021).
- Josuttis, N.M. The C++ Standard Library: A Tutorial and Reference, 3rd ed.; Addison-Wesley: Philadelphia, PA, USA, 2000. [Google Scholar]
- NVCC Compiler. Available online: https://docs.nvidia.com/cuda/cuda-compiler-driver-nvcc/ (accessed on 16 February 2021).
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with QUANTUM ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giannozzi, P.; Baseggio, O.; Bonfà, P.; Brunato, D.; Car, R.; Carnimeo, I.; Cavazzoni, C.; de Gironcoli, S.; Delugas, P.; Ferrari Ruffino, F.; et al. Quantum ESPRESSO toward the exascale. J. Chem. Phys. 2020, 152, 154105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blaha, P.; Hofstätter, H.; Koch, O.; Laskowski, R.; Schwarz, K. Iterative diagonalization in augmented plane wave based methods in electronic structure calculations. J. Comput. Phys. 2010, 229, 453–460. [Google Scholar] [CrossRef]
- Chandran, A.K. A Performance Study of Quantum ESPRESSO’s Diagonalization Methods on Cutting Edge Computer Technology for High-Performance Computing. Master’s Thesis, Scuola Internazionale Superiore di Studi Avanzati (SISSA), Trieste, Italy, 2017. [Google Scholar]
- Gulans, A. Implementation of Davidson Iterative Eigen-solver for LAPW. to be published.
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Sim, P.G.; Sinn, E. First manganese(III) spin crossover, first d4 crossover. Comment on cytochrome oxidase. J. Am. Chem. Soc. 1981, 103, 241–243. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).