On the Conic Convex Approximation to Locate and Size Fixed-Step Capacitor Banks in Distribution Networks
Abstract
:1. Introduction
1.1. General Context
1.2. Motivation
1.3. Revision of the State-of-the-Art
1.4. Contribution and Scope
1.5. Document Organization
2. Exact MINLP Formulation
2.1. Objective Function
2.2. Set of Constraints
3. MI-SOCP Relaxation
SOCP Approximation for the Power Flow Equations
4. Solution Methodology
5. Test System and Simulation Cases
5.1. IEEE 33-Node System
5.2. 69-Bus System
6. Computational Validation
6.1. Power Loss Analyses of the Proposed MI-SOCP Model
6.2. Economic Assessment of the Proposed MI-SOCP Model
- ✓
- For both test feeders, the CBGA and the proposed MI-SOCP reach the same numerical solution; however, the effectiveness of the CBGA was 5% in the IEEE 33-bus system and 12% for the IEEE 69-bus system when 100 consecutive evaluations were executed. These results imply that there exists less than 88% probability that in only one execution of the CBGA, it effectively reaches the optimal objective function value, while the MI-SOCP, due to the convexity of the solution space, finds the global optimum without recurring in any statistical evaluation.
- ✓
- Numerical results with the GAMS solver confirm that the MINLP model that represents the studied problem is hard to solve owing to the non-convexity of the power flow equations. Note that for both test feeders, the GAMS software is stuck in locally optimal solutions.
- ✓
- Regarding the total processing times, the MI-SOCP approach takes about 6.85 s to solve the studied problem in the IEEE 33-bus system and 26.99 s in the case of the IEEE 69-bus system, which can be considered fast processing times owing to the large size of the solution space explored (e.g., one million possible solutions), confirming the effectiveness of the proposed mixed-integer conic approximation to find the global optimal solution of complex MINLP models for distribution grids, which is clearly not ensurable with metaheuristic methods.
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ridzuan, M.I.M.; Fauzi, N.F.M.; Roslan, N.N.R.; Saad, N.M. Urban and rural medium voltage networks reliability assessment. SN Appl. Sci. 2020, 2, 241. [Google Scholar] [CrossRef] [Green Version]
- Kien, L.C.; Nguyen, T.T.; Pham, T.D.; Nguyen, T.T. Cost reduction for energy loss and capacitor investment in radial distribution networks applying novel algorithms. Neural Comput. Appl. 2021, 33, 15495–15522. [Google Scholar] [CrossRef]
- Riaño, F.E.; Cruz, J.F.; Montoya, O.D.; Chamorro, H.R.; Alvarado-Barrios, L. Reduction of Losses and Operating Costs in Distribution Networks Using a Genetic Algorithm and Mathematical Optimization. Electronics 2021, 10, 419. [Google Scholar] [CrossRef]
- Lavorato, M.; Franco, J.F.; Rider, M.J.; Romero, R. Imposing Radiality Constraints in Distribution System Optimization Problems. IEEE Trans. Power Syst. 2012, 27, 172–180. [Google Scholar] [CrossRef]
- Paz-Rodríguez, A.; Castro-Ordoñez, J.F.; Montoya, O.D.; Giral-Ramírez, D.A. Optimal Integration of Photovoltaic Sources in Distribution Networks for Daily Energy Losses Minimization Using the Vortex Search Algorithm. Appl. Sci. 2021, 11, 4418. [Google Scholar] [CrossRef]
- Águila, A.; Ortiz, L.; Orizondo, R.; López, G. Optimal location and dimensioning of capacitors in microgrids using a multicriteria decision algorithm. Heliyon 2021, 7, e08061. [Google Scholar] [CrossRef] [PubMed]
- Madruga, E.P.; Canha, L.N. Allocation and integrated configuration of capacitor banks and voltage regulators considering multi-objective variables in smart grid distribution system. In Proceedings of the 2010 9th IEEE/IAS International Conference on Industry Applications—INDUSCON 2010, Sao Paulo, Brazil, 8–10 November 2010. [Google Scholar] [CrossRef]
- Pareja, L.A.G.; Lezama, J.M.L.; Carmona, O.G. Optimal Placement of Capacitors, Voltage Regulators, and Distributed Generators in Electric Power Distribution Systems. Ingeniería 2020, 25, 334–354. [Google Scholar] [CrossRef]
- Mishra, S.; Das, D.; Paul, S. A comprehensive review on power distribution network reconfiguration. Energy Syst. 2016, 8, 227–284. [Google Scholar] [CrossRef]
- Dhivya, S.; Arul, R. Demand Side Management Studies on Distributed Energy Resources: A Survey. Trans. Energy Syst. Eng. Appl. 2021, 2, 17–31. [Google Scholar] [CrossRef]
- Valencia, A.; Hincapie, R.A.; Gallego, R.A. Optimal location, selection, and operation of battery energy storage systems and renewable distributed generation in medium–low voltage distribution networks. J. Energy Storage 2021, 34, 102158. [Google Scholar] [CrossRef]
- Sirjani, R.; Jordehi, A.R. Optimal placement and sizing of distribution static compensator (D-STATCOM) in electric distribution networks: A review. Renew. Sustain. Energy Rev. 2017, 77, 688–694. [Google Scholar] [CrossRef]
- Tamilselvan, V.; Jayabarathi, T.; Raghunathan, T.; Yang, X.S. Optimal capacitor placement in radial distribution systems using flower pollination algorithm. Alex. Eng. J. 2018, 57, 2775–2786. [Google Scholar] [CrossRef]
- Gil-González, W.; Montoya, O.D.; Rajagopalan, A.; Grisales-Noreña, L.F.; Hernández, J.C. Optimal Selection and Location of Fixed-Step Capacitor Banks in Distribution Networks Using a Discrete Version of the Vortex Search Algorithm. Energies 2020, 13, 4914. [Google Scholar] [CrossRef]
- Griot, S.; Moreau, A. Vacuum circuit breakers electrical life for shunt capacitor switching. In Proceedings of the 24th ISDEIV 2010, Braunschweig, Germany, 30 August–3 September 2010. [Google Scholar] [CrossRef]
- Velásquez, R.M.A.; Lara, J.V.M. Reliability, availability and maintainability study for failure analysis in series capacitor bank. Eng. Fail. Anal. 2018, 86, 158–167. [Google Scholar] [CrossRef]
- Benson, H.Y.; Sağlam, Ü. Mixed-Integer Second-Order Cone Programming: A Survey. In Theory Driven by Influential Applications; INFORMS: Catonsville, MD, USA, 2013; pp. 13–36. [Google Scholar] [CrossRef] [Green Version]
- Abdelaziz, A.Y.; Ali, E.S.; Elazim, S.M.A. Flower Pollination Algorithm for Optimal Capacitor Placement and Sizing in Distribution Systems. Electr. Power Components Syst. 2016, 44, 544–555. [Google Scholar] [CrossRef]
- Abril, I.P. Capacitors placement in distribution systems with nonlinear load by using the variables’ inclusion and interchange algorithm. Dyna 2021, 88, 13–22. [Google Scholar] [CrossRef]
- Augugliaro, A.; Dusonchet, L.; Favuzza, S.; Ippolito, M.G.; Mangione, S.; Sanseverino, E.R. A Modified Genetic Algorithm for Optimal Allocation of Capacitor Banks in MV Distribution Networks. Intell. Ind. Syst. 2015, 1, 201–212. [Google Scholar] [CrossRef] [Green Version]
- El-Fergany, A.A.; Abdelaziz, A.Y. Capacitor placement for net saving maximization and system stability enhancement in distribution networks using artificial bee colony-based approach. Int. J. Electr. Power Energy Syst. 2014, 54, 235–243. [Google Scholar] [CrossRef]
- Prakash, K.; Sydulu, M. Particle Swarm Optimization Based Capacitor Placement on Radial Distribution Systems. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007. [Google Scholar] [CrossRef]
- Ogita, Y.; Mori, H. Parallel Dual Tabu Search for Capacitor Placement in Smart Grids. Procedia Comput. Sci. 2012, 12, 307–313. [Google Scholar] [CrossRef] [Green Version]
- Shuaib, Y.M.; Kalavathi, M.S.; Rajan, C.C.A. Optimal capacitor placement in radial distribution system using Gravitational Search Algorithm. Int. J. Electr. Power Energy Syst. 2015, 64, 384–397. [Google Scholar] [CrossRef]
- Devabalaji, K.; Yuvaraj, T.; Ravi, K. An efficient method for solving the optimal sitting and sizing problem of capacitor banks based on cuckoo search algorithm. Ain Shams Eng. J. 2018, 9, 589–597. [Google Scholar] [CrossRef] [Green Version]
- Heliodore, F.; Nakib, A.; Ismail, B.; Ouchraa, S.; Schmitt, L. Performance Evaluation of Metaheuristics. In Metaheuristics for Intelligent Electrical Networks; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2017; pp. 43–58. [Google Scholar] [CrossRef]
- Rocktäschel, S. A basic Branch-and-Bound algorithm for (MOMICP). In A Branch-and-Bound Algorithm for Multiobjective Mixed-integer Convex Optimization; Springer Fachmedien Wiesbaden: Berlin/Heidelberg, Germany, 2020; pp. 17–39. [Google Scholar] [CrossRef]
- Borchers, B.; Mitchell, J.E. An improved branch and bound algorithm for mixed integer nonlinear programs. Comput. Oper. Res. 1994, 21, 359–367. [Google Scholar] [CrossRef]
- YUAN, Z.; Hesamzadeh, M.R. Second-order cone AC optimal power flow: Convex relaxations and feasible solutions. J. Mod Power Syst. Clean Energy 2018, 7, 268–280. [Google Scholar] [CrossRef] [Green Version]
- Kaur, S.; Kumbhar, G.; Sharma, J. A MINLP technique for optimal placement of multiple DG units in distribution systems. Int. J. Electr. Power Energy Syst. 2014, 63, 609–617. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, A.; Kansal, S. To Improve the Voltage Profile of Distribution System with the Optimal Placement of Capacitor. Indian J. Sci. Technol. 2017, 10, 1–7. [Google Scholar] [CrossRef]
- Molina-Martin, F.; Montoya, O.D.; Grisales-Noreña, L.F.; Hernández, J.C. A Mixed-Integer Conic Formulation for Optimal Placement and Dimensioning of DGs in DC Distribution Networks. Electronics 2021, 10, 176. [Google Scholar] [CrossRef]
- Garces, A.; Gil-González, W.; Montoya, O.D.; Chamorro, H.R.; Alvarado-Barrios, L. A Mixed-Integer Quadratic Formulation of the Phase-Balancing Problem in Residential Microgrids. Appl. Sci. 2021, 11, 1972. [Google Scholar] [CrossRef]
- Alizadeh, F.; Goldfarb, D. Second-order cone programming. Math. Program. 2003, 95, 3–51. [Google Scholar] [CrossRef]
- Karmarkar, N. A new polynomial-time algorithm for linear programming. Combinatorica 1984, 4, 373–395. [Google Scholar] [CrossRef]
- Atamtürk, A.; Gómez, A. Submodularity in Conic Quadratic Mixed Optimization. Oper. Res. 2020. [Google Scholar] [CrossRef] [Green Version]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming, Version 2.1. 2014. Available online: http://cvxr.com/cvx (accessed on 3 July 2021).
- Abul’Wafa, A.R. Optimal capacitor allocation in radial distribution systems for loss reduction: A two stage method. Electr. Power Syst. Res. 2013, 95, 168–174. [Google Scholar] [CrossRef]
- Abul’Wafa, A.R. Optimal capacitor placement for enhancing voltage stability in distribution systems using analytical algorithm and Fuzzy-Real Coded GA. Int. J. Electr. Power Energy Syst. 2014, 55, 246–252. [Google Scholar] [CrossRef]
- Sultana, S.; Roy, P.K. Optimal capacitor placement in radial distribution systems using teaching learning based optimization. Int. J. Electr. Power Energy Syst. 2014, 54, 387–398. [Google Scholar] [CrossRef]
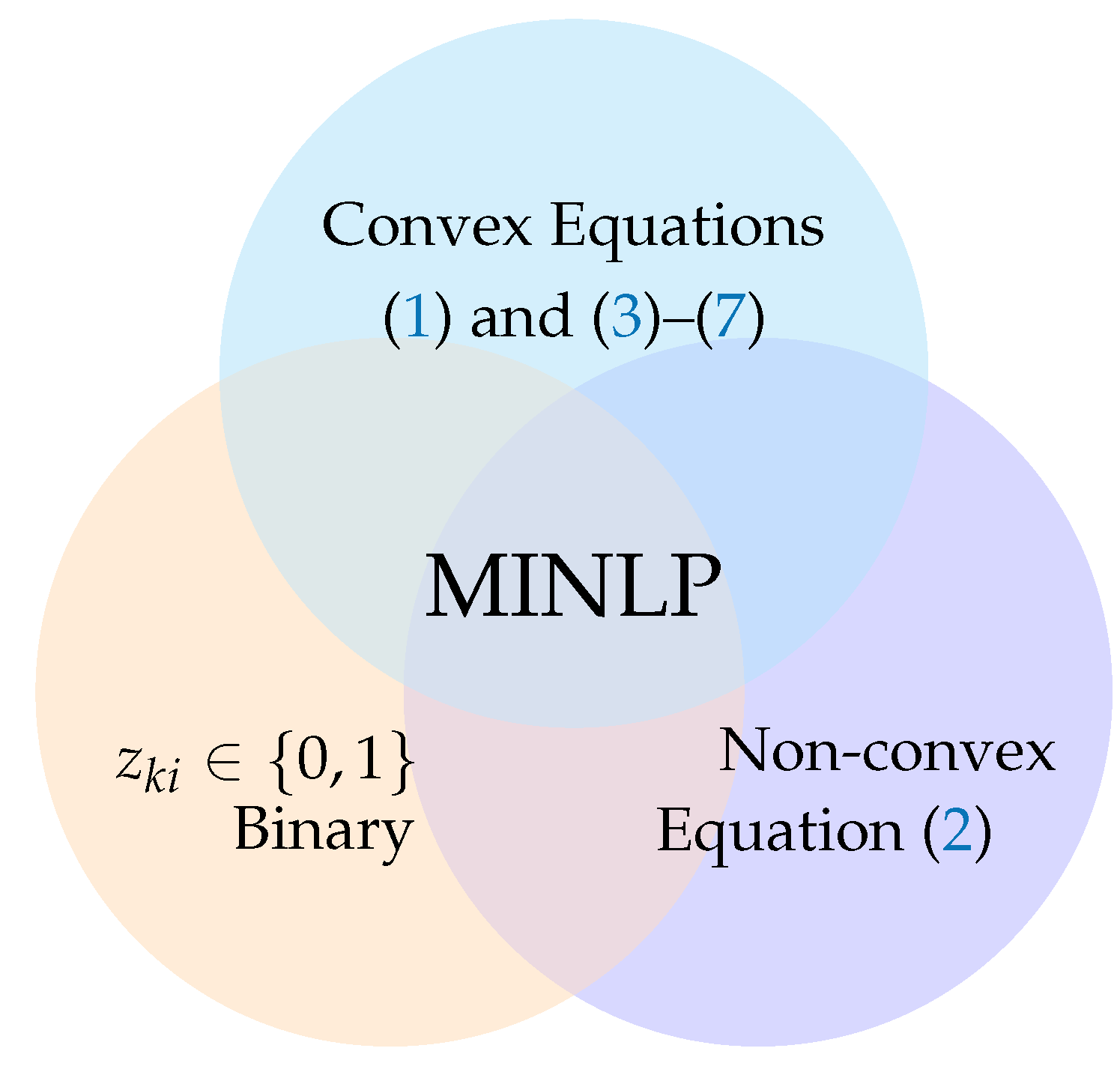
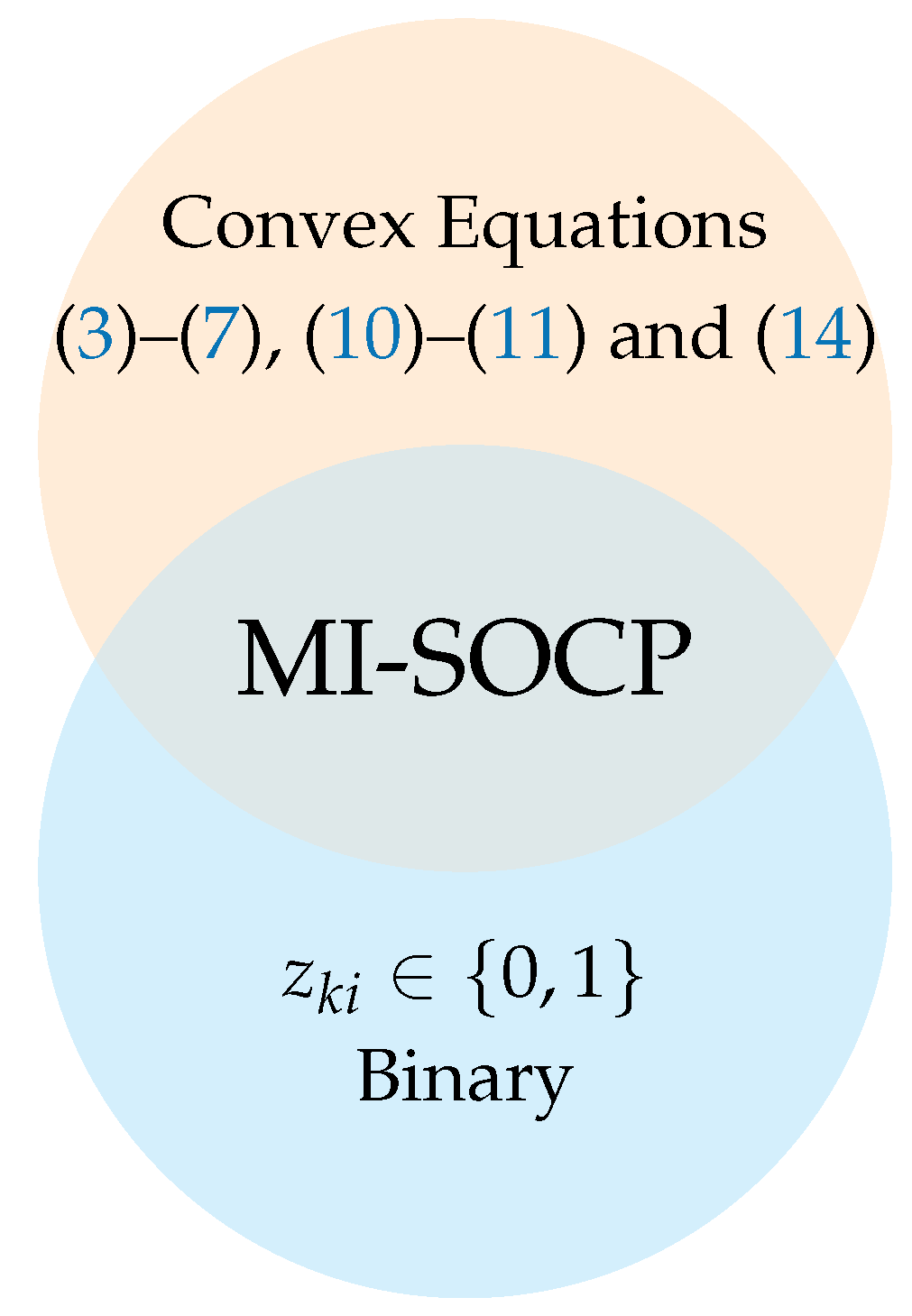


| Node i | Node j | () | () | (kW) | (kvar) | Node i | Node j | () | () | (kW) | (kvar) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 0.0922 | 0.0477 | 100 | 60 | 17 | 18 | 0.7320 | 0.5740 | 90 | 40 |
| 2 | 3 | 0.4930 | 0.2511 | 90 | 40 | 2 | 19 | 0.1640 | 0.1565 | 90 | 40 |
| 3 | 4 | 0.3660 | 0.1864 | 120 | 80 | 19 | 20 | 1.5042 | 1.3554 | 90 | 40 |
| 4 | 5 | 0.3811 | 0.1941 | 60 | 30 | 20 | 21 | 0.4095 | 0.4784 | 90 | 40 |
| 5 | 6 | 0.8190 | 0.7070 | 60 | 20 | 21 | 22 | 0.7089 | 0.9373 | 90 | 40 |
| 6 | 7 | 0.1872 | 0.6188 | 200 | 100 | 3 | 23 | 0.4512 | 0.3083 | 90 | 50 |
| 7 | 8 | 1.7114 | 1.2351 | 200 | 100 | 23 | 24 | 0.8980 | 0.7091 | 420 | 200 |
| 8 | 9 | 1.0300 | 0.7400 | 60 | 20 | 24 | 25 | 0.8960 | 0.7011 | 420 | 200 |
| 9 | 10 | 1.0400 | 0.7400 | 60 | 20 | 6 | 26 | 0.2030 | 0.1034 | 60 | 25 |
| 10 | 11 | 0.1966 | 0.0650 | 45 | 30 | 26 | 27 | 0.2842 | 0.1447 | 60 | 25 |
| 11 | 12 | 0.3744 | 0.1238 | 60 | 35 | 27 | 28 | 1.0590 | 0.9337 | 60 | 20 |
| 12 | 13 | 1.4680 | 1.1550 | 60 | 35 | 28 | 29 | 0.8042 | 0.7006 | 120 | 70 |
| 13 | 14 | 0.5416 | 0.7129 | 120 | 80 | 29 | 30 | 0.5075 | 0.2585 | 200 | 600 |
| 14 | 15 | 0.5910 | 0.5260 | 60 | 10 | 30 | 31 | 0.9744 | 0.9630 | 150 | 70 |
| 15 | 16 | 0.7463 | 0.5450 | 60 | 20 | 31 | 32 | 0.3105 | 0.3619 | 210 | 100 |
| 16 | 17 | 1.2860 | 1.7210 | 60 | 20 | 32 | 33 | 0.3410 | 0.5302 | 60 | 40 |
| Node i | Node j | () | () | (kW) | (kvar) | Node i | Node j | () | () | (kW) | (kvar) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 0.0005 | 0.0012 | 0 | 0 | 3 | 36 | 0.0044 | 0.0108 | 26 | 18.55 |
| 2 | 3 | 0.0005 | 0.0012 | 0 | 0 | 36 | 37 | 0.0640 | 0.1565 | 26 | 18.55 |
| 3 | 4 | 0.0015 | 0.0036 | 0 | 0 | 37 | 38 | 0.1053 | 0.1230 | 0 | 0 |
| 4 | 5 | 0.0251 | 0.0294 | 0 | 0 | 38 | 39 | 0.0304 | 0.0355 | 24 | 17 |
| 5 | 6 | 0.3660 | 0.1864 | 2.6 | 2.2 | 39 | 40 | 0.0018 | 0.0021 | 24 | 17 |
| 6 | 7 | 0.3810 | 0.1941 | 40.4 | 30 | 40 | 41 | 0.7283 | 0.8509 | 1.2 | 1 |
| 7 | 8 | 0.0922 | 0.0470 | 75 | 54 | 41 | 42 | 0.3100 | 0.3623 | 0 | 0 |
| 8 | 9 | 0.0493 | 0.0251 | 30 | 22 | 42 | 43 | 0.0410 | 0.0475 | 6 | 4.3 |
| 9 | 10 | 0.8190 | 0.2707 | 28 | 19 | 43 | 44 | 0.0092 | 0.0116 | 0 | 0 |
| 10 | 11 | 0.1872 | 0.0619 | 145 | 104 | 44 | 45 | 0.1089 | 0.1373 | 39.22 | 26.3 |
| 11 | 12 | 0.7114 | 0.2351 | 145 | 104 | 45 | 46 | 0.0009 | 0.0012 | 39.22 | 26.3 |
| 12 | 13 | 1.0300 | 0.3400 | 8 | 5 | 4 | 47 | 0.0034 | 0.0084 | 0 | 0 |
| 13 | 14 | 1.0440 | 0.3450 | 8 | 5.5 | 47 | 48 | 0.0851 | 0.2083 | 79 | 56.4 |
| 14 | 15 | 1.0580 | 0.3496 | 0 | 0 | 48 | 49 | 0.2898 | 0.7091 | 384.7 | 274.5 |
| 15 | 16 | 0.1966 | 0.0650 | 45.5 | 30 | 49 | 50 | 0.0822 | 0.2011 | 384.7 | 274.5 |
| 16 | 17 | 0.3744 | 0.1238 | 60 | 35 | 8 | 51 | 0.0928 | 0.0473 | 40.5 | 28.3 |
| 17 | 18 | 0.0047 | 0.0016 | 60 | 35 | 51 | 52 | 0.3319 | 0.1114 | 3.6 | 2.7 |
| 18 | 19 | 0.3276 | 0.1083 | 0 | 0 | 9 | 53 | 0.1740 | 0.0886 | 4.35 | 3.5 |
| 19 | 20 | 0.2106 | 0.0690 | 1 | 0.6 | 53 | 54 | 0.2030 | 0.1034 | 26.4 | 19 |
| 20 | 21 | 0.3416 | 0.1129 | 114 | 81 | 54 | 55 | 0.2842 | 0.1447 | 24 | 17.2 |
| 21 | 22 | 0.0140 | 0.0046 | 5 | 3.5 | 55 | 56 | 0.2813 | 0.1433 | 0 | 0 |
| 22 | 23 | 0.1591 | 0.0526 | 0 | 0 | 56 | 57 | 1.5900 | 0.5337 | 0 | 0 |
| 23 | 24 | 0.3460 | 0.1145 | 28 | 20 | 57 | 58 | 0.7837 | 0.2630 | 0 | 0 |
| 24 | 25 | 0.7488 | 0.2475 | 0 | 0 | 58 | 59 | 0.3042 | 0.1006 | 100 | 72 |
| 25 | 26 | 0.3089 | 0.1021 | 14 | 10 | 59 | 60 | 0.3861 | 0.1172 | 0 | 0 |
| 26 | 27 | 0.1732 | 0.0572 | 14 | 10 | 60 | 61 | 0.5075 | 0.2585 | 1244 | 888 |
| 3 | 28 | 0.0044 | 0.0108 | 26 | 18.6 | 61 | 62 | 0.0974 | 0.0496 | 32 | 23 |
| 28 | 29 | 0.0640 | 0.1565 | 26 | 18.6 | 62 | 63 | 0.1450 | 0.0738 | 0 | 0 |
| 29 | 30 | 0.3978 | 0.1315 | 0 | 0 | 63 | 64 | 0.7105 | 0.3619 | 227 | 162 |
| 30 | 31 | 0.0702 | 0.0232 | 0 | 0 | 64 | 65 | 1.0410 | 0.5302 | 59 | 42 |
| 31 | 32 | 0.3510 | 0.1160 | 0 | 0 | 11 | 66 | 0.2012 | 0.0611 | 18 | 13 |
| 32 | 33 | 0.8390 | 0.2816 | 14 | 10 | 66 | 67 | 0.0047 | 0.0014 | 18 | 13 |
| 33 | 34 | 1.7080 | 0.5646 | 19.5 | 14 | 12 | 68 | 0.7394 | 0.2444 | 28 | 20 |
| 34 | 35 | 1.4740 | 0.4873 | 6 | 4 | 68 | 69 | 0.0047 | 0.0016 | 28 | 20 |
| Method | Nodes | Size [kvar] | Total Losses [kW] |
|---|---|---|---|
| Base case | - | - | 210.987 |
| GSA [24] | 171.780 | ||
| TSM [38] | 144.040 | ||
| FRCGA [39] | 141.240 | ||
| FPA [13] | 139.075 | ||
| MI-SOCP | 138.416 |
| Method | Nodes | Size [kvar] | Losses [kW] |
|---|---|---|---|
| Base case | - | - | 225.072 |
| GSA [24] | 163.280 | ||
| TSM [38] | 148.910 | ||
| TBLO [40] | 146.350 | ||
| FPA [13] | 145.860 | ||
| MI-SOCP | 145.397 |
| Option | (kvar) | Cost ($/kvar-Year) | Option | (kvar) | Cost ($/kvar-Year) |
|---|---|---|---|---|---|
| 1 | 150 | 0.500 | 8 | 1200 | 0.170 |
| 2 | 300 | 0.350 | 9 | 1350 | 0.207 |
| 3 | 450 | 0.253 | 10 | 1500 | 0.201 |
| 4 | 600 | 0.220 | 11 | 1650 | 0.193 |
| 5 | 750 | 0.276 | 12 | 1800 | 0.870 |
| 6 | 900 | 0.183 | 13 | 1950 | 0.211 |
| 7 | 1050 | 0.228 | 14 | 2100 | 0.176 |
| Method | Size (Node) (Mvar) | Losses (kW) | C. Caps. US$ | C. Total US$ |
|---|---|---|---|---|
| IEEE 33-bus system | ||||
| GAMS | {0.30(14),0.45(24),1.05(30)} | 139.292 | 458.25 | 23,859.313 |
| CBGA | {0.45(12),0.45(24),1.05(30)} | 138.416 | 467.10 | 23,721.108 |
| MI-SOCP | {0.45(12),0.45(24),1.05(30)} | 138.416 | 467.10 | 23,721.108 |
| IEEE 69-bus system | ||||
| GAMS | {0.45(11),0.15(27),1.20(61)} | 145.738 | 392.85 | 24,876.910 |
| CBGA | {0.45(12),0.15(22),1.20(61)} | 145.521 | 392.85 | 24,840.347 |
| MI-SOCP | {0.45(12),0.15(21),1.20(61)} | 145.520 | 392.85 | 24.840.189 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montoya, O.D.; Gil-González, W.; Garcés, A. On the Conic Convex Approximation to Locate and Size Fixed-Step Capacitor Banks in Distribution Networks. Computation 2022, 10, 32. https://doi.org/10.3390/computation10020032
Montoya OD, Gil-González W, Garcés A. On the Conic Convex Approximation to Locate and Size Fixed-Step Capacitor Banks in Distribution Networks. Computation. 2022; 10(2):32. https://doi.org/10.3390/computation10020032
Chicago/Turabian StyleMontoya, Oscar Danilo, Walter Gil-González, and Alejandro Garcés. 2022. "On the Conic Convex Approximation to Locate and Size Fixed-Step Capacitor Banks in Distribution Networks" Computation 10, no. 2: 32. https://doi.org/10.3390/computation10020032
APA StyleMontoya, O. D., Gil-González, W., & Garcés, A. (2022). On the Conic Convex Approximation to Locate and Size Fixed-Step Capacitor Banks in Distribution Networks. Computation, 10(2), 32. https://doi.org/10.3390/computation10020032








