Length-Gauge Optical Matrix Elements in WIEN2k

Abstract

Hybrid exchange-correlation functionals provide superior electronic structure and optical properties of semiconductors or insulators as compared to semilocal exchange-correlation potentials due to admixing a portion of the non-local exact exchange potential from a Hartree–Fock theory. Since the non-local potential does not commute with the position operator, the momentum matrix elements do not fully capture the oscillator strength, while the length-gauge velocity matrix elements do. So far, length-gauge velocity matrix elements were not accessible in the all-electron full-potential WIEN2k package. We demonstrate the feasibility of computing length-gauge matrix elements in WIEN2k for a hybrid exchange-correlation functional based on a finite difference approach. To illustrate the implementation we determined matrix elements for optical transitions between the conduction and valence bands in GaAs, GaN, (CH${}_3$NH${}_3$)PbI${}_3$ and a monolayer MoS${}_2$. The non-locality of the Hartree–Fock exact exchange potential leads to a strong enhancement of the oscillator strength as noticed recently in calculations employing pseudopotentials (Laurien and Rubel: arXiv:2111.14772 (2021)). We obtained an analytical expression for the enhancement factor for the difference in eigenvalues not captured by the kinetic energy. It is expected that these results can also be extended to other non-local potentials, e.g., a many-body $GW$ approximation.

1. Introduction

Calculations of linear optical properties of solids require matrix elements for electric dipole transitions. Momentum matrix elements

$${\mathbf{p}}_{mn}\left(\mathbf{k}\right)=⟨m,\mathbf{k}|-i{\nabla }_{\mathbf{r}}|n,\mathbf{k}⟩$$

(1)

are widely used in full-potential codes with periodic boundary conditions [1] when optical properties are computed with local potentials (e.g., LDA (see end of the paper for the full list of abbreviations) or GGA XC functionals) and referred to in the literature as a velocity gauges. (Atomic units will be used throughout the paper.)

Starace [2] emphasised the limitations of Equation (1) when representing matrix elements for electric dipole transitions. Instead, the more general velocity matrix elements should be used

$${\mathbf{v}}_{mn}\left(\mathbf{k}\right)=⟨m,\mathbf{k}|i[\widehat{H},\mathbf{r}]|n,\mathbf{k}⟩$$

(2)

with the velocity operator [2]

$$\widehat{\mathbf{v}}=i[\widehat{H},\mathbf{r}]=\widehat{\mathbf{p}}+i[{\widehat{V}}_{\mathrm{NL}}(\mathbf{r},{\mathbf{r}}^{\prime }),\mathbf{r}],$$

(3)

which contains an additional commutator term $[{\widehat{V}}_{\mathrm{NL}}(\mathbf{r},{\mathbf{r}}^{\prime }),\mathbf{r}]$ to account for non-local potentials (e.g., the Hartree-Fock exchange in hybrid XC functionals). With $|n,\mathbf{k}⟩$ and $E_n\left(\mathbf{k}\right)$ being eigenstates of the Hamiltonian $\widehat{H}$, the alternative (length gauge) matrix elements can be expressed as [2]

$$⟨m,\mathbf{k}|i[\widehat{H},\mathbf{r}]|n,\mathbf{k}⟩=i[E_m\left(\mathbf{k}\right)-E_n\left(\mathbf{k}\right)]⟨m,\mathbf{k}\left|\mathbf{r}\right|n,\mathbf{k}⟩.$$

(4)

Since the position operator is not well defined for periodic systems, the following substitution is used instead: [3,4]

$$\mathbf{r}=\underset{q\to 0}{lim}(e^{iq\mathbf{r}}-1)/iq,$$

(5)

which leads to a practical expression for the velocity matrix elements in the long wavelength limit [5,6]

$$v_{mn}^{\left(\alpha \right)}\left(\mathbf{k}\right)=\underset{q\to 0}{lim}\frac{1}{q}⟨m,\mathbf{k}+{\mathbf{q}}_{\alpha }|{\mathrm{e}}^{i{\mathbf{q}}_{\alpha }·\mathbf{r}}|n,\mathbf{k}⟩[E_m(\mathbf{k}+{\mathbf{q}}_{\alpha })-E_n\left(\mathbf{k}\right)].$$

(6)

Here, $\alpha =x,y,z$ is a Cartesian direction, m and n are band indices, and ${\mathbf{q}}_x=q\widehat{\mathbf{x}}$, where $\widehat{\mathbf{x}}$ is a unit vector in the direction of the x axis.

WIEN2k [7,8] is one of the most used full-potential all-electron DFT codes for solids. It offers many XC functionals to open the band gap, including hybrids with a non-local Hartree-Fock potential [9]. So far, however, WIEN2k has implemented only momentum matrix elements to compute optical properties as a part of the optic module [1]. Laurien and Rubel [10] showed that neglecting the second term in Equation (3) when using hybrid functionals can lead to an underestimation of the squared magnitude of matrix elements for electric dipole transitions between conduction and valence band edges by ca. 30%.

Here, we present a scheme for the calculation of the length-gauge optical matrix elements in WIEN2k based on a finite difference Equation (6) with the help of overlap matrix elements

$$M_{mn}(\mathbf{k},\mathbf{q})=⟨u_{\mathbf{k},n}|u_{\mathbf{k}+\mathbf{q},m}⟩\equiv ⟨{\psi }_{\mathbf{k},n}|{\mathrm{e}}^{-i\mathbf{q}·\mathbf{r}}|{\psi }_{\mathbf{k}+\mathbf{q},m}⟩$$

(7)

that come from the wien2wannier module [11]. This development opens an avenue for the calculation of optical properties (frequency-dependent dielectric tensor, absorption spectrum, optical conductivity, refractive index, reflectively, loss function) in the independent particle approximation with hybrid functionals in WIEN2k.

2. Methods

DFT [12,13] calculations were performed with the WIEN2k package (version 21.1) and the Yukawa screened hybrid (YSH) functional [9]. It was shown that by choosing an appropriate screening length $\lambda$ in the Yukawa potential the YSH functional gives very similar results as the common HSE06 XC functional [14,15]. Important parameters are summarized in Table 1. Experimental structural parameters were used for all solids (Figure 1) with internal atomic positions optimized at the PBE level when permitted by symmetry. Spin-orbit coupling (SOC) was included in all calculations. The structure of (CH${}_3$NH${}_3$)PbI${}_3$ was represented by a pseudo-cubic cell taken from Ref. [16], scaled to experimental lattice parameters at 350 K [17,18], followed by a subsequent relaxation of atomic positions while retaining the experimental lattice parameters. The pseudo-cubic structure means that the following constrains $a=b=c$, $\alpha =\beta =\gamma ={90}^{°}$ are applied to lattice parameters, while the formal symmetry of the structure (spacegroup P1) is not cubic.

Table 1. Structural and calculation parameters.

Parameters	GaAs	GaN	(CH${}_3$NH${}_3$)PbI${}_3$	1L-MoS${}_2$
Space group	F$\overline{4}$3m (216)	P6${}_3$mc (186)	P1 (1)	P$\overline{6}$m2 (187)
Lattice param. (Å)	5.653 [19]	3.18, 5.166 [20]	6.31 [17,18]	3.16 [21], 29.0
			(pseudo-cubic)
$R_{\mathrm{MT}}$ (bohr)	2.23 (Ga)	1.90 (Ga)	0.68 (H)	2.36 (Mo)
	2.23 (As)	1.64 (N)	1.34 (C)	2.03 (S)
			1.26 (N)
			2.50 (Pb)
			2.50 (I)
$n_{\mathrm{val}}$	13 (Ga)	19 (Ga)	4 (C)	14 (Mo)
	15 (As)	5 (N)	5 (N)	6 (S)
			18 (Pb)
			17 (I)
$R_{{\mathrm{MT}}_{\min }}{K}_{\max }$	8.0	8.0	3.0	8.0
$G_{\max }$	12	12	20	12
$l_{\max }$	10 (all structures)
$l_{{\mathrm{vns}}_{\max }}$	6 (all structures)
k mesh	$8\times 8\times 8$	$8\times 8\times 4$	$3\times 3\times 3$	$9\times 9\times 1$
	($\mathsf{\Gamma }$ centered)	($\mathsf{\Gamma }$ centered)	(shifted)	($\mathsf{\Gamma }$ centered)
Energy (Ry) and	${10}^{-4}$ (all structures)
charge converg.	${10}^{-3}$ (all structures)

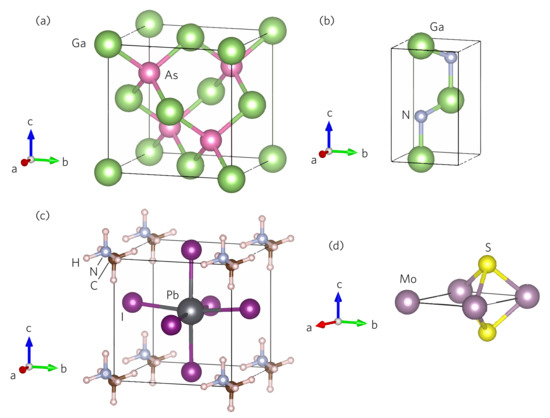
Figure 1. Crystal structures: (a) GaAs, (b) GaN, (c) quasi-cubic (CH${}_3$NH${}_3$)PbI${}_3$, and (d) monolayer MoS${}_2$.

Velocity-gauge optical matrix elements ${\mathbf{p}}_{mn}\left(\mathbf{k}\right)$ were calculated using the optic module [1] in WIEN2k. Length-gauge optical matrix elements ${\mathbf{v}}_{mn}\left(\mathbf{k}\right)$ were obtained with the forward

$$v_{mn}^{\left(\alpha \right)}\left(\mathbf{k}\right)\approx \frac{1}{q}⟨u_{\mathbf{k},n}|u_{\mathbf{k}+{\mathbf{q}}_{\alpha },m}⟩[E_m(\mathbf{k}+{\mathbf{q}}_{\alpha })-E_n\left(\mathbf{k}\right)]$$

(8)

and central

$$v_{mn}^{\left(\alpha \right)}\left(\mathbf{k}\right)\approx \frac{1}{q}⟨u_{\mathbf{k}-\frac{1}{2}{\mathbf{q}}_{\alpha },n}|u_{\mathbf{k}+\frac{1}{2}{\mathbf{q}}_{\alpha },m}⟩[E_m(\mathbf{k}+\frac{1}{2}{\mathbf{q}}_{\alpha })-E_n(\mathbf{k}-\frac{1}{2}{\mathbf{q}}_{\alpha })]$$

(9)

finite difference method. The overlap matrix elements $⟨u_{\mathbf{k},n}|u_{{\mathbf{k}}^{\prime },m}⟩$ between the cell-periodic parts of the Bloch functions were generated by the wien2wannier module [11] (case.mmn output file). The length-gauge optical matrix elements for GaAs computed with YSH were additionally verified using VASP [22], HSE06 and projector augmented-wave potentials [22,23,24]. Sample scripts that illustrate a detailed workflow can be found in the Supporting Information section.

The logarithmic percent change

$$\mathsf{\Delta }=ln\left(\frac{\sum |v_{mn}^{\left(\alpha \right)}{|}^2}{\sum |p_{mn}^{\left(\alpha \right)}{|}^2}\right)100\%$$

(10)

was used to evaluate differences between matrix elements. This approach has the following advantages: (i) does not require a reference, (ii) is more suitable for large changes (greater than a few percents), (iii) it has additive properties, and (iv) in the limit of small changes it reduces to the classical ratio of the relative change to the reference.

3. Results

3.1. Finite Difference Calibration and Validation for Local XC

We selected GaAs and the local PBE XC potential [25] to prove the feasibility of computing the length-gauge optical matrix elements using the finite difference methods given by Equations (8) and (9). The local potential is selected here since both the length- and velocity-gauge should lead to identical results under these circumstances. It is also important to get a feeling for the step size q at which the finite difference approximation converges to the accurate result given by the momentum matrix element. Here GaAs serves as an important benchmark since the conduction band and light holes are very sharp and non-parabolic (see Figure 2a).

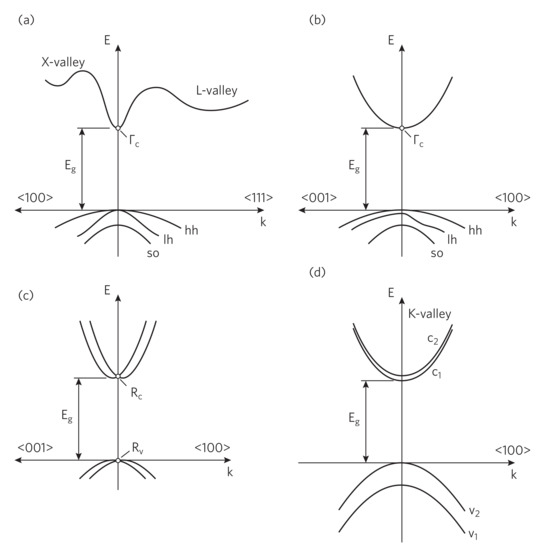
Figure 2. Schematic band structures of materials studied with SOC: (a) GaAs, (b) GaN, (c) quasi-cubic (CH${}_3$NH${}_3$)PbI${}_3$, and (d) monolayer MoS${}_2$. The band indices ‘c’, ‘hh’, ‘lh’, and ‘so’ stand for conduction, valence heavy-hole, light-hole, and split-off bands, respectively. The scale of band splittings is exaggerated.

Results presented in Table 2 suggest that both, the forward and the central finite differences reproduce the values of the momentum matrix element within a 3% error. The central finite difference converges faster (at the wave vector shift of $q\approx 0.003$ rad bohr${}^{-1}$) and will be used to derive matrix elements for the remaining part of this paper. The numerical noise of the finite difference starts to show up at $q<{10}^{-6}$ rad bohr${}^{-1}$.

Table 2. Length-gauge velocity matrix elements $|v_{mn}^{\left(x\right)}{|}^2$ (at.u.) in GaAs calculated using the finite difference approximations (forward vs. central) Equations (8) and (9) with various step sizes q. These values are compared with the velocity-gauge momentum matrix elements $|p_{mn}^{\left(x\right)}{|}^2$ (at.u.) from the optic module. The local (GGA-PBE) XC functional wa used, which made the velocity and the length gauges identical. The band degeneracy is given as a superscript in parentheses and the meaning of the subscripts is made clear in Figure 2a.

Transition	$\sum |{\mathit{v}}_{\mathit{m}\mathit{n}}^{\left(\mathit{x}\right)}{|}^2$		$\sum |{\mathit{p}}_{\mathit{m}\mathit{n}}^{\left(\mathit{x}\right)}{|}^2$
	$(\mathit{q}=(\mathbf{16}.\mathbf{0}/\mathbf{3}.\mathbf{5}/\mathbf{1}.\mathbf{2}/\mathbf{0}.\mathbf{0006})\times {\mathbf{10}}^{-\mathbf{3}}{\mathbf{rad}\mathbf{bohr}}^{-\mathbf{1}})$
	Forward FD	Central FD
${\mathsf{\Gamma }}_{lh,hh}^{(\times 4)}-{\mathsf{\Gamma }}_c^{(\times 2)}$	0.264/0.402/0.420/0.402	0.412/0.422/0.422/0.402	0.417
${\mathsf{\Gamma }}_{so}^{(\times 2)}-{\mathsf{\Gamma }}_c^{(\times 2)}$	0.217/0.202/0.200/0.221	0.209/0.201/0.200/0.221	0.206

3.2. Validation for Non-Local XC

After validating our approach with the local potential, we applied it to the non-local YSH XC functional. Again we evaluated the velocity-gauge (momentum) matrix elements and length-gauge (velocity) matrix elements in GaAs. Now we did not expect the two matrix elements to agree given the arguments presented in Section 1. To cross-check our results, we also computed the velocity matrix elements with VASP, which should be comparable with our $v_{mn}^{\left(\alpha \right)}$ values.

Our YSH calculations for GaAs gave a band gap of $E_{\mathrm{g}}^{\mathrm{YSH}}=1.24$ eV vs $E_{\mathrm{g}}^{\exp }=1.52$ eV [26] and previously reported $E_{\mathrm{g}}^{\mathrm{HSE}06}=1.33$ eV [27], which was a significant improvement over PBE. The band structure is shown schematically in Figure 2a where bands are labeled according to the convention. The results presented in Table 3 confirmed the agreement between WIEN2k and VASP for length-gauge matrix elements within less than a 2% deviation. The total length-gauge oscillator strength between valence and conduction band corresponded to $m_0\sum {\left|v_{cv}^{\left(x\right)}\right|}^2\approx 21$ eV, which agreed well with the 20 eV quoted by (Yu and Cardona [28], Section 2.6) for III-V semiconductors. The momentum (velocity-gauge) matrix elements significantly underestimated the strength of optical transitions, which had previously been reported and quantified in Ref. [10]. The values of $|p_{cv}{|}^2$ were almost identical to those obtained with PBE (Table 2), even though the momentum matrix elements were derived from YSH wave functions.

Table 3. Length-gauge $|v_{mn}^{\left(x\right)}{|}^2$ and velocity-gauge $|p_{mn}^{\left(x\right)}{|}^2$ matrix elements (at.u.) in GaAs calculated using WIEN2k (with YSH) and VASP (with HSE06). Due to the non-local potential the velocity and the length gauges are not identical. The band degeneracy is given as a superscript in parentheses and the subscripts are explained in Figure 2a. The logarithmic deviation between $\sum |p_{vc}^{\left(x\right)}{|}^2$ and $\sum |v_{vc}^{\left(x\right)}{|}^2$ is given in parentheses ($\mathsf{\Delta }$ as per Equation (10)).

Transition	$\sum |{\mathit{v}}_{\mathit{m}\mathit{n}}^{\left(\mathit{x}\right)}{|}^2$		$\sum |{\mathit{p}}_{\mathit{m}\mathit{n}}^{\left(\mathit{x}\right)}{|}^2$
	WIEN2k	VASP
${\mathsf{\Gamma }}_{lh,hh}^{(\times 4)}-{\mathsf{\Gamma }}_c^{(\times 2)}$	0.534	0.541	0.420
${\mathsf{\Gamma }}_{so}^{(\times 2)}-{\mathsf{\Gamma }}_c^{(\times 2)}$	0.255	0.256	0.208
Total	0.789 (+23%)	0.797	0.628

3.3. Illustrative Applications

In the previous subsection we showed that calculations of optical properties for GaAs with the non-local hybrid XC functional (YSH or HSE06) require length-gauge optical matrix elements. If the momentum matrix elements had been used instead, the strength of optical transitions would have been underestimated by 23%. Next, we showed that a similar enhancement of the strength of direct optical transitions was also observed in other semiconductors, such as GaN, (CH${}_3$NH${}_3$)PbI${}_3$, and monolayer MoS${}_2$. The corresponding band structures are shown schematically in Figure 2b–d.

The band gap of GaN is well reproduced with YSH: $E_{\mathrm{g}}^{\mathrm{YSH}}=3.19$ eV vs. $E_{\mathrm{g}}^{\exp }=3.30$ eV [29]. Compared to GaAs, the optical matrix elements in Table 4 showed an even larger disparity between the length-gauge velocity and the momentum matrix elements.

Table 4. Length-gauge $|v_{mn}^{\left(\alpha \right)}{|}^2$ and velocity-gauge $|p_{mn}^{\left(\alpha \right)}{|}^2$ matrix elements (at.u.) in GaN calculated using the YSH XC functional.

Transition	$\sum |{\mathit{v}}_{\mathit{m}\mathit{n}}^{\left(\mathit{x}\right)}{|}^2$	$\sum |{\mathit{v}}_{\mathit{m}\mathit{n}}^{\left(\mathit{z}\right)}{|}^2$	$\sum |{\mathit{p}}_{\mathit{m}\mathit{n}}^{\left(\mathit{x}\right)}{|}^2$	$\sum |{\mathit{p}}_{\mathit{m}\mathit{n}}^{\left(\mathit{z}\right)}{|}^2$
${\mathsf{\Gamma }}_{hh}^{(\times 2)}-{\mathsf{\Gamma }}_c^{(\times 2)}$	0.211	0	0.183	0
${\mathsf{\Gamma }}_{lh}^{(\times 2)}-{\mathsf{\Gamma }}_c^{(\times 2)}$	0.256	0.055	0.163	0.042
${\mathsf{\Gamma }}_{so}^{(\times 2)}-{\mathsf{\Gamma }}_c^{(\times 2)}$	0.026	0.507	0.018	0.377
Total	0.493 (+30%)	0.562 (+29%)	0.364	0.419

The monolayer MoS${}_2$ had a direct band gap at the $K=(1/3,1/3,1/3)$ point. Due to large excitonic effects [30], direct comparison of the YSH band gap $E_{\mathrm{g}}^{\mathrm{YSH}}=2.22$ eV with experiment was not possible. Thus, we used a many-body result $E_{\mathrm{g}}^{G_0{W}_0}=2.53$ eV [31,32] as a reference. Similarly to other materials, the monolayer MoS${}_2$ showed strong enhancement of the matrix elements (Table 5) with the YSH XC functional. Spin selection rules disabled half of the in-plane $v_{cv}^{\left(x\right)}$ matrix elements, while the out-of-plane matrix elements $v_{cv}^{\left(z\right)}$ were zero for transitions at the band edges due to symmetry arguments.

Table 5. Length-gauge $|v_{mn}^{\left(x\right)}{|}^2$ and velocity-gauge $|p_{mn}^{\left(x\right)}{|}^2$ matrix elements (at.u.) in monolayer MoS${}_2$ calculated using YSH XC functional.

Transition	$\sum |{\mathit{v}}_{\mathit{m}\mathit{n}}^{\left(\mathit{x}\right)}{|}^2$	$\sum |{\mathit{p}}_{\mathit{m}\mathit{n}}^{\left(\mathit{x}\right)}{|}^2$
$K_{v_1}-K_{c_1}$	0	0
$K_{v_2}-K_{c_1}$	0.107	0.075
$K_{v_1}-K_{c_2}$	0.106	0.074
$K_{v_2}-K_{c_2}$	0	0
Total	0.213 (+36%)	0.149

The pseudo-cubic (CH${}_3$NH${}_3$)PbI${}_3$ had a direct gap at $R=(1/2,1/2,1/2)$. The calculated band gap $E_{\mathrm{g}}^{\mathrm{YSH}}=1.03$ eV is an improvement relative to the PBE band gap (0.46 eV), but it is still far from the experimental 1.5–1.6 eV for the tetragonal phase [33,34]. This underestimation was due to the lack of stochastic thermal distortions of the PbI${}_6$ octahedra, which further opened the gap by ca. 0.5 eV at room temperature [35,36]. Table 6 captures the matrix elements and their anisotropy caused by the reduced (pseudo-cubic) symmetry of the unit cell. Among all materials studied here, this material showed the lowest enhancement of the velocity matrix elements compared to the momentum matrix elements.

Table 6. Length-gauge $|v_{mn}^{\left(\alpha \right)}{|}^2$ and velocity-gauge $|p_{mn}^{\left(\alpha \right)}{|}^2$ matrix elements (at.u.) in pseudo-cubic (CH${}_3$NH${}_3$)PbI${}_3$ calculated using the YSH XC functional.

Transition	$\sum |{\mathit{v}}_{\mathit{m}\mathit{n}}^{(\mathit{x},\mathit{y},\mathit{z})}{|}^2$	$\sum |{\mathit{p}}_{\mathit{m}\mathit{n}}^{(\mathit{x},\mathit{y},\mathit{z})}{|}^2$
$R_v^{(\times 2)}-R_c^{(\times 2)}$	0.195, 0.150, 0.128 (+11, +11, +8%) ${}^a$	0.174, 0.135, 0.118

^a The true enhancement should be about 22% due to inaccuracies in $|{\mathit{p}}_{\mathit{m}\mathit{n}}^{(\mathit{x},\mathit{y},\mathit{z})}{|}^2$ values. See text below for more details.

It should be mentioned that the momentum matrix elements calculated with the optic module in the presence of SOC had an inaccuracy that progressively increased for heavier elements. The discrepancy between $|p_{mn}^{(x,y,z)}{|}^2$ values calculated at the PBE level (including SOC) with the optic module and using the finite difference overlap matrix reached ca. 12% in the case of (CH${}_3$NH${}_3$)PbI${}_3$. The discrepancy fully vanished when SOC was excluded. After crosschecking the matrix elements with VASP we concluded that the finite difference results were correct. Since the optic module overestimated $|p_{mn}^{(x,y,z)}{|}^2$ values at PBE with SOC, the same applied to YSH with the SOC results presented in Table 6. After including this error, the true enhancement of YSH matrix elements for (CH${}_3$NH${}_3$)PbI${}_3$ were about 22% (10% average enhancement in Table 6 and 12% optic error for this material). Additional calculations with VASP and HSE06 XC functional with SOC produced a very similar result (23% enhancement of the matrix elements).

4. Discussion

YSH length-gauge $|v_{m,n}^{\mathrm{YSH}}{|}^2$ matrix elements were systematically greater than the momentum matrix elements $|p_{m,n}^{\mathrm{YSH}}{|}^2$. The enhancement ranged from 22 to 36% in the following order: (CH${}_3$NH${}_3$)PbI${}_3$, GaAs, GaN, and MoS${}_2$ (from the smaller to higher enhancement). This trend prompted the hypothesis that the enhancement was related to the localization of states involved in the optical transition. (CH${}_3$NH${}_3$)PbI${}_3$ has the most extended 5p-I and 6p-Pb states, while MoS${}_2$ had the most localized 4d-Mo and 3p-S states at the band edges.

To gain further insight into the difference between $|p_{m,n}^{\mathrm{YSH}}{|}^2$ and $|v_{m,n}^{\mathrm{YSH}}{|}^2$ we wote the momentum matrix element in the length gauge. The corresponding operator was expressed as the commutator

$$\widehat{\mathbf{p}}=i[\widehat{T},\mathbf{r}],$$

(11)

where $\widehat{T}$ is the kinetic energy operator. Following the same logic that leads to Equation (4), we derived an equivalent expression for the momentum matrix element in the length-gauge

$${\mathbf{p}}_{m,n}\left(\mathbf{k}\right)=i[T_m\left(\mathbf{k}\right)-T_n\left(\mathbf{k}\right)]⟨m,\mathbf{k}\left|\mathbf{r}\right|n,\mathbf{k}⟩.$$

(12)

After dividing Equation (4) by (12) we obtain

$${\mathbf{v}}_{m,n}\left(\mathbf{k}\right)={\mathbf{p}}_{m,n}\left(\mathbf{k}\right)\frac{E_m\left(\mathbf{k}\right)-E_n\left(\mathbf{k}\right)}{T_m\left(\mathbf{k}\right)-T_n\left(\mathbf{k}\right)}.$$

(13)

Thus, the 10 to 36% enhancement of the absolute squared magnitude of velocity matrix elements vs momentum matrix elements in calculations with YSH was directly related to the difference in eigenvalues not captured by the kinetic energy. In contrast, we expected the difference in eigenvalues to be fully captured by the kinetic energy, i.e., $[E_m\left(\mathbf{k}\right)-E_n\left(\mathbf{k}\right)]/[T_m\left(\mathbf{k}\right)-T_n\left(\mathbf{k}\right)]=1$, when a local potential was employed. Interestingly, Equation (13) predicts an isotropic renormalization factor shared by all Cartesian directions ($\alpha =x,y,z$). Indeed, materials with anisotropic $v_{mn}^{\left(\alpha \right)}$—GaN (Table 4) and (CH${}_3$NH${}_3$)PbI${}_3$ (Table 6)—showed a material-dependent yet isotropic enhancement factor, which was an indirect proof of the validity of Equation (13).

The renormalization of momentum matrix elements should have had implications for optical properties calculated with non-local potentials (hybrid or quasi-particle $GW$). The velocity matrix elements entered the frequency-dependent dielectric tensor (an imaginary part of the inter-band contribution) that took the following form in the independent-particle approximation [5]

$${ϵ}_{\alpha \beta }^{″}\left(\omega \right)\propto \sum _{v,c}{\int }_{\mathbf{k}\in \mathrm{BZ}}\frac{v_{v,c}^{\left(\alpha \right)}\left(\mathbf{k}\right)v_{c,v}^{\left(\beta \right)}\left(\mathbf{k}\right)}{{\omega }^2}\delta [E_c\left(\mathbf{k}\right)-E_v\left(\mathbf{k}\right)-\omega ]d\mathbf{k}.$$

(14)

However, length-gauge ${\mathbf{v}}_{c,v}$ matrix elements are more difficult to compute than ${\mathbf{p}}_{c,v}$, especially at the quasi-particle $GW$ level of theory where the finite difference method seems the only available technique [3]. Equation (13) opens a convenient possibility to use renormalized momentum matrix elements instead

$${ϵ}_{\alpha \beta }^{″}\left(\omega \right)\propto \sum _{v,c}{\int }_{\mathbf{k}\in \mathrm{BZ}}\frac{p_{v,c}^{\left(\alpha \right)}\left(\mathbf{k}\right)p_{c,v}^{\left(\beta \right)}\left(\mathbf{k}\right)}{{[T_c\left(\mathbf{k}\right)-T_v\left(\mathbf{k}\right)]}^2}\delta [E_c\left(\mathbf{k}\right)-E_v\left(\mathbf{k}\right)-\omega ]d\mathbf{k},$$

(15)

provided that eigenstates are consistent with the potential, and their kinetic energy is known. The last expression should be valid not only for hybrid XC functionals but also for the quasi-particle $GW$ level of theory.

Finally, we would like to comment on the renormalization of optical transition matrix elements proposed by Levine and Allan [37]

$$v_{v,c}^{GW}=v_{v,c}^{\mathrm{LDA}/\mathrm{PBE}}\frac{{(E_c-E_v)}^{GW}}{{(E_c-E_v)}^{\mathrm{LDA}/\mathrm{PBE}}}$$

(16)

that is further used in the literature [5,38]. If we apply Equation (16) to the ${\mathsf{\Gamma }}_{so}-{\mathsf{\Gamma }}_c$ transition in GaAs, one would expect the absolute squared magnitude of the velocity matrix element to increase by the ratio of ${[(E_c^{\mathrm{YSH}}-E_{so}^{\mathrm{YSH}})/(E_c^{\mathrm{PBE}}-E_{so}^{\mathrm{PBE}})]}^2$ which amounts to +151%. This result contradicts the +23% difference between $|p_{so,c}^{\mathrm{PBE}}{|}^2$ and $|v_{so,c}^{\mathrm{YSH}}{|}^2$ we observed (compare Table 2 and Table 3). At the same time, the dipole matrix element $|⟨{\mathsf{\Gamma }}_{so}\left|\mathbf{r}\right|{\mathsf{\Gamma }}_c{⟩|}^2$ becomes 127% smaller in YSH relative to PBE and counterbalances (partly) the effect of the gap opening. We further identified contributions of the muffin-tin spheres and of the interstitial volume to the value of the dipole matrix element $⟨{\mathsf{\Gamma }}_{so}\left|\mathbf{r}\right|{\mathsf{\Gamma }}_c⟩$ at PBE and YSH levels of theory: 25% Ga, 44% As, and 31% interstitial. All contributions are in phase with each other, and the proportions remain unchanged from PBE to YSH. Equation (16), in contrast, implies the equality of dipole matrix elements ${⟨m,\mathbf{k}\left|\mathbf{r}\right|n,\mathbf{k}⟩}^{\mathrm{LDA}/\mathrm{PBE}}={⟨m,\mathbf{k}\left|\mathbf{r}\right|n,\mathbf{k}⟩}^{GW}$ (see Equation (4). Note that $v_{m,n}^{\mathrm{LDA}/\mathrm{PBE}}=p_{m,n}^{\mathrm{LDA}/\mathrm{PBE}}\approx p_{m,n}^{GW}$ [10]) leads to a gross overestimation of $v_{m,n}^{GW}$ matrix elements making them inconsistent with the band curvature [10].

5. Conclusions

Strong material-dependent enhancement of the oscillator strength (22–36% in the absolute squared magnitude) was observed in the electronic structure calculations of semiconductors with a hybrid XC functional. The origin of the enhancement was traced to the non-local Hartee–Fock exchange potential. The enhancement of the absolute squared magnitude of velocity matrix elements $|v_{m,n}^{\mathrm{YSH}}{|}^2$ vs momentum matrix elements $|p_{m,n}^{\mathrm{YSH}}{|}^2$ in calculations with non-local potentials was directly related to the difference in eigenvalues not captured by the kinetic energy, i.e., ${[E_m\left(\mathbf{k}\right)-E_n\left(\mathbf{k}\right)]}^2/{[T_m\left(\mathbf{k}\right)-T_n\left(\mathbf{k}\right)]}^2$. This enhancement is isotropic and can be readily included in a calculation of the dielectric function. Our enhancement factor was much more accurate than that previously proposed by Levine and Allan ${(E_{\mathrm{g}}^{GW}/E_{\mathrm{g}}^{\mathrm{LDA}})}^2$, which leads to nonphysically large $v_{m,n}^{GW}$ matrix elements.