A Comparison between Task Distribution Strategies for Load Balancing Using a Multiagent System
Abstract
1. Introduction
- We implemented the software solution that supports the execution of the proposed experiments, with full support for metric definition, task generation, and configuration of processing agents;
- Based on the conducted research, we proposed and implemented a series of distribution strategies in order to have a broader perspective on the relationship between the context, task particularities and the strategy that is suitable in a given scenario;
- We proposed, implemented and evaluated the experiments that are going to be detailed below.
2. Related Work
2.1. Task Distribution
2.2. Load Balancing
3. Methodology
3.1. Problem Description
- All the processors are available to receive tasks from time zero of the simulation;
- Each processor has an available processing power that is 100% at the beginning of the simulation;
- Each processor is able to process multiple tasks at the same time;
- The time needed to process a task does not change based on the load of the processor;
- Each processor is able to spawn a certain number of helper processors;
- Each helper processor has a reduced processing power compared to the main processors;
- The list of tasks is available from time zero of the simulation;
- Each task from the list has two requirements: the processing power needed and the time needed for the task to be processed;
- The tasks do not have priorities;
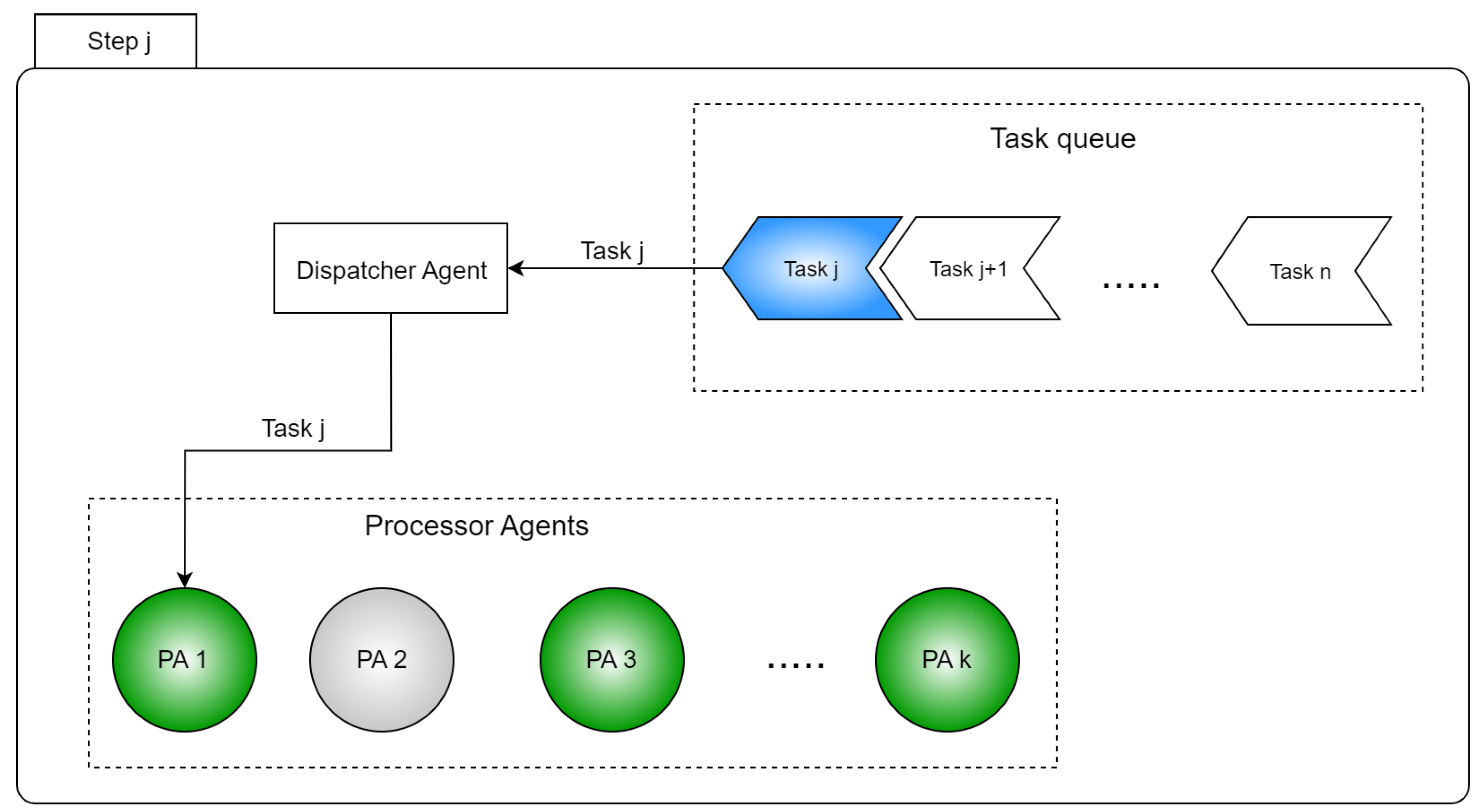
- The tasks are distributed sequentially in the order in which they are placed in the distribution queue.
3.2. System Description
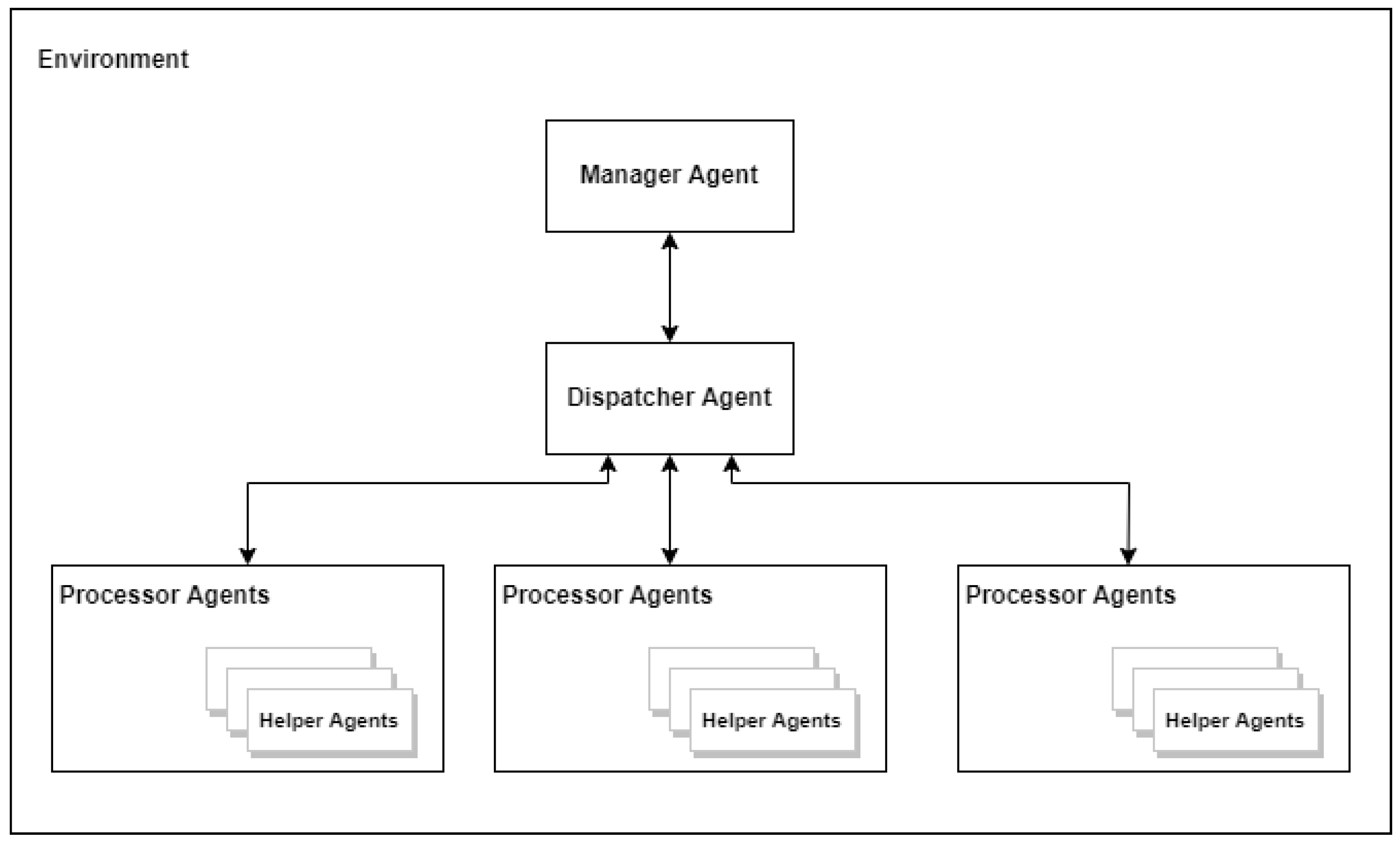
3.2.1. System Structure
- Environment represents the place where simulations run. This component is responsible for generating the rest of the agents based on the specified configurations;
- Manager Agent generates the tasks to be distributed and communicates with the dispatcher agent to stop the simulation after the distribution of the tasks;
- Dispatcher Agent is the component that handles the communication with the processor agents in order to apply the distribution strategy and to distribute the tasks in the queue;
- Processor Agent (PA) or worker agent is responsible for receiving tasks and processing them, possibly assisted by the helper agents;
- Helper Agents (HAs) are occasionally spawned when a processor agent needs to be assisted in processing a task for which it does not have sufficient resources. Each processor agent is able to spawn a predefined number (the same for all the processor agents) of helper agents that will be alive until the task that they were spawned for is finished.
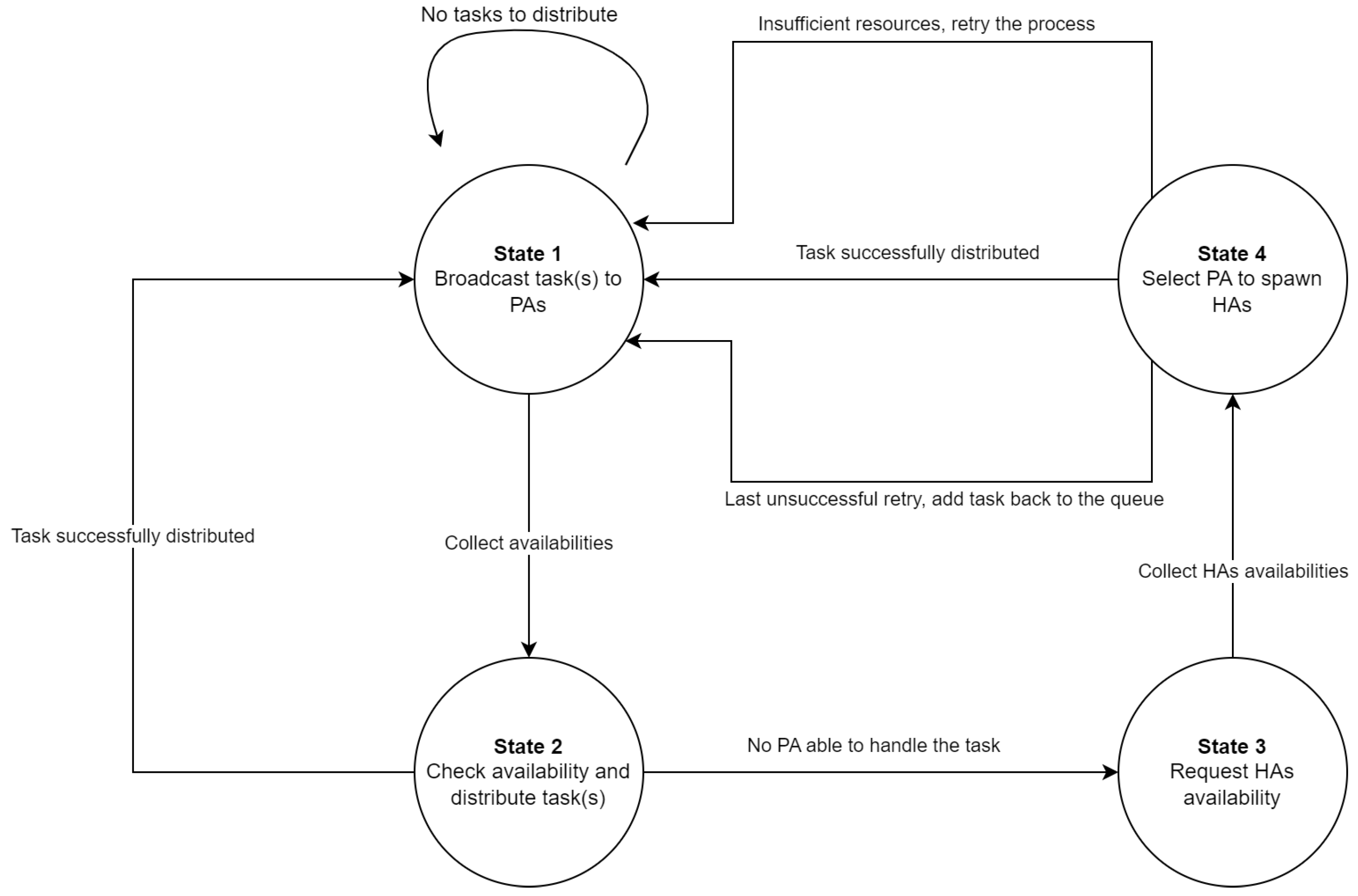
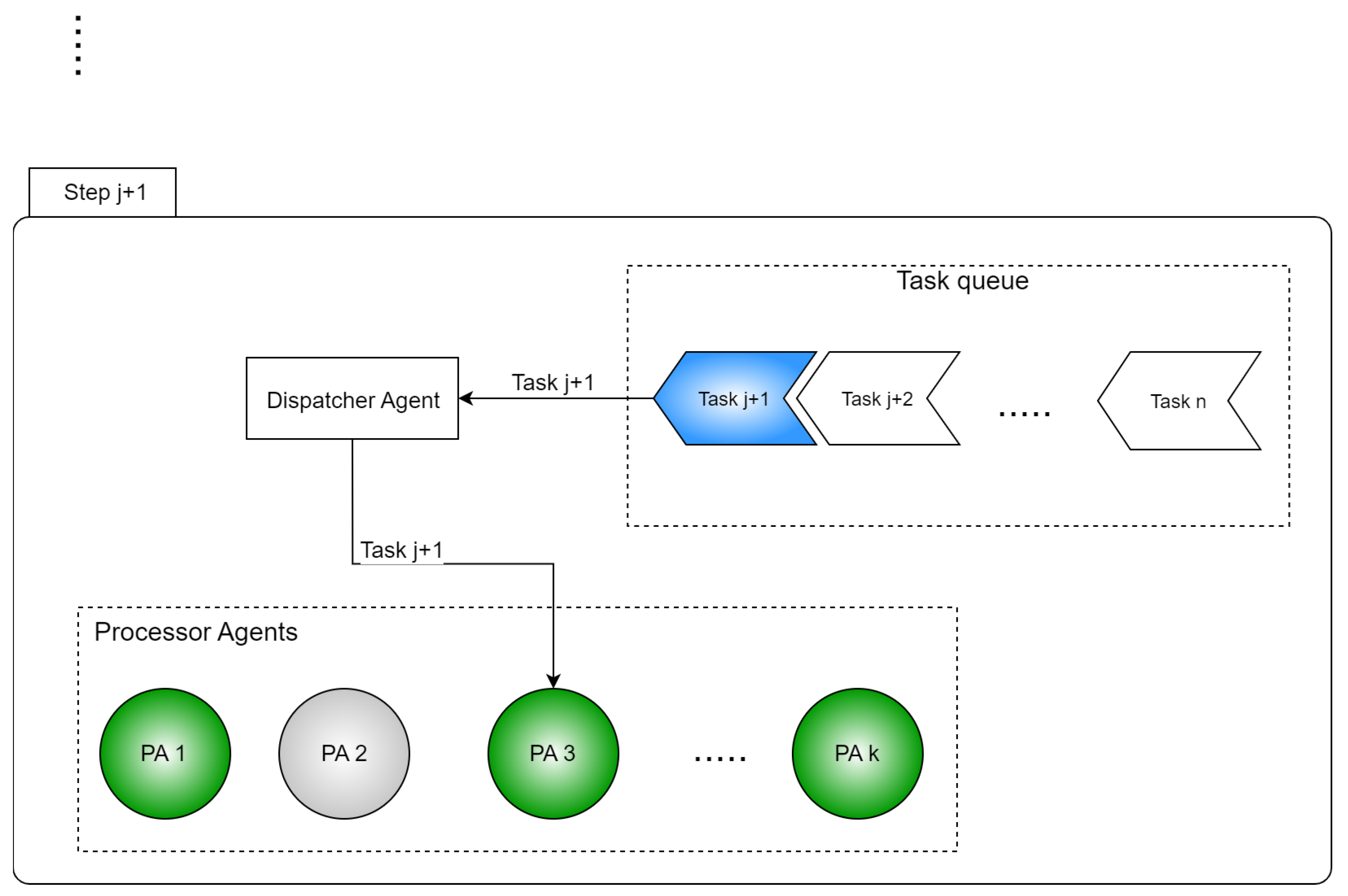
3.2.2. Task Distribution Process
- State 1: If the task queue contains some tasks, the distributor agent selects the first task (or more tasks, depending on the distribution strategy) and broadcasts it to all the PAs. If no task is available, the dispatcher remains in the current state, waiting for a task to appear in the queue;
- State 2: After collecting the responses from the PAs, the dispatcher agent distributes the task(s) to the PA selected based on the distribution strategy and returns to the first state. If there is no PA available to handle the task(s), the dispatcher goes to next state;
- State 3: In this state, the dispatcher broadcasts a message to all the PAs, requesting the HAs availability;
- State 4: If the dispatcher reaches this state, the best scenario happens if the task can be processed by a PA with the help of its corresponding HAs. After the successful distribution, the dispatcher is ready to go to the first state in order to try the distribution of another task. If there is no PA able to handle the current task even with the help from HAs, then the distributor goes back to the first state, retrying the whole process with the current task. The number of retries is empirically chosen to be 3. If the task reaches the maximum number of retries, it is added to the end of the queue and the dispatcher goes to the first state.
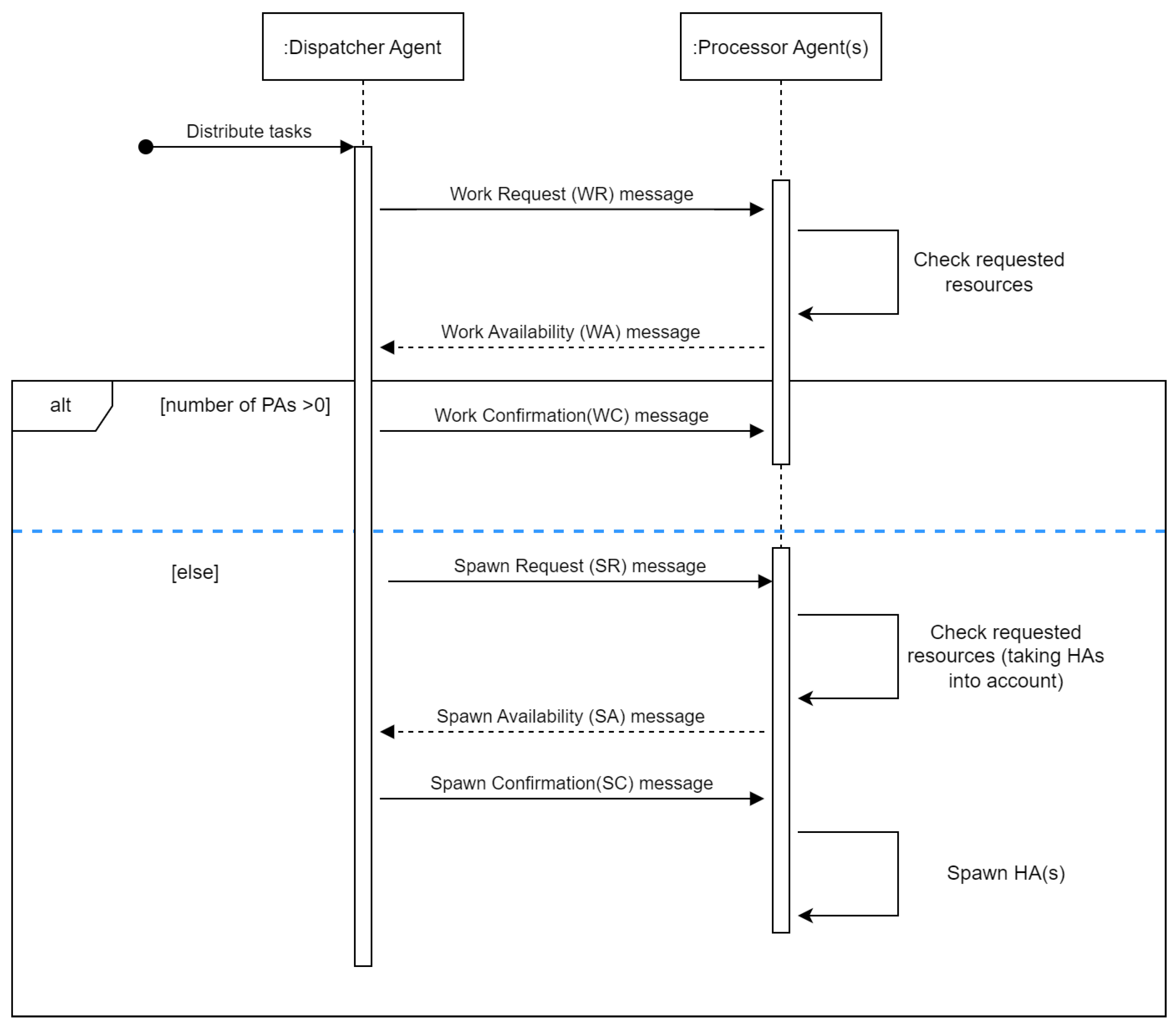
3.2.3. Communication Protocol
- Work Request (WR) represents the message broadcast by the dispatcher to PAs with details regarding the current task(s) that need(s) to be processed;
- Work Availability (WA) is the response sent by each PA agent and contains information about the available processing power that a PA agent has;
- Work Confirmation (WC) is the message sent by the dispatcher after applying the distribution strategy in order to determine the PA designated to process a given task. The message only contains the ID of the task, and it is sent only to the PA selected to handle the task. The other participant PAs do not receive any rejection message;
- Spawn Request (SR) is the message sent by the dispatcher if there are no available PAs to handle the current task. It is similar to the WR message and requests the availability of the PAs but this time taking into account the availability of the HAs too;
- Spawn Availability (SA) is sent by PAs and offers information about the availability but taking into account also the potential of the HAs;
- Spawn Confirmation (SC) is the message sent by the dispatcher to a PA after the distribution strategy is applied, and the PA selected to handle the task with the help of its HAs is determined.
- The presence of the two main classes of participants in the communication process: one that initiates the dialogue and calls for proposals, and the other one that receives the message, analyzes the requirement and responds to the proposal;
- The flow of the messages is similar, following the main pattern of the CNP with “request–response” messages.
- The PAs do not send a reject message if the requirements from the Dispatcher cannot be fulfilled. The PAs send only a single type of message that is not specifically a reject or a proposal, but it is an informative message with the current availability of the agent;
- The Dispatcher does not send a specific reject message to the PAs that were not selected to process the request;
- The PA that was selected to process the request does not send a confirmation or a cancel message to the Dispatcher;
- The protocol supports a different round of messages exchanged between the agents in some scenarios.
- UniqueId or task name represents a unique identifier used for each task;
- Required Load is a numeric value that represents the number of resources required for a PA in order to process a task;
- Required Time represents the value that measures how long a PA will process the current task.
3.3. Distribution Strategies
3.3.1. Round Robin
3.3.2. Max-Utility
3.3.3. Max-Availability
3.3.4. Random
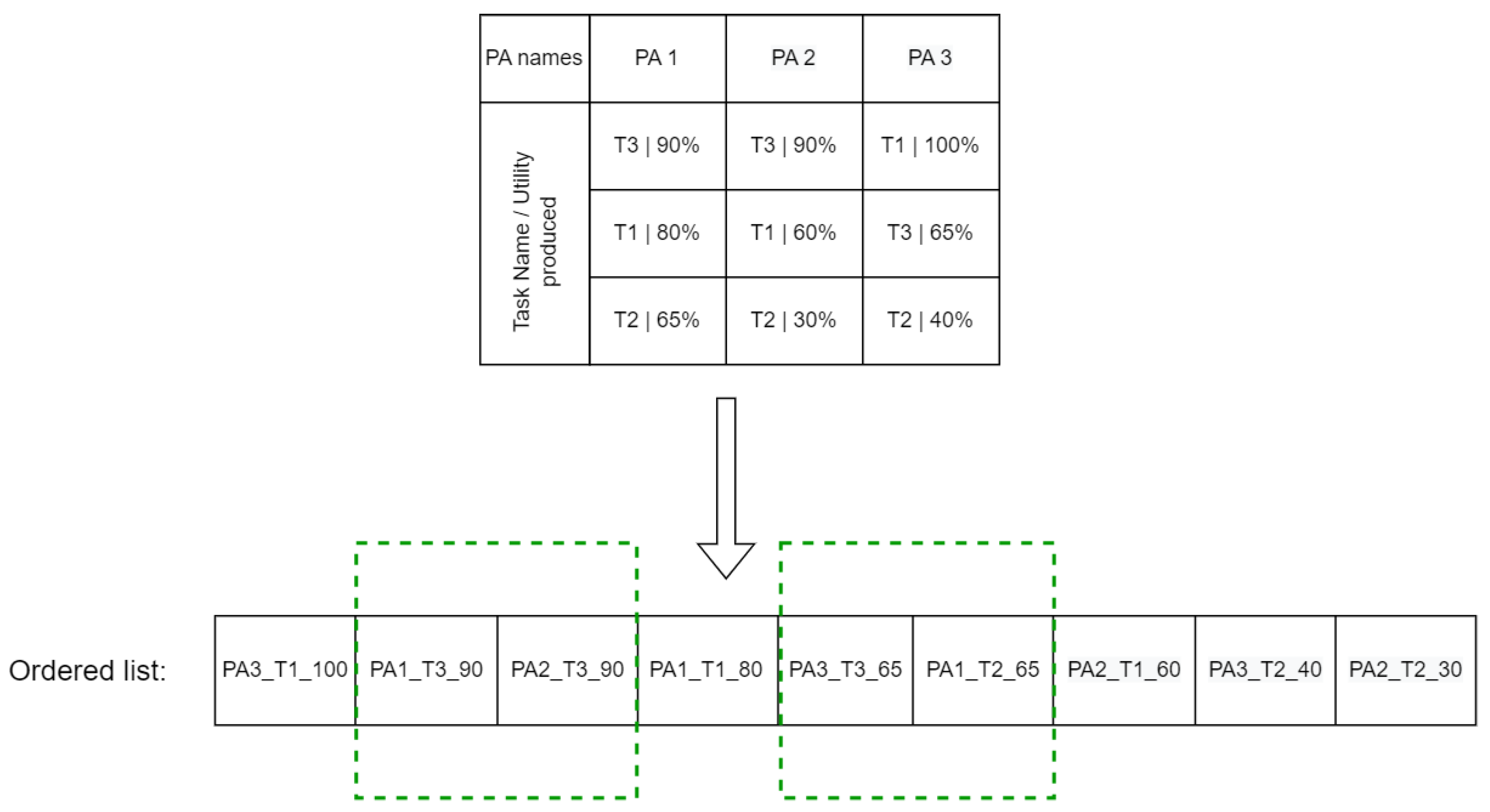
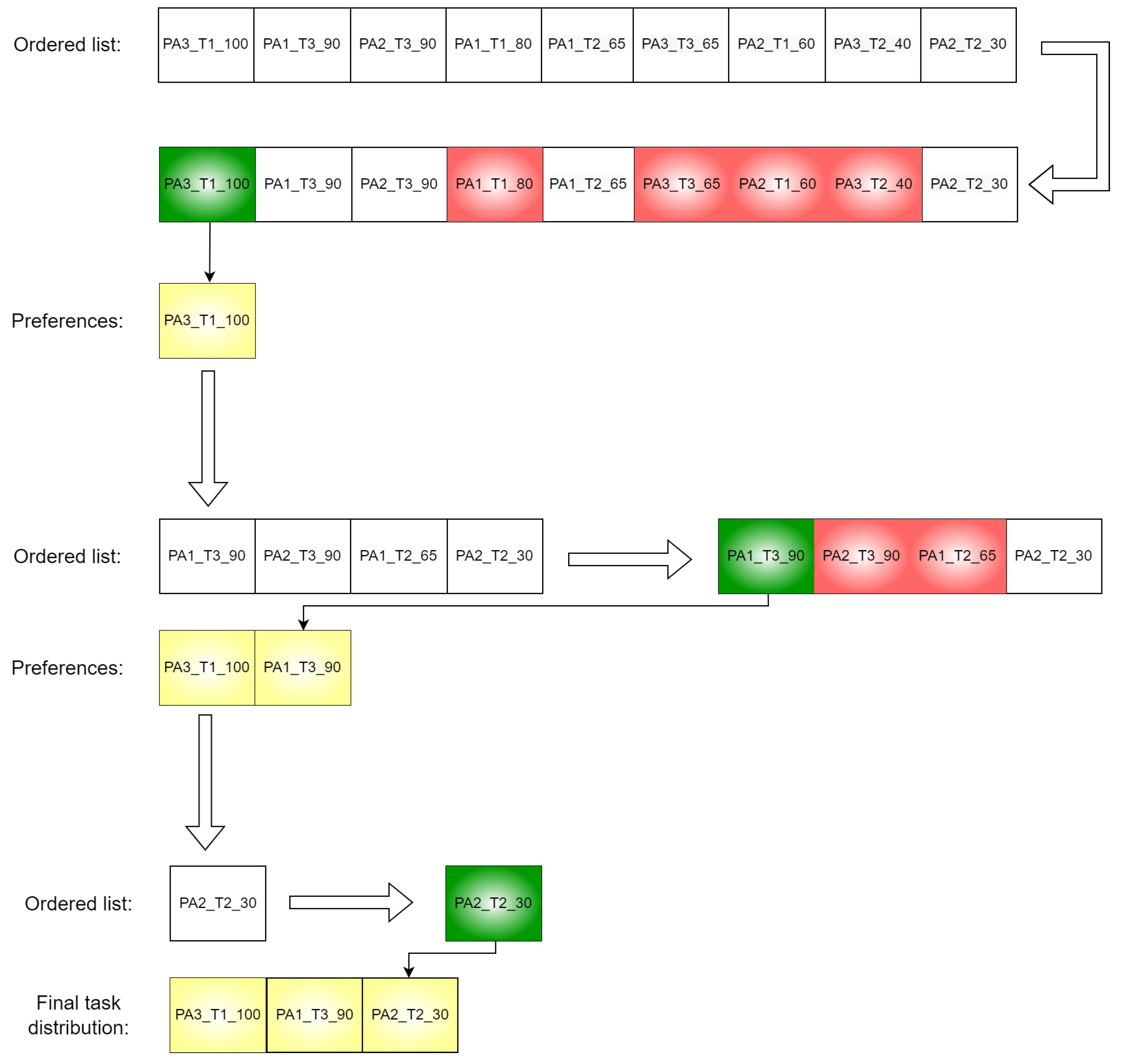
3.3.5. Agents Preferences
3.4. Metrics Description
4. Experimental Results and Discussion
- The number of tasks that are used in the experiments is 500;
- The number of simulation steps is 50;
- The number of PAs is always 5. The processing power of a PA is 100 (this can be regarded as 100% available processing power);
- The maximum number of HAs per PA is 3. The capacity of one HA is 5. In other words, one HA is able to handle 5% of the total available processing power of a PA;
- The minimum and maximum task times (the time is expressed as the number of turns) are varied to produce 3 intervals: [1; 5] (small processing time required), [3; 15] (broad processing time required), and [10; 15] (large processing time required);
- The minimum and maximum task resources required represent the numbers that show how much the availability of a PA will decrease after the task will be accepted. As for the time required, these are varied to produce 3 intervals: [1; 20] (small number of resources required), [1; 40] (broad processing power required), and [20; 40] (high processing capacity required).
- Agents preferences (AP);
- Max-utility (Mu);
- Max-availability (Ma);
- Random (Rnd);
- Round Robin (RR).
4.1. Description of Results
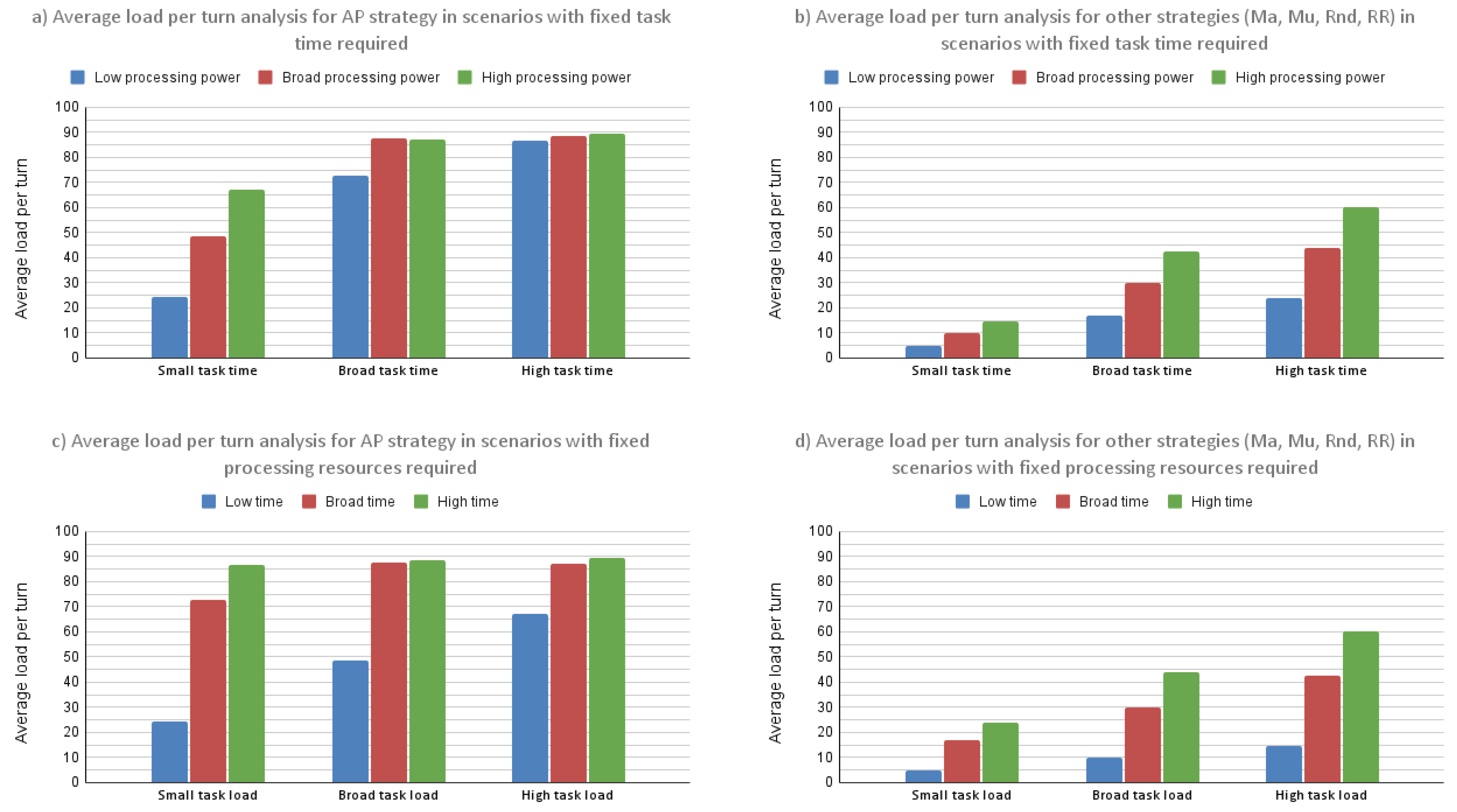
4.2. Analysis and Interpretation of Results
- The average required processing power per task of 9.78 produces an average load per turn equal to ≈24.2, meaning that the average load per turn is ≈2.49 times higher than the average processing power required per task;
- The average required processing power per task of 19.6 generates an average load per PA equal to ≈48.7, which means that the average load per PA is ≈2.48 times higher than the average required processing per task;
- The average required processing power per task of 29.52 results in an average load per PA equal to ≈67.4, resulting in an average load per PA ≈2.28 times higher than the average processing power required by a task.
- The average required processing power per task of 9.78 produces an average load per turn equal to ≈4.93, resulting in an average load per turn ≈1.98 times lower than the average required processing power per task;
- The average required processing power per task of 19.6 generates an average load per PA equal to ≈10.12, resulting in an ≈1.93 times difference between the two;
- The average required processing power per task of 29.52 results in an average load per PA equal to ≈14.7, generating an ≈2 times difference between them.
4.3. Brief Summary of Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pinedo, M. Scheduling. Theory, Algorithms, and Systems, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Zhang, A.-N.; Shu-Chuan, C.; Song, P.; Wang, H.; Pan, J. Task Scheduling in Cloud Computing Environment Using Advanced Phasmatodea Population Evolution Algorithms. Electronics 2022, 11, 1451. [Google Scholar] [CrossRef]
- Gawali; Bhatu, M.; Shinde, S.K. Task Scheduling and Resource Allocation in Cloud Computing Using a Heuristic Approach. J. Cloud Comput. 2018, 7, 1–16. [Google Scholar] [CrossRef]
- Filho, S.; Pinheiro, M.; Albuquerque, P.; Rodrigues, J. Task Allocation in Distributed Software Development: A Systematic Literature Review. Complexity 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Filho, S.; Pinheiro, M.; Albuquerque, P.; Simão, A.; Azevedo, E.; Sales Neto, R.; Nunes, L. A Multicriteria Approach to Support Task Allocation in Projects of Distributed Software Development. Complexity 2019, 2019, 1–22. [Google Scholar] [CrossRef]
- Gu, M.; Zheng, J.; Hou, P.; Dai, Z. Task Allocation for Product Development Projects Based on the Knowledge Interest. In Proceedings of the 6h International Conference on Information Science and Control Engineering (ICISCE), Shanghai, China, 20–22 December 2019; pp. 600–604. [Google Scholar] [CrossRef]
- William, P.; Pardeep Kumar, G.S.; Vengatesan, C.K. Task Allocation in Distributed Agile Software Development Using Machine Learning Approach. In Proceedings of the International Conference on Disruptive Technologies for Multi-Disciplinary Research and Applications (CENTCON), Online, 22–24 December 2021; pp. 168–172. [Google Scholar] [CrossRef]
- Heidari, A.; Jabraeil Jamali, M.A.; Jafari Navimipour, N.; Akbarpour, S. Deep Q-Learning Technique for Offloading Offline/Online Computation in Blockchain-Enabled Green IoT-Edge Scenarios. Appl. Sci. 2022, 12, 8232. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Fe, I.; Brito, C.; Kaliappan, V.K.; Choi, E.; Min, D.; Lee, J.W.; Silva, F.A. Performability Evaluation of Load Balancing and Fail-over Strategies for Medical Information Systems with Edge/Fog Computing Using Stochastic Reward Nets. Sensors 2021, 21, 6253. [Google Scholar] [CrossRef]
- Leon, F. Self-organization of Roles Based on Multilateral Negotiation for Task Allocation. In Proceedings of the Ninth German Conference on Multi-Agent System Technologies (MATES 2011), Berlin, Germany, 4–7 October 2011; Lecture Notes in Artificial Intelligence, LNAI 6973. Springer: Berlin/Heidelberg, Germany, 2011; pp. 173–180. [Google Scholar] [CrossRef]
- Heidari, A.; Jabraeil Jamali, M.A. Internet of Things intrusion detection systems: A comprehensive review and future directions. Cluster Comput. 2022. [Google Scholar] [CrossRef]
- Yan, S.-R.; Pirooznia, S.; Heidari, A.; Navimipour, N.J.; Unal, M. Implementation of a Product-Recommender System in an IoT-Based Smart Shopping Using Fuzzy Logic and Apriori Algorithm. IEEE Trans. Eng. Manag. 2022. [Google Scholar] [CrossRef]
- Yichuan, J. A Survey of Task Allocation and Load Balancing in Distributed Systems. IEEE Trans. Parallel Distrib. Syst. 2016, 27, 585–599. [Google Scholar] [CrossRef]
- Lim, J.; Lee, D. A Load Balancing Algorithm for Mobile Devices in Edge Cloud Computing Environments. Electronics 2020, 9, 686. [Google Scholar] [CrossRef]
- Shahbaz, A.; Kavitha, G. Load balancing in cloud computing -A hierarchical taxonomical classification. J. Cloud Comput. 2019, 8. [Google Scholar] [CrossRef]
- Keivani, A.; Tapamo, J.R. Task scheduling in cloud computing: A review. In Proceedings of the 2019 International Conference on Advances in Big Data, Computing and Data Communication Systems (icABCD), Lesotho, South Africa, 5–6 August 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Kumar, M.; Sharma, S.C.; Goel, A.; Singh, S.P. A comprehensive survey for scheduling techniques in cloud computing. J. Netw. Comput. Appl. 2019, 143, 1–33. [Google Scholar] [CrossRef]
- Alam Siddique, M.T.; Sharmin, S.; Ahammad, T. Performance Analysis and Comparison Among Different Task Scheduling Algorithms in Cloud Computing. In Proceedings of the 2020 2nd International Conference on Sustainable Technologies for Industry 4.0 (STI), Dhaka, Bangladesh, 19–20 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Rodrigo, N.; Calheiros, R.R.; Beloglazov, A.; De Rose, C.A.F.; Buyya, R. CloudSim: A toolkit for modeling and simulation of cloud computing environments and evaluation of resource provisioning algorithms. Softw. Pract. Expert 2011, 41, 23–50. [Google Scholar] [CrossRef]
- Joo, T.; Jun, H.; Shin, D. Task Allocation in Human–Machine Manufacturing Systems Using Deep Reinforcement Learning. Sustainability 2022, 14, 2245. [Google Scholar] [CrossRef]
- Oliehoek, F.A.; Amato, C. A Concise Introduction to Decentralized POMDPs. In SpringerBriefs in Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Liu, Y.; Wang, L.; Wang, Y.; Wang, X.; Zhang, L. Multi-agent-based scheduling in cloud manufacturing with dynamic task arrivals. Procedia CIRP 2018, 72. [Google Scholar] [CrossRef]
- Jensen, T.R.; Bjarne, T. Graph Coloring Problems; Wiley-Interscience: Hoboken, NJ, USA, 1995. [Google Scholar]
- Mostafaie, T.; Modarres, K.; Farzin, N.N. A systematic study on meta-heuristic approaches for solving the graph coloring problem. Comput. Oper. Res. 2019, 120, 104850. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Mirjalili, S. Evolutionary Algorithms and Neural Networks: Theory and Applications; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Wang, C.-N.; Yang, F.-C.; Nguyen, V.T.T.; Vo, N.T.M. CFD Analysis and Optimum Design for a Centrifugal Pump Using an Effectively Artificial Intelligent Algorithm. Micromachines 2022, 13, 1208. [Google Scholar] [CrossRef]
- Nguyen, T.; Huynh, T.; Vu, N.; Chien, K.V.; Huang, S.-C. Optimizing compliant gripper mechanism design by employing an effective bi-algorithm: Fuzzy logic and ANFIS. Microsyst. Technol. 2021, 27, 1–24. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant Colony Optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Deng, W.; Xu, J.; Zhao, H. An Improved Ant Colony Optimization Algorithm Based on Hybrid Strategies for Scheduling Problem. IEEE Access 2019, 7, 20281–20292. [Google Scholar] [CrossRef]
- Mbarek, F.; Volodymyr, M. Hybrid Nearest-Neighbor Ant Colony Optimization Algorithm for Enhancing Load Balancing Task Management. Appl. Sci. 2021, 11, 10807. [Google Scholar] [CrossRef]
- Zhiyuan, Y.; Zihan, D.; Clausen, T. Multi-Agent Reinforcement Learning for Network Load Balancing in Data Center. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management (CIKM’22); Association for Computing Machinery: New York, NY, USA, 2022; pp. 3594–3603. [Google Scholar] [CrossRef]
- Rashid, T.; Samvelyan, M.; Witt, C.S.D.; Farquhar, G.; Jakob, N.; Shimon, F.W. QMIX: Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning. arXiv 2018, arXiv:abs/1803.11485. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. In Proceedings of the 36th International Conference on Machine Learning, Stockolm, Sweden, 10–15 July 2018. [Google Scholar]
- Miao, R.; Zeng, H.; Kim, C.; Lee, J.; Yu, M. SilkRoad: Making Stateful Layer-4 Load Balancing Fast and Cheap Using Switching ASICs. In Proceedings of the Conference of the ACM Special Interest Group on Data Communication (SIGCOMM’17); Association for Computing Machinery: New York, NY, USA, 2017; pp. 15–28. [Google Scholar] [CrossRef]
- Eisenbud, D.E.; Cheng, Y.; Contavalli, C.; Smith, C.; Kononov, R.; Mann-Hielscher, E.; Cilingiroglu, A.; Cheyney, B.; Shang, W.; Hosein, J.D. Maglev: A Fast and Reliable Software Network Load Balancer; NSDI: New York, NY, USA, 2016. [Google Scholar]
- Aghdai, A.; Chu, C.-Y.; Xu, Y.; Dai, D.H.; Xu, J.; Chao, H.J. Spotlight: Scalable Transport Layer Load Balancing for Data Center Networks. IEEE Trans. Cloud Comput. 2022, 10, 2131–2145. [Google Scholar] [CrossRef]
- Goren, G.; Shay, V.; Yoram, M. Distributed Dispatching in the Parallel Server Model. arXiv 2020, arXiv:abs/2008.00793. [Google Scholar] [CrossRef]
- Linux Virtual Server. Job Scheduling Algorithms in Linux Virtual Server. 2011. Available online: http://www.linuxvirtualserver.org/docs/scheduling.html (accessed on 6 October 2022).
- Kwa, H.L.; Leong, K.J.; Bouffanais, R. Balancing Collective Exploration and Exploitation in Multi-Agent and Multi-Robot Systems: A Review. Front. Robot. AI 2022, 8, 771520. [Google Scholar] [CrossRef] [PubMed]
- Leon, F. ActressMAS, a .NET Multi-Agent Framework Inspired by the Actor Model. Mathematics 2022, 10, 382. [Google Scholar] [CrossRef]
- Smith, S. The Contract Net Protocol: High-Level Communication and Control in a Distributed Problem Solver. IEEE Trans. Comput. 1980, C-29, 1104–1113. [Google Scholar] [CrossRef]
- Mostafa, S.M.; Hirofumi, A. Dynamic Round Robin CPU Scheduling Algorithm Based on K-Means Clustering Technique. Appl. Sci. 2020, 10, 5134. [Google Scholar] [CrossRef]
- Alhaidari, F.; Balharith, T.Z. Enhanced Round-Robin Algorithm in the Cloud Computing Environment for Optimal Task Scheduling. Computers 2021, 10, 63. [Google Scholar] [CrossRef]
- Kemptechnologies.com. Round Robin Load Balancing. Available online: https://kemptechnologies.com/load-balancer/round-robin-load-balancing (accessed on 30 July 2022).
- Nginx.com. HTTP Load Balancing. Available online: https://docs.nginx.com/nginx/admin-guide/load-balancer/http-load-balancer/ (accessed on 30 July 2022).
- Haas, C.; Hall, M.; Vlasnik, S.L. Finding Optimal Mentor-Mentee Matches: A Case Study in Applied Two-Sided Matching. Heliyon 2018, 4, e00634. [Google Scholar] [CrossRef]
- Ren, J.; Feng, X.; Chen, X.; Liu, J.; Hou, M.; Shehzad, A.; Sultanova, N.; Kong, X. Matching Algorithms: Fundamentals, Applications and Challenges. IEEE Trans. Emerg. Top. Comput. Intell. 2021, 5, 332–350. [Google Scholar] [CrossRef]
| The Number of Simulation Steps | |
|---|---|
| The number of processor agents | |
| The maximum number of helper agents | |
| The list of all processor agents | A |
| The list of all tasks | T |
| The list of loads per simulation step j for a given PA, | , i = , j = |
| The list with number of HAs per simulation step j for a given PA, | , i = , j = |
| The required processing power for a given task | , i = |
| The required time (turns) for a given task | , i = |
| The Average Load per Turn for One PA, (%) | = , i = |
|---|---|
| The average load per turn aggregated on all PAs (%) | = |
| The maximum difference between PAs average load per turn | = max() − min(), i = |
| The number of turns with at least one HA per turn for a PA, | = count(), i = , j = |
| The average number of turns with at least one HA per turn | = |
| The average number of HAs per turn for a PA, | = , i = , |
| The average number of HAs per turn aggregated on all PAs | = |
| The average required processing power per task | = |
| The average required time (turns) per task | = |
| Metrics | Task Times | Task Loads = [1; 20] | ||||
|---|---|---|---|---|---|---|
| Distribution Strategy | ||||||
| AP | Ma | Mu | Rnd | RR | ||
| [1; 5] | 1.76 | 0.21 | 0.66 | 0.21 | 1.14 | |
| [3; 15] | 6.45 | 0.25 | 9.47 | 0.60 | 4.04 | |
| [10; 15] | 3.91 | 0.36 | 9.07 | 0.81 | 4.36 | |
| [1; 5] | 24.19 | 4.93 | 4.93 | 4.93 | 4.93 | |
| [3; 15] | 72.95 | 16.85 | 16.83 | 16.84 | 16.90 | |
| [10; 15] | 86.73 | 23.79 | 23.67 | 23.63 | 23.76 | |
| [1; 5] | - | - | - | - | - | |
| [3; 15] | - | - | - | 0.06 | - | |
| [10; 15] | 0.34 | - | - | 0.55 | - | |
| [1; 5] | - | - | - | - | - | |
| [3; 15] | - | - | - | 0.20 | - | |
| [10; 15] | 1.40 | - | - | 1.67 | - | |
| Metrics | Task Times | Task Loads = [1; 40] | ||||
|---|---|---|---|---|---|---|
| Distribution Strategy | ||||||
| AP | Ma | Mu | Rnd | RR | ||
| [1; 5] | 1.19 | 0.36 | 1.11 | 0.18 | 2.05 | |
| [3; 15] | 3.30 | 0.51 | 4.59 | 1.35 | 5.02 | |
| [10; 15] | 4.80 | 0.69 | 0.75 | 3.44 | 10.41 | |
| [1; 5] | 48.69 | 10.12 | 10.11 | 9.79 | 10.12 | |
| [3; 15] | 87.53 | 31.69 | 31.57 | 25.53 | 30.38 | |
| [10; 15] | 88.43 | 48.40 | 48.35 | 32.52 | 46.34 | |
| [1; 5] | - | - | - | 0.35 | - | |
| [3; 15] | 8.86 | - | - | 14.72 | - | |
| [10; 15] | 51.61 | - | - | 44.43 | - | |
| [1; 5] | - | - | - | 1.51 | - | |
| [3; 15] | 2.52 | - | - | 1.78 | - | |
| [10; 15] | 2.66 | - | - | 1.90 | - | |
| Metrics | Task Times | Task Loads = [20; 40] | ||||
|---|---|---|---|---|---|---|
| Distribution Strategy | ||||||
| AP | Ma | Mu | Rnd | RR | ||
| [1; 5] | 1.28 | 0.21 | 2.31 | 0.78 | 2.29 | |
| [3; 15] | 3.18 | 0.72 | 1.13 | 2.72 | 8.72 | |
| [10; 15] | 3.43 | 0.58 | 2.54 | 2.80 | 6.05 | |
| [1; 5] | 67.37 | 14.77 | 14.77 | 14.03 | 14.77 | |
| [3; 15] | 87.08 | 48.91 | 48.83 | 29.22 | 43.62 | |
| [10; 15] | 89.44 | 69.04 | 70.18 | 37.28 | 64.85 | |
| [1; 5] | - | - | - | 0.70 | - | |
| [3; 15] | 29.14 | - | - | 38.01 | - | |
| [10; 15] | 80.44 | 11.88 | 1.44 | 89.20 | - | |
| [1; 5] | - | - | - | 1.54 | - | |
| [3; 15] | 2.76 | - | - | 1.93 | - | |
| [10; 15] | 2.67 | 1.02 | 2.32 | 1.93 | - | |
| Task Times | Task Loads | ||
|---|---|---|---|
| [1; 20] | [1; 40] | [20; 40] | |
| 9.78 | 19.6 | 29.52 | |
| 10.16 | 19.78 | 29.51 | |
| 10.14 | 20.49 | 29.68 | |
| Task Times | Task Loads | ||
|---|---|---|---|
| [1; 20] | [1; 40] | [20; 40] | |
| 2.55 | 2.55 | 2.52 | |
| 8.39 | 8.27 | 8.50 | |
| 11.90 | 11.98 | 12.10 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vecliuc, D.-D.; Leon, F.; Logofătu, D. A Comparison between Task Distribution Strategies for Load Balancing Using a Multiagent System. Computation 2022, 10, 223. https://doi.org/10.3390/computation10120223
Vecliuc D-D, Leon F, Logofătu D. A Comparison between Task Distribution Strategies for Load Balancing Using a Multiagent System. Computation. 2022; 10(12):223. https://doi.org/10.3390/computation10120223
Chicago/Turabian StyleVecliuc, Dumitru-Daniel, Florin Leon, and Doina Logofătu. 2022. "A Comparison between Task Distribution Strategies for Load Balancing Using a Multiagent System" Computation 10, no. 12: 223. https://doi.org/10.3390/computation10120223
APA StyleVecliuc, D.-D., Leon, F., & Logofătu, D. (2022). A Comparison between Task Distribution Strategies for Load Balancing Using a Multiagent System. Computation, 10(12), 223. https://doi.org/10.3390/computation10120223









