Precision Calibration of Omnidirectional Camera Using a Statistical Approach

Abstract

Omnidirectional optoelectronic systems (OOES) find applications in many areas where a wide viewing angle is crucial. The disadvantage of these systems is the large distortion of the images, which makes it difficult to make wide use of them. The purpose of this study is the development an algorithm for the precision calibration of an omnidirectional camera using a statistical approach. The calibration approach comprises three basic stages. The first stage is the formation of a cloud of points characterizing the view field of the virtual perspective camera. In the second stage, a calibration procedure that provides the projection function for the camera calibration is performed. The projection functions of traditional perspective lenses and omnidirectional wide-angle fisheye lenses with a viewing angle of no less than 180° are compared. The construction of the corrected image is performed in the third stage. The developed algorithm makes it possible to obtain an image for part of the field of view of an OOES by correcting the distortion from the original omnidirectional image.Using the developed algorithm, a non-mechanical pivoting camera based on an omnidirectional camera is implemented. The achieved mean squared error of the reproducing points from the original omnidirectional image onto the image with corrected distortion is less than the size of a very few pixels.

1. Introduction

In areas where a large viewing angle is critical, OOES are used. However, these systems have a large image distortion: which makes their use difficult in the case of measuring and observing in television systems [1,2,3].

Omnidirectional imaging systems find applications in many areas where a wide viewing angle is crucial. Their main areas of application are in the field of mobile robot navigation and surveillance systems. Over the last decade, the use of mobile robots in our society has grown significantly. The robots need sensor systems to extract information from the environment to solve mapping and localization problems. Cameras have become one of the most widespread options in mobile robotics owing to the big amount of information that they provide to the robot. For the solution of this complex task for simultaneous localization and mapping (the so-called SLAM) these systems are increasingly used alone or in configuration with other sensor systems [4].

Some works focus on the use of omnidirectional imaging as the only source of information for solving mapping and localization tasks. Such is the study of Caruso et al. [5] which presents a method for performing visual odometry with a rover. Garcia-Fidalgo et al. [6] presented a study of mapping and localization methods using visual systems. They allow for various configurations, such as single cameras, stereo cameras, multi-camera systems, catadioptric systems, and more. Catadioptric vision systems consist of a single camera aimed at a convex mirror. This configuration allows for image capturing with a 360-degree field of view around the mirror axis.

Corke [7] developed large-scale SLAM using also omnidirectional cameras. An approach for the efficient reduction of information lost and the creation of a map is proposed, as well. Often the visual information is combined with other sources of data such as GPS (global positioning system), IMU (inertial measuring device), LiDARS, pressure sensors, encoders, and others [4,8]. In [9] a system for the navigation and control of mobile robots is introduced which includes a camera, IMU, and encoder. Oriolo et al. [9] presented a method for locating robots using a monocular camera, IMU, encoders, and pressure sensors. In [10] and [11] systems are proposed for Optical 3D Object Recognition in autonomous driving applications. The systems combine data from a stereo camera system, LiDAR, IMU, Encoder, and GNSS (Global Navigation Satellite System), to incorporate the 3D object information into a mapping framework.

In recent years, various approaches have been presented for robust feature extraction from images taken with catadioptric visual systems [4,10,12]. Surveillance has a wide variety of applications, ranging from applications requiring high security to those used in our daily life, such as healthcare surveillance. Accordingly, many researchers in the field of imaging and video technology have paid great attention to the study and development of highly advanced surveillance systems [11,13].

Despite the wide variety of surveillance products on the market, most systems have a limitation in the angle of surveillance of the camera. Many studies have proposed two main approaches to increase the viewing angle—mechanical and optical. Mechanical approaches typically use a mechanically rotating and moving chamber system [14].

Some surveillance products use the so-called Pan-Tilt-Zoom (PTZ) cameras. They can move back and forth, up, and down, and increase the viewing area. The main disadvantages of mechanical approaches, however, are the high cost, the need for moving parts, and accurate positioning. Therefore, longer scene scanning, and synchronization time are required to obtain an omnidirectional image. For capturing omnidirectional images alternatively, the optical approach can be used. For example, a fisheye lens can provide a $360°$ viewing angle by refracting the omnidirectional scene in the camera sensor. However, the fisheye lens distorts the image which is not immediately understandable due to geometric distortion [15].

Another proposed approach is the use of a one-way mirror as a hyperbolic mirror. The 360-degree omnidirectional scene on the surveillance site is reflected in the camera and the image is captured. Examples that use a hyperbolic mirror to extend the viewing angle are: (i) folded catadioptric cameras by Nayar and Peri [16], (ii) an integrated surveillance system using multiple omnidirectional vision sensors by Ng et al. [17], and (iii) non-targeted surveillance system proposed in the work of Wong et al. [18]. The system consists of a hyperbolic mirror that is attached face-to-face with the webcam in a vertical direction using a construction bracket. It can capture a 360° area in a horizontal plane at once. A hyperbolic mirror is used because it is cheaper than a fisheye lens with almost the same image quality.

Along with the presented main applications, there are many others. Electric power generation forecasting is of particular interest. Electric power load forecasting has been an integral part of managing electrical energy markets and infrastructure for many decades. The cost of generating power from other than traditional energy sources can be reduced through the integration of solar energy into the classical energy supply structures. However, such integration has its challenges and costs. The forecasting of distributed photovoltaic (PV) power generation, requires both intra-hour and day-ahead forecasting of solar irradiance [19]. For the PV systems, global irradiation (GI) on the inclined surface is required.

For different time horizons, however, different approaches are required.

For a very short time (<30 min), a range of ground-based imaging techniques was developed for GI using the information on cloud positioning and deterministic models [20,21].

Hensel et al. [22] describe a systematic approach for a precise short-time cloud coverage prediction based on an optical system. The images are based on a sky imager system with a fish-eye lens optic to cover a maximum area. After a calibration step, the image is rectified to enable linear prediction of cloud movement. In a subsequent step, the clear sky model is estimated based on actual high dynamic range images and combined with a threshold-based approach to segment clouds from the sky. In the final stage, a multi-hypothesis linear tracking framework estimates cloud movement, velocity, and possible coverage of a given photovoltaic power station. A Kalman filter framework, which efficiently operates on the rectified images, is used. The evaluation of real-world data suggests high coverage prediction accuracy above 75%.

The goal of this research is to develop a mathematically valid model and efficient practical approach for calibrating and correcting distortion in fisheye cameras.

2. Methodology

This section explains the technical details of the perspective geometry model and the calibration methods used and sets out the framework for implementing the proposed approach.

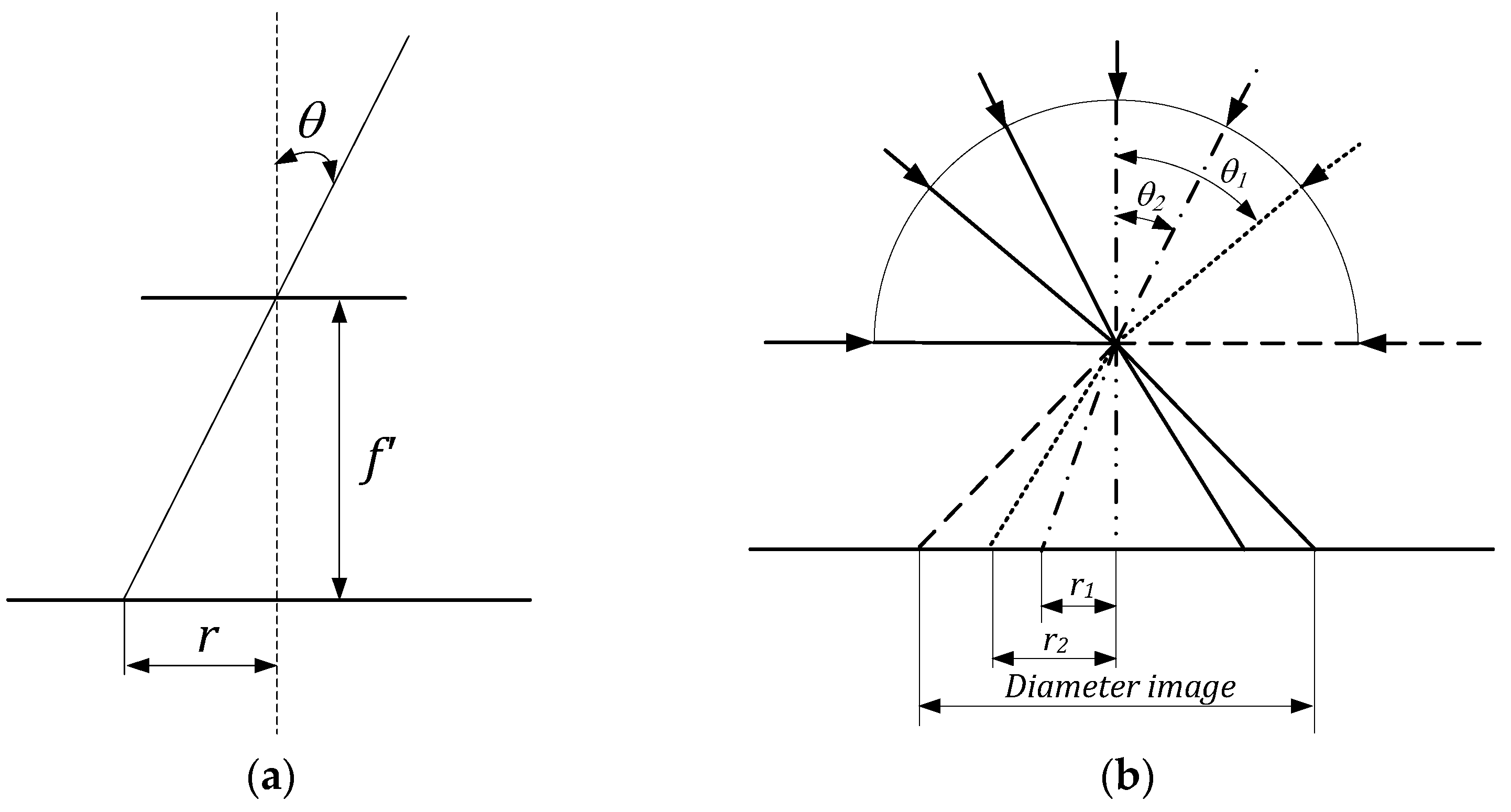
2.1. The Perspective Geometric Model

Most recent optical systems can be described with sufficient precision by a perspective geometric model (Figure 1a). In this case, distortion will be considered a deviation from this model. The projection function of such systems is expressed as follows:

$$tan\theta =\frac{r}{-f^{\prime }},$$

(1)

where $r$ is the image radius; $f^{\prime }$ is the focal length; $\theta$ is the ray incidence angle. The relationship (1) shows that when the ray incident angle is 90°, then the image radius becomes infinite.

It follows that ultra-wide-angle fisheye lenses with a viewing angle of at least 180° cannot be described by derivation from this model.

M. M. Rusinov proposed in [23], a projection function for super-wide-angle fisheye lenses in which the image radius is proportional to the angle at which the ray falls (Figure 1b):

$$\theta =\frac{r}{-f^{\prime }}.$$

(2)

In previous papers [24], this function is used in the algorithms implemented by many other authors [22,25,26]. However, it became obvious that in practice the transfer function varies with the specific lens model and, in general, it is not known in advance.

To solve this problem, algorithms have been developed for converting images received by omnidirectional cameras into images with corrected distortion; these images correspond to those obtained by the classical perspective model using a calibration procedure. By omnidirectional optoelectronic systems (omnidirectional cameras), we mean optoelectronic systems, in which the field of view, reaches $360°$, at least in one of the planes (meridional or sagittal).

There are three common types of omnidirectional optical systems:

• Optical systems with super-wide fisheye lenses with a view angle of no less than $180°$, capable of capturing at least a hemisphere of the surrounding space.
• Mirror-lens (catadioptric) optical systems are cameras with a conventional lens with a nozzle mounted on it in the form of a mirror with rotational symmetry. The shape of the mirror surface can vary from cone to ellipse.
• Multi-chamber systems, whose large field of view is achieved using several chambers with overlapping fields of view.

Herein only single-chamber optical-electronic systems, i.e., cameras with fisheye lenses and catadioptric cameras, are considered. The main purpose of this work is the development of an algorithm for the transformation of images, obtained from cameras with omnidirectional lenses, into classic perspective views with corrected distortion. The goal was to develop a module for the so-called Typhoon program for an optoelectronic surveillance system that implements, on an omnidirectional camera, the function of a non-mechanical PTZ camera operating on a motion detector.

In this respect, there are additional requirements for the algorithm:

• It should work with omnidirectional cameras with a fisheye lens, as well as with catadioptric optical systems.
• The calibration process should be accessible for unqualified users of the system and should not require the use of special technical means.

The algorithm can be deployed in video surveillance systems that can use different models of cameras and lenses, but a simple calibration procedure will be needed. Besides, the algorithm can be used in various areas of robotics, where a wide viewing angle is important, but the distortion, typical for omnidirectional cameras, has to be eliminated [27,28].

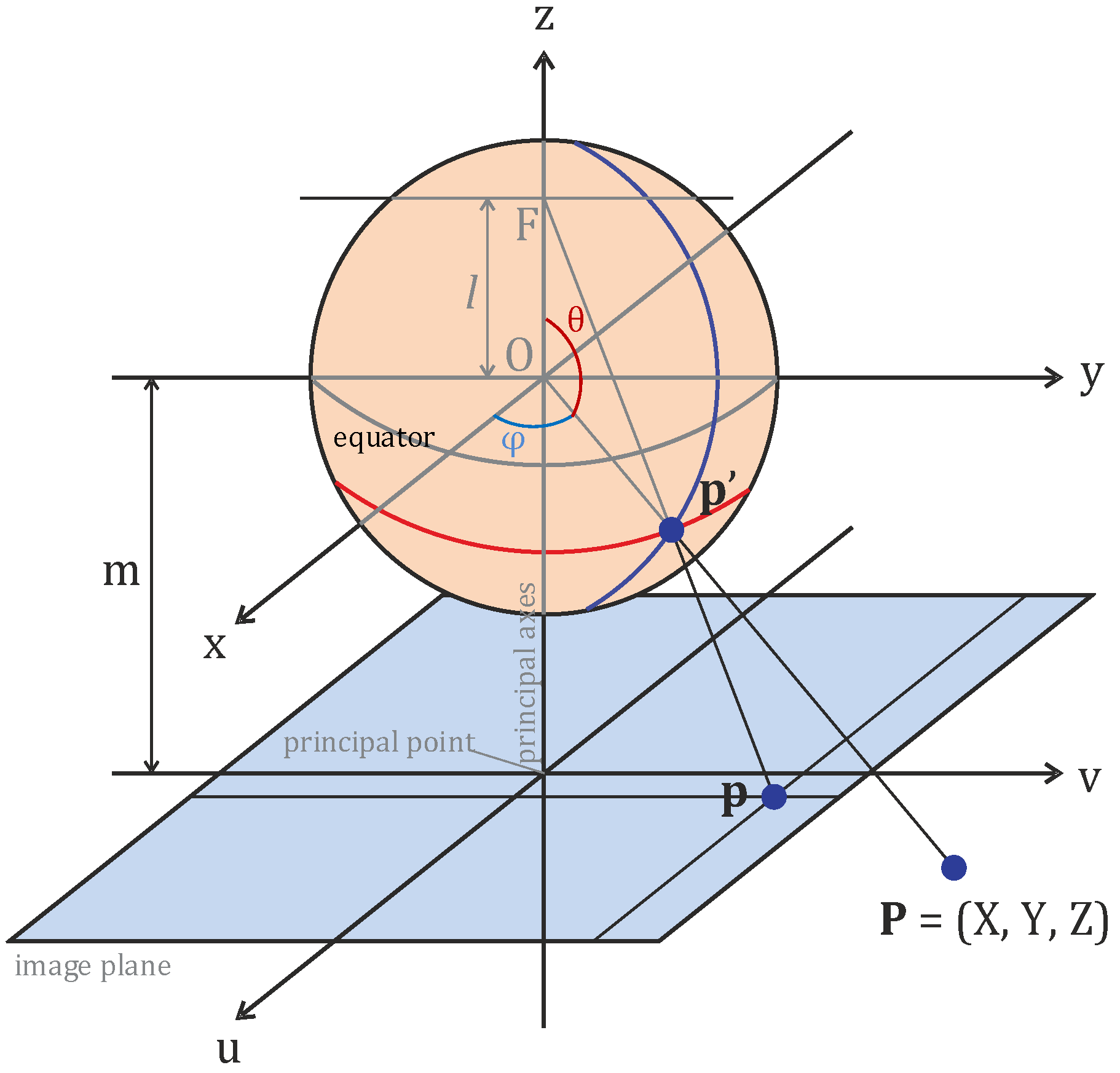
2.2. Methods for Calibration of Omnidirectional Optical Systems

The omnidirectional optical systems calibration is built on the Unifying Theory of Geyer and Daniilidis [29] for Central Panoramic Systems, according to which every perspective and catadioptric projection can be centered by mapping a three-dimensional sphere in the effective pixel. Ying and Hu [30] extended this theory for fisheye lenses with a viewing angle of $<180°.$

The unified imaging model provides a suitable framework for considering different camera types, such as standard, catadioptric perspective, and diverse fisheye lens types. The two-step process and the interrelationships are shown in Figure 2.

A spherical type of projection of world point $\mathit{P}$ by a ray onto the surface of the unit sphere ${\mathit{p}}^{\prime }=\left(x, y, z\right)$ is the first step.

A two-parameter minimal representation for a surface point of a sphere $\left(\theta ,\phi \right)$ includes the colatitude angle measured from the North pole $\theta$ with $r=\sqrt{x^2+y^2 }$ and the azimuth $\phi$.

$$\theta =\arcsin r, \theta \in \left[0,\pi \right],$$

(3)

$$\phi =\arctan \frac{y}{x}, \phi \in \left[-\pi ,\pi \right].$$

(4)

The viewpoint $\mathit{O}$ is the center of the sphere, which is along its normal $z$-axis at a distance $m$ from the image plane (Figure 2).

In the second step the point ${\mathit{p}}^{\prime }=\left(\theta ,\phi \right)$ is projected onto the image plane with the viewpoint $\mathit{F},$ which is located at a distance $l \left(l\in \left(0,1\right)\right)$ along the $z$ axis above $\mathit{O}.$ $\mathit{p}=\left(r,\phi \right)$ are the polar coordinates of the image plane point where

$$r=\frac{sin \theta \times \left(l+m\right)}{l-cos \theta }.$$

(5)

There are two basic parameters $l$ and $m$ for the unified imaging model. For $m=f^{\prime }$ (where $f^{\prime }$ is the focal length of the lens), depending on the values of the parameter $l$ three types of imaging can be distinguished [7]:

• Stereographic for $l=1$.
• Perspective for $l=0$.
• Fisheye for $l>0$.

A coordinate system transformation is needed for the relationship identification between the pixel position of the image and the position of the spatial center:

• Linear transformation to the camera coordinate system from the world coordinate system.
• Nonlinear transformation from the camera coordinate system to the image plane. To approximate the fisheye lens model a Taylor polynomial is used [7].

The key issue for the image transformation algorithm is setting the lens transfer function which connects the coordinates (in three dimensions) of a point in the object space with the coordinates of its image in the plane of the receiver. To address this task, the omnidirectional optical system is calibrated.

The different methods for calibrating OOES are presented and compared in detail in [7,31].

What is needed is a technique that does not require any special technical equipment and can be employed by unskilled operators. The method of Scaramuzza described in [32] was selected as the most easy-to-use.

This approach is implemented through the MATLAB “OCamCalib” toolkit. For calibration, it is necessary to take several images positioned in a chessboard form with a calibrated optic system. What follows is a calculation of the calibration parameters (such as polynomial coefficients and mean coordinates) for two functions that define a connection between the three-dimensional coordinates of the point in object space and the coordinates of its image in the coordinate system of the image sensor $\left(\left[\begin{array}{c}{u}^{\prime }\\ v^{\prime }\end{array}\right]\right)=\mathrm{world}2\mathrm{cam}\left(\left[\begin{array}{c}x\\ y\\ z\end{array}\right]\right)$ and $\left(\left[\begin{array}{c}x\\ y\\ z\end{array}\right]\right)=cam2world\left(\left[\begin{array}{c}{u}^{\prime }\\ v^{\prime }\end{array}\right]\right)$. A detailed calibration process is described in [32,33,34].

3. Proposed Geometric Projection Approach for Omnidirectional Optical System Calibration

The omnidirectional camera geometric projection model used for calibration is shown in Figure 3.

Here, $\mathit{X},\mathit{Y},\mathit{Z}$ is a coordinate system in the object space; $\mathit{U},\mathit{V}$—the coordinate system in the plane of the image sensor; $\left[x,y,z\right]$—point coordinates in the object space; $\mathit{p}$—point image; $\left[u,v\right]$—image coordinates of this point in the plane of the image sensor; $\mathit{P}$—vector originating from the coordinate system origin and directed at the point in the object space.

The model is based on the following assumptions:

• The catadioptric camera is a centered optical system; therefore, there is a point at which all the reflected rays intersect. This [0,0,0] point is the coordinate system origin $X,Y,Z.$
• The optical system focal plane has to coincide with the plane of the image sensor, only minor deviations are permissible.
• The mirror has rotational symmetry about the optical axis.
• The distortion of the lens in the model is not considered since the mirror used in an omnidirectional camera requires a long focal length of the lens. Thus, this lens distortion can be neglected. However, in the case of the fisheye lens, the distortion must be included in the calculated projection function.

Since we suppose that the focal plane of the optical system coincides with the image sensor plane, it follows that $x$ and $y$ are proportional to $u$ and $v$, respectively:

$$\left[\begin{array}{c}x\\ y\end{array}\right]=\alpha \times \left[\begin{array}{c}u\\ v\end{array}\right],$$

(6)

where $\alpha$ is a scaling factor, $\alpha >0$.

The purpose of calibration is to find a function that will describe the correspondence between the point images $p$ and the three-dimensional vector $\mathit{P}$. Thus,

$$\mathit{P}=\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{c}\alpha \times u\\ \alpha \times v\\ f\left(u,v\right)\end{array}\right].$$

(7)

When assigning $u=\alpha ·u$ and, $v=\alpha ·v$ then

$$\mathit{P}=\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{c}u\\ v\\ f\left(u,v\right)\end{array}\right].$$

(8)

Because the vector $\mathit{P}$ is not a point, but only a direction to it, the latter simplification is permissible. Moreover, as the mirror is rotationally symmetric (as well as the distortion of the fisheye lens), the function $f\left(u,v\right)$ depends only on the distance $\rho$ between the point image and the image center:

$$\mathit{P}=\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{c}u\\ v\\ f\left(\rho \right)\end{array}\right],$$

(9)

where $\rho =\sqrt{u^2+v^2}.$

The calculation of the coefficients of the polynomial $f\left(\rho \right)$ is carried out by the method of least squares:

$$f\left(\rho \right)={\alpha }_0+{\alpha }_1\rho +{\alpha }_2{\rho }^2+\cdot \cdot +{\alpha }_n{\rho }^n.$$

(10)

However, to obtain its coefficients $a_0,a_1,a_2,a_3,\dots ,a_n$ we need to consider the distortions caused by the discretization of the image sensor and the fact that the pixels do not always have a square form. Thus, the border of the circular image takes the form of an ellipse (Figure 4). To account for these distortions, we complement our model with affine transformations:

$$\left[\begin{array}{c}{u}^{\prime }\\ v^{\prime }\end{array}\right]=\left[\begin{array}{cc}c& d\\ e& 1\end{array}\right]\times \left[\begin{array}{c}u\\ v\end{array}\right]+\left[\begin{array}{c}{x}_c^{\prime }\\ y_c^{\prime }\end{array}\right],$$

(11)

where $u^{\prime },v^{\prime }$ are the true coordinates in the coordinate system of the image sensor, $u,v$ coordinates without distortions, $x_c^{\prime },y_c^{\prime }$ center coordinates of the circular image.

As a result of using the calibration toolbox [33], we obtain all the necessary parameters for Equation (12). That function is specifying the relationship of the three-dimensional coordinates of the object points in the objects space and the coordinates of its image in the image sensor coordinate system (hereinafter, we will assume that these functions already contain the calculated parameters):

$$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=f\left(x,y,z,{\alpha }_0,{\alpha }_1,{\alpha }_2,{\alpha }_3,..{\alpha }_n,x_c^{\prime },y_c^{\prime },c,d,e\right)=cam2world\left(\begin{array}{c}{u}^{\prime }\\ v^{\prime }\end{array}\right).$$

(12)

4. Algorithm of Image Conversion for Omnidirectional Optoelectronic Systems

The algorithm has three basic parts (Figure 5).

The first part is the formation of a cloud of three-dimensional points in the object space corresponding to the field of view of, a kind of virtual perspective camera. We suggest that this camera has desirable characteristics: α is the angle of the virtual camera view; φ is the rotation angle of the virtual camera around the Z axis; θ is the tilt angle of the virtual camera from the Z axis.

In the second part, the coordinates of the images of these points in the plane of the image sensor are determined. For this purpose, the transfer function of the OOES found using the omnidirectional camera calibration procedure is used.

The third part is the elementwise (pixel) formation of the output image from the original omnidirectional image using the coordinates found in the second part.

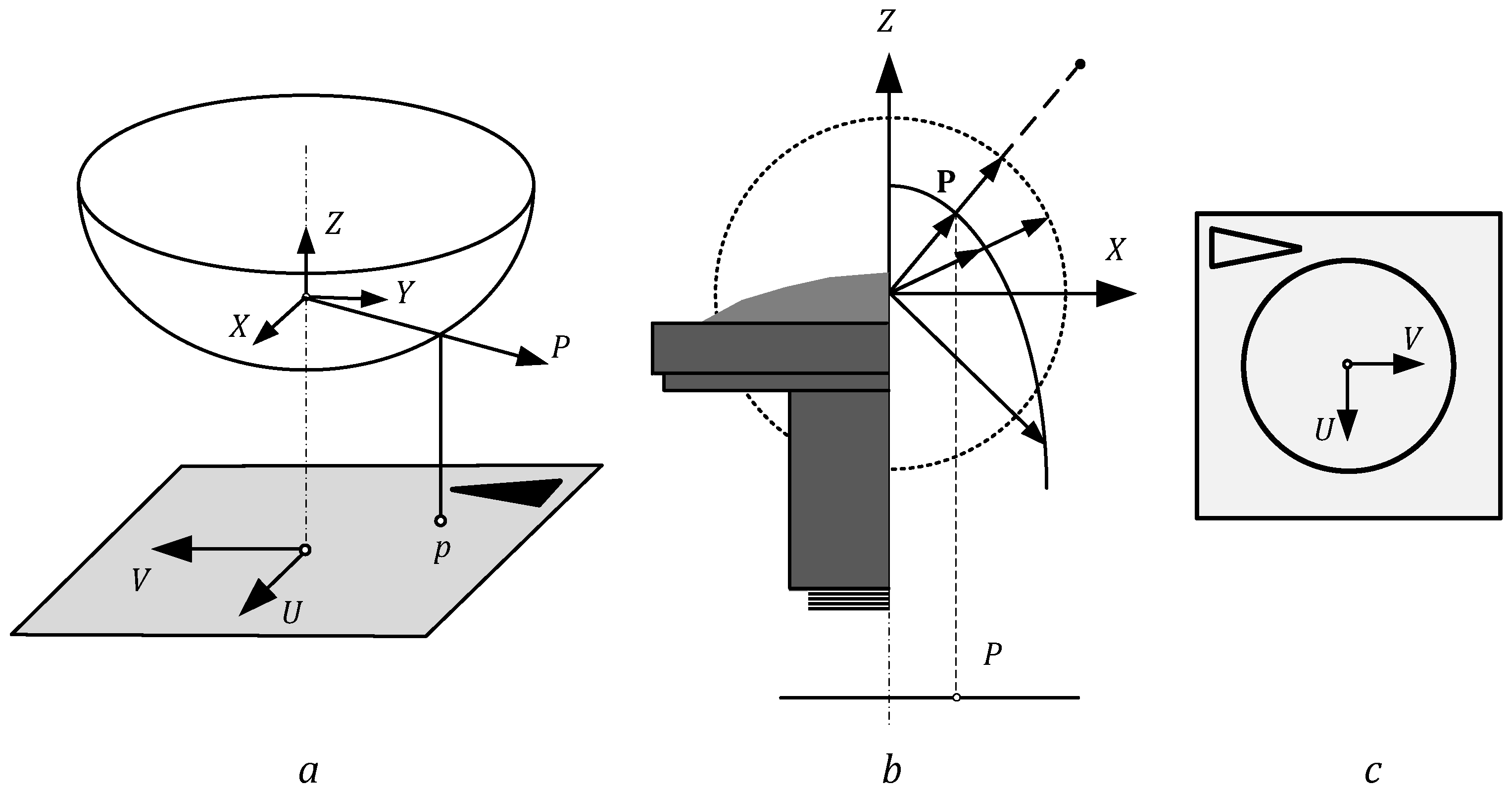
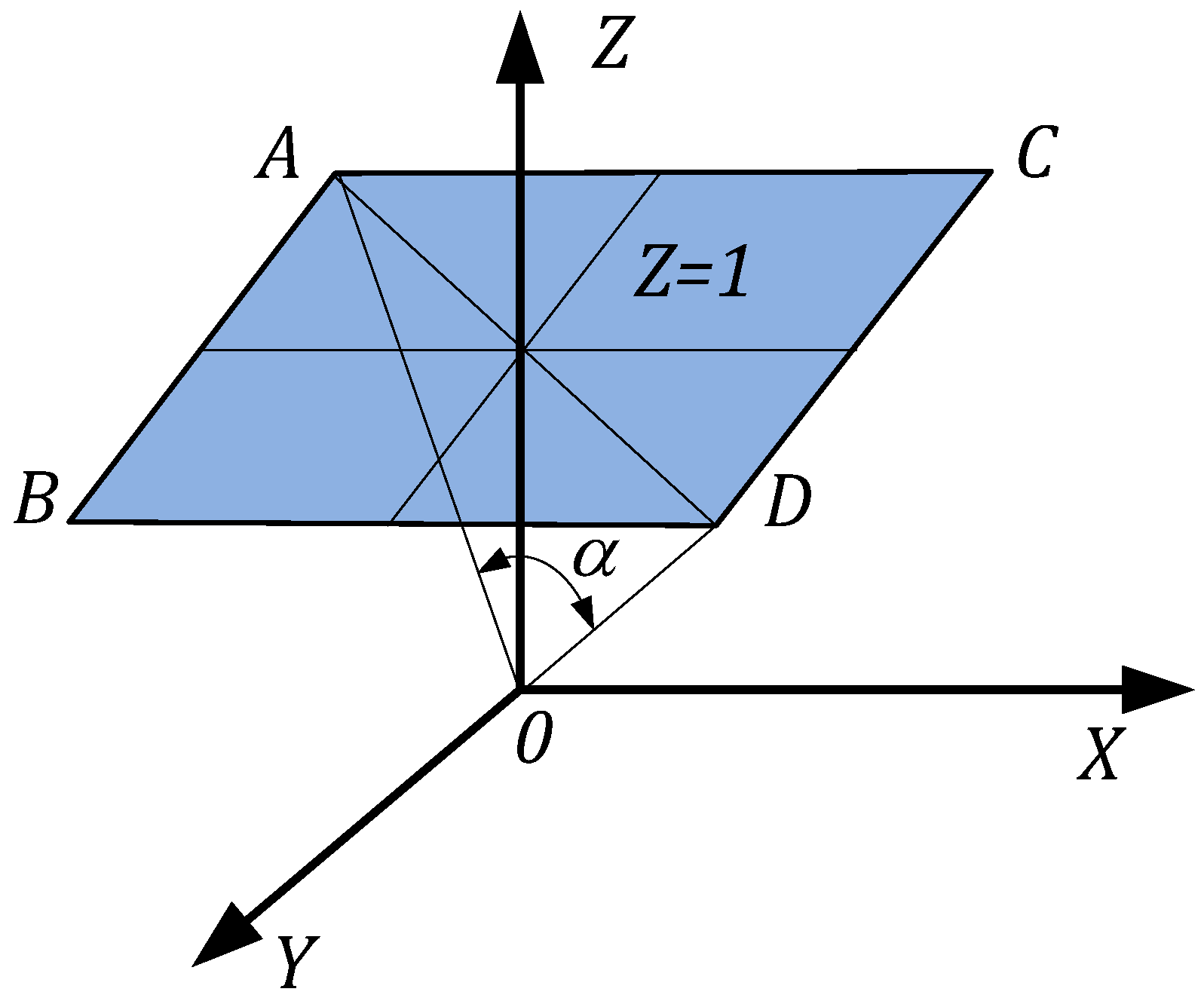
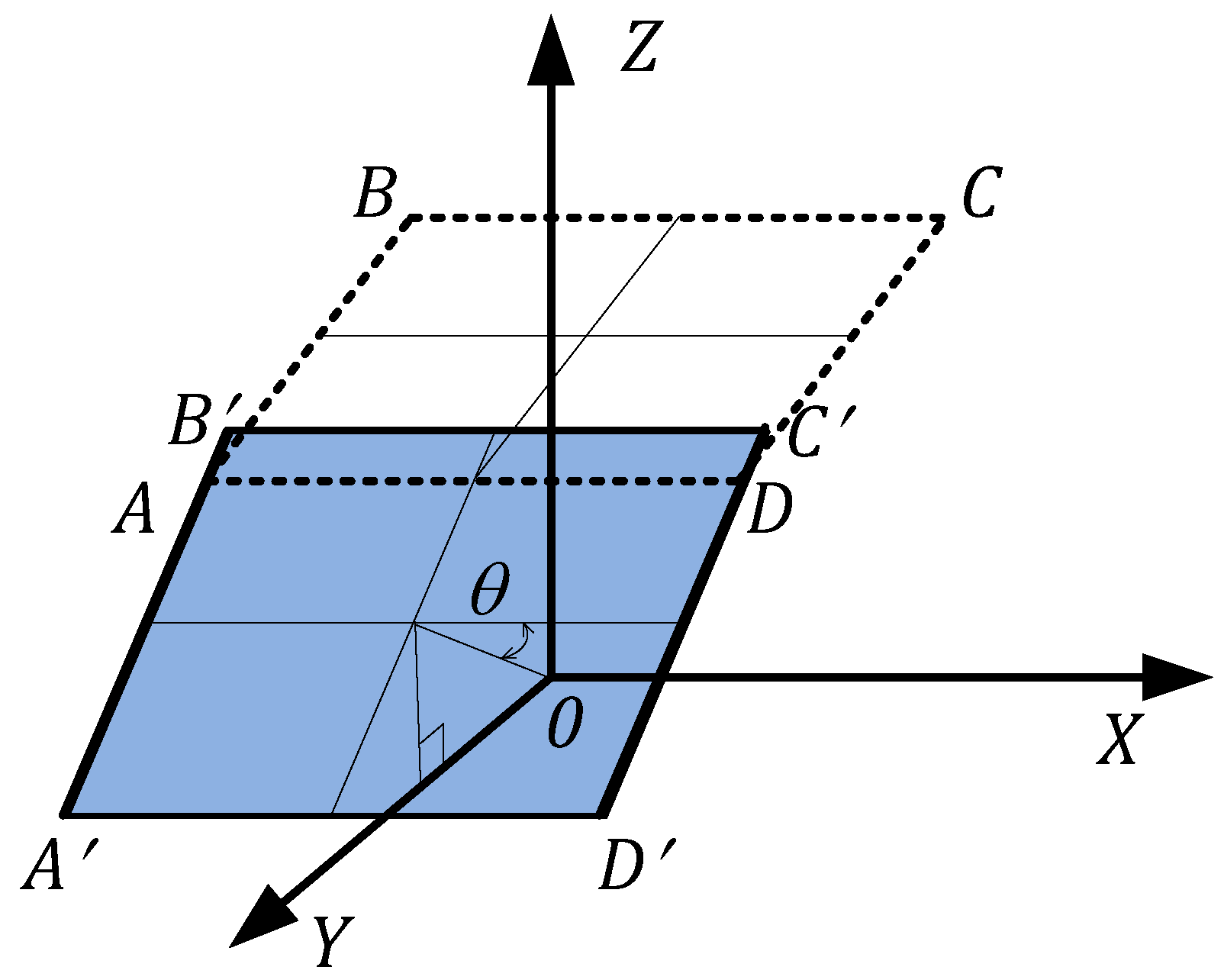
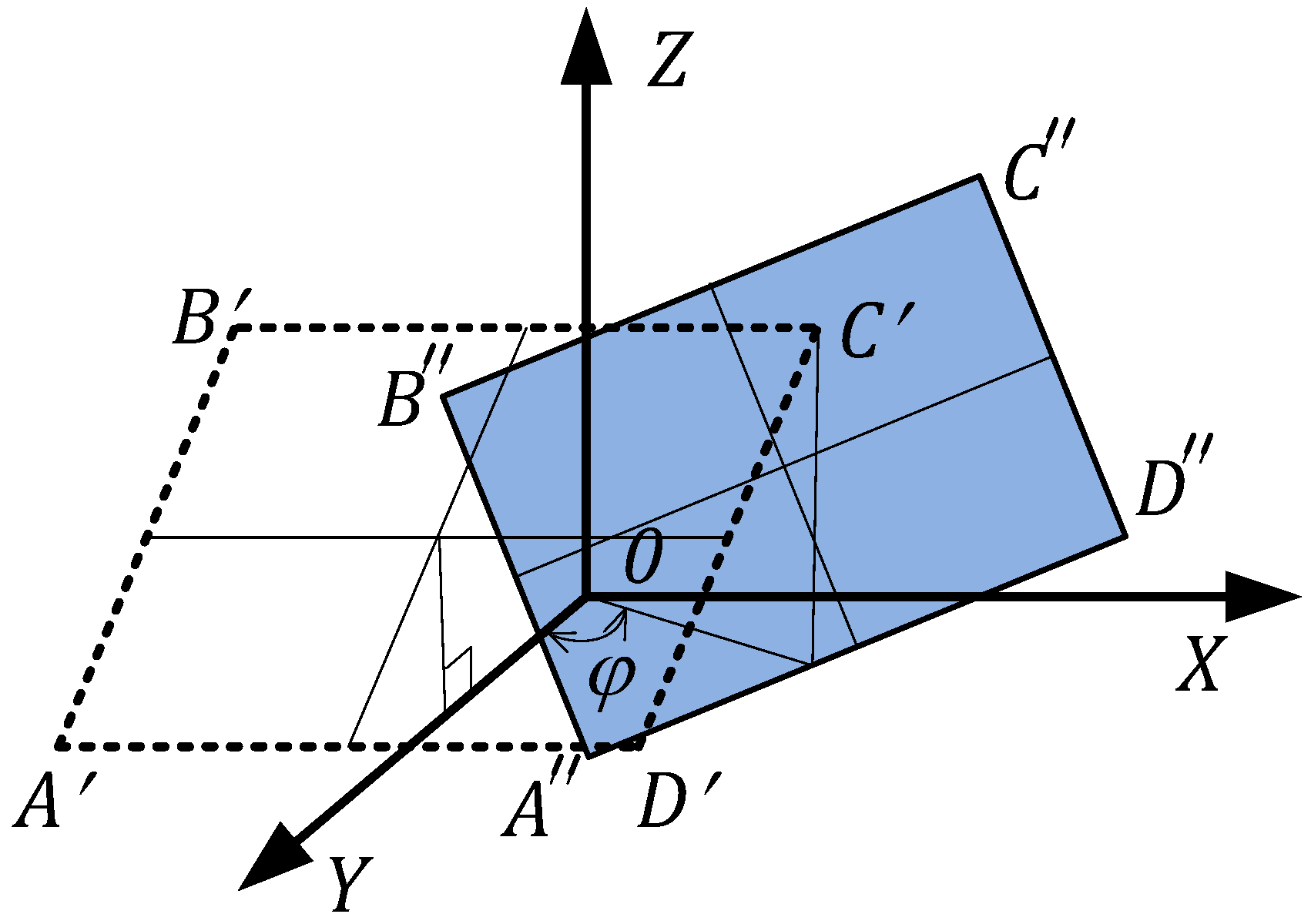
4.1. The First Stage: Formation of a Cloud of Points Characterizing the Field of View of the Virtual Perspective Camera

To implement the first stage, we need to set the characteristics of this camera:

$H_{res}$—horizontal resolution;

$K_{res}$—side ratio (for example, 4/3 or 16/9);

$V_{res}=\frac{H_{res}}{K_{res}}$—vertical resolution;

$\alpha$ is the angle of the virtual camera view;

$\phi$ is the rotation angle of the virtual camera around the $Z$ axis;

$\theta$ is the tilt angle of the virtual camera from the $Z$ axis.

The $Z$ axis coincides with the omnidirectional camera optical axis. First, we calculate the field view of the virtual camera with $\phi =0, \theta =0$ (Figure 6). Since when passing through the lens, we lose information about the distance to the object, we can place the plane of the virtual camera’s field of view at an arbitrary distance. To simplify calculations, a distance of $1 m$ is assumed.

In this way, the virtual camera field of view will be the rectangular area defined by the points ABCD, located parallel to the $\mathit{O}\mathit{x}\mathit{y}$ plane at a unit distance.

The rectangular area $ABCD$ is represented as an array $\mathit{M}$ of size $H_{res}$ by $V_{res}$ containing the coordinates of three-dimensional points ${\mathit{P}}_{\mathit{i},\mathit{j}},$:

$$\mathit{M}=\left[\begin{array}{ccc}{P}_{0,0}& \cdots & P_{H_{res}-1,0}\\ ⋮& ⋮& ⋮\\ P_{0,V_{res}-1}& \cdots & P_{H_{res}-1,V_{res}-1}\end{array}\right],$$

(13)

where

$${\mathit{P}}_{\mathit{i},\mathit{j}}=\left[\begin{array}{c}{x}_{i,j}\\ y_{i,j}\\ z_{i,j}\end{array}\right].$$

(14)

Thus, point $A$ corresponds to $P_{0,0}$, $B\to P_{0, V_{res}-1}$, $C\to P_{H_{res}-1, 0}$, $D\to P_{H_{res}-1,V_{res}-1}.$ We calculate the geometric dimensions of the region $ABCD$ as follows:

$$\begin{gathered} \mathit{A}\mathit{D}=2tan \left(\frac{\alpha }{2}\right), \\ \mathit{A}\mathit{C}=\sqrt{\mathit{A}{\mathit{D}}^2-\mathit{A}{\mathit{B}}^2}=\sqrt{\frac{{\left(2\cdot tan \alpha \right)}^2\times K_{res}^2}{K_{res}^2+1}}, \\ \mathit{A}\mathit{B}=\frac{\mathit{A}\mathit{C}}{K_{res}}=\sqrt{\frac{{\left(2\cdot tan \alpha \right)}^2\times K_{res}^2}{K_{res}^2+1}.} \end{gathered}$$

(15)

Then the coordinates of the vertices $A,B,C,D$ are to be calculated:

$$\begin{gathered} \mathit{A}={\mathit{P}}_{\mathit{0},\mathit{0}}=\left[\begin{array}{c}{x}_{0,0}\\ y_{0,0}\\ z_{0,0}\end{array}\right]=\left[\begin{array}{c}-AC/2\\ -AB/2\\ 1\end{array}\right], \\ \mathit{B}=P_{0,V_{res}-1}=\left[\begin{array}{c}{x}_{0,V_{res}-1}\\ y_{0,V_{res}-1}\\ z_{0,V_{res}-1}\end{array}\right]=\left[\begin{array}{c}-AC/2\\ AB/2\\ 1\end{array}\right], \\ \mathit{C}=P_{H_{res}-1,0}=\left[\begin{array}{c}{x}_{H_{res}-1,0}\\ y_{H_{res}-1,0}\\ z_{H_{res}-1,0}\end{array}\right]=\left[\begin{array}{c}AC/2\\ -AB/2\\ 1\end{array}\right], \\ \mathit{D}=P_{H_{res}-1,V_{res}-1}=\left[\begin{array}{c}{x}_{H_{res}-1,V_{res}-1}\\ y_{H_{res}-1,V_{res}-1}\\ z_{H_{res}-1,V_{res}-1}\end{array}\right]=\left[\begin{array}{c}AC/2\\ AB/2\\ 1\end{array}\right]. \end{gathered}$$

(16)

Taking into consideration that $x_{i,0}=x_{i,1}=\cdots =x_{i,V_{res}-1}, y_{0,j}=y_{1,j}=\cdots =y_{H_{res}-1,j,} z=1$ for all points ${\mathit{P}}_{\mathit{i},\mathit{j}},$ we obtain

$$\begin{gathered} x_i=-\frac{AC}{2}+\frac{AC}{H_{res}-1}\times i, \\ {y}_j=-\frac{AB}{2}+\frac{AB}{V_{res}-1}\times j, \\ {\mathit{P}}_{\mathit{i},\mathit{j}}=\left[\begin{array}{c}{x}_{i,j}\\ y_{i,j}\\ 1\end{array}\right]. \end{gathered}$$

(17)

Next, we need to calculate the field of view ABCD by the angles of rotation $\phi$ and slope $\theta$ (Figure 7). First, we rotate the field of view ABCD by an angle $\theta$, while $x_i$ remains unchanged:

$${\mathit{P}}_{\mathit{i},\mathit{j}}^{\prime }=\left[\begin{array}{c}{x}_i^{\prime }\\ y_j^{\prime }\\ z_j^{\prime }\end{array}\right]=\left[\begin{array}{c}{x}_i\\ -zsin \theta +y_{j}cos \theta \\ zcos \theta +y_{j}sin \theta \end{array}\right]=\left[\begin{array}{c}{x}_i\\ y_{i}cos \theta -sin \theta \\ y_{i}sin \theta +cos \theta \end{array}\right].$$

(18)

Next, we rotate the $A^{\prime }{B}^{\prime }{C}^{\prime }{D}^{\prime }$ relative to the $Z$ axis by an angle $\phi$ (Figure 8), while $z_j^{\prime }$ remains unchanged:

$${\mathit{P}}_{\mathit{i},\mathit{j}}^{″}=\left[\begin{array}{c}{x}_i^{″}\\ y_j^{″}\\ z_j^{″}\end{array}\right]=\left[\begin{array}{c}{x}_i^{\prime }cos \phi +y_j^{\prime }sin \phi \\ -x_i^{\prime }sin \phi +y_j^{\prime }cos \phi \\ z_j^{\prime }\end{array}\right].$$

(19)

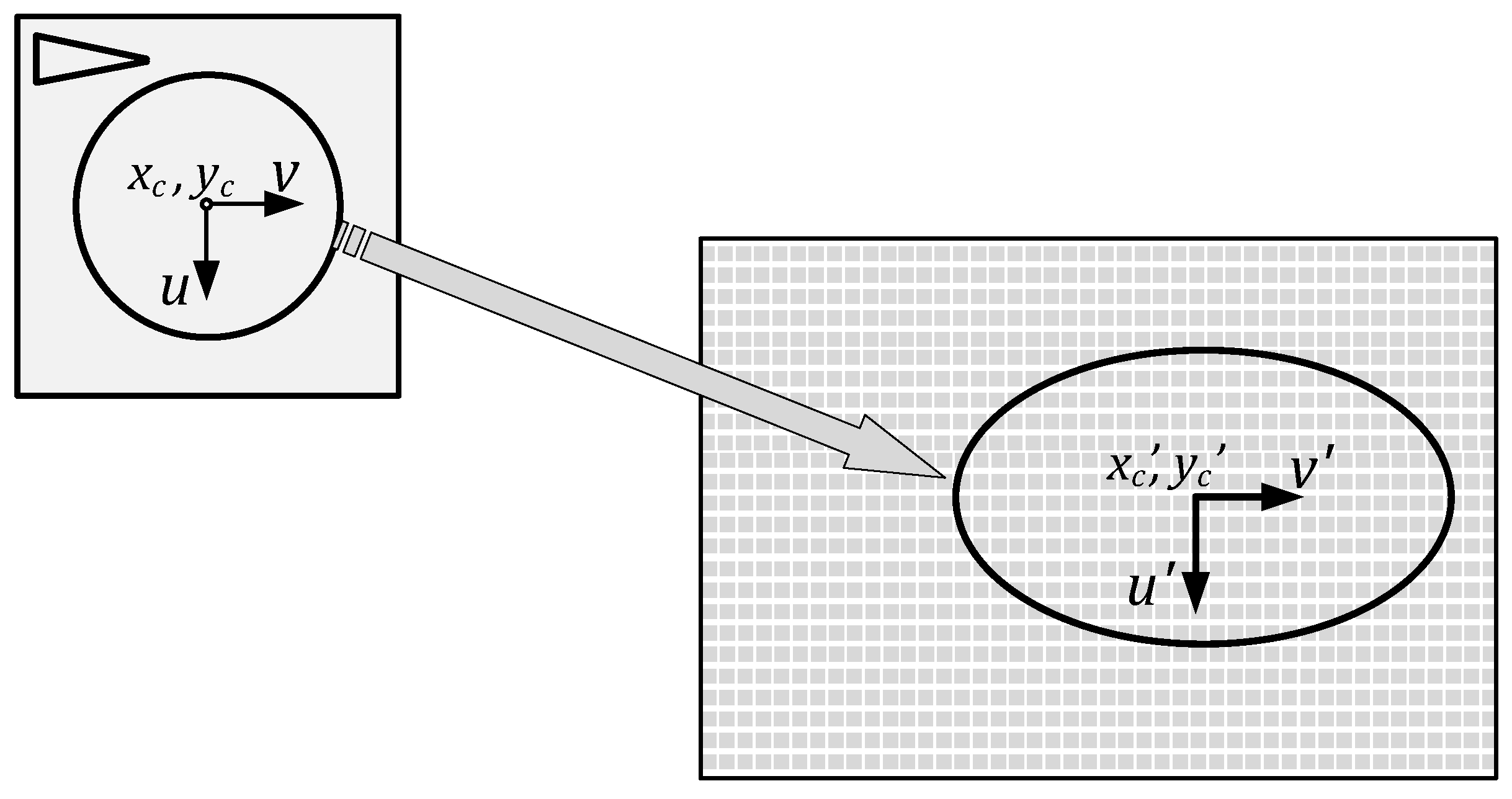
4.2. The Second Stage: Search for the Coordinates of the Point Images

To obtain the relationship between the spatial coordinates of the point $P_{i,j}^{″},$ obtained in Equation (19), and pixel coordinates $p^{\prime }$ of its image in the coordinate system of the image sensor, we apply the function of a direct correspondence between coordinates of the coordinates (9), with parameters calculated because of calibration:

$${\mathit{p}}_{\mathit{i},\mathit{j}}^{\prime }=\left[\begin{array}{c}{u}_{i,j}^{\prime }\\ v_{i,j}^{\prime }\end{array}\right]=world2cam\left(P_{i,j}^{\prime }\right)=world2cam\left(\left[\begin{array}{c}{x}_{i,j}^{\prime }\\ y_{i,j}^{\prime }\\ z_{i,j}^{\prime }\end{array}\right]\right).$$

(20)

Thus, we obtain an array ${\mathit{M}}^{\prime }$ containing pixel coordinates of the images of the points for the calculated field of view:

$${\mathit{M}}^{\prime }=\left[\begin{array}{ccc}\left[\begin{array}{c}{u}_{0,0}^{\prime }\\ v_{0,0}^{\prime }\end{array}\right]& \cdots & \left[\begin{array}{c}{u}_{H_{res}-1,0}^{\prime }\\ v_{H_{res}-1,0}^{\prime }\end{array}\right]\\ :& :& :\\ \left[\begin{array}{c}{u}_{0,V_{res}-1}^{\prime }\\ v_{0,V_{res}-1}^{\prime }\end{array}\right]& \cdots & \left[\begin{array}{c}{u}_{H_{res}-1,V_{res}-1}^{\prime }\\ v_{H_{res}-1,V_{res}-1}^{\prime }\end{array}\right]\end{array}\right].$$

(21)

4.3. The Third Stage: Construction of the Corrected Image

The last third step is to form the resulting image pixel using a pixel from the original omnidirectional image:

$${\mathit{I}}^{\prime }=\left[\begin{array}{ccc}L\left(u_{0,0}^{\prime },v_{0,0}^{\prime }\right)& \cdots & L\left(u_{H_{res}-1,0}^{\prime },v_{H_{res}-1,0}^{\prime }\right)\\ :& :& :\\ L\left(u_{0,V_{res}-1}^{\prime },v_{0,V_{res}-1}^{\prime }\right)& \cdots & L\left(u_{H_{res}-1,V_{res}-1}^{\prime },v_{H_{res}-1,V_{res}-1}^{\prime }\right)\end{array}\right]$$

(22)

where $L$ is the signal level in each pixel of the image sensor (or the original omnidirectional image) with coordinates $u_{i,j}^{\prime },v_{i,j}^{\prime }$. The resulting image can be improved by any anti-aliasing method since we are dealing with fractional coordinate values.

5. Experimental Results

The omnidirectional camera was calibrated using the OCamCalib toolkit. For this purpose, nine images of a test object were taken in the form of a chessboard on a calibrated camera. In the calibration experiments, it was found that usually, nine images were sufficient to stabilize the determined coefficients. A two-megapixel IP camera was used with a super wide-angle lens of fisheye mounted on it (Fujinon FE185CO46HA-1: Focal length 1.4 mm, Iris range F1.4–F16, Angle of view 1/2”) [35]. This approach can be applied to catadioptric setup too.

After calibration and setting of the input parameters for the camera (Figure 5) the following coordinates were obtained:

• center of the circular image (pixel) coordinates:
• $x_c^{\prime }=580718\cdot {10}^{-3}$, $y_c^{\prime }=770693\cdot {10}^{-3};$
• standard deviation of re-projection (pixel): $0.7948;$
• affine coefficients:

  $$c=999779\times {10}^{-6}, d=913037\times {10}^{-10},e=-374671\times {10}^{-9};$$
• polynomial coefficients:

  $$\begin{gathered} a_0=-338295\times {10}^{-6}, a_1=0, a_2=106759\times {10}^{-12}, \\ {a}_3=-755634\times {10}^{-16},a_4=-1593\times {10}^{-16}. \end{gathered}$$

As seen, the mean squared error of re-projection (in other words, the error of the function of the direct connection of the coordinates of world2cam) turned out to be less than the size of a pixel; this is shown in Figure 9b. Such accuracy is sufficient for both the tasks of observation and most calculation tasks.

Further, the parameters found because of the calibration were used in the algorithm implemented in the module for the Typhoon system [36]. The module is implemented based on an omnidirectional non-mechanical PTZ camera, turning after moving objects. Figure 10 shows an example of the program operation.

Thus, using the developed algorithm, we implemented a non-mechanical pivoting camera based on an omnidirectional camera, while the mean squared error of the reproducing points from the original omnidirectional image onto the image with corrected distortion was less than pixel size.

The proposed precision calibration using a statistical approach is also applied to a digital camera with a fisheye lens of the type “cnAICO-Fisheye Lens/1/2”—Focal Length 1.4 mm, F1.4 Manuel Iris—182 Degree [37].

In Figure 11 the output wide-angle image is shown, which clearly shows the distortions and the test object for calibration.

After calibration, the following results were obtained:

• input image size $=\left(2592, 1920\right)$;
• center of the circular image (pixel) coordinates: $x_c^{\prime }=1284.93, y_c^{\prime }=1114.8$;
• standard deviation of re-projection (pixel): 2.476;
• average error = 2.476 pixel;
• polynomial coefficients:

  $$\begin{gathered} a_0=-6.470\times {10}^2, a_1=0, a_2=5.652\times {10}^4, \\ {a}_3=-8.358\times {10}^{-8}, a_4=1.059\times {10}^{-10}. \end{gathered}$$

After applying the algorithm for virtual fields of view of 90 and 120 degrees, the images shown in Figure 12a,b are obtained where the distortions are removed.

6. Conclusions

This paper presents a practical approach for calibrating and correcting distortion for fisheye cameras. The only requirement is that the lens can be modeled by a Taylor series expansion of a spherical perspective model.

Based on some assumptions, an algorithm has been developed for converting images received by omnidirectional cameras into images with corrected distortion corresponding to the classical projection geometric models. This algorithm makes it possible to obtain an image with corrected distortion. It is suitable for both types of omnidirectional cameras: the ones with catadioptric optical systems and those with fisheye lenses.

The algorithm was successfully applied in a software module for a “Typhoon” optical-electronic observation system, implemented based on an omnidirectional non-mechanical camera, turning after moving objects [36].

The algorithm was applied in a software module for a “Typhoon” CCTV system, implementing a PTZ camera, turning after moving objects based on an omnidirectional camera with a fisheye lens.

The algorithm can be applied also in various fields of robotics, where a wide viewing angle is important, but the elimination of distortion, inherent in omnidirectional cameras, is needed. It can also be used to create 360-degree videos for the YouTube platform, see example—https://www.youtube.com/watch?v=j34Ut0QHNYA (accessed on 3 October 2022).

The transformation of images from fisheye cameras into an equiangular representation moves the trajectory estimation problem from a nonlinear motion model to a linear one that can be treated with classical algorithms such as the Kalman filter.