Abstract
The purpose of this study is to describe a methodology for assessing the geotechnical stability of agricultural facilities, enabling prediction of the state of the geotechnical system, taking into account the influence of external factors and combinations of reactions of the geotechnical system under study. According to the methodology, the heterogeneous geotechnical monitoring data obtained are used in an adjusted geotechnical system model, allowing a bifurcation analysis to be carried out. The bifurcation analysis determines critical values of influencing factors, and the limits of stability of the geotechnical system studied parameters are adjusted. The developed methodology was used to assess and predict the geotechnical stability of agricultural facilities during the processing of geoelectric, resistive acoustic, accelerometric and strain-gauge control data obtained in the period from 2016 to 2021. A feature of the geotechnical system under study is the periodic flooding of the building basement caused by the processes of reclamation and irrigation, leading to changes in the groundwater level. The results show that the permissible calculated elastic limit of the foundation elements (32.2–35.1 MPa) before the loss of stability should be significantly reduced with a change in the water content coefficient (W) of the soil base: at W = 0.15 Eb = 30.7–32.0 MPa; at W = 0.35 Eb = 26.8–28.2 MPa; at W = 0.55 Eb = 24.9–25.3 MPa.
1. Introduction
Geotechnical stability is a complex indicator that characterizes the parameters of the reliable functioning of elements in the “ground foundation—foundation—structure” system. Currently, standards and regulatory documents define structural schemes for monitoring and managing engineering systems of buildings and structures that allow monitoring their geotechnical stability [1,2,3,4], which are based on the task of monitoring periodic variations in climatic, physical and mechanical parameters of the geotechnical system and the environment. However, inadequate attention is paid to monitoring and assessing the geotechnical stability of objects of the agro-industrial complex (AIC), the operating conditions of which are complicated by the presence of additional impacts on the soil base that are not taken into account in existing methodologies, namely:
- Reduction in the strength characteristics of the soil base due to the dynamic nature of the hydrogeological regime during the reclamation and irrigation activities.
- High vibratory load due to the operation of machinery on arable land and farmland located near the infrastructure of the geotechnical system of the agro-industrial complex (processing and production workshops, livestock facilities).
- Activation of destructive processes of the soil base due to the storage and processing of animal waste.
As a result, the process of long-term operation of agricultural geotechnical systems is associated with a constant change in the qualitative and quantitative indicators of the physical and mechanical parameters of their elements, due to changes in the overall loads on the soil base, fatigue phenomena in the properties of materials, as well as the presence of external periodic agrotechnical and climatic influences.
Currently, the processes of soil erosion, due to the dynamics of hydrogeological parameters, are considered in the aspect of the impact on geotechnical stability in various industrial areas around the world [1,2,3,4]. It may be noted that the processes of soil erosion are also actively occurring in the territories of agricultural lands due to reclamation and irrigation measures, changing the parameters of the stability of the soil base. However, modern scientists in the field of agricultural technologies assess the process of soil erosion only in terms of the impact on agricultural fertility indicators [5,6], without taking into account the loss of geotechnical stability and the development of emergency situations, which determines the relevance of research within the scope of this article. The authors of the article propose to assess the impact of agrotechnical load on the geotechnical stability of agricultural facilities, including the presence of hydrogeological dynamic load and erosion processes.
In the practice of construction and supervision of the operation of engineering structures of industrial and residential type, calculations of limit loads are provided until the structure and the geotechnical system as a whole maintain their stability [7,8]. However, there are cases of the development of pre-emergency and emergency situations that are the result of an insignificant output of one or more physical and mechanical parameters of the structure beyond the calculated values [9,10], or the synergetic effect of factors not taken into account in the construction calculations [11,12]. This is due to the incompleteness of the mathematical model adopted in the theory of material resistance, which underlies most traditional methodologies for assessing the stability of structures [13]. Models of this type, as a rule, do not take into account possible combinations of external factors on the geotechnical system, as well as possible combinations of its reactions that have additional mutual influence on the elements of the geotechnical system. It is precisely such conditions that lead to the development of hidden destructive processes in geotechnical systems, since the unaccounted total effects of certain factors, or their combinations, lead to changes in the permissible limit loads and stability limits established in the construction documentation of the object.
One of the priority tasks of monitoring geotechnical stability is the prediction and observation of the initial phases of the development of hidden destructive processes occurring in geotechnical systems. In solving problems of this class, the scientific and practical results have been obtained, described in the works of Russian and foreign authors [14,15,16,17]. The priority direction in this case is the integration of geodynamic and deformation monitoring of elements of the geotechnical system (soil foundation, foundations and structures) [18,19]. However, the effectiveness of this approach lies in the quality of the elaboration of algorithms for complex processing of geodynamic and deformation monitoring data, as well as the achievement of the adequacy of models used in predicting geotechnical stability, which also determines the relevance of this work.
The purpose of the study is to evolve a methodology for assessing the geotechnical stability of agricultural facilities, including a model and data processing algorithms based on the theory of bifurcations and allowing the prediction of the state of the geotechnical system, taking into account combinations of external factors and combinations of reactions of the geotechnical system under study.
2. Materials and Methods
Hidden destructive processes occurring in geotechnical systems are characterized by a gradual degradation of the physical and mechanical state of the materials of the structures and the soil base, and do not manifest themselves until the development of irreversible destruction processes. One of the reasons for their occurrence is the impact on the geotechnical system of one or more external factors (hydrogeological, vibration, temperature, climate, wind load, etc.), as well as the reaction of elements of the geotechnical system to the various effects (changes in stress fields, deformations, load redistribution).
Within the framework of the developed methodology, it is proposed to adjust the permissible limits of the load on the elements of the geotechnical system of agro-industrial complex (permissible loads of snow masses on the roofs of buildings, permissible levels of vibration noise, etc.), revealed at the stage of design calculations, taking into account the synergetic effect of many factors that reduce the overall limit of stability. It is proposed to present a geotechnical system in the form of a set of elementary modules that differ in the laws of transformation of incoming quantities, as well as their coefficients. In this case, possible combinations of elementary (basic) modules and the interrelations between them make it possible to form a model of a geotechnical system of any complexity (on-spot, local, regional levels) (Figure 1).
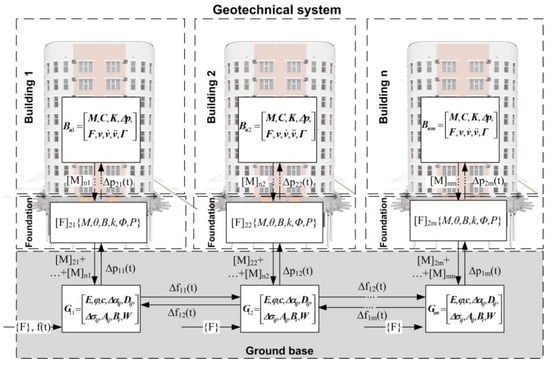
Figure 1.
A model of a geotechnical system.
The system includes the components are given in Table 1.

Table 1.
The system components.
The main agrotechnical influences that can affect the stability conditions of the geotechnical system of the agro-industrial complex, as mentioned earlier, include climatic and hydrogeological factors (dynamics of moisture saturation of the geological environment, wind exposure, temperature regime) and operational loads on local areas of the soil base (operation of the control object, neighboring buildings and structures, vibration load from agricultural machinery, dissolution of the ground rocks of the base due to the processing of biological waste of livestock) [20,21].
A change in the hydrogeological regime during land reclamation measures leads to the liquefaction of soils composing the soil base of the geotechnical system. As a result, under the influence of vibration and wind load, unsteady forced oscillations arise. We propose carrying out their study and control by the method of bifurcation analysis. This will make it possible to determine the maximum values of the structure displacement as a result of the complex impact of external factors and to identify not only their permissible level in these conditions, but also the most vulnerable sections of the structure.
The equation describing the displacements of the structure of the system under study can be written as [22]:
where M is the mass matrix of the i-element of the geotechnical system; C is the attenuation matrix of the i-element of the geotechnical system; K is the stiffness matrix of the i-element of the geotechnical system; v is the displacement vector; is the dynamic load vector (vibration noise).
The problem under consideration for a geotechnical system using the finite element method (FEM) procedure is reduced to solving a system of linear integro-differential equations
where is a vector of the desired displacement amplitudes of the i-element of the geotechnical system, is a vector of velocity of the i-element of the geotechnical system, is a vector of accelerations, displacements of the i-element of the geotechnical system, is the core of relaxation of the system [23], is the vector sum of the static loads (mass forces, hydrostatic water pressure, etc.)
The solution of the system of integro-differential equations with initial conditions , is carried out by Newmark method [23].
According to the mathematical model shown in Figure 1, the total external action vector {F} and the dynamic load vector affect the displacement and stiffness parameters [K] of the geotechnical system element. Moving from module to module of the geotechnical system, the parameters of the vibration effect ∆p(t) change taking into account the attenuation function [C]. Thus, the external impact creates favorable conditions for stress concentration at the weakest points of the soil foundation or structural elements, which leads to a loss of stability of the geotechnical system at significantly less short-term dynamic impacts than in static conditions established in construction design models.
Within the framework of the methodology, it is proposed to use methods of hydrological, geoelectric, vibroacoustic, accelerometric and strain-gauge control to ensure monitoring of the geotechnical stability of agricultural facilities. As noted earlier, the optimal solution to the problem of multiparametric analysis is the use of a bifurcation approach [12,24,25], which allows us to identify critical levels of influencing factors and reactions of the geotechnical system, leading to its abrupt transition to an unstable state. The terms “foundation serviceability” and “limit states” denote the ability to operate the building in normal mode (without the danger of violating operational standards), as well as the limiting state, which is on the verge of the transition of operational properties to emergency.
To implement this approach, an algorithm was developed (Figure 2), according to which a mathematical model of a geotechnical system was initially constructed based on the main model [26]. It takes into account the features and limitations inherent in a specific geotechnical system, among which, in general, it is necessary to distinguish:
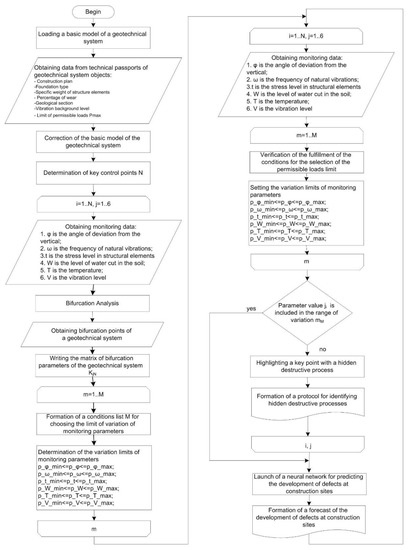
Figure 2.
An identification algorithm for hidden destructive processes in geotechnical systems.
- Construction plan;
- Type of foundation;
- The specific weight of the structural elements;
- Percentages of wear;
- Geological section;
- Vibration background level;
- The level of permissible limit loads.
The obtained data arrays are loaded into the basic model, which is a set of vectors describing the relationship of the components of the geotechnical system. Next, a system of differential equations is constructed and solved according to the basic rules of the bifurcation analysis method and the additions described in [25,26,27]. During the bifurcation analysis, bifurcation points are determined: a combination of system parameters leading to its transition to an unstable state, which further form a matrix of bifurcation parameters.
The provision of monitoring systems is proposed to be carried out at key control points that are the most informative and determined according to the approach described in [26]. In this case, the transfer functions of the components of the geotechnical system (ground base—foundation—structure) are analyzed [28] and, as a result, destructive processes are localized.
It is proposed to observe the physical and mechanical parameters of the structure using a deformation monitoring system that allows recording the axes deviation angle from the vertical, natural and forced oscillation frequencies, accelerograms, the level of mechanical stresses and forces in the structural elements. A system of this class includes a network of accelerometric and strain gauges located at the control points of the structure. It is proposed to register the level of exposure to external factors using a geoelectric monitoring system [29], which allows recording the parameters of moisture saturation and vibration background in the soil base.
The adaptive process of heterogeneous geotechnical monitoring data is carried out according to the approach described in [30]. After that, the data obtained are used by an adjusted model of the geotechnical system, allowing for bifurcation analysis. Bifurcation analysis determines critical values of influencing factors, as well as the physical and mechanical parameters of the materials of the geotechnical system, a small variation of which leads to the transition of the geotechnical system into an unstable state. As a result, modeling of multiple interactions and reactions of a geotechnical system make it possible to identify the most informative among a set of physical and mechanical parameters of elements of a geotechnical system, as well as a set of influencing factors which are subject to further monitoring. Based on the obtained bifurcation diagrams, the limits of variation in the studied parameters of the geotechnical system, as well as the limits of its stability, are adjusted.
3. Results
The developed methodology was used to assess and predict the geotechnical stability of agricultural facilities during the processing of geoelectric, resistive acoustic, accelerometric and strain-gauge control data obtained during geotechnical monitoring in the period from 2016 to 2021. The object of the study is a three-story building (part of the agro-industrial complex), built on a brick ribbon foundation (Figure 3a,b). The observations were carried out from September 2016 to February 2021. A feature of the geotechnical system under study is the periodic flooding of the building basement caused by the processes of reclamation and irrigation, leading to changes in the groundwater level, as well as the presence of cracks on the facade elements.
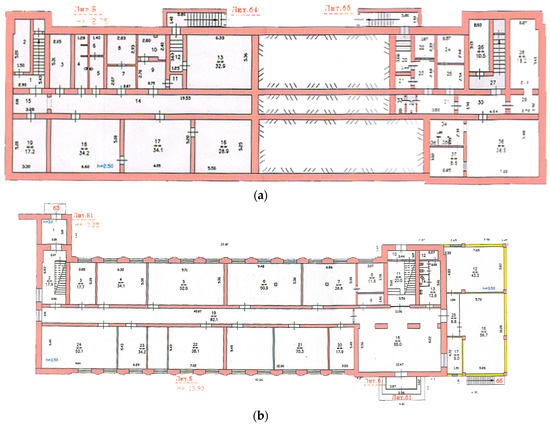
Figure 3.
The plan of 3-story brick building with a ribbon foundation under study: (a) The building basement plan; (b) The 1st floor plan.
Accelerometric sensors were placed at the control points to register the vibration frequencies and angles of deviation from the vertical line (red dots in Figure 4, the number of sensors was n = 28). Strain gauges were placed at the control points of the structure (blue dots in Figure 4, the number of sensors n = 18) (Figure 4) to register stresses and forces. Trends in the parameters of water saturation of the soil base and the level of vibration noise were recorded by means of geoelectric monitoring, with a frequency of 4 times a day [29].
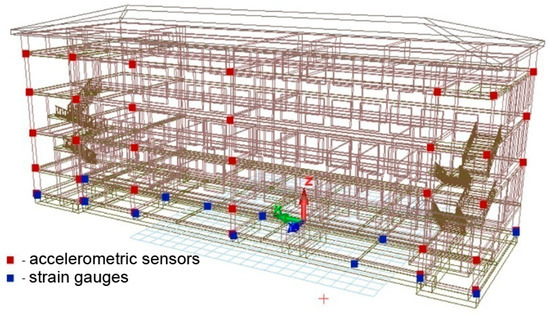
Figure 4.
Placement of the sensor network of the geotechnical monitoring system.
According to the results of the data analysis during the period from 2016 to 2018, the most vulnerable key points of the structure were identified (marked in red in Figure 5 below), in which hidden destructive processes were presumably developing. These processes were due to the dynamics of the water level of the soil base caused by reclamation and irrigation measures on agricultural land.
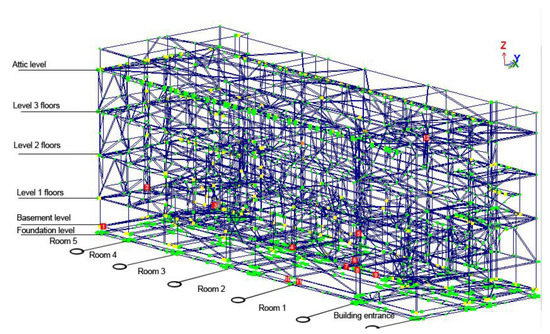
Figure 5.
The most vulnerable key points with the development of hidden destructive processes.
Based on the developed methodology, stress modeling was carried out in the structure of the building foundation with a change in the proportion of natural humidity of the upper layers of the soil.
A ground cross section diagram is shown in Figure 6. The soil base consisted of five layers; the characteristics of each layer are shown in Table 2.
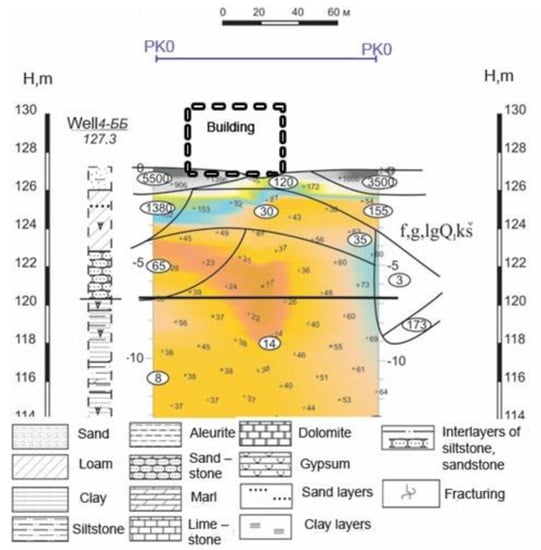
Figure 6.
A ground cross section diagram.

Table 2.
The soil base characteristics.
During the simulation, the moisture fractions changed in increments of 10 units, while the specific gravity of the soil increased proportionally. The calculation was carried out taking into account the own weight of all structural elements of the building under study according to the Coulomb–Mohr law, which takes into account the deformation of the soil base (Figure 7).
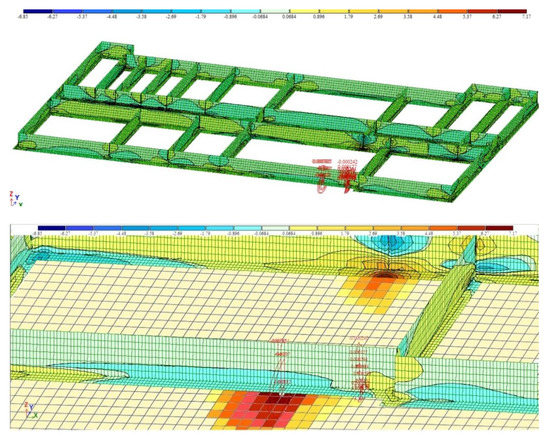
Figure 7.
Simulation results for a soil base with a moisture content of W = 0.25.
In May 2019, it was decided to introduce an additional local monitoring system present in the area with the highest density of vulnerable control points 4, 5, 6, 7, 10, 11 (Figure 5). This system included a set of three accelerometric and three strain gauges.
During further observations of the dynamics of the physical and mechanical parameters of the geotechnical system under study in October 2019, the fact of crack formation in the structure of the external load-bearing wall of the basement and the first floor of the building was noted, which coincides with the key points No. 4,7,10,11 (located in the plane of the load-bearing wall of the 1st floor of the building under study).
4. Discussion
During the data analysis, according to the developed methodology and the bifurcation approach, a significant decrease in the permissible values of the elastic limit of the object under study, located in the territory of the agro-industrial complex, was confirmed at key points of the foundation structure No. 1–12 (according to Figure 5), with small variations in the water content coefficient of the soil base. The obtained results correlate well with similar studies in the field of deformation monitoring [31].
Modeling has shown that when the moisture saturation of the soil base increases during reclamation activities, deformations occur at key points No. 4,10,11 (according to Figure 5), leading to the occurrence of stress isofields concentrations in the most vulnerable structural elements, which is fully consistent with the results obtained using the developed algorithm for identifying hidden destructive processes.
According to the obtained results, the calculated elastic limit of the foundation elements (32.2–35.1 MPa) before the loss of stability has significantly reduced with a change in the water content coefficient of the soil base (Figure 8):
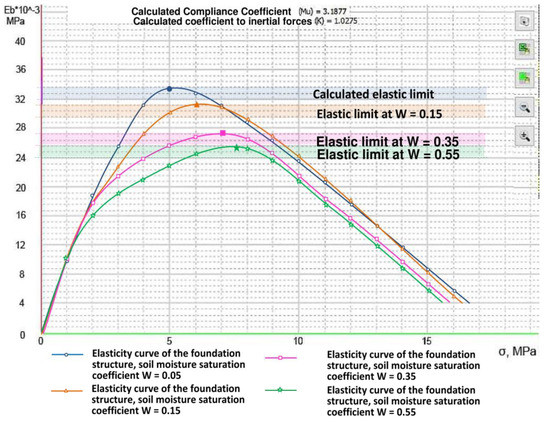
Figure 8.
Dependences of the change in the elastic limit of the structure foundation materials on the arising mechanical stresses, taking into account the level of waterlogging of the soil base.
- at W = 0.05 Eb =32.2–35.1 MPa (design conditions);
- at W = 0.15 Eb = 30.7–32.0 MPa;
- at W = 0.35 Eb = 26.8–28.2 MPa;
- at W = 0.55 Eb = 24.9–25.3 MPa.
The diagram in Figure 6 illustrates the ground section, including the groundwater pattern. This confirms their high content at the point of crack development on the foundation (point 120 in Figure 6). This comprehensive study is aimed at confirming the need to take into account the water cut of the foundation of structures in order to adjust the level of permissible loads on the wells.
The main beneficiaries of the proposed methodology are the building supervision and geotechnical monitoring services.
The proposed methodology makes it possible to revise the limiting operating strain standards for building structures that are in special operating conditions (increased dynamics of the hydrogeological regime, other geodynamic processes). Additionally, this methodology will be of interest to specialist developers of geotechnical monitoring systems as a mathematically and conceptually new approach to the problem being solved.
5. Conclusions
As a result of the research, a methodology for assessing the geotechnical stability of agricultural facilities was developed and described, taking into account the peculiarities of exogenous agrotechnical load. The use of the methodology made it possible to identify the development of a hidden destructive process on the example of a real agricultural infrastructure object, which was also consistent with the simulation results. This makes it possible not only to locate the areas of the geotechnical system with the least stability, but also to identify the factors that have the greatest impact on the stability of the geotechnical system as a whole.
The application of the developed methodology proves the need for the organization of geotechnical monitoring of agricultural facilities, taking into account the agrotechnical impact. It will also allow us to dynamically adjust the permissible limits obtained in the design calculations, the limits of variation in the physical and mechanical parameters of the stability of the geotechnical system, taking into account the current level of loads and the effects of external factors.
Author Contributions
Data curation, A.G.; Formal analysis, A.G. and M.S.; Investigation, A.G.; Supervision, A.G. and E.K.; Writing—original draft, A.G.; Writing—review & editing, A.G., E.K. and A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Higher Education of the Russian Federation in accordance with agreement No. 075-15-2020-905 date 16 November 2020 on providing a grant in the form of subsidies from the Federal budget of the Russian Federation. The grant was provided for state support for the establishing and development of a world-class Scientific Center “Agrotechnologies for the Future”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The simulation results can be found at the link: https://yadi.sk/d/bQJm6Tb4QKNd-Q (accessed on 1 September 2022).
Acknowledgments
The research was supported by the Ministry of Science and Higher Education of the Russian Federation in accordance with agreement No. 075-15-2020-905 date 16 November 2020 on providing a grant in the form of subsidies from the Federal budget of the Russian Federation. The grant was provided for state support for the establishment and development of a world-class Scientific Center “Agrotechnologies for the Future”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Saliba, F.; Nassar, R.B.; Khoury, N.M.; Maalouf, Y. Geotechnics of Soil Erosion. In Proceedings of the Eighth International Conference on Case Histories in Geotechnical Engineering, Philadelphia, PA, USA, 24–27 March 2019. [Google Scholar] [CrossRef]
- Tao, J.; Tao, H. Factors Affecting Piping Erosion Resistance: Revisited with a Numerical Modeling Approach. Int. J. Geomech. 2017, 17, 04017097. [Google Scholar] [CrossRef]
- Phuong, T.T.; Shrestha, R.P.; Chuong, H.V. Simulation of Soil Erosion Risk in the Upstream Area of Bo River Watershed. Redefining Divers. Dyn. Nat. Resour. Manag. Asia 2017, 3, 87–99. [Google Scholar]
- Kiani-Harchegani, M.; Najafi, S.; Ghahramani, A. Measuring and mapping excessive linear soil erosion features: Rills and gullies. In Precipitation: Earth Surface Responses and Processes; Elsevier: Amsterdam, The Netherlands, 2021; Chapter 18; pp. 419–438. [Google Scholar]
- Seenivasan, D.; Padmavathy, P. Role of Chemical Sciences in Technology and Development for Sustainability; Immortal Publications Prasadampadu: Vijayawada, India, 2020. [Google Scholar]
- Kaushal, R.; Mandal, D.; Panwar, K.; Kumar, P.; Tomar, J.M.S.; Mehta, H. Soil and water conservation benefits of agroforestry. In Forest Resources Resilience and Conflicts; Elsevier: Amsterdam, The Netherlands, 2021; Chapter 20; pp. 259–275. [Google Scholar]
- GOST R 22.1.12-2005; Safety in Emergency Situations. Structured System of Monitoring and Management of Engineering Systems of Buildings and Structures. Stroyizdatinform: Moscow, Russia, 2005; p. 34.
- Federal Law of the Russian Federation No. 384-FZ Technical Regulations on the Safety of Buildings and Structures; CIS Legislation: Moscow, Russia, 2009; p. 22.
- Kolesnikov, A.O.; Kostyuk, T.N.; Popov, V.N. Calculation of the vertical rigidity of the foundation taking into account the mutual influence of piles. Constr. Mech. Eng. Struct. 2019, 3, 229–236. [Google Scholar] [CrossRef]
- Inozemtsev, V.K.; Zhestkova, S.A. Bifurcation problems of stability of a high-altitude object. Constr. Mech. Eng. Struct. 2016, 4, 53–57. [Google Scholar]
- Nazarov, D.I. Destruction of structures of a mining building, energy and bifurcation analysis. Min. Form. Anal. Bull. 2015, 7, 95–100. [Google Scholar]
- Monteiro, L.H.A. A discrete-time dynamic system with four types of codimension-one bifurcations. Appl. Math. Comput. 2019, 354, 189–191. [Google Scholar]
- GOST R ISO 10137-2016; Fundamentals of Calculation of Building Structures. Operational Reliability of Buildings under the Influence of Vibration. Publishing house of Standartinform: Moscow, Russia, 2017; p. 40.
- Smirnov, V.V.; Zemenkov, Y.D.; Toropov, S.Y.; Seroshtanov, I.V.; Nikiforov, V.N. Prospects for the development of geotechnical monitoring systems. GIAB 2014, 4, 325–350. [Google Scholar]
- Ayberk, K. Geotechnical assessment of a slope stability pro blem in the Citlakkale residential area (Giresun, NE Turkey). Bulletin of Engineering Geology and the Environment. Off. J. Int. Assoc. Eng. Geol. Environ. 2017, 3, 875–889. [Google Scholar]
- Fan, Y.B.; Yang, S.W.; Xu, L.K.; Feng, C.; Liang, B.F. Real time monitoring instrument designed for the deformation and sliding period of colluvial landslides. Bulletin of Engineering Geology and the Environment. Off. J. Int. Assoc. Eng. Geol. Environ. 2017, 3, 829–838. [Google Scholar]
- Lebedev, M.O. Safety provision in the construction of a two-track subway tunnel in quaternary deposits. GIAB 2019, 3, 88–96. [Google Scholar] [CrossRef]
- Konyushkov, V.V.; Veselov, A.A.; Kondratieva, L.N. Complex analysis of the results of engineering surveys for the design, construction and operation of structures in areas with slope processes. Izv. TPU 2017, 11, 111–125. [Google Scholar]
- Kuleshov, A.P.; Pendin, V.V. On the issue of processing the results of geotechnical monitoring of structure settlement. Proc. TPU 2019, 8, 203. [Google Scholar]
- Boardman, J.; Evans, R.; Poesen, J. Socio-economic factors in soil erosion and conservation. Environ. Sci. Policy 2003, 6, 1–6. [Google Scholar] [CrossRef]
- Ge, Y.; Jun-Yan, Z. Analysis of the impact on ecosystem and environment of marine reclamation-A case study in Jiaozhou Bay. Energy Procedia 2005, 5, 105–111. [Google Scholar] [CrossRef]
- Litvinova, E.V. Determination of parameters of the dynamic vibration characteristics of building con-structions, buildings and structures. Constr. Technog. Saf. 2017, 9, 93–99. [Google Scholar]
- Ilyushin, A.A.; Pobedrya, B.E. Fundamentals of the mathematical theory of thermo-viscoelasticity. Mosc. Nauka 1970, 8, 280. [Google Scholar]
- Panasyuk, L.N.; Dumbai, V.A.; Morozova, A.K.; Livinsky, D.R. Estimation of the accuracy of direct methods of integrating equations of motion. IVD 2019, 9, 312–316. [Google Scholar]
- Dorofeev, N.V.; Romanov, R.V.; Grecheneva, A.V.; Pankina, E.S. Improving the Reliability of The Results of Automated Forecasting of Emissions in Geotechnical Systems Based on the Bifurcation Approach. In Proceedings of the Iop Conference Series: Materials Science and Engineering Krasnoyarsk Science and Tech-nology City Hall of the Russian Union of Scientific and Engineering Associations, Krasnoyarsk, Russia, 16–18 April 2020; pp. 520–570. [Google Scholar]
- Dorofeev, N.V.; Romanov, R.V.; Grecheneva, A.V.; Pankina, E.S. Algorithm for Predicting of The Transition of A Key Point of Geodynamic Control to the Risk Zone. In Proceedings of the Iop Conference Series: Earth And Environmental Science Iii International Scientific Conference: Agritech-Iii-2020: Agribusiness, Environmental Engineering and Biotechnologies. Krasnodar Science and Technology City Hall of The Russian Union of Scientific and Engineering Associations, Krasnoyarsk, Russia, 18–20 June 2020; pp. 520–568. [Google Scholar]
- Dorofeev, N.V.; Grecheneva, A.V.; Pankina, E.S.; Romanov, R.V. Modeling and Bifurcation Analysis of the Stability of a Geotechnical System under the Influence of Vibration Factors. Autom. Control. Processes 2020, 3, 92–100. [Google Scholar]
- Vasiliev, G.S.; Kuzichkin, O.R.; Grecheneva, A.V.; Dorofeev, N.V.; Surzhik, D.S. Analysis of the Combined Transfer Functions for Geotechnical Control. In Proceedings of the 18th International Multidisciplinary Scientific GeoconferencesSgem 2018 Conference Proceedings, Albena, Bulgaria, 2–8 July 2018; pp. 43–50. [Google Scholar]
- Dorofeev, N.V.; Kuzichkin, O.R.; Grecheneva, A.V.; Romanov, R.V. Conducting Geotechnical Moni-toring In Karst Areas Based on Joint Geoelectric And Accelerometric Measurements. Bull. Volgogr. State Univ. Archit. Civ. Eng. Ser. Constr. Archit. 2018, 54, 20–31. [Google Scholar]
- Pankina, E.S.; Dorofeev, N.V.; Romanov, R.V. Adaptive Processing of Heterogeneous Geotechnical Monitoring Data. Proc. Tula State Univ. Tech. Sci. 2020, 7, 226–236. [Google Scholar]
- Zhelnin, M.S.; Prokhorov, A.E.; Kostina, A.A.; Plekhov, O.A. Experimental and theoretical study of mechanical deformations in freezing moisture-saturated soil. Bull. PNRPU Mech. 2019, 4, 213–218. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).