A New Nearest Centroid Neighbor Classifier Based on K Local Means Using Harmonic Mean Distance
Abstract
1. Introduction
- Efficient classification considers not only the distance proximity of k nearest neighbors, but also takes their symmetrical allocation around the query sample into account.
- The proposed framework includes local centroid mean vectors of k nearest neighbors in each class, effectively showing robustness to existing outliers.
- Finally, using Harmonic mean distance as a distance metric, it accounts for more reliable local means in different classes, making the proposed method less sensitive to parameter k.
- Extensive experiments on real world datasets show that our non-parametric framework has better classification accuracy compared to traditional KNN based classifiers.
2. Related Work
2.1. LMKNN Classifier
- Step 1.
- Search the k nearest neighbors from the set TR of each class for the query pattern x. Let be the set of KNNs for x in the class using the Euclidean distance metric , where .
- Step 2.
- Calculate the local mean vector from the class , using the set .
- Step 3.
- Assign x to class c if the distance between the local mean vector for c and the query sample in Euclidean space is minimum.
2.2. Harmonic Mean Distance
2.3. KNCN Classifier
- Step 1.
- Search k-nearest centroid neighbors of x from TS using NCN concept,
- Step 2.
- Assign x to the class c, which is most frequently represented by the centroid neighbors in the set (resolve ties randomly).where is the class label for the nth centroid neighbor , and δ(cj = ), the Kronecker delta function, takes a value of one if = , and zero otherwise.
3. The Proposed LMKHNCN Method
3.1. Motivation of LMKHNCN
3.2. Description of LMKHNCN
- Step 1:
- Find the set of KNCNs from the set TS of each class for the query sample x,using NCN criterion. Note that the value of .
- Step 2:
- Compute the local centroid mean vector from each class using the set
- Step 3:
- Calculate the harmonic mean distance HMDS (x, ) between x and each local centroid mean vector .
- Step 4:
- Classify x to the class c, which has the minimum harmonic mean distance between its local centroid mean vector and the query sample x.
| Algorithm 1. The proposed MLM-KHNN classifier. |
| Input: |
| x: a query sample, k: the neighborhood size. |
| : a training set, N1, …, NM: the number of training samples in TS. |
| : class cj training set with Nj training samples. |
| M: the number of classes, c1, c2, …, cM: class labels in TS, |
| : the number of training samples in TS. |
| Output: |
| c: the classification result of query sample x. |
| Procedures: |
| Step 1: Calculate the distances of training samples in each class ci to x. |
| for j = 1 to Ni do |
| end for |
| Step 2: Find the first nearest centroid neighbor of x in each class ci, say |
| [min_index,min_dist] = min(d(x, pij)) |
| = pmin_index |
| Set = { ∈ Rm} |
| Step 3: Search k nearest centroid neighbors of except the first one, , in each class ci. |
| for j = 2 to k do |
| Set Si(x) = TR − (x) |
| Si(x) = , Li(x) = length(Si(x)) |
| Compute the sum of the previous j − 1 nearest centroid neighbors. |
| = |
| Calculate the centroids in the set Si for . |
| for l = 1 to Li(x) do |
| = 1/j (pil + (x)) |
| (x, ) = |
| end for |
| Find the jth nearest centroid neighbor. |
| [min_indexNCN, min_distNCN] = min((x, )) |
| = xmin_indexNCN |
| Add to the set . |
| end for |
| Set = (x). |
| Step 4: Calculate the k-local centroid mean vector in set for each class ci. |
| = 1/r |
| Step 5: Compute the harmonic mean distance HMDS(x,) between and local centroid mean vector for each class ci, |
| for j = 1 to M do |
| HMD(x, ) = k//d(x, ) |
| end for |
| Step 6: Assign to the class c with a minimum harmonic mean distance. |
| c = argminciHMDS(x, ) |
3.3. Comparison with Traditional KNN Based Classifiers
4. Experiment Results and Discussion
4.1. Performance Evaluation
4.2. Description of the Datasets
4.3. Experimental Procedure
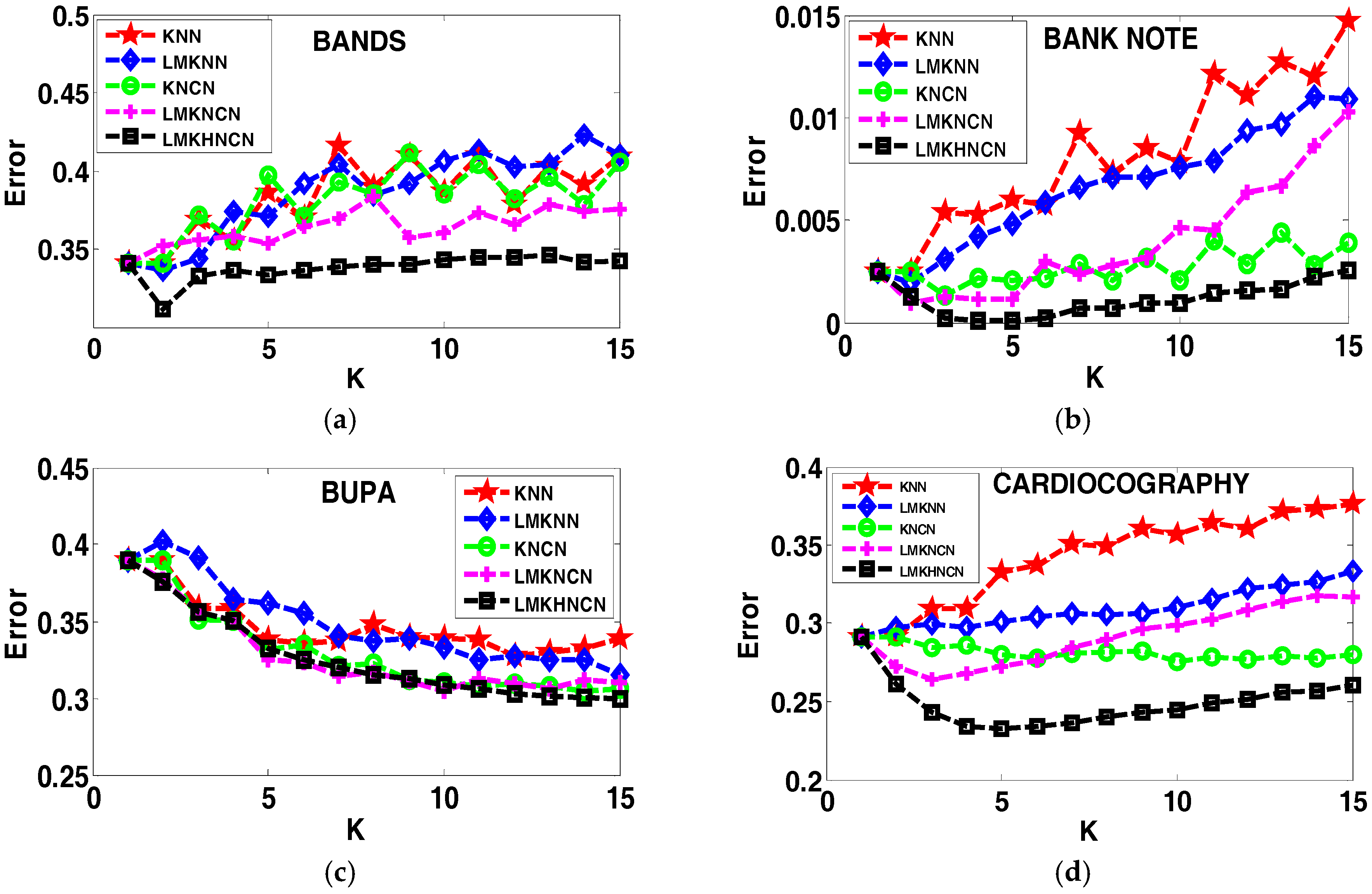
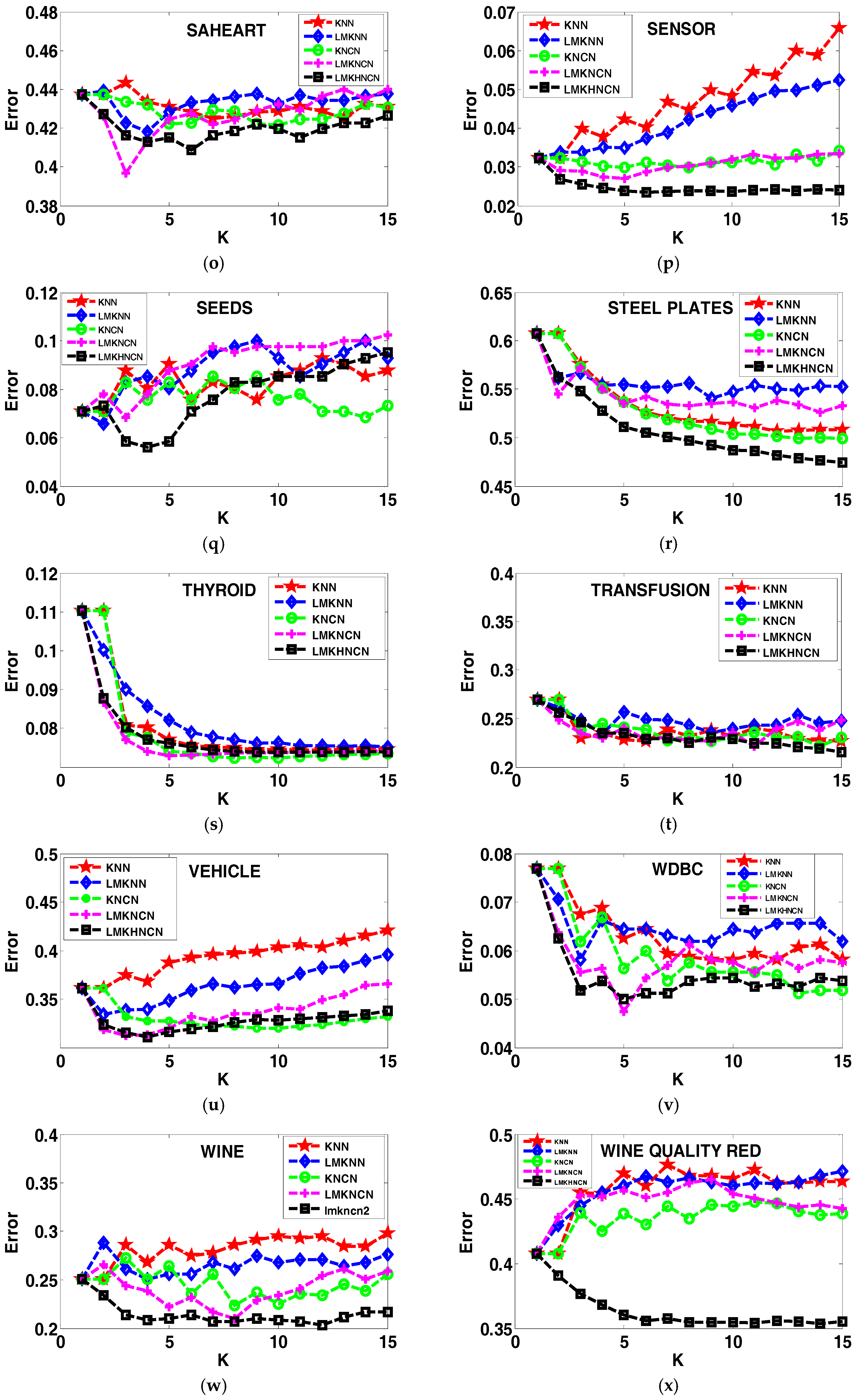
4.4. Analyzing the Error Rates Results with Corresponding K Value
4.5. Results of the Sensitivity to the Neighborhood Size K
4.6. Analyzing the Effect of Distance on Classification Performance
4.7. Analyzing the Computational Complexity
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theor. 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Liu, Z.G.; Pan, Q.; Dezert, J. A new belief-based K-nearest neighbor classification method. Pattern Recognit. 2013, 46, 834–844. [Google Scholar] [CrossRef]
- Mitani, Y.; Hamamoto, Y. A local mean-based nonparametric classifier. Pattern Recognit. Lett. 2006, 27, 1151–1159. [Google Scholar] [CrossRef]
- Gou, J.; Yi, Z.; Du, L.; Xiong, T. A local mean-based k-nearest centroid neighbor classifier. Comput. J. 2011, 55, 1058–1071. [Google Scholar] [CrossRef]
- Sánchez, J.S.; Pla, F.; Ferri, F.J. On the use of neighbourhood-based non-parametric classifiers1. Pattern Recognit. Lett. 1997, 18, 1179–1186. [Google Scholar] [CrossRef]
- Samsudin, N.A.; Bradley, A.P. Nearest neighbour group-based classification. Pattern Recognit. 2010, 43, 3458–3467. [Google Scholar] [CrossRef]
- Shanableh, T.; Assaleh, K.; Al-Rousan, M. Spatio-temporal feature-extraction techniques for isolated gesture recognition in Arabic sign language. IEEE Trans. Syst. Man Cybern. Part B 2007, 37, 641–650. [Google Scholar] [CrossRef]
- Xu, J.; Yang, J.; Lai, Z. K-local hyperplane distance nearest neighbor classifier oriented local discriminant analysis. Inf. Sci. 2013, 232, 11–26. [Google Scholar] [CrossRef]
- Maji, P. Fuzzy–rough supervised attribute clustering algorithm and classification of microarray data. IEEE Trans. Syst. Man Cybern. Part B 2011, 41, 222–233. [Google Scholar] [CrossRef] [PubMed]
- Raymer, M.L.; Doom, T.E.; Kuhn, L.A.; Punch, W.F. Knowledge discovery in medical and biological datasets using a hybrid bayes classifier/evolutionary algorithm. IEEE Trans. Syst. Man Cybern. Part B 2003, 33, 802–813. [Google Scholar] [CrossRef] [PubMed]
- Dudczyk, J.; Kawalec, A.; Owczarek, R. An application of iterated function system attractor for specific radar source identification. In Proceedings of the 17th International Conference on Microwaves, Radar and Wireless Communications, Wroclaw, Poland, 19–21 May 2008; pp. 1–4. [Google Scholar]
- Dudczyk, J.; Kawalec, A.; Cyrek, J. Applying the distance and similarity functions to radar signals identification. In Proceedings of the 2008 International Radar Symposium, Wroclaw, Poland, 21–23 May 2008; pp. 1–4. [Google Scholar]
- Dudczyk, J.; Wnuk, M. The utilization of unintentional radiation for identification of the radiation sources. In Proceedings of the 34th European Microwave Conference, Amsterdam, The Netherlands, 12–14 October 2004; pp. 777–780. [Google Scholar]
- Dudczyk, J. A method of feature selection in the aspect of specific identification of radar signals. Bull. Pol. Acad. Sci. Tech. Sci. 2017, 65, 113–119. [Google Scholar] [CrossRef]
- Mensink, T.; Verbeek, J.; Perronnin, F.; Csurka, G. Distance-based image classification: Generalizing to new classes at near-zero cost. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2624–2637. [Google Scholar] [CrossRef] [PubMed]
- Frigui, H.; Gader, P. Detection and discrimination of land mines in ground-penetrating radar based on edge histogram descriptors and a possibilistic k-nearest neighbor classifier. IEEE Trans. Fuzzy Syst. 2009, 17, 185–199. [Google Scholar] [CrossRef]
- Ma, L.; Crawford, M.M.; Tian, J. Local manifold learning-based k-nearest-neighbor for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4099–4109. [Google Scholar] [CrossRef]
- Manavalan, B.; Shin, T.H.; Lee, G. PVP-SVM: Sequence-based prediction of phage virion proteins using a support vector machine. Front. Microbiol. 2018. [Google Scholar] [CrossRef] [PubMed]
- Manavalan, B.; Subramaniyam, S.; Shin, T.H.; Kim, M.O. Machine-learning-based prediction of cell-penetrating peptides and their uptake efficiency with improved accuracy. J. Proteome Res. 2018, 17, 2715–2726. [Google Scholar] [CrossRef] [PubMed]
- Manavalan, B.; Shin, T.H.; Lee, G. DHSpred: Support-vector-machine-based human DNase I hypersensitive sites prediction using the optimal features selected by random forest. Oncotarget 2018, 9, 1944–1956. [Google Scholar] [CrossRef] [PubMed]
- Manavalan, B.; Shin, T.H.; Kim, M.O.; Lee, G. AIPpred: Sequence-based prediction of anti-inflammatory peptides using random forest. Front. Pharmacol. 2018, 9, 276. [Google Scholar] [CrossRef] [PubMed]
- Fukunaga, K. Introduction to Statistical Pattern Recognition; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Bhattacharya, G.; Ghosh, K.; Chowdhury, A.S. A probabilistic framework for dynamic k estimation in kNN classifiers with certainty factor. In Proceedings of the 2015 8th International Conference on Advances in Pattern Recognition, Kolkata, India, 4–7 January 2015. [Google Scholar]
- Chai, J.; Liu, H.; Chen, B.; Bao, Z. Large margin nearest local mean classifier. Signal Process. 2010, 90, 236–248. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, L.; Yang, J.Y.; Zhang, D. From classifiers to discriminators: A nearest neighbor rule induced discriminant analysis. Pattern Recognit. 2011, 44, 1387–1402. [Google Scholar] [CrossRef]
- Zeng, Y.; Yang, Y.; Zhao, L. Pseudo nearest neighbor rule for pattern classification. Expert Syst. Appl. 2009, 36, 3587–3595. [Google Scholar] [CrossRef]
- Gou, J.; Zhan, Y.; Rao, Y.; Shen, X.; Wang, X.; He, W. Improved pseudo nearest neighbor classification. Knowl. Based Syst. 2014, 70, 361–375. [Google Scholar] [CrossRef]
- Xu, Y.; Zhu, Q.; Fan, Z.; Qiu, M.; Chen, Y.; Liu, H. Coarse to fine K nearest neighbor classifier. Pattern Recognit. Lett. 2013, 34, 980–986. [Google Scholar] [CrossRef]
- Chen, L.; Guo, G. Nearest neighbor classification of categorical data by attributes weighting. Expert Syst. Appl. 2015, 42, 3142–3149. [Google Scholar] [CrossRef]
- Lin, Y.; Li, J.; Lin, M.; Chen, J. A new nearest neighbor classifier via fusing neighborhood information. Neurocomputing 2014, 143, 164–169. [Google Scholar] [CrossRef]
- Chaudhuri, B.B. A new definition of neighborhood of a point in multi-dimensional space. Pattern Recognit. Lett. 1996, 17, 11–17. [Google Scholar] [CrossRef]
- Grabowski, S. Limiting the set of neighbors for the k-NCN decision rule: Greater speed with preserved classification accuracy. In Proceedings of the International Conference Modern Problems of Radio Engineering, Telecommunications and Computer Science, Lviv-Slavsko, Ukraine, 24–28 Feburary 2004. [Google Scholar]
- Sánchez, J.S.; Pla, F.; Ferri, F.J. Improving the k-NCN classification rule through heuristic modifications. Pattern Recognit. Lett. 1998, 19, 1165–1170. [Google Scholar] [CrossRef]
- Bailey, T.; Jain, A.K. A note on distance-weighted k-nearest neighbor rules. IEEE Trans. Syst. Man Cybern. 1978, 311–313. [Google Scholar] [CrossRef]
- Yu, J.; Tian, Q.; Amores, J.; Sebe, N. Toward robust distance metric analysis for similarity estimation. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; pp. 316–322. [Google Scholar]
- Gou, J.; Du, L.; Zhang, Y.; Xiong, T. A new distance-weighted k-nearest neighbor classifier. J. Inf. Comput. Sci. 2012, 9, 1429–1436. [Google Scholar]
- Wang, J.; Neskovic, P.; Cooper, L.N. Improving nearest neighbor rule with a simple adaptive distance measure. Pattern Recognit. Lett. 2007, 28, 207–213. [Google Scholar] [CrossRef]
- Pan, Z.; Wang, Y.; Ku, W. A new k-harmonic nearest neighbor classifier based on the multi-local means. Expert Syst. Appl. 2017, 67, 115–125. [Google Scholar] [CrossRef]
- Manavalan, B.; Shin, T.H.; Kim, M.O.; Lee, G. PIP-el: A new ensemble learning method for improved proinflammatory peptide predictions. Front. Immunol. 2018, 9, 1783. [Google Scholar] [CrossRef] [PubMed]
- Alcalá-Fdez, J.; Fernández, A.; Luengo, J.; Derrac, J.; Garcí, S.; Sánchez, L.; Herrera, F. Keel data-mining software tool: Data set repository, integration of algorithms and experimental analysis framework. J. Mult.-Valued Log. Soft Comput. 2011, 17, 255–287. [Google Scholar]
- Bache, K.; Lichman, M. Uci machine learning repository [http://archive. ics. uci. edu/ml]. irvine, ca: University of california, school of information and computer science. begleiter, h. neurodynamics laboratory. state university of new york health center at brooklyn. ingber, l.(1997). statistical mechanics of neocortical interactions: Canonical momenta indicatros of electroencephalography. Phys. Rev. E 2013, 55, 4578–4593. [Google Scholar]


| Classifier | Distance Proximity | Spatial Distribution | Local Mean Used | Type of Nearest Neighbors | Distance Similarity |
|---|---|---|---|---|---|
| KNN | √ | × | × | NN | E D |
| KNCN | √ | √ | × | NCN | E D |
| LMKNN | √ | × | Local mean of NNs | NN | E D |
| LMKNCN | √ | √ | Local mean of NCNs | NCN | E D |
| LMKHNCN | √ | √ | Local mean of NCNs | NCN | H M D |
| DATASET | SAMPLES | ATTRIBUTES | CLASSES | TESTING SET |
|---|---|---|---|---|
| DIABTIC | 1151 | 20 | 2 | 68 |
| HILL VALLEY | 1212 | 101 | 2 | 150 |
| ILPD | 583 | 10 | 2 | 69 |
| PLRX | 182 | 13 | 2 | 65 |
| WPBC | 198 | 32 | 2 | 58 |
| TRANSFUSION | 748 | 5 | 2 | 155 |
| BANK NOTE | 1372 | 5 | 2 | 3315 |
| CARDIOCOGRAPHY 10 | 2126 | 22 | 10 | 176 |
| THYROID | 7200 | 22 | 3 | 2400 |
| SENSOR | 5456 | 5 | 4 | 26 |
| QUALITATIVE BANKKRUPTCY | 250 | 7 | 3 | 60 |
| WDBC | 569 | 31 | 2 | 169 |
| PHONEME | 5406 | 6 | 2 | 60 |
| SONAR | 208 | 60 | 2 | 66 |
| WINEQUALITYRED | 1599 | 12 | 4 | 76 |
| STEEL PLATES | 1941 | 28 | 7 | 65 |
| FOREST TYPES | 523 | 28 | 4 | 112 |
| BALANCE SCALE | 625 | 5 | 3 | 96 |
| RING | 7400 | 21 | 2 | 125 |
| BANDS | 365 | 20 | 2 | 78 |
| SEEDS | 210 | 8 | 3 | 99 |
| VEHICLE1812 | 846 | 18 | 4 | 282 |
| WINE | 178 | 14 | 3 | 59 |
| GLASS | 214 | 11 | 2 | 53 |
| MICE | 1080 | 72 | 8 | 117 |
| DATASET | KNN | LMKNN | KNCN | LMKNCN | LMKHNCN | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| DIABTIC | 34.08 ± 0.0169 | [13] | 33.91 ± 0.0158 | [14] | 31.18 ± 0.0256 | [10] | 30.48 ± 0.0231 | [15] | 30.32 ± 0.0237 | [14] |
| HILL VALLEY | 40.67 ± 0.0193 | [1] | 39.23 ± 0.0112 | [2] | 40.67 ± 0.0426 | [1] | 30.17 ± 0.0270 | [9] | 25.77 ± 0.0425 | [16] |
| ILPD | 29.85 ± 0.0212 | [10] | 30.36 ± 0.0171 | [14] | 30.26 ± 0.0199 | [16] | 29.03 ± 0.0176 | [14] | 28.77 ± 0.0221 | [13] |
| PLRX | 36.75 ± 0.0154 | [1] | 36.75 ± 0.0237 | [1] | 36.75 ± 0.0154 | [1] | 36.75 ± 0.0159 | [1] | 35 ± 0.0134 | [15] |
| PHONEME | 12.08 ± 0.0183 | [1] | 12.08 ± 0.0112 | [1] | 12.08 ± 0.0124 | [1] | 12.08 ± 0.0290 | [1] | 11.75 ± 0.0137 | [2] |
| SONAR | 17.42 ± 0.0606 | [1] | 16.36 ± 0.0170 | [2] | 16.97 ± 0.0398 | [7] | 14.7 ± 0.0255 | [4] | 12.88 ± 0.0123 | [4] |
| TRANSFUSION | 22.69 ± 0.0137 | [7] | 23.38 ± 0.0095 | [4] | 22.15 ± 0.0140 | [15] | 22.15 ± 0.0119 | [12] | 21.54 ± 0.0144 | [16] |
| BANK NOTE | 0.25 ± 0.0038 | [1] | 0.20 ± 0.0029 | [2] | 0.13 ± 0.0029 | [3] | 0.0009 ± 0.0008 | [2] | 0.0001 ±0.0008 | [4] |
| CARDIOCOGRAPHY | 29.13 ± 0.092 | [1] | 29.12 ± 0.0124 | [1] | 27.55 ± 0.0048 | [11] | 26.95 ± 0.0183 | [3] | 23.28 ± 0.0152 | [5] |
| THYROID | 7.44 ± 0.0123 | [12] | 7.53 ± 0.0105 | [16] | 7.24 ± 0.0130 | [9] | 7.30 ± 0.0098 | [5] | 7.38 ± 0.0097 | [13] |
| SENSOR | 3.22 ± 0.0100 | [1] | 3.22 ± 0.0072 | [1] | 2.99 ± 0.0012 | [5] | 2.7 ± 0.0021 | [5] | 2.34 ± 0.0022 | [7] |
| QUALITATIVE | 0.33 ± 0.0030 | [3] | 0.33 ± 0.0023 | [2] | 0.33 ± 0.0028 | [5] | 0.33 ± 0.0023 | [3] | 0.33 ± 0.0023 | [5] |
| WINEQUALITYRED | 40.8 ± 0.0209 | [1] | 40.8 ± 0.01169 | [1] | 40.8 ± 0.0127 | [1] | 40.8 ± 0.0134 | [1] | 35.39 ± 0.0161 | [15] |
| WDBC | 5.81 ± 0.0075 | [10] | 5.81 ± 0.0080 | [3] | 5.13 ± 0.0117 | [14] | 4.75 ± 0.0076 | [16] | 5.0 ± 0.0076 | [5] |
| STEEL PLATES | 50.66 ± 0.0353 | [13] | 54.07 ± 0.0151 | [10] | 49.92 ± 0.0378 | [16] | 52.66 ± 0.0207 | [15] | 47.43 ± 0.0376 | [16] |
| FOREST TYPES | 10.06 ± 0.0074 | [4] | 9.45 ± 0.0090 | [8] | 9.5 ± 0.0099 | [11] | 9.28 ± 0.0073 | [10] | 9.06 ± 0.0076 | [16] |
| BALANCE SCALE | 15.06 ± 0.0711 | [16] | 10.94 ± 0.0684 | [10] | 11.89 ± 0.0858 | [16] | 9.94 ± 0.0682 | [4] | 9.06 ± 0.0719 | [16] |
| RING | 26.32 ± 0.0623 | [1] | 10.23 ± 0.0783 | [3] | 5.39 ± 0.1063 | [4] | 7.94 ± 0.0740 | [2] | 7.58 ± 0.0809 | [3] |
| BANDS | 34.08 ± 0.0247 | [1] | 33.68 ± 0.0276 | [2] | 34.08 ± 0.0221 | [1] | 34.08 ± 0.0117 | [1] | 31.2 ± 0.0083 | [2] |
| SEEDS | 7.07 ± 0.0071 | [1] | 6.59 ± 0.0101 | [2] | 6.83 ± 0.0058 | [15] | 6.83 ± 0.0113 | [3] | 5.61 ± 0.0126 | [4] |
| VEHICLE1812 | 36.11 ± 0.0189 | [1] | 33..39 ± 0.0189 | [2] | 31.97 ± 0.0132 | [10] | 31.24 ± 0.0181 | [3] | 31.11 ± 0.0119 | [12] |
| Wine | 27.29 ± 0.0150 | [1] | 25.42 ± 0.0101 | [9] | 22.71 ± 0.0196 | [14] | 21.02 ± 0.0191 | [11] | 19.49 ± 0.0224 | [16] |
| WPBC1 | 29.31±0.0164 | [12] | 31.55 ± 0.0084 | [7] | 29.14 ± 0.0166 | [11] | 28.28 ± 0.0160 | [9] | 28.45 ± 0.0162 | [11] |
| GLASS | 20.56 ± 0.0307 | [1] | 18.32 ± 0.0197 | [2] | 20.56 ± 0.0161 | [1] | 19.72 ± 0.0141 | [2] | 17.78 ± 0.0131 | [3] |
| MICE | 3.72 ± 0.0638 | [1] | 3.58 ± 0.01380 | [2] | 3.72 ± 0.0080 | [1] | 3.25 ± 0.0312 | [2] | 3 ± 0.0041 | [3] |
| k | Classifier | Class 1 | Class 2 | Class 3 | Classification Result | |
|---|---|---|---|---|---|---|
| 1 | LMKNN | 2.247 | 1.714 | 1.000 | 3 | √ |
| LMKNCN | 2.247 | 1.714 | 1.000 | 3 | √ | |
| LMKHNCN | 2.247 | 1.714 | 1.000 | 3 | √ | |
| 2 | LMKNN | 2.414 | 1.091 | 1.523 | 2 | × |
| LMKNCN | 2.414 | 1.054 | 1.423 | 2 | × | |
| LMKHNCN | 2.202 | 1.032 | 0.837 | 3 | √ | |
| 3 | LMKNN | 2.941 | 1.742 | 1.774 | 2 | × |
| LMKNCN | 2.941 | 1.125 | 2.333 | 2 | × | |
| LMKHNCN | 2.854 | 1.121 | 1.047 | 3 | √ | |
| 4 | LMKNN | 3.173 | 1.436 | 1.754 | 1 | × |
| LMKNCN | 3.112 | 1.247 | 0.250 | 3 | √ | |
| LMKHNCN | 3.061 | 1.061 | 0.000 | 3 | √ | |
| 5 | LMKNN | 4.166 | 1.314 | 1.846 | 2 | × |
| LMKNCN | 4.087 | 1.194 | 1.283 | 2 | × | |
| LMKHNCN | 4.021 | 1.020 | 0.000 | 3 | √ | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehta, S.; Shen, X.; Gou, J.; Niu, D. A New Nearest Centroid Neighbor Classifier Based on K Local Means Using Harmonic Mean Distance. Information 2018, 9, 234. https://doi.org/10.3390/info9090234
Mehta S, Shen X, Gou J, Niu D. A New Nearest Centroid Neighbor Classifier Based on K Local Means Using Harmonic Mean Distance. Information. 2018; 9(9):234. https://doi.org/10.3390/info9090234
Chicago/Turabian StyleMehta, Sumet, Xiangjun Shen, Jiangping Gou, and Dejiao Niu. 2018. "A New Nearest Centroid Neighbor Classifier Based on K Local Means Using Harmonic Mean Distance" Information 9, no. 9: 234. https://doi.org/10.3390/info9090234
APA StyleMehta, S., Shen, X., Gou, J., & Niu, D. (2018). A New Nearest Centroid Neighbor Classifier Based on K Local Means Using Harmonic Mean Distance. Information, 9(9), 234. https://doi.org/10.3390/info9090234






