Perceptual Hashing Based Forensics Scheme for the Integrity Authentication of High Resolution Remote Sensing Image
Abstract
:1. Introduction
2. Related Works
2.1. Overview of Perceptual Hash Algorithm
- (1)
- Robustness: The robustness is the most striking difference between the perceptual hash algorithm and the cryptographic hash function. The cryptographic hash function implements the authentication of the image at the binary level, while the perceptual hash algorithm considers whether the available content of the image has been changed.
- (2)
- Sensitivity to tampering: The perceptual hash algorithm has to be sensitive to malicious tampering operations, which means the visually distinct images should have significantly different hash sequences.
- (3)
- Security: The effective content of the image content cannot be obtained from the perceptual hash sequence, that is, the calculation of image hashing depends on a secret key.
- (4)
- Compactness: When the above characteristics are satisfied, the perceptual hash sequence generated by the algorithm should be as compact as possible. A short perceptual hash sequence is convenient for storage, transfer, and use.
- (5)
- Tamper localization: In some applications, the perceptual hash algorithm should also be able to locate where the image was tampered with.
- Image statistical information based algorithms generally utilize statistical features such as histogram mean and variance of image blocks. Xiang et al. [2] propose a robust perceptual hash algorithm by using the invariance of the image histogram shape to geometric deformations. The robustness of the algorithm is achieved by using the histogram shape invariance. Xu et al. [3] propose a robust image hash scheme using a multi-resolution histogram for image copy detection, which is invariant to rigid motions and robust to noise. Tang et al. [4] propose a perceptual hash algorithm based on statistical features for color images, which extracts local color features by calculating the block mean and variance. Fang et al. [5] use image statistical information based perceptual hashing for person re-identification, which generates the perceptual hash vector by calculating the average gray value of all pixels. These kinds of algorithms have the advantages of simple principle and good robustness, but the attacker can modify the image content while keeping the image statistical information unchanged, and the security is insufficient. Moreover, there is a certain deficiency in the compactness of the algorithms.
- Rough representation of image based algorithms mostly make use of the coarse features of the image to be perceptual of the valid content. Swaminathan et al. [6] propose an image perceptual hash algorithm based on Fourier transform features and controlled randomization, which is resilient to content-preserving modifications, such as moderate geometric and filtering distortions. Saad et al. [7] propose a content-based image authentication scheme, which exploits the scalability of a structural digital signature to achieve a good trade off between security and image transfer for networked image applications. Ahmed et al. [8] propose a hash-based image authentication scheme that uses a secret key to randomly modulate image pixels to create a transformed feature space. This type of method has robust to subtle image modifications, but is more vulnerable to local malicious tampering.
- Transform domain coefficients based algorithms mainly take the invariant relationship between the coefficients of the image after discrete cosine transform (DCT) or discrete wavelet transform (DWT) as the perceptual feature. Lin et al. [9] present a method for image authentication based on the invariance of the relationships between DCT coefficients at the same position in separate blocks of an image. Lu et al. [10] present an image authentication scheme by making use of the interscale relationship of wavelet coefficients. Zhang et al. [11] propose an authentication signature method for image based on Hotelling’s T-square Statistic (HTS) via a Principal Component Analysis (PCA) of block DCT coefficients. Wang et al. [12] present a perceptual hashing for image copy-move forgery detection scheme, which generates the perceptual hash feature based on the DCT coefficient of the fixed-size image blocks. Yang et al. [13] propose an image hash algorithm based on wave atom transform (WAT) using distributed source coding, providing a better performance than existing WAT. This type of approach is relatively insufficient for the geometric transformation of images.
- Feature point based algorithms. Monga et al. [14] propose an image hashing paradigm based on an iterative feature detector to extract significant geometry preserving feature points. Liu et al. [15] propose an image hash algorithm based on the SIFT operator, which is robust to geometric attacks. In this algorithm, the image digest is constructed through filtering and compressing the SIFT feature vector, which is followed by the quantization based on the centroid of feature vector. Wang et al. [16] propose an image forensic approach for content authenticity analysis. In the proposed method, adaptive Harris corner detection algorithm is used to extract image feature points, then the statistics of the feature point neighborhood are used to construct a forensic signature. Zhao et al. [17] propose a second-order image hash approach based on SIFT for image retrieval. Feature point based algorithms have relatively good robustness, while there are ubiquitous deficiencies in computational complexity. Moreover, those methods cannot prove the uniqueness of image content, that is, images with the same feature point may not have the same content, which makes the security of the perceptual hash algorithm insufficient.
- Matrix decomposition based algorithms. Kozat et al. [18] propose an image hash algorithm based on singular value decomposition. Sun et al. [19] present a perceptual hash method based on non-negative matrix factorizations (NMF) and principal component analysis (PCA), in which NMF is used to capture the local features of the image. Xiang et al. [20] improve the NMF based perceptual hash algorithm by constraining blocking range and adopting appropriate block size, which provides a satisfactory robustness to image rotation. Tang et al. [21] designed an image hashing based on nonnegative matrix factorization (NMF) and ring partition, which has good discriminative capability. In general, matrix decomposition based perceptual hash algorithms are more sensitive to geometric attacks.
- Other algorithms. Chen et al. [22] developed an image hash algorithm based on invariants of radial Tchebichef moments. It generates an image hash sequence by adaptive quantization of the invariants of radial Tchebichef moments. Qin et al. [23] designed a hybrid feature extraction based perceptual hashing scheme for color images, in which image normalization, Gaussian low-pass filtering, SVD and Canny operator are applied on the image to improve the robustness of the scheme. Chen et al. [24] propose a novel compressive sensing based perceptual hash algorithm for visual tracking, which constructs a perceptual feature by means of intensity histogram and DCT based on illumination and contour profile. Cui et al. [25] proposed a 3D images hash algorithm by selecting suitable Dual-tree complex wavelet transform coefficients. Yang et al. [26] proposed a perceptual image hashing algorithm by combining latent low-rank representation and rotation invariant uniform local binary patterns.
2.2. High Resolution Remote Sensing Image
2.3. Multi-Scale Edge Feature Extraction for HRRS
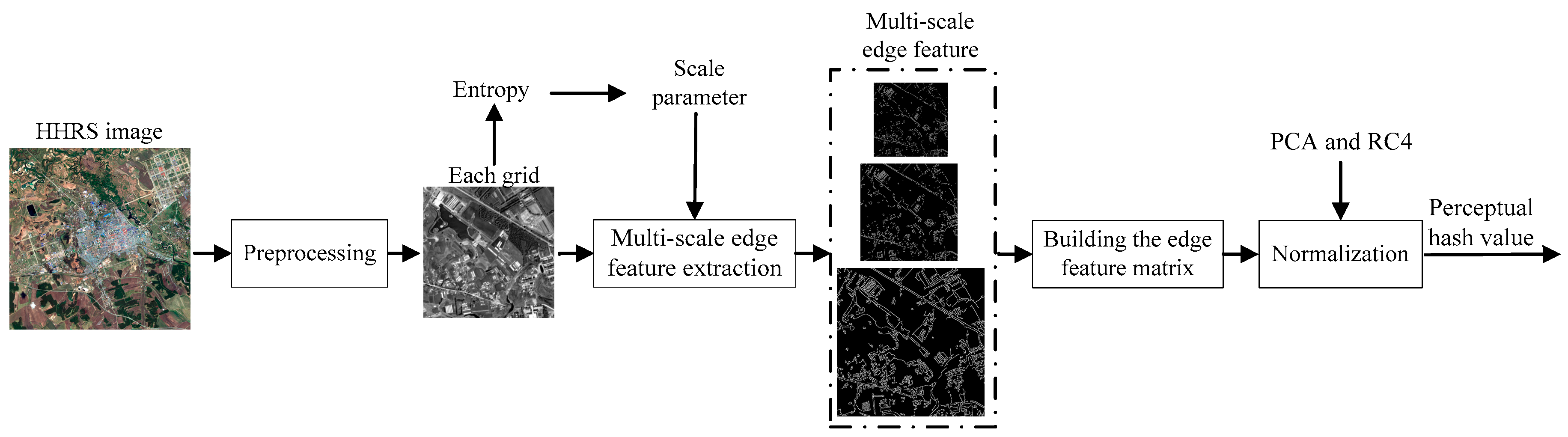
3. Proposed Scheme
3.1. HRRS Image Preprocessing
3.2. Multi-Scale Edge Feature Extraction
- (1)
- Computation of the gradient magnitude and edge direction maps. Canny operator is firstly performed on Pl to get an edge map El. Then, the edge pixels on El are recorded in a set Pl and roughly sorted in the descending order according to the gradient magnitudes G, which can be obtained by the formula G = where Gx and Gy are the horizontal and vertical gradients of the edge pixel.
- (2)
- The foremost unprocessed edge pixel in Pl is selected as the initial seed pixel pseed, whose 8-neighbors are then searched. If there exists an 8-neighbor and unprocessed edge pixel, we consider it as the next seed pixel and add it into the current edge chain.
- (3)
- The seed growing of the current edge chain is conducted iteratively until all the pixels in the chain is processed, and then we begin with another edge chain from the rest of Pl.The set of edge chains on Pl is denoted as Cl.
- (1)
- Traversing the grid cell Qij to detect the candidate edge pixel. For each pixel Qij(x0,y0) of the grid cell, if there is a corresponding scaled pixel Pl(xl,yl) = (x0/2l, y0/2l) on any layer of the image pyramid is an edge pixel, we consider Qij(x0,y0) to be a candidate edge pixel. For all these candidate edge pixels, a mask image with the same size of Qij is created.
- (2)
- Processing non-maximum suppression [38] on the pixel of the mask image to get real edge pixels, in which the gradient orientation of each pixel is defined as that of the corresponding pixels on the original grid cell Qij. The real edge pixels are the anchors.
- (3)
- Connecting the anchors to get the fused edge feature. We simply go from one anchor to the next by proceeding over the cordillera peak of the gradient map mountain, which is guided by the gradient magnitude and edge direction maps.
3.3. The Generation of Perceptual Hash Sequence
3.4. Forensics of Tampering for HRRS Image
4. Experiments and Discussions
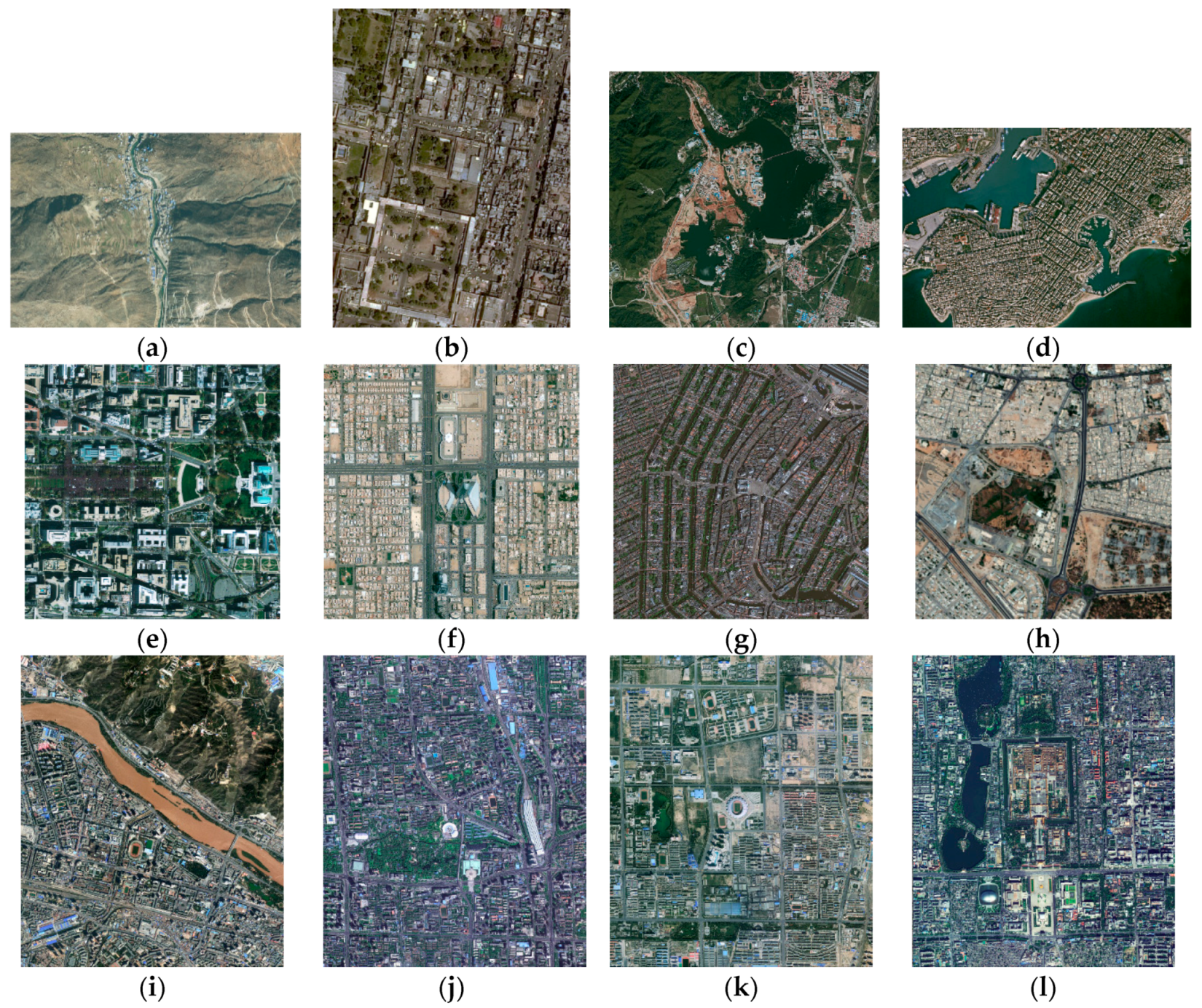
4.1. Experiments Setting
4.2. Sensitivity to Tampering Experiments and Analysis
4.3. Robust Experiments and Analysis
4.4. Computational Efficiency Experiments and Analysis
4.5. Analysis of Algorithm Safety
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Niu, X.M.; Jiao, Y.H. An Overview of Perceptual Hashing. Acta Electron. Sin. 2008, 36, 1405–1411. [Google Scholar]
- Xiang, S.; Kim, H.J.; Huang, J. Histogram-based image hashing scheme robust against geometric deformations. In Proceedings of the 9th Workshop on Multimedia & Security, Dallas, TX, USA, 20–21 September 2007; pp. 121–128. [Google Scholar]
- Xu, Z.; Ling, H.; Zou, F.; Li, P. Robust image copy detection using multi-resolution histogram. In Proceedings of the International Conference on Multimedia Information Retrieval, Philadelphia, PA, USA, 29–31 March 2010; pp. 129–136. [Google Scholar]
- Tang, Z.J.; Zhang, X.Q.; Dai, X.; Yang, J.Z.; Wu, T.X. Robust image hash function using local color features. AEU Int. J. Electron. Commun. 2013, 67, 717–722. [Google Scholar] [CrossRef]
- Fang, W.; HU, H.M.; Hu, Z.; Liao, S.C.; Li, B. Perceptual hash-based feature description for person re-identification. Neurocomputing 2018, 272, 520–531. [Google Scholar] [CrossRef]
- Swaminathan, A.; Mao, Y.; Wu, M. Robust and secure image hashing. IEEE Trans. Inf. Forensics Secur. 2006, 1, 215–230. [Google Scholar] [CrossRef] [Green Version]
- Saad, S.M. Design of a robust and secure digital signature scheme for image authentication over wireless channels. IET Inf. Secur. 2009, 3, 1–8. [Google Scholar] [CrossRef]
- Ahmed, F.; Siyal, M.Y.; Abbas, V.U. A secure and robust hash-based scheme for image authentication. Signal Process. 2010, 90, 1456–1470. [Google Scholar] [CrossRef]
- Lin, C.Y.; Chang, S.F. A robust image authentication method distinguishing JPEG compression from malicious manipulation. EEE Trans. Circuits Syst. Video Technol. 2001, 11, 153–168. [Google Scholar]
- Lu, C.S.; Liao, H.Y.M. Structural digital signature for image authentication: An incidental distortion resistant scheme. IEEE Trans. Multimed. 2003, 5, 161–173. [Google Scholar]
- Zhang, Y.D.; Tang, S.; Li, J.T. Secure and Incidental Distortion Tolerant Digital Signature for Image Authentication. J. Comput. Sci. Technol. 2007, 22, 618–625. [Google Scholar] [CrossRef]
- Wang, H.; Wang, H.X. Perceptual Hashing-Based Image Copy-Move Forgery Detection. Secur. Commun. Netw. 2018, 2018, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Zhou, J.; Duan, F.; Liu, F.; Cheng, L.M. Wave atom transform based image hashing using distributed source coding. J. Inf. Secur. Appl. 2016, 31, 75–82. [Google Scholar] [CrossRef]
- Monga, V.; Evans, B.L. Perceptual image hashing via feature points: Evaluation and tradeoffs. IEEE Trans. Image Process. 2006, 15, 3452–3465. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.Q.; Li, Q.; Liu, J.R.; Peng, X.Y. SIFT based image hashing algorithm. Chin. J. Sci. Instrum. 2011, 32, 2024–2028. [Google Scholar]
- Wang, X.F.; Xue, J.R.; Zheng, Z.Q.; Liu, Z.L.; Li, N. Image forensic signature for content authenticity analysis. J. Vis. Commun. Image Represent. 2012, 23, 782–797. [Google Scholar] [CrossRef]
- Zhao, X.H.; Li, Z.R.; Yi, J.K. SIFT Feature-Based Second-Order Image Hash Retrieval Approach. J. Softw. 2018, 13, 103–116. [Google Scholar] [CrossRef]
- Kozat, S.S.; Venkatesan, R.; Mihcak, M.K. Robust perceptual image hashing via matrix invariants. In Proceedings of the 2004 International Conference on Image Processing (ICIP), Singapore, 24–27 October 2004; pp. 3443–3446. [Google Scholar]
- Sun, R.; Gao, J. Image Hashing method via combination of NMF and PCA. J. Electron. Meas. Instrum. 2009, 23, 52–57. [Google Scholar] [CrossRef]
- Xiang, S.J.; Yang, J.Q. NMF-Based Image Hashing Algorithm Using Restricted Random Blocking. J. Electron. Inf. Technol. 2011, 33, 337–341. [Google Scholar] [CrossRef]
- Tang, Z.J.; Zhang, X.Q.; Zhang, S.C. Perceptual Image Hashing Based on Ring Partition and NMF. IEEE Trans. Knowl. Data Eng. 2014, 26, 711–724. [Google Scholar] [CrossRef]
- Chen, Y.C.; Yu, W.Y.; Feng, J.C. Robust image hashing using invariants of Tchebichef moments. Opt. Int. J. Light Electron Opt. 2014, 125, 5582–5587. [Google Scholar] [CrossRef]
- Qin, C.; Sun, M.; Chang, C.C. Perceptual Hashing for Color Images Based on Hybrid Extraction of Structural Features. Signal Process. 2017, 142, 194–205. [Google Scholar] [CrossRef]
- Chen, L.; Li, Z.; Yang, J.F. Compressive perceptual hashing tracking. Neurocomputing 2017, 239, 69–80. [Google Scholar] [CrossRef]
- Cui, C.; Mao, H.; Niu, X.; Zhang, L.X.; Hayat, T.; Alsaedi, A. A novel hashing algorithm for Depth-image-based-rendering 3D images. Neurocomputing 2016, 191, 1–11. [Google Scholar] [CrossRef]
- Yang, H.; Yin, J.; Jiang, M. Perceptual Image Hashing Using Latent Low-Rank Representation and Uniform LBP. Appl. Sci. 2018, 8, 317. [Google Scholar] [CrossRef]
- Ding, K.M.; Zhu, C.Q.; Lu, F.Q. An adaptive grid partition based perceptual hash algorithm for remote sensing image authentication. Wuhan Daxue Xuebao 2015, 40, 716–720. [Google Scholar]
- Ding, K.M.; Zhu, C.Q. Perceptual hash algorithm for integrity authentication of remote sensing image. J. Southeast Univ. 2014, 44, 723–727. [Google Scholar]
- Ding, K.M.; Chen, S.P.; Meng, F. A Novel Perceptual Hash Algorithm for Multispectral Image Authentication. Algorithms 2018, 11, 6. [Google Scholar] [CrossRef]
- Cihan, T.; Cuneyt, A. Edge Drawing: A combined real-time edge and segment detector. J. Vis. Commun. Image R. 2012, 23, 862–872. [Google Scholar]
- Bruzzone, L.; Carlin, L. A Multilevel Context-Based System for Classification of Very High Spatial Resolution Images. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2587–2600. [Google Scholar] [CrossRef] [Green Version]
- Lopez-Molina, C.; Baets, B.D.; Bustince, H.; Sanz, J.; Barrenechea, E. Multiscale edge detection based on Gaussian smoothing and edge tracking. Knowl. Based Syst. 2013, 44, 101–111. [Google Scholar] [CrossRef]
- Witkin, A.P. Scale-space Filtering. Read. Comput. Vis. 1987, 42, 329–332. [Google Scholar]
- Coleman, S.A.; Scotney, B.W.; Suganthan, S. Multi-scale edge detection on range and intensity images. Pattern Recognit. 2011, 44, 821–838. [Google Scholar] [CrossRef]
- Shih, M.Y.; Tseng, D.C. A wavelet-based multiresolution edge detection and tracking. Image Vis. Comput. 2005, 23, 441–451. [Google Scholar] [CrossRef]
- Xiang, Y.; Wang, F.; Wan, L.; You, H. An Advanced Multiscale Edge Detector Based on Gabor Filters for SAR Imagery. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1522–1526. [Google Scholar] [CrossRef]
- Antunes, S.; Esposito, A.; Palmisano, A.; Colantoni, C.; Cerutti, S.; Rizzo, G. Cardiac Multi-detector CT Segmentation Based on Multiscale Directional Edge Detector and 3D Level Set. Ann. Biomed. Eng. 2016, 44, 1487–1501. [Google Scholar] [CrossRef] [PubMed]
- Jin, G.; Wan, X. An improved method for SIFT-based copy–move forgery detection using non-maximum value suppression and optimized J-Linkage. Signal Process. Image Commun. 2017, 57, 113–125. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, J.; Jiang, X.; Fang, X.; Cai, Z. Spectral-Spatial Feature Extraction of Hyperspectral Images Based on Propagation Filter. Sensors 2018, 18, 6. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Gao, S.; Li, M. A novel PCA-based microstructure descriptor for heterogeneous material design. Comput. Mater. Sci. 2017, 130, 39–49. [Google Scholar] [CrossRef]
- Báscones, D.; González, C.; Mozos, D. Hyperspectral Image Compression Using Vector Quantization, PCA and JPEG2000. Remote Sens. 2018, 10, 6. [Google Scholar] [CrossRef]





| Algorithm Based on DCT | Algorithm Based on Wavelet Transform | Algorithm Based on SVD | Algorithm in Paper [28] | Our Scheme | |
|---|---|---|---|---|---|
| Figure 4b | Undetected | Undetected | Detected | Detected | Detected |
| Figure 4c | Detected | Detected | Detected | Detected | Detected |
| Figure 4d | Detected | Detected | Detected | Detected | Detected |
| Figure 5b | Detected | Detected | Detected | Detected | Detected |
| Figure 5c | Undetected | Detected | Undetected | Detected | Detected |
| Figure 5d | Detected | Detected | Detected | Detected | Detected |
| Figure 6b | Undetected | Undetected | Undetected | Detected | Detected |
| Figure 6c | Undetected | Undetected | Undetected | Undetected | Detected |
| Figure 6d | Undetected | Undetected | Undetected | Detected | Detected |
| Figure 7b | Undetected | Undetected | Undetected | Undetected | Detected |
| Figure 7c | Undetected | Undetected | Undetected | Detected | Detected |
| Figure 7d | Undetected | Undetected | Undetected | Undetected | Detected |
| Manipulation | Format Conversion (TIFF to BMP) | Lossless Compression (PNG Compressing) | Digital Watermarking (LSB) |
|---|---|---|---|
| Image A (6 × 4 partition) | 100% | 100% | 100% |
| Image B (4 × 6 partition) | 100% | 100% | 100% |
| Image C (6 × 6 partition) | 100% | 100% | 100% |
| Image D (24 × 16 partition) | 100% | 100% | 100% |
| Image E (10 × 10 partition) | 100% | 100% | 100% |
| Image F (10 × 10 partition) | 100% | 100% | 100% |
| Image G (10 × 10 partition) | 100% | 100% | 100% |
| Image H (16 × 16 partition) | 100% | 100% | 100% |
| Image I (12 × 16 partition) | 100% | 100% | 100% |
| Image J (12 × 16 partition) | 100% | 100% | 100% |
| Image K (12 × 16 partition) | 100% | 100% | 100% |
| Image L (12 × 16 partition) | 100% | 100% | 100% |
| Manipulation | JPEG Compression (98%) | JPEG Compression (90%) | Brightness Adjustment (5% Reduction) |
|---|---|---|---|
| Image A (6 × 4 partition) | 91.7% | 86.1% | 83.3% |
| Image B (4 × 6 partition) | 91.7% | 84.4% | 81.3% |
| Image C (6 × 6 partition) | 88.9% | 86.1% | 80.6% |
| Image D (24 × 16 partition) | 91.1% | 83.9% | 79.4% |
| Image E (10 × 10 partition) | 92.0% | 86.0% | 83.0% |
| Image F (10 × 10 partition) | 93.0% | 82.0% | 81.0% |
| Image G (10 × 10 partition) | 92.0% | 80.0% | 84.0% |
| Image H (16 × 16 partition) | 91.0% | 85.9% | 81.6% |
| Image I (12 × 16 partition) | 89.6% | 85.9% | 80.7% |
| Image J (12 × 16 partition) | 93.8% | 86.5% | 82.3% |
| Image K (12 × 16 partition) | 89.6% | 85.9% | 81.8% |
| Image L (12 × 16 partition) | 91.2% | 83.9% | 80.7% |
| DWT-Based Algorithm | Algorithm in [28] | Our Scheme | |
|---|---|---|---|
| Image A (6 × 4 partition) | 0.85 | 1.56 | 4.56 |
| Image C (6 × 6 partition) | 1.33 | 2.25 | 6.71 |
| Image D (24 × 16 partition) | 18.34 | 31.56 | 73.34 |
| Image G (10 × 10 partition) | 3.78 | 6.09 | 17.38 |
| Image L (12 × 16 partition) | 7.05 | 12.36 | 33.12 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, K.; Meng, F.; Liu, Y.; Xu, N.; Chen, W. Perceptual Hashing Based Forensics Scheme for the Integrity Authentication of High Resolution Remote Sensing Image. Information 2018, 9, 229. https://doi.org/10.3390/info9090229
Ding K, Meng F, Liu Y, Xu N, Chen W. Perceptual Hashing Based Forensics Scheme for the Integrity Authentication of High Resolution Remote Sensing Image. Information. 2018; 9(9):229. https://doi.org/10.3390/info9090229
Chicago/Turabian StyleDing, Kaimeng, Fan Meng, Yueming Liu, Nan Xu, and Wenjun Chen. 2018. "Perceptual Hashing Based Forensics Scheme for the Integrity Authentication of High Resolution Remote Sensing Image" Information 9, no. 9: 229. https://doi.org/10.3390/info9090229





