The (T, L)-Path Model and Algorithms for Information Dissemination in Dynamic Networks
Abstract
1. Introduction
2. Related Work
2.1. Dynamic Network Models
2.2. Information Dissemination Algorithms
3. System Model and Problem Definition
3.1. System Model
3.2. Problem Definition
- Termination: each node in the network should eventually terminate the execution of the algorithm.
- Accuracy: each node gets all the k tokens at the end of the algorithm execution.
4. The Proposed Dynamic Network Models
4.1. Instant Path
- : the minimum accumulation of node number variance of ρt(u, v) from t to t′ (t′ > t), i.e.,
- : the maximum variance of node order of ρt(u, v) from t to t′ (t′ > t), i.e.,
4.2. The (T, l)-Path Model
4.3. The (T, l)*-Path Model
4.4. The Relationship between the (T, l)-Path and (T, l)*-Path
4.5. The Relationship between (T, l)-Path and T-Interval Connectivity
5. The Algorithm for Token Dissemination in (T, l)-Path
5.1. Algorithm 1: 1-Token Dissemination in (T, l)-Path
| Algorithm 1: 1-token dissemination in the (T, l)-path. |
| Initialization of per node: |
| broNumber ← −1 |
| For nodeu: |
| broNumber ← l + 1 |
| fori = 0, …, l + 1 do |
| broadcasts msg(c, broNumber) |
| broNumber ← broNumber-1 |
| endfor |
| For any nodevin roundi*T + r: |
| ifbroNumber ≠ 0 |
| broadcasts msg(c, broNumbe) |
| broNumber ← broNumber-1 |
| endif |
| receive msg(c, broNumber) from neighbors |
| set TR ← msg(c, broNumber) |
| ifTR is not an empty set |
| set m ← max(broNumber) in TR |
| if broNumber = −1 |
| set broNumber ← |
| endif |
| if broNumber = 0 and m≥2 or broNumber ≤m-2 |
| set broNumber ← m-1 |
| endif |
| endif |
5.2. Algorithm 2: K-Token Dissemination in (T, l)-Path
| Algorithm 2:k-token dissemination in the (T, l)-path. |
| Initialization of per node: |
| TC ← |
| TS ← |
| TR ← |
| broNumber ← l + 1 |
| c ← the token c that the node has in the beginning |
| For any nodevin roundi*T + r: |
| ift is not an empty set |
| broadcasts msg(c, broNumbe) |
| broNumber ← broNumber-1 |
| endif |
| receive msg(c′, broNumber) from neighbors |
| TR ← {msg(c′, broNumber)} |
| TA ← {c′} in TR |
| ifTR is not an empty set |
| minID ← minimal ID of token c′ in TR |
| if minID < ID of token c and i<(n-1)* p (the ranks of c′) |
| broNumber ← max(, (n-1)*p-i*T-r) |
| c ← c |
| TS ← TA − {c1, c2,... ci}, which ID of c i is not smaller than minID in TA |
| endif |
| if minID = ID of token c |
| set m ← max(broNumber) in TR |
| if broNumber ≤ m-2 |
| set broNumber ← m-1 |
| endif |
| endif |
| ifbroNumber = 0 |
| set TS=TSc |
| c ← min(TA-TS) |
| broNumber ← l+1 |
| endif |
6. The Algorithm for K-Token Dissemination in (T, L)*-Path
6.1. Algorithm 3: 1-Token Dissemination in (T, l)*-Path
| Algorithm 3: 1-token dissemination in the (T, l)*-path. |
| For nodeu: |
| fori = 0, …, l do |
| broadcasts msg(c) |
| endfor |
| For any nodev: |
| if node v receives token c for the first time in round r |
| for i = r+1, …,r+ l + 1 do |
| broadcasts msg(c) |
| endfor |
| endif |
6.2. Algorithm 4: K-Token Dissemination in (T, l)*-Path
| Algorithm 4:k-token dissemination in the (T, l)*-path. |
| Initialization of per node: |
| TC ← |
| TS ← |
| broNumber ← −1 |
| broID ← MAX |
| For any other nodevin roundi: |
| IDt ← min(TC-TS) |
| if broNumber = −1 or (broNumber ≠ −1 and broID> IDt) |
| broID ← IDt |
| broadcast c to neighbors |
| broNumber ← k |
| TS=TS-{IDj}(which IDj > IDt) |
| endif |
| if broNumber ≠ −1 and broID ≤ IDt |
| broadcast c′ to neighbors (ID of token c′ is broID) |
| broNumber ← broNumber-1 |
| endif |
| if broNumber = 0 |
| set TS=TSbroID |
| broNumber ← −1 |
| borID ← MAX |
| endif |
| receive c1, ..., cs from neighbors |
| TC←TC{c1, ..., cs} |
7. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Grindrod, P.; Higham, D.J. Evolving graphs: Dynamical models, inverse problems and propagation. Proc. R. Soc. Lond. Ser. A 2010, 466, 753–770. [Google Scholar] [CrossRef]
- Erlebach, T.; Hoffmann, M.; Kammer, F. On temporal graph exploration. In Proceedings of the International Colloquium on Automata, Languages and Programming, Kyoto, Japan, 6–10 July 2015; pp. 444–455. [Google Scholar]
- Datta, S.; Giannella, C.; Kargupta, H. K-means clustering over a large, dynamic network. In Proceedings of the Sixth SIAM International Conference on Data Mining, Bethesda, MD, USA, 20–22 April 2006; pp. 153–164. [Google Scholar]
- Vaidya, N.H.; Krishna, P.; Chatterjee, M.; Pradhan, D.K. A Cluster-based approach for routing in dynamic networks. ACM SIGCOMM Comput. Commun. Rev. 1997, 27, 49–64. [Google Scholar]
- Michail, O.; Chatzigiannakis, I.; Spirakis, P.G. Naming and counting in anonymous unknown dynamic networks. In Proceedings of the 26th International Symposium on Distributed Computing (DISC), Salvador, Brazil, 16–18 October 2012; pp. 437–438. [Google Scholar]
- Kuhn, F.; Oshman, R. Dynamic networks: Models and algorithms. ACM SIGACT News 2011, 42, 82–96. [Google Scholar] [CrossRef]
- Van de Bovenkamp, R.; kuipers, F.; van Mieghem, P. Gossip-based counting in dynamic networks. In Proceedings of the 11th International IFIP TC 6 Networking Conference, Prague, Czech Republic, 21–25 May 2012; pp. 404–417. [Google Scholar]
- O’Dell, R.; Wattenhofer, R. Information dissemination in highly dynamic graphs. In Proceedings of the 9th Joint Workshop on Foundations of Mobile Computing, Cologne, Germany, 2 September 2005; pp. 104–110. [Google Scholar]
- Haeupler, B.; Karger, D. Faster information dissemination in dynamic networks via network coding. In Proceedings of the ACM SIGACT-SIGOPS Symposium on Principles of Distributed Computing, San Jose, CA, USA, 6–8 June 2011; pp. 381–390. [Google Scholar]
- Kuhn, F.; Lynch, N.; Oshman, R. Distributed computation in dynamic networks. In Proceedings of the 42nd ACM Symposium on Theory of Computing, Cambridge, MA, USA, 6–8 June 2010; pp. 513–522. [Google Scholar]
- Kempe, D.; Kleinberg, J.; Kumar, A. Connectivity and inference problems for temporal networks. In Proceedings of the 32nd Annual ACM Symposium on Theory of Computing (STOC), Portland, OR, USA, 21–23 May 2000; pp. 504–513. [Google Scholar]
- Casteigts, A.; Flocchini, P.; Quattrociocchi, W.; Santoro, N. Time-Varying graphs and dynamic networks. Int. J. Parallel Emerg. Distrib. Syst. 2012, 27, 387–408. [Google Scholar] [CrossRef]
- Shang, Y. Multi-agent coordination in directed moving neighbourhood random networks. Chin. Phys. B 2010, 19, 070201. [Google Scholar]
- Shang, Y. Consensus in averager-copier-voter networks of moving dynamical agents. Chaos Interdisciplin. J. Nonlinear Sci. 2017, 27, 215–233. [Google Scholar] [CrossRef] [PubMed]
- Clementi, A.; Macci, C.; Monti, A.; Pasquale, F.; Silvestri, R. Flooding time in edge-markovian dynamic graphs. In Proceedings of the 27th ACM Symposium on Principles of Distributed Computing, Toronto, ON, Canada, 18–21 August 2008; pp. 213–222. [Google Scholar]
- Avin, C.; Koucky, M.; Lotker, Z. How to explore a fast-changing world (cover time of a simple random walk on evolving graphs). In Proceedings of the 35th International Colloquium on Automata, Languages and Programming, Reykjavik, Iceland, 7–11 July 2008; pp. 121–132. [Google Scholar]
- Pittel, B. On spreading a rumor. SIAM J. Appl. Math. 1987, 47, 213–223. [Google Scholar] [CrossRef]
- Clementi, A.; Monti, A.; Silvestri, R. Flooding over Manhattan. In Proceedings of the 29th ACM Symposium on Principles of Distributed Computing, Zurich, Switzerland, 25–28 July 2010. [Google Scholar]
- Shang, Y. The Estrada index of evolving graphs. Appl. Math. Comput. 2015, 250, 415–423. [Google Scholar] [CrossRef]
- Shang, Y. Laplacian Estrada and normalized Laplacian Estrada indices of evolving graphs. PLoS ONE 2015, 10, e0123426. [Google Scholar] [CrossRef] [PubMed]
- Wehmuth, K.; Fleury, E.; Ziviani, A. On multiaspect graphs. Theor. Comput. Sci. 2016, 651, 50–61. [Google Scholar] [CrossRef]
- Ahmadi, M.; Ghodselahi, A.; Kuhn, F.; Molla, A.R. The cost of global broadcast in dynamic radio networks. In Proceedings of the International Conference on Principles of Distributed Systems, Rennes, France, 14–17 December 2015. [Google Scholar]
- Yang, Z.; Wu, W.; Chen, Y.; Li, X.; Cao, J. (Q, S)-distance model and counting algorithms in dynamic distributed systems. Int. J. Distrib. Sens. Netw. 2018, 14. [Google Scholar] [CrossRef]
- Jelasity, M.; Guerraoui, R.; Kermarrec, A.; Steem, M. The peer sampling service: Experimental evaluation of unstructured gossip-based implementations. In Proceedings of the 5th ACM/IFIP/USENIX International Conference on Middleware, Toronto, ON, Canada, 18–22 October 2004; pp. 79–98. [Google Scholar]
- Clementi, A.; Crescenzi, P.; Doerr, C.; Fraigniaud, P.; Pasquale, F.; Silvestri, R. Rumor spreading in random evolving graphs. Random Struct. Algorithms 2016, 48, 290–312. [Google Scholar] [CrossRef]
- Acan, H.; Collevecchio, A.; Mehrabian, A.; Wormald, N. On the push & pull protocol for rumor spreading. SIAM J. Discret. Math. 2017, 31, 647–668. [Google Scholar]
- Augustine, J.; Chen, A.; Liaee, M.; Pandurangan, G.; Rajaraman, R. Information spreading in dynamic networks under oblivious adversaries. In Proceedings of the International Symposium on Distributed Computing, Paris, France, 27–29 September 2016; pp. 399–413. [Google Scholar]

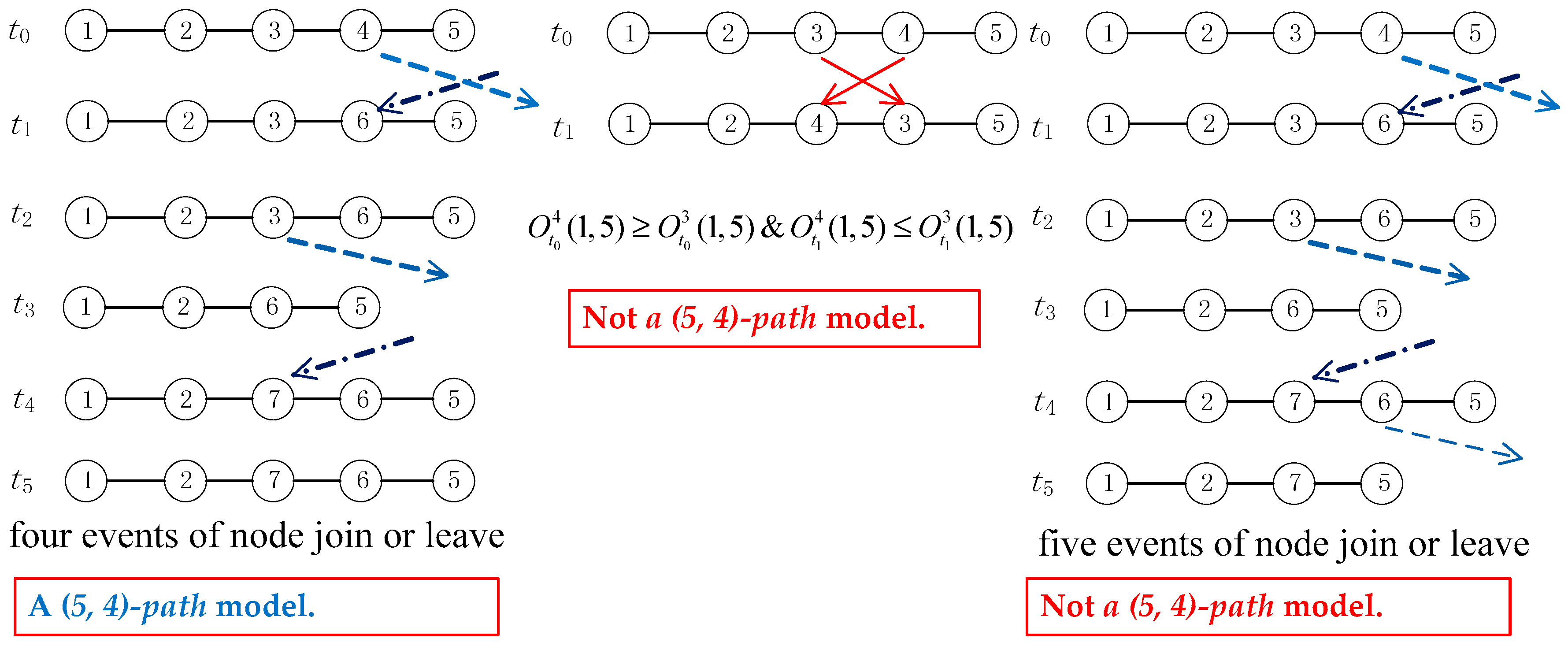

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Wu, W. The (T, L)-Path Model and Algorithms for Information Dissemination in Dynamic Networks. Information 2018, 9, 212. https://doi.org/10.3390/info9090212
Yang Z, Wu W. The (T, L)-Path Model and Algorithms for Information Dissemination in Dynamic Networks. Information. 2018; 9(9):212. https://doi.org/10.3390/info9090212
Chicago/Turabian StyleYang, Zhiwei, and Weigang Wu. 2018. "The (T, L)-Path Model and Algorithms for Information Dissemination in Dynamic Networks" Information 9, no. 9: 212. https://doi.org/10.3390/info9090212
APA StyleYang, Z., & Wu, W. (2018). The (T, L)-Path Model and Algorithms for Information Dissemination in Dynamic Networks. Information, 9(9), 212. https://doi.org/10.3390/info9090212



