Abstract
Multiswarm comprehensive learning particle swarm optimization (MSCLPSO) is a multiobjective metaheuristic recently proposed by the authors. MSCLPSO uses multiple swarms of particles and externally stores elitists that are nondominated solutions found so far. MSCLPSO can approximate the true Pareto front in one single run; however, it requires a large number of generations to converge, because each swarm only optimizes the associated objective and does not learn from any search experience outside the swarm. In this paper, we propose an adaptive particle velocity update strategy for MSCLPSO to improve the search efficiency. Based on whether the elitists are indifferent or complex on each dimension, each particle adaptively determines whether to just learn from some particle in the same swarm, or additionally from the difference of some pair of elitists for the velocity update on that dimension, trying to achieve a tradeoff between optimizing the associated objective and exploring diverse regions of the Pareto set. Experimental results on various two-objective and three-objective benchmark optimization problems with different dimensional complexity characteristics demonstrate that the adaptive particle velocity update strategy improves the search performance of MSCLPSO significantly and is able to help MSCLPSO locate the true Pareto front more quickly and obtain better distributed nondominated solutions over the entire Pareto front.
1. Introduction
Multiobjective optimization optimizes multiple conflicting objectives simultaneously. A multiobjective optimization problem can be formulated with the following minimization form without loss of generality [1]:
where x is the D-dimensional decision vector; Ω is the search space; M is the number of objectives; and fm (m = 1, 2, …, M) is the function or procedure used for evaluating the performance of x on the mth objective. The set is the objective space. Given two points u = (u1, u2, …, uM) and v = (v1, v2, …, vM) in Θ, v dominates u if vm ≤ um for each m = 1, 2, …, M and v ≠ u. A point u in Θ is nondominated if no other point in Θ dominates u; in other words, improvement on one objective of a nondominated point leads to deterioration on at least one other objective. A point x in Ω is Pareto-optimal if f(x) is nondominated in Θ; the set of all the nondominated points in Θ is the Pareto front and the set of all the Pareto-optimal points in Ω is the Pareto set.
In absence of the preferences of conflicting objectives, there is no way to say whether one nondominated solution is better than another nondominated solution, because a nondominated solution does not outperform on all the objectives. Accordingly, for many real-world applications, a number of nondominated solutions, well distributed over the entire span of the Pareto front, must be identified for selecting the final tradeoff. Metaheuristics have been recognized as promising and competitive for approximating the Pareto front [2,3]. A metaheuristic is essentially a collection of one or more intelligent search strategies inspired by nature principles from, e.g., biology, chemistry, ethology, and physics [2,3,4,5]. Metaheuristics were originally proposed for single-objective optimization [4,5], and have been extended to address multiobjective optimization recently [2,3]. A metaheuristic usually solves the single-objective or multiobjective optimization problem using a population of individuals, with each individual representing a candidate solution and iteratively evolving. Compared with traditional optimization methods such as linear programming, nonlinear programming, and optimal control theory, metaheuristics do not require characteristics such as continuity, differentiability, linearity, and convexity on the optimization problem; in addition, population-based metaheuristics can find multiple nondominated solutions in just one run for multiobjective optimization. Existing metaheuristics solve a multiobjective optimization problem by either treating the multiobjective problem as whole [6,7,8,9,10,11,12,13,14,15,16,17,18] or involving decomposition (i.e., decomposing the multiobjective problem into multiple single-objective problems) [1,19,20,21,22,23,24,25,26,27].
Particle swarm optimization (PSO) is a class of metaheuristics inspired by ethology and simulates the movements of zooids in a bird flock or fish school [1,7,20,21,28,29,30,31,32]. In PSO, the population is termed as a swarm, and an individual is termed as a particle. All the particles of the swarm can be considered to be “flying” in the search space Ω. Each particle is thus associated with a position, a velocity, and a fitness indicating the particle’s search performance. The particles are initialized randomly. Each particle adjusts its velocity in each iteration (or generation) based on the historical best search experience (i.e., personal best position) of the particle itself and/or the personal best positions of other particles. In our recent work [1], we have proposed multiswarm comprehensive learning PSO (MSCLPSO) for multiobjective optimization. Decomposition is employed in MSCLPSO; multiple swarms are used and each swarm independently optimizes a separate original objective by a state-of-the-art single-objective comprehensive learning PSO (CLPSO) algorithm [29]. Nondominated solutions found so far (also called elitists) are stored in an external repository. Mutation and differential evolution are applied to the elitists. The experimental results reported in [1] demonstrate that the decomposition, mutation and differential evolution strategies help MSCLPSO discover the true Pareto front in just one run. However, the experimental results also indicate that MSCLPSO needs a large number of generations to converge on benchmark problems with either simple or complex Pareto sets; in other words, MSCLPSO is inefficient. The underlying reason is that each swarm just tries to optimize the associated objective and does not learn from any other swarm or the elitists for the particles’ velocity update. This particle velocity update strategy contributes to the search of the extreme nondominated solutions on the Pareto front, but does not benefit locating the other nondominated solutions on the Pareto front. Therefore, in this paper, we propose an adaptive particle velocity update strategy for MSCLPSO to improve the search efficiency. According to whether the elitists are indifferent or complex on each dimension, each particle adaptively determines to only learn from some particles in the same swarm, or additionally, from the difference of some pair of elitists for the velocity update on that dimension, in an attempt to achieve a tradeoff between optimizing the associated single objective and exploring the Pareto set.
Metaheuristics need to store elitists either internally (i.e., within the population) or externally (i.e., using one or more separate repositories) when dealing with multiobjective optimization. However, none of the existing metaheuristics [1,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27], including MSCLPSO, have differentiated the indifferent and complex cases for the elitists on each dimension when evolving the individuals. If the elitists are indifferent on a dimension, the Pareto-optimal decision vectors are expected to be indifferent on that dimension, and learning from the historical search experience related to optimizing an objective benefits moving close to the indifferent Pareto-optimal decision vectors. On the other hand, when the elitists differ considerably on a dimension, the Pareto-optimal decision vectors are expected to be complex on that dimension, and it is important to persistently exert different forces on the evolution of each individual for the purpose of exploring the Pareto set. Accordingly, judging whether the elitists are indifferent or complex on each dimension and letting the individuals evolve differently in either case is critical to improve the search efficiency for multiobjective metaheuristics.
The rest of this paper is organized as follows. In Section 2, related work on multiobjective metaheuristics is discussed. Section 3 briefly reviews MSCLPSO and details the implementation of the adaptive particle velocity update strategy. The improved algorithm is referred to as adaptive MSCLPSO (AMCLPSO). In Section 4, AMCLPSO is evaluated on various two-objective and three-objective benchmark optimization problems and its performance is compared with MSCLPSO, as well as several other state-of-the-art multiobjective metaheuristics. Section 5 concludes the paper.
2. Related Work
A lot of metaheuristics have been proposed in the literature to address multiobjective optimization. These metaheuristics either treat the multiobjective optimization problem as a whole or involve decomposition. In addition, these metaheuristics differ in the strategies adopted to guide the search towards the true Pareto front and to obtain well distributed nondominated solutions.
Metaheuristics usually use a population of individuals that evolve iteratively. In each iteration, each individual is compared with its evolved value in order to decide whether the individual needs to be replaced by its evolved value. For metaheuristics that treat the multiobjective optimization problem as whole [6,7,8,9,10,11,12,13,14,15,16], the comparison is based on Pareto dominance. As Pareto dominance is a partial order, an inappropriate selection of the value to stay in the population would negatively affect discovering the true Pareto front. Metaheuristics that involve decomposition decompose the multiobjective optimization problem into multiple different single-objective problems and use multiple populations/individuals, with each single-objective problem being independently optimized by a separate population/individual. As a result, the comparison of each individual with the evolved value is determined simply based on the optimized single objective. The multiple populations/individuals exchange information and collaborate to derive nondominated solutions. For vector evaluated genetic algorithm [19], vector evaluated PSO [20], co-evolutionary multiswarm PSO (CMPSO) [21], and MSCLPSO [1], multiple populations are used and each population focuses on optimizing a separate original objective. Multiobjective evolutionary algorithm based on decomposition (MOEA/D) [22,23,24,25,26,27] is a framework that lets each individual handle a different single-objective problem; an aggregation technique (e.g., weighted sum) is applied to attain each single objective.
To guide the search towards the true Pareto front, most metaheuristics encourage each individual to learn from diverse exemplars [6,7,19,20,21,22,23,24,25,26]. The exemplars exert different forces on the evolution of the individual. The exemplars can be the individual itself [6,7,19,20,21,22,23,24,25,26], another individual [6,7,19,20,21,22,23,24,25,26], and/or an externally stored elitist [7,21]. For elitists stored in an external repository, the repository can be considered as a separate population of individuals, thus the elitists can also be appropriately evolved to help discover the true Pareto front [1,21].
To obtain well distributed nondominated solutions on the Pareto front, metaheuristics need to promote the diversity of the elitists using techniques such as adaptive grid [12,13], clustering [14], crowding distance [6], fitness sharing [8], maximin sorting [15], vicinity distance [9,16], nearest neighbor density estimation [10], and weighted sum aggregation [22,23,24,25,26]. The weighted sum aggregation technique employed in the MOEA/D framework is the most efficient and assumes that the predefined uniformly distributed weight vectors result in reasonably distributed nondominated solutions; however, this assumption may be violated in cases where the Pareto front is discontinuous or has a shape of sharp peak and low tail [26].
Robustness and search efficiency are also important concerns for metaheuristics. The initialization and evolution of the individuals involve random influence; therefore, the set of nondominated solutions obtained by a metaheuristic might be quite different for each run. Agent swarm optimization [11] improves the robustness by using a framework with various population-based metaheuristics coexist, working like a multi-agent system. A number of adaptive strategies have been adopted recently in literature metaheuristics to enhance the search efficiency [17,18,26,27].
3. Adaptive Multiswarm Comprehensive Learning Particle Swarm Optimization
3.1. Multiswarm Comprehensive Learning Particle Swarm Optimization
MSCLPSO [1] involves decomposition and uses M swarms, with each swarm m (m = 1, 2, …, M) optimizing a separate original objective (i.e., objective fm) by CLPSO [29]. There are N particles in each swarm. For each particle i (i = 1, 2, …, N) in each swarm m, i is associated with a position Pm,i = (Pm,i,1, Pm,i,2, …, Pm,i,D) and a velocity Vm,i = (Vm,i,1, Vm,i,2, …, Vm,i,D). Vm,i and Pm,i are updated on each dimension d (d = 1, 2, …, D) as follows in each generation.
where w is the inertia weight that somewhat keeps the previous flying direction with the use of the term , which decreases from 0.9 to 0.4 linearly; Em,i = (Em,i,1, Em,i,2, …, Em,i,D) is the guidance vector; c is the acceleration coefficient fixed at 1.5; and rm,i,d is a random number within the range [0, 1] and the term aims to pull i towards Em,i. CLPSO encourages learning from different guidance exemplars Em,i,d (d = 1, 2, …, D) on different dimensions. Em,i,d is dimension d of i’s personal best position Bm,i or dimension d of the personal best position of some other particle selected from swarm m. Bm,i is actually i’s historical best search experience. In each generation, the fitness of Pm,i is evaluated and replaces Bm,i if Pm,i gives a better fitness value than Bm,i.
Elitists are stored in an external repository shared by all the swarms. The repository is initialized to be empty and has a fixed maximum size Lmax. When the number of the elitists is larger than Lmax, the elitists with larger crowding distances (for two-objective optimization problems) [6] or vicinity distances (for multiobjective optimization problems with more objectives) [16] are allowed to stay in the repository, thereby facilitating preserving the diversity of the elitists.
The Pareto set of a multiobjective optimization can be simple or complex on each dimension d, i.e., the Pareto-optimal decision vectors are indifferent or differ considerably on that dimension. During the maintenance of the external repository, MSCLPSO applies mutation to maximally elitists randomly selected from the repository on a dimension selected randomly and adds the mutated elitists that are nondominated into the repository. The mutation strategy takes advantage of the particles’ personal best positions and the elitists. Each swarm m optimizes objective fm; therefore, for each particle i in the swarm, i’s personal best position Bm,i is exactly the single-objective global optimum or close to the single-objective global optimum on fm after a sufficient number of generations. The single-objective global optimum on fm is also a multiobjective Pareto-optimal decision vector and is extreme on the Pareto front. If the Pareto set is simple on dimension d, as Bm,i,d is exactly the same as or close to dimension d of the single-objective optimum on fm, learning from Bm,i,d benefits the search of the Pareto-optimal decision vectors on dimension d. On the other hand, if the Pareto set is complex on dimension d, the personal best positions of particles in different swarms often differ noticeably on that dimension; accordingly, learning from the particles’ personal best positions leads to the exploration of different regions of the Pareto set on dimension d. Additionally, the dimensional difference of two different elitists selected from the repository is often small when the Pareto set is simple on a dimension and could be large in the complex case; hence, learning from the elitists’ differences also helps search the Pareto set. The chances of mutating an elitist based on a personal best position or the difference of two elitists on each dimension are, respectively, 0.5.
MSCLPSO also applies differential evolution to maximally extreme and least crowded elitists in the external repository on all the D dimensions and adds the differentially evolved elitists that are nondominated into the repository. MSCLPSO differentially evolves an elitist by a large search step size or a small search step size with the same possibilities 0.5, for the purpose of achieving a balance between exploring and exploiting the Pareto set. The application of differential evolution to the extreme and least crowded elitists helps to improve the diversity of the elitists.
Let kmax be the predefined maximum number of generations and k be the generation counter, the working procedure of MSCLPSO is briefed in Algorithm 1. More details about MSCLPSO can be found in [1].
| Algorithm 1. The brief working procedure of MSCLPSO. |
|
3.2. Adaptive Particle Velocity Update
Let the number of elitists in the external repository be L. For each elitist l (l = 1, 2, …, L) in the repository, l’s decision vector is denoted as Ql = (Ql,1, Ql,2, …, Ql,D). On each dimension d, AMCLPSO calculates and which are respectively the maximum and minimum decision variable values relevant to all the elitists stored in the repository, i.e.,
If Equation (6) is true, the elitists are deemed to be indifferent on dimension d; otherwise, the elitists differ considerably on dimension d.
where Δabs is the absolute bound and is a small positive number; Δrel is the relative ratio and is a positive number much smaller than 1; and and are, respectively, the lower and upper bounds of the search space on dimension d. As the dimensional search space can be very large, the combined use of the absolute bound and relative ratio ensures that the elitists are indifferent on dimension d. The concepts of absolute bound and relative ratio were introduced in [31]; and differ from the “normative interval” determined in [31] in that and are relevant to the elitists, whereas the normative interval relates to the personal best positions. Empirical values chosen for Δabs and Δrel are 2 and 0.06 respectively.
The shared external repository provides an indirect information exchange mechanism among the swarms. For each particle i in each swarm m, i can learn from three types of search experience during the flight, i.e., i’s personal best position Bm,i, the personal best positions of other particles in swarm m, and the elitists stored in the repository. The search experience of i and that of other particles in swarm m benefit the single-objective optimization on objective fm. The search experience of the elitists might hinder the single-objective optimization on fm; however, it could contribute to the discovery of the Pareto set if the Pareto-optimal decision vectors differ considerably. Accordingly, on each dimension d, i’s velocity Vm,i,d is adaptively updated as follows.
where c1 and c2 are the acceleration coefficients used for the particle velocity update on dimension d when the elitists differ considerably on that dimension; αm,i,d and βm,i,d are two random numbers in [0, 1]; and l1 and l2 are two elitists randomly selected from the repository, and l1 ≠ l2 when the number of elitists L ≥ 2. Note that the same pair of l1 and l2 are used for all the dimensions. As can be seen from Equation (7), if Equation (6) is true, the Pareto set is expected to be simple on dimension d, thus i focuses on searching the optimal decision variable value with respect to objective fm on dimension d, because such a value is close to the Pareto-optimal decision vectors on that dimension. On the other hand, if Equation (6) is false, the Pareto set is expected to be complex on dimension d; as illustrated in Figure 1, the term guides i to fly towards the exemplar Em,i,d on dimension d and helps to locate the extreme nondominated solution that is optimal on fm, while the other term performs perturbation based on the difference of the two elitists l1 and l2 and lets the particle to explore the Pareto set on dimension d. It is much more important to conduct perturbation than extremity search for the particle velocity update when the Pareto set is expected to be complex on dimension d, hence c2 is much larger than c1. c1 and c2 are, respectively, set as 0.3 and 3 empirically.
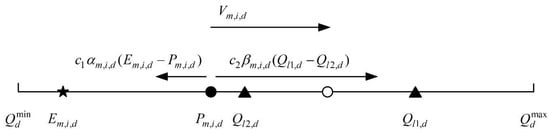
Figure 1.
Illustration of the adaptive particle velocity update strategy.
The adaptive particle velocity update strategy is able to improve the search efficiency of MSCLPSO. When the Pareto-optimal decision vectors differ considerably on a significant number of dimensions, updating the particles’ flight trajectories using Equation (2) does not contribute much to exploring the complex Pareto set, and MSCLPSO solely relies on the mutation and differential evolution of the externally stored elitists to discover the complex Pareto set; as a result, the computational effort spent on evolving the particles is mostly wasted. With the judgment of the complexness of the elitists on each dimension, the adaptive particle velocity update strategy dynamically determines the appropriate rule to update the particles’ velocities and positions on each dimension, helping to find the Pareto-optimal decision vectors on each dimension. The adaptive particle velocity update strategy also contributes to cases where at least one objective is multimodal and the Pareto-optimal decision vectors are indifferent on a significant number of dimensions. As it is difficult to locate the single-objective global optimum for the multimodal objective, the algorithm would encounter many local optima corresponding to the multimodal objective and the single-objective local optima would be stored as temporary elitists. The local optima could be quite different and Equation (6) may be false. Updating the particle’s flight trajectories based on the elitists’ differences helps to explore the search space, escape the local optima, and accelerate approaching the global optimum.
Calculating the maximum and minimum decision variable values relevant to all the elitists on all the dimensions requires O(LmaxD) basic operations. The judgment of the complexities of the Pareto set on all the dimensions needs O(D) basic operations. Hence the adaptive particle velocity update strategy incurs an additional computational burden of O(LmaxD) basic operations in each generation. The time complexity of MSCLPSO is O((MN + Lmax + Nmut + Nde)2D) basic operations and O(MN + Nmut + Nde) function evaluations (FEs) in each generation [1]. If the adaptive particle velocity update strategy can help MSCLPSO discover the true Pareto front with a noticeably smaller number of generations, a lot of computation time can be saved.
4. Experimental Studies
4.1. Performance Metric
Inverted generational distance (IGD) [1,6,21] is adopted as the metric for evaluating the performance of multiobjective metaheuristics in this paper, as it can reflect both the convergence of the resulting nondominated solutions to the true Pareto front and the diversity of the solutions over the entire Pareto front. As expressed in Equation (8), the IGD metric measures the average distance in the objective space Θ from a number of uniformly distributed points sampled along the true Pareto front to the nondominated solutions obtained.
where is the external repository; is the true Pareto front; u is a point sampled along ; the function dist() calculates the Euclidean distance between u and the nondominated solution in that is nearest to u; and gives the number of points in . Clearly, the IGD metric value would be small if the nondominated solutions stored in are well distributed over the true Pareto front.
4.2. Multiobjective Benchmark Optimization Problems
The following multiobjective benchmark optimization problems are chosen for evaluating multiobjective metaheuristics: ZDT2 and ZDT3 from the ZDT test set [33], ZDT4-V1 and ZDT4-V2 which are modified versions of ZDT4 [1], WFG1 from the WFG test set [34], UF1, UF2, UF7, UF8, and UF9 from the UF test set [35], a hybrid version of ZDT2 and UF1 called ZDT2-UF1, and a hybrid version of ZDT4 and UF2 called ZDT4-UF2. Equations (9) and (10) respectively describe the ZDT2-UF1 and ZDT4-UF2 problems.
For ZDT2-UF1, D = 30. The search space is . The Pareto set is . The Pareto front is nonconvex. f1 is unimodal and f2 is multimodal.
For ZDT4-UF2, D = 30. The search space is
The Pareto set is
The Pareto front is convex. f1 and f2 are both multimodal.
For ZDT2, ZDT3, ZDT4-V1, ZDT4-V2, and WFG1, the Pareto set is complex on dimension 1 and simple on the other D − 1 dimensions. With regard to UF1, UF2, UF7, UF8, and UF9, the Pareto set is complex on all the dimensions. Concerning ZDT2-UF1 and ZDT4-UF2, the Pareto set is simple on D/2 − 1 dimensions (i.e., dimension 2 to dimension D/2) and complex on D/2 + 1 dimensions (i.e., dimension 1 and dimension D/2 + 1 to dimension D). UF8 and UF9 are three-objective, while all the other benchmark problems are two-objective.
4.3. Metaheuristics Compared and Parameter Settings
AMCLPSO is compared with MSCLPSO [1] in order to investigate whether the proposed adaptive particle velocity update strategy can help MSCLPSO improve the search efficiency. The algorithm parameters of MSCLPSO take the recommended values given in [1]. The algorithm parameters of AMCLPSO take the same values as those of MSCLPSO, except that the empirical values of the parameters related to the adaptive particle velocity update strategy have been given in Section 3. The maximum number of elitists stored in the external repository is set as 100 and 300, respectively, on the two-objective benchmark optimization problems and three-objective problems. The number of points sampled along the true Pareto front is set as 1000 for the two-objective problems and 10,000 for three-objective problems. ε-dominance [36] is adopted. Given two points u = (u1, u2, …, uM) and v = (v1, v2, …, vM) in the objective space Θ, v ε-dominances u if vm ≤ um + ε for each m = 1, 2, …, M, and at least one m exists such that vm < um + ε, where ε is a given very small positive number. ε is set as 0.0001. As the problems exhibit different difficulty levels, the metaheuristics take different numbers of FEs on the problems. The FEs values are listed in Table 1. AMCLPSO and MSCLPSO are run for 30 independent times on each problem. MSCLPSO was compared with several state-of-the-art multiobjective metaheuristics including CMPSO [21], MOEA/D [22], and nondominated sorting genetic algorithm II (NSGA-II) and was ranked the best in [1], we can thus understand whether CMPSO outperforms the CMPSO, MOEA/D, and NSGA-II algorithms based on the comparison between AMCLPSO and MSCLPSO.

Table 1.
FEs used on the benchmark problems.
4.4. Experimental Results and Discussions
Table 2 lists the statistical (i.e., mean, standard deviation, best, and worst) IGD results calculated from the 30 runs of AMCLPSO and MSCLPSO on all the benchmark optimization problems. The better results of the two metaheuristics on all the problems are marked in bold in Table 2. The IGD results of AMCLSO in all 30 runs are compared with those of MSCLPSO using the Wilcoxon rank sum test with the significance level 0.05 on each benchmark problem. The test p-value results are listed in Table 3 and p-value results less than 0.05 are marked in bold. The best single-objective solutions obtained by different swarms of AMCLPSO on all the problems are listed in Table 4. Table 5 gives the statistical IGD results of AMCLPSO using some different parameters settings of the adaptive particle velocity update strategy. Standard deviation is abbreviated as “sd” for convenience in Table 1, Table 4 and Table 5. The nondominated solutions obtained by AMCLPSO and MSCLPSO in the worst runs on all the problems are illustrated in Figure 2, with the hollow circle and solid triangle curves respectively representing AMCLPSO and MSCLPSO.

Table 2.
Statistical IGD results of AMCLPSO and MSCLPSO on the benchmark problems.

Table 3.
Wilcoxon rank sum test p-value results on the benchmark problems.

Table 4.
Best single-objective solutions obtained by different swarms of AMCLPSO on the benchmark problems.

Table 5.
Statistical IGD results of AMCLPSO using some different parameter settings of the adaptive particle velocity update strategy.
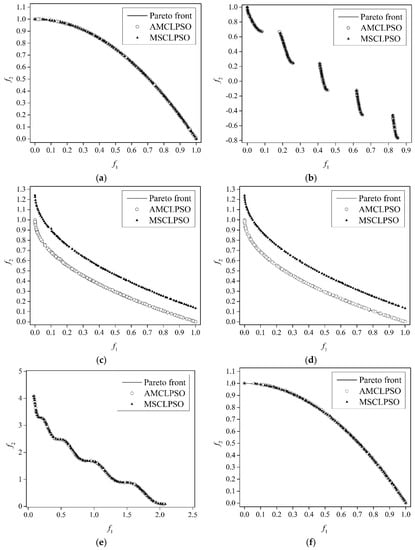
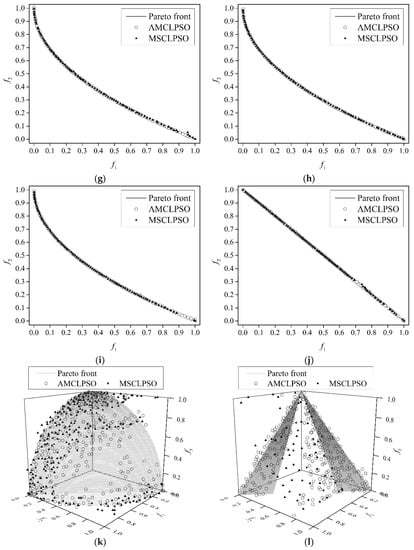
Figure 2.
Nondominated solutions obtained by AMCLPSO and MSCLPSO in the worst runs on the benchmark problems: (a) ZDT2; (b) ZDT3; (c) ZDT4-V1; (d) ZDT4-V2; (e) WFG1; (f) ZDT2-UF1. (g) ZDT4-UF2; (h) UF1; (i) UF2; (j) UF7; (k) UF8; (l) UF9.
The adaptive particle velocity update strategy: As can be observed from Table 2, AMCLPSO outperforms MSCLPSO on 10 problems with respect to each type of statistical IGD result. AMCLPSO is slightly worse than MSCLPSO in terms of the mean IGD result on ZDT2 and ZDT4-UF1, the standard deviation IGD result on ZDT2 and WFG1, the best IGD result on ZDT4-V2 and ZDT2-UF1, and the worst IGD result on ZDT2 and WFG1. For the Wilcoxon rank sum test, the null hypothesis is that the two arrays of data samples have identical distributions. A p-value result less than the significance level 0.05 supports the alternative hypothesis and means that the data distributions are significantly different. It can be observed from the Wilcoxon rank sum test p-value results given in Table 3 that the IGD results of AMCLPSO are significantly better than those of MSCLPSO on 6 problems i.e., ZDT4-UF2, UF1, UF2, UF7, UF8, and UF9. According to the nondominated solutions illustrated in Figure 2, AMCLPSO can approximate the true Pareto front even in the worst run on all 12 problems, and the nondominated solutions obtained by AMCLPSO in the worst run are well distributed over the entire Pareto front on 10 problems (i.e., except UF8 and UF9). MSCLPSO locates a local Pareto front which is considerably far from the true Pareto front in the worst run on the ZDT4-V1, ZDT4-V2, UF8, and UF9 problems. The nondominated solutions derived by MSCLPSO exhibit a worse distribution over the entire Pareto front than those by AMCLPSO on the ZDT4-UF2, UF2, and UF7 problems. The best single-objective solutions given in Table 4 show that AMCLPSO can find the global optimum or a near-optimum for one objective on the ZDT2, ZDT3, WFG1, ZDT2-UF1, and ZDT4-UF2 problems, for two objectives on the ZDT4-V1, ZDT4-V2, UF1, UF2, UF7, and UF9 problems, and for three objectives on the UF8 problem. A dimension is said to be simple if the Pareto-optimal decision vectors are indifferent on that dimension, and is complex if the vectors differ considerably. The particles’ personal best positions obtained by AMCLPSO related to at least one objective are close to the Pareto-optimal decision vectors on simple dimensions, while the personal best positions regarding all the objectives are located in rather different regions of the search space on complex dimensions. All the observations verify that: (1) the personal best positions carry useful information about the Pareto set, and the mutation strategy that learns from the personal best positions benefits discovering the true Pareto set; (2) there are many local Pareto fronts encountered and the elitists differ considerably on many dimensions during the initial search process for the ZDT4-V1 and ZDT4-V2 problems that feature many simple dimensions and difficult extremity search, the adaptive particle velocity update strategy accelerates the extremity search through incorporating perturbation; (3) the perturbation mechanism in the adaptive particle velocity update strategy enables to explore the Pareto set on complex dimensions; and (4) the adaptive particle velocity update strategy thus helps AMCLPSO to converge towards the true Pareto front more quickly and to obtain better distributed nondominated solutions over the entire Pareto front than MSCLPSO.
The strategy parameters: As we can observe from the statistical IGD results given in Table 5, the performance of the adaptive particle velocity update strategy is quite sensitive to the values selected for the parameters. The appropriate values of the strategy parameters are determined based on trials on all the problems. AMCLPSO is likely to get stuck in a terrible local Pareto front in the worst run on the ZDT4-V2 problem with the relative ratio Δrel = 0.1, on the WFG1 problem with the acceleration coefficient c1 = 0, and on the UF9 problem with c1 = 1. The distribution of the nondominated solutions obtained by AMCLPSO with the acceleration coefficient c2 = 0.3 is much worse than that with c2 = 3. The observations accordingly indicate that: (1) when the interval of the elitists is sufficiently small on dimension d, the elitists can be considered as indifferent on that dimension; and (2) the particle velocity update process needs to take a tradeoff between the extremity search and the perturbation, and it is more much important to conduct the perturbation than the extremity search when the elitists differ considerably on a dimension.
Comparison of AMCLPSO with other state-of-the-art multiobjective metaheuristics: In [1], we compared MSCLPSO with CMPSO, MOEA/D, and NSGA-II on the ZDT2, ZDT4, ZDT4-V1, ZDT4-V2, WFG1, UF1, UF2, UF7, UF8, and UF9 problems. The FEs used in [1] are significantly more than those used in this paper on all the problems. It was demonstrated in [1] that CMPSO, MOEA/D, and NSGA-II cannot approximate the true Pareto front on ZDT4-V1, ZDT4-V2, WFG1, UF1, UF2, UF7, UF8, and UF9 in some or all of the runs, while MSCLPSO is able to find nondominated solutions well distributed over the true Pareto front on all the problems in all the runs. MSCLPSO significantly beats CMPSO, MOEA/D, and NSGA-II on 9 out of the 10 problems in terms of the statistical IGD results [1]. As AMCLPSO outperforms MSCLPSO, AMCLPSO also performs better than the state-of-the-art metaheuristics such as CMPSO, MOEA/D, and NSGA-II.
5. Conclusions
In this paper, we have proposed AMCLPSO with an adaptive particle velocity update strategy to improve the search efficiency of MSCLPSO. When the elitists are indifferent on a dimension, each particle only learns from some particle in the same swarm on that dimension for flight trajectory update; otherwise, when the elitists are complex on a dimension, each particle additionally learns from the difference of some pair of elitists on that dimension. The adaptive particle velocity update strategy achieves a tradeoff between optimizing each single objective and exploring the Pareto set. Experimental results on various multiobjective benchmark optimization problems have demonstrated that the adaptive particle velocity update strategy is able to help AMCLPSO converge more quickly towards the true Pareto front and derive better distributed nondominated solutions over the entire Pareto front than MSCLPSO. In the future, we will further enhance the performance of AMCLPSO. A possible direction is to investigate an adaptive different evolution strategy of the elitists as differential evolution is not equally useful for the simple and complex dimensions.
Author Contributions
Conceptualization, X.Y.; Methodology, X.Y.; Validation, X.Y.; Writing—Original Draft Preparation, X.Y.; Visualization, X.Y. and C.E.; Writing—Review & Editing, C.E.
Funding
This research was funded by the Jiangxi Province Key Laboratory for Water Information Cooperative Sensing and Intelligent Processing Open Foundation Project (2016WICSIP011), the National Natural Science Foundation of China Project (61703199), and the Network of the European Union, Latin America and the Caribbean Countries on Joint Innovation and Research Activities Project (ELAC2015/T10-076).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Yu, X.; Zhang, X.-Q. Multiswarm comprehensive learning particle swarm optimization for solving multiobjective optimization problems. PLoS ONE 2017, 12, e0172033. [Google Scholar] [CrossRef] [PubMed]
- Jones, D.F.; Mirrazavi, S.K.; Tamiz, M. Multi-objective meta-heuristics: An overview of the current state-of-the-art. Eur. J. Oper. Res. 2002, 137, 1–9. [Google Scholar] [CrossRef]
- Zavala, G.R.; Nebro, A.J.; Luna, F.; Coello, C.A.C. A survey of multi-objective metaheuristics applied to structural optimization. Struct. Multidiscip. Optim. 2014, 49, 537–558. [Google Scholar] [CrossRef]
- Fister, I., Jr.; Yang, X.-S.; Fister, I.; Brest, J.; Fister, D. A brief review of nature-inspired algorithms for optimization. Elektrotehniski Vestnik 2013, 80, 116–122. [Google Scholar]
- Boussaïd, I.; Lepagnot, J.; Siarry, P. A survey on optimization metaheuristics. Inf. Sci. 2013, 237, 82–117. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Huang, V.L.; Suganthan, P.N.; Liang, J.J. Comprehensive learning particle swarm optimizer for solving multiobjective optimization problems. Int. J. Intell. Syst. 2006, 21, 209–226. [Google Scholar] [CrossRef]
- Horn, J.; Nafpliotis, N.; Goldberg, D.E. A niched Pareto genetic algorithm for multiobjective optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Orlando, FL, USA, 27–29 June 1994; pp. 82–87. [Google Scholar]
- Yang, D.-D.; Jiao, L.-C.; Gong, M.-G.; Feng, J. Adaptive ranks clone and k-nearest neighbor list-based immune multi-objective optimization. Comput. Intell. 2010, 26, 359–385. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm; ETH: Zurich, Switzerland, 2001; pp. 1–21. [Google Scholar]
- Montalvo, I.; Izquierdo, J.; Pérez-García, R.; Herrera, M. Water distribution system computer-aided design by agent swarm optimization. Comput.-Aided Civ. Infrastruct. Eng. 2014, 29, 433–448. [Google Scholar] [CrossRef]
- Knowles, J.D.; Corne, D.W. The Pareto archived evolution strategy: A new baseline algorithm for Pareto multiobjective optimisation. In Proceedings of the IEEE Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999; pp. 98–105. [Google Scholar]
- Knowles, J.D.; Corne, D.W. Approximating the nondominated front using the Pareto archived evolution strategy. Evol. Comput. 2000, 8, 149–172. [Google Scholar] [CrossRef] [PubMed]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Pires, E.J.S.; de Moura Oliveira, P.B.; Machado, J.A.T. Multi-objective maximin sorting scheme. In Proceedings of the International Conference on Evolutionary Multi-Criterion Optimization, Guanajuato, Mexico, 9–11 March 2005; pp. 165–175. [Google Scholar]
- Kukkonen, S.; Deb, K. A fast and effective method for pruning of non-dominated solutions in many-objective problems. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Reykjavik, Iceland, 9–13 September 2006; pp. 553–562. [Google Scholar]
- Hu, W.; Yen, G.G. Adaptive multiobjective particle swarm optimization based on parallel cell coordinate system. IEEE Trans. Evol. Comput. 2015, 19, 1–18. [Google Scholar]
- Qiu, X.; Xu, J.-X.; Tan, K.C.; Abbass, H.A. Adaptive cross-generation differential evolution operators for multiobjective optimization. IEEE Trans. Evol. Comput. 2016, 20, 232–244. [Google Scholar] [CrossRef]
- Schaffer, J.D. Multiple objective optimization with vector evaluated genetic algorithms. In Proceedings of the International Conference on Genetic Algorithms, Pittsburgh, PA, USA, 24–26 July 1985; pp. 93–100. [Google Scholar]
- Parsopoulos, K.E.; Tasoulis, D.K.; Vrahatis, M.N. Multiobjective optimization using parallel vector evaluated particle swarm optimization. In Proceedings of the IASTED International Conference on Artificial Intelligence & Applications, Innsbruck, Austria, 16–18 February 2004; pp. 823–828. [Google Scholar]
- Zhan, Z.-H.; Li, J.-J.; Cao, J.-N.; Zhang, J.; Chung, H.S.-H.; Shi, Y.-H. Multiple populations for multiple objectives: A coevolutionary technique for solving multiobjective optimization problems. IEEE Trans. Cybern. 2013, 43, 445–463. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.-F.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q.-F. Multiobjective optimization problems with complicated Pareto sets, MOEA/D and NSGA-II. IEEE Trans. Evol. Comput. 2009, 13, 284–302. [Google Scholar] [CrossRef]
- Zhang, Q.-F.; Liu, W.-D.; Li, H. The performance of a new version of MOEA/D on CEC09 unconstrained MOP test instances. In Proceedings of the IEEE Congress on Evolutionary Computation, Tronhdeim, Norway, 18–21 May 2009; pp. 203–208. [Google Scholar]
- Tan, Y.-Y.; Jiao, Y.-C.; Li, H.; Wang, X.-K. A modification to MOEA/D-DE for multiobjective optimization problems with complicated Pareto sets. Inf. Sci. 2012, 213, 14–38. [Google Scholar] [CrossRef]
- Qi, Y.-T.; Ma, X.-L.; Liu, F.; Jiao, L.-C.; Sun, J.-Y.; Wu, J.-S. MOEA/D with adaptive weight adjustment. Evol. Comput. 2014, 22, 231–264. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Fialho, A.; Kwong, S.; Zhang, Q.-F. Adaptive operator selection with bandits for a multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2014, 18, 114–130. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 Novmber–1 December 1995; pp. 1942–1948. [Google Scholar]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Zhan, Z.-H.; Zhang, J.; Li, Y.; Shi, Y.-H. Orthogonal learning particle swarm optimization. IEEE Trans. Evol. Comput. 2011, 15, 832–847. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, X.-Q. Enhanced comprehensive learning particle swarm optimization. Appl. Math. Comput. 2014, 242, 265–276. [Google Scholar] [CrossRef]
- Montalvo, I.; Izquierdo, J.; Pérez-García, R.; Herrera, M. Improved performance of PSO with self-adaptive parameters for computing the optimal design of water supply systems. Eng. Appl. Artif. Intell. 2010, 23, 727–735. [Google Scholar] [CrossRef]
- Zitzler, E.; Deb, K.; Thiele, L. Comparison of multiobjective evolutionary algorithms: Empirical results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef] [PubMed]
- Huband, S.; Hingston, P.; Barone, L.; While, L. A review of multiobjective test problems and a scalable test problem toolkit. IEEE Trans. Evol. Comput. 2006, 10, 477–506. [Google Scholar] [CrossRef]
- Zhang, Q.-F.; Zhou, A.-M.; Zhao, S.-Z.; Suganthan, P.N.; Liu, W.-D.; Tiwari, S. Multiobjective Optimization Test Instances for the CEC 2009 Special Session and Competition; University of Essex: Colchester, UK, 2009; pp. 1–30. [Google Scholar]
- Laumanns, M.; Thiele, L.; Deb, K.; Zitzler, E. Combining convergence and diversity in evolutionary multiobjective optimization. Evol. Comput. 2002, 10, 263–282. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).