1. Introduction
With the development of the Internet and network technologies, the digital divide between businesses is being addressed. In this situation, companies are using strategies to enhance outsourcing to focus on core competences along with information. In particular, such rapid developments in information technology are pushing many companies into a race that transcends time and space. Furthermore, the global business environment surrounding corporations is changing from competition between individual companies to competition between supply chains. In order to ensure the competitive edge of the supply chain, companies have tried to find the right suppliers offering higher quality, reduced costs, and shorter lead times. Therefore, in supply chain management, selecting the right suppliers is one of the most important decision-making processes for improving corporate competitiveness [
1,
2,
3].
In many cases, a single supplier may not be able to meet the buyer’s requirements. In such cases, selecting multiple suppliers—multiple sourcing—would be a reasonable alternative [
4]. Whereas single sourcing significantly increases the disruption risk in the supply chain, multiple sourcing increases the fixed cost in terms of administrative and negotiating costs [
5]. However, multiple sourcing is preferred over a single sourcing, ensuring order flexibility [
6]. Therefore, multiple sourcing inevitably includes the problem of order allocation. Furthermore, the relationship between the buyer and supplier is influenced by order allocation decisions based on strategic purchase decisions [
7]. Therefore, the overall supplier selection problem should not only cover the selection of the right supplier but also the determination of the orders assigned to the selected supplier based on the given objectives and constraints [
8]. To date, however, only a few mathematical programming models to analyze such decisions have been published [
9,
10,
11,
12]. In the field of supply chain management, it is necessary to develop a precise decision support model which simultaneously considers supplier selection and order allocation. In particular, researchers need to advance research in this direction to guide the decision-maker (DM)’s rational choice.
Supplier selection is inherently a multi-criteria decision-making (MCDM) problem since some conflicting performance criteria have an influence on the selection of suppliers [
13,
14]. It is also considered one of the most familiar problems in MCDM [
15]. This problem has been studied from a variety of perspectives, such as green supplier selection [
6,
16] and global supplier selection [
17]. Generally, the performance criteria involves the factors such as cost, quality, and lead time. Each supplier has its own strengths and weaknesses, so it is very difficult to select a superior supplier at all dimensions of criteria. Thus, supplier selection problem has made MCDM a very challenging task. Ho et al. [
18] provided comprehensive reviews for MCDM approaches to vendor selection problems between 2000 and 2008. In addition, a more recent review from Chai et al. [
19] provides guidelines for a MCDM-based supplier selection model.
For solving a multiobjective optimization (MOO) problem in MCDM, the DM seeks a compromise solution which provides the greatest satisfaction in the presence of conflicting objectives. Thus, the DM’s preference information plays a critical role in finding the solution. In the literature, the DM’s preference information can enter the solving process of MOO problems in three different ways: (1) a priori; (2) a posteriori; and (3) progressive (interactive) articulation [
20,
21]. For an a priori setting, multiple objective functions combined with preference convert into one single objective. For an a posteriori setting, the DM’s preference information is articulated after optimization process by selecting the most preferred one from a set of non-dominated solutions, usually called a Pareto optimal set. For progressive optimization, the preference of the DM is incorporated into the solution search process. Iterative dialogues between the DM and optimization model contribute to find the most satisfactory solution in this optimization approach. For this reason, the progressive articulation approach is also referred to as the interactive approach.
Most studies in supplier selection and order allocation are categorized into the prior approach by the MOO categorization scheme. However, the prior approach may decrease the reliability of solutions because of the unrealistic assumption that the DM can specify the preference information in advance. Although the interactive approach has been broadly applied to various fields as an alternative to overcome this limitation on the DM’s preference, it is rarely used to solve supplier selection and order allocation problems. To the best of the author’s knowledge, Demirtas and Üstün [
4]’s research is the only material related to using the interactive MOO method to solve supplier selection and order allocation problem. Demirtas and Üstün [
4] proposed an interactive MOO method, and a reservation level driven Tchebycheff procedure. In this model, the solution process makes the DM express adjusting some or all of reservation values of objective functions, by generating candidate solutions with sampling weights. The interactive method that we propose in this paper has something in common with Demirtas and Üstün [
4]’s research in terms of a kind of objective space reduction. Also, two methods share the Tchebycheff framework to find a solution by utilizing the concept of distance to the ideal vector. However, the proposed approach provides an integrated use of the desirability function approach in response to surface methodology and the step method (STEM). Our model has advantages in that it reflects the satisfaction of the DM more realistically by using the concept of desirability function, and it reduces the burden on the DM to express preference information.
Based on the above-mentioned background, the purpose of the research is summarized as follows. We aim to solve the multiple sourcing problem which deals with order allocation at the same time as supplier selection by using an interactive MOO method. The devised method, which progressively articulates the DM’s preference information, is applied to a problem with three important criteria: cost, quality, and delivery. Also, to intuitively utilize the level of satisfaction, we borrow the concept of desirability from the research field of product and process design. We show that our method can be utilized effectively in the supplier selection and order allocation problem.
The organization of this paper is as follows.
Section 2 presents previous works to be addressed in this study. The proposed interactive desirability function approach to supplier selection is presented in
Section 3.
Section 4 analyzes results and provides discussions. Conclusions are provided in
Section 5.
3. Proposed Model
Across fifty years of evaluating suppliers, many researchers have proposed different sets of criteria.
The first set of criteria was proposed by Dickson [
14], who identified 23 different criteria evaluated in supplier selection. Evans [
34] and Shipley [
35] agreed that price, quality and delivery are the most important criteria for evaluating suppliers. Ellram [
36] proposed that the quality dimension should be divided into product quality and service quality, and it is suggested to use them with price and delivery time to select suppliers. Weber et al. [
37] surveyed based on Dickson’s 23 criteria and concluded that price, delivery, quality, production capacity, and localization are the most important criteria. Pi and Low [
38] proposed quality, delivery, price and service for supplier evaluation. Amid et al. [
39] uses price, quality, and service, and Jadidi et al. [
11] utilized price, quality, and lead time to the supplier selection and order allocation model. As shown by the literature, the most important criteria for supplier selection problems are cost, quality, and delivery. We also use those criteria by using the measures: total purchasing costs, the number of rejects, and the number of late delivery for cost, quality, and delivery, respectively. We assume the buyer considers a single item that should be purchased under known total demand. Also, information about criteria and production capacity is already known for a set of potential suppliers. The notations of the proposed model are presented in
Table 1.
There are three original objective functions:
f1 (minimizing total purchasing cost),
f2 (minimizing total number of defects),
f3 (minimizing the number of late delivery). Each objective function can be shown as follows:
Using the functions defined above, MOO problem considering the supplier selection with order allocation can be formulated as follows [
12]:
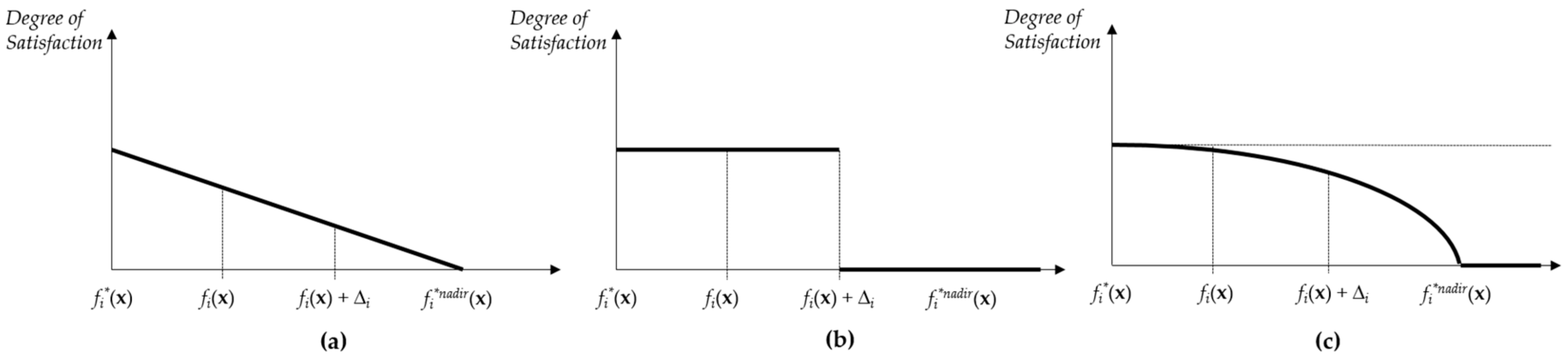
The first and second constraint present demand satisfaction and capacity restriction, respectively, and the last constraint ensures non-negativity of the decision variables. Now we transform the original objective functions into the desirability functions. Because all original objective functions are to be minimized (STB type), the individual desirability is defined as
where
fimax are the maximum values of the objective functions as obtained from the payoff table and
fi*(
x) are the ideal points from maximizing the objective functions individually.
Table 2 presents the payoff table that includes
fimax and
fi*(
x). For a STB type function,
fimax are recognized as the
nadir points which are maximum values from each column in the payoff table, and the ideal values are on the diagonal of the table.
We represent the desirability-based supplier selection problem in the form of a MOO problem:
The individual desirability functions di (i = 1, …, k) are objective functions to be maximized simultaneously.
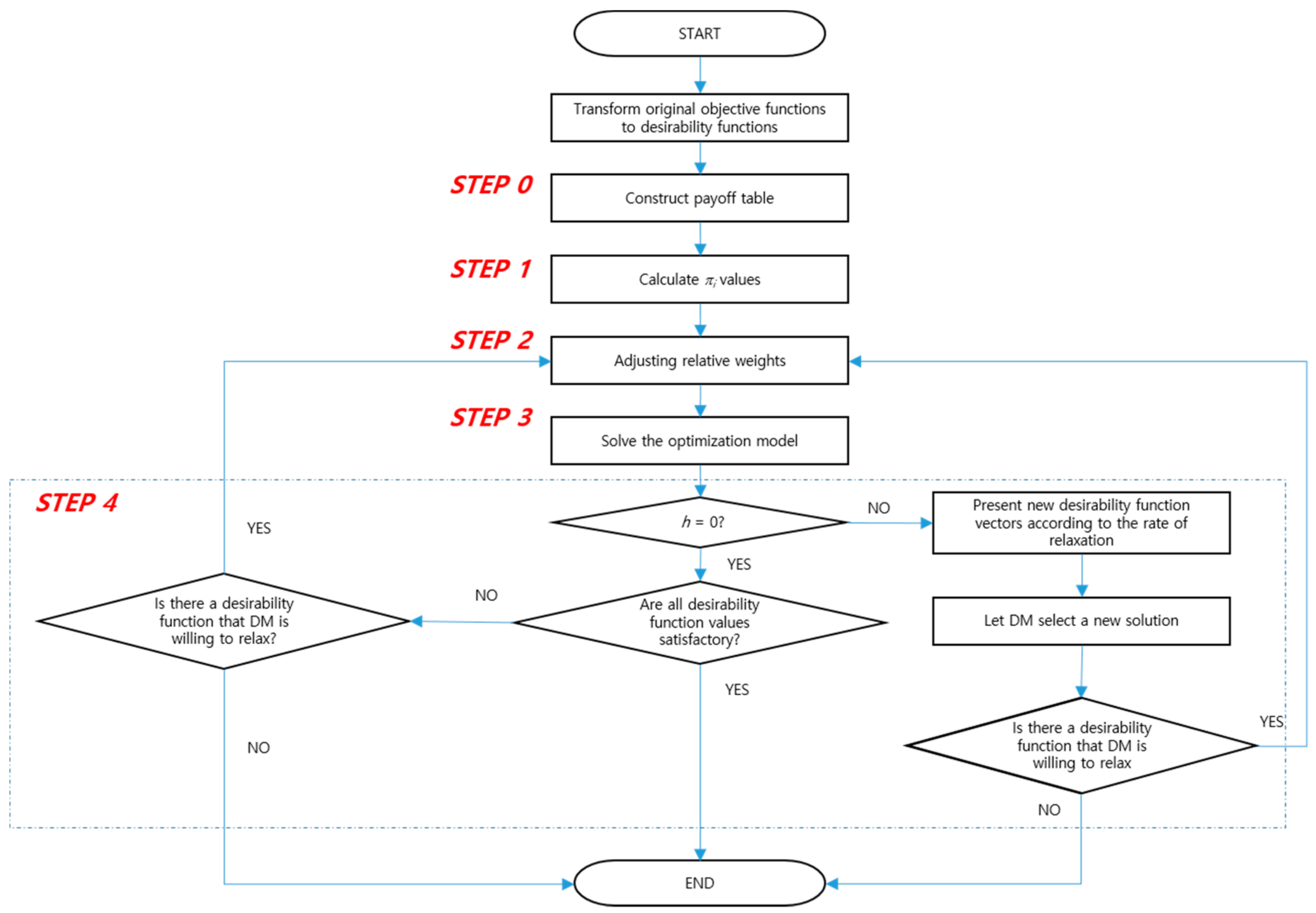
The optimization process consists of five major steps. The overall procedure is presented in
Figure 1. In addition, a pseudo code is described in Algorithm 1 to aid readers understanding.
| Algorithm 1. Pseudo code of the proposed method. |
| begin | |
| | initialize: h ← 0 |
| | initialize: J = ∅ |
| | calculate d* and n* |
| | calculate πi values |
| | compute relative weights |
| | compute an initial solution dh |
| | ask if there is a desirability function value want to relax (j) |
| | while the preferred solution has not been found do |
| | | J = {j} |
| | | compute relative weights |
| | | compute potential solutions based on the preferences of the DM |
| | | present the solutions to the DM |
| | | ask the most preferred solution dh* from potential solutions |
| | | ask if there is a desirability function value want to relax (j) |
| | | h ← h + 1 |
| | endwhile |
| end | |
4. Summary of Results and Discussion
This study successfully applied the concept of desirability function in response surface methodology, which is used in product and process design, to supplier selection problems. The desirability function diverts the DM’s recognition system for each objective function from linear coupling and realistically reflects the degree of satisfaction for each objective function. Since the proposed method assumes that the DM’s preference information is not completely known, it is difficult to discuss the superiority of solutions by directly comparing the results with other methods. However, we explain the advantages of the proposed method by comparing them with the solutions from two weighting methods: the weighted sum method and weighted geometric method. Several weighting vectors are assumed for the purpose of comparing solutions. We adopted three sets of weighting parameter
w, proposed be Jadidi et al. [
11] for the same supplier selection problem. The results are shown in
Table 8.
The results of the weighted sum method show that the more weights are assigned to the first objective function (minimizing total purchasing costs), the larger the contribution is made to the value of the first desirability function. However, when w1 is larger than 0.6, the individual desirability value for f2 equals to 0. Namely, the second objective function, the number of late delivery, has the worst value. Furthermore, there is no differences between w = (0.6, 0.2, 0.2) and w = (0.8, 0.1, 0.1), although the overall objective function values ∑widi differ. These extreme results show that the DM may not satisfied with the results.
Next, we also tested the weighted geometric model using the same set of
w. In fact, the weighted geometric mean is a popular method for unifying individual desirability functions to a single function in desirability function approach. The weighted geometric method results in a somewhat balanced solution avoiding extreme values in one objective function, even if the weight is to one side. This method, however, also may result in a controversial solution. In
Table 8, we found the third desirability value for late delivery increases as
w3 decreases. Thus, the results do not necessarily guarantee that the DM can find the most satisfactory solution even if he/she can decide preference information in advance at one time. The proposed method can complement the shortcomings of these methods because the DM directly checks the degree of desirability and learns a preference structure through improved solutions. In other words, the advantage of the proposed method is that the solution changes in the object function space can be detected through the DM’s preference information.
The last row section in
Table 8 summarizes the solutions from the proposed method. The results show that the proposed method prevents the emergence of extreme values in two ways. First, the initial solution
d0 describes this characteristic. In each case, for
r, the initial solution is a neutral compromise solution because it is calculated by using the Tchebycheff metric without preference information. This setting eliminates the unnecessary iteration that causes a desirability function value to deviate from an extreme value. The results in the 12th and 15th row show reasonable levels of desirability functions, for both cases,
r = 1 and
r = 2. Second, the proposed method also prevents the extreme value in the problem-solving process. The original STEM allows the DM to relax one objective function, which may lead to significantly improved values than expected. In such a case, the DM might want to relax an excessively improved value for the purpose of adjustment. However, the proposed method does not ask the DM directly for the amount of relaxation, so it induces the satisfactory solution to find the change of desirability functions according to the rate of relaxation. Accordingly, the DM can choose the most satisfactory solution among the various possible solutions. Therefore, it helps to avoid occurrence of an extreme value by showing the alternatives that the DM can choose.
The proposed method presents the changes of the desirability function values to the DM according to the rate of relaxation of a particular desirability function in the form of a table. If a MOO method requires preference information that is difficult for the DM to express—for example, specific numerical information—it may be difficult to find the satisfactory solution. In this regard, the information presentation of the proposed method provides an additional advantage in that it can ease the burden of the DM by showing a set of expected candidate solutions and selecting the most satisfactory solution rather than requiring specific values. If the number of desirability functions increases, it is recommended to use the graph form. The graph form may also be more useful because the scales of the desirability are all the same. An alternative interactive MOO approach to supplier selection and order allocation is Demirtas and Üstün [
4]. In this interactive method, the DM can control objective values directly in a similar way to our research. The authors uses the reservation level that represents an objective function value which must be equaled or exceeded to be considered acceptable, in the maximization context. The method repeatedly reduces the objective space by adjusting reservations level from the DM’s preference information. Although there are differences in, for example, how local weights are used and how the DM expresses preference information, both studies show that interactive MOO approaches can help supplier selection and order allocation problems. We expect that a variety of interactive MOO methods can be used for supplier selection and order allocation problems.