A Novel Rough WASPAS Approach for Supplier Selection in a Company Manufacturing PVC Carpentry Products
Abstract
:1. Introduction
2. Literature Review
2.1. Applications of Weighted Aggregated Sum Product Assessment (WASPAS) Method
2.2. Applications of Rough Sets in Multiple Criteria Decision Making (MCDM)
3. Methods
3.1. Rough Set Theory
3.2. A Novel Rough WASPAS Approach
4. Supplier Selection in a Company Manufacturing Polyvinyl Chloride (PVC) Carpentry
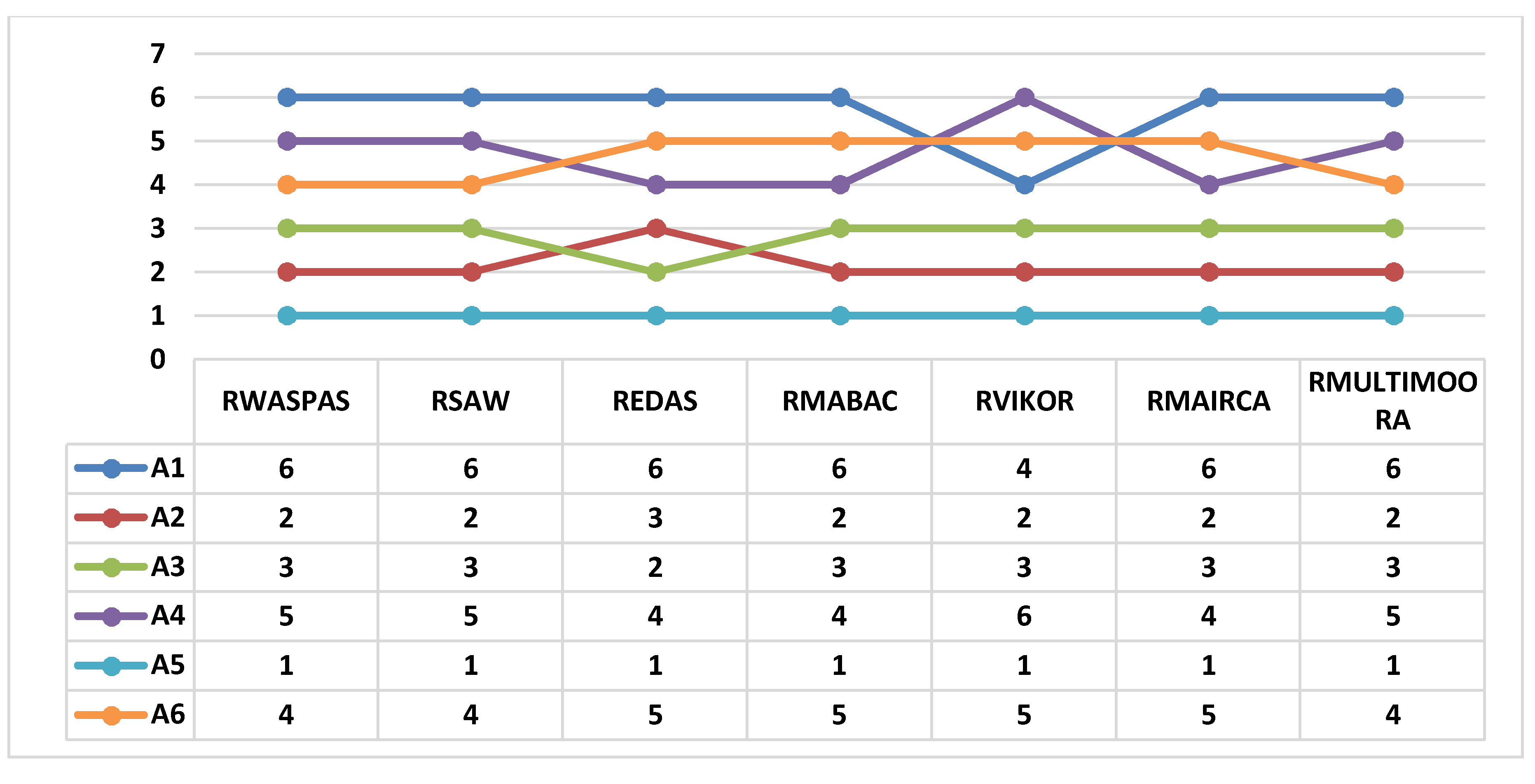
5. Sensitivity Analysis
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Petrovic, D.; Xie, Y.; Burnham, K.; Petrovic, R. Coordinated control of distribution supply chains in the presence of fuzzy customer demand. Eur. J. Oper. Res. 2008, 185, 146–158. [Google Scholar] [CrossRef]
- Monczka, R.M.; Handfield, R.B.; Giunipero, L.C.; Patterson, J.L. Purchasing and and Supply Chain Management; Cengage Learning: Boston, MA, USA, 2015; ISBN 978-1-285-86968-1. [Google Scholar]
- Zhong, L.; Yao, L. An ELECTRE I-based multi-criteria group decision making method with interval type-2 fuzzy numbers and its application to supplier selection. Appl. Soft Comput. 2017, 57, 556–576. [Google Scholar] [CrossRef]
- Bai, C.; Sarkis, J. Evaluating supplier development programs with a grey based rough set methodology. Expert Syst. Appl. 2011, 38, 13505–13517. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J.; Zakarevicius, A. Optimization of weighted aggregated sum product assessment. Elektron. Elektrotech. 2012, 122, 3–6. [Google Scholar] [CrossRef]
- Ighravwe, D.E.; Oke, S.A. A fuzzy-grey-weighted aggregate sum product assessment methodical approach for multi-criteria analysis of maintenance performance systems. Int. J. Syst. Assur. Eng. Manag. 2017, 8, 961–973. [Google Scholar] [CrossRef]
- Mathew, M.; Sahu, S.; Upadhyay, A.K. Effect of normalization techniques in robot selection using weighted aggregated sum product assessment. Int. J. Innov. Res. Adv. Stud. 2017, 4, 59–63. [Google Scholar]
- Bagočius, V.; Zavadskas, E.K.; Turskis, Z. Multi-person selection of the best wind turbine based on the multi-criteria integrated additive-multiplicative utility function. J. Civ. Eng. Manag. 2014, 20, 590–599. [Google Scholar] [CrossRef]
- Yazdani, M. New approach to select materials using MADM tools. Int. J. Bus. Syst. Res. 2018, 12, 25–42. [Google Scholar] [CrossRef]
- Hashemkhani Zolfani, S.; Aghdaie, M.H.; Derakhti, A.; Zavadskas, E.K.; Varzandeh, M.H.M. Decision making on business issues with foresight perspective; an application of new hybrid MCDM model in shopping mall locating. Expert Syst. Appl. 2013, 40, 7111–7121. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Kalibatas, D.; Kalibatiene, D. A multi-attribute assessment using WASPAS for choosing an optimal indoor environment. Arch. Civ. Mech. Eng. 2016, 16, 76–85. [Google Scholar] [CrossRef]
- Suresh, R.K.; Krishnaiah, G.; Venkataramaiah, P. An experimental investigation towards multi objective optimization during hard turning of tool steel using a novel MCDM technique. Int. J. Appl. Eng. Res. 2017, 12, 1899–1907. [Google Scholar]
- Džiugaitė-Tumėnienė, R.; Lapinskienė, V. The multicriteria assessment model for an energy supply system of a low energy house. Eng. Struct. Technol. 2014, 6, 33–41. [Google Scholar] [CrossRef]
- Turskis, Z.; Daniūnas, A.; Zavadskas, E.K.; Medzvieckas, J. Multicriteria evaluation of building foundation alternatives. Comput. Aided Civ. Infrastruct. Eng. 2016, 31, 717–729. [Google Scholar] [CrossRef]
- Emovon, I. A Model for determining appropriate speed breaker mechanism for power generation. J. Appl. Sci. Process Eng. 2018, 5, 256–265. [Google Scholar]
- Madić, M.; Gecevska, V.; Radovanović, M.; Petković, D. Multicriteria economic analysis of machining processes using the WASPAS method. J. Prod. Eng. 2014, 17, 1–6. [Google Scholar]
- Turskis, Z.; Zavadskas, E.K.; Antucheviciene, J.; Kosareva, N. A hybrid model based on fuzzy AHP and fuzzy WASPAS for construction site selection. Int. J. Comput. Commun. Control 2015, 10, 113–128. [Google Scholar] [CrossRef]
- Madic, M.; Antucheviciene, J.; Radovanovic, M.; Petkovic, D. Determination of manufacturing process conditions by using MCDM methods: Application in laser cutting. Eng. Econ. 2016, 27, 144–150. [Google Scholar] [CrossRef]
- Vafaeipour, M.; Zolfani, S.H.; Varzandeh, M.H.M.; Derakhti, A.; Eshkalag, M.K. Assessment of regions priority for implementation of solar projects in Iran: New application of a hybrid multi-criteria decision making approach. Energy Convers. Manag. 2014, 86, 653–663. [Google Scholar] [CrossRef]
- Ghorshi Nezhad, M.R.; Zolfani, S.H.; Moztarzadeh, F.; Zavadskas, E.K.; Bahrami, M. Planning the priority of high tech industries based on SWARA-WASPAS methodology: The case of the nanotechnology industry in Iran. Econ. Res.-Ekon. Istraz. 2015, 28, 1111–1137. [Google Scholar] [CrossRef]
- Yazdani, M.; Hashemkhani Zolfani, S.; Zavadskas, E.K. New integration of MCDM methods and QFD in the selection of green suppliers. J. Bus. Econ. Manag. 2016, 17, 1097–1113. [Google Scholar] [CrossRef]
- Urosevic, S.; Karabasevic, D.; Stanujkic, D.; Maksimovic, M. An approach to personnel selection in the tourism industry based on the SWARA and the WASPAS methods. Econ. Comput. Econ. Cybern. Stud. Res. 2017, 51, 75–88. [Google Scholar]
- Mardani, A.; Nilashi, M.; Zakuan, N.; Loganathan, N.; Soheilirad, S.; Saman, M.Z.M.; Ibrahim, O. A systematic review and meta-Analysis of SWARA and WASPAS methods: Theory and applications with recent fuzzy developments. Appl. Soft Comput. 2017, 57, 265–292. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. Selecting a contractor by using a novel method for multiple attribute analysis: Weighted Aggregated Sum Product Assessment with grey values (WASPAS-G). Stud. Inform. Control 2015, 24, 141–150. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Amiri, M.; Esmaeili, A. Multi-criteria evaluation of green suppliers using an extended WASPAS method with interval type-2 fuzzy sets. J. Clean. Prod. 2016, 137, 213–229. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Antuchevičienė, J. Assessment of third-party logistics providers using a CRITIC–WASPAS approach with interval type-2 fuzzy sets. Transport 2017, 32, 66–78. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Baušys, R.; Stanujkic, D.; Magdalinovic-Kalinovic, M. Selection of lead-zinc flotation circuit design by applying WASPAS method with single-valued neutrosophic set. Acta Montan. Slov. 2016, 21, 85–92. [Google Scholar]
- Baušys, R.; Juodagalvienė, B. Garage location selection for residential house by WASPAS-SVNS method. J. Civ. Eng. Manag. 2017, 23, 421–429. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Antucheviciene, J.; Hajiagha, S.H.R.; Hashemi, S.S. Extension of weighted aggregated sum product assessment with interval-valued intuitionistic fuzzy numbers (WASPAS-IVIF). Appl. Soft Comput. 2014, 24, 1013–1021. [Google Scholar] [CrossRef]
- Nie, R.X.; Wang, J.Q.; Zhang, H.Y. Solving solar-wind power station location problem using an extended weighted aggregated sum product assessment (WASPAS) technique with interval neutrosophic sets. Symmetry 2017, 9, 106. [Google Scholar] [CrossRef]
- Song, W.; Ming, X.; Wu, Z.; Zhu, B. A rough TOPSIS approach for failure mode and effects analysis in uncertain environments. Qual. Reliab. Eng. Int. 2014, 30, 473–486. [Google Scholar] [CrossRef]
- Roy, J.; Chatterjee, K.; Bandhopadhyay, A.; Kar, S. Evaluation and selection of Medical Tourism sites: A rough AHP based MABAC approach. arXiv, 2016; arXiv:1606.08962. [Google Scholar]
- Pamučar, D.; Stević, Ž.; Zavadskas, E.K. Integration of interval rough AHP and interval rough MABAC methods for evaluating university web pages. Appl. Soft Comput. 2018, 67, 141–163. [Google Scholar] [CrossRef]
- Song, W.; Ming, X.; Wu, Z. An integrated rough number-based approach to design concept evaluation under subjective environments. J. Eng. Des. 2013, 24, 320–341. [Google Scholar] [CrossRef]
- Stević, Ž.; Pamučar, D.; Vasiljević, M.; Stojić, G.; Korica, S. Novel integrated multi-criteria model for supplier selection: Case study construction company. Symmetry 2017, 9, 279. [Google Scholar] [CrossRef]
- Cao, J.; Song, W. Risk assessment of co-creating value with customers: A rough group analytic network process approach. Expert Syst. Appl. 2016, 55, 145–156. [Google Scholar] [CrossRef]
- Vasiljevic, M.; Fazlollahtabar, H.; Stevic, Z.; Veskovic, S. A rough multicriteria approach for evaluation of the supplier criteria in automotive industry. Decis. Mak. Appl. Manag. Eng. 2018, 1, 82–96. [Google Scholar] [CrossRef]
- Karavidic, Z.; Projovic, D. A multi-criteria decision-making (MCDM) model in the security forces operations based on rough sets. Decis. Mak. Appl. Manag. Eng. 2018, 1, 97–120. [Google Scholar] [CrossRef]
- Stević, Ž.; Pamučar, D.; Zavadskas, E.K.; Ćirović, G.; Prentkovskis, O. The selection of wagons for the internal transport of a logistics company: A novel approach based on Rough BWM and Rough SAW Methods. Symmetry 2017, 9, 264. [Google Scholar] [CrossRef]
- Chai, J.; Liu, J.N. A novel believable rough set approach for supplier selection. Expert Syst. Appl. 2014, 41, 92–104. [Google Scholar] [CrossRef]
- Zhai, L.Y.; Khoo, L.P.; Zhong, Z.W. Design concept evaluation in product development using rough sets and grey relation analysis. Expert Syst. Appl. 2009, 36, 7072–7079. [Google Scholar] [CrossRef]
- Khoo, L.P.; Tor, S.B.; Zhai, L.Y. A rough-set based approach for classification and rule induction. Int. J. Adv. Manuf. Technol. 1999, 15, 438–444. [Google Scholar] [CrossRef]
- Pamučar, D.; Mihajlović, M.; Obradović, R.; Atanasković, P. Novel approach to group multi-criteria decision making based on interval rough numbers: Hybrid DEMATEL-ANP-MAIRCA model. Expert Syst. Appl. 2017, 88, 58–80. [Google Scholar] [CrossRef]
- Duntsch, I.; Gediga, G. The rough set engine GROBIAN. In Proceedings of the 15th IMACS World Congress; Sydow, A., Ed.; Berlin Wissenschaft und Technik Verlag: Berlin, Germany, 1997; Volume 4, pp. 613–618. [Google Scholar]
- Khoo, L.-P.; Zhai, L.-Y. A prototype genetic algorithm enhanced rough set-based rule induction system. Comput. Ind. 2001, 46, 95–106. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Zhu, G.N.; Hu, J.; Qi, J.; Gu, C.C.; Peng, J.H. An integrated AHP and VIKOR for design concept evaluation based on rough number. Adv. Eng. Inform. 2015, 29, 408–418. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough Sets: Theoretical Aspects of Reasoning about Data; Springer: Berlin, Germany, 1991. [Google Scholar]
- Pawlak, Z. Anatomy of conflicts. Bull. Eur. Assoc. Theor. Comput. Sci. 1993, 50, 234–247. [Google Scholar]
- Stević, Ž. Integrisani Model Vrednovanja Dobavljača u Lancima Snabdevanja. Ph.D. Thesis, Univerzitet u Novom Sadu, Fakultet Tehničkih Nauka, Novi Sad, Serbia, 2018. (In Bosnian). [Google Scholar]
- Zhai, L.Y.; Khoo, L.P.; Zhong, Z.W. A rough set based QFD approach to the management of imprecise design information in product development. Adv. Eng. Inform. 2009, 23, 222–228. [Google Scholar] [CrossRef]

| Linguistic Scale | For Criteria of Type Max (Benefit Criteria) | For Criteria of Type Min (Cost Criteria) |
|---|---|---|
| Very Poor—VP | 1 | 9 |
| Poor—P | 3 | 7 |
| Medium—M | 5 | 5 |
| Good—G | 7 | 3 |
| Very Good—VG | 9 | 1 |
| E1 | E2 | |||||||||||||||||
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | |
| C1 | 1.00 | 7.00 | 2.00 | 5.00 | 6.00 | 4.00 | 3.00 | 3.00 | 8.00 | 1.00 | 8.00 | 2.00 | 6.00 | 6.00 | 4.00 | 5.00 | 3.00 | 9.00 |
| C2 | 0.14 | 1.00 | 0.17 | 0.33 | 0.50 | 0.33 | 0.25 | 0.17 | 2.00 | 0.13 | 1.00 | 0.14 | 0.25 | 0.50 | 0.33 | 0.25 | 0.17 | 2.00 |
| C3 | 0.50 | 6.00 | 1.00 | 4.00 | 5.00 | 6.00 | 2.00 | 2.00 | 7.00 | 0.50 | 7.00 | 1.00 | 4.00 | 5.00 | 6.00 | 2.00 | 2.00 | 7.00 |
| C4 | 0.20 | 3.00 | 0.25 | 1.00 | 2.00 | 0.50 | 0.33 | 0.25 | 4.00 | 0.20 | 4.00 | 0.25 | 1.00 | 2.00 | 0.50 | 0.33 | 0.25 | 4.00 |
| C5 | 0.17 | 2.00 | 0.20 | 0.50 | 1.00 | 0.33 | 0.25 | 0.20 | 3.00 | 0.17 | 2.00 | 0.20 | 0.50 | 1.00 | 0.33 | 0.25 | 0.20 | 3.00 |
| C6 | 0.25 | 3.00 | 0.17 | 2.00 | 3.00 | 1.00 | 0.50 | 0.33 | 5.00 | 0.17 | 3.00 | 0.17 | 2.00 | 3.00 | 1.00 | 0.50 | 0.33 | 5.00 |
| C7 | 0.33 | 4.00 | 0.50 | 3.00 | 4.00 | 2.00 | 1.00 | 0.50 | 5.00 | 0.20 | 4.00 | 0.50 | 3.00 | 4.00 | 2.00 | 1.00 | 0.50 | 5.00 |
| C8 | 0.33 | 6.00 | 0.50 | 4.00 | 5.00 | 3.00 | 2.00 | 1.00 | 6.00 | 0.33 | 6.00 | 0.50 | 4.00 | 5.00 | 3.00 | 2.00 | 1.00 | 6.00 |
| C9 | 0.13 | 0.50 | 0.14 | 0.25 | 0.33 | 0.20 | 0.20 | 0.17 | 1.00 | 0.11 | 0.50 | 0.14 | 0.25 | 0.33 | 0.20 | 0.20 | 0.17 | 1.00 |
| E3 | E4 | |||||||||||||||||
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | |
| C1 | 1.00 | 8.00 | 1.00 | 6.00 | 6.00 | 4.00 | 5.00 | 3.00 | 8.00 | 1.00 | 6.00 | 0.50 | 4.00 | 5.00 | 4.00 | 2.00 | 2.00 | 7.00 |
| C2 | 0.13 | 1.00 | 0.14 | 0.25 | 0.50 | 0.33 | 0.25 | 0.17 | 1.00 | 0.17 | 1.00 | 0.14 | 0.33 | 0.50 | 0.33 | 0.25 | 0.17 | 2.00 |
| C3 | 1.00 | 7.00 | 1.00 | 6.00 | 6.00 | 4.00 | 5.00 | 3.00 | 8.00 | 2.00 | 7.00 | 1.00 | 5.00 | 6.00 | 6.00 | 3.00 | 3.00 | 8.00 |
| C4 | 0.20 | 4.00 | 0.20 | 1.00 | 2.00 | 0.50 | 0.33 | 0.25 | 4.00 | 0.25 | 3.00 | 0.20 | 1.00 | 2.00 | 0.50 | 0.33 | 0.25 | 4.00 |
| C5 | 0.17 | 2.00 | 0.17 | 0.50 | 1.00 | 0.33 | 0.25 | 0.20 | 3.00 | 0.20 | 2.00 | 0.17 | 0.50 | 1.00 | 0.33 | 0.25 | 0.20 | 3.00 |
| C6 | 0.17 | 3.00 | 0.17 | 2.00 | 3.00 | 1.00 | 0.50 | 0.33 | 5.00 | 0.25 | 3.00 | 0.17 | 2.00 | 3.00 | 1.00 | 0.50 | 0.33 | 5.00 |
| C7 | 0.20 | 4.00 | 0.20 | 3.00 | 4.00 | 2.00 | 1.00 | 0.50 | 5.00 | 0.50 | 4.00 | 0.33 | 3.00 | 4.00 | 2.00 | 1.00 | 0.50 | 5.00 |
| C8 | 0.33 | 6.00 | 0.33 | 4.00 | 5.00 | 3.00 | 2.00 | 1.00 | 6.00 | 0.50 | 6.00 | 0.33 | 4.00 | 5.00 | 3.00 | 2.00 | 1.00 | 6.00 |
| C9 | 0.13 | 1.00 | 0.13 | 0.25 | 0.33 | 0.20 | 0.20 | 0.17 | 1.00 | 0.14 | 0.50 | 0.13 | 0.25 | 0.33 | 0.20 | 0.20 | 0.17 | 1.00 |
| E5 | ||||||||||||||||||
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | ||||||||||
| C1 | 1.00 | 6.00 | 0.50 | 4.00 | 5.00 | 4.00 | 2.00 | 2.00 | 7.00 | |||||||||
| C2 | 0.17 | 1.00 | 0.14 | 0.33 | 0.50 | 0.33 | 0.25 | 0.17 | 2.00 | |||||||||
| C3 | 2.00 | 7.00 | 1.00 | 5.00 | 6.00 | 6.00 | 3.00 | 3.00 | 8.00 | |||||||||
| C4 | 0.25 | 3.00 | 0.20 | 1.00 | 2.00 | 0.50 | 0.33 | 0.25 | 4.00 | |||||||||
| C5 | 0.20 | 2.00 | 0.17 | 0.50 | 1.00 | 0.33 | 0.25 | 0.25 | 3.00 | |||||||||
| C6 | 0.25 | 3.00 | 0.17 | 2.00 | 3.00 | 1.00 | 0.50 | 0.50 | 5.00 | |||||||||
| C7 | 0.50 | 4.00 | 0.33 | 3.00 | 4.00 | 2.00 | 1.00 | 1.00 | 5.00 | |||||||||
| C8 | 0.50 | 6.00 | 0.33 | 4.00 | 4.00 | 2.00 | 1.00 | 1.00 | 5.00 | |||||||||
| C9 | 0.14 | 0.50 | 0.13 | 0.25 | 0.33 | 0.20 | 0.20 | 0.20 | 1.00 | |||||||||
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | |
|---|---|---|---|---|---|---|---|---|---|
| C1 | [1, 1] | [6.47, 7.53] | [0.81, 1.61] | [4.47, 5.53] | [5.36, 5.84] | [4, 4] | [2.63, 4.23] | [2.36, 2.84] | [7.36, 8.25] |
| C2 | [0.14, 0.16] | [1, 1] | [0.14, 0.15] | [0.28, 0.32] | [0.5, 0.5] | [0.33, 0.33] | [0.25, 0.25] | [0.17, 0.17] | [1.64, 1.96] |
| C3 | [0.81, 1.61] | [6.64, 6.96] | [1, 1] | [4.36, 5.25] | [5.36, 5.84] | [5.28, 5.92] | [2.4, 3.67] | [2.36, 2.84] | [7.36, 7.84] |
| C4 | [0.21, 0.23] | [3.16, 3.64] | [0.21, 0.23] | [1, 1] | [2, 2] | [0.5, 0.5] | [0.33, 0.33] | [0.25, 0.25] | [4, 4] |
| C5 | [0.17, 0.19] | [2, 2] | [0.17, 0.19] | [0.5, 0.5] | [1, 1] | [0.33, 0.33] | [0.25, 0.25] | [0.2, 0.22] | [3, 3] |
| C6 | [0.2, 0.24] | [3, 3] | [0.17, 0.17] | [2, 2] | [3, 3] | [1, 1] | [0.5, 0.5] | [0.34, 0.4] | [5, 5] |
| C7 | [0.27, 0.43] | [4, 4] | [0.3, 0.44] | [3, 3] | [4, 4] | [2, 2] | [1, 1] | [0.52, 0.68] | [5, 5] |
| C8 | [0.36, 0.44] | [6, 6] | [0.36, 0.44] | [4, 4] | [4.64, 4.96] | [2.64, 2,96] | [1.64, 1,96] | [1, 1] | [5.64, 5.96] |
| C9 | [0.12, 0.14] | [0.52, 0.68] | [0.13, 0.14] | [0.25, 0.25] | [0.33, 0.33] | [0.2, 0.2] | [0.2, 0.2] | [0.17, 0.18] | [1, 1] |
| A1 | A2 | A3 | |||||||||||||
| E1 | E2 | E3 | E4 | E5 | E1 | E2 | E3 | E4 | E5 | E1 | E2 | E3 | E4 | E5 | |
| C1 | 7 | 9 | 5 | 5 | 7 | 7 | 7 | 3 | 5 | 7 | 5 | 3 | 5 | 7 | 5 |
| C2 | 1 | 1 | 1 | 3 | 1 | 3 | 3 | 5 | 1 | 3 | 7 | 9 | 3 | 5 | 7 |
| C3 | 3 | 3 | 1 | 3 | 1 | 7 | 9 | 5 | 5 | 7 | 7 | 7 | 3 | 5 | 5 |
| C4 | 9 | 7 | 7 | 9 | 9 | 9 | 5 | 5 | 7 | 9 | 5 | 1 | 7 | 7 | 5 |
| C5 | 1 | 9 | 1 | 3 | 3 | 3 | 7 | 3 | 5 | 5 | 7 | 5 | 3 | 5 | 9 |
| C6 | 3 | 7 | 3 | 3 | 7 | 5 | 7 | 5 | 3 | 7 | 7 | 5 | 3 | 5 | 9 |
| C7 | 5 | 5 | 3 | 3 | 5 | 5 | 3 | 5 | 1 | 5 | 7 | 7 | 5 | 3 | 7 |
| C8 | 3 | 5 | 1 | 1 | 7 | 5 | 7 | 3 | 3 | 9 | 5 | 5 | 5 | 3 | 9 |
| C9 | 3 | 7 | 3 | 1 | 7 | 3 | 5 | 1 | 3 | 5 | 7 | 5 | 3 | 5 | 7 |
| A4 | A5 | A6 | |||||||||||||
| C1 | 5 | 3 | 7 | 7 | 5 | 5 | 3 | 5 | 7 | 5 | 3 | 5 | 3 | 5 | 5 |
| C2 | 3 | 7 | 5 | 3 | 5 | 9 | 9 | 5 | 5 | 9 | 7 | 7 | 7 | 5 | 7 |
| C3 | 3 | 3 | 1 | 3 | 1 | 9 | 9 | 5 | 7 | 7 | 7 | 9 | 3 | 5 | 7 |
| C4 | 5 | 3 | 7 | 5 | 5 | 3 | 1 | 5 | 5 | 1 | 3 | 3 | 3 | 5 | 3 |
| C5 | 7 | 5 | 5 | 5 | 9 | 7 | 5 | 9 | 7 | 9 | 5 | 5 | 3 | 3 | 5 |
| C6 | 3 | 3 | 5 | 3 | 9 | 5 | 5 | 3 | 7 | 5 | 3 | 5 | 3 | 5 | 9 |
| C7 | 9 | 7 | 5 | 3 | 9 | 9 | 7 | 5 | 3 | 9 | 3 | 3 | 1 | 3 | 3 |
| C8 | 5 | 5 | 3 | 3 | 7 | 5 | 5 | 5 | 5 | 7 | 3 | 5 | 3 | 5 | 5 |
| C9 | 5 | 5 | 5 | 3 | 9 | 7 | 5 | 5 | 5 | 9 | 3 | 1 | 5 | 5 | 3 |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | |
|---|---|---|---|---|---|---|---|---|---|
| A1 | [5.72, 7.51] | [1.08, 1.72] | [1.72, 2.68] | [7.72, 8.68] | [1.88, 5.16] | [3.64, 5.56] | [3.72, 4.68] | [1.91, 4.96] | [2.81, 5.64] |
| A2 | [4.88, 6.66] | [2.3, 3.7] | [5.72, 7.51] | [5.93, 8.07] | [3.72, 5.51] | [4.49, 6.28] | [2.88, 4.66] | [3.91, 6.96] | [2.49, 4.28] |
| A3 | [4.3, 5.7] | [4.84, 7.51] | [4.49, 6.28] | [3.67, 6.2] | [4.49, 7.16] | [4.49, 7.16] | [4.88, 6.66] | [4.38, 6.48] | [4.49, 6.28] |
| A4 | [4.49, 6.28] | [3.72, 5.51] | [1.72, 2.68] | [4.3, 5.7] | [5.34, 7.12] | [3.42, 5.96] | [5.04, 8.09] | [3.72, 5.51] | [4.38, 6.48] |
| A5 | [4.3, 5.7] | [6.44, 8.36] | [6.49, 8.28] | [1.93, 4.07] | [6.49, 8.28] | [4.3, 5.7] | [5.04, 8.09] | [5.08, 5.72] | [5.34, 7.12] |
| A6 | [3.72, 4.68] | [6.28, 6.92] | [4.84, 7.51] | [3.08, 3.72] | [3.72, 4.68] | [3.8, 6.33] | [2.28, 2.92] | [3.72, 4.68] | [2.49, 4.28] |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | |
|---|---|---|---|---|---|---|---|---|---|
| A1 | [0.76, 1.31] | [0.63, 1.59] | [0.21, 0.41] | [0.22, 0.48] | [0.23, 0.8] | [0.51, 1.24] | [0.46, 0.93] | [0.27, 0.98] | [0.39, 1.06] |
| A2 | [0.65, 1.16] | [0.29, 0.75] | [0.69, 1.16] | [0.24, 0.63] | [0.45, 0.85] | [0.63, 1.4] | [0.36, 0.92] | [0.56, 1.37] | [0.35, 0.8] |
| A3 | [0.57, 1] | [0.14, 0.36] | [0.54, 0.97] | [0.31, 1.01] | [0.54, 1.1] | [0.63, 1.59] | [0.6, 1.32] | [0.63, 1.28] | [0.63, 1.18] |
| A4 | [0.6, 1.1] | [0.2, 0.46] | [0.21, 0.41] | [0.34, 0.87] | [0.64, 1.1] | [0.48, 1.33] | [0.62, 1.61] | [0.53, 1.08] | [0.62, 1.21] |
| A5 | [0.57, 1] | [0.13, 0.27] | [0.78, 1.28] | [0.47, 1.93] | [0.78, 1.28] | [0.6, 1.27] | [0.62, 1.61] | [0.73, 1.13] | [0.75, 1.33] |
| A6 | [0.5, 0.82] | [0.16, 0.27] | [0.58, 1.16] | [0.52, 1.21] | [0.45, 0.72] | [0.53, 1.41] | [0.28, 0.58] | [0.53, 0.92] | [0.35, 0.8] |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | |
|---|---|---|---|---|---|---|---|---|---|
| A1 | [0.61, 1.3] | [0.06, 0.15] | [0.17, 0.41] | [0.04, 0.09] | [0.03, 0.1] | [0.12, 0.31] | [0.17, 0.39] | [0.14, 0.54] | [0.03, 0.08] |
| A2 | [0.52, 1.16] | [0.03, 0.07] | [0.57, 1.16] | [0.04, 0.12] | [0.06, 0.11] | [0.15, 0.36] | [0.13, 0.38] | [0.28, 0.76] | [0.02, 0.06] |
| A3 | [0.46, 0.99] | [0.01, 0.03] | [0.44, 0.97] | [0.06, 0.2] | [0.07, 0.15] | [0.15, 0.41] | [0.22, 0.55] | [0.32, 0.7] | [0.04, 0.08] |
| A4 | [0.48, 1.09] | [0.02, 0.04] | [0.17, 0.41] | [0.06, 0.17] | [0.08, 0.14] | [0.12, 0.34] | [0.23, 0.67] | [0.27, 0.6] | [0.04, 0.09] |
| A5 | [0.46, 0.99] | [0.01, 0.03] | [0.64, 1.28] | [0.09, 0.37] | [0.1, 0.17] | [0.15, 0.32] | [0.23, 0.67] | [0.37, 0.62] | [0.05, 0.1] |
| A6 | [0.4, 0.81] | [0.01, 0.03] | [0.48, 1.16] | [0.1, 0.23] | [0.06, 0.09] | [0.13, 0.36] | [0.1, 0.24] | [0.27, 0.51] | [0.02, 0.06] |
| λ × Qi | (1 − λ) × Pi | Ai | Crisp Ai | Rank | |
|---|---|---|---|---|---|
| A1 | [0.687, 1.963] | [0.002, 0.031] | [0.689, 1.995] | 1.342 | 6 |
| A2 | [0.908, 2.422] | [0.005, 0.093] | [0.914, 2.515 | 1.714 | 2 |
| A3 | [0.894, 2.367] | [0.005, 0.083] | [0.899, 2.450] | 1.675 | 3 |
| A4 | [0.739, 2.061] | [0.002, 0.037] | [0.741, 2.098] | 1.419 | 5 |
| A5 | [1.053, 2.636] | [0.009, 0.119] | [1.063, 2.755 | 1.909 | 1 |
| A6 | [0.790, 2.026] | [0.004, 0.044] | [0.793, 2.070] | 1.432 | 4 |
| λ = 0 | λ = 0.1 | λ = 0.2 | λ = 0.3 | λ = 0.4 | λ = 0.5 | λ = 0.6 | λ = 0.7 | λ = 0.8 | λ = 0.9 | λ = 1.0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 0.033 | 0.267 | 0.501 | 0.735 | 0.969 | 1.203 | 1.437 | 1.671 | 1.905 | 2.139 | 2.374 |
| A2 | 0.100 | 0.389 | 0.678 | 0.967 | 1.255 | 1.544 | 1.833 | 2.122 | 2.411 | 2.699 | 2.989 |
| A3 | 0.090 | 0.374 | 0.658 | 0.942 | 1.225 | 1.509 | 1.792 | 2.076 | 2.359 | 2.643 | 2.927 |
| A4 | 0.040 | 0.287 | 0.534 | 0.781 | 1.028 | 1.275 | 1.521 | 1.768 | 2.015 | 2.262 | 2.509 |
| A5 | 0.131 | 0.449 | 0.768 | 1.086 | 1.405 | 1.724 | 2.042 | 2.361 | 2.680 | 2.998 | 3.317 |
| A6 | 0.048 | 0.296 | 0.545 | 0.793 | 1.041 | 1.289 | 1.537 | 1.785 | 2.034 | 2.282 | 2.530 |
| Methods | RWASPAS | RSAW | REDAS | RMABAC | RVIKOR | RMAIRCA | RMULTI-MOORA | Average |
|---|---|---|---|---|---|---|---|---|
| RWASPAS | 1.000 | 1.000 | 0.886 | 0.943 | 0.829 | 0.943 | 1.000 | 0.943 |
| RSAW | - | 1.000 | 0.886 | 0.943 | 0.829 | 0.943 | 1.000 | 0.933 |
| REDAS | - | - | 1.000 | 0.943 | 0.714 | 0.943 | 0.886 | 0.897 |
| RMABAC | - | - | - | 1.000 | 0.771 | 1.000 | 0.943 | 0.929 |
| RVIKOR | - | - | - | - | 1.000 | 0.771 | 0.829 | 0.867 |
| RMAIRCA | - | - | - | - | - | 1.000 | 0.943 | 0.971 |
| RMULTI-MOORA | - | - | - | - | - | - | 1.000 | 1.000 |
| Overall average | 0.934 | |||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stojić, G.; Stević, Ž.; Antuchevičienė, J.; Pamučar, D.; Vasiljević, M. A Novel Rough WASPAS Approach for Supplier Selection in a Company Manufacturing PVC Carpentry Products. Information 2018, 9, 121. https://doi.org/10.3390/info9050121
Stojić G, Stević Ž, Antuchevičienė J, Pamučar D, Vasiljević M. A Novel Rough WASPAS Approach for Supplier Selection in a Company Manufacturing PVC Carpentry Products. Information. 2018; 9(5):121. https://doi.org/10.3390/info9050121
Chicago/Turabian StyleStojić, Gordan, Željko Stević, Jurgita Antuchevičienė, Dragan Pamučar, and Marko Vasiljević. 2018. "A Novel Rough WASPAS Approach for Supplier Selection in a Company Manufacturing PVC Carpentry Products" Information 9, no. 5: 121. https://doi.org/10.3390/info9050121
APA StyleStojić, G., Stević, Ž., Antuchevičienė, J., Pamučar, D., & Vasiljević, M. (2018). A Novel Rough WASPAS Approach for Supplier Selection in a Company Manufacturing PVC Carpentry Products. Information, 9(5), 121. https://doi.org/10.3390/info9050121








