Auction-Based Cloud Service Pricing and Penalty with Availability on Demand

Abstract

Availability is one of the main concerns of cloud users, and cloud providers always try to provide higher availability to improve user satisfaction. However, higher availability results in higher provider costs and lower social welfare. In this paper, taking into account both the users’ valuation and desired availability, we design resource allocation, pricing and penalty mechanisms with availability on demand. Considering two scenarios: public availability in which the desired availabilities of all users are public information, and private availability in which the desired availabilities are private information of users, and, analyzing the possible behaviours of users, we design a truthful deterministic mechanism with 2-approximation in public availability scenario and a universal truthful mechanism with $\frac{1}{1+\gamma }$ approximation in private availability scenario, where $\gamma$ is the backup ratio of resources with the highest availability. The experiment results show that our mechanisms significantly improve the social welfare compared to the mechanism without considering availability demand of users.

1. Introduction

Quality of service is a significant factor affecting the service selection of cloud users, which has attracted the attention of many researchers [1,2,3]. As a crucial metric for quality of service, availability is the most discussed attribute, which is included in almost all cloud service level agreements (SLAs). According to Pan et al. [4], above about 70 percent of user/provider SLA included availability concerns. Thus, many research works focused on improving the availability by various optimization approaches [5,6,7,8]. To improve the user satisfaction, the infrastructure as a service (IaaS) cloud provider provides higher and higher availability for their users, and provides a penalty when the SLA is violated. Figure 1 shows the penalty named service credit in different clouds [9,10,11], which is a percentage of the corresponding price.

However, in terms of the types of applications, users might have different availability demands. For instance, a non-critical web hosting service always has a lower availability demand than a mission-critical banking service. According to the discussion in literature [12], all high availability techniques increase administrative costs and resource needs. Therefore, existing solutions in the cloud center, which try to provide higher and higher availability without considering different availability demand, will result in higher provider costs and consume more resources. Especially in the scenario of insufficient resources, it will make more users lose service. Thus, the social welfare, which is the sum of users’ valuation, will decrease. Figure 2a shows the resource allocation for the service requests with fixed availability and price.

To overcome the shortcomings above, some researchers have noticed the importance of resources allocation according to users’ demands on availability. Shen et al. [13] proposed a mechanism named availability on demand (AoD), which allows data center users to specify dynamically availability requirements, and dynamically manages computing resources using an availability-aware scheduler based on user-specified requirements. Shahrad et al. [14] proposed the Availability Knob (AK), which provides user-defined availability in IaaS clouds, allowing the IaaS cloud user to express their desire for availability to the cloud provider. This approach can reduce provider costs, increase provider profit, and improve user satisfaction when compared to that without considering different availability demands. In the system of user-selected availability, the penalty mechanism is another important ingredient that affects the users’ service selection. The negotiations on availability generally include the penalty, which should be paid by the cloud provider if the cloud cannot meet the requested availability. Yuan et al. [15] proposed a competitive penalty model and a corresponding penalty based profit maximization algorithm for cloud providers. In [14], considering service credit as a penalty to the user when her requested availability cannot be met, the authors proposed the pricing strategy based on game theory. However, the studies above did not consider the valuation of services to users, resulting in low social welfare. Taking the service valuation to users into account, auctions have been applied widely [16,17,18,19,20,21]. Mashayekhy et al. [16] proposed mechanisms consisting of a winner determination algorithm that selects the users, and provisions the virtual machines (VMs) to physical machines; Zhang et al. [21] considered a flexible pricing model for instance reservation. However, most of those works investigate the allocation of resources without worrying about the availability demands of users.

In this paper, taking both the users’ valuation and desired availability into account, we investigate resource allocation, pricing and penalty mechanism to maximize the social welfare based on the works in [13,14,16]. Figure 2b shows a cloud scheduler that allocates resources according to different availability demands and valuation of users with different prices. We allow each user to request the desired availability and report the valuation that she is willing to pay for the service with requested availability. As shown in Figure 2, user 1 would like to pay $5 to the service with 99.9% availability. In our work, we consider two scenarios: (1) the desired availabilities of all users are public information of users (public availability); and (2) the desired availabilities are private information of users (private availability). Then, by analyzing the possible behaviours of users, we design a truthful deterministic mechanism in a public availability scenario and a universal truthful mechanism in a private availability scenario for resource allocation, pricing and penalty.

The rest of the paper is organized as follows. Section 2 introduces the problem model. In Section 3, we design a truthful deterministic mechanism in a public availability scenario and a universal truthful mechanism in a private availability scenario. In Section 4, we compare the proposed mechanisms to optimal resource allocation and an allocation mechanism without considering the availability demand. Finally, Section 5 concludes our work in this paper.

2. System Model

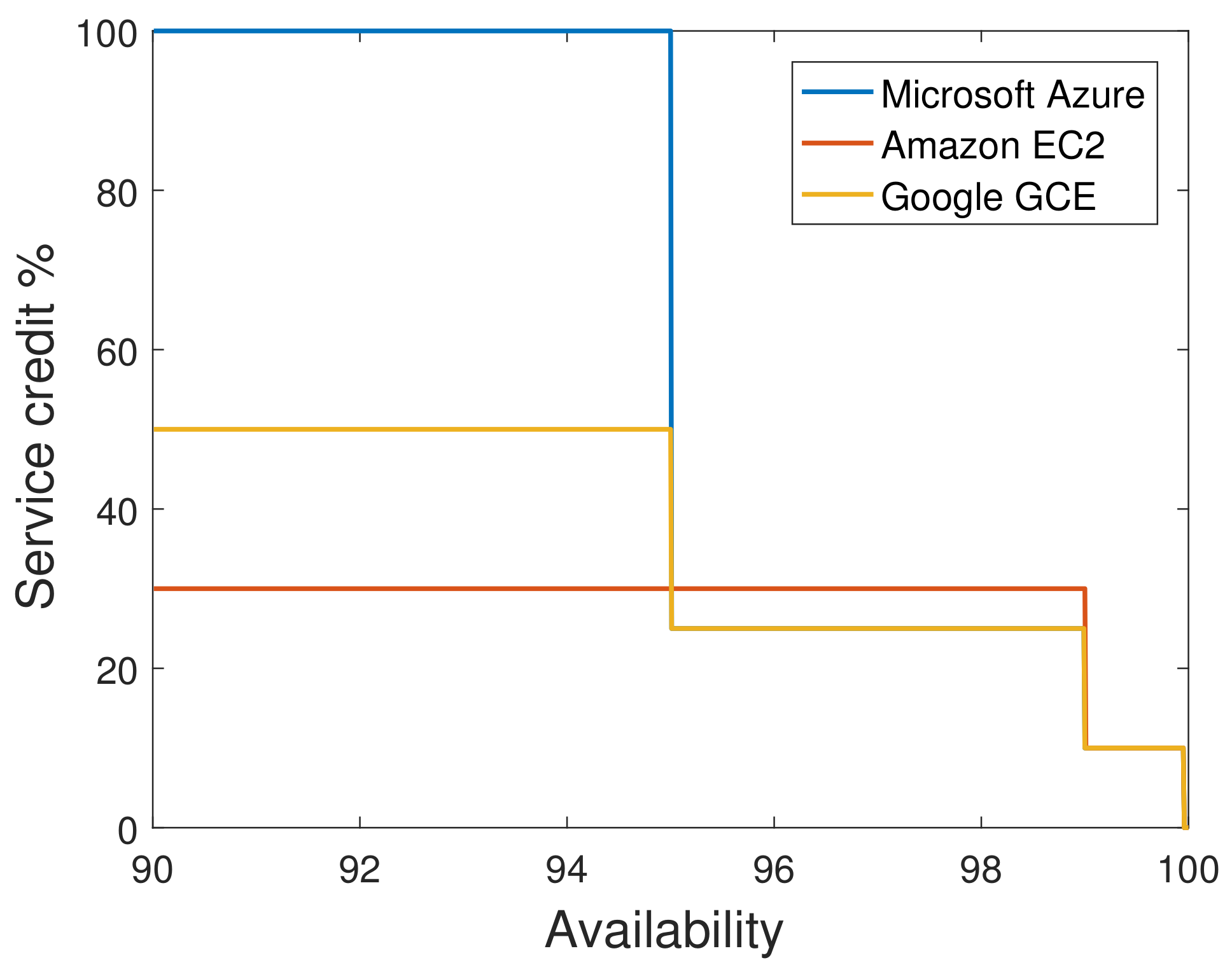
2.1. Availability on Demand and Service Credit

Availability of an application can be measured as the fraction of its uptime in a specified period of time, which can be expressed by

$$\mathrm{Availability}=\frac{\mathrm{service}\mathrm{uptime}}{\mathrm{service}\mathrm{uptime}+\mathrm{service}\mathrm{downtime}},$$

where service uptime is the duration during which the system delivers the given service, while service downtime is the period during which the service is not delivered [22].

Providers always adopt different fault tolerance schemes to realize different availabilities of a given application. In [23], it shows that most of the cloud providers use redundancy models with 1-active and 1-standby, 1-active and X-standby, and X-active assignments. We denote the set of all availability options by A, $A=\{A_1,A_2,\dots ,A_L\}$, where $A_1$ is the lowest option, and $A_L$ is the highest availability. Each Availability option $A_l$ corresponds to a backup ratio of virtual machine $\phi (A_l)\in [0,X]$.

On the other side, SLA templates are always provided by cloud providers in most clouds. When a user agrees to purchase a service, it also implies that she has signed the service level agreement with the provider. When the cloud services cannot meet availability commitment of the SLA, providers would pay back service credits to make up for their violation, which is also included in the SLA. Service credit is calculated in different manners. Figure 1 shows the service credit functions of Amazon EC2, Google GCE, and Microsoft Azure. Of course, cloud providers can use other penalty schemes such as linear function, arbitrary function, etc. These penalty mechanism only applies to the scenarios with fixed availability provisioning.

In our work, we assume that the provider only provisions one type of virtual machine. The resource (virtual machine) number needed by the user i is $n_i$. To simplify, we call it resource demand $n_i$. Each user can select an availability from set A according to the service demand. We assume that the total resource number occupied by each user i denoted by $n_i(1+\phi (a_i))$ is no more than total capacity of the cloud. The definition of desired availability is as follows:

Definition 1 (Desired Availability).

Given the resource demand $n_i$, $a_i$ is desired availability of user i if $\forall a<a_i,V_i(n_i,a)=0$ and $\forall a\ge a_i,V_i(n_i,a)=v_i$, where $V_i(·)$ is the valuation function of user i, $v_i$ is a constant.

Our resource allocation for service requests with desired availability is named as Allocation with Availability on Demand. Then, we denote $S{C}_{A_i}^k(A_j)$ as the absolute service credit for service k, where $A_i$, $A_j$ are the requested availability and delivered availability, respectively. It implies that, when the requested availability is $A_i$, the provider needs to pay back service credit $S{C}_{A_i}^k(A_j)$ if the delivered availability is $A_j$ and $A_j<A_i$. Of course, $S{C}_{A_i}^k(A_j)=0$ if $A_i\le A_j$.

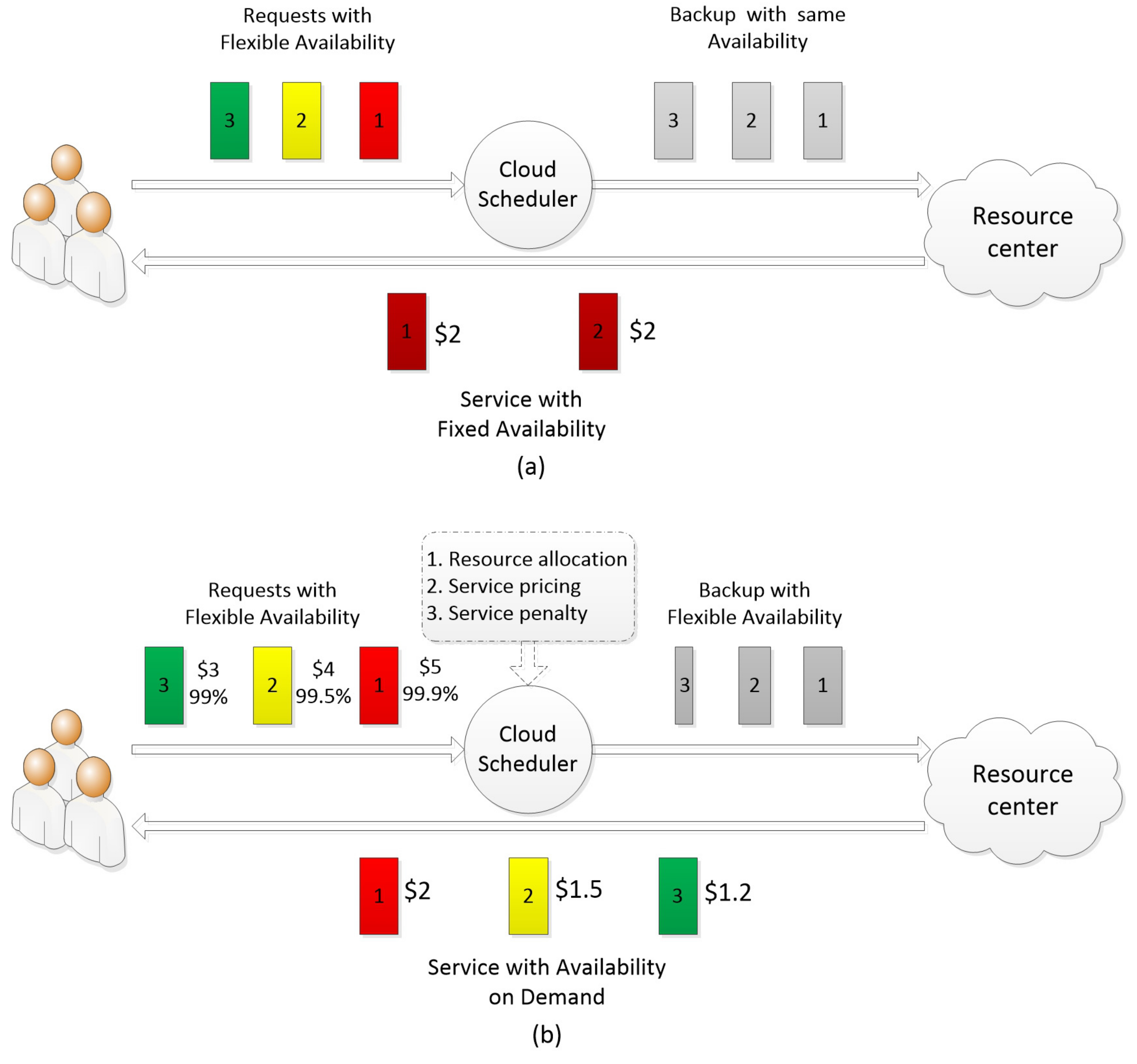
2.2. Description of the Problem

Let $\mathcal{N}$ denote a set of cloud users who want to request services. The type of user i can be expressed by $(n_i,a_i,v_i)$, where $a_i\in A$ is the desired availability, $n_i$ is the resource demand and $v_i$ is the service valuation to user i. In our work, we assume that all the bidders are single-minded, the definition of which is as follows:

Definition 2 (Single-minded).

A valuation function V is called single-minded if there exists a number of items $n^{\ast }$, an availability $a^{\ast }$ and a value $v^{\ast }\in {\mathcal{R}}^{+}$ such that $V(n,a)=v^{\ast }$ for all $n\ge n^{\ast }$ and $a\ge a^{\ast }$ and $V(n,a)=0$ for all other $(n,a)$. A single-minded bid is the pair $(n^{\ast },a^{\ast },v^{\ast })$.

In this paper, we design resource auction mechanisms for the cloud center, and the objective is to maximize the sum of users’ valuation, which is the social welfare. The formalization problem can be expressed as follows:

$$\begin{array}{cc}& \max \sum _{i\in \mathcal{N}}{x}_i{v}_i,\hfill \\ \hfill s.t.& \sum _{i\in \mathcal{N}}{x}_i{n}_i(1+\phi (a_i))\le C,\hfill \\ & x_i=0or1,\forall i\in \mathcal{N},\hfill \end{array}$$

(1)

where C is the total capacity in cloud, $x_i$ is the allocation outcome for user i. $x_i=1$ if user i is allocated; otherwise, $x_i=0$.

Now, the critical work is to obtain a mechanism including resource allocation, pricing and penalty. To achieve the objective in problem (1), the mechanism should be truthful so that it can incentivize all users to bid their true type.

Let $b_i$ be the true type of user i, $b_{-i}$ the true type of other users. Let bid ${\widehat{b}}_i$ be the report type of user i, ${\widehat{b}}_{-i}$ the report type of other users. The utility function of i is denoted by $u_i(·)$. The definition of truthfulness of an auction mechanism is as follows:

Definition 3 (Truthful).

An auction mechanism is truthful if bidding true type maximizes the utility of any user i irrespective of the bid of other users. Formally, $\forall {\widehat{b}}_i,{\widehat{b}}_{-i}$,

$$u_i(b_i,{\widehat{b}}_{-i})\ge u_i({\widehat{b}}_i,{\widehat{b}}_{-i}).$$

Intuitively, it means that user i whose type is $b_i$ would prefer “telling the truth” $b_i$ to the mechanism rather than any possible “lie” ${\widehat{b}}_i$ , since this gives her higher utility.

In the next section, we will design truthful mechanisms under two scenarios: public availability in which the desired availabilities of all users are public information, and private availability in which the desired availabilities are private information of users.

3. Truthful Auction Mechanism with Availability on Demand

3.1. Public Availability

In this subsection, we consider the setting that the desired availability of each user is public information to the auctioneer, and the valuation function is single-minded. Then, $b_i=(n_i,v_i)$, it becomes a two parameter mechanism design problem. The problem is very similar to the knapsack problem. Our auction mechanism for public availability is presented in Algorithm 1.

Algorithm 1: Auction for multi-unit request: HalfGreedy.

Algorithm 1 begins by computing two candidate allocation set. The first candidate allocation set denoted by $S_1$ is the singleton set that only consists of the user $i_1$ who has the highest valuation among all the users, and $V_1$ denotes the valuation of $S_1$. The computing process of first candidate allocation set and corresponding valuation is shown in Lines 2–4 of Algorithm 1. The second candidate allocation set $S_2$ is computed as following steps. First, we select all users whose requested capacity is less than $C/2$ to set $U^{\prime }$ in Line 5. Let value density of user i be $\frac{v_i}{n_i(1+\phi (a_i))}$. Then, we select the cloud users from set $U^{\prime }$ to $S_2$ based on a greedy approach with respect to the value density of users in Lines 6–10. Lastly, we calculate the total valuation $V_2$ about the second allocation in Line 12. It is worth noting that $V_2$ is not the overall valuation from set $S_2$, but the maximal sum of valuation allocated in exactly half of the capacity. After computing two candidate allocation sets, in Lines 13–17, we choose an optimal one as a final allocation. According to the maximal valuation between $V_1$ and $V_2$, we select either the user in $S_1$ or all users in $S_2$. In Line 19, according to the Myerson payment rule, we calculate the payment $p_i$ for each winner i:

$$p_i=v_i{x}_i-{\int }_0^{v_i}{x}_i((n_i,a_i,u),b_{-i})du,$$

where, $x_i((n_i,a_i,u),b_{-i})$ presents the allocation of user i in Algorithm 1 when the bid of user i is $(n_i,a_i,u)$, and the bid of others is $b_{-i}$.

To prove the truthfulness of our mechanism in Algorithm 1, firstly we introduce a truthfulness Theorem [24].

Theorem 1.

A mechanism for single-minded bidders in which losers pay 0 is truthfulness if and only if it satisfies the following two conditions:

(i) 

Monotonicity: A bidder who wins with bid $(o_i^{\ast },v_i^{\ast })$ keeps winning for any $v_i^{\prime }>v_i^{\ast }$ and for any $o^{\prime }⪯o^{\ast }$ (for any fixed settings of the other bids).

(ii) 

Critical Payment: A bidder who wins pays the minimum value needed for winning: the minimum of all values $v_i^{\prime }$ such that $(o_i^{\ast },v_i^{\ast })$ still wins.

Theorem 2.

The auction mechanism in Algorithm 1 is truthful.

Proof of Theorem 2.

First, we use $w_i$ instead of $n_i(1+\phi (a_i))$ in Algorithm 1, and the bid changes to $(w_i,v_i)$. According to the results in [25], the changed algorithm is loser-independent and monotonic with respect to the bid $(w_i,v_i)$ of every user. Since $w_i$ is monotonic in $n_i,a_i$, and $a_i$ is public information, Algorithm 1 is also monotonic in $n_i,v_i$.

The payment $p_i=v_i{x}_i-{\int }_0^{v_i}{x}_i((n_i,a_i,u),b_{-i})du$ is the minimum value, which can make user i obtain allocation.

According to the Theorem 1, Algorithm 1 is truthful. ☐

Theorem 3.

The auction mechanism in Algorithm 1 is 2-approximation.

Proof of Theorem 3.

Assume that $V_{opt}$ is the optimal valuation, and $S^{\ast }$ is the set of allocated users. Recall that $V_1$ is the highest bid valuation among all users and $V_2$ the maximum sum of valuation allocated in half of capacity.

Case 1: If $S^{\ast }$ includes a user $i^{\ast }$ whose required total capacity $n_{i^{\ast }}(1+\phi (a_{i^{\ast }}))$ is more than $\frac{C}{2}$, since $V_1\ge v_{i^{\ast }}$ and $V_2\ge {\sum }_{i\in S^{\ast }\setminus \left\{i^{\ast }\right\}}{v}_i$, it follows that

$$\max \{V_1,V_2\}\ge \frac{1}{2}(V_1+V_2)\ge \frac{1}{2}(v_{i^{\ast }}+\sum _{i\in S^{\ast }\setminus \left\{i^{\ast }\right\}}{v}_i)=\frac{1}{2}{V}_{opt}.$$

Case 2: If all the users in $S^{\ast }$ require the resource capacity less than half of whole capacity, it follows that

$$\max \{V_1,V_2\}\ge V_2\ge \frac{1}{2}{V}_{opt}.$$

 ☐

In Algorithm 1, we obtain a truthful 2-approximation mechanism if each desired availability $a_i$ is a public information. However, in many scenarios, cloud providers cannot obtain the desired availability of users. It needs the users to tell their availabilities to the mechanism. In that case, a user might make some other strategies to improve her utility.

Studies [26,27,28] have shown, and one of the root causes of failure is software in computer systems. Such possible software failures can affect the availability of the VM, and it is difficult to distinguish software-induced failures from failures caused by hardware [14]. Therefore, if the user is unhealthy, to obtain service credit, she can adopt some strategy to reduce the availability of herself. Shahrad et al. [14] consider that a user can either run defective software that reduces the availability from ${\widehat{a}}_i$ to desired availability $a_i$, resulting in some service credit return, or instead run healthy, reliable software and originally request the true desired availability $a_i$. The former users we name unhealthy users, and the latter are healthy users.

In Algorithm 1, when the users are unhealthy, for any nonzero service credit approach, it cannot make each user truthfully report the desired availability $a_i$ in any case if $a_i$ is private information. For example, in Algorithm 1, if $V_1>V_2$ and $i^{\ast }\in S_1$, we can obtain a critical payment of $i^{\ast }$ denoted by $p_{i^{\ast }}^c$. Obviously, if $i^{\ast }$ reports its availability ${\widehat{a}}_{i^{\ast }}>a_{i^{\ast }}$, she still can obtain allocation. Therefore, when there is a service credit, $i^{\ast }$ will request higher availability and then reduce it to the desired availability by running defective software to get both the service credit and valuation of the service.

To address the above problem, in the next subsection, we will design another pricing and penalty mechanism that can avoid unhealthy users to misreport their desired availability.

3.2. Private Availability

In this section, we deal with the setting that users’ availabilities are private information. Firstly, the penalty in practice is no more than the payment, which will be followed in our work. In terms of that, we can deduce that each user hopes to obtain the service with the availability not lower than her desired availability. This is because the user obtains the zero valuation if the delivered availability is lower than the desired availability according to the definition of desired availability, and the penalty cannot be larger than the payment. Therefore, if the delivered availability is lower than the desired availability, the user cannot obtain positive utility.

However, since there is a service credit if the availability cannot be satisfied, an unhealthy user might adopt some strategies to improve her utility. As described in [14], an unhealthy user can reduce the availability from requested availability ${\widehat{a}}_i$ (${\widehat{a}}_i>a_i$) to desired availability $a_i$ to get service credit $S{C}_{{\widehat{a}}_i}(a_i)$. Although a cloud provider can use measures to investigate the cause of a downtime incident, it might not be accurate and can increase the work of the cloud. Price and penalty mechanisms can be effective tools to solve the above problem, which make all users truthfully report their true type including resource demand $n_i$, desired availability $a_i$ and valuations $v_i$, and run healthy, reliable software.

Let $p_i(·)$ be the payment function of user i, and the bid of user i $b_i=(n_i,a_i,v_i)$. First, we can obtain the following theorem.

Theorem 4.

When a mechanism M is truthful without service credit, it is still truthful with service credit if it satisfies the service credit $S{C}_{{\widehat{a}}_i}(a_i)$ of each winner being less than $p_i(({\widehat{n}}_i,{\widehat{a}}_i,{\widehat{v}}_i),{\widehat{b}}_{-i})-p_i(({\widehat{n}}_i,a_i,{\widehat{v}}_i),{\widehat{b}}_{-i})$ for any ${\widehat{n}}_i,{\widehat{v}}_i,{\widehat{b}}_{-i}$ and ${\widehat{a}}_i>a_i$.

Proof of Theorem 4.

Since a mechanism M is truthful without service credit, we can have that:

$$u(b_i,{\widehat{b}}_{-i})\ge u({\widehat{b}}_i,{\widehat{b}}_{-i}),\forall {\widehat{b}}_i,{\widehat{b}}_{-i},$$

where the utility $u_i(·)$ is the difference of the valuation $V_i(·)$ and the payment $p_i(·)$. Next, we discuss two cases: the user is healthy, and the user is unhealthy. Recall that all users hope to obtain efficient service and cloud providers do their best to meet the availability demand for required service. Therefore, in this paper, we do not consider the cases that the cloud provider cannot meet the requested availability because of her own reasons.

First, if the user is healthy who runs healthy, reliable, software, and the cloud provider provisions the service with requested availability; in this case, there is no violation. Since $u(b_i,{\widehat{b}}_{-i})\ge u({\widehat{b}}_i,{\widehat{b}}_{-i})$, the mechanism is truthful.

Second, if the user is unhealthy who runs defective software, the requested availability ${\widehat{a}}_i$ will be reduced to desired availability $a_i$ even if the cloud provider provisions the service with requested availability ${\widehat{a}}_i>a_i$. Then, the unhealthy user will obtain a service credit $S{C}_{{\widehat{a}}_i}(a_i)$. The utility of the user is:

$$u_i({\widehat{b}}_i,{\widehat{b}}_{-i})=V_i({\widehat{n}}_i,a_i)-p({\widehat{b}}_i,{\widehat{b}}_{-i})+S{C}_{{\widehat{a}}_i}(a_i).$$

For any ${\widehat{n}}_i,{\widehat{v}}_i$ and the bid of others ${\widehat{b}}_{-i}$, if the service credit $S{C}_{{\widehat{a}}_i}(a_i)$ is less than $p_i(({\widehat{n}}_i,{\widehat{a}}_i,{\widehat{v}}_i),{\widehat{b}}_{-i})-p_i(({\widehat{n}}_i,a_i,{\widehat{v}}_i),{\widehat{b}}_{-i})$, for any ${\widehat{a}}_i>a_i$, we have that:

$$\begin{array}{cc}\hfill u_i(({\widehat{a}}_i,{\widehat{v}}_i),{\widehat{b}}_{-i})& =V_i({\widehat{n}}_i,a_i)-p(({\widehat{n}}_i,{\widehat{a}}_i,{\widehat{v}}_i),{\widehat{b}}_{-i})+S{C}_{{\widehat{a}}_i}(a_i)\hfill \\ \hfill & \le V_i({\widehat{n}}_i,a_i)-p_i(({\widehat{n}}_i,{\widehat{a}}_i,{\widehat{v}}_i),{\widehat{b}}_{-i})+p_i(({\widehat{n}}_i,{\widehat{a}}_i,{\widehat{v}}_i),{\widehat{b}}_{-i})-p_i(({\widehat{n}}_i,a_i,{\widehat{v}}_i),{\widehat{b}}_{-i})\hfill \\ \hfill & =V_i({\widehat{n}}_i,a_i)-p_i(({\widehat{n}}_i,a_i,{\widehat{v}}_i),{\widehat{b}}_{-i})\hfill \\ \hfill & =u_i(({\widehat{n}}_i,a_i,{\widehat{v}}_i),{\widehat{b}}_{-i}).\hfill \end{array}$$

$u_i(({\widehat{n}}_i,a_i,{\widehat{v}}_i),{\widehat{b}}_{-i})$ is the utility of user i if she asks for truthful availability and runs healthy, reliable software. It means that the unhealthy users cannot improve the utility by adopting improper strategy for any resource demand ${\widehat{n}}_i$, valuation ${\widehat{v}}_i$ and the bid of the others $b_{-i}$.

The theorem is proved. ☐

Our auction is presented in Algorithm 2. Basically, it is a combination of the following two basic auctions:

• With the probability $\mu$, we run Auction A: Agent $i_1$ with highest value of $\frac{v_i}{1+\phi (a_i)}$ gets the allocation and needs to pay $p_{i_1}=v_{i_2}\frac{1+\phi (a_{i_1})}{1+\phi (a_{i_2})}$, where $i_2$ is the user with second highest value of $v_i/(1+\phi (a_i))$. Obviously, $p_i$ is not higher than the valuation $v_{i_1}$. The service credit for $i_1$ is $S{C}_{a_{i_1}}^{i_1}(A_j)=\beta \frac{v_{i_2}}{1+\phi (a_{i_2})}(\phi (a_{i_1})-\phi (A_j)),\beta \le 1$ if the delivered availability $A_j$ is lower than the desired availability $a_{i_1}$.
• With the probability $1-\mu$, we run Auction B: according to the value density $\frac{v_i}{n_i(1+\phi (a_i))}$, we allocate the VMs to the users based on a greedy approach with respect to the value density of users until there is no sufficient capacity, and the payment of each i is $p_i=x_i·n_i(1+\phi (a_i))\rho$, where $\rho$ = $\frac{v_k}{n_k(1+\phi (a_k))}$ is the highest value density with which the user loses the allocation in Auction B. The service credit for user i is $S{C}_{a_i}^i(A_j)=\beta \rho n_i(\phi (a_i)-\phi (A_j)),\beta \le 1$ if the delivered availability $A_j$ is lower than the desired availability $a_i$.

In this mechanism, $\beta$ is a penalty coefficient selected by cloud provider. Generally, increasing $\beta$ can attract more users, but it will raise the penalty cost. How to choose $\beta$ is another important problem, but it is not involved in our work. To prove the truthfulness of the auction mechanism in Algorithm 2, we first obtain the following two lemmas.

Lemma 1.

Auction A is truthful.

Proof of Lemma 1.

First, we consider the case without service credit. According to the allocation algorithm of Auction A, given bids of the other users, the user with type $(n_i^{\prime },a_i^{\prime },v_i^{\prime })$ can win allocation for any $n_i^{\prime }\le n_i$, $a_i^{\prime }\le a_i$ and $v_i^{\prime }>v_i$, if she wins allocation with type $(n_i,a_i,v_i)$. Let $o_i=(n_i,a_i)$. Define a partial-order ⪯ on $o_i$:

$$o_i^{\prime }⪯o_i\equiv (n_i^{\prime }\le n_i)\wedge (a_i^{\prime }\le a_i).$$

It satisfies the monotonicity shown in Theorem 1.

Let $i_1$ be the bidder with the highest value of $\frac{v_i}{1+\phi (a_i)}$, and $i_2$ the second highest one. The critical value for winner $i_1$ is $\frac{v_{i_2}}{1+\phi (a_{i_2})}(1+\phi (a_{i_1}))$. According to Theorem 1, it is truthful without service credit.

Next, we prove that Auction A satisfies the service credit $S{C}_{{\widehat{a}}_i}(a_i)$ being less than $p_i(({\widehat{n}}_i,{\widehat{a}}_i,{\widehat{v}}_i),{\widehat{b}}_{-i})-p_i(({\widehat{n}}_i,a_i,{\widehat{v}}_i),{\widehat{b}}_{-i})$, for any ${\widehat{n}}_i,{\widehat{v}}_i,{\widehat{b}}_{-i}$ and ${\widehat{a}}_i>a_i$.

Assume that the winner i, whose requested availability ${\widehat{a}}_i$ is larger than $a_i$ has run defective software that reduced the delivered availability to her desired availability $a_i$. In Line 7 of Algorithm 2, the service credit $S{C}_{{\widehat{a}}_i}(a_i)=\beta \frac{v_{i_2}}{1+\phi (a_{i_2})}(\phi ({\widehat{a}}_i)-\phi (a_i)),{\widehat{a}}_i>a_i,\beta \le 1$. We have that

$$\begin{array}{cc}\hfill S{C}_{{\widehat{a}}_i}(a_i)& =\beta \frac{v_{i_2}}{1+\phi (a_{i_2})}((1+\phi ({\widehat{a}}_i))-(1+\phi (a_i)))\hfill \\ & =\beta (p_i(({\widehat{n}}_i,{\widehat{a}}_i,{\widehat{v}}_i),{\widehat{b}}_{-i})-p_i(({\widehat{n}}_i,a_i,{\widehat{v}}_i),{\widehat{b}}_{-i}))\hfill \\ \hfill & \le p_i(({\widehat{n}}_i,{\widehat{a}}_i,{\widehat{v}}_i),{\widehat{b}}_{-i})-p_i(({\widehat{n}}_i,a_i,{\widehat{v}}_i),{\widehat{b}}_{-i}).\hfill \end{array}$$

(2)

According to Theorem 4, Auction A is truthful. ☐

Algorithm 2: Auction for private availability: RandomGreedy.

Lemma 2.

Auction B is truthful.

Proof of Lemma 2.

First, we still consider the case without service credit. The analysis of monotonicity is similar to that of Auction A. According to the allocation algorithm of Auction B, given bids of the other users, the user with type $(n_i^{\prime },a_i^{\prime },v_i^{\prime })$ can win allocation for any $n_i^{\prime }\le n_i$, $a_i^{\prime }\le a_i$ and $v_i^{\prime }>v_i$, if she wins allocation with type $(n_i,a_i,v_i)$. Thus, it satisfies monotonicity.

The payment $p_i=\rho n_i(1+\phi (a_i))$ is the critical value which makes i win allocation, where $\rho =\frac{v_k}{n_k(1+\phi (a_k))}$ is the highest value density among losers. Thus, Auction B is a truthful mechanism if all users are healthy.

Next, we discuss the possible utility of an unhealthy winner. As discussed above, assume that a winner i has reduced the availability from requested availability ${\widehat{a}}_i$ to her desired availability $a_i({\widehat{a}}_i>a_i)$. In Line 22 of Algorithm 2, the service credit in such case is $S{C}_{{\widehat{a}}_i}(a_i)=\beta \rho (({\widehat{n}}_i,{\widehat{a}}_i,{\widehat{v}}_i),{\widehat{b}}_{-i}){\widehat{n}}_i(\phi ({\widehat{a}}_i)-\phi (a_i)),{\widehat{a}}_i>a_i$.

Give any ${\widehat{n}}_i,{\widehat{v}}_i,{\widehat{b}}_{-i}$, obviously, we have $\rho (({\widehat{n}}_i,{\widehat{a}}_i,{\widehat{v}}_i),{\widehat{b}}_{-i})\ge \rho (({\widehat{n}}_i,a_i,{\widehat{v}}_i),{\widehat{b}}_{-i})$, which implies that the price of unit resource when the user requests higher availability ${\widehat{a}}_i$ is not less than that of when she requests her desired availability $a_i$. Then, we have that

$$\begin{array}{cc}\hfill S{C}_{{\widehat{a}}_i}(a_i)& =\beta \rho (({\widehat{n}}_i,{\widehat{a}}_i,{\widehat{v}}_i),b_{-i}){\widehat{n}}_i(\phi ({\widehat{a}}_i)-\phi (a_i))\hfill \\ \hfill & \le \rho (({\widehat{n}}_i,{\widehat{a}}_i,{\widehat{v}}_i),{\widehat{b}}_{-i}){\widehat{n}}_i(1+\phi ({\widehat{a}}_i))-\rho (({\widehat{n}}_i,{\widehat{a}}_i,{\widehat{v}}_i),b_{-i}){\widehat{n}}_i(1+\phi (a_i))\hfill \\ \hfill & \le \rho (({\widehat{n}}_i,{\widehat{a}}_i,{\widehat{v}}_i),{\widehat{b}}_{-i}){\widehat{n}}_i(1+\phi ({\widehat{a}}_i))-\rho (({\widehat{n}}_i,a_i,{\widehat{v}}_i),b_{-i}){\widehat{n}}_i(1+\phi (a_i))\hfill \\ \hfill & =p_i(({\widehat{n}}_i,{\widehat{a}}_i,{\widehat{v}}_i),{\widehat{b}}_{-i})-p_i(({\widehat{n}}_i,a_i,{\widehat{v}}_i),{\widehat{b}}_{-i}).\hfill \end{array}$$

According to Theorem 4, Auction B is truthful. ☐

Theorem 5.

The mechanism in Algorithm 2 is universally truthful.

Proof of Theorem 5.

The auction is a probabilistic combination of two auctions. According to Lemmas 1 and 2, since both the auctions are truthful, we can draw the conclusion. ☐

Theorem 6.

Let $\frac{1+\phi (A_L)}{1+\phi (A_1)}=\gamma ,\gamma >1$. Choosing $\mu =\frac{\gamma }{1+\gamma }$, the approximation ratio of Algorithm 2 is at most $\frac{1}{1+\gamma }$.

Proof of Theorem 6.

In Algorithm 2, $i_1$ is the user with highest value of $\frac{v_i}{1+\phi (a_i)}$. Thus, for any $i^{\prime }\ne i_1$, it satisfies $\frac{v_{i_1}}{1+\phi (a_{i_1})}\ge \frac{v_{i^{\prime }}}{1+\phi (a_{i^{\prime }})}\ge \frac{v_{i^{\prime }}}{1+\phi (A_L)}$. So, $v_{i_1}\ge \frac{v_{i^{\prime }}(1+\phi (a_{i_1}))}{1+\phi (A_L)}\ge \frac{v_{i^{\prime }}(1+\phi (A_1))}{1+\phi (A_L)}$.

Let $V_{opt}$ be the optimal valuation. If ${\max }_i{v}_i=\alpha ·V_{opt}$, the valuation obtained by Auction A is larger than $\alpha ·V_{opt}·\frac{1+\phi (A_1)}{1+\phi (A_L)}=\frac{\alpha V_{opt}}{\gamma }$.

In addition, the valuation obtained by Auction B in Algorithm 2 is more than $(1-\alpha )·V_{opt}$. The total expected social welfare is at least

$$\mu \frac{\alpha V_{opt}}{\gamma }+(1-\mu )(1-\alpha )V_{opt}.$$

Substituting $\mu$ with $\frac{\gamma }{1+\gamma }$ and simplifying, the above expression is $\frac{V_{opt}}{1+\gamma }$. We can have that the approximation ratio is at most $\frac{1}{1+\gamma }$. ☐

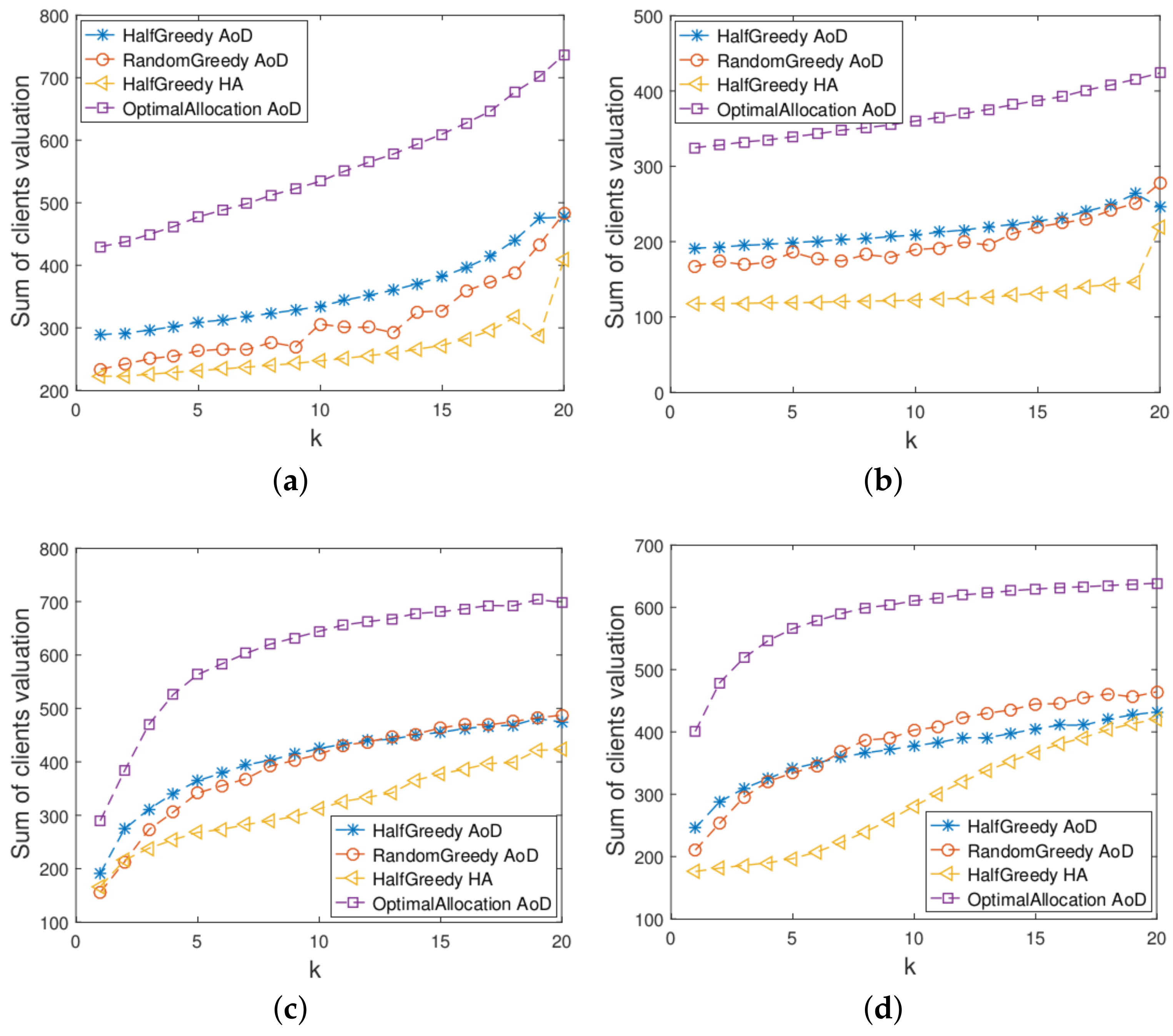
4. Experiment Results

In this section, we evaluate the performance including social welfare and service credits of our proposed mechanisms for availability on demand. We compare four mechanisms: (1) Half Greedy Auction with availability on demand; (2) Random Greedy auction with availability on demand; (3) Half Greedy Auction with highest availability; and (4) Optimal allocation with availability on demand.

• Half Greedy Auction with availability on demand (HalfGreedy AoD) is our proposed deterministic mechanism, which is a truthful mechanism if the availability is public information or all users are healthy.
• Random Greedy Auction with availability on demand (RandomGreedy AoD) is our proposed nondeterministic mechanism, which is truthful mechanism even if users might be unhealthy.
• Similar to the mechanism proposed by [16], Half Greedy Auction with highest availability (HalfGreedy HA) is the benchmark allocation without considering user-selection availability. Different from HalfGreedy AoD, this allocation provisions the highest availability for all users.
• Optimal allocation with availability on demand (OptimalAllocation AoD) is the benchmark allocation mechanism without considering the strategies of users. Since the optimization problem is a well-known NP-hard problem in this scenario, we obtain a relaxed optimal solution by allowing fraction allocation and using a greedy algorithm.

To evaluate the performance in various scenarios, we generate test data with different distributions as shown in

Table 1. Parameter distribution in data settings.

Data Setting	Resource Demand ${\mathit{n}}_{\mathit{i}}$	Availability on Demand ${\mathit{a}}_{\mathit{i}}$	Unit Resource Valuation ${\mathit{v}}_{\mathit{i}}$
DS1	uniform distribution	uniform distribution	uniform distribution
	in [1,C/k]	in $[A_1,A_2,\dots ,A_L]$	in [0,1]
DS2	uniform distribution	uniform distribution	Gaussian Distribution
	in [1,C/k]	in $[A_1,A_2,\dots ,A_L]$	with $\mu =0.5,\sigma =0.5$
DS3	Exponential Distribution	uniform distribution	uniform distribution
	$\lambda =k·100/C$	in $[A_1,A_2,\dots ,A_L]$	in [0,1]
DS4	Exponential Distribution	uniform distribution	Gaussian Distribution
	$\lambda =k·100/C$	in $[A_1,A_2,\dots ,A_L]$	with $\mu =0.5,\sigma =0.5$

. In Data settings DS1 and DS2, the resource demand $n_i$ follows uniform distribution in $[1,C/k]$, and the valuation for unit resource follows uniform distribution in [0,1] in DS1 and Gaussian distribution with expectation $\mu =0.5$, standard deviation $\sigma =0.5$ in DS2. In Data settings DS3 and DS4, the resource demand $n_i$ follows exponential distribution with parameter $\lambda =k·100/C$, and the valuation for unit resource follows uniform distribution in [0,1] in DS3 and Gaussian distribution with expectation $\mu =0.5$, standard deviation $\sigma =0.5$ in DS4. In the experiments, we select $C=1000$, and change the parameter k from 1 to 20.

Assume that each user has a job to be processed in the cloud, and each job consists of multiple tasks. Similar to the description in [13], in our experiments, the users’ options of availability can be as follows:

• No Backup: This option does not use any high availability techniques.
• Random-k Backup: Under this option, the cloud provider will use the Active/Active (AA) technique to improve the availability of the jobs: for each task, it will have a k% (i.e., 30) probability to add an AA backup task that runs for the entire duration of the job (each task corresponds to a virtual machine).
• Active/Active Backup : Under this option, the cloud provider will use the Active/Active (AA) backup for the tasks.

Since the objective of our work is to maximize the social welfare (the sum of users’ valuation), firstly we compare the social welfare obtained by four approaches under different data settings. The experiment results are shown in Figure 3. The value of the y-axis is the sum of the users’ valuation, and the value of the x-axis is the parameter k that changes the distribution of requested number $n_i$ shown in Table 1. Each point in the Figure 3 is the average social welfare obtained by 10,000 random experiments.

This shows that our proposed mechanisms with availability on demand always obtain higher total valuation than the mechanism with highest availability. Comparing HalfGreedy AoD to RandomGreedy AoD, we can see that the social welfare of the former is better than that of the latter when the k is small. It is worth noting that the maximal resource demand of a single user rises if k rises. With the rising of k, the difference of performances between HalfGreedy AoD and RandomGreedy AoD mechanisms decreases. It implies that RandomGreedy AoD also has a higher social welfare and even exceeds HalfGreedy AoD when there is some user with a larger number of requested resources.

Next, we will compare the possible service credits and increased payment brought by an unhealthy strategy in RandomGreedy AoD. The unhealthy strategy is that user i requests the availability ${\widehat{a}}_i$ and runs defective software to reduce the availability from requested availability ${\widehat{a}}_i$ to desired availability $a_i({\widehat{a}}_i>a_i)$, resulting in service credit. Firstly, we randomly choose one user who can be served when she truthfully reports the desired availability and valuation. Then, keeping the bids of others unchanged, we raise the requested availability of the user, and calculate the new payment and service credit if she adopts an unhealthy strategy, until she cannot be served. The experiment is respectively repeated 20 times in four data settings. All of the experiment results show that each user cannot improve utility by adopting an unhealthy strategy.

Table 2. The comparison of increased payment and service credit caused by misreporting availability.

Backup Ratio	Served or Not	Payment	Increased Payment	Service Credit
0.1	Yes	82.6717	0	0
0.2	Yes	89.7892	7.1175	7.1175
0.3	Yes	99.3982	16.7265	14.6010
0.4	Yes	106.6987	24.0270	21.9014
0.5	Yes	117.2437	34.5720	30.0330
0.6	No	0	0	0

shows one of the experiment results. The backup ratio corresponding to the true availability in the experiment is 0.1. Then, the user raises her requested availability to obtain both the valuation and service credit by adopting an unhealthy strategy. We choose penalty coefficient $\beta =1$, which is the maximal service credit in our mechanism. However, on the other hand, requesting higher availability also results in higher payment in our mechanism. Table 2 compares the increased payment and service credit when the user adopts that strategy. In the table, “Backup ratio” corresponds to requested availability, and the higher the requested availability is, the higher the backup ratio is; “Served or not” presents whether the user can be served if the requested availability increases; “Increased payment” presents the difference of payment with requested availability and desired availability; “Service credit” is the penalty brought by the unhealthy strategy.

In Table 2, we can see that the user will lose the allocation if she increases her requested availability and makes the backup ratio be larger than 0.6. It is because the value density of the user decreases when she raises the requested availability. Furthermore, for each backup ratio in which the user can be served, the service credit is always no more than the increased payment, which implies that the user cannot improve utility by adopting unhealthy strategies. Thus, in our mechanism, each user will truthfully request the desired availability even if the availability is private information for users.

5. Conclusions

To reduce providers’ costs and improve the sum of users’ valuation (social welfare), we proposed resource pricing and penalty mechanisms based on auctions. In our mechanisms, we allow users to request their desired availability, and allocate resources with availability on demand. Considering intelligent and rational users, we designed two mechanisms: a deterministic HalfGreedy AoD mechanism for a public availability scenario and a nondeterministic RandomGreedy AoD mechanism for a private availability scenario. The experiment results showed that our mechanisms have higher social welfare than the HalfGreedy with highest availability.

However, this is only an initial work in exploring resource allocation, pricing and penalty mechanism design in the user-selected availability scenario, and there are also some problems that need to be solved. Since, in our work, the desired availability of each user is fixed and it only deals with single time resource allocation. In the future work, we will focus on resource pricing and penalty in the online and dynamic user-selected availability environment.