Next Article in Journal
Random Linear Network Coding for 5G Mobile Video Delivery
Previous Article in Journal
IPv6 Convergence for IoT Cyber–Physical Systems
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Information
Volume 9
Issue 4
10.3390/info9040071
information-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Characteristics and Classification of Topological Spatial Relations in 3-D Cadasters

by
Lili Fu
1,
Pengcheng Yin
2,
Gang Li
1,*,
Zhifeng Shi
3,
Youzhi Liu
3 and
Jiyi Zhang
3
1
School of Environmental Science and Spatial Informatics, China University of Mining and Technology, Xuzhou 221008, China
2
Bureau of Land and Resources of Xuzhou, Xuzhou 221006, China
3
Bureau of Land and Resources of Xinyi, Xuzhou 221400, China
*
Author to whom correspondence should be addressed.
Information 2018, 9(4), 71; https://doi.org/10.3390/info9040071
Submission received: 12 February 2018 / Revised: 18 March 2018 / Accepted: 22 March 2018 / Published: 27 March 2018
Browse Figures
Versions Notes

Abstract

:
The application of a 3-D topology to cadasters is becoming increasingly important as 3-D cadasters continue to develop and cadastral data applications increase. This study discusses spatial topological relations related to 3-D cadasters, the geometric objects used in 3-D cadastral spatial modelling, and the characteristics of the spatial data. The characteristics of the topological relations for a 3-D cadaster are summarized, and a classification method is proposed. Research on the classification of topological spatial relations in 3-D cadasters provides guidance for the analysis and computation of the topological spatial relations, changing of cadastral parcels, and topological consistency in cadastral spatial data.

1. Introduction

Topological relation analysis for cadasters involves the application of traditional topological spatial analysis to cadastral spatial objects. Because of the expanding use of cadasters, cadastral topological spatial analysis has become increasingly important [1,2,3,4,5]. Many studies have been conducted on topological relations for cadastral spatial objects using standard topological spatial analysis [6,7,8,9,10,11,12]. Zhou et al. extended the four-intersection model to a double four-intersection model that is applicable to 2-D cadastral topological relations. This method can represent 31 topological spatial relations, both simple and complex [13]. Using the double four-intersection model with the software Oracle Spatial and its spatial relationship query functions, Zhou et al. identified 31 topological spatial relations among cadastral zones [14]. Xu et al. classified topological relations among 2-D cadastral objects and studied the classes of cadastral parcel alterations and the changes in the topological relations resulting from these alterations based on the topological relations among the objects [15]. Ye proposed a logic model for 2-D cadastral spatial objects based on the nine-intersection model by analyzing the boundary points and segments and the topological relations among parcels in a 2-D cadaster [16]. Based on the Boolean operation of cadaster objectives, Zhou et al. investigated a computational method for topological relations of cadastral objects based on Voronoi zones and Euler numbers [17]. This method was applied to updates of a cadastral database. Shi studied the basic topological relations among points, curves, triangles, and tetrahedrons in 3-D cadasters [18].
In general, previous research on cadastral topological spatial relations has focused on 2-D cadasters and not 3-D cadasters. Since the 3-D cadaster register demand is increasing, a specific international standard, Land Administration Domain Model (LADM), is proposed to guide worldwide cadastral development [19]. Worldwide researchers and cadastral department managers have made lots of efforts to develop a feasible 3-D cadastral solution [20,21,22,23,24,25,26,27,28,29]. These research results can be divided into three categories as following: cadastral registration system model, legal framework, and technical implementation. However, few studies have examined the topological spatial relations in 3-D cadasters which is one of the essential factor for 3-D cadastral objects’ validation and representation. The topological analysis of 3-D cadasters is an application of 3-D topological spatial analysis to cadastral management. Therefore, the characteristics of the 3-D cadastral data should be taken into consideration in a topological analysis of a 3-D cadaster. Identifying the topological spatial relations in 3-D cadasters allows for more efficient access, storage, and updating of 3-D cadastral data and greater use of cadastral data in the design of cities, intelligent transportation systems, and underground pipeline systems. Consequently, public works and economic development projects could make greater use of 3-D cadasters and thus expand the use of cadasters.
This study investigates the unique characteristics of the topological relations in 3-D cadastral data and a classification method for 3-D cadastral topological relations. The topological relations are classified and grouped based on the dimensional characteristics of the 3-D cadastral data.

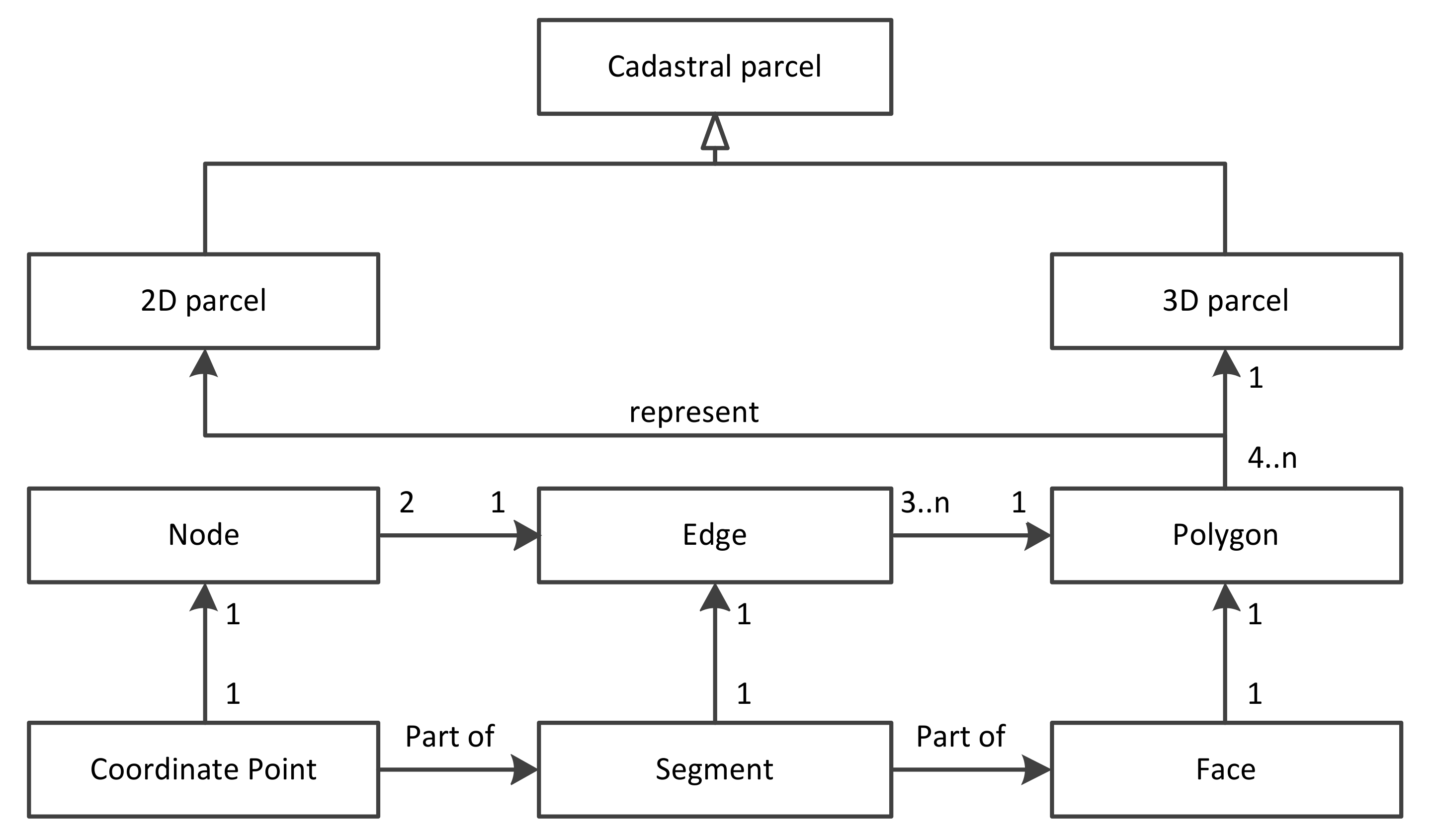
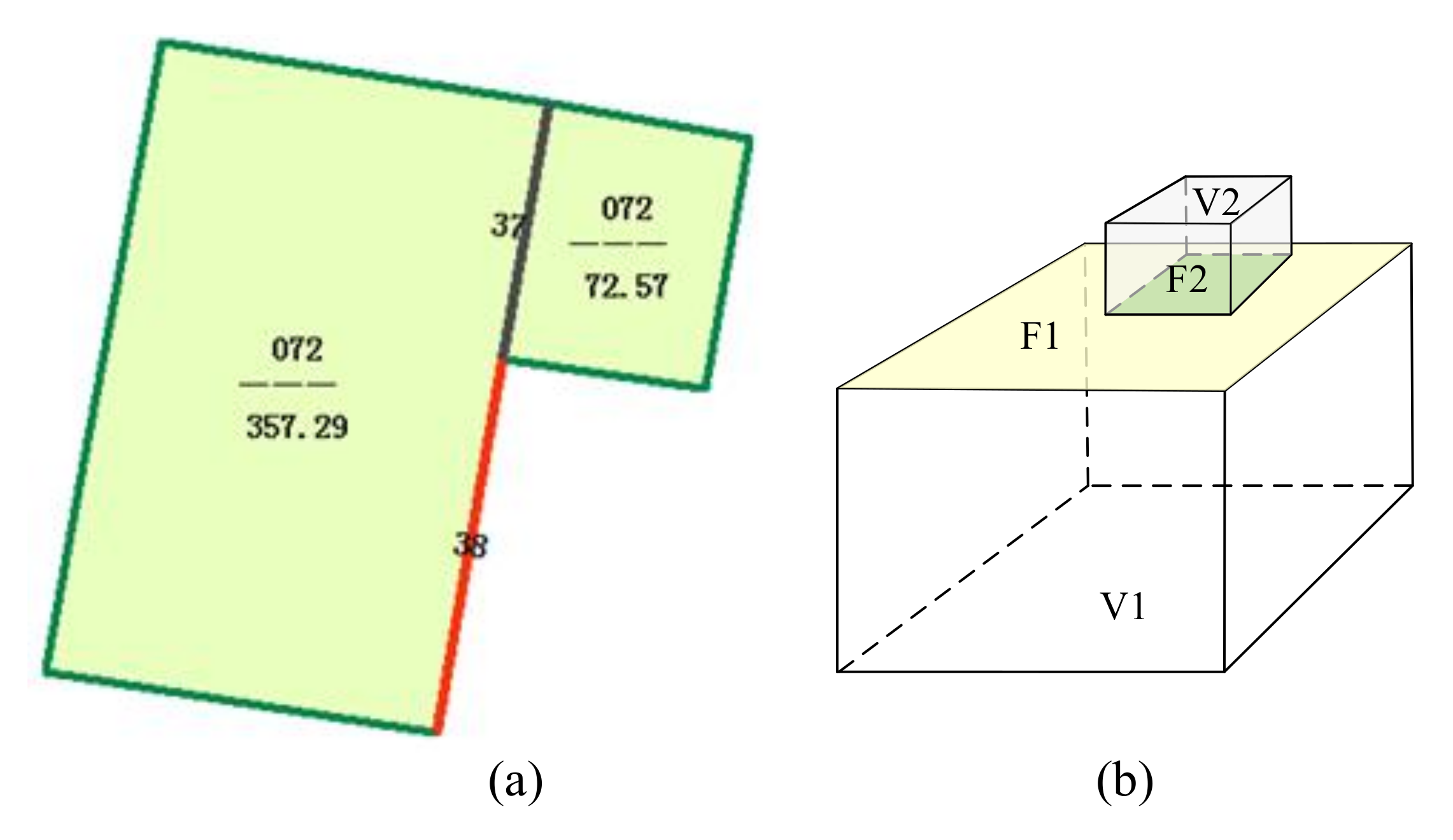
2. Characteristics of 3-D Cadastral Data

A traditional 2-D cadastral parcel within a 3-D cadastral space is referred to as a parcel face, and a 3-D cadastral object is referred to as a parcel solid. A cadastral parcel includes both a 2-D parcel face and a 3-D parcel solid. The parcel solid is the basic management unit of a 3-D cadaster. The parcel solid has a fixed spatial location and shape and is a closed and independent 3-D space with property rights in a legally recognized boundary. A solid is a combination of a physical building entity and an area with legally recognized ownership that does not depend on the ground face. Ownership of a cadastral parcel is not divisible; i.e., ownership within a cadastral parcel is consistent. The boundary of ownership is the primary basis by which cadastral parcels are separated.
The relationship among geometric elements and their topological equivalents in 3-D cadastral space is shown in Figure 1. The geometric objects that delineate a cadastral parcel include boundary points with coordinate, boundary segments, boundary faces, and parcel solids. The boundary face can not only represent a 2-D cadastral face but also define the ownership boundary of a 3-D cadastral parcel. Node, edge, and polygon are the basic topological elements. It should be noted that the segment in Figure 1 is equivalent to the LA_BoundaryFaceString class and the face is equivalent to the LA_BoundaryFace.
The geographic information in the cadastral data is used to identify and maintain the ownership of the relevant rights holder. Therefore, the representation of cadastral parcels and the topological relations must clearly and accurately describe the boundaries and the ownership of the parcels so that the legal rights of the rights holders can be protected. This requirement results in significant differences between the topological spatial relations in a 3-D cadaster and those in a simple 3-D space. For example, the isolated point and segment shown in Figure 2 are not allowed in 3-D cadastral data. The isolated point does not belong to any boundary segments, boundary faces, or parcel solids, the isolated segment does not belong to any boundary faces or parcel solids, and the isolated face is neither an independent 2-D boundary face nor a part of any 3-D parcel solid. In addition, to clearly define the ownership boundaries of each parcel, an element that intersects two parcels must be divided where it crosses the boundary, as shown in Figure 3.
These characteristics of cadastral data ensure that in a 3-D cadastral database, the ownership boundaries between parcels are clear and unique and no isolated cadastral elements exist independently from cadastral parcels. The geometric elements used to define cadastral parcels can occur only on the cadastral boundaries, and no isolated cadastral elements can exist independently within cadastral parcels. Therefore, two inferences can be made: (a) Because isolated cadastral boundary objects do not exist within the parcels of a 3-D cadaster, the topological relations among the objects within a 3-D cadaster in fact reflect the topological relations among the elements on the ownership boundaries; (b) Cadastral parcels are a complete division of the cadastral space; thus, ownership of cadastral parcels does not overlap, and no gaps exist between neighboring parcels, which are standard requirements in cadastral management.

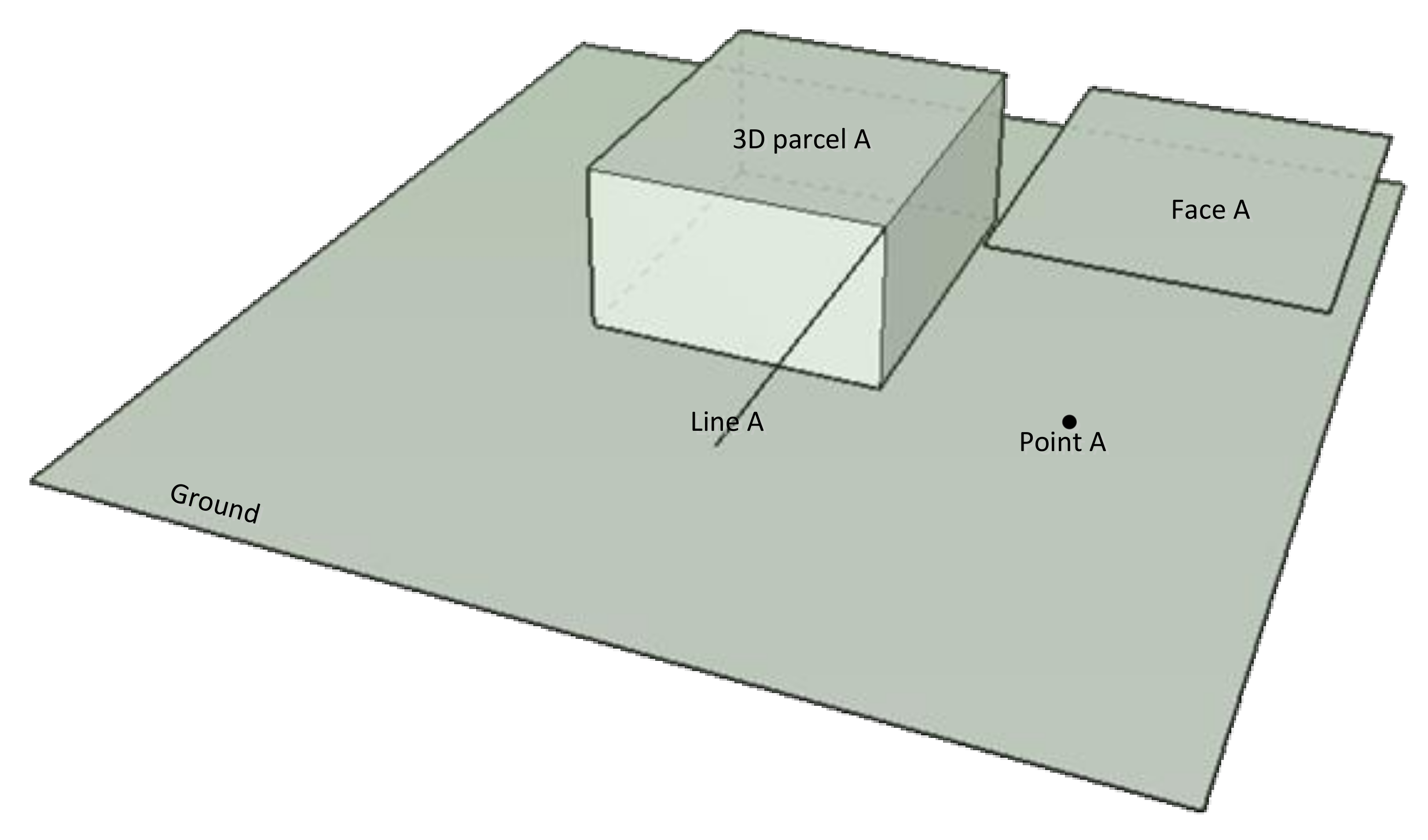
3. Topological Relations in 3-D Spaces

Topological relations can be represented in two ways: an intersection model based on the point-set topology and the region connection calculus (RCC) model based on spatial calculation. The RCC model can represent topological relations among objects within a region. However, this model is restricted to simple spatial objects and is not applicable to a topological analysis in 3-D space. Intersection models based on the point-set topology include mainly the four-intersection model, the nine-intersection model, and the 3-D point-set intersection model. In the four-intersection model, the topological relations among objects are determined by comparisons between the boundaries and the interior spaces of the objects. This model can effectively represent topological relations among 2-D objects, but it cannot effectively represent topological relations among 3-D objects. To expand the domain of topological relations that can be represented, Egenhofer and Herring included the exterior spaces of spatial objects and extended the four-intersection model to create the nine-intersection model, which consists of the intersections of the boundaries and the interior and exterior spaces of spatial objects [30]. Although both the four- and nine-intersection models can qualitatively describe topological relations, neither model can effectively identify the dimensions of the intersections. Clementini et al. proposed the dimensionally extended nine-intersection model, which classifies the topological relations among spatial objects based on the dimensions of the intersections [31]. Using the topological relations among 3-D points, segments, faces, and solids, Zlatanova identified 159 3-D spatial topological relations [32]. Zhang et al. analyzed the topological relations among 3-D points, segments, faces, and solids and simplified the nine-intersection model in 3-D space by excluding impossible topological relations [33].

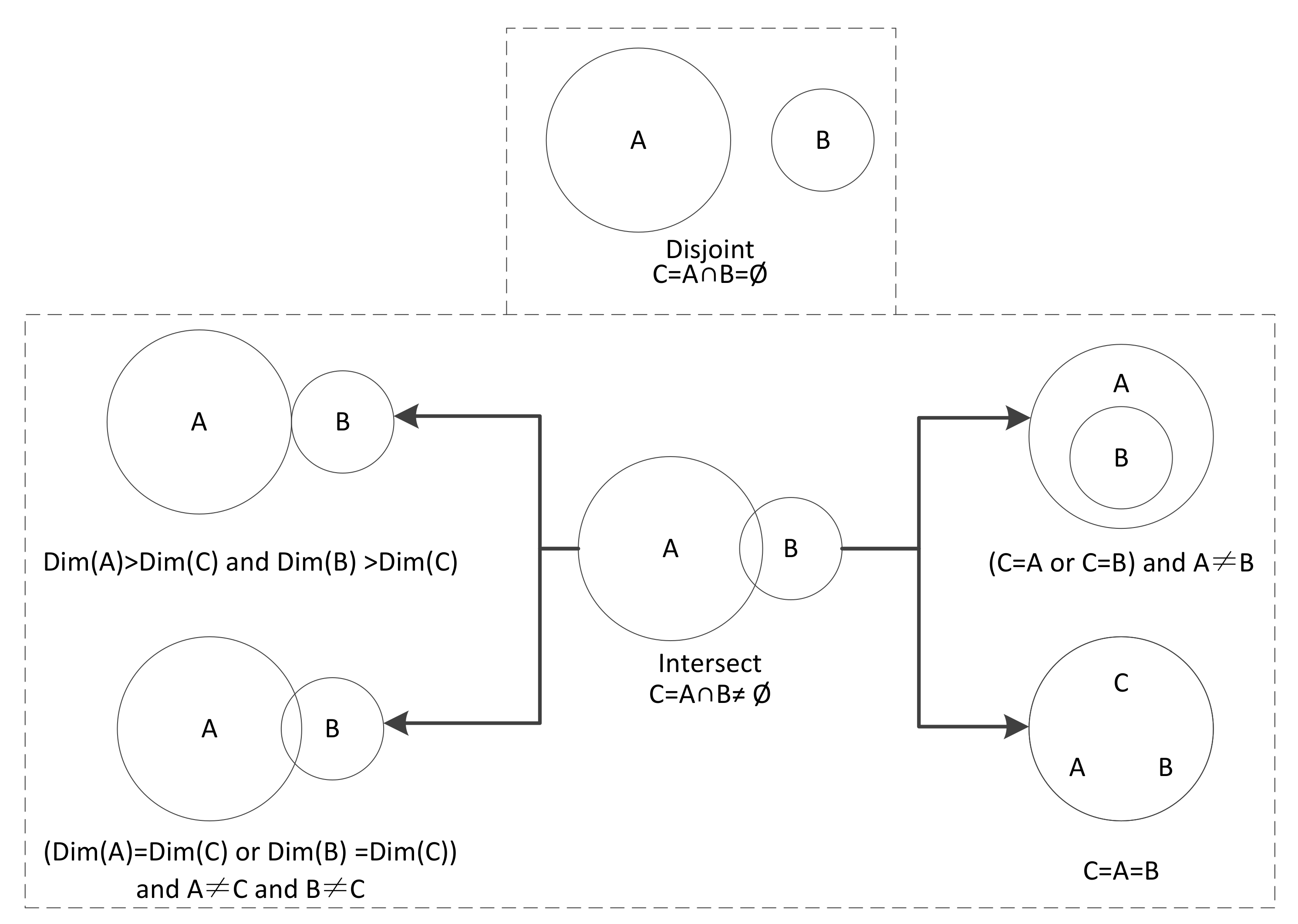
4. Classification of 3-D Cadastral Topological Relations

Although various methods have been proposed for representing topological relations, these relations can be categorized into one of two classes (disjoint and intersect) based on whether the spatial objects intersect. The intersect class can be further divided into the subclasses touch, overlap, contain, or equal. Figure 4 illustrates the various classes of topological relations among spatial objects.
Cadastral topological relations are traditional topological relations applied to cadastral management. The topological relations in 3-D cadasters can be separated into the disjoint and intersect classes based on whether the objects intersect. Since overlaps are not allowed in cadastral management, the intersect class of topological relations in a cadastral space does not include the overlap or contain subclasses; only the touch and equal subclasses are valid. The cadastral topological relation classes are illustrated in Figure 4. Because of the unique characteristics of cadastral spatial data shown in Figure 5, there are fewer topological relations in 3-D cadasters (only disjoint, touch, and equal) than in a general 3-D space, and the relations are less complex.
The topological relations for the various geometric objects in 3-D cadasters are shown in Table 1. Disjoint relations can exist between all types of objects, touch relations can exist between objects with different dimensions, and equal relations can occur between objects with the same dimension.
In cadastral management, to obtain an accurate description of the spatial relations among the parcels, it is necessary to determine whether the cadastral objects share points, lines, or faces. Two cadastral objects A and B share points when A and B both contain the same point. Objects A and B share lines when A or an element of A exists on the extension of one segment of B or vice versa. Objects A and B share faces when A or an element of A exists on the extension of one face of B or vice versa. The topological relations of disjoint and touch in 3-D cadastral space can be categorized from the perspective of whether exist the share elements. Theoretically, there are four disjoint types between two cadastral objects: share a line and a face (LFD), only share a line (LNFD), only share a face (NLFD) and have no share elements (NLNFD). These disjoint relations are illustrated in Table 2. The touch relation between two cadastral objects include seven categories in theory: touch by a point and share a line and a face at the same time (PLFT), touch by a point and only share a face (PNLFT), touch by a point and only share a line (PLNFT), touch by a point with no share parts (PNLNFT), touch by a line and share a face (LFT), touch by a line and with no share faces (LNFT), touch by a face (FT). All those touch relations are illustrated in Table 3.
It should be noted, however, that the above disjoint and touch relations do not exist in all cadastral objects. Two cadastral objects can share points, lines, or faces only if the sum of the dimensions of the two objects is greater than the dimension of the shared element. For example, the sum of the dimensions of two points is two, so there can be no shared segments. Similarly, the sum of the dimensions of a point and a segment is three, so the two elements cannot share a face; a shared face is possible only if the sum of the dimensions of two cadastral objects is greater than three.
According to whether the cadastral objects share points, lines, or faces, as illustrated in Table 2, the disjoint topological relation class in 3-D cadastral spaces includes 30 types, which are shown in Table 4. It follows that a shared-point disjoint relation cannot exist. Therefore, in the analysis of cadastral disjoint relations, only shared lines and shared faces must be considered. The analysis for this type proceeds as follows. (1) If the object with the higher dimension is a face or a solid, the possibilities of a shared line and a shared face are considered. If the object with the higher dimension is a segment, only a shared line is possible. (2) After the object with the higher dimension is determined, if the other object is a point or a segment, then there is no possibility of a shared face, only a shared line. If the other object is not a point or a segment, then the possible crossing of a shared face and a shared line must be considered. (3) If both objects are points, then there is only one disjoint relation.
Similarly, the touch topological relation class includes 30 types, which are defined according to whether the cadastral objects share points, lines, or faces, as shown in Table 5. The touch relation cannot exist between two points, and a point object can have a touch relation with shared points in other objects. The touch relation between two segments is manifested as a shared point, and two segments with a shared point must be on a shared face. Thus, relations between two segments can exist only where there are shared lines. A touch relation between a segment and a face can exist only when there is a shared point. In addition, if a segment and a face are touching with only a shared point (no shared face), there must be no shared lines because two segments with shared lines and shared points must share a face, which contradicts the premise that there is no shared face. Therefore, one of three possible touch relations may exist between a segment and a face. Topological relations between two faces include touch relations with shared points and with shared lines, for which there are four cases with shared points and two cases with shared lines. Since the touch relations between 3-D cadastral objects normally involve the surfaces of the objects, the types of relations include shared faces in addition to the six relations between faces. Since the touch relations between 3-D cadastral objects primarily involve surfaces, the touch relations between segments and faces or solids are identical. Similarly, the touch relations between two faces and between faces and solids are identical.

5. Discussion

Characteristics and classification of topological spatial relations research in 3-D cadastral space is important for verifying topological consistency of 3-D cadastral data which concern the cadastral database quality and efficiency. An important component of verifying topological consistency of 3-D cadastral data is the spatial topology inspection. The differences among requirements for different cadastral software, cadastral data organizations and expressions, cadastral data acquisition precisions, and technical methods leads to the difficulty making universal and efficient topological validation rules for cadastral data. Problems in a cadastral database including redundant, repetitive, or unnecessary processing are highly related to topological validation rules. Topological relations categories research in cadastral space will make the way of cadastral data organization more reasonable, which will be beneficial to improve the efficiency of cadastral data retrieval and analysis and formulate efficient validation rules. Studying the topological relations in 3-D cadasters not only advances the development of 3-D cadasters but also broadens the possible applications of 3-D cadastral spatial data. The topological relations in 3-D cadasters can provide a means to assess the consistency of the spatial data and improve the efficiency and the accuracy of an assessment. Furthermore, a clear classification of the topological relations in 3-D cadasters is essential for performing queries and analysing topological relations in 3-D cadasters.

6. Conclusions

This study examined the characteristics and the classification of topological spatial relations in 3-D cadasters. The characteristics of the topological spatial relations in 3-D cadasters were analyzed within the constraints of cadastral management and 3-D cadastral spatial data. The topological spatial relations for 3-D cadasters can be classified as either disjoint or intersect depending on whether the cadastral objects intersect. Intersect relations include several types. The topological spatial relations for 3-D cadasters can be classified as disjoint, touch, or equal. There are 30 specific types in each of the disjoint and touch relation classes.
The research results in this paper can be used to design a computational framework for topological relations and conduct spatial analyzation in 3-D cadastral space. Future research can be carried out in the following directions: 3-D cadastral topological relation computation, geometrical and topological validation for 3-D cadastral objects, 3-D cadastral objects visualization based on topological relations, and so on.

Acknowledgments

This work was supported by China Land Surveying and Planning Institute Outsourcing Project (grant No. 5P147782), surveying and mapping Geographic Information Research Foundation of Jiangsu Province (grant No. JSCHKY201711). The authors also wish to thank the editors and reviewers for their interesting and constructive comments.

Author Contributions

All six authors have contributed to the work presented in this paper. Lili Fu, Pengcheng Yin, and Gang Li constructed the overall framework for 3-D cadastral topological spatial relations. Youzhi Liu, Jiyi Zhang, and Zhifeng Shi contributed in the discussion section. All authors worked collaboratively on writing this paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Guo, R.Z.; Ying, S.; Li, L. Automatic Construction of 3-D Valid Solids for 3-D Cadastral Objects Based on Facet Sets. Acta Geod. Cartogr. Sin. 2012, 41, 620–626. [Google Scholar]
  2. He, B.; Li, L.; Guo, R.Z.; Shi, Y. 3-D Topological Reconstruction of Heterogeneous Buildings Considering Exterior Topology. Geomat. Inf. Sci. Wuhan Univ. 2011, 36, 579–583. [Google Scholar]
  3. Li, L.; Zhao, Z.G.; Guo, R.; He, B. 3-D Topological Construction for Spatial Physical Object. Geomat. Inf. Sci. Wuhan Univ. 2012, 37, 719–723. [Google Scholar]
  4. Shi, Y.F.; He, B. Research and Implementation of a Three Dimensional Cadastral Spatial Topology Data Model. Sci. Surv. Mapp. 2013, 38, 12–14. [Google Scholar]
  5. Shi, Y.F.; Zhang, L.L.; He, B. A 3-D Cadastral Space Consolidation and Segmentation Algorithm Based on a Topological Data Model. Sci. Surv. Mapp. 2013, 38, 106–109. [Google Scholar]
  6. Egenhofer, M.; Franzosa, R.D. Point-set topological spatial relations. Int. J. Geogr. Inf. Syst. 1991, 5, 161–174. [Google Scholar] [CrossRef]
  7. Chen, J.; Li, C.; Li, Z.; Gold, C. A Voronoi-based nine-intersection model for spatial relations. Int. J. Geogr. Inf. Sci. 2001, 15, 201–220. [Google Scholar] [CrossRef]
  8. Deng, M.; Zhang, X.S.; Lin, Z.J. Modeling Topological Relations Based on Euler Characteristics. Geomat. Inf. Sci. Wuhan Univ. 2004, 29, 872–876. [Google Scholar]
  9. Guo, W.; Chen, J. The formal description of topological spatial relationship in 3-D based on point set topology. Acta Geod. Cartogr. Sin. 1997, 26, 122–127. [Google Scholar]
  10. Randell, D.; Cui, Z.; Cohn, A. A spatial logic based on regions and connection. In Proceedings of the 3rd International Conference on Principles of Knowledge Representation and Reasoning, Cambridge, MA, USA, 23–25 October 1992; pp. 165–176. [Google Scholar]
  11. Gao, L.X.; Zhao, B.; Liu, W. RCC Topological Relations between Vague Regions Based on Rough Sets. Geogr. Geo-Inf. Sci. 2008, 24, 16–19. [Google Scholar]
  12. Yu, Q.Y.; Liu, D.Y.; Liu, Y.B. An Expanded Egg-Yolk Model between Intermediate Regions. Acta Electron. Sin. 2004, 32, 610–615. [Google Scholar]
  13. Zhou, X.G.; Chen, J.; Jiang, J.; Zhu, J. Description of topological relationships between cadastral landforms. Acta Geod. Cartogr. Sin. 2003, 32, 356–361. [Google Scholar]
  14. Zhou, X.G.; Yue, G.S.; Wei, J.Z.; Zhao, R.L.; Zhu, J.J. A Computation Method of Parcels’ Topological Relations Based on Oracle Spatial. J. Cent. South Univ. (Sci. Technol.) 2005, 36, 317–322. [Google Scholar]
  15. Xu, Z.H.; Bian, F.L. Cadastral Spatial Entities and Their Spatiotemporal Topological Relations. Geomat. Inf. Sci. Wuhan Univ. 2002, 27, 522–527. [Google Scholar]
  16. Ye, J. Research on Cadastral Dynamic Management Technology Based on Spatial Object Relationship Analysis; Zhejiang University: Hangzhou, China, 2006. [Google Scholar]
  17. Zhou, X.; Chen, J.; Li, Z. Calculation of Topological Relations Based on Euler numbers. Acta Geod. Cartogr. Sin. 2006, 35, 291–298. [Google Scholar]
  18. Shi, Y. Study on a 3-D Cadastral Spatial Data Model and Its Key Techniques; Wuhan University: Wuhan, China, 2009. [Google Scholar]
  19. ISO TC211. ISO 19152 Geographic Information—Land Administration Domain Model (LADM); ISO: Geneva, Switzerland, 2012. [Google Scholar]
  20. Ying, S.; Guo, R.; Li, L. 3-D Cadasters; Science Press: Beijing, China, 2014. [Google Scholar]
  21. Van Oosterom, P.J.M.; Stoter, J.E.; Ploeger, H.D.; Thompson, R.J.; Karki, S. World-wide inventory of the status of 3-D cadasters in 2010 and expectations for 2014. In Proceedings of the 3-D-Cadasters at the FIG Working Week, Marrakech, Morocco, 18–22 May 2011. [Google Scholar]
  22. Aien, A.; Kalantari, M.; Rajabifard, A.; Williamson, I.; Bennett, R. Advanced principles of 3-D cadastral data modeling. In Proceedings of the 2nd International Workshop on 3-D Cadasters, Delft, The Netherlands, 16–18 November 2011. [Google Scholar]
  23. Stoter, J.; Ploeger, H. Property in 3-D—Registration of multiple use of space: Current practice in Holland and the need for a 3-D cadaster. Comput. Environ. Urban Syst. 2003, 27, 553–570. [Google Scholar] [CrossRef]
  24. Paulsson, J. Reasons for introducing 3-D property in a legal system—Illustratedby the Swedish case. Land Use Policy 2013, 33, 195–203. [Google Scholar] [CrossRef]
  25. Paulsson, J.; Paasch, J.M. 3-D property research from a legal perspective. Comput. Environ. Urban Syst. 2013, 40, 7–13. [Google Scholar] [CrossRef]
  26. Ho, S.; Rajabifard, A.; Stoter, J.; Kalantari, M. Legal barriers to 3-D cadaster implementation: What is the issue? Land Use Policy 2013, 35, 379–387. [Google Scholar] [CrossRef]
  27. Karki, S.; Thompson, R.; McDougall, K.; Cumerford, N.; Van Oosterom, P.J.M. ISO Land Administration Domain Model and LandXML in the Development of Digital Survey Plan Lodgement for 3-D Cadaster in Australia. In Proceedings of the 2nd International Workshop on 3-D Cadasters, Delft, The Netherlands, 16–18 November 2011. [Google Scholar]
  28. Aiena, A.; Kalantaria, M.; Rajabifard, A.; Williamson, I.; Bennett, R. Utilising data modelling to understand the structure of 3-D cadasters. J. Spat. Sci. 2013, 58, 215–234. [Google Scholar] [CrossRef]
  29. Shojaei, D.; Olfat, H.; Faundez, S.I.Q.; Kalantari, M.; Rajabifard, A.; Briffa, M. Geometrical data validation in 3-D digital cadaster—A case study for Victoria, Australia. Land Use Policy 2017, 68, 638–648. [Google Scholar] [CrossRef]
  30. Egenhofer, M.; Herring, J. Categorizing Binary Topological Relations between Regions, Lines, and Points in Geographic Databases; Technical Report; Department of Surveying Engineering, University of Maine: Orono, ME, USA, 1991. [Google Scholar]
  31. Clementini, E.; Felice, P.D.; Oosterom, P.V. A small set of formal topological relationships suitable for end-user interaction. In Proceedings of the Advances in Spatial Data-Third International Symposium (SSD’93), Singapore, 23–25 June 1993, 2nd ed.; Abel, D., Ooi, B.C., Eds.; Lecture Notes in Computer Science; Springer: Berlin, Germany, 1993; Volume 62, pp. 277–295. [Google Scholar]
  32. Zlatanova, S. 3-D GIS for Urban Development; ITC: Enschede, The Netherlands, 2000. [Google Scholar]
  33. Zhang, J.; Qin, X.; Bao, L. Method for simplifying 3-D spatial nine-intersection model. J. Nanjing Univ. Aeronaut. Astronaut. 2006, 38, 335–340. [Google Scholar]
Information 09 00071 g001 550
Figure 1. Geometrical and topological structure for cadastral parcel in a 3-D space.
Figure 1. Geometrical and topological structure for cadastral parcel in a 3-D space.
Information 09 00071 g001
Information 09 00071 g002 550
Figure 2. Examples of isolated objects in a cadastral space.
Figure 2. Examples of isolated objects in a cadastral space.
Information 09 00071 g002
Information 09 00071 g003 550
Figure 3. The boundary objects in cadastral management. (a) Example of divided boundary edges 37 and 38 between two 2-D parcels; (b) example of divided boundary polygon F1 and F2 between two 3-D parcels.
Figure 3. The boundary objects in cadastral management. (a) Example of divided boundary edges 37 and 38 between two 2-D parcels; (b) example of divided boundary polygon F1 and F2 between two 3-D parcels.
Information 09 00071 g003
Information 09 00071 g004 550
Figure 4. Classes of topological relations for spatial objects.
Figure 4. Classes of topological relations for spatial objects.
Information 09 00071 g004
Information 09 00071 g005 550
Figure 5. Classes of topological relations in cadastral spaces.
Figure 5. Classes of topological relations in cadastral spaces.
Information 09 00071 g005
Table
Table 1. Classes of topological relations for 3-D cadastral objects.
Table 1. Classes of topological relations for 3-D cadastral objects.
PointSegmentFaceSolid
Pointdisjoint/equaldisjoint/touchdisjoint/touchdisjoint/touch
Segmentdisjoint/touchdisjoint/equaldisjoint/touchdisjoint/touch
Facedisjoint/touchdisjoint/touchdisjoint/equaldisjoint/touch
Soliddisjoint/touchdisjoint/touchdisjoint/touchdisjoint/equal
Table
Table 2. The disjoint topological relation for objects in a 3-D cadaster.
Table 2. The disjoint topological relation for objects in a 3-D cadaster.
TypeExample
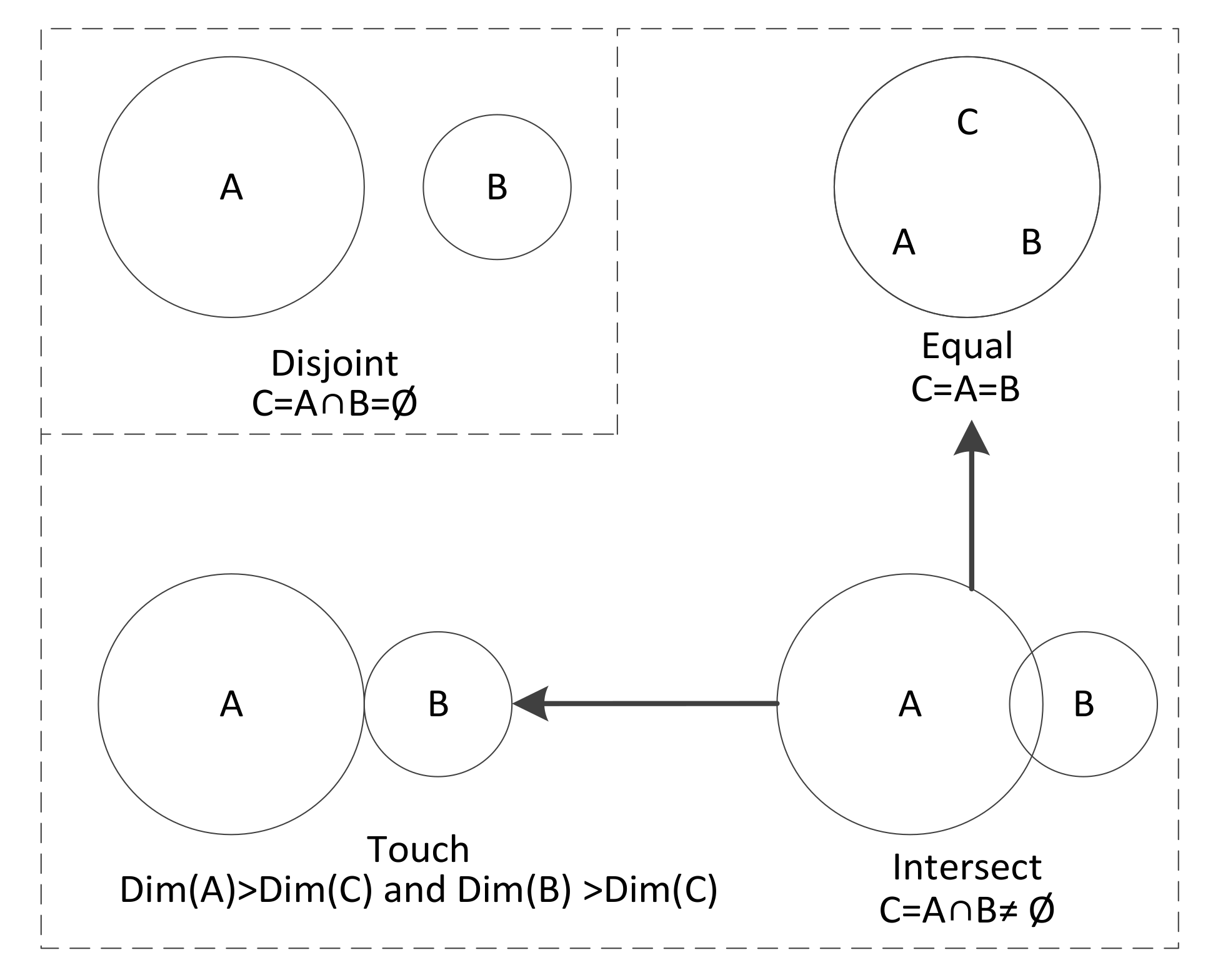
LFD 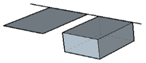Information 09 00071 i001
NLFD Information 09 00071 i002
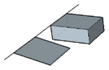LNFD Information 09 00071 i003
NLNFD Information 09 00071 i004
Note: D represents disjoint, L represent shared lines, NL represents no shared lines, F represents shared faces, and NF represents no shared faces.
Table
Table 3. The touch topological relation for objects in a 3-D cadaster.
Table 3. The touch topological relation for objects in a 3-D cadaster.
TypeExample
PLFT 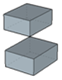Information 09 00071 i005
PNLFT Information 09 00071 i006
PLNFT Information 09 00071 i007
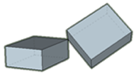PNLNFT Information 09 00071 i008
LFT Information 09 00071 i009
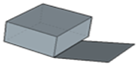LNFT Information 09 00071 i010
FT Information 09 00071 i011
Note: PT represents touch with shared points, P represents shared points, L represent shared lines, NL represents no shared lines, F represents shared faces, and NF represents no shared faces.
Table
Table 4. Disjoint topological relation among objects in a 3-D cadaster.
Table 4. Disjoint topological relation among objects in a 3-D cadaster.
DisjointPointSegmentFaceSolid
PointDLFD/NLFDLFD/NLFD/NLNFDLFD/NLFD/NLNFD
SegmentLFD/NLFDLFD/NLFD/NLNFDLFD/NLFD/NLNFDLFD/NLFD/NLNFD
FaceLFD/NLFD/NLNFDLFD/NLFD/NLNFDLFD/NLFD/LNFD/NLNFDLFD/NLFD/LNFD/NLNFD
SolidLFD/NLFD/NLNFDLFD/NLFD/NLNFDLFD/NLFD/LNFD/NLNFDLFD/NLFD/LNFD/NLNFD
Table
Table 5. The touch topological relation for objects in a 3-D cadaster.
Table 5. The touch topological relation for objects in a 3-D cadaster.
TouchPointSegmentFaceSolid
Point-PTPTPT
SegmentPTPLFT/PNLFTPLFT/PNLFT/PNLNFTPLFT/PNLFT/PNLNFT
FacePTPLFT/PNLFT/PNLNFTPLFT/PNLFT/PLNFT/PNLNFT/LFT/LNFTPLFT/PNLFT/PLNFT/PNLNFT/LFT/LNFT
SolidPTPLFT/PNLFT/PNLNFTPLFT/PNLFT/PLNFT/PNLNFT/LFT/LNFTPLFT/PNLFT/PLNFT/PNLNFT/LFT/LNFT/FT

Share and Cite

MDPI and ACS Style

Fu, L.; Yin, P.; Li, G.; Shi, Z.; Liu, Y.; Zhang, J. Characteristics and Classification of Topological Spatial Relations in 3-D Cadasters. Information 2018, 9, 71. https://doi.org/10.3390/info9040071

AMA Style

Fu L, Yin P, Li G, Shi Z, Liu Y, Zhang J. Characteristics and Classification of Topological Spatial Relations in 3-D Cadasters. Information. 2018; 9(4):71. https://doi.org/10.3390/info9040071

Chicago/Turabian Style

Fu, Lili, Pengcheng Yin, Gang Li, Zhifeng Shi, Youzhi Liu, and Jiyi Zhang. 2018. "Characteristics and Classification of Topological Spatial Relations in 3-D Cadasters" Information 9, no. 4: 71. https://doi.org/10.3390/info9040071

APA Style

Fu, L., Yin, P., Li, G., Shi, Z., Liu, Y., & Zhang, J. (2018). Characteristics and Classification of Topological Spatial Relations in 3-D Cadasters. Information, 9(4), 71. https://doi.org/10.3390/info9040071

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop