Abstract
Network coding approaches typically consider an unrestricted recoding of coded packets in the relay nodes to increase performance. However, this can expose the system to pollution attacks that cannot be detected during transmission, until the receivers attempt to recover the data. To prevent these attacks while allowing for the benefits of coding in mesh networks, the cache coding protocol was proposed. This protocol only allows recoding at the relays when the relay has received enough coded packets to decode an entire generation of packets. At that point, the relay node recodes and signs the recoded packets with its own private key, allowing the system to detect and minimize the effect of pollution attacks and making the relays accountable for changes on the data. This paper analyzes the delay performance of cache coding to understand the security-performance trade-off of this scheme. We introduce an analytical model for the case of two relays in an erasure channel relying on an absorbing Markov chain and an approximate model to estimate the performance in terms of the number of transmissions before successfully decoding at the receiver. We confirm our analysis using simulation results. We show that cache coding can overcome the security issues of unrestricted recoding with only a moderate decrease in system performance.
1. Introduction
Mobile Ad-hoc Networks (MANET) constitute an infrastructure-less network architecture for mobile devices. In MANETs, network coding has been shown to increase reliability and throughput [1]. In network coding, data are encoded in a sender and transmitted through a network to be decoded at one or multiple receivers. Intermediate nodes in the network can also recombine coded packets (recode) without decoding the original data. Network coding can be considered as a generalized routing, in which relay nodes not only store and forward packets, but also combine packets received from multiple input paths before sending them to any output path [2,3]. Random Linear Network Coding (RLNC) is a simple, yet asymptotically optimal method, where packets are linearly combined using coefficients drawn uniformly at random from the elements of a finite field [2] and then transmitted through the network [4].
However, RLNC with unrestricted and unsupervised recoding is vulnerable to pollution attacks. A pollution attack occurs when a malicious or faulty node injects invalid linear combinations of generation into the network [5]. These invalid coded packets can quickly propagate into other packets via recoding in relay nodes and can prevent the destination node from decoding properly [6]. To prevent pollution attacks, homomorphic signatures, which are preserved through linear combination and recoding, can be used [7,8,9]. This method allows the system to check the integrity of network coded data and also to track and find malicious nodes in the network. However, due to high processing cost, this method is not practical [6]. While there exist alternatives for preventing pollution attacks with reduced processing costs, these solutions place limitations on topologies, require loose clock synchronization on the order of 100 ms, limit the hop count, require large field sizes or demand new public keys to be generated per generation. These requirements are not feasible in dynamic MANET networks. Thus, a new integrity mechanism is needed to mitigate pollution attacks [10].
As an alternative, the authors of [5] proposed a protocol solution called cache coding. Cache coding allows certified relay nodes to recode data only when they have decoded an entire generation. At that time, the relay nodes can generate new recoded packets and sign them with their own identifier. This mechanism generates trusted packets from both the source node and the trusted relay nodes, thus allowing the network to detect pollution attacks before they propagate.
Although [5] presents the protocol to cope with this vulnerability and identifies some bounds on the number of transmissions, a precise analytical model to characterize the performance of cache coding in multi-relay networks is missing. This performance analysis is critical to understand the security-delay trade-off imposed by the protocol. This paper provides two models for analysis of the cache coding protocol. The first model is a simple, yet accurate approximation to predict the number of required transmissions. The second model is based on an absorbing Markov chain inspired by previous works (e.g., [11]) and is used to accurately characterize the total number of transmissions in the system, as well as the number of linearly independent packets in all nodes after some constant transmissions from the source node. Although we focus on a simple relay policy from the cache coding protocol, future work can exploit the Markov chain structure of the problem to derive optimal policies using Markov Decision Processes (MDP) as in recent RLNC work (e.g., [12,13,14]).
We validate our analytical models using simulation results showing the difference between the absorbing Markov chain model, and the simulation results are negligible for all analyzed generation sizes and packet loss rates. For moderate loss rates, there is a 10% deviation in terms of the square average of the difference between our heuristic model and the simulation results. However, the heuristic model loses accuracy for high loss rates. Finally, we show that the cache coding protocol is at most 12% worse than RLNC with unrestricted recoding in terms of the number of transmissions. However, on average, there is only a 7% deviation in terms of the square average of the difference between the expected number of transmissions of cache coding and unrestricted coding protocols.
This paper is organized as follows. In Section 2, we discuss the system model and different coding methods in relay nodes. In Section 3 and Section 4, we discuss our two analytical models, while Section 5 focuses on validating those models using simulation results. We present our conclusions in Section 6.
2. System Model
We consider a network topology with one source node S, two relay nodes and and a destination node D. A total number of n packets must be sent from S to D. This transmission occurs by using the links shown in Figure 1. Each link has a fixed packet loss rate, e. The packet loss rates are considered constant throughout the transmission and independent of each other.

Figure 1.
The topology of a two-relay network.
We define the Degrees of Freedom (DoF ) of a node as the number of linearly independent packets received by that node. In any topology, the transmission will be carried on until the DoF of the destination node are equal to the generation size, i.e., when the destination has enough information to decode the original data. We also define the generation size (n packets) as the number of original data packets that are linearly combined to generate network coded packets.
S generates packets using RLNC. It uses data packets , ,..., in the generation to create a linear combination with coding coefficients , ,..., , i.e., . These coefficients are randomly selected from q elements of a Galois field, i.e., [12]. If the field size is not considered very large, there is a chance that a packet received by D is not innovative and hence does not increase the DoF of D. However, in our analysis, we assume that the field size is large enough so that the probability of generating a linearly dependent coded packets for and is negligible until they decode the generation.
Data are sent in three broadcast transmissions in three time slots as shown in Figure 2, with and indicating the transmission and reception of data, respectively. The first time slot is used for broadcasting from S to both and . The second and third time slots are used by and to broadcast to D, respectively. This whole process is called a transmission round. We assume a shared channel between all nodes for sending data in this topology, and the TDMA protocol is used to manage each node’s access to this shared channel.

Figure 2.
A transmission round.
We assume that whenever a relay node receives a packet, it is permitted to transmit a packet. This packet is determined by one of the following three coding methods.
Source coding (): Upon reception of a transmission from S, and/or send a packet to D, which is identical to the packet received from S. Thus, D receives only one independent packet if it receives packets from more than one relay in the same time slot. Repeated coded packets are discarded.
Unrestricted coding (): In this method, and receive encoded packets from S. and recode packets with previously received coded packets in each relay’s buffer and send the newly generated recoded packet to D. Each relay transmits a recoded packet when they receive a coded packet from S.
Cache coding (): In this method, and will act like the source coding method until its DoF is equal to the generation size (n). Then, the relay decodes the whole generation. After decoding all packets, the mentioned relay recodes the original packets and sends recoded data to D. This mechanism continues until the end of transmission, where the DoF of D are equal to the generation size (n).
3. Heuristic
This section derives an approximation to evaluate the performance of the three coding methods described in Section 2 in a system with the topology of Figure 1. We address each method in different subsections. We focus on the expected number of transmissions from S until D decodes a generation of n packets, as well as the expected total number of transmissions in all links in the network.
3.1. Source Coding
The probability that a packet is received by D from and the probability of receiving a packet by D from are:
Meanwhile, the probability of receiving a packet by D from both and is:
Since the assumption is based on a high field size, a new packet is innovative at D if it is received from either or . This probability is equal to . Thus, the probability of receiving a linearly independent packet by D is:
Using Equation (3), the expected number of required transmissions from S to decode the generation completely in D is:
where n is the size of the generation that D needs to decode and is the number of required transmissions from S to have n linearly independent packets in D. In source coding, every transmission round includes a transmission from S; therefore, this metric is equal to the total number of transmission rounds in the system.
The expected number of transmissions in all links requires us to determine the expected number of transmissions from each relay. Since each relay transmits a packet when it receives a packet from S, the expected number of transmissions from each relay is equal to . Hence, the expected number of transmissions in all links is:
Note that the expected number of linearly dependent packets received in D, i.e., coded packets received by D from both and in the case of this scheme, is given by:
3.2. Unrestricted Coding
In the analysis of unrestricted coding, our assumption is that the system operates optimally, i.e., each transmitted coded packet from S is linearly independent for D, as well as for the joint information of both and . The latter means that if a transmission from S is successfully received by at least one of or and increases their joint DoF, then it is considered a useful transmission. Thus, the approximations derived for the expected number of transmission rounds and total expected number of transmissions in this section are lower bounds to the experimental values. Although this optimal scheme is achievable, from a practical perspective, it may impose increased signaling requirements in the network. A practical scheme requires the same or more coded packet transmissions.
Since the probability that neither nor receive the coded packet from S is , hence the probability of receiving a transmitted packet from S by either or is . As we require and to receive n packets, the expected number of transmissions from S to and is:
D requires n packets to decode the whole generation. As the probability of receiving a packet by D from a relay node is , the expected number of transmissions from and to D until D can decode the whole generation is:
3.3. Cache Coding
For the cache coding protocol, the total number of transmissions from all links can be separated into three separate contributions, as follows.
- The probability of receiving a packet by a relay node or is . As we need n packets in each relay node, the expected number of transmissions from S to and until the relays decode the whole generation is equal to .
- Until and decode the whole generation, they forward the packets received from S. As each relay node receives n packets until decoding the whole generation, each relay node forwards n coded packets received from S. Thus, the expected number of transmissions from and to D until both and have decoded the whole generation is equal to .
- The expected number of transmissions from and to D after they have decoded the whole generation requires us to determine the expected number of linearly independent packets received by D before and have decoded the whole generation. Before the relay nodes decode the whole generation, the expected number of packets received by D from is equal to . Meanwhile, the expected number of packets received by D only from is equal to . Hence, the expected number of linearly independent packets in D, before the relay nodes decode the whole generation, is equal to . In order to decode the whole generation, D needs a total of n linearly independent packets; hence, after and have decoded the whole generation, D must receive another linearly dependent packets. Since the probability of receiving a packet by D from and the probability of receiving a packet by D from is , the expected number of transmissions from and to D after they have decoded the whole generation is equal to .
Summing these three equations, we can calculate the expected number of transmissions in all links as:
While the expected number of transmission rounds in the system is:
The expected number of transmission rounds before and have decoded the data equals the expected number of transmissions from S to and , i.e., . Moreover, the expected number of transmission rounds after and have decoded the data is equal to the expected number of transmissions from and to D divided by the number of relays.
In order to determine the expected number of linearly dependent packets in D, we use the fact that the expected number of packets received by D from or is equal to and that the expected number of packets received by D from only one of and is equal to . Thus, the expected number of linearly dependent packets is equal to the subtraction of these two equations.
4. Absorbing Markov Chain Model
This section provides a full characterization of the cache coding protocol using an analytical model based on an absorbing Markov chain. We define the states as a triple , where and are the DoFs in and , respectively, and r represents the DoFs in D. Note that based on these states. The absorbing states are the states where . This absorbing Markov chain will also include a cost matrix C alongside the matrix of transition probabilities P. While indicates the transition probability from state i to state j, is the total number of transmissions in all links required for the transition from state i to state j. We have derived closed-form expressions for each element of these two matrices.
4.1. Transition Probabilities
The transition probabilities between states and are dependent on the the cache coding protocol’s stage in the communication process. Thus, we organize the transition probabilities into five cases as follows. In each case, we show how to derive one of the probabilities. Other probabilities are derived in the same way.
- andNo single relay node has decoded the data or decodes the data after receiving the new coded packet. Thus, both relays receive the coded packet and forward the received packet to D. Thus,In this case, for example, consider the probability where , and . This case is the union of three possibilities.
- and receive from S. D receives from both and . In this case, all receptions are successful, so the probability of this incident is equal to .
- and receive from S. D receives only from . In this case, three of four receptions are successful, so the probability of this incident is equal to
- and receive from S. D receives only from . In this case, three of four receptions are successful, so the probability of this incident is equal to .
- and or and .In this case, if one the relay node with DoFs equal to receives a new packet, it decodes the generation completely and starts to send recoded data to D. However, the other relay node still forwards the received coded packet. Thus,In this case, for example, consider the probability where , and . This case occurs when and both receive a packet from S and D receives a packet from both and . Therefore, all four transmissions must be successful; hence, this incident must have a probability of .
- andIn this case, recodes and sends data to D, while forwards the received coded packets. Even if receives a new packet and decodes data completely (the case ), it recodes data and sends a recoded packet to the destination, which is different from the packet sent by . The difference between this case and Case 2 is the fact that sends a recoded packet to D whether or not it receives a packet from S. However, this event does not occur in Case 2. Thus,In this case, consider the probability where , and . If , this incident occurs when receives a packet from S, and also D receives a packet from either or . Each of these incidents have a probability of . Hence, the total probability is equal to .
- Case 4 : andIn this case, recodes and sends data to D, while forwards the received coded packets. Even if receives a new packet and decodes data completely (the case ), it recodes data and sends a recoded packet to the destination, which is different from the packet sent by . The difference between this case and Case 2 is the fact that sends a recoded packet to D whether or not it receives a packet from S. However, this event does not occur in Case 2. The probabilities in this case are identical to the previous case. Thus,
- Case 5 : andIn this case, both and have decoded the data. Therefore, S will not transmit any longer to or , while and will recode the decoded data and send different coded packets to D.
4.2. Cost of Transitions
The cost of any transition is 0, 1, 2 or 3 depending on the number of broadcast transmissions that occur. Using the cases introduced in Section 4.1, we can derive the cost of transitions. The cost of transition is derived using these two facts.
- S sends a packet unless the DoF of both and is equal to n.
- and send a packet when their DoF is equal to n or they receive a packet from S.
Thus, the cost of transitions is as follows.
- and
- and or and
- and
- and
- and
4.3. Performance Analysis Using the Markov Chain
4.3.1. Calculation of the Number of Transitions
After establishing all transition probabilities in a transition matrix, we can build the fundamental matrix F as follows [15]:
where t is the number of transient (non-absorbing) states and r is the number of absorbing states. Q is the matrix of transition probabilities between transient states. R is the matrix of transition probabilities from transient states to absorbing states. I is the identity matrix, and Z is an all-zero matrix. After building this matrix, the mean number of transitions can be calculated using Definition 1.
Definition 1.
The expected number of transitions before being absorbed when starting in a transient state i is the i-th element of the column vector:
where I is the identity matrix with the same dimensions as Q and Γ is an all-one vector [16].
4.3.2. Calculation of the Number of Transmissions in All Links
The expected number of transmissions in all links is calculated using both transition matrix A and cost matrix C.
Definition 2.
For an absorbing Markov chain in state i, the expected number of transmissions in its next transition is equal to [17]:
Theorem 1.
For an absorbing Markov chain with state probability π, the expected number of transmissions in the next transition is equal to:
where represents the element to element multiplication between two matrices A and C and Γ is an all-one column vector.
Proof-sketch of Theorem 1.
Using Definition 2, for a system in state i, the expected number of transmissions is equal to . As shows the probability for the system to be in state i, so the expected number of transmissions in the system is equal to . ☐
5. Results
In this section, we assess the validity of the proposed models and compare the three recoding schemes using various performance measures. We simulate the network topology of Figure 1 using the KODO library [18] in C++ to perform encoding/decoding operations. We have carried 1000 independent experiments for each generation size and packet loss rate and report the average of these measurements. These experiments were carried out by using Galois Field () for encoding/decoding operations. In this section, the deviation between two plots is calculated by the square average between two vectors. The calculation is carried out by using the second vector as a reference vector for calculating the square average. For example “the deviation of x and y is 5%” means that if x and y have n entries, then .
We have calculated the expected number of transmissions in all links in source coding. Using Equation (5) in Section 3, we can approximate the expected number of transmission in all links for source coding. Figure 3 compares the simulation results with our heuristics, showing a deviation of 10% between heuristics and simulation. This fact shows that the approximated model can estimate this metric within 90–110% of the real value for a wide range of generation sizes and packet loss rates. This difference comes from the fact that additional transmissions from S to both and occur, while these packets are not innovative for D.

Figure 3.
Average number of transmissions in all links in source coding.
Figure 4 shows the expected number of transmissions in all links for unrestricted coding. This figure shows that there is a 20% deviation between our heuristic model and simulation results for all generation sizes and packet loss rates. However, for a moderate loss rate, which means less than a 20% loss rate, there is only a 10% deviation between heuristic and simulation results. This gap is created because the proposed heuristic is a lower bound for unrestricted coding.

Figure 4.
Average number of transmissions in all links in unrestricted coding.
Figure 5 illustrates the expected number of transmission rounds in order to decode the data in D for different generation sizes in cache coding. We compare our simulation results with the two proposed models. Figure 6 shows the expected number of transmission rounds for different generation sizes in cache coding. In both of these metrics, there is at most a 10% deviation between heuristics and simulation. The deviation between the absorbing Markov chain and simulation is at most 6%. The absorbing Markov chain model is more precise than the heuristics, because we did not consider the number of relay nodes in our heuristic model. Table 1 and Table 2 summarize our key results for cache coding.
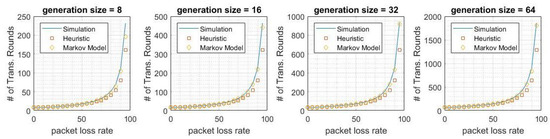
Figure 5.
Average number of transmission rounds in cache coding.
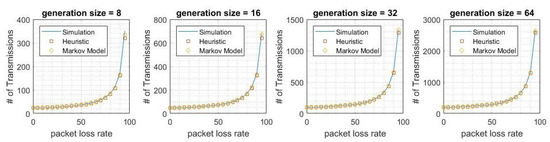
Figure 6.
Average number of transmissions in all links in cache coding.

Table 1.
Total number of transmission rounds in cache coding.

Table 2.
Total number of transmissions in all links in cache coding.
Figure 7 and Figure 8 show the expected number of linearly dependent packets received in D for cache coding and source coding, respectively. As shown, this number decreases by increasing the packet loss rate. This comes from the fact that there is a lower probability of receiving the same packets by and for higher packet loss rates, which decreases the probability of receiving non-innovative packets in D.
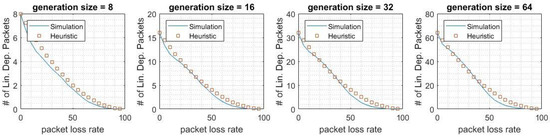
Figure 7.
Number of linearly dependent packets in D in cache coding.

Figure 8.
Number of linearly dependent packets in D in source coding.
We also compare the performance of cache coding and unrestricted coding. In Figure 9 and Figure 10, we show the expected number of transmissions in all links for these coding schemes. The results for the simulation confirm that there is only a 5% deviation between cache coding and unrestricted coding in terms of expected total number of transmissions. This gap is larger for the results of the heuristics. There is at most a 9% derivation between heuristic models of cache coding and unrestricted coding. These results also show that the deviation between cache coding and unrestricted coding is only 12% in the worst case.
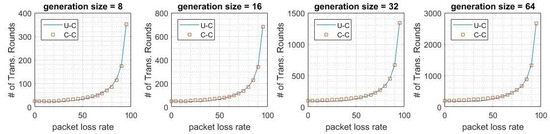
Figure 9.
Average number of transmissions in cache coding and unrestricted coding by the
simulation results.
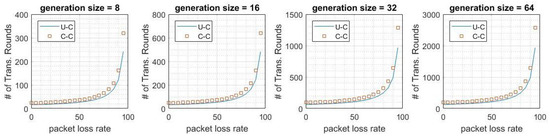
Figure 10.
Average number of transmissions in cache coding and unrestricted coding by the
heuristic results.
6. Conclusions and Future Work
This paper presents a model and full characterization for the cache coding protocol presented in [5], as well as an approximated, yet accurate model for this protocol and other protocols of interest. This analysis also considers an achievable lower bound for the number of transmissions in the network, which serves as the gold standard to measure various protocols, including the cache coding protocol.
Using our models and simulation results, we have confirmed that the cache coding protocol, which was originally designed to overcome the security issues of unrestricted coding, can overcome the security issues with a negligible decrease in the performance of the two-relay system analyzed in this paper. Although this fact had been shown by simulations [5], our paper provides the first confirmation using analytical models to describe the system.
Our future work will consider closed-form expressions for other performance metrics, such as the number of linearly dependent packets received by the destination node. Moreover, we will consider extensions of the analytical model to systems with more than two relays. Regarding the probabilistic method, we will take the impact of field size on the probability of receiving an uninnovative packet by the relay and destination nodes into consideration.
Acknowledgments
This work was partially financed by the Aarhus Universitets Forskningsfond Starting Grant Project AUFF-2017-FLS-7-1, and Aarhus University’s DIGIT Centre.
Author Contributions
The mathematical analysis of source coding and cache coding and the simulation of all the methods was done by Behnaz Maboudi. The analytical part for Markov chain method was carried out by Hadi Sehat and Behnaz Maboudi. Hadi Sehat was responsible for writing and editing the paper with Behnaz’s help. The analysis and simulation were done under the supervision of Peyman Pahlevani and Daniel E. Lucani.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, C.; Fang, Y.; Zhu, X. Throughput-Delay Tradeoffs in Large-Scale MANETs with Network Coding. In Proceedings of the IEEE INFOCOM 2009, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 199–207. [Google Scholar]
- Ahlswede, R.; Cai, N.; Yeng, R.W. Network information flow. IEEE Trans. Inform. Theory 2000, 46, 1204–1216. [Google Scholar] [CrossRef]
- Koetter, R.; Medard, M. An algebraic approach to network coding. IEEE ACM Trans. Netw. 2003, 46, 782–795. [Google Scholar] [CrossRef]
- Ho, T.; Medrad, M.; Koetter, D.; Karager, D.R. A Random Linear Network Coding Approach to Multicast. IEEE Trans. Inform. Theory 2006, 11, 4413–4430. [Google Scholar] [CrossRef]
- Joy, J.; Yu-Ting, Y.; Perez, V.; Lu, D.; Gerla, M. A new approach to coding in content-based MANETs. In Proceedings of the 2014 International Conference on Computing, Networking and Communications (ICNC), Honolulu, HI, USA, 3–6 February 2014; pp. 173–177. [Google Scholar]
- Esfahani, A.; Mantas, G.; Rodriguez, J.; Neves, J.C. An efficient homomorphic MAC-based scheme against data and tag pollution attacks in network coding-enabled wireless networks. Int. J. Inf. Secur. 2017, 16, 4413–4430. [Google Scholar] [CrossRef]
- Lee, S.H.; Gerla, M.; Krawczyk, H.; Lee, K.W.; Quaglia, E. Performance evaluation of secure network coding using homomorphic signature. In Proceedings of the International Symposium on Network Coding, Beijing, China, 25–27 July 2011; pp. 1–6. [Google Scholar]
- Gennaro, R.; Katz, J.; Krawczyk, H.; Rabin, T. Secure network coding over the integers. In Proceedings of the 13th International Conference on Practice and Theory in Public Key Cryptography, Paris, France, 26–28 May 2010; pp. 142–160. [Google Scholar]
- Agrawal, S.; Boneh, D. Homomorphic MACs: MAC-Based Integrity for Network Coding. In Proceedings of the 7th Applied Cryptography and Network Security, (ACNS 2009), Paris, France, 2–5 June 2009; pp. 292–305. [Google Scholar]
- Dong, J.; Curtmola, R.; Nita-Rotaru, C. Practical defenses against pollution attacks in intra-flow network coding for wireless mesh networks. In Proceedings of the Second ACM Conference on Wireless Network Security, Zurich, Switzerland, 16–19 March 2009; pp. 111–122. [Google Scholar]
- Lucani, D.E.; Médard, M.; Stojanovic, M. Broadcasting in time-division duplexing: A random linear network coding approach. In Proceedings of the Network Coding, Theory, and Applications, 2009, (NetCod’09), Lausanne, Switzerland, 15–16 June 2009; pp. 62–67. [Google Scholar]
- Khamfroush, H.; Pahlevani, P.; Lucani, D.E.; Hundeboll, M. On the coded packet relay network in the presence of neighbors: Benefits of speaking in a crowded room. In Proceedings of the IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014; pp. 1928–1933. [Google Scholar]
- Khamfroush, H.; Lucani, D.E.; Pahlevani, P.; Barros, J. On optimal policies for network-coded cooperation: Theory and implementation. IEEE J. Sel. Area Commun. 2015, 33, 199–212. [Google Scholar] [CrossRef]
- Khamfroush, H.; Lucani, D.E.; Barros, J.; Pahlevani, P. Network-Coded Cooperation over Time-Varying Channels. IEEE Trans. Commun. 2014, 62, 4413–4425. [Google Scholar] [CrossRef]
- Kemeny, J.G.; Snell, J.L. Finite Markov Chains; D. Van Nostrand: New York, NY, USA, 1960. [Google Scholar]
- Garrido, P.; Lucani, D.E.; Agüero, R. Markov chain model for the decoding probability of sparse network coding. IEEE Trans. Commun. 2017, 65, 1675–1685. [Google Scholar] [CrossRef]
- Lucani, D.E.; Medard, M.; Stojanovic, M. On coding for delay—Network coding for time-division duplexing. IEEE Trans. Inform. Theory 2012, 58, 2330–2348. [Google Scholar] [CrossRef]
- Pedersen, M.V.; Heide, J.; Fitzek, F.H. Kodo: An open and research oriented network coding library. In Proceedings of the International Conference on Research in Networking, Valencia, Spain, 9–13 May 2011; pp. 145–152. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).