A Caching Strategy for Transparent Computing Server Side Based on Data Block Relevance
Abstract
:1. Introduction
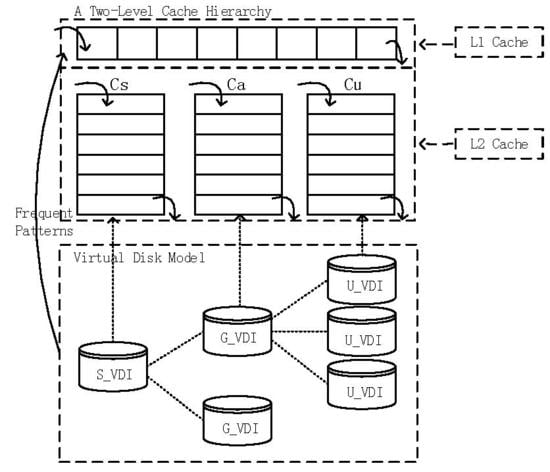
2. Preliminary
3. Caching Strategy Based on Relevance
3.1. Description of FP-Stream
- Build FP-tree and mine frequent patterns.
- (a)
- Scan the current batch of data , and create the header table f_list according to the frequency of items in . If , only the items whose support counts are larger than are stored in f_list. If , all the items in are stored in f_list with their support counts, without filtering.
- (b)
- The FP-tree is a prefix tree storing compressed data information from each batch of data. If the FP-tree is not null, empty the FP-tree. Sort each transaction in according to the item order in f_list, and compress sorted data into the FP-tree from the root.
- (c)
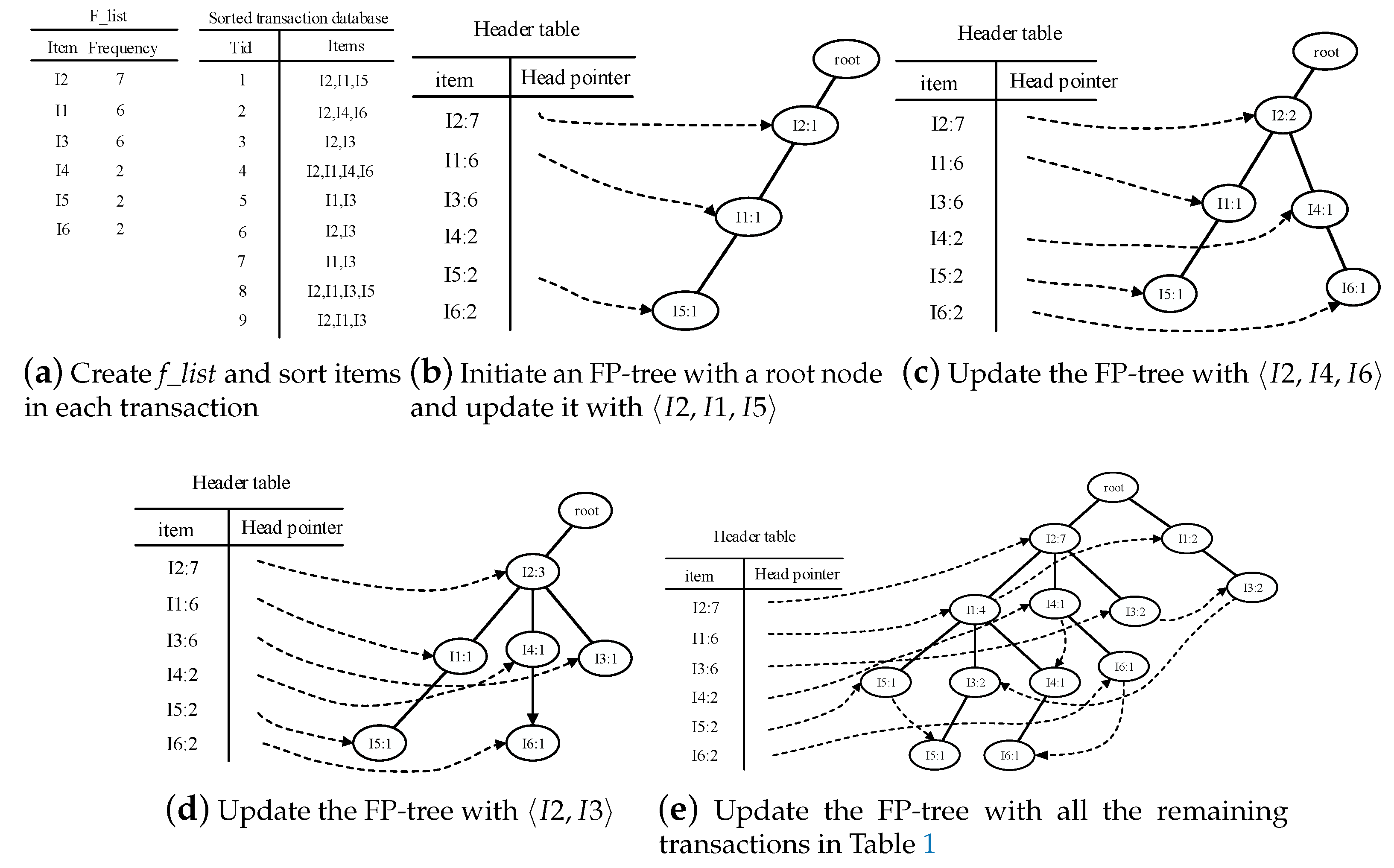
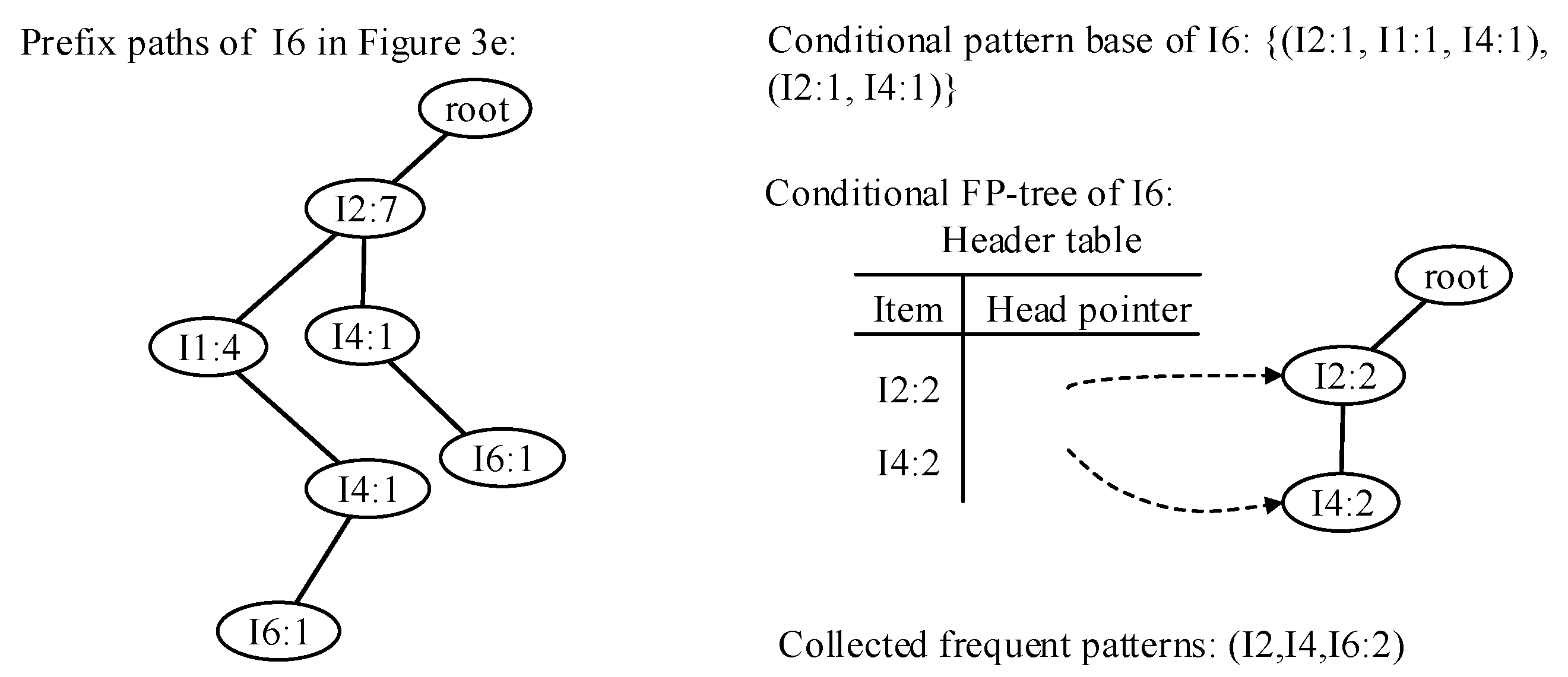
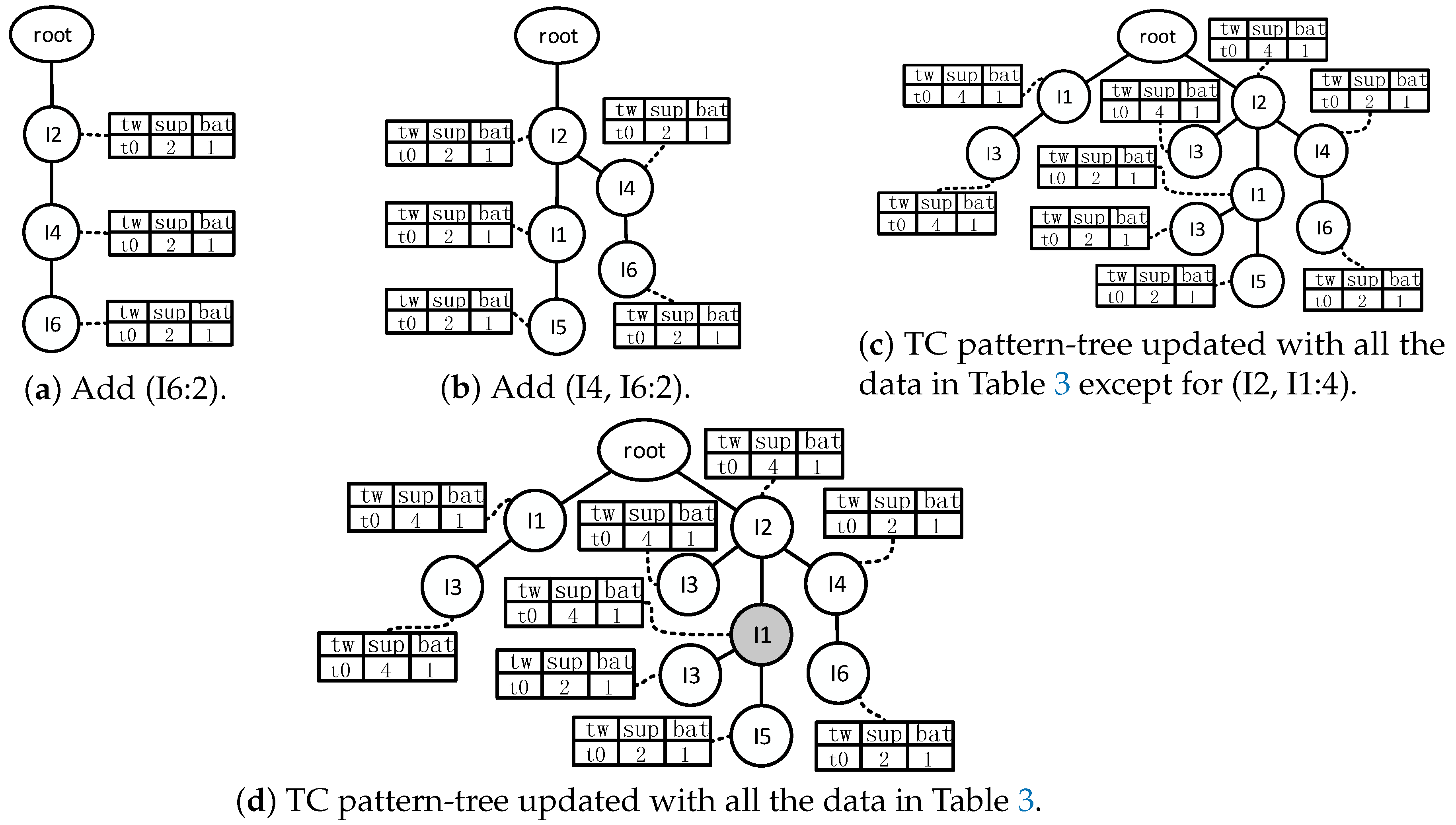
- Traverse the FP-tree from the node corresponding to the last item in f_list with FP-growth. Mine frequent patterns out gradually while the FP-tree is essentially producing one level of recursion at a time, until recursion to the root.Example 1.Suppose the minimum support is 0.2 and the maximum support error is 0.01. If the data in Table 1 are one batch of original data, where data are recorded as some transactions, we can build an FP-tree with these data following the steps shown in Figure 3. Here, frequent items are the items whose support count is not less than in the transaction database. First, the transaction database is scanned once, and the f_list is created with frequent items in descending-frequency order. Then items in each transaction are sorted according to the sequence in f_list. The created f_list and sorted transaction database are shown in Figure 3a. Next, the sorted transaction database is scanned individually, and the FP_tree is initiated. An empty node is set as the root node of the FP_tree. Figure 3b shows that the first transaction is used to build a branch of the tree, with the presented frequency 1 on every node. The second transaction has the same prefix as the first transaction. Thus the frequency of the node (I2:1) is incremented by 1. The remaining string derives two new nodes as a downward branch of 〈I2:2〉, with presented frequency 1. The results are shown in Figure 3c. The third transaction has the same prefix as the existing branches. Thus the frequency of the node (I2:2) is incremented by 1 again, and derives a new node as the child node of (I2:3), with frequency 1. By analogy, an FP-tree can be built as shown in Figure 3d with all the data in Table 1. Every time a new node is created, it will be linked with the last node that has the same name as the new node. If there is no node to link, the new node will be linked with the corresponding head pointer in the header table. Following these node sequences starting from the header table, we can mine out complete frequent patterns, for example, from the FP-tree in Figure 3e. This starts from the bottom of the header table.The process of mining frequent patterns based on I6 are shown in Figure 4. Figure 3e shows that I6 is at the bottom of the header table. Following the sequence that starts from I6 in the header table, we can obtain two nodes with the name I6, and both of them have the frequency count 1. Hence, a one-frequent-item set can be mined out: . In Figure 3e, there are two prefix paths of I6: and . As the number of times I6 appears, the paths indicate that items in the strings and have appeared once together. Hence, just the paths and count when the mining is based on I6. Then is called I6’s conditional pattern base. With the conditional pattern base of I6, the conditional FP-tree of I6 can be built as shown in Figure 4a. Because the accumulated frequency of I1 in is 1, which is less than the minimum support count of 1.71, I1 is discarded when the conditional FP-tree of I6 is built. So far the first layer of recursion has finished. The second layer of recursion starts from scanning the header table in the conditional FP-tree of I6. Figure 4b shows the second layer of recursion. Similarly to the analysis of I6 in the global FP-tree that can be found in Figure 3e, the second layer of recursion is based on I2 and I4 in the conditional FP-tree of I6. Thus the second recursion involves mining two items I4 and I2 in sequence. The first item I4 derives a frequent pattern (I4, I6:2) by combining with I6. Next, the conditional pattern base and conditional FP-tree of (I4, I6) can be created according to the prefix path of I4 in the conditional FP-tree of I6. With the conditional FP-tree of (I4, I6), the third layer of recursion can be derived. The second item I2 derives a frequent pattern (I2, I6:2) by combining with I6. Then the conditional pattern base and conditional FP-tree of (I2, I6) can be created according to the prefix path of (I2) in the conditional FP-tree of I6. In fact, the parent node of (I2) is a root node; thus the search for frequent patterns associated with (I2, I6) terminates. Figure 4c indicates that the third layer of recursion is based on I2 in the conditional FP-tree of (I4, I6). The item I2 derives a frequent pattern (I2, I4, I6:2) by combining with (I4, I6). Because the parent of (I2) is the root node, the search for frequent patterns associated with string (I2, I4, I6) terminates. By traversing the FP-tree in Figure 3 with FP-growth, the frequent patterns mined out are presented in Table 2.
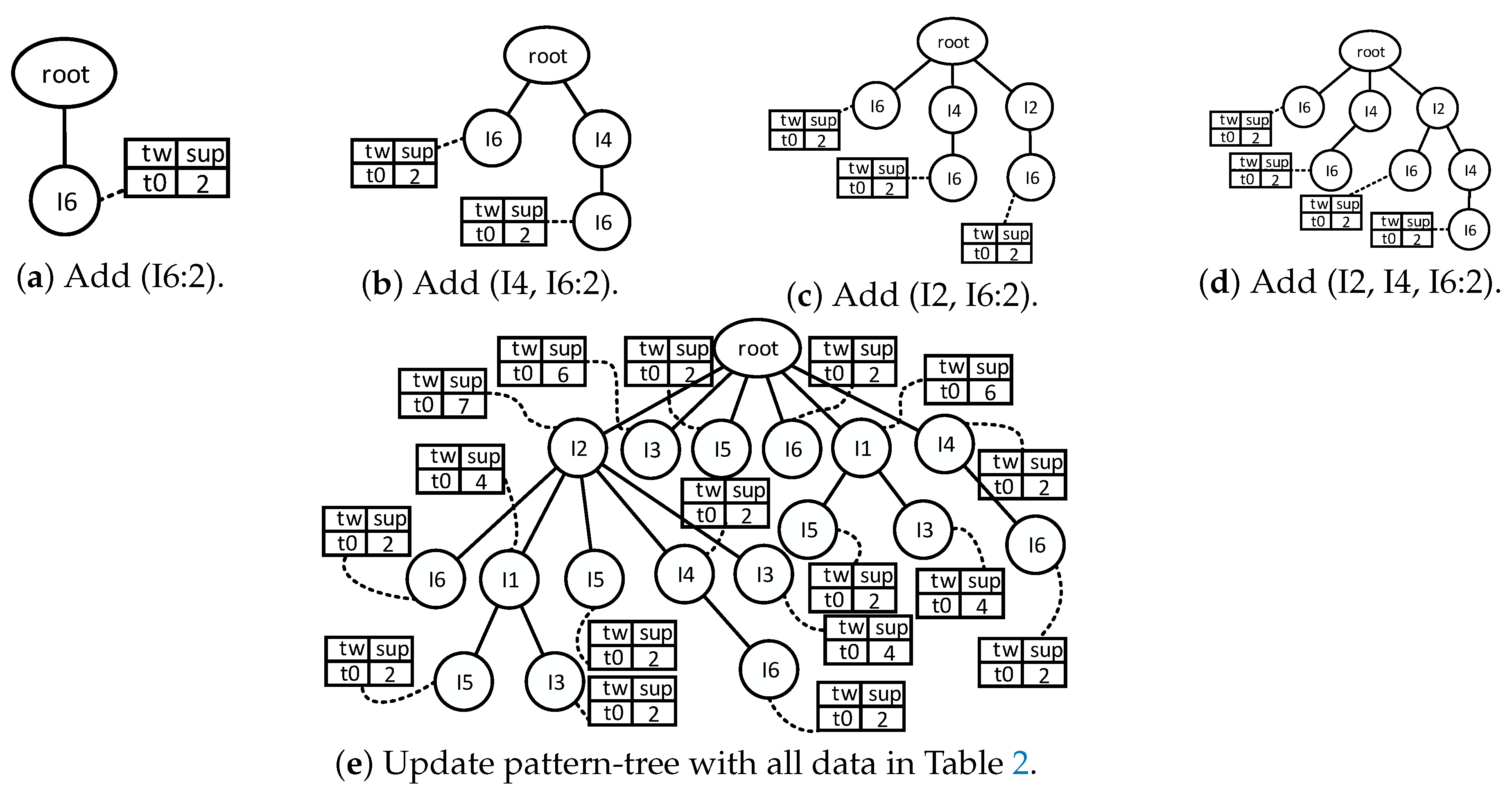
- Update time-sensitive pattern-tree on the basis of the frequent patterns that have been mined out in step 1.
- (a)
- Every time we come to the end of the data batch, update the pattern-tree with the frequent patterns that have been mined out in step 1. Suppose one of the frequent patterns is I. If I has existed in the pattern-tree, just update the titled-time window corresponding to the frequent pattern I with its support count. If there is no path corresponding to I in the pattern-tree and the support count of I is more than , insert I into the pattern-tree. Otherwise, stop mining the supersets of I.
- (b)
- Traverse the pattern-tree in depth-first order and check whether or not each time-sensitive window of the item set has been updated. If not, insert zero into the time-sensitive window that has not been updated.
- (c)
- Drop tails of time-sensitive windows to save space. Given the window that records the information about the latest time window, the window that records the information about the oldest time window, and the support counts , , , …, , which indicate the present frequencies of one certain item set from to , retain , , , …, and abandon , , , …, as long as the following condition is satisfied:
- (d)
- Traverse pattern-tree and check whether or not there are empty time-sensitive windows. Drop the node and its child nodes, if the node’s time-sensitive window is empty.
3.2. Optimizing the FP-Stream
| Algorithm 1: Mining frequent patterns with changed FP-growth. |
| Input : An FP-tree constructed by original data: FP-tree. Output: Frequent patterns. 1 Tree ← FP-tree; ← null; 2 if Tree contains a single path p and all nodes in the path p have the same support s then 3 denote the combination of the nodes in the path p as ; 4 generate pattern with support s; 5 return; 6 else 7 for each in the header of Tree do 8 generate pattern with support ; 9 if α is not null then 10 output frequent pattern ; 11 end 12 construct conditional FP-tree ; 13 if is not null then 14 Tree ; 15 mine frequent patterns out of from the second row in Algorithm 1; 16 end 17 end 18 end |
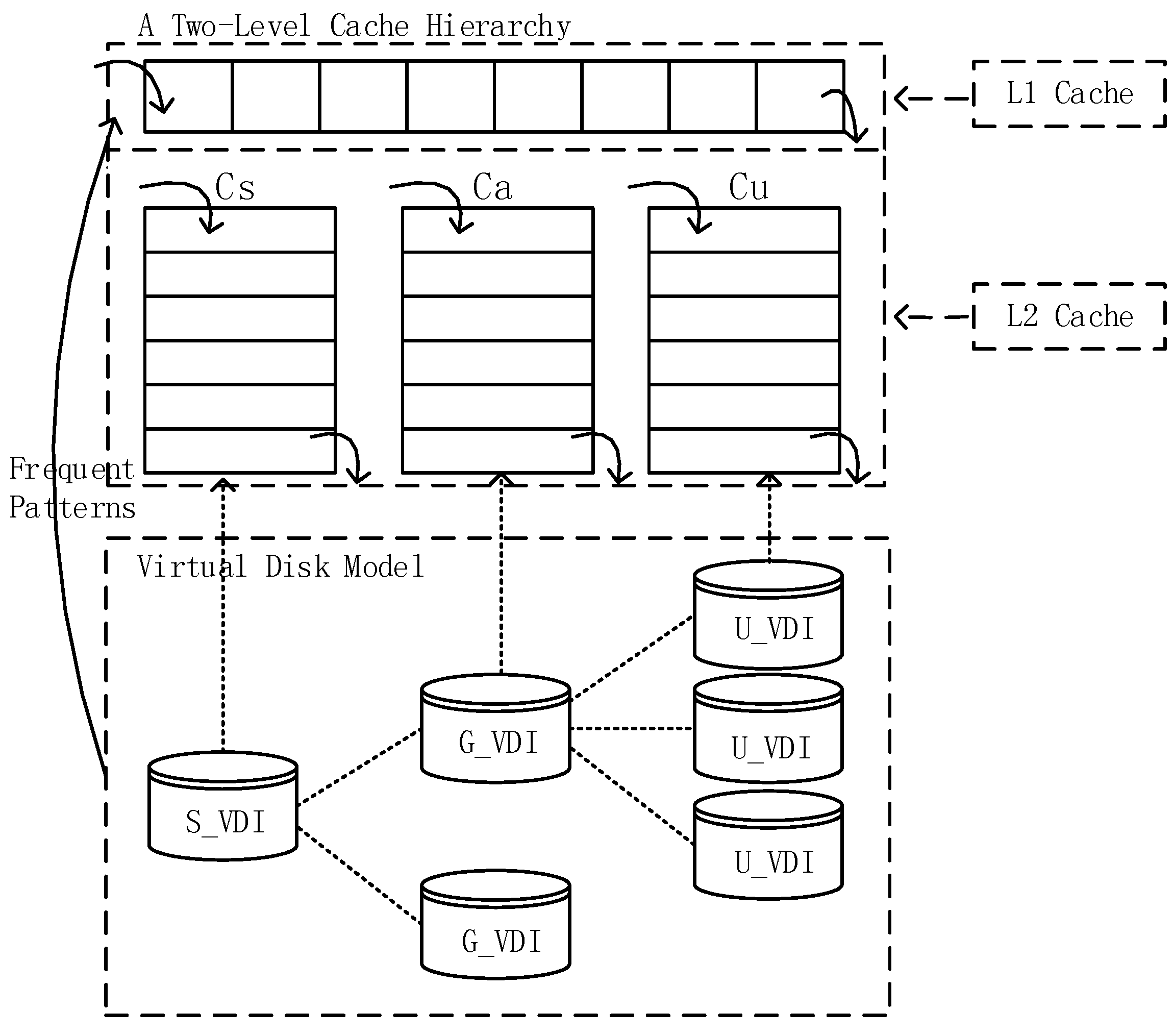
3.3. Caching Strategy
| Algorithm 2: Correlation pattern-based caching strategy. |
| Input : The data block being accessed currently: db; A pattern-tree structure storing frequent patterns: pattern-tree; Output: Null; 1 if db is hit in L1 then 2 move db to the front of the queue in L1; 3 return; 4 else if db is hit in then 5 move db to the front of the queue in ; 6 return; 7 else 8 denote the set of data blocks being prefetched from virtual disk as PDB; 9 PDB ← null; 10 if db exists in pattern-tree then 11 for each node (denoted as pnode) representing db in pattern-tree do 12 add all the nodes in pnode’s prefix path to PDB; 13 if pnode has children nodes then 14 for each node (denoted as cnode) in pnode’s children nodes do 15 call extractSet (cnode, PDB); 16 end 17 end 18 end 19 place data blocks in PDB at the front of the queue in L1; 20 return; 21 else 22 prefetch data blocks db from virtual disk; 23 place db at the front of the queue in ; 24 return; 25 end 26 end 27 Procedure extractSet (node, PDB){ add node to PDB; if node has child nodes then for each node (denoted as cnode) in node’s child nodes do call extractSet (cnode, PDB); end end } |
4. Experimental Analysis
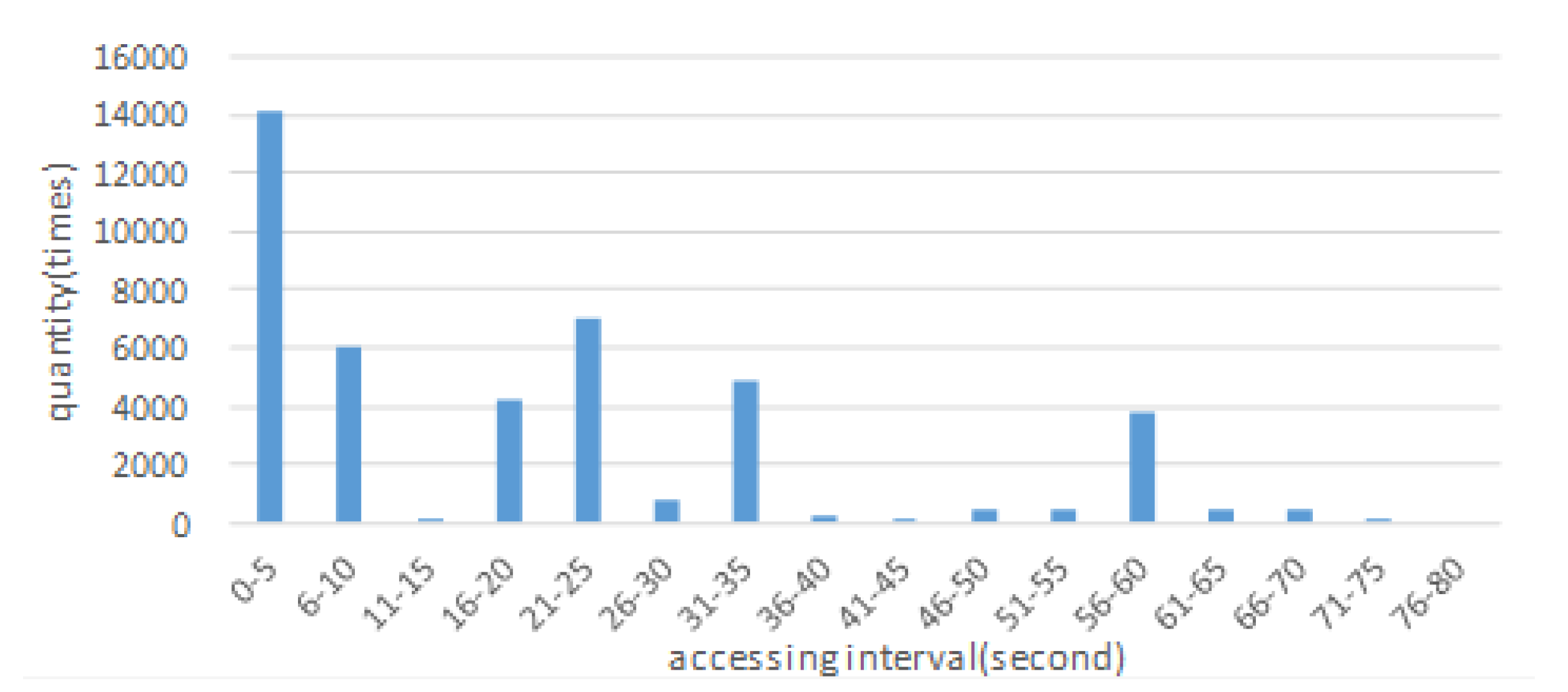
4.1. Cache Simulation
4.2. Parameter Configuration
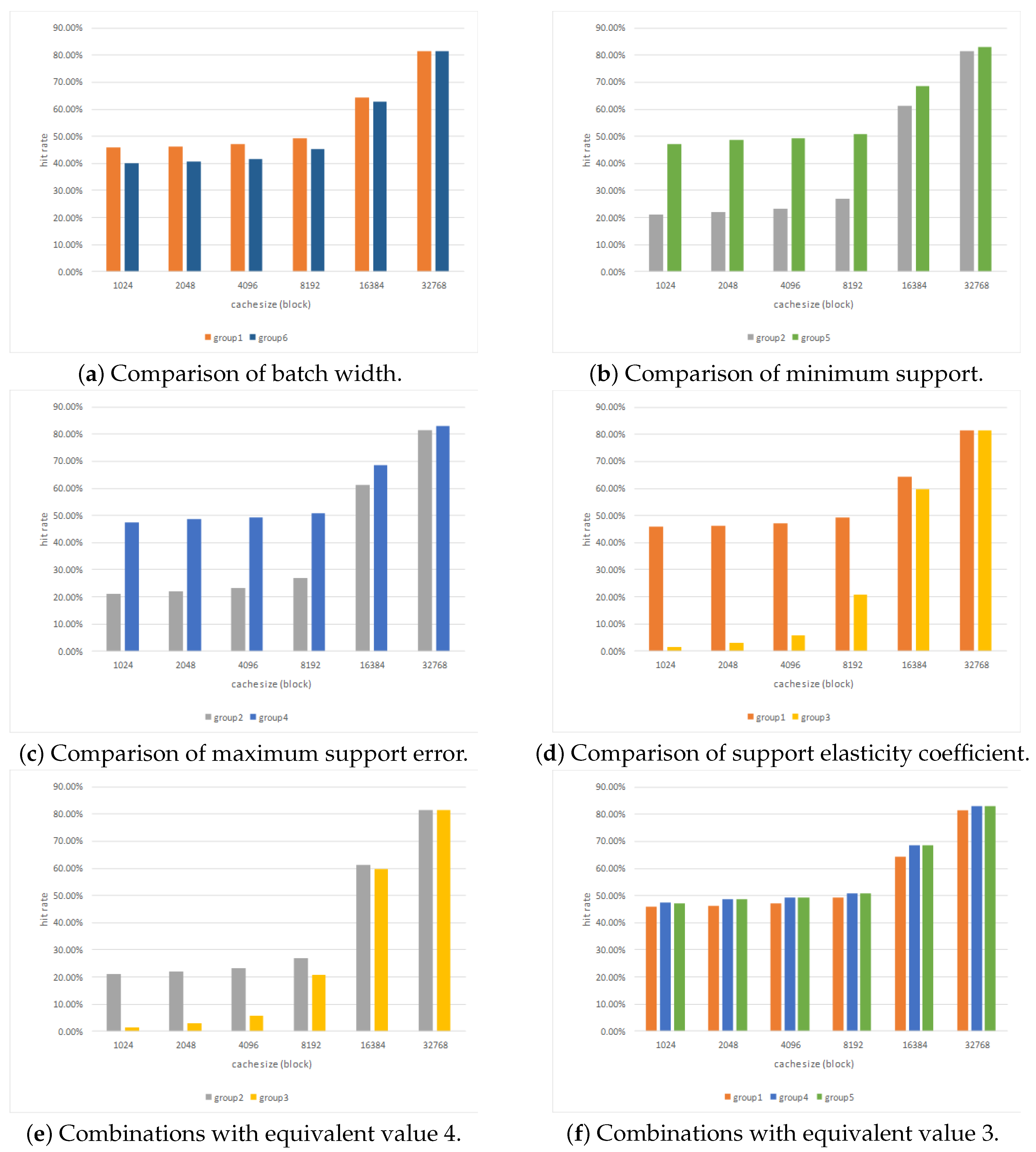
4.3. Comparison of Runtime
4.4. Caching Efficiency
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, X.; Chen, M.; Taleb, T.; Ksentini, A.; Leung, V. Cache in the air: Exploiting content caching and delivery techniques for 5G systems. IEEE Commun. Mag. 2014, 52, 131–139. [Google Scholar] [CrossRef]
- Markakis, E.; Negru, D.; Bruneau-Queyreix, J.; Pallis, E.; Mastorakis, G.; Mavromoustakis, C. P2P Home-Box Overlay for Efficient Content Distribution. In Emerging Innovations in Wireless Networks and Broadband Technologies; IGI Global: Hershey, PA, USA, 2016; pp. 199–220. [Google Scholar]
- Shi, W.; Cao, J.; Zhang, Q.; Li, Y.; Xu, L. Edge Computing: Vision and Challenges. IEEE Internet Things J. 2016, 3, 637–646. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Y. Transparent Computing: A New Paradigm for Pervasive Computing; Springer: Berlin, Germany, 2006. [Google Scholar]
- Zhang, Y.; Guo, K.; Ren, J.; Zhou, Y.; Wang, J.; Chen, J. Transparent Computing: A Promising Network Computing Paradigm. Comput. Sci. Eng. 2017, 19, 7–20. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, Y.; Zhou, Y. Performance Analysis of Virtual Disk System for Transparent Computing. In Proceedings of the 9th International Conference on Ubiquitous Intelligence and Computing and 9th International Conference on Autonomic and Trusted Computing, Fukuoka, Japan, 4–7 September 2012; pp. 470–477. [Google Scholar]
- Gao, Y.; Zhang, Y.; Zhou, Y. A Cache Management Strategy for Transparent Computing Storage System; Springer: Berlin, Germany, 2006; pp. 651–658. [Google Scholar]
- Tang, Y.; Guo, K.; Tian, B. A block-level caching optimization method for mobile transparent computing. Peer Peer Netw. Appl. 2017, 1–12. [Google Scholar] [CrossRef]
- Guo, K.; Tang, Y.; Ma, J.; Zhang, Y. Optimized dependent file fetch middleware in transparent computing platform. Future Gener. Comput. Syst. 2015, 74, 199–207. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, Y.; Zhang, D. TranSim: A Simulation Framework for Cache-Enabled Transparent Computing Systems. IEEE Trans. Comput. 2016, 65, 3171–3183. [Google Scholar] [CrossRef]
- Lin, K.W.; Chung, S.; Lin, C. A fast and distributed algorithm for mining frequent patterns in congested networks. Computing 2016, 98, 235–256. [Google Scholar] [CrossRef]
- Agrawal, R.; Srikant, R. Fast Algorithms for Mining Association Rules in Large Databases. In Proceedings of the 20th International Conference on Very Large Data Bases, Santiago de Chile, Chile, 12–15 September 1994; pp. 487–499. [Google Scholar]
- Han, J.; Pei, J.; Yin, Y. Mining Frequent Patterns without Candidate Generation. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 16–18 May 2000; pp. 1–12. [Google Scholar]
- Leung, C.K.; Khan, Q.I.; Li, Z.; Hoque, T. CanTree: a canonical-order tree for incremental frequent-pattern mining. Knowl. Inf. Syst. 2007, 11, 287–311. [Google Scholar] [CrossRef]
- Koh, Y.S.; Pears, R.; Dobbie, G. Extrapolation Prefix Tree for Data Stream Mining Using a Landmark Model; Springer: Berlin, Germany, 2012; pp. 340–351. [Google Scholar]
- Chen, X.j.; Ke, J.; Zhang, Q.q.; Song, X.p.; Jiang, X.m. Weighted FP-Tree Mining Algorithms for Conversion Time Data Flow. Int. J. Database Theor. Appl. 2016, 9, 169–184. [Google Scholar] [CrossRef]
- Ölmezoğulları, E.; Arı, İ.; Çelebi, Ö.F.; Ergüt, S. Data stream mining to address big data problems. In Proceedings of the Signal Processing and Communications Applications Conference (SIU), Haspolat, Turkey, 24–26 April 2013; pp. 1–4. [Google Scholar]
- Giannella, C.; Han, J.; Pei, J.; Yan, X.; Yu, P.S. Mining frequent patterns in data streams at multiple time granularities. Next Gener. Data Min. 2003, 212, 191–212. [Google Scholar]
- Zhang, Y. Transparence computing: Concept, architecture and example. Acta Electron. Sin. 2004, 32, 169–174. [Google Scholar]
- Zhang, Y.; Zhou, Y. 4VP: A Novel Meta OS Approach for Streaming Programs in Ubiquitous Computing. In Proceedings of the 21st International Conference on Advanced Information Networking and Applications (AINA 2007), Niagara Falls, ON, Canada, 21–23 May 2007; pp. 394–403. [Google Scholar]
- Zhang, Y.; Zhou, Y. Separating computation and storage with storage virtualization. Comput. Commun. 2011, 34, 1539–1548. [Google Scholar] [CrossRef]
- Chadha, V.; Figueiredo, R.J.O. ROW-FS: A User-Level Virtualized Redirect-on-Write Distributed File System for Wide Area Applications; Springer: Berlin, Germany, 2007; pp. 21–34. [Google Scholar]
- Ayres, J.; Flannick, J.; Gehrke, J.; Yiu, T. Sequential PAttern mining using a bitmap representation. In Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Edmonton, AB, Canada, 23–26 July 2002; pp. 429–435. [Google Scholar]
- Chen, Y.; Dong, G.; Han, J.; Wah, B.W.; Wang, J. Multi-Dimensional Regression Analysis of Time-Series Data Streams. In Proceedings of the 28th International Conference on Very Large Data Bases, Hong Kong, China, 20–23 August 2002; pp. 323–334. [Google Scholar]







| Transaction Number | Items |
|---|---|
| 1 | I1,I2,I5 |
| 2 | I2,I4,I6 |
| 3 | I2,I3 |
| 4 | I1,I2,I4,I6 |
| 5 | I1,I3 |
| 6 | I2,I3 |
| 7 | I1,I3 |
| 8 | I1,I2,I3,I5 |
| 9 | I1,I2,I3 |
| Frequent Patterns | Support Count |
|---|---|
| 2 | |
| 2 | |
| 2 | |
| 2 | |
| 2 | |
| 2 | |
| 2 | |
| 2 | |
| 2 | |
| 2 | |
| 6 | |
| 4 | |
| 2 | |
| 4 | |
| 6 | |
| 4 | |
| 7 |
| Frequent Patterns | Support Count |
|---|---|
| 2 | |
| 2 | |
| 2 | |
| 4 | |
| 4 | |
| 2 | |
| 4 |
| Group | Batch Width (s) | Minimum Support | Maximum Support Error | Support Elasticity Coefficient |
|---|---|---|---|---|
| Group 1 | 30 | 0.19 | 0.02 | 0.6 |
| Group 2 | 40 | 0.19 | 0.02 | 0.6 |
| Group 3 | 30 | 0.19 | 0.02 | 0.8 |
| Group 4 | 40 | 0.19 | 0.05 | 0.6 |
| Group 5 | 40 | 0.17 | 0.02 | 0.6 |
| Group 6 | 20 | 0.19 | 0.02 | 0.6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Chen, L.; Li, W.; Sheng, J. A Caching Strategy for Transparent Computing Server Side Based on Data Block Relevance. Information 2018, 9, 42. https://doi.org/10.3390/info9020042
Wang B, Chen L, Li W, Sheng J. A Caching Strategy for Transparent Computing Server Side Based on Data Block Relevance. Information. 2018; 9(2):42. https://doi.org/10.3390/info9020042
Chicago/Turabian StyleWang, Bin, Lin Chen, Weimin Li, and Jinfang Sheng. 2018. "A Caching Strategy for Transparent Computing Server Side Based on Data Block Relevance" Information 9, no. 2: 42. https://doi.org/10.3390/info9020042
APA StyleWang, B., Chen, L., Li, W., & Sheng, J. (2018). A Caching Strategy for Transparent Computing Server Side Based on Data Block Relevance. Information, 9(2), 42. https://doi.org/10.3390/info9020042