1. Introduction
Ideological polarization has been addressed as a potential problem for healthy societies. There has been an increase in the attention given to the subject in recent years with a particular focus on various political disagreements and how to resolve them. These considerations have been modeled in various paradigms such as the spatial segregation model [
1] (Schelling model), direct survey analysis [
2], ideological exchanges [
3,
4,
5], as well as other approaches. Given the recent discussion of a possible association between this increase in polarization and the use of online social networks, questions about the particular features that might have caused this change are becoming extremely important. Online social networks provide a means for the exploration of a wider community with reduced costs of connecting over longer distances and if this ease of connection is not properly investigated, its negative side effects may potentially grow. The question explored here is whether there is valid concern that a combination of access to a larger size of potential friends with tendencies towards homophily (ideological) can produce a network that is more polarized than if the accessibility were more constrained to a set of random set of associations (local view). Recent results that have been discussed suggest different outcomes in relation to polarization and this work aims to extend a general purpose model to explore the outcomes of the dynamics of opinion exchange in randomly produced graphs according to varying degrees of access towards friends and homophily. The vital extension is the explicit representation of the discussion groups upon which many of the premises rely. The ability to connect through a homophilic bias relies on group interactions and the existence of common ideological standpoints implies a platform for exchange between like-minded individuals. The examination of this element in the model and simulation shows that the results can change from amplifying the effects or dampening them. This work also provides investigation into situations where more than two ideologies are present, both within the original Davies model and with the discussion extensions.
The work presented here addresses some of the shortcomings and extends the model produced in [
6]. Referred to in this paper as the Davies model (Davies [
6]), a methodology for producing social networks using the concepts of local associates, accessibility, homophily [
7] and ideological label assignments. The results of this research are important to thoroughly investigate as they provide evidence against the conclusions widely accepted in the well known work of Axelrod [
8]. The work reinforces alternative conclusions that an increase in range will facilitate greater polarization [
9] and that different parameterizations of the model can change the predictions [
10]. The deficiencies of the model and presentation are addressed to support certain aspects that can support a change of perspective regarding the association of accessibility and homophily with the production of polarization in the ideological separation between members of a network. From the extended presentation of the results, it becomes evident that the conclusions which seek to overturn many previously published articles can be concluded from only a partial view of a simulation trace. Namely, although this model is apparently simple, it can display two phases under certain parameter settings: an increase in “polarization” (ideological segregation) followed by a single phase of decrease in that effect towards ideological consensus over the whole network. Segregation can arise from a multitude of reasons and given the model framework it will be a result of ideological polarization. A more complete picture of the behavior of the simulations becomes evident and the potential misconceptions from working with such models can be avoided in future use, which is of importance. Although consensus is shown to be arrived at, the initial increase can be a significant feature if there are thresholds in which social cohesion can be at threat due to increases.
The necessary features lacking in the model of Davies is the representation of a group/organization that is presumed, and this work presents the extended Davies model that incorporates this. A full presentation of the results allows some of the previous questions and comments to be answered. Mainly the question about the final state and significance of the polarization increases through a full trajectory plot can be answered. The discussion groups, modeled as randomly allocated memberships and those based around ideological identification with two and four different ideological groups, are shown.
It is assumed that the ideologies are a discrete label set similar to the discussion threads organized by hashtags, rather than a placement within a continuous domain of ideological memberships, as in [
11]. The impact of discussion threads is explored in depth in [
12], which shows that homophilic attractors (echo-chambers) can intensify the distance between different network members without the need for the negative influence. The model does not account for the particularities of the means of communication or the dynamics of exchange between certain ideological labels. This may at first appear to be a deficiency and in terms of real world applicability for understanding particular dynamics related to polarization it may be, but here the question of the role that social networks may play is the main focus of the investigation. It is a question as to whether there is an intrinsic feature of online social networks that could facilitate an increase of polarization. One of the core revolutionary features of online social networks is that it provides greater access to people around the world in terms of breadth of potential candidate friendships and depth of the information. The work of Mark [
13] discusses how these memberships into different groups (application to culture) can form and evolve to produce a homophilic attraction as competition between cultures. This paradigm is taken into account with the application of the ideological label swappings permitted in the stochastic simulation.
The Davies model produces a set of local associates, i.e., members of society who a person (node within the context of a network) is randomly allocated through work affiliations or spatial proximities of pairs of people. Then, a graph of friends for each node is produced where a local associate is chosen at random, or one node uniformly (randomly) from the rest of the nodes in the graph. This choice between the sets of nodes is then made based on the parameter of
accessibility and the individual friendship selection is made based upon the parameter of
homophily. In summary, the results from the Davies model show that an increase in the accessibility of a user, a greater range of choice of contacts, in the presence of homophily will produce an increase the measure of assortativity [
14] (polarization of ideologies within the network structure shown by separations). The findings of Davies [
6] allude to conclusions that there is an association of greater accessibility with an increase of polarization (ideological segregation). Therefore, the topic warrants a careful examination as well as confirmatory efforts. Since online platforms facilitate communication at a reduced cost and latency, if there is a byproduct of this efficiency over time and space in a way that polarization can be reinforced. In light of this potential, further research within this area is necessary. Assortativity captures segregation between members in the network and it is used as a proxy for the interpretation of polarization as an edge set which does not connect different ideological members.
An independent implementation of the Davies model has been produced and simulations produced from it. The provided code on GitHub was used to ensure that the description in the paper was understood correctly but the implementation was produced independently to avoid duplication of mistakes that may have been present in the original implementation (one measure of independence was to choose a different programming language).
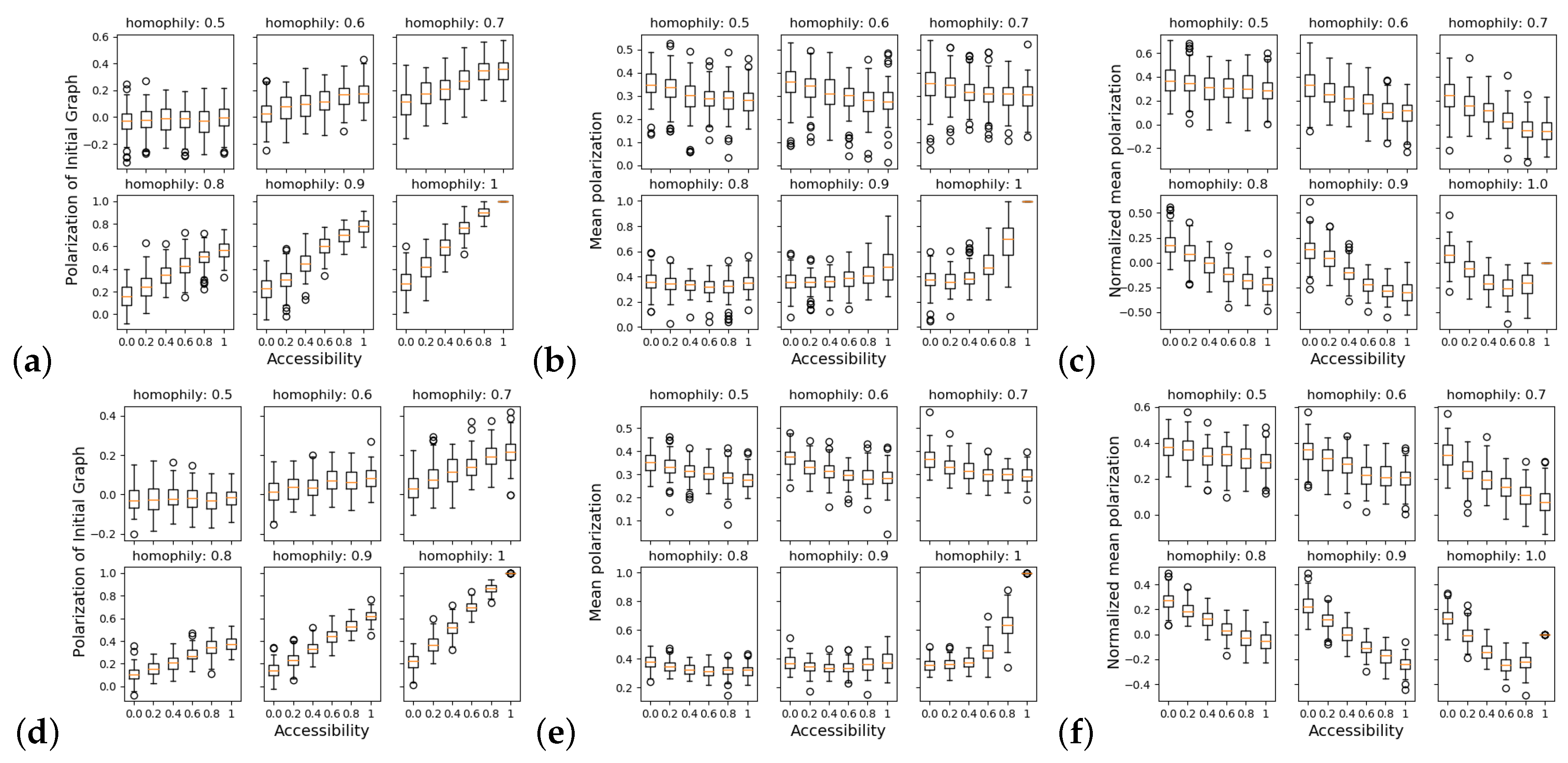
Figure 1 presents the results of the independent simulations, which confirm the results shown in the first panel of Figure 2 in [
6]. The main feature is that an increase of accessibility can be associated with an increase in polarization (measured by assortativity).
Figure 1a shows a panel of plots representing the initial state of the friendship graphs after all friendship edges have been assigned using the accessibility and homophily parameters. It can be seen that larger values of homophily and accessibility can produce a greater value of polarization (measured via the Newman assortativity).
Figure 1b,c displays the results of using the Binary Voting Model (BVM), where there is an exchange of ideological labels.
Figure 1b shows the mean value of the polarization from Iteration 50 to the final iteration and
Figure 1c the mean through until the last iteration minus the values from the initial state. In this figure, it can be seen that the model creates an initially polarized arrangement of connections so that those “users” who had homophilic preferences and a high degree of accessibility produce more polarization than those with less accessibility. Using a standard manner of ideological exchange, this effect can be reduced when the edge connectivity remains constant. The methodology for the creation of the network and the simulation details are presented in
Section 2.
Figure 1d–f shows an equivalent analysis but with an increase in the number of ideologies from two to four. With the set of ideologies being mutually exclusive to each other, the effect of a larger discussion can be examined where the network is not completely anchored upon a single topic. The effects can be seen to reduce the magnitudes of the assortativity (polarization), although the same features are found. From these results, it is not clear if the ideological consensus is reached given a larger number of iterations or averaging over a larger run will reduce the impact of the phases of polarization initially and the initial increases.
The reproduced results from the Davies model demonstrates that accessibility can facilitate nodes to develop a greater proportion of homogeneous friendships in the graphs when label associations exist, and there are homophilic preferences in connections according to the labels. During the initialization phase of the friendship graph, an increase in assortativity as a proxy for polarization in this model shows that accessibility and homophily can induce polarization. For a certain number of iterations of the model, this state of polarization can continue according to the results in [
6]. This is used to provide a counterargument to the conclusions of the model in [
8] that accessibility reduces polarization and that this conclusion may not always hold, which brings into question whether negative effects from boundless accessibility exists and that new Internet platforms could then provide an avenue for increased polarization.
What is absent from [
6] is an examination of the trace from the simulations to examine the stability of the network polarization values where accessibility can be shown to increase polarization. The results then describe a more complex situation where there are configurations of the parameters that allow for a initial phase of increase in polarization followed by a decay phase that results in complete homogenization. Although some statistics for the various phases of the simulation can present an overall increased assortativity value from initialization, this would not exist for longer simulation runs where the homogeneous region comprises a longer period of simulation time points. Insight into the feature reveals an artifact that is frequently observed in multiple simulation scenarios. Namely, adjacent ideological exchanges occur at a different expected stage in the simulation compared to the cross cluster assignments.
In [
6], analogs from society are used to motivate the difference between local associates and those that are outside the affiliations from being a functional member of society. Those outside yet accessible depend upon a parameter value that controls the probability that such a connection can occur and certain platforms change that probability. From the societal analogs described as example from where the facility to access non-local associates can arise from, examples such as Twitter communities, Rotary Clubs and others are mentioned (examples of this in real world scenarios are discussed in [
15,
16]). These aggregations of users provide a meeting place for the choice process of new friendships to occur outside of the pre-existing locality and provide the means for the accessibility but are not explicitly modeled. It is therefore necessary to explore the effect of the introduction of such a feature to ensure that the process which produces the results shown continues to support the same conclusions. Even if the qualitative results show that an increase in accessibility is able produce more polarization, it is a requirement to see if the presence of groups/community organizations invalidates the results or whether any effect is produced.
Section 2 provides a more thorough presentation of the methodology and the extended model that addresses the gap in the model paradigm with a clear overview of the simulation trajectories. The important finding is that the previous findings were based upon an isolated view of the simulation ignoring the complete simulation trajectory. By investigating the complete trajectory, a change in the conclusion previously established is derived, i.e., in general, polarization will inevitably be reduced but there are situations where topological arrangements can induce short-lived increases in polarization. The conclusions here are supported by the results in [
17], which discusses how the question of increased personalization and homophilic interactions can induce higher degrees of polarization based upon mechanisms of rejection or persuasion. Although not explored in this work, it is noted that the exploration done reinforces the findings in [
17] that large networks fail to display the polarization phenomena for many of the parameterizations that result in polarization for smaller networks. Discussion groups comprised of randomly allocated ideological members and those according to a homophilic parameter are examined assess their impact given two or four different ideologies.
This can mirror the conclusions in [
18] where long range ties prompted negative interactions and that those in close proximity become more similar, self reinforcing their identification. The use of the discussion threads/groups corresponds to this close proximity tie set and where a small-world network model was used here the structure follows a Erdos–Reyni graph instead. There is a single dimension for the ideological shift during exchanges between network members to model a polarized system in [
6]. Homophily here represents an individual’s willingness to develop a friendship connection with another person who shares a differing ideological opinion. More specifically,
H represents the probability that a friendship will be generated with an individual of similar ideological alignment and
represents the probability that a friendship will be generated with an individual of opposite ideological alignment. Dynamics of political polarization is discussed in [
19] for a heterogeneous opinion set in reference to a commonly shared issue but with the possibility for different label allocations. In the investigation, the dynamics of “takeoff” issues, in which there is more than a single dimension to a topic, is introduced. This is explored in the simulation studies given that, during unrest, a homogeneity amongst the members during a “takeoff” is not expected to exist. Flache and Macy [
18] acknowledges how the elements of intercultural differences (perturbations) can significantly change the results and perturbation examination is performed here to test the stability of the results. The time points in the simulations here represent a unit of time for which ideological exchange can occur. The rate at which exchanges can occur in between people in the environment (digital or not) is the unit represented here.
2. Methodology
The Davies model (as referred to here) is presented in [
6], and aims to investigate the effect of three parameters in the creation of networks where a single ideology (from a set of ideologies) can be held by each node. These three parameters are
accessibility,
homophily and
dynamic balancing. Using these parameters, networks of a fixed number of nodes (hypothetical users) are able to produce a friendship network from a set of local associates and those outside based upon the amount of accessibility offered, which is increased through online services/platforms. Each network consists of 40 nodes in the Davies model and the same number was used here; presumably taken as the second Dunbar number [
20] (which is more recently confirmed in an analysis of microblogs [
21]). The
dynamic rebalancing is not presented in this work, as the Davies results and those produced independently show no new qualitative insights from its use. Two different ideologies were considered to label users in the initialization of the first stages of the network creation and that users change these labels according to the classic Binary Voter Model (BVM) [
22]. An extension of the Davies model was developed and presented to incorporate the facility of the networks referred to in [
6] of group memberships and organisations. In that work, Rotary Clubs, political parties, Twitter communities and others are mentioned as memberships which provide means to access those with similar ideologies, although that effect is not accounted for, but is included in the model presented here.
The parameter of accessibility, A, regulates the probability of choosing between the local associates produced in the generation of the ER graph for initial neighbors and the chance of using a medium such as the Internet to sample connections outside of that initial locality provided. Sampling a friendship from the local neighbor set is done with probability and draws a neighboring edge within the ER graph that is not already present. For a node i, is that node’s position in the ER graph and represents the number of edges (friendships) i will produce that are distributed between those in (given local associates) and those sampled outside of that set . This probability regulates the ratio of the friendships that are associated with a process of regular association with surrounding individuals rather than those that can be independently searched for. The friendship graph will maintain the number of edges for each vertex, , so that the accessibility replaces friendships that would otherwise be included from the local associate set supplied by default. It can be considered that the local associates still exist and should still be considered explicitly but those in that are no longer included in will have no ideological influence in the simulation (it is possible to be an associate but not a friend with ideological influence).
Given the set of nodes to sample from (local associates or outside of that group), that set is then differentiated into those with the same or different ideological labels.
Homophily,
H, is the probability that an edge is produced between nodes with the same ideology, and
for choosing a node with the opposite label (type of heterophily). For a homophilic friendship assignment,
(same ideology), otherwise probability
a different ideological node is chosen,
. An edge in the friendship graph is added
according to:
Here, the reference to is the intermediate set of nodes that differentiate between the choices of local associates and those outside that group.
In Algorithm 1, the steps of the Davies model are presented in a different manner to what is originally provided with the aim that the model can more easily be understood. Steps 1–4 initialize the network where the main components of accessibility and homophily determine the ratio of friend candidates chosen from local associates or those outside of that group uniformly and from those candidates the homophily parameter is then used to choose according to that probability that such a node with the same or different ideology is included in their friendship graph
. The selection of candidate nodes as friends may end up being void for certain iterations, such as when the initial
associates graph produces zero edges for a node and then the addition of edges is bypassed. Step 5 corresponds to the operation of the classic BVM, which draws uniform samples of the nodes in a friendship graph, and then allows a node to propagate its ideology deterministically. The main feature which relates the accessibility to the homophily is that the accessibility allows for a greater number of homogeneous nodes to be discovered when creating the friendship graph.
| Algorithm 1 Previous approach: Outline of the methodological approach of the Davies model for the initialization of graphs of social inconnectivity based upon the parameters of accessibility A and homophily H. The purpose it to examine whether accessibility and homophily can produce unexpected changes in the assortativity (polarization) amongst nodes with specific ideologies. The interplay of accessibility and homophily can produce different results when interactions are found and developed through online platforms that provide a greater means for users to fill their social circle with a greater proportion of like minded individuals. |
Generate an undirected Erdos–Reyni graph according to a chosen p, to produce a Local Associates Graph, ( where ) Uniformly assign each node an ideology from set of ideologies , Generate corresponding Friendship Graph, with and initialize for every to have , For add friends to while Select: - (a)
With probability A (accessibility), sample a candidate edge uniformly among non-current associates (non-neighbors), , and with probability choose an edge uniformly from the Local Associates Graph - (b)
Assign to each potential friendship node probability H, if (same ideology), otherwise probability , - (c)
Include edges between candidates and according to the probability
Simulate the Binary Voter Model (BVM) for T iterations while - (a)
- (b)
- (c)
Change ideology of according to:
|
The
assortativity coefficient [
14] was used to examine the magnitude of polarization, since it quantifies the lack of connectivity between users of different ideological labels. Its values range between −1 and +1, and for the edge pairs in the friendship graph,
where the node pairs are
, those edges between identical ideologies are denoted as
when
. We consider
to be represented as a matrix that allows the assortativity to then be given by:
with
being the trace of the ideology matrix between nodes that are connected. A value close to 1 is indicative of strong homophily and −1 that of heterophily with 0 corresponding to a lack of bias.
Extension of Davies Model
This subsection describes the alterations of the Davies model which accounts for the presence of discussion groups as well as the changes in assortativity values in the simulation. The modeling design does not affect the dynamics of the network initializations and has an effect when nodes interact in an ideological exchange. The explicit representation of a negative interaction between users of different ideological memberships is not produced as this approach adopts from the conclusions of Mäs and Flache [
12] in that homophily between users in closer proximity can create a polarized state from others based upon a common issue.
The procedural elements of the
extended Davies model are presented in Algorithms 2 and 3. In Algorithm 2, the steps to initialize the network based upon the accessibility
A, homophily
H, and the introduction of the new feature where users are assigned to discussion groups based upon similar ideologies are described. This new feature can be seen as a uniform sample across the
ideologies available and the number of
discussions where a user of a particular ideology can be placed subsequently. This discussion group membership in the initialization stage does not affect the edge creation between nodes as the accessibility and homophily do. This membership will play a role in the simulation of the ideological exchange in the iterations post initialization. As the edge productions are not affected by the presence of a discussion group membership or absence of membership, the assortativity (polarization) measurement at initialization will not be altered. Here, the discussion groups for the simulations conducted will follow that of the Davies investigation of two groups of ideologies, but this effect can easily take a different number of group memberships for equality testing. This premise is also comparable to the group similarity verification which is done at the micro level in models of residential dynamics such as the Schelling model [
1].
Algorithm 3 shows the procedures of the extension of the BVM which accounts for the presence of the discussion groups introduced in Algorithm 2. One important point to consider is that “None” is a possible option in assignment of discussions in Algorithm 2. In
Section 3, two different implementations are provided with different values used to control the rate at which None is assigned as a discussion. The standard BVM is a direct asymmetric label propagation between non-identical ideological associations in which structural information of the network is not taken into account in terms of the neighbor influences. It is considered that the neighboring label set will play a role in the ability of a node to change the ideology of another node, as noted in [
23,
24]. This information is brought into the model by the membership of a node in a discussion group based upon similar ideologies. It is also considered that it is through these discussion groups that the accessibility for edge creations, outside of the locality, makes it possible to facilitate a search based upon the parameter of Homophily. Since the simple random sample is not representative of the intelligent optimal association searches that platforms offer services for. The quantitative effect of the membership on the BVM is that the probability of a successful ideological conversion will then be inversely proportional to the size of the group.
| Algorithm 2 Extended Davies initialization algorithm. |
procedureInitializeGraph() for all do end for for all do while do if then else end if for all do if then else end if end for end while end for return end procedure
|
| Algorithm 3 Binary Voter Model (BVM) extended to consider discussion group effects. |
procedureBVM() for do if then end if end for end procedure
|
3. Results
Here, the results of the simulations of the Davies model, shown in Algorithm 1, and the extended Davies model described in Algorithms 2 and 3, are presented. The main feature that differentiates the two models is that the extension accounts for the membership of users in discussion groups (communities, echo-chambers, clubs, etc.), in which the participation is associated with a homophilic interaction. From the simulations, a comparison was made as to what impact this can make upon the trajectories of the simulation that are based upon the Binary Voter Model (BVM). Each of the simulation runs included a network of 40 agents, the same value as in [
6], again presumably in accordance with the second Dunbar number from [
20].
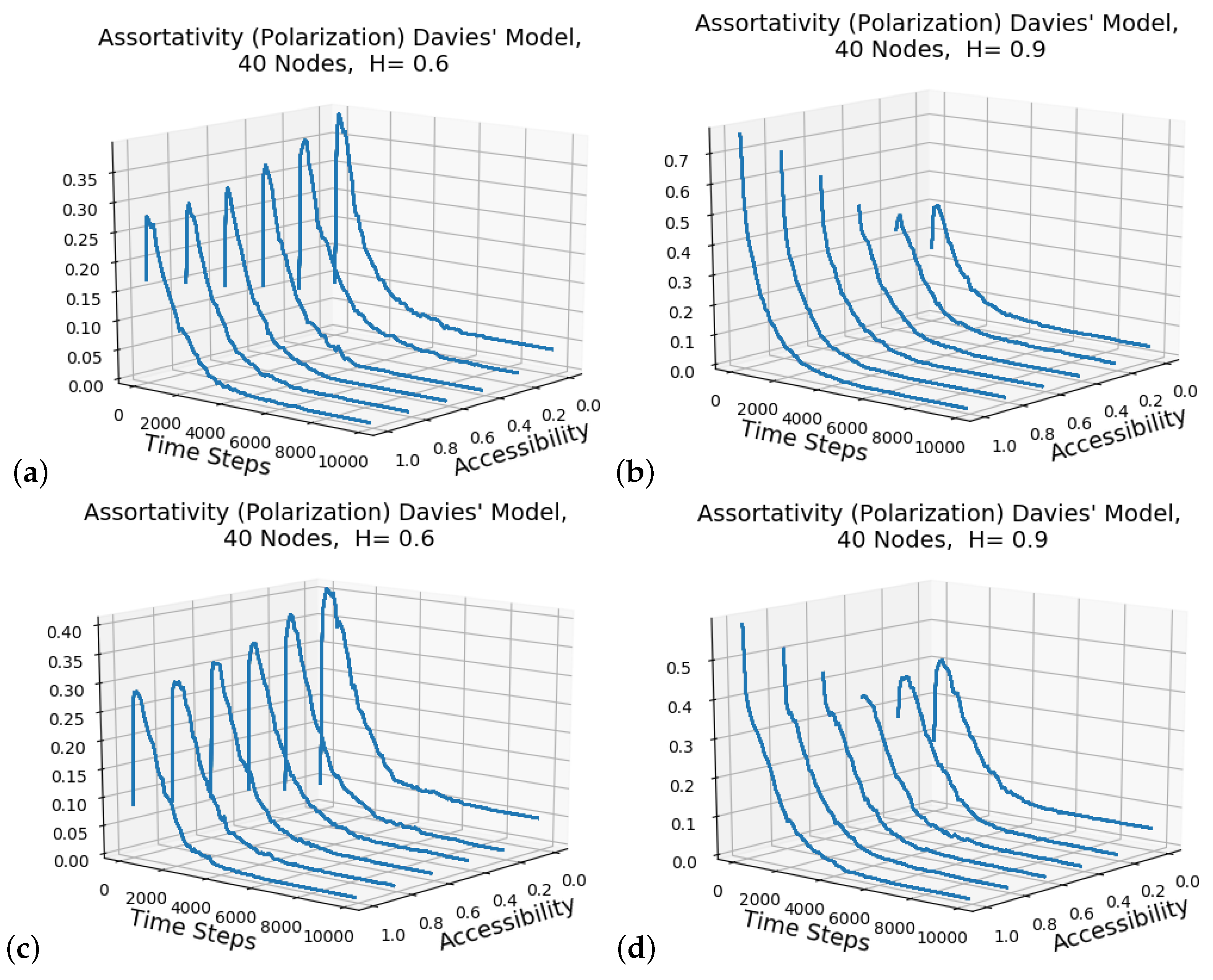
Figure 2 displays a set of trajectories of the Davies model for two different values of the homophilic affinity of ideological connectivity beyond a node’s locality with values
and
(
Figure 2a,b, respectively) for a range of accessibility values
. These plots are meant to expand upon the results presented in
Figure 1, which are presented in the Davies paper and are averages over 500 independent simulations for the different
parameter values. The iteration number for the simulation is plotted against the assortativity that provides a quantification for the amount of “polarization” between nodes of different ideologies in the network. It is interesting to point out that there are parameterizations for which there can be an increase in the polarization from the initial values and also that the increase in the accessibility values introduces greater initial polarization prior to the process of ideological homogenization, which begins with iterations of the BVM. In
Figure 2a, the lower
A values produce increases in the assortativity early in the simulations, and this is seen as well in
Figure 2b for
. The reason this feature has increased presence with lower
A values and
H is that the initial networks are less interconnected due to members having fewer “long-range” associations so that the communities/clusters in a first stage of ideological label agreements do so without a network wide consensus. The cluster homogeneity forms first before the non-local associations become the predominate cause for the label switching during the BVM. Therefore, this can be seen as a dual phase process with the local community associations conforming to a uniform ideological adoption prior to the full network. In the second phase, the networks proceed towards homogenization with a monotonic decrease in the polarization along the iterations (ignoring the stochasticity inherent of the process, which may produce sporadic irregularities in that pattern). The main feature is that the polarization is increased at the initialization merely by permitting users to explore beyond their local associates when homophilic interactions are a choice.
Figure 2c,d shows the results from having four ideological labels for the nodes. Examining the values in both pairs of figures shows that the increase in the number of ideologies corresponds to a reduction in the assortativity values and more so with
.
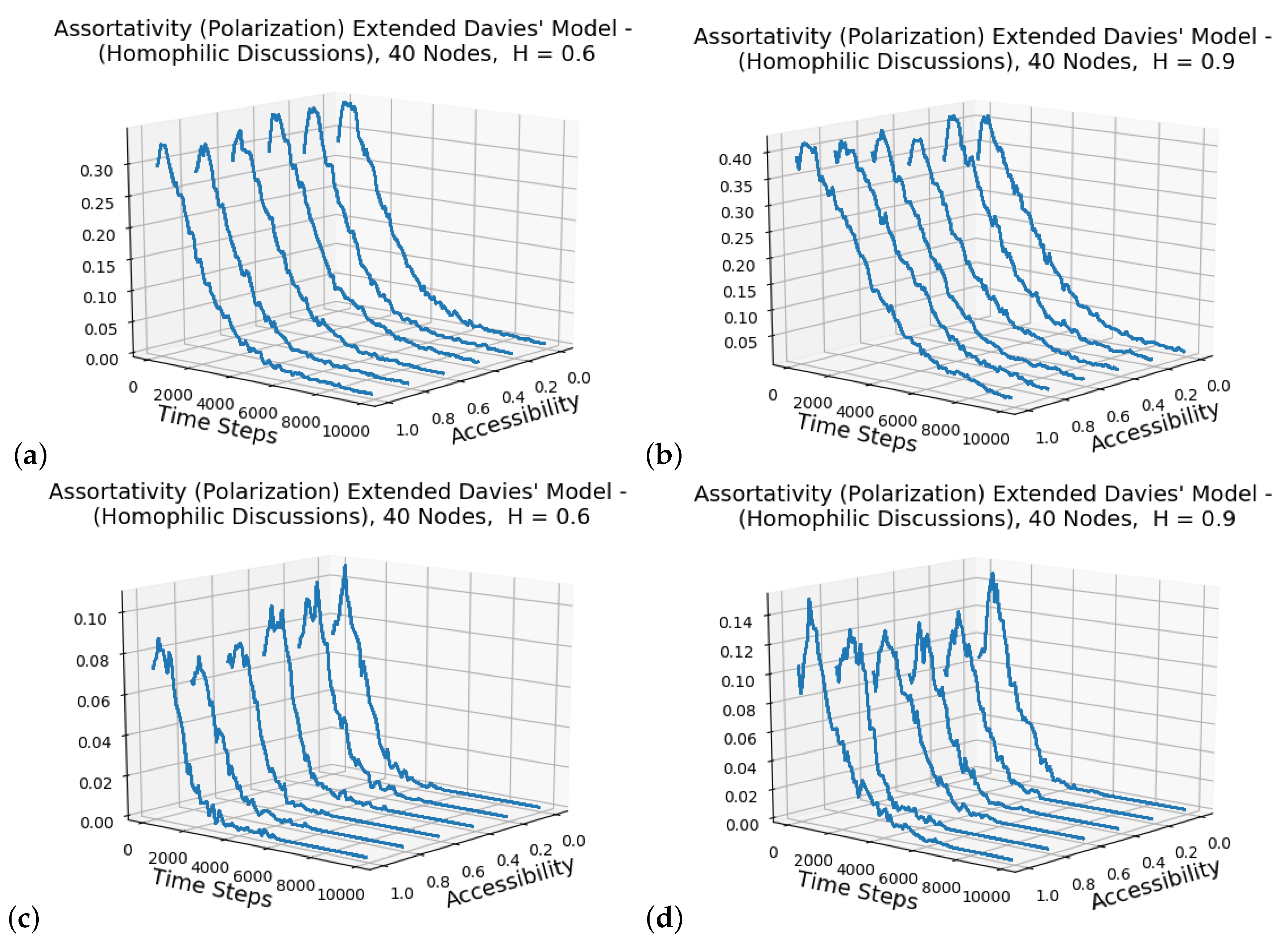
Figure 3 provides the traces for the simulations on the same parameter values
applied the extended Davies model, which includes the creation of randomly allocated discussion groups, as outlined in Algorithm 3. The number of discussion groups in the simulation was equal to the number of ideologies for each run.
Figure 3a,b looks at the the initialization parameters for the network,
and
, respectively, with a range of accessibility values
. Each of the trajectories is an average over 500 independent runs. As noted in the Davies model simulation, for both chosen values of homophily in the network creation, shown in
Figure 2, there is a decrease in the assortativity measure towards the end of the simulation as the BVM stochasticity ends up producing a monolithic ideology amongst all users. The initial values are comparable and the same modes seen in
(
Figure 3a) and for
(
Figure 3b) with
are also seen with the original Davies model results (
Figure 2). The main feature that showcases the difference between the simulation with the discussion groups is that interaction assortativity values are greater with the extension. Since the initial values are similar, the discussion groups introduce a dampening effect upon the reduction of the ideological homogenization process. This corresponds to the expected effects of “echo chambers”, “group think” and incubation of ideas that isolate users from independent ideological exchange.
Figure 3c,d shows the results for four ideologies allocated to the nodes during initialization. The results of the assortativity are lower and the difference between the two sets of figures is greater than the differences noted in
Figure 2.
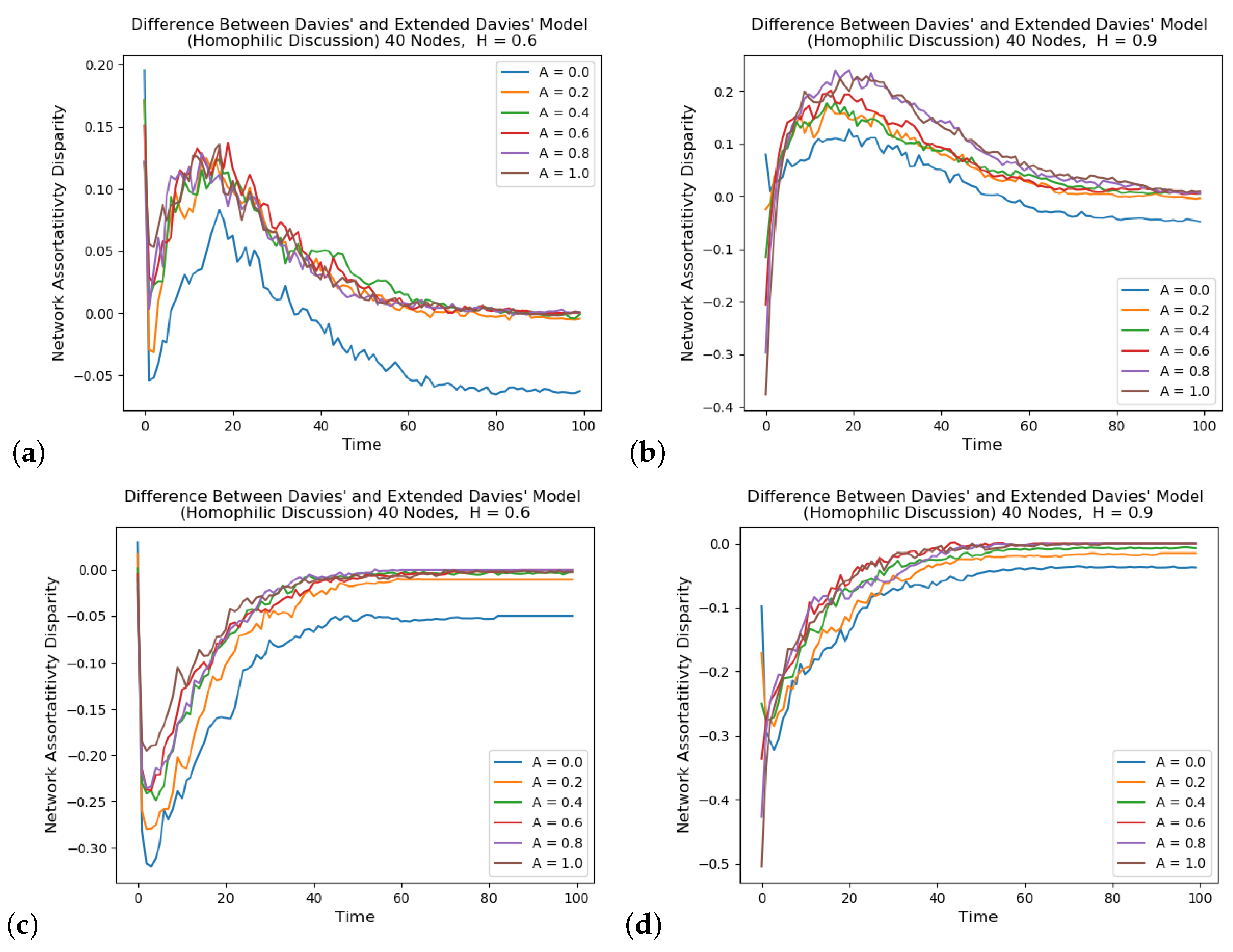
Figure 4 displays the results of the investigation into the difference between values of the network assortativity between the Davies model and the extended Davies model, which accounts for discussion groups (clusters). Of the two simulations presented, the homophily parameter values used in the initializations are
and
in
Figure 4a,b, respectively. A range of accessibility values are chosen and shown in the legend,
. Both models for each parameter pair values were run for 10,000 iterations and the differences are plotted at each 10-iteration step. For both simulations with
and
, the differences at the initialization are low, which is expected since the discussion groupings/clusters were not based upon homophily, which does not affect any edge construction process. Each subfigure traces a set for different accessibility values, which shows an increase in values that then diminishes towards the end of the simulations. That both simulations began at approximately the same point and then ended at the same point is expected, but what is important to notice is the increase in relative assortativity values of the extended Davies model in the first half. Looking at the results in
Figure 2 and
Figure 3, it is evident that the addition of the discussion groups to the formation of the initial network delays the process of the BVM in reducing the assortativity (polarization). Although the accessibility increases this disparity between the models at their maximum difference, it is seen even for low parameter values of
A. The reason the dynamics of the BVM result in an altered trajectory is because the influence of the single points of contact for a change in opinion are outweighed by the aggregate of a discussion group which can mimic the “echo-chamber” and require more messages (iterations) to shift an ideology. These curves having the right tail skew are akin to the complex phenomena observed in many systems.
Figure 4c,d shows the differences in the values in comparing the analogous cases having four ideologies. It can be seen that higher values of H produce an increased disparity between the models, however an unexpected result is that, with four ideologies, the discussion groups actually increase the rate of consensus. While this at first seems counterintuitive, the reason for this change is due to the reduction in effectiveness of the resistance to ideological change when the membership is distributed across more discussions. With more competing ideologies, each individual ideology is weaker in terms of its control of the whole group. This allows for the first ideological group that gains an advantage to snowball its control more quickly than with two ideologies or without discussions at all.
The exact reasons there can be a sporadic increase in polarization during initial stages of the simulation for certain parameterizations are shown in the work of Banisch and Olbrich [
25] (Figure 9). The presence of densely connected homophilic components can be generated through the initialization and the first stages of the simulation will increase the homophily of these clusters, and the “long-range” ties between heterogeneous clusters will take a longer period to stabilize towards a uniform consensus.
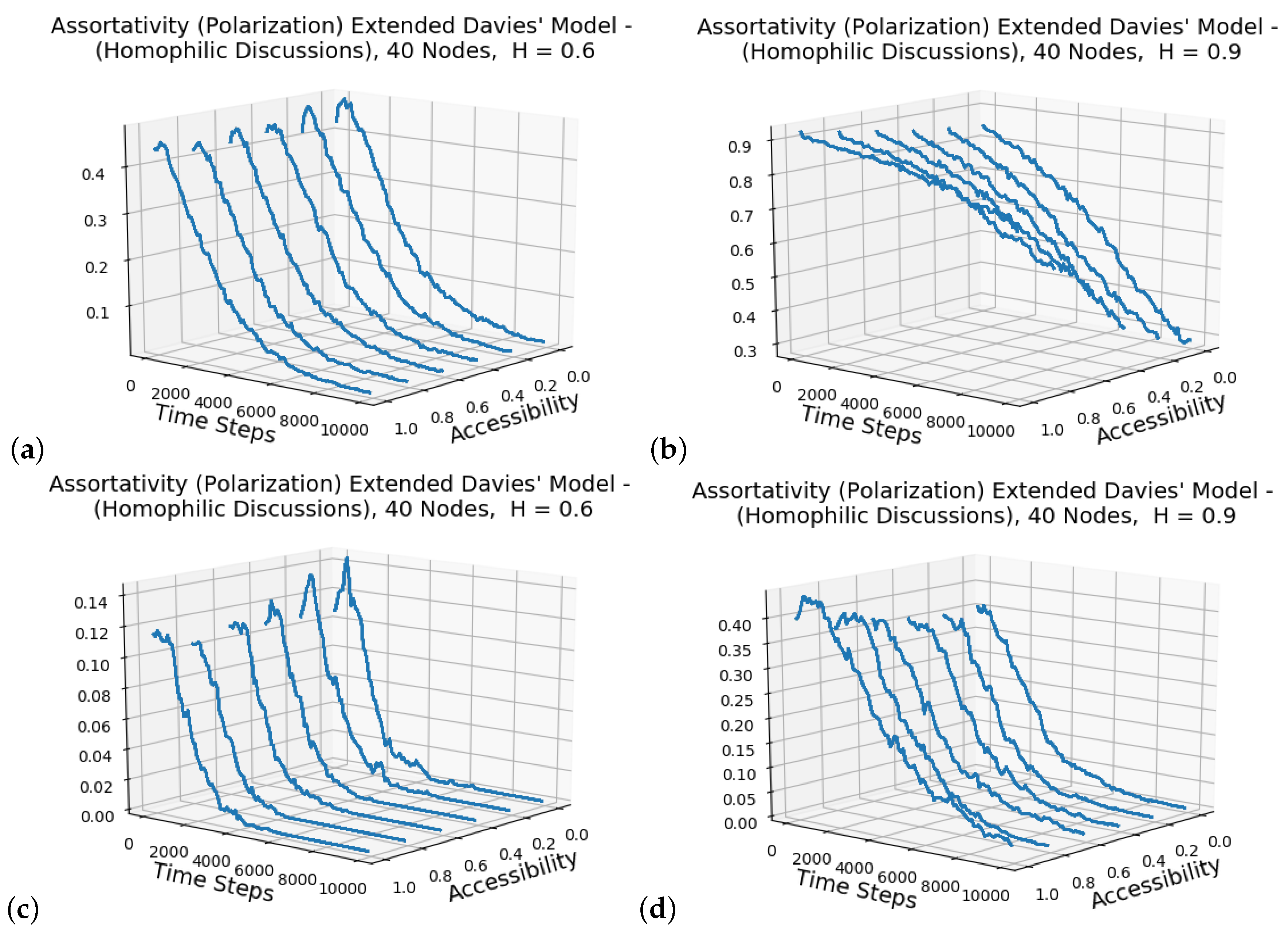
Homophilic Assigned Discussions
Here, the model of the discussion groups are modified from that of the previous usage. In the previous description, the discussion group members were comprised of users assigned to discussions in accordance with their ideological affiliation, but the rate of assignment to a discussion was purely random. In this particular implementation, the rate was 0.5. This default base case scenario was intended to show that the effect of the discussions was significant even when considering only a reduced set of the network. It is also reasonable to assume that not every member of an ideological exchange would be a member of an ideologically associated discussion. In the following implementation, instead of assigning the discussions at a random rate, the rate was chosen to be H. This decision was made due to the likelihood that more homophilically-minded individuals would be more likely to join an ideological discussion.
Figure 5 shows the simulation traces for the homophilic discussion groups in a network undergoing ideological exchange. Whereas the previous simulations demonstrated the effects of the introduction of the discussion groups with random allocation having an effect on the trajectory of the assortativity values for ideological exchange, a comparison can be seen in
Figure 5a–d with
Figure 5a,b being for two ideologies and
Figure 5c,d for four ideologies. In
Figure 5a,b, it can be seen that the homophilic discussion groups increase the assortativity values and the time towards ideological convergence so that these echo-chambers which discussion groups can represent are facilitating increased polarization through assisting in a network segregation. For
, this can be seen easily and therefore the identification of a large number of ideological echo-chambers can be an indication of a delay and/or increase in assortativity upon two competing ideologies. In
Figure 5c,d, the opposite effect can be seen where the values are lower and the decay takes less time. This provides support that a single topic of concern in a network can induce greater levels of segregation between members of the network.
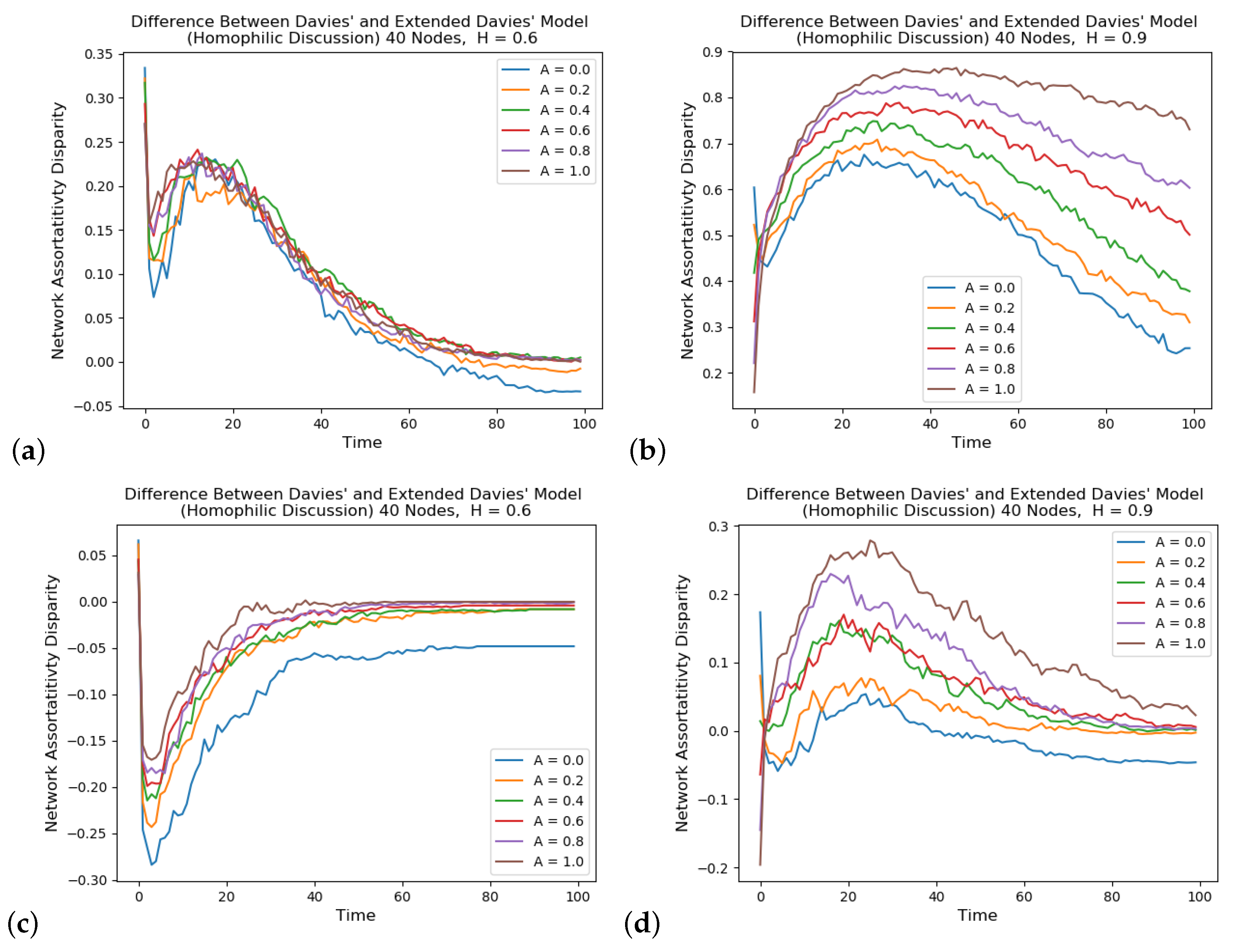
Figure 6 shows a difference in the assortativity values from the simulation trajectories of the original Davies model and the extended version with homophilic discussion groups. The number of discussion groups in the simulation is equal to the number of ideologies for each run.
Figure 6a,b shows the differences when there are two ideologies and
Figure 6c,d when there are four ideologies. The comparison with
Figure 4 provides an indication for the changes brought about from having homophilic produced discussion groups. With lower
H values,
Figure 6a,c does not display a large change between the results of the two implementations, but the comparisons in
Figure 6b,d appear to have a greater effect since the composition of the discussions have a more uniform composition. We can also see that in contrast with
Figure 4,
Figure 6d also shows a delay in consensus. This shows that, with the homophilic assignment of discussions and a high level of homophily (0.9 in this case), the network with four ideologies is again delayed from reaching consensus compared with the results without any discussion. The reasoning is similar to that for the results in
Figure 4, however instead of the first to gain an advantage being able to snowball more quickly, the network is more sparse and the number of discussion members is significantly increased. The number of BVM exchanges between individuals who both disagree and are not members of discussions is significantly lower.
4. Discussion
The work presented by the authors explores the results of a recent study [
6] that investigated the choice mechanism of establishing a friendship graph and the assortativity of ideologies when they are mutually exclusive labels per individual. This mechanism of developing friendship networks relies upon each member having an initial set of local associates who are provided through a random allocation as being a functioning member of society. Subsequently, a set of friends are chosen based upon the accessibility that a member can access potential friends outside of their local associates and the choice within these two pools is biased according to the value of homophily. After the friendship graph is generated, it is assumed that only this set can influence the ideologies of a node regardless of whether a node is a member of the local associates and not in the group of designated friends. This work investigated the relationship of
accessibility and
homophily with the change of values of
assortativity that quantifies polarization. These associations will have potentially large impacts on society given that there is an increase in friendship developments online [
26,
27], which have been provided to users of platforms and there is also research indicating an increase of polarization surrounding sensitive societal choices in recent years that can be associate with certain types of isolation [
28].
The results of the previous research (Davies model) provides support for an idea that an increase in accessibility can increase the assortativity values due to users having access to a large pool of candidate friends with whom homophilic interactions can produce friendships at an increased rate. In that model, the exchange of ideological labels due to friendship interactions is governed by the classic Binary Voting Model (BVM) [
22]. Since these results can alter the conclusions in previous publications [
8], the work here presents an independent implementation of the model after careful examination of its description provided and the code on GitHub. This independent implementation was written in a different programming language, and can confirm the validity of those results shown in
Figure 1.
There are two important explorations in [
6] that are required to appreciate the insight it can bring towards understanding the impact of accessibility in online social networks upon measures of polarization. The first is that, although the initialization of a network, given increased accessibility, can produce an increase in polarization, and that, during the simulation of the BVM, these polarized states can be found, the full trajectory of the BVM simulation upon these networks is not provided. Such a set of plots will provide insight into states of convergence and different modes of the model. These are provided in
Figure 2 and show that the initial networks follow the pattern that increased accessibility in the presence of homophily creates increases in assortativity and that early stages of the simulation produce temporary increases in the assortativity mostly for lower homophily. This is due to the relatively lower initial assortativity that exists in comparison to larger
H, as the BVM homogenizes local clusters before the macroscopic homogenization process begins. The most important feature to note in the inspection of a full run of the BVM on the Davies model is that the BVM does proceed to reduce the heterogeneous clusters. The second feature explored in this work is that, in [
6], the increased accessibility offered is motivated by the presence of offline or online clubs, communities and organizations where members can find these pools of homophilic affiliations in ideological labels. This is not present in the Davies model and it is uncertain whether their introduction would disrupt the results presented. An extension of the Davies model is developed in
Section 2, where discussion group memberships are represented, and the results are shown in
Figure 3. It can be seen that the presence of discussion groups reinforces the results of the Davies model and adds to the degree to which polarization can be manifested with accessibility increases and even the discussion groups.
Figure 4 provides an indication of the increase in assortativity during the simulation in the initial phases of the BVM in a manner. As both models provide an increase and then homogenization, it can be said that the results in [
6] are reliable and can provide insight into a possible negative effect that accessibility may have in the presence of homophily over initial stages of the onset of the differentiation. The topological setting of the network association and discussion arrangements reflect the results of the one-dimensional version of the Axelrod model simulation conducted in [
29] which shows that a single label state will emerge in convergence when the noise (ideological perturbations) are limited. These results of a global mono-culture emerging from an influence mechanism are also found in [
30], supporting the concept that accessibility can only in specific situations induce increases in polarization or a separation of ideological communities.
The social implications of this work is that even if consensus is expected to be obtained from an ideological exchange there are situations in which initial increases in polarization can occur. Depending upon the topics of concern, this may reach a threshold in which a disruption to society is created. The fact that the discussion may inevitably reach consensus is dependent upon the dialogue continuing uninterrupted by events that may result due to the disagreements. The discussion groups that emerge have an effect upon the decay of the societal separation that are sensitive to how much homophily values are in their composition. Randomly allocated discussion groups have a different impact than those generated with a preference for a common perspective. Therefore, the number of discussion groups that cater to particular ideologies will be an indicator for the delay in ideological consensus.
Future work entails expanding on the model of opinion exchange to examine the sensitivity of the various conclusions based on how ideologies are exchanged or interacted with. The work in [
25] incorporates feedback of opinions and the model in [
31] uses a multi-level model for the formation of the opinion labels. These aspects of the model can change the rate at which the “long-range” ties between clusters of nodes exchange labels as other features can induce a delay or accelerate the exchange over these essential edges for the phenomenon examined.