A Soft Body Physics Simulator with Computational Offloading to the Cloud
Abstract
1. Introduction
2. Methods and Materials
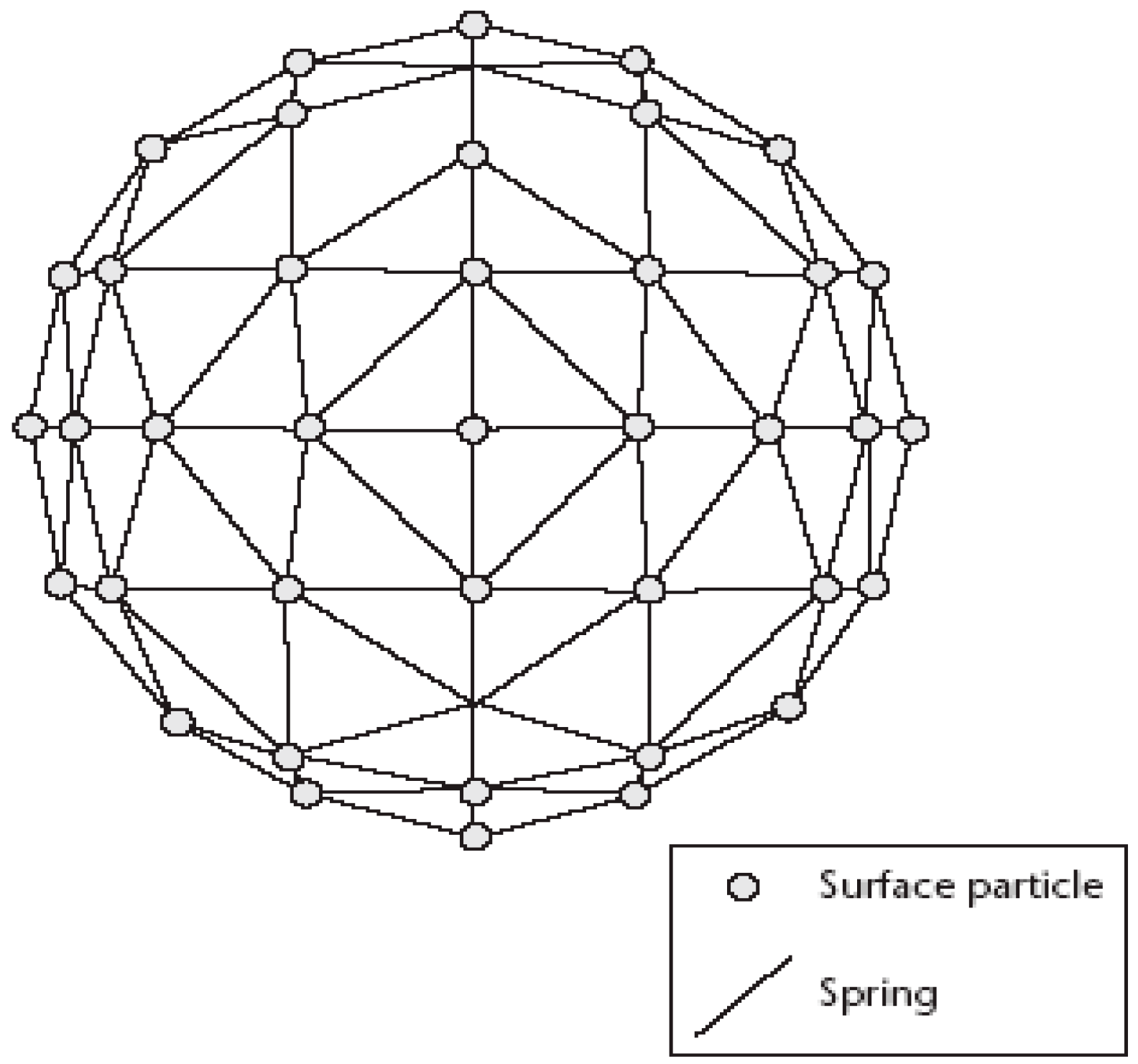
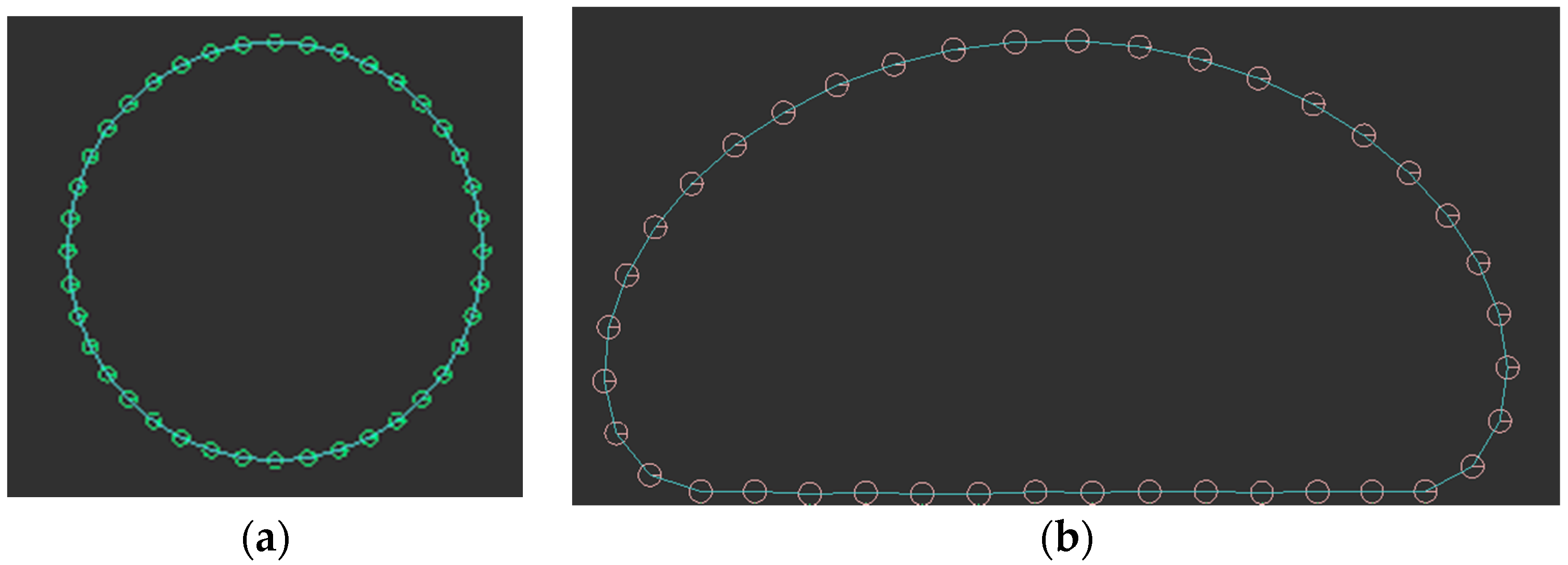
2.1. Soft Body Physics
2.2. Game Implementation
| Algorithm 1 |
|
| Algorithm 2 |
|
2.3. Game Architecture
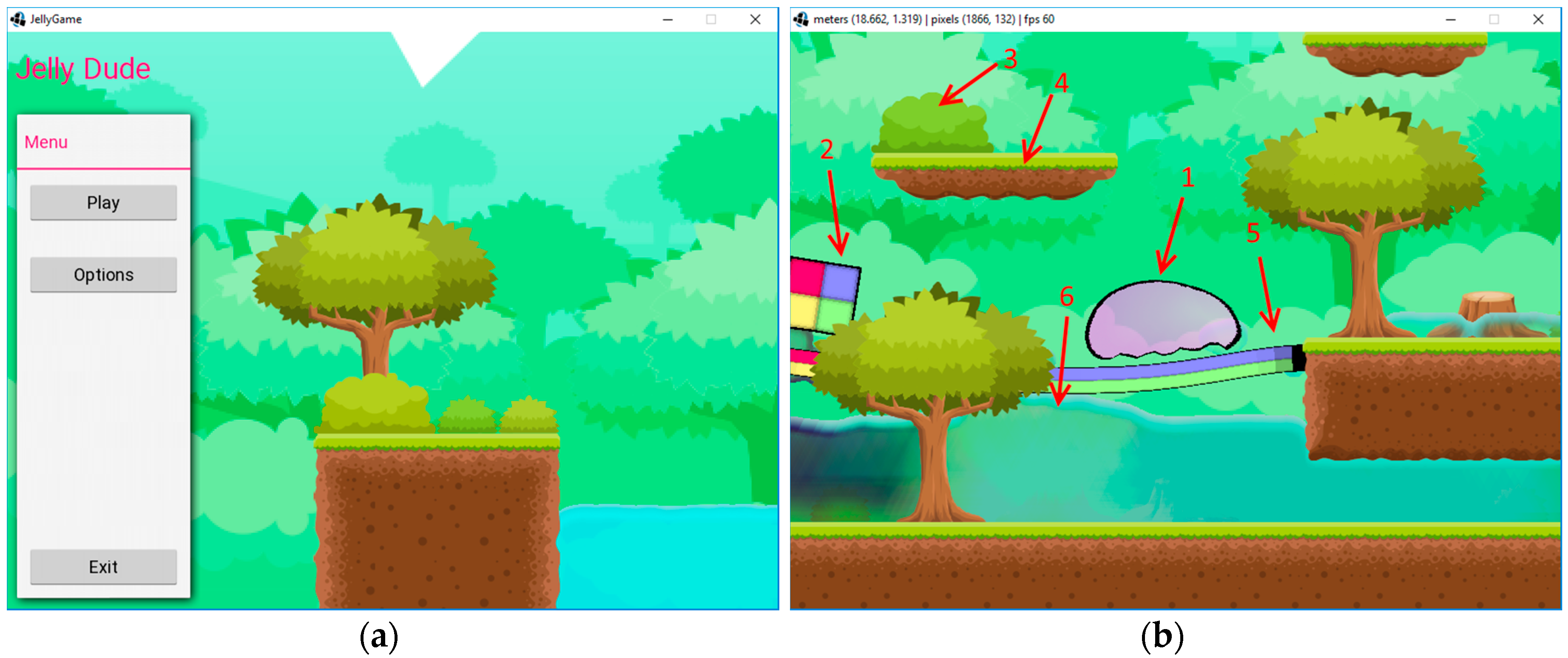
2.4. Game Interface and Main Elements
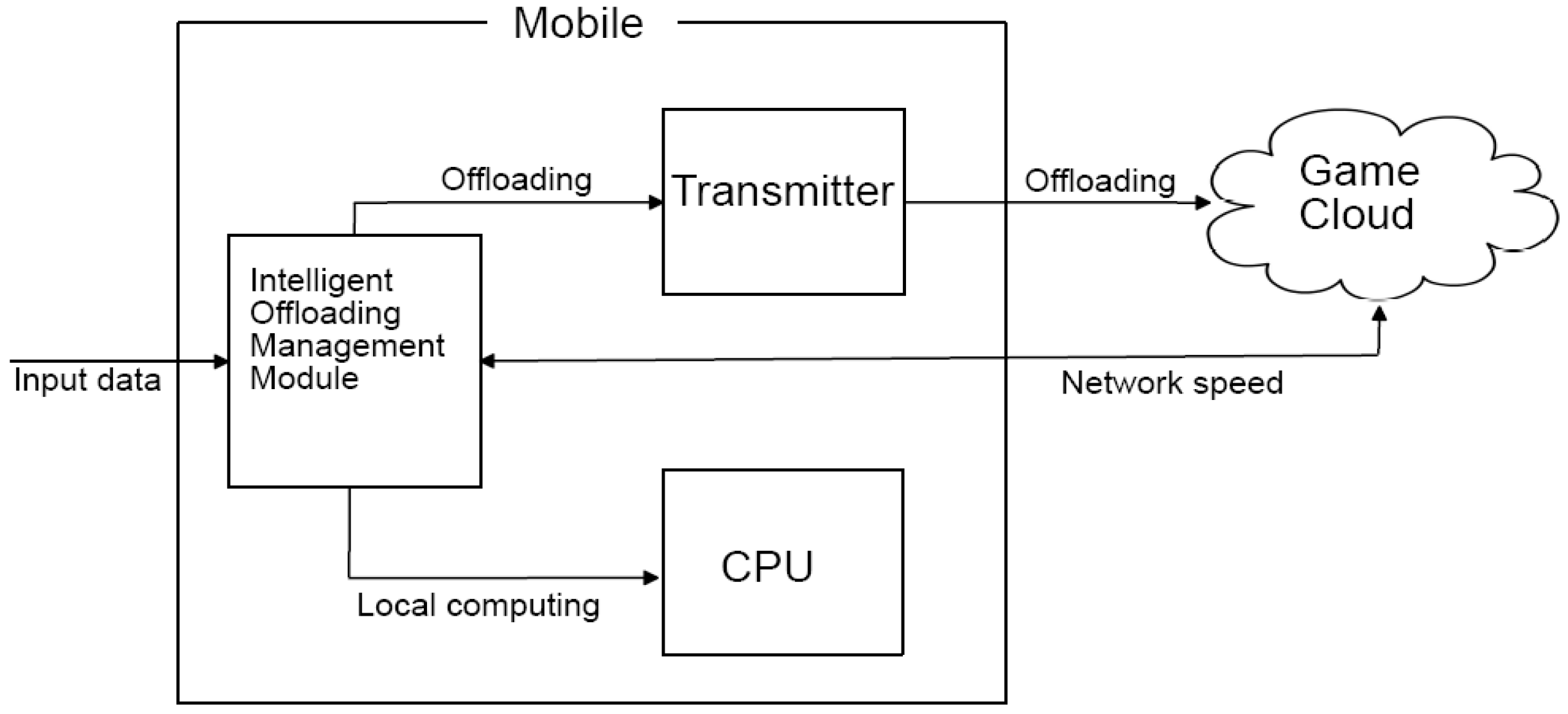
2.5. Computational Offloading Model and Offloading Decision Scheme
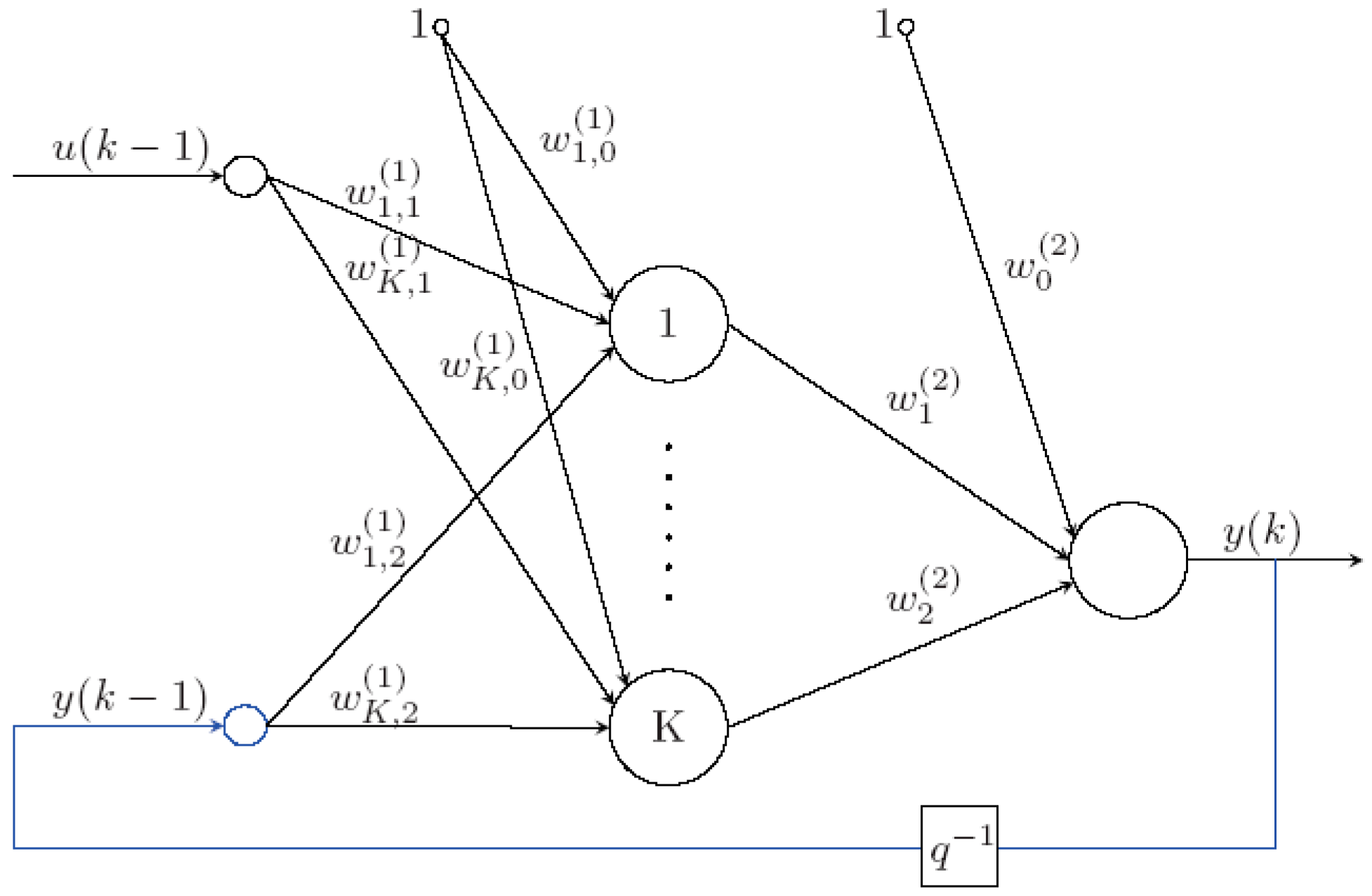
2.6. Implementation of Intelligent Cloud Offloading
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nixon, D.; Lobb, R. A Fluid-Based Soft-Object Model. IEEE Comput. Graph. Appl. 2002, 22, 68–75. [Google Scholar] [CrossRef]
- Song, M.; Grogo, P. A framework for dynamic deformation of uniform elastic two-layer 2D and 3D objects in OpenGL. In Proceedings of the 2008 C3S2E Conference (C3S2E ’08), Montreal, QC, Canada, 12–13 May 2008; pp. 145–158. [Google Scholar] [CrossRef]
- Nebel, J.-C. Soft Tissue Modelling from 3D Scanned Data. In Deformable Avatars; Springer: New York, NY, USA, 2001; pp. 85–97. [Google Scholar]
- Kriegman, S.; Cappelle, C.; Corucci, F.; Bernatskiy, A.; Cheney, N.; Bongard, J.C. Simulating the evolution of soft and rigid-body robots. In Proceedings of the Genetic and Evolutionary Computation Conference Companion (GECCO ’17), Berlin, Germany, 15–19 July 2017. [Google Scholar]
- Panthalookaran, V. Gamification of physics themes to nurture engineering professional and life skills. In Proceedings of the IEEE Global Engineering Education Conference (EDUCON), Tenerife, Spain, 17–20 April 2018; pp. 931–939. [Google Scholar] [CrossRef]
- Ullman, T.D.; Spelke, E.; Battaglia, P.; Tenenbaum, J.B. Mind Games: Game Engines as an Architecture for Intuitive Physics. Trends Cognitive Sci. 2017, 21, 649–665. [Google Scholar] [CrossRef] [PubMed]
- Pérez, F.Q. Applying of gamification tools in physics and chemistry of secondary education. Opcion 2016, 32, 327–348. [Google Scholar]
- Tembo, T.T.; Lee, C. Using 2D simulation applications to motivate students to learn STEAM. In Proceedings of the 25th International Conference on Computers in Education: Technology and Innovation: Computer-Based Educational Systems for the 21st Century (ICCE 2017), Christchurch, New Zealand, 4–8 December 2017; pp. 403–409. [Google Scholar]
- Oyesiku, D.; Adewumi, A.; Misra, S.; Ahuja, R.; Damasevicius, R.; Maskeliunas, R. An Educational Math Game for High School Students in Sub-Saharan Africa. In Communications in Computer and Information Science; Springer: Cham, Switzerland, 2018; pp. 228–238. [Google Scholar]
- Raziunaite, P.; Miliunaite, A.; Maskeliunas, R.; Damasevicius, R.; Sidekerskiene, T.; Narkeviciene, B. Designing an educational music game for digital game based learning: A Lithuanian case study. In Proceedings of the 41st International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 21–25 May 2018; pp. 800–805. [Google Scholar] [CrossRef]
- Chittaro, L.; Ieronutti, L. A visual tool for tracing users’ behavior in Virtual Environments. In Proceedings of the Working Conference on Advanced Visual Interfaces (AVI ’04), Gallipoli, Italy, 25–28 May 2004; pp. 40–47. [Google Scholar] [CrossRef]
- Sookhanaphibarn, K.; Thawonmas, R. A Movement Data Analysis and Synthesis Tool for Museum Visitors’ Behaviors. In Proceedings of the 10th Pacific Rim Conference on Multimedia (PCM 2009), Bangkok, Thailand, 15–18 December 2009; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2009; Volume 5879, pp. 144–154. [Google Scholar] [CrossRef]
- Tsiropoulou, E.E.; Thanou, A.; Papavassiliou, S. Modelling museum visitors’ Quality of Experience. In Proceedings of the 2016 11th International Workshop on Semantic and Social Media Adaptation and Personalization (SMAP), Thessaloniki, Greece, 20–21 October 2016; pp. 77–82. [Google Scholar] [CrossRef]
- Tsiropoulou, E.E.; Thanou, A.; Papavassiliou, S. Quality of Experience-based museum touring: A human in the loop approach. Soc. Netw. Anal. Min. 2017, 7, 33. [Google Scholar] [CrossRef]
- Slivar, I.; Suznjevic, M.; Skorin-Kapov, L. Game Categorization for Deriving QoE-Driven Video Encoding Configuration Strategies for Cloud Gaming. ACM Trans. Multimedia Comput. Commun. Appl. 2018, 14, 1–24. [Google Scholar] [CrossRef]
- Jarschel, M.; Schlosser, D.; Scheuring, S.; Hoßfeld, T. Gaming in the clouds: QoE and the users’ perspective. Math. Comput. Model. 2013, 57, 2883–2894. [Google Scholar] [CrossRef]
- Maggiorini, D.; Ripamonti, L.A.; Sauro, F. Unifying Rigid and Soft Bodies Representation: The Sulfur Physics Engine. Int. J. Comput. Games Technol. 2014, 2014. [Google Scholar] [CrossRef]
- Xie, J. The research on mobile game engine. In Proceedings of the International Conference on Image Analysis and Signal Processing, Wuhan, China, 21–23 October 2011; pp. 635–639. [Google Scholar] [CrossRef]
- Ali, Z.; Usman, M. A framework for game engine selection for gamification and serious games. In Proceedings of the FTC 2016—Future Technologies Conference, San Francisco, CA, USA, 6–7 December 2016; pp. 1199–1207. [Google Scholar] [CrossRef]
- Połap, D.; Kęsik, K.; Książek, K.; Woźniak, M. Obstacle Detection as a Safety Alert in Augmented Reality Models by the Use of Deep Learning Techniques. Sensors 2017, 17, 2803. [Google Scholar] [CrossRef] [PubMed]
- Buzys, R.; Maskeliūnas, R.; Damaševičius, R.; Sidekerskienė, T.; Woźniak, M.; Wei, W. Cloudification of Virtual Reality Gliding Simulation Game. Information 2018, 9, 293. [Google Scholar] [CrossRef]
- James, D.L.; Fatahalian, K. Precomputing interactive dynamic deformable scenes. ACM Trans. Graph. (TOG) 2003, 22, 879–887. [Google Scholar] [CrossRef]
- Wyvill, G.; McPheeters, C.; Wyvill, B. Data Structures for Soft Objects. Vis. Comput. 1986, 2, 227–234. [Google Scholar] [CrossRef]
- Terzopoulos, D.; Fleischer, K. Modeling Inelastic Deformation: Viscoelasticity, Plasticity, Fracture. ACM Comput. Graph. 1988, 22, 269–278. [Google Scholar] [CrossRef]
- James, D.; Pai, D. ArtDefo—Accurate Real Time Deformable Objects. In Proceedings of the Computer Graphics (Proc. Siggraph 99), Los Angeles, CA, USA, 8–13 August 1999; ACM Press: New York, NY, USA, 1999; pp. 65–72. [Google Scholar]
- Miller, G. The Motion Dynamics of Snakes and Worms. ACM Comput. Graph. 1988, 22, 169–177. [Google Scholar] [CrossRef]
- Matyka, M.; Ollila, M. Pressure Model of Soft Body Simulation. In Proceedings of the Annual SIGRAD Conference, Umeå, Sweden, 20–21 November 2003; pp. 29–32. [Google Scholar]
- Kenwright, B. Scalable Real-Time Vehicle Deformation for Interactive Environments. Available online: http://www.xbdev.net/misc_demos/demos/vehicle_deformation/paper.pdf (accessed on 9 December 2018).
- McAdams, A.; Zhu, Y.; Selle, A.; Empey, M.; Tamstorf, R.; Teran, J.; Sifakis, E. Efficient elasticity for character skinning with contact and collisions. In Proceedings of the ACM SIGGRAPH ’11, Vancouver, BC, Canada, 7–11 August 2011; pp. 37:1–37:12. [Google Scholar]
- Martin, S.; Thomaszewski, B.; Grinspun, E.; Gross, M. Example-based elastic materials. ACM Trans. Graph. 2011, 30, 72:1–72:8. [Google Scholar] [CrossRef]
- Wu, X.; Mukherjee, R.; Wang, H. A unified approach for subspace simulation of deformable bodies in multiple domains. ACM Trans. Graph. 2015, 34, 241. [Google Scholar] [CrossRef]
- Coumans, E. Bullet physics simulation. In Proceedings of the ACM SIGGRAPH 2015 Courses—SIGGRAPH ’15, Los Angeles, CA, USA, 9–13 August 2015; ACM Press: New York, NY, USA, 2015. [Google Scholar]
- Parker, E.G.; O’Brien, J.F. Real-time deformation and fracture in a game environment. In Proceedings of the SCA ’09 2009 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, New Orleans, LA, USA, 1–2 August 2009; pp. 165–175. [Google Scholar] [CrossRef]
- Tasora, A.; Serban, R.; Mazhar, H.; Pazouki, A.; Melanz, D.; Fleischmann, J.; Negrut, D. Chrono: An Open Source Multi-physics Dynamics Engine. In Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; pp. 19–49. [Google Scholar] [CrossRef]
- Itterheim, S. Soft-Body Physics. In Learn SpriteBuilder for iOS Game Development; Apress: Berkeley, CA, USA, 2014. [Google Scholar]
- Kwon, Y.-W.; Tilevich, E. Facilitating the Implementation of Adaptive Cloud Offloading to Improve the Energy Efficiency of Mobile Applications. In Proceedings of the 2nd ACM International Conference on Mobile Software Engineering and Systems, Florence, Italy, 16–17 May 2015; pp. 94–104. [Google Scholar] [CrossRef]
- Chen, X.; Jiao, L.; Li, W.; Fu, X. Efficient multi-user computation offloading for mobile-edge cloud computing. IEEE/ACM Trans. Netw. 2016, 24, 2795–2808. [Google Scholar] [CrossRef]
- Gu, F.; Niu, J.; Qi, Z.; Atiquzzaman, M. Partitioning and offloading in smart mobile devices for mobile cloud computing: State of the art and future directions. J. Netw. Comput. Appl. 2018, 119, 83–96. [Google Scholar] [CrossRef]
- Li, W.; You, X.; Jiang, Y.; Yang, J.; Hu, L. Opportunistic computing offloading in edge clouds. J. Parallel Distrib. Comput. 2019, 123, 69–76. [Google Scholar] [CrossRef]
- Georgy, M.E.; Chang, L.-M.; Zhang, L. Prediction of Engineering Performance: A Neurofuzzy Approach. J. Constr. Eng. Manag. 2005, 131, 548–557. [Google Scholar] [CrossRef]
- Wysocki, A.; Lawrynczuk, M. Jordan neural network for modelling and predictive control of dynamic systems. In Proceedings of the 2015 20th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 24–27 August 2015. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]



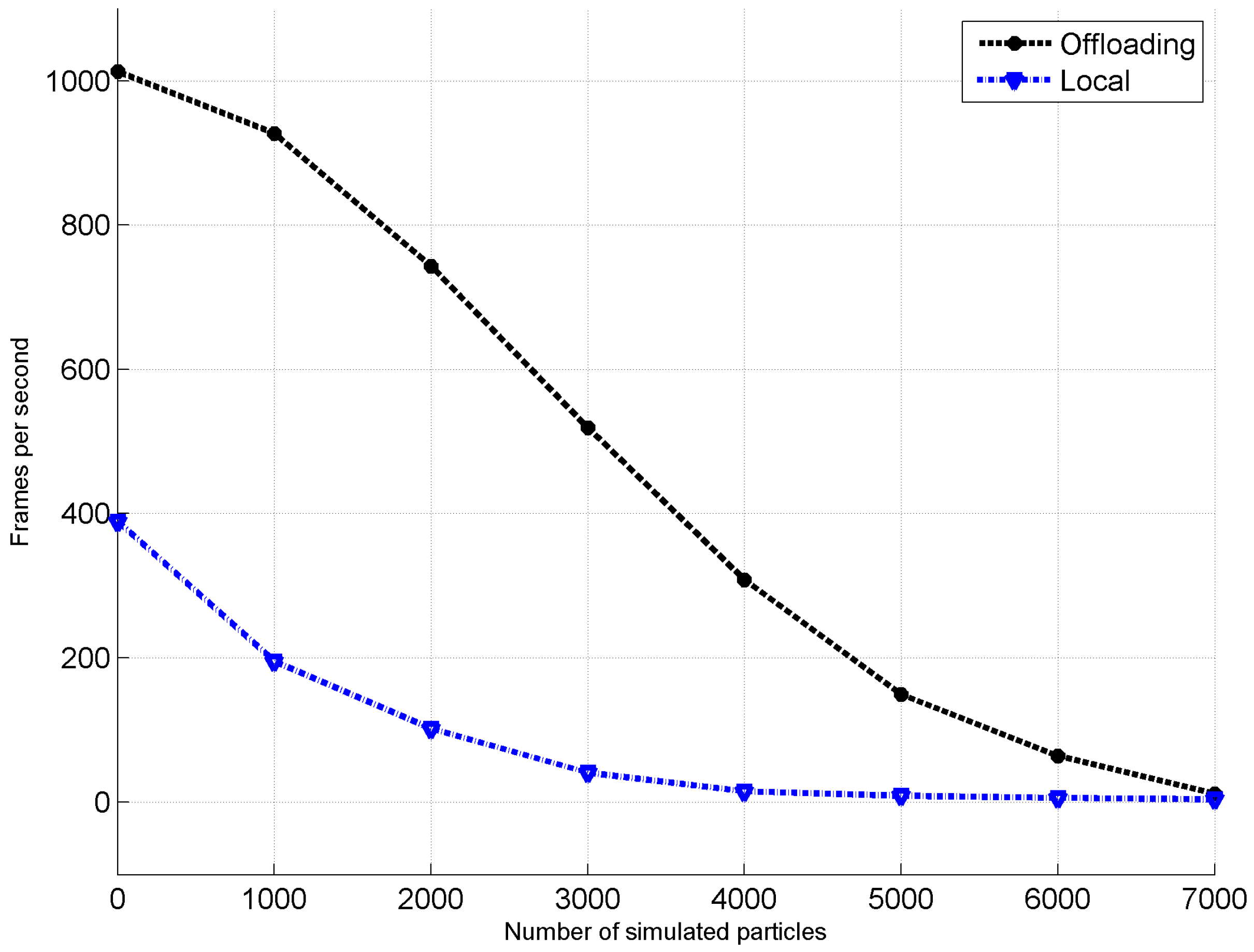
| Computation Scheme | Load Time (s) | FPS (min) | FPS (max) | FPS (mean) |
|---|---|---|---|---|
| Local computation | 4 | 14 | 138 | 40 |
| Offloading (cloud) | 2.9 | 192 | 656 | 277 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danevičius, E.; Maskeliūnas, R.; Damaševičius, R.; Połap, D.; Woźniak, M. A Soft Body Physics Simulator with Computational Offloading to the Cloud. Information 2018, 9, 318. https://doi.org/10.3390/info9120318
Danevičius E, Maskeliūnas R, Damaševičius R, Połap D, Woźniak M. A Soft Body Physics Simulator with Computational Offloading to the Cloud. Information. 2018; 9(12):318. https://doi.org/10.3390/info9120318
Chicago/Turabian StyleDanevičius, Edvinas, Rytis Maskeliūnas, Robertas Damaševičius, Dawid Połap, and Marcin Woźniak. 2018. "A Soft Body Physics Simulator with Computational Offloading to the Cloud" Information 9, no. 12: 318. https://doi.org/10.3390/info9120318
APA StyleDanevičius, E., Maskeliūnas, R., Damaševičius, R., Połap, D., & Woźniak, M. (2018). A Soft Body Physics Simulator with Computational Offloading to the Cloud. Information, 9(12), 318. https://doi.org/10.3390/info9120318






