An Inter-Frame Forgery Detection Algorithm for Surveillance Video
Abstract
1. Introduction
2. Feature Extraction
2.1. 2-D Phase Congruency
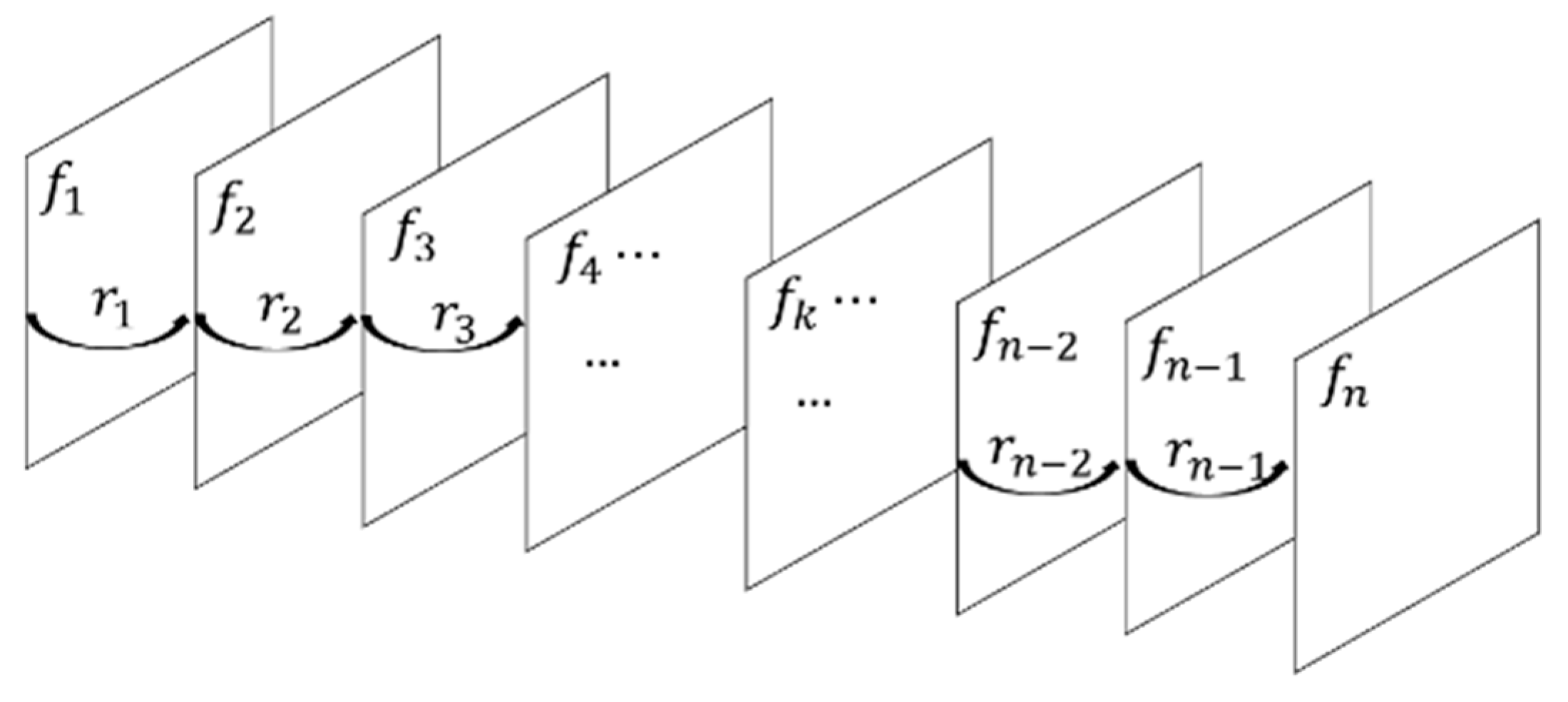
2.2. The Correlation of Adjacent Frames
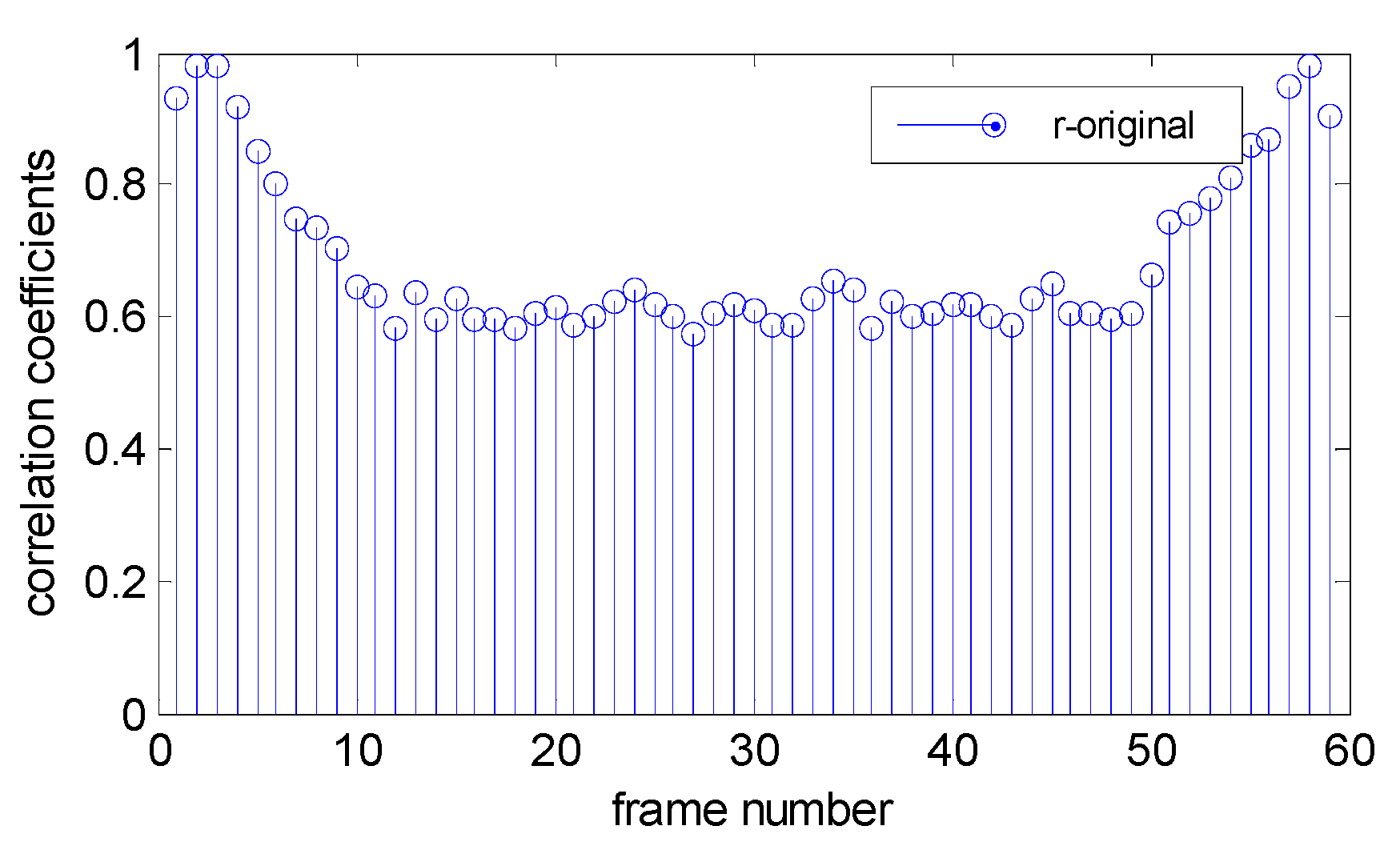
2.3. The Variation of Consecutive Correlation Coefficients
3. Detection Scheme for Abnormal Points
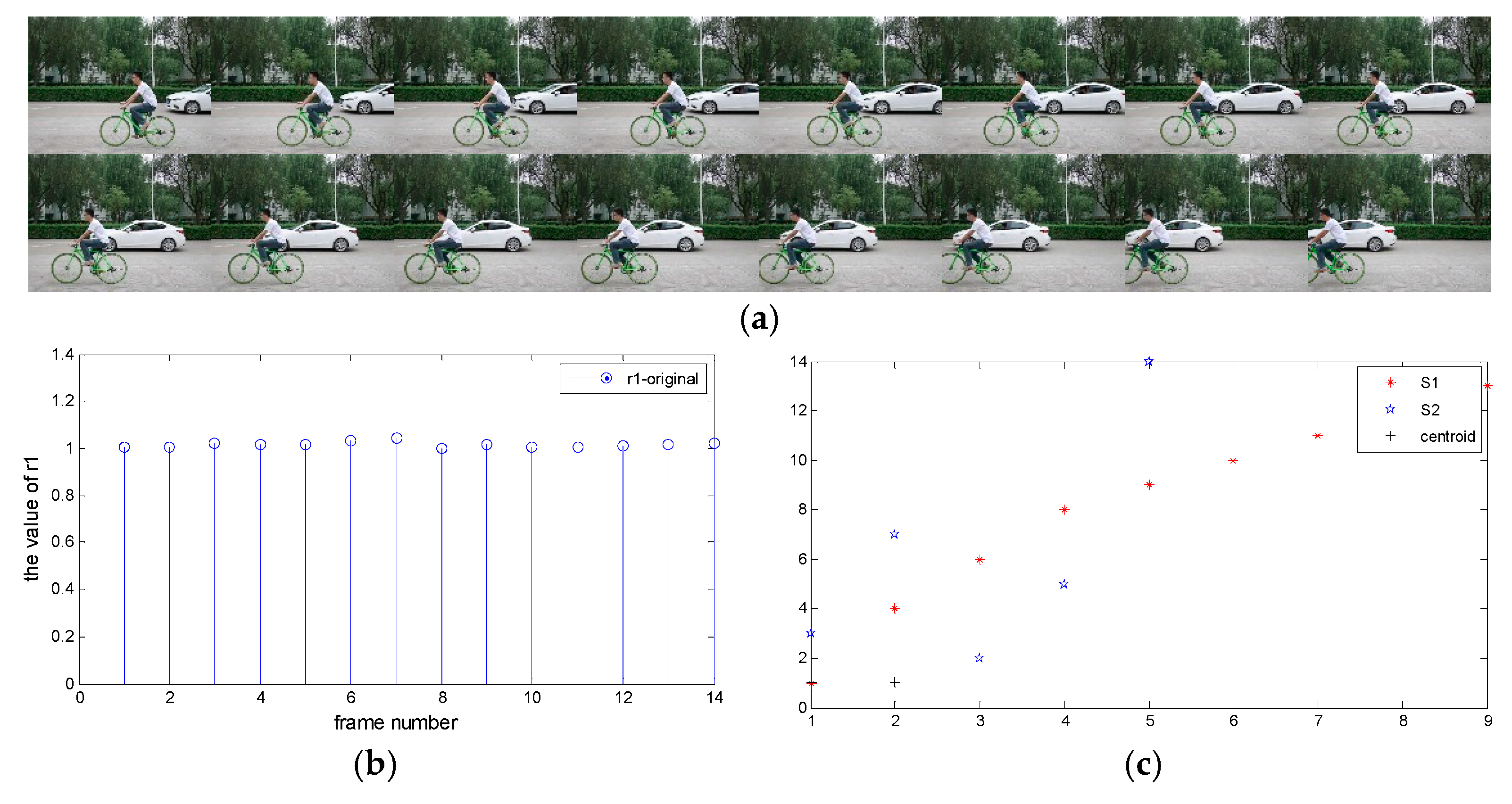
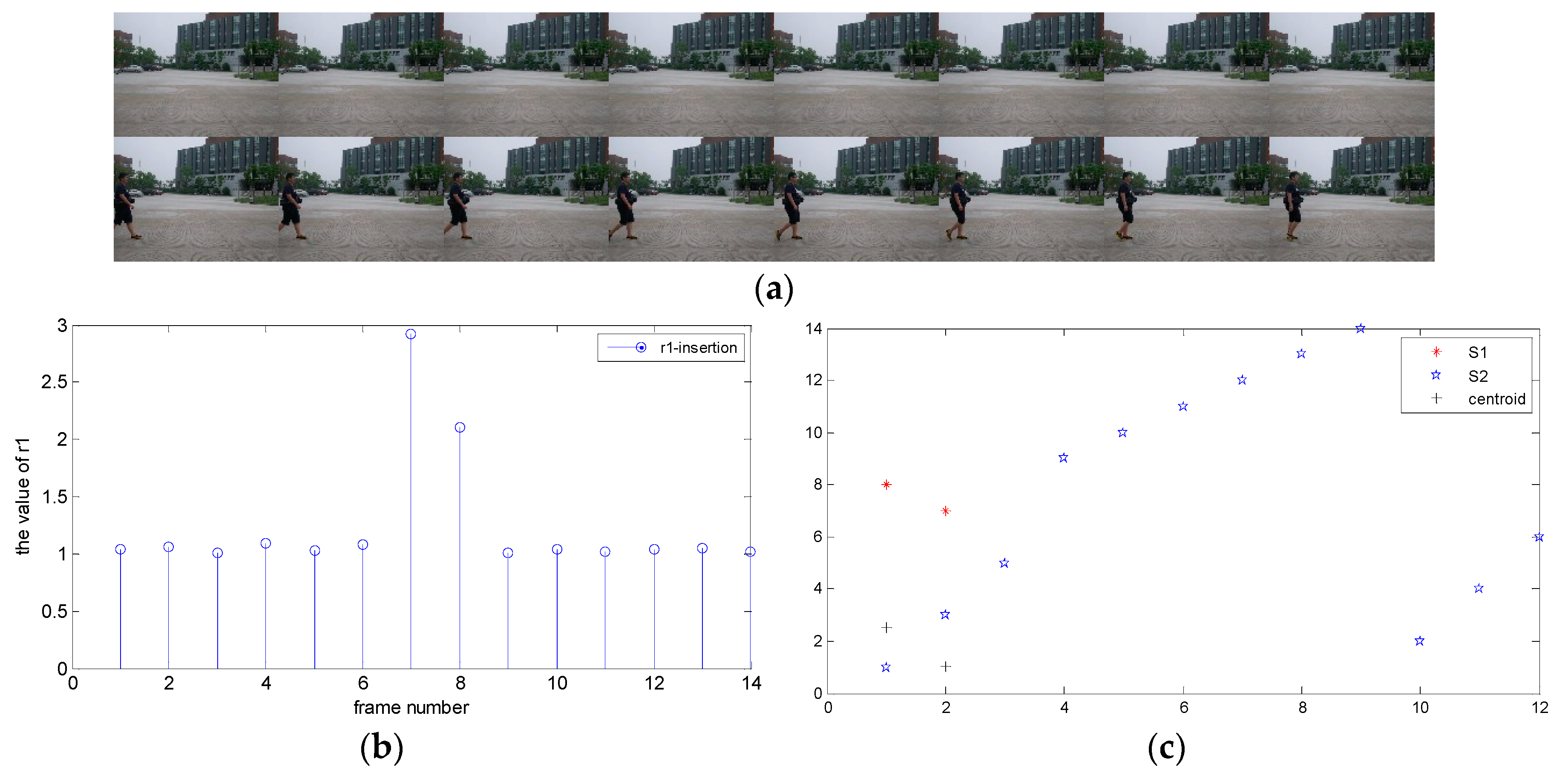
3.1. The k-Means Clustering Algorithm
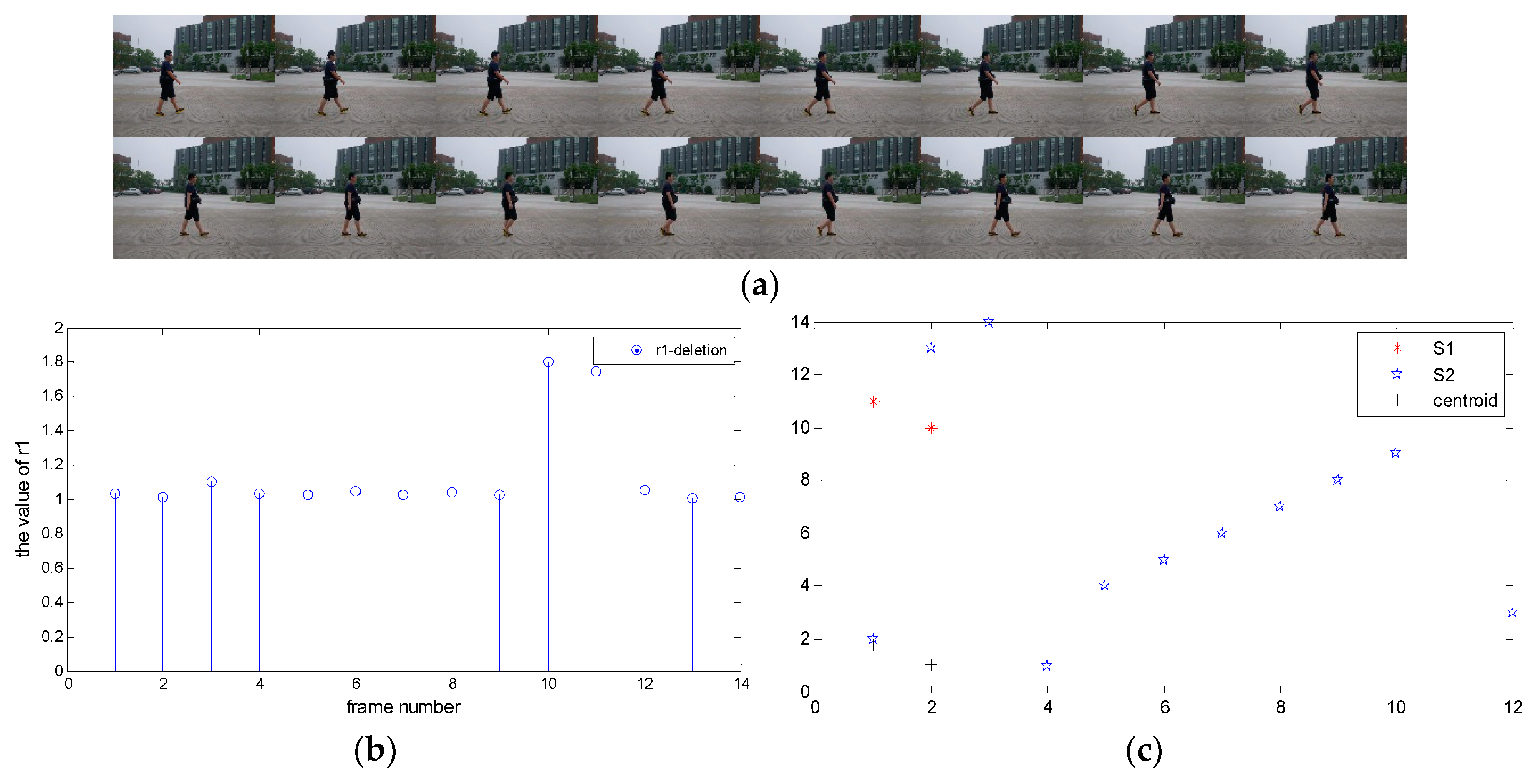
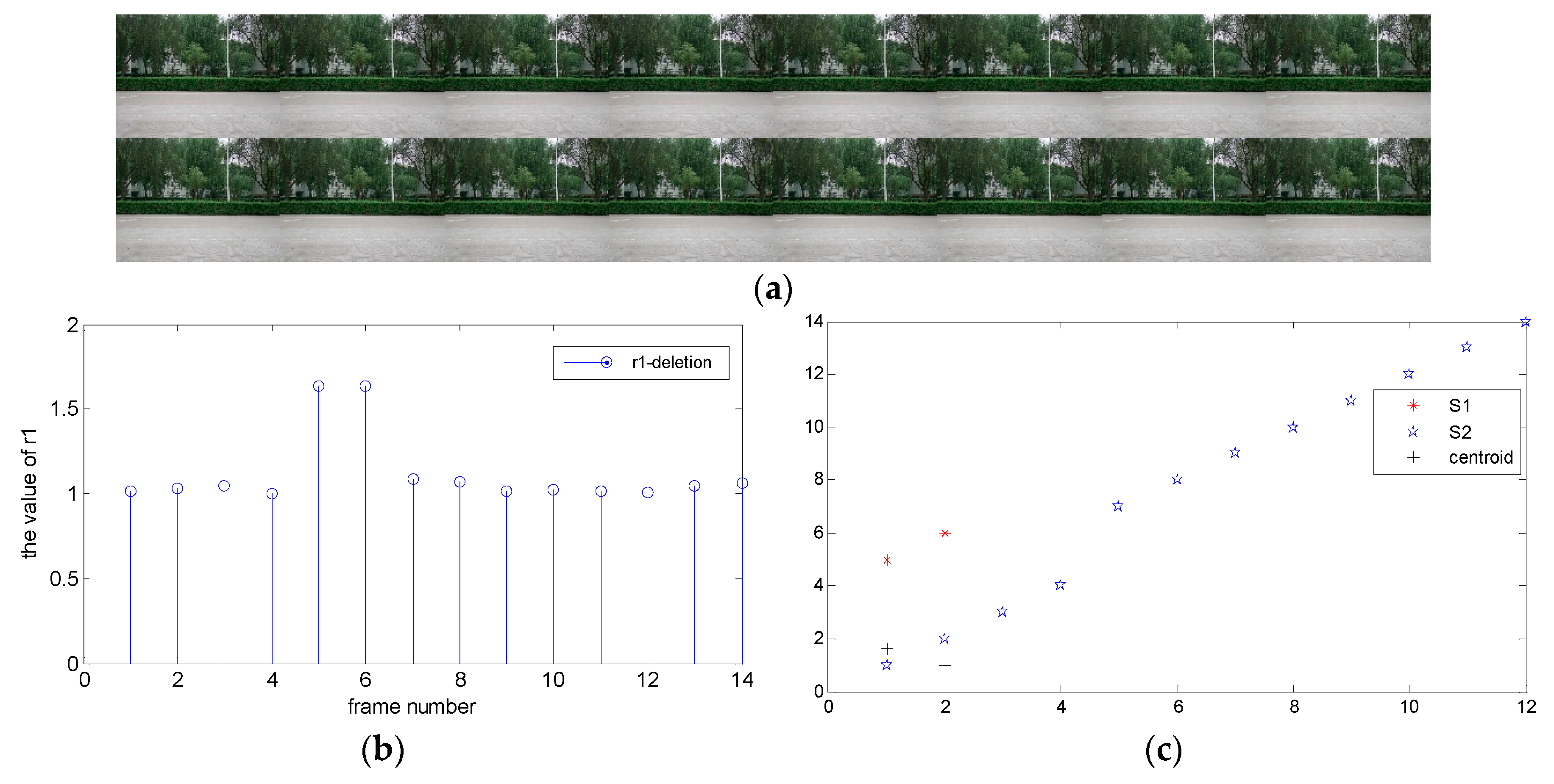
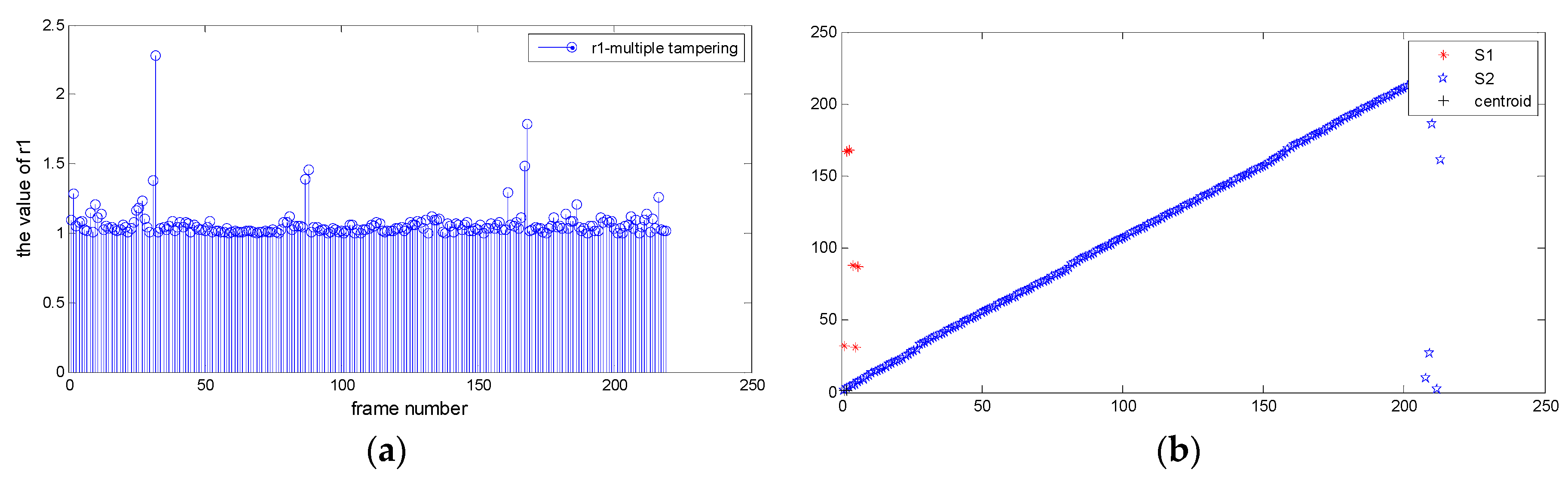
3.2. Abnormal Points Detection Based on KM
3.2.1. Clustering Results of Original Video
3.2.2. Clustering Results of Forged Video by Frame Insertion
3.2.3. Clustering Results of Forged Video by Frame Deletion
3.2.4. Clustering Results of Forged Video by Multiple Tampering
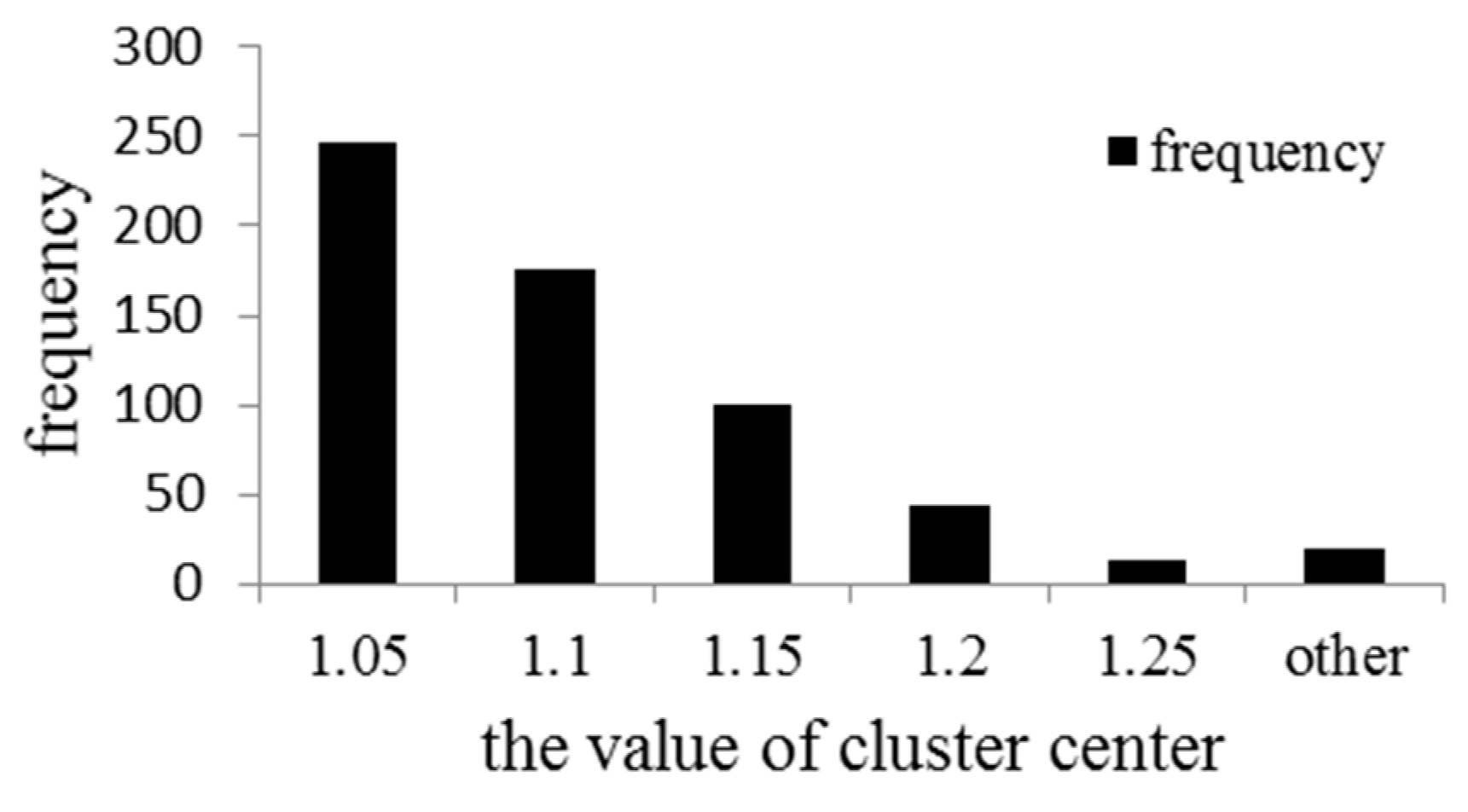
3.3. Threshold Decision
4. Experimental Results and Discussion
4.1. Dataset
4.2. Evaluation Metrics and Method Assessment Procedure
4.3. Experimental Results
4.4. Time Complexity Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Katsaounidou, A.; Dimoulas, C.; Veglis, A. Cross-Media Authentication and Verification: Emerging Research and Opportunities; IGI Global: Hershey, PA, USA, 2018; pp. 155–188. [Google Scholar]
- Arab, F.; Abdullah, S.M.; Hashim, S.Z.M.; Manaf, A.A.; Zamani, M. A robust video watermarking technique for the tamper detection of surveillance systems. Multimed. Tools Appl. 2016, 75, 10855–10885. [Google Scholar] [CrossRef]
- Chen, S.; Pande, A.; Zeng, K.; Mohapatra, P. Live video forensics: Source identification in lossy wireless networks. IEEE Trans. Inf. Forensics Secur. 2015, 10, 28–39. [Google Scholar] [CrossRef]
- Amerini, I.; Caldelli, R.; Del Mastio, A.; Di Fuccia, A.; Molinari, C.; Rizzo, A.P. Dealing with video source identification in social networks. Signal Process. Image Commun. 2017, 57, 1–7. [Google Scholar] [CrossRef]
- Tao, J.J.; Jia, L.L.; You, Y. Review of passive-blind detection in digital video forgery based on sensing and imaging techniques. Proc. SPIE 2017, 10244, 102441C. [Google Scholar]
- Li, Z.H.; Jia, R.S.; Zhang, Z.Z.; Liang, X.Y.; Wang, J.W. Double HEVC compression detection with different bitrates based on co-occurrence matrix of PU types and DCT coefficients. In Proceedings of the ITM Web of Conferences, Guangzhou, China, 26–28 May 2017; p. 01020. [Google Scholar]
- He, P.; Jiang, X.; Sun, T.; Wang, S. Double compression detection based on local motion vector field analysis in static-background videos. J. Vis. Commun. Image R 2016, 35, 55–66. [Google Scholar] [CrossRef]
- Zheng, J.; Sun, T.; Jiang, X.; He, P. Double H.264 compression detection scheme based on prediction residual of background regions. In Intelligent Computing Theories and Application; Springer: Cham, Switzerland, 2017; pp. 471–482. [Google Scholar]
- Li, L.; Wang, X.; Zhang, W.; Yang, G.; Hu, G. Detecting removed object from video with stationary background. In Proceedings of the International Workshop on Digital Forensics and Watermarking, Auckland, New Zealand, 1–4 October 2013. [Google Scholar]
- Lin, C.S.; Tsay, J.J. A passive approach for effective detection and localization of region-level video forgery with spatio-temporal coherence analysis. Digit. Investig. 2014, 11, 120–140. [Google Scholar] [CrossRef]
- Chen, R.C.; Yang, G.B.; Zhu, N.B. Detection of object-based manipulation by the statistical features of object contour. Forensic Sci. Int. 2014, 236, 164–169. [Google Scholar]
- Su, L.; Huang, T.; Yang, J. A video forgery detection algorithm based on compressive sensing. Multimed. Tools Appl. 2015, 74, 6641–6656. [Google Scholar] [CrossRef]
- Mulla, M.U.; Bevinamarad, P.R. Review of techniques for the detection of passive video forgeries. Int. J. Sci. Res. Comput. Sci. Eng. Inf. Technol. 2017, 2, 199–203. [Google Scholar]
- Mizher, M.A.; Ang, M.C.; Mazhar, A.A.; Mizher, M.A. A review of video falsifying techniques and video forgery detection techniques. Int. J. Electron. Secur. Digit. Forensics 2017, 9, 191–208. [Google Scholar] [CrossRef]
- Han, Y.X.; Sun, T.F.; Jiang, X.H. Design and performanc optimization of surveillance video Inter-frame forgery detection system. Commun. Technol. 2018, 51, 215–220. [Google Scholar]
- Su, Y.T.; Ning, W.Z.; Zhang, C.Q. A frame tampering detection algorithm for MPEG videos. In Proceedings of the IEEE Joint International Information Technology and Artificial Intelligence Conference, Chongqing, China, 20–22 August 2011; pp. 461–464. [Google Scholar]
- Dong, Q.; Yang, G.B.; Zhu, N.B. A MCEA based passive forensics scheme for detecting frame-based video tampering. Digit. Investig. 2012, 9, 151–159. [Google Scholar] [CrossRef]
- Shanableh, T. Detection of frame deletion for digital video forensics. Digit. Investig. 2013, 10, 350–360. [Google Scholar] [CrossRef]
- Feng, C.; Xu, Z.; Jia, S.; Zhang, W.; Xu, Y. Motion-adaptive frame deletion detection for digital video forensics. IEEE Trans. Circuits Syst. Video Technol. 2017, 27, 2543–2554. [Google Scholar] [CrossRef]
- Kang, X.; Liu, J.; Liu, H.; Wang, Z.J. Forensics and counter anti-forensics of video inter-frame forgery. Multimed. Tools Appl. 2016, 75, 13833–13853. [Google Scholar] [CrossRef]
- Chao, J.; Jiang, X.H.; Sun, T.F. A novel video Inter-frame forgery model detection scheme based on optical flow consistency. In Digital Forensics and Watermaking; Springer: Berlin/Heidelberg, Germany, 2013; pp. 267–281. [Google Scholar]
- Wu, Y.; Jiang, X.; Sun, T.; Wang, W. Exposing video inter-frame forgery based on velocity field consistency. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 2674–2678. [Google Scholar]
- Zhang, Z.; Hou, J.; Li, Z.; Li, D. Inter-frame forgery detection for static-background video based on MVP consistency. Proc. Lect. Notes Comput. Sci. 2016, 9569, 94–106. [Google Scholar]
- Zhang, Z.; Hou, J.; Ma, Q.; Li, Z. Efficient video frame insertion and deletion detection based on inconsistency of correlations between local binary pattern coded frames. Secur. Commun. Netw. 2015, 8, 311–320. [Google Scholar] [CrossRef]
- Zhang, X.L.; Huang, T.Q.; Lin, J.; Huang, W. Video tamper detection method based on nonnegative tensor factorization. Chin. J. Netw. Inf. Secur. 2017, 3, 42–49. [Google Scholar]
- Zhao, Y.; Pang, T.; Liang, X.; Li, Z. Frame-deletion detection for static-background video based on multi-scale mutual information. In Proceedings of the International Conference on Cloud Computing and Security (ICCCS), Nanjing, China, 16–18 June 2017; pp. 371–384. [Google Scholar]
- Chen, W.; Shi, Y.Q.; Su, W. Image splicing detection using 2-D phase congruency and statistical moments of characteristic function. Proc. SPIE 2007, 6505, 65050–65058. [Google Scholar]
- Morrone, M.C.; Ross, J.; Burr, D.C.; Owens, R. Mach bands are phase dependent. Nature 1986, 324, 250–253. [Google Scholar] [CrossRef]
- Morrone, M.C.; Burr, D.C. Feature detection in human vision: A phase-dependent energy model. Proc. R. Soc. Lond. B 1988, 235, 221–245. [Google Scholar] [CrossRef] [PubMed]
- Kovesi, P. Image features from phase congruency. J. Comput. Vis. Res. 1999, 1, 1–26. [Google Scholar]
- Huang, T.Q.; Chen, Z.W.; Su, L.C.; Zheng, Z.; Yuan, X.J. Digital video forgeries detection based on content continuity. J. Nanjing Univ. (Nat. Sci.) 2011, 47, 493–503. [Google Scholar]
- k-Means Clustering. Available online: https://en.wikipedia.org/wiki/K-means_clustering#cite_note-lloyd1957-3 (accessed on 22 November 2018).
- Schuldt, C.; Laptev, I.; Caputo, B. Recognizing human actions: A local SVM approach. Pattern Recognit. 2004, 33, 32–36. [Google Scholar]
- Qadir, G.; Yahaya, S.; Ho, A.T.S. Surrey university library for forensic analysis (SULFA) of video content. In Proceedings of the IET Conference on Image Processing, London, UK, 3–4 July 2012; pp. 1–6. [Google Scholar]



| Source | Frame Rate | Resolution | Number of Original Videos | Number of Forged Videos |
|---|---|---|---|---|
| SULFA [34] | 30fps | 320 × 240 | 120 | 120 |
| Camera | 30fps | 640 × 480 | 120 | 120 |
| Source | TPL | Precision | F1 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Original | - | 579 | 20 | - | - | - | 0.9666 | - | - | - | - |
| 25 frames inserted | 599 | - | - | 0 | 582 | 1.00 | - | - | - | - | 0.9716 |
| 100 frames inserted | 599 | - | - | 0 | 581 | 1.00 | - | - | - | - | 0.9699 |
| 25 frames deleted | 550 | - | - | 49 | 500 | 0.9182 | - | - | - | - | 0.9091 |
| 100 frames deleted | 586 | - | - | 12 | 560 | 0.9799 | - | - | - | - | 0.9556 |
| Average | 584 | 579 | 20 | 15 | 556 | 0.9750 | 0.9666 | 0.9669 | 0.9708 | 0.9724 | 0.9520 |
| Source | TPL | Precision | F1 | LP | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| SULFA | 114 | 111 | 9 | 6 | 109 | 0.95 | 0.925 | 0.9268 | 0.9375 | 0.9383 | 0.9561 |
| Camera | 112 | 110 | 10 | 8 | 105 | 0.9333 | 0.9167 | 0.9180 | 0.925 | 0.9256 | 0.9375 |
| All | 226 | 221 | 19 | 14 | 214 | 0.9417 | 0.9208 | 0.9224 | 0.9313 | 0.9320 | 0.9469 |
| Method | Recall | Precision | F1 | LP |
|---|---|---|---|---|
| Reference [24] | 0.8673 | 0.8954 | 0.8811 | 0.8896 |
| Reference [25] | 0.9272 | 0.9455 | 0.9363 | 0.9361 |
| Proposed method | 0.9584 | 0.9447 | 0.9522 | 0.9495 |
| Video Resolution | Frame Number | Time of Feature Extract (s) | Time of Clustering (s) |
|---|---|---|---|
| 320 × 240 | 500 | 185.56 | 0.0545 |
| 640 × 480 | 500 | 373.15 | 0.0632 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Wang, R.; Xu, D. An Inter-Frame Forgery Detection Algorithm for Surveillance Video. Information 2018, 9, 301. https://doi.org/10.3390/info9120301
Li Q, Wang R, Xu D. An Inter-Frame Forgery Detection Algorithm for Surveillance Video. Information. 2018; 9(12):301. https://doi.org/10.3390/info9120301
Chicago/Turabian StyleLi, Qian, Rangding Wang, and Dawen Xu. 2018. "An Inter-Frame Forgery Detection Algorithm for Surveillance Video" Information 9, no. 12: 301. https://doi.org/10.3390/info9120301
APA StyleLi, Q., Wang, R., & Xu, D. (2018). An Inter-Frame Forgery Detection Algorithm for Surveillance Video. Information, 9(12), 301. https://doi.org/10.3390/info9120301






