2. Preliminaries
Under the PMC model [
5,
23], to diagnose a system
, two adjacent nodes in
G can perform tests on each other. For two adjacent nodes
u and
v in
, the test performed by
u on
v is represented by the ordered pair
The outcome of a test
is 1 (respectively, 0) if
u evaluate
v as faulty (respectively, fault-free). We assume that the test result is reliable (respectively, unreliable) if the node
u is fault-free (respectively, faulty). A test assignment
T for
G is a collection of tests for every adjacent pair of vertices. It can be modeled as a directed testing graph
), where
implies that
u and
v are adjacent in
G. The collection of all test results for a test assignment
T is called a syndrome. Formally, a syndrome is a function
. The set of all faulty processors in
G is called a faulty set. This can be any subset of
. For a given syndrome
, a subset of vertices
is said to be consistent with
if syndrome
can be produced from the situation that, for any
such that
,
if and only if
. This means that
F is a possible set of faulty processors. Since a test outcome produced by a faulty processor is unreliable, a given set
F of faulty vertices may produce a lot of different syndromes. On the other hand, different faulty sets may produce the same syndrome. Let
denote the set of all syndromes which
F is consistent with. Under the PMC model, two distinct sets
and
in
are said to be indistinguishable if
; otherwise,
and
are said to be distinguishable. Besides, we say
is an indistinguishable pair if
; else,
is a distinguishable pair.
In the MM model, a processor sends the same task to a pair of distinct neighbors and then compares their responses to diagnose a system G. The comparison scheme of is modeled as a multigraph, denoted by , where L is the labeled-edge set. A labeled edge represents a comparison in which two vertices u and v are compared by a vertex w, which implies . We usually assume that the testing result is reliable (respectively, unreliable) if the node u is fault-free (respectively, faulty). If and , then . If and , then . If and , then . If , then . The collection of all comparison results in is called the syndrome of the diagnosis, denoted by . If the comparison disagrees, then . Otherwise, . Hence, a syndrome is a function from L to . The MM* is a special case of the MM model and each node must test its any pair of adjacent nodes, i.e., if , then . The set of all faulty processors in the system is called a faulty set. This can be any subset of . For a given syndrome , a faulty subset of vertices is said to be consistent with if syndrome can be produced from the situation that, for any such that , if and only if or or under the MM model. Let denote the set of all syndromes which F is consistent with. Let and be two distinct faulty sets in . If , we say is an indistinguishable pair under the MM model; else, is a distinguishable pair under the MM model.
Definition 1. A system is g-good-neighbor t-diagnosable if and are distinguishable under the PMC (MM) model for each distinct pair of g-good-neighbor faulty subsets and of V with and . The g-good-neighbor diagnosability of G is the maximum value of t such that G is g-good-neighbor t-diagnosable under the PMC (MM) model.
A multiprocessor system and network is modeled as an undirected simple graph
, whose vertices (nodes) represent processors and edges (links) represent communication links. Given a nonempty vertex subset
of
V, the induced subgraph by
in
G, denoted by
, is a graph, whose vertex set is
and the edge set is the set of all the edges of
G with both endpoints in
. For any vertex
v, we define the neighborhood
of
v in
G to be the set of vertices adjacent to
v. For
,
u is called a neighbor vertex or a neighbor of
v. We denote the numbers of vertices and edges in
G by
and
. The degree
of a vertex
v is the number of neighbors of
v in
G. The minimum degree of a vertex in
G is denoted by
. Let
. We use
to denote the set
. For neighborhoods and degrees, we usually omit the subscript for the graph when no confusion arises. A path in
G is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. The path with a length of
n is denoted by
n-path. The length of a shortest path between
x and
y is called the distance between
x and
y, denoted by
. A complete graph
is a graph in which any two vertices are adjacent on
n vertices. A graph
is isomorphic to another graph
(denoted by
) if and only if there exists a bijection
such that for any two vertices
,
if and only if
. A graph
G is said to be
k-regular if for any vertex
v,
. Let
G be connected. The connectivity
of
G is the minimum number of vertices whose removal results in a disconnected graph or only one vertex left when
G is complete. Let
and
be two distinct subsets of
V, and let the symmetric difference
. For graph-theoretical terminology and notation not defined here, we follow [
33].
Let be connected. A fault set is called a g-good-neighbor faulty set if for every vertex v in . A g-good-neighbor cut of G is a g-good-neighbor faulty set F such that is disconnected. The minimum cardinality of g-good-neighbor cuts is said to be the g-good-neighbor connectivity of G, denoted by . A connected graph G is said to be g-good-neighbor connected if G has a g-good-neighbor cut.
For two positive integers n and k, let denote the set and denote the set . Let be a set of arrangements of k elements in , that is, : for and for , .
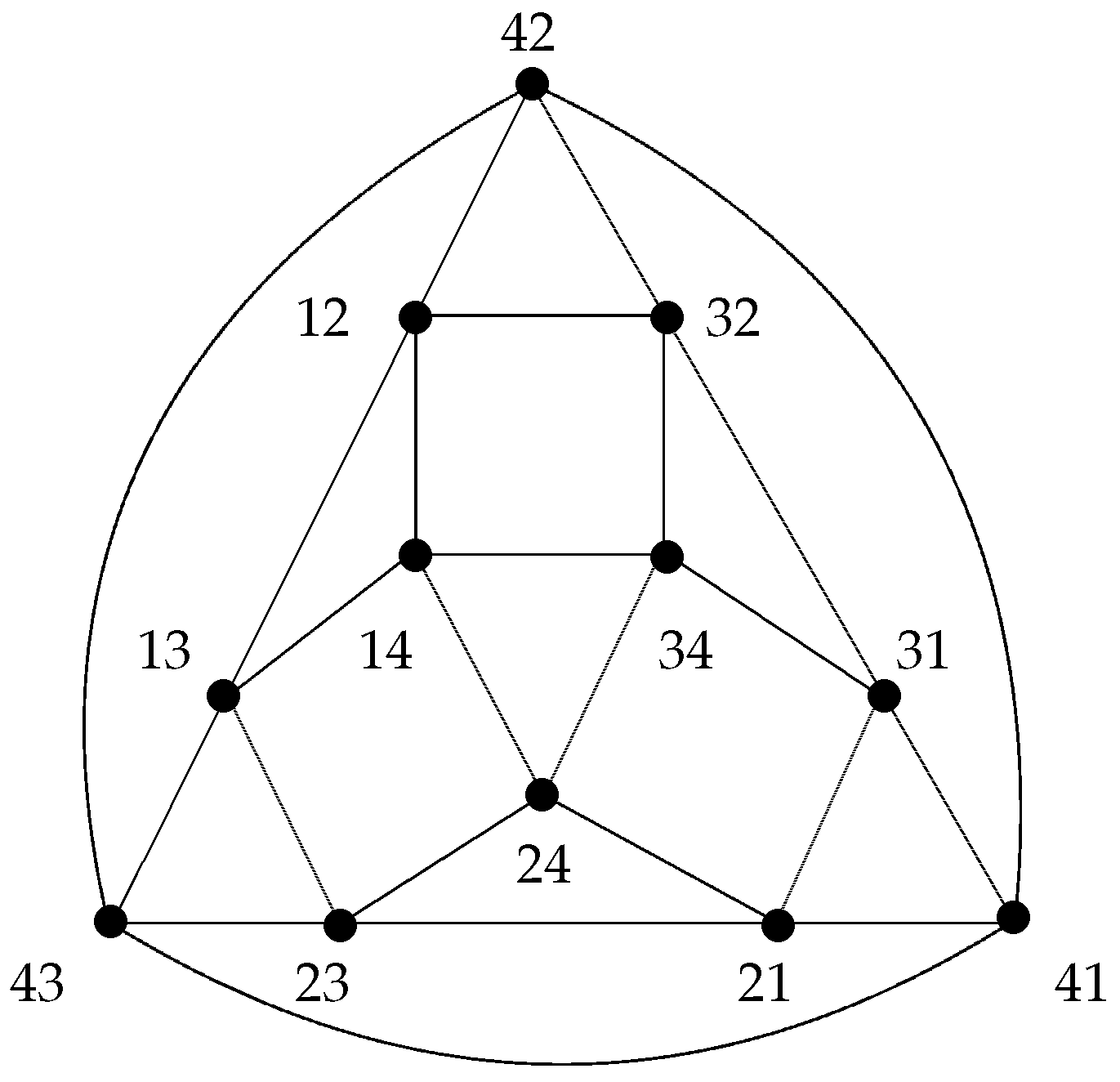
Definition 2. Given two positive integers n and k with . The -arrangement graph, denoted by , has vertex set , and edge set with for some and for all .
From the definition, we know that the vertices of
are the arrangements of
k elements in
, and the edges of
connect arrangements which differ in exactly one of their
k positions.
is a regular graph of degree
with
vertices.
Figure 1 shows the arrangement graph
.
Definition 3 ([
26]).
A graph is vertex-transitive if and only if for any pair of its vertices u and v, there exists an automorphism of the graph that maps u to v. A graph is edge-transitive if and only if for any pair of its edges and , there exists an automorphism of the graph that maps to . Lemma 1 ([
26]).
is vertex-transitive and edge-transitive. Lemma 2 ([
26]).
for . Lemma 3 ([
28]).
and , , and . Lemma 4 ([
28]).
and , , and . Lemma 5 ([
28]).
For , , and, for , . Lemma 6 ([
28]).
Let be positive integers such that , . Then, An edge cut of a graph G is a set of edges whose removal makes the remaining graph no longer connected. The edge connectivity of G is the minimum cardinality of an edge cut of G.
Lemma 7 ([
33]).
. According to Lemmas 2 and 7, we get the following corollary.
Corollary 1. The edge connectivity for .
For , , let be the set of all vertices in with the jth position being i, that is, with . It is easy to check that each is a subgraph of , and we say that is decomposed into n subgraphs according to the jth position. For simplicity, we shall take j as the last position k, and use to denote . Then, with and for for . It is easy to see that is a complete graph .
Proposition 1 ([
34]).
Let . For each , is isomorphic to where . For any vertex , in this paper, we say that is the set of inner neighbors of u, which is denoted by and is the set of outer neighbors of u, which is denoted by .
Proposition 2 ([
31]).
Let , . For any two vertices u, v in the subgraph , and . Furthermore, the vertices of are distributed in distinct subgraphs. Proposition 3. For any vertex , let be the set of outer neighbors of u. Then, is isomorphic to the complete graph .
Proof. By Lemma 1, is vertex-transitive. Without loss of generality, let . By the definition of arrangement graphs, . Then, . Note that u, ,…, and are only different in last position. By the definition of arrangement graphs, any pair of vertices of u ,…, and are adjacent. Thus, is a complete graph. Note that . Thus, is isomorphic to . □
Definition 4. Let , and let be the symmetric group on containing all permutations of . The alternating group is the subgroup of containing all even permutations. It is well known that is a generating set for . The n-dimensional alternating group graph is the graph with vertex set = in which two vertices u, v are adjacent if and only if or , .
Definition 5. The n-dimensional star graph denoted by . The vertex set of is is a permutation of . Vertex adjacency is defined as follows: is adjacent to for all .
Lemma 8 ([
29]).
(1). The arrangement graph is isomorphic to the n-dimensional alternating group graph . (2). The arrangement graph is isomorphic to the n-dimensional star graph . Lemma 9 ([
31]).
For any two distinct vertices u and v in the arrangement graph , we have the following results:- 1.
If , then ;
- 2.
If and , then ;
- 3.
If and , then ; and
- 4.
If , then .
3. The g-Good-Neighbor Diagnosability of Arrangement Graphs under the PMC Model
In this section, we show the
g-good-neighbor diagnosability of arrangement graphs under the PMC model (
Figure 2).
Theorem 1 ([
23]).
A system is g-good-neighbor t-diagnosable under the model if and only if there is an edge with and for each distinct pair of g-good-neighbor faulty subsets and of V with and . Lemma 10 ([
28]).
For and , , and . Lemma 11 ([
28]).
For , , and, for , . Lemma 12 ([
27]).
Let and let T be a subset of the vertices of such that . Then, is either connected or has a large component and small components with at most two vertices or and has a large component and a four-cycle. Lemma 13 ([
28]).
Let be positive integers such that . Then, Let , and . Let and and neither i nor j occurs in . Clearly, , and . Since any symbol that does not occur in can serve as the last symbol in a vertex in , . Thus, the graph induced by is a complete graph of order . Let and such that . Notice that . Then, is a complete graph .
Lemma 14. Let be positive integers such that , , , and let be the arrangement graph. Let X be defined as above, and let , . Then, , , and .
Proof. Let
X be defined as above. By the process of the proof of Lemma 13 in [
28],
is a
g-good-neighbor cut of
and
. Since
,
. □
Lemma 15. Let , and . Then, the g-good-neighbor diagnosability of the arrangement graph under the PMC model is less than or equal to , i.e., .
Proof. Let X be defined as above, and let , . By Lemma 14, , , and . Therefore, and are g-good-neighbor faulty sets of with and .
We prove that is not g-good-neighbor -diagnosable. Since and , there is no edge of between and . By Theorem 1, we can show that is not g-good-neighbor -diagnosable under the PMC model. Hence, by the definition of the g-good-neighbor diagnosability, we show that the g-good-neighbor diagnosability of is less than , i.e., . □
Lemma 16. Let be positive integers such that , . Then, the arrangement graph is g-good-neighbor -diagnosable under the PMC model.
Proof. By Theorem 1, to prove is g-good-neighbor -diagnosable, it is equivalent to prove that there is an edge with and for each distinct pair of g-good-neighbor faulty subsets and of with and .
We prove this statement by contradiction. Suppose that there are two distinct g-good-neighbor faulty subsets and of with and , but the vertex set pair is not satisfied with the condition in Theorem 1, i.e., there are no edges between and . Without loss of generality, suppose that .
Case 1. .
Note that . Since , . Let . Then, for and .
Assume . We have that . When , . Note for . Thus, . In fact, when . This is a contradiction. Therefore, .
Case 2.
According to the hypothesis, there are no edges between and . Since is a g-good-neighbor faulty set and has two parts and , we have that and . Similarly, when . Therefore, is also a g-good-neighbor faulty set. Since there are no edges between and , is also a g-good-neighbor cut. When , is also a g-good-neighbor faulty set. Since there are no edges between and , is a g-good-neighbor cut. By Lemma 13, . Since , . Therefore, , which contradicts with that . Thus, is g-good-neighbor -diagnosable. By the definition of , . The proof is complete. □
Combining Lemmas 15 and 16, we have the following theorem.
Theorem 2. Let be positive integers such that , . Then, under the PMC model.
Theorem 3. Let be the arrangement graph with . Then, the diagnosability under the PMC model.
Proof. Let . Then, is a cut of and . Let , . Then, , , and . Therefore, and are 0-good-neighbor faulty sets of with and . We will prove is not 0-good-neighbor -diagnosable. Since and , there is no edge of between and . By Theorem 1, we can show that is not 0-good-neighbor -diagnosable under the PMC model. Hence, by the definition of the 0-good-neighbor diagnosability, we conclude that the 0-good-neighbor diagnosability of is less than , i.e., .
By Theorem 1, to prove is 0-good-neighbor -diagnosable, it is equivalent to prove that there is an edge with and for each distinct pair of 0-good-neighbor faulty subsets and of with and .
We prove this statement by contradiction. Suppose that there are two distinct 0-good-neighbor faulty subsets and of with and , but the vertex set pair is not satisfied with the condition in Theorem 1, i.e., there are no edges between and . Without loss of generality, suppose that .
Assume . We have that . When , , a contradiction. Therefore, . When , . Note and for . Thus, . In fact, when . This is a contradiction. Therefore, .
According to the hypothesis, there are no edges between and . Since is a 0-good-neighbor faulty set and has two parts and , we have that and . Similarly, when . Therefore, is also a 0-good-neighbor faulty set. Since there are no edges between and , is also a 0-good-neighbor cut. When , is also a 0-good-neighbor faulty set. Since there are no edges between and , is a 0-good-neighbor cut. By Lemma 2, . Since , . Therefore, , which contradicts with that . Thus, is 0-good-neighbor -diagnosable. By the definition of , . Therefore, . □
Lemma 17. Let and . Then, under the PMC model.
Proof. By Theorem 1, to prove is 1-good-neighbor -diagnosable, it is equivalent to prove that there is an edge with and for each distinct pair of g-good-neighbor faulty subsets and of with and .
We prove this statement by contradiction. Suppose that there are two distinct 1-good-neighbor faulty subsets and of with and , but the vertex set pair is not satisfied with the condition in Theorem 1, i.e., there are no edges between and . Without loss of generality, assume that .
Assume . We have that . When , . Note for . Thus, . In fact, when . This is a contradiction. When , . In fact, when . This is a contradiction. Therefore, .
According to the hypothesis, there are no edges between and . Since is a 1-good-neighbor faulty set and has two parts and , we have that and . Similarly, when . Therefore, is also a 1-good-neighbor faulty set. Since there are no edges between and , is also a 1-good-neighbor cut. When , is also a 1-good-neighbor faulty set. Since there are no edges between and , is a 1-good-neighbor cut. By Lemma 10, . Since , . Therefore, , which contradicts with that . Thus, is 1-good-neighbor -diagnosable. By the definition of , . □
Combining Lemmas 15 and 17, we have the following theorem.
Theorem 4. Let and . Then, under the PMC model.
Lemma 18. Let and . Then, under the PMC model.
Proof. By Theorem 1, to prove is 2-good-neighbor -diagnosable, it is equivalent to prove that there is an edge with and for each distinct pair of g-good-neighbor faulty subsets and of with and .
We prove this statement by contradiction. Suppose that there are two distinct g-good-neighbor faulty subsets and of with and , but the vertex set pair is not satisfied with the condition in Theorem 1, i.e., there are no edges between and . Without loss of generality, assume that .
Assume . We have that . When , . Note for . Thus, . In fact, when . This is a contradiction. Therefore, .
According to the hypothesis, there are no edges between and . Since is a 2-good-neighbor faulty set and has two parts and , we have that and . Similarly, when . Therefore, is also a 2-good-neighbor faulty set. Since there are no edges between and , is also a 2-good-neighbor cut. When , is also a 2-good-neighbor faulty set. Since there are no edges between and , is a 2-good-neighbor cut. By Lemma 11, . Since , . Therefore, , which contradicts with that . Thus, is 2-good-neighbor -diagnosable. By the definition of , . □
Combining Lemmas 15 and 18, we have the following theorem.
Theorem 5. Let and . Then, under the PMC model.
For , is decomposed into n subgraphs . By Proposition 1, is isomorphic to for . Let . Then, , , , , and , and is a 4-cycle of .
Lemma 19. For and , let be defined as above, and let , . Then, , , and .
Proof. Note that . Then, . Since is a four-cycle of , . Since , and . Thus, . □
Lemma 20. For , under the PMC model.
Proof. Let X be defined in Lemma 19, and let , . By Lemma 19, , , and . Therefore, and are 2-good-neighbor faulty sets of with and .
We will prove is not 2-good-neighbor -diagnosable. Since and , there is no edge of between and . By Theorem 1, we can deduce that is not 2-good-neighbor -diagnosable under the PMC model. Hence, by the definition of the 2-good-neighbor diagnosability, we conclude that the 2-good-neighbor diagnosability of is less than , i.e., . □
Lemma 21. For , under the PMC model.
Proof. By Theorem 1, to prove is 2-good-neighbor -diagnosable, it is equivalent to prove that there is an edge with and for each distinct pair of 2-good-neighbor faulty subsets and of with and .
We prove this statement by contradiction. Suppose that there are two distinct 2-good-neighbor faulty subsets and of with and , but the vertex set pair is not satisfied with the condition in Theorem 1, i.e., there are no edges between and . Without loss of generality, assume that .
Assume . We have that , a contradiction to . Therefore, .
According to the hypothesis, there are no edges between and . Since is a 2-good-neighbor faulty set and has two parts and , we have that and . Similarly, when . Therefore, is also a 2-good-neighbor faulty set. Since there are no edges between and , is also a 2-good-neighbor cut. When , is also a 2-good-neighbor faulty set. Since there are no edges between and , is a 2-good-neighbor cut. By Lemma 11, . If , then, by Lemma 12, . If or , then , a contradiction to that . Therefore, , which contradicts with that . Thus, is 2-good-neighbor -diagnosable. By the definition of , . □
Combining Lemmas 20 and 21, we have the following theorem.
Theorem 6. Let . Then, under the PMC model.
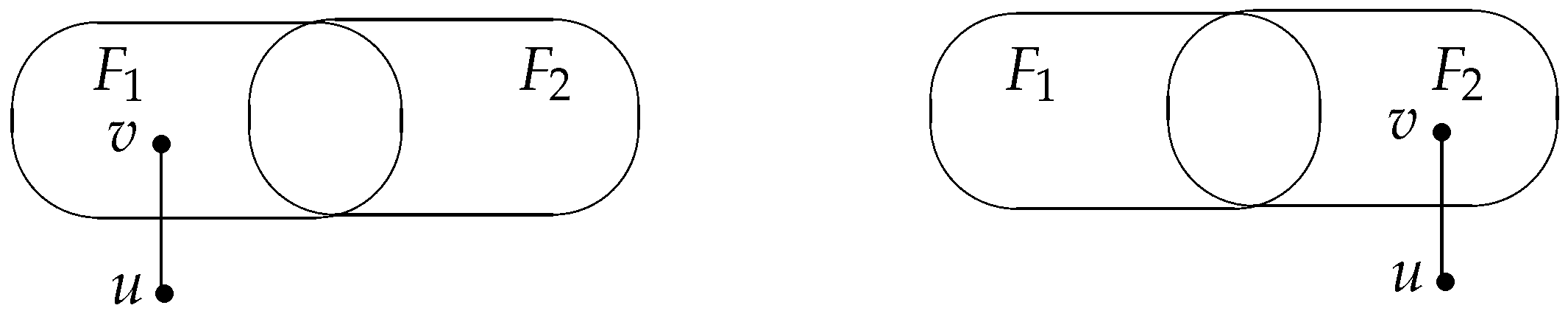
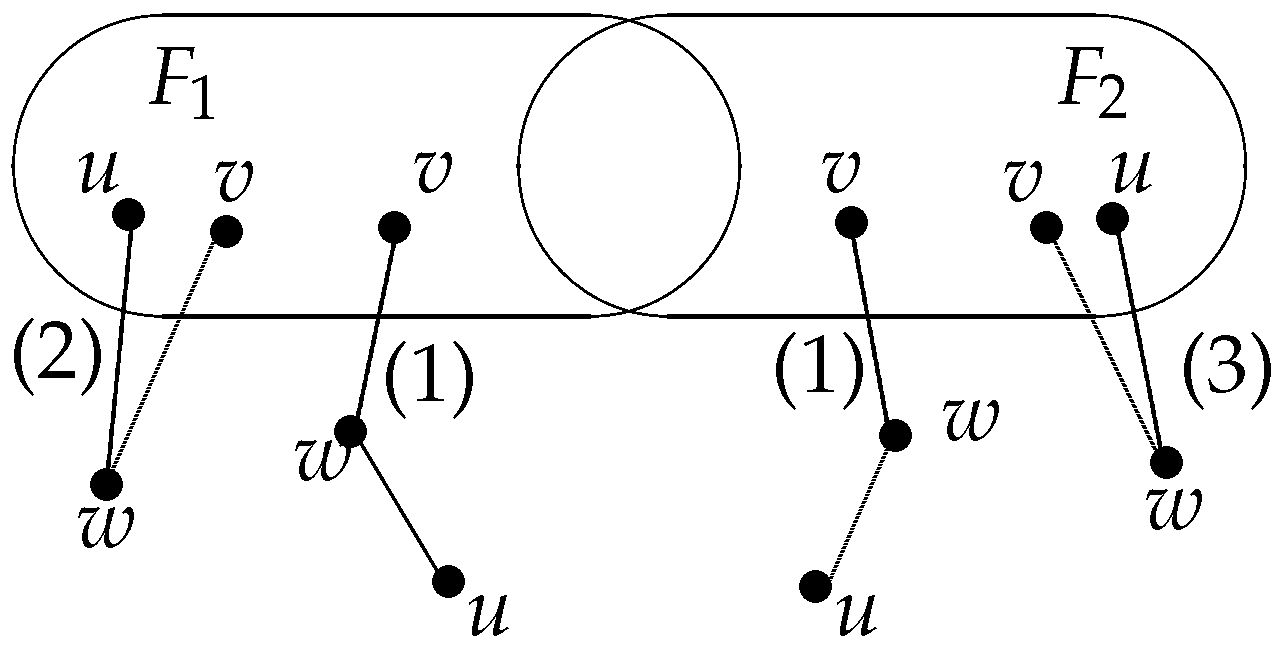
4. The g-Good-Neighbor Diagnosability of Arrangement Graphs under the MM* Model
Before discussing the
g-good-neighbor diagnosability of the arrangement graph
under the MM
model (
Figure 3), we first give an existing result.
Theorem 7 ([
1,
23]).
A system is g-good-neighbor t-diagnosable under the model if and only if for each distinct pair of g-good-neighbor faulty subsets and of V with and satisfies one of the following conditions. (1) There are two vertices and there is a vertex such that and . (2) There are two vertices and there is a vertex such that and . (3) There are two vertices and there is a vertex such that and . Lemma 22. Let , and . Then, the g-good-neighbor diagnosability of the arrangement graph under the MM* model is less than or equal to , i.e., .
Proof. Let X be defined in Lemma 15, and let , . By Lemma 14, , , and . Therefore, and are g-good-neighbor faulty sets of with and .
We will prove that is not g-good-neighbor -diagnosable. Since and , there is no edge of between and . By Theorem 7, we can show that is not g-good-neighbor -diagnosable under the MM* model. Hence, by the definition of the g-good-neighbor diagnosability, we show that the g-good-neighbor diagnosability of is less than , i.e., . □
Lemma 23. Let be positive integers such that , . Then, the arrangement graph is g-good-neighbor -diagnosable under the MM* model.
Proof. By the definition of the g-good-neighbor diagnosability, it is sufficient to show that is g-good-neighbor -diagnosable for .
By Theorem 7, suppose, on the contrary, that there are two distinct g-good-neighbor faulty subsets and of with and , but the vertex set pair is not satisfied with any condition in Theorem 7. Without loss of generality, assume that Similar to the discussion on in Lemma 16, we can show .
Claim 1. has no isolated vertex.
Since is a g-good neighbor faulty set, for an arbitrary vertex , . Suppose, on the contrary, that has at least one isolated vertex x. Since is a g-good neighbor faulty set and , there are at least two vertices such that are adjacent to x. According to the hypothesis, the vertex set pair is not satisfied with any condition in Theorem 7, by Condition (3) of Theorem 7, a contradiction. Therefore, there are at most one vertex such that u are adjacent to x. Thus, , a contradiction to that is a g-good neighbor faulty set, where . Thus, has no isolated vertex. The proof of Claim 1 is complete.
Let . By Claim 1, . Since the vertex set pair is not satisfied with any condition in Theorem 7, by the condition (1) of Theorem 7, for any pair of adjacent vertices , there is no vertex such that and . It follows that u has no neighbor in . Since u is taken arbitrarily, there is no edge between and .
Since and is a g-good-neighbor faulty set, we have that , and . Since both and are g-good-neighbor faulty sets, and there is no edge between and , is a g-good-neighbor cut of . By Lemma 13, we have . Therefore, , which contradicts . Therefore, is g-good-neighbor -diagnosable and . The proof is complete. □
Combining Lemmas 22 and 23, we have the following theorem.
Theorem 8. Let be positive integers such that , . Then, under the MM* model.
Theorem 9 ([
34]).
Let be an n-dimensional arrangement graph and . Then, the diagnosability of is , i.e., under the MM* model. Lemma 24 ([
30]).
is hamiltonian for . A component of a graph G is odd according as it has an odd number of vertices. We denote by the number of odd component of G.
Theorem 10 ([
33]).
A graph has a perfect matching if and only if for all . Lemma 25. Let and . Then, under the MM model.
Proof. By the definition of 1-good-neighbor diagnosability, it is sufficient to show that is 1-good-neighbor -diagnosable.
By Theorem 7, suppose, on the contrary, that there are two distinct 1-good-neighbor faulty subsets and of with and , but the vertex set pair is not satisfied with any condition in Theorem 7. Without loss of generality, suppose that Assume . We have that . When , , a contradiction to . Therefore, . When , . Note for . Thus, . In fact, when . This is a contradiction. Therefore, .
Claim 1. has no isolated vertex.
Suppose, on the contrary, that has at least one isolated vertex w. Since is a 1-good-neighbor faulty set, there is a vertex such that u is adjacent to w. Since the vertex set pair is not satisfied with any condition in Theorem 7, there is at most one vertex such that u is adjacent to w. Thus, there is just a vertex such that u is adjacent to w. Similarly, we can show that there is just a vertex such that v is adjacent to w when . Suppose . Then, . Since is a 1-good neighbor faulty set, has no isolated vertex. Therefore, as follows. Let be the set of isolated vertices in , and let H be the subgraph induced by the vertex set . Then, for any , there are neighbors in . Since is even and Lemma 24, has a perfect matching. By Theorem 10, . In particular, when . When , . This is a contradiction to . Thus, . When , . Note for . Note that . This is a contradiction to . Thus, . Since the vertex set pair is not satisfied with the condition (1) of Theorem 7, and any vertex of is not isolated in H, we show that there is no edge between and . Thus, is a vertex cut of and , i.e., is a 1-good-neighbor cut of . By Lemma 10, . Because , , and neither nor is empty, we have . Let and . Then, for any vertex , w are adjacent to and . Suppose that is adjacent to . Then, is a three-cycle and , a contradiction. Therefore, suppose that is not adjacent to . According to Lemma 9, there are at most two common neighbors for any pair of vertices in , it follows that there are at most three isolated vertices in , i.e., .
Suppose that there is exactly one isolated vertex v in . Let and be adjacent to v. Then, and . Note that and . By Lemma 9, It follows that , which contradicts .
Suppose that there are exactly two isolated vertices
v and
w in
. Let
and
be adjacent to
v and
w, respectively. Since
, by Lemma 9,
. Note that
. If
, then
, a contradiction. Thus,
. Since
,
. If
, then, by Lemma 9, a contradiction to
. Suppose that
. Then,
. By the proof of Lemma 3.2 ([
18]),
has no isolated vertex. Suppose that
. Then,
. By Lemma 1, let
.Without loss of generality, suppose
and
. Then, the vertex
is not adjacent to
v and
w. Thus,
, a contradiction. The proof of Claim 1 is complete.
Let . By Claim 1, u has at least one neighbor in . Since the vertex set pair is not satisfied with any condition in Theorem 7, by the condition (1) of Theorem 7, for any pair of adjacent vertices , there is no vertex such that and . It follows that u has no neighbor in . Since u is taken arbitrarily, there is no edge between and . Since and is a 1-good-neighbor faulty set, and . Since both and are 1-good-neighbor faulty sets, and there is no edge between and , is a 1-good-neighbor cut of . By Lemma 10, we have . Therefore, , which contradicts . Therefore, is 1-good-neighbor -diagnosable and . The proof is complete. □
Combining Lemmas 22 and 25, we have the following theorem.
Theorem 11. Let . Then, under the MM model.
Lemma 26. Let and . Then, under the MM model.
Proof. By the definition of the 2-good-neighbor diagnosability, it is sufficient to show that is g-good-neighbor -diagnosable.
By Theorem 7, suppose, on the contrary, that there are two distinct g-good-neighbor faulty subsets and of with and , but the vertex set pair is not satisfied with any condition in Theorem 7. Without loss of generality, suppose that Similar to the discussion on in Lemma 18, we have .
Claim 1. has no isolated vertex.
Since is a 2-good neighbor faulty set, for an arbitrary vertex , . Suppose, on the contrary, that has at least one isolated vertex x. Since is a 2-good neighbor faulty set, there are at least two vertices such that are adjacent to x. According to the hypothesis, the vertex set pair is not satisfied with any condition in Theorem 7, by the condition (3) of Theorem 7, a contradiction. Therefore, there are at most one vertex such that u are adjacent to x. Thus, , a contradiction to that is a 2-good neighbor faulty set. Thus, has no isolated vertex. The proof of Claim 1 is complete.
Let . By Claim 1, . Since the vertex set pair is not satisfied with any condition in Theorem 7, by the condition (1) of Theorem 7, for any pair of adjacent vertices , there is no vertex such that and . It follows that u has no neighbor in . Since u is taken arbitrarily, there is no edge between and .
Since and is a 2-good-neighbor faulty set, we have that , and . Since both and are 2-good-neighbor faulty sets, and there is no edge between and , is a 2-good-neighbor cut of . By Lemma 11, we have . Therefore, , which contradicts . Therefore, is 2-good-neighbor -diagnosable and . The proof is complete. □
Combining Lemmas 22 and 26, we have the following theorem.
Theorem 12. Let and . Then, under the MM model.
Lemma 27. For , under the MM model.
Proof. Let X be defined in Lemma 19, and let , . By Lemma 19, , , and . Therefore, and are 2-good-neighbor faulty sets of with and .
We will prove is not 2-good-neighbor -diagnosable. Since and , there is no edge of between and . By Theorem 7, we show that is not 2-good-neighbor -diagnosable under the MM model. Hence, by the definition of the 2-good-neighbor diagnosability, we show that the 2-good-neighbor diagnosability of is less than , i.e., . □
Lemma 28. For , under the MM model.
Proof. By the definition of the 2-good-neighbor diagnosability, it is sufficient to show that is 2-good-neighbor -diagnosable.
By Theorem 7, suppose, on the contrary, that there are two distinct 2-good-neighbor faulty subsets and of with and , but the vertex set pair is not satisfied with any condition in Theorem 7. Without loss of generality, suppose that Similar to the discussion on in Lemma 21, we have .
Claim 1. has no isolated vertex.
Since is a 2-good neighbor faulty set, for an arbitrary vertex , . Suppose, on the contrary, that has at least one isolated vertex x. Since is a 2-good neighbor faulty set, there are at least two vertices such that are adjacent to x. According to the hypothesis, the vertex set pair is not satisfied with any condition in Theorem 7, by the condition (3) of Theorem 7, a contradiction. Therefore, there are at most one vertex such that u are adjacent to x. Thus, , a contradiction to that is a 2-good neighbor faulty set. Thus, has no isolated vertex. The proof of Claim 1 is complete.
Let . By Claim 1, . Since the vertex set pair is not satisfied with any condition in Theorem 7, by the condition (1) of Theorem 7, for any pair of adjacent vertices , there is no vertex such that and . It follows that u has no neighbor in . Since u is taken arbitrarily, there is no edge between and .
Since and is a 2-good-neighbor faulty set, we have that , and . Since both and are 2-good-neighbor faulty sets, and there is no edge between and , is a 2-good-neighbor cut of . By Lemma 11, we have . If , then, by Lemma 12, . If or , then , a contradiction to that . Therefore, , which contradicts with that . Therefore, is 2-good-neighbor -diagnosable and . The proof is complete. □
Combining Lemmas 27 and 28, we have the following theorem.
Theorem 13. Let . Then, under the MM model.