Sensor Alignment for Ballistic Trajectory Estimation via Sparse Regularization
Abstract
:1. Introduction
2. Estimates of Trajectory and Systematic Errors via Sparse Regularization
3. Regularization Parameter Selection
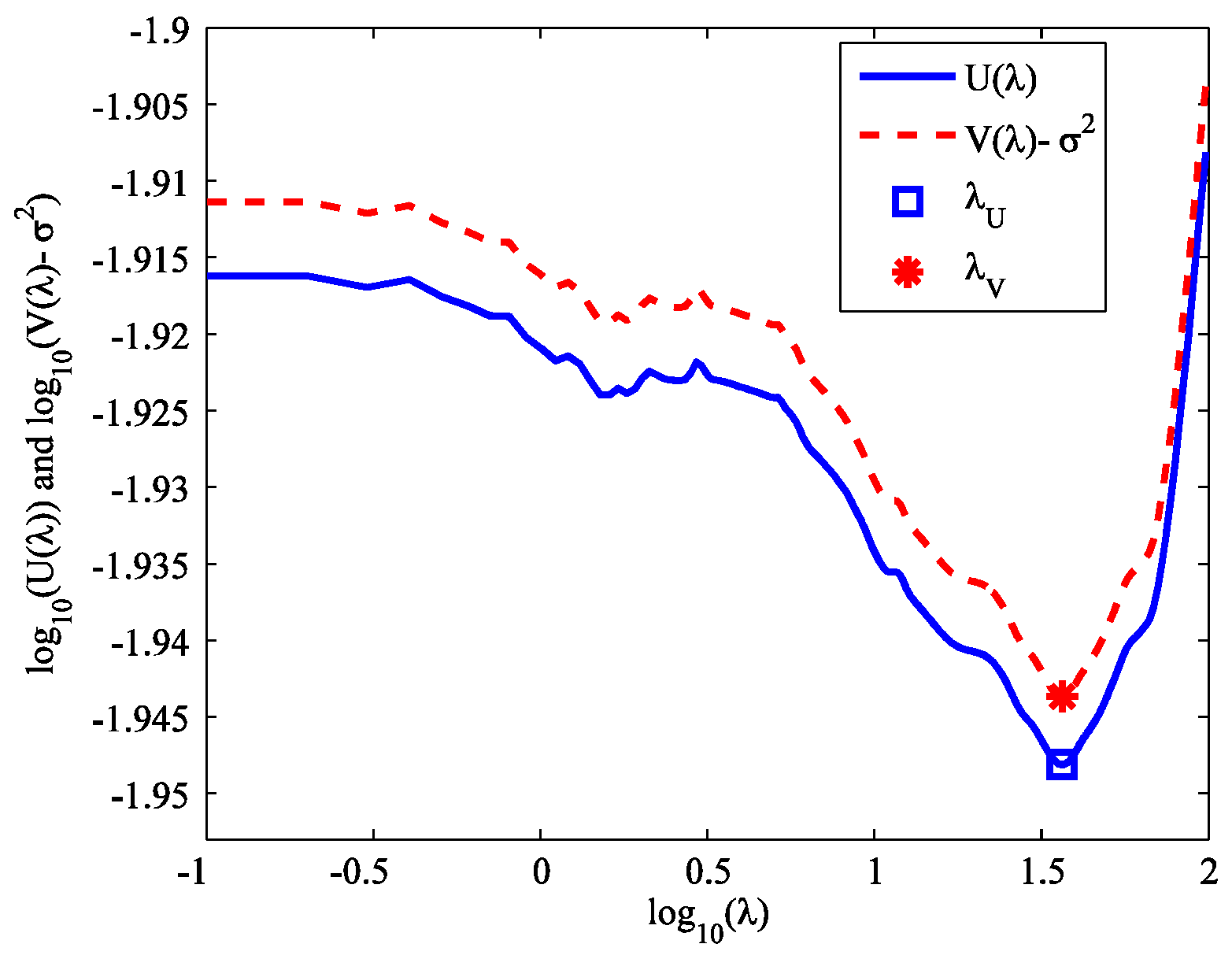
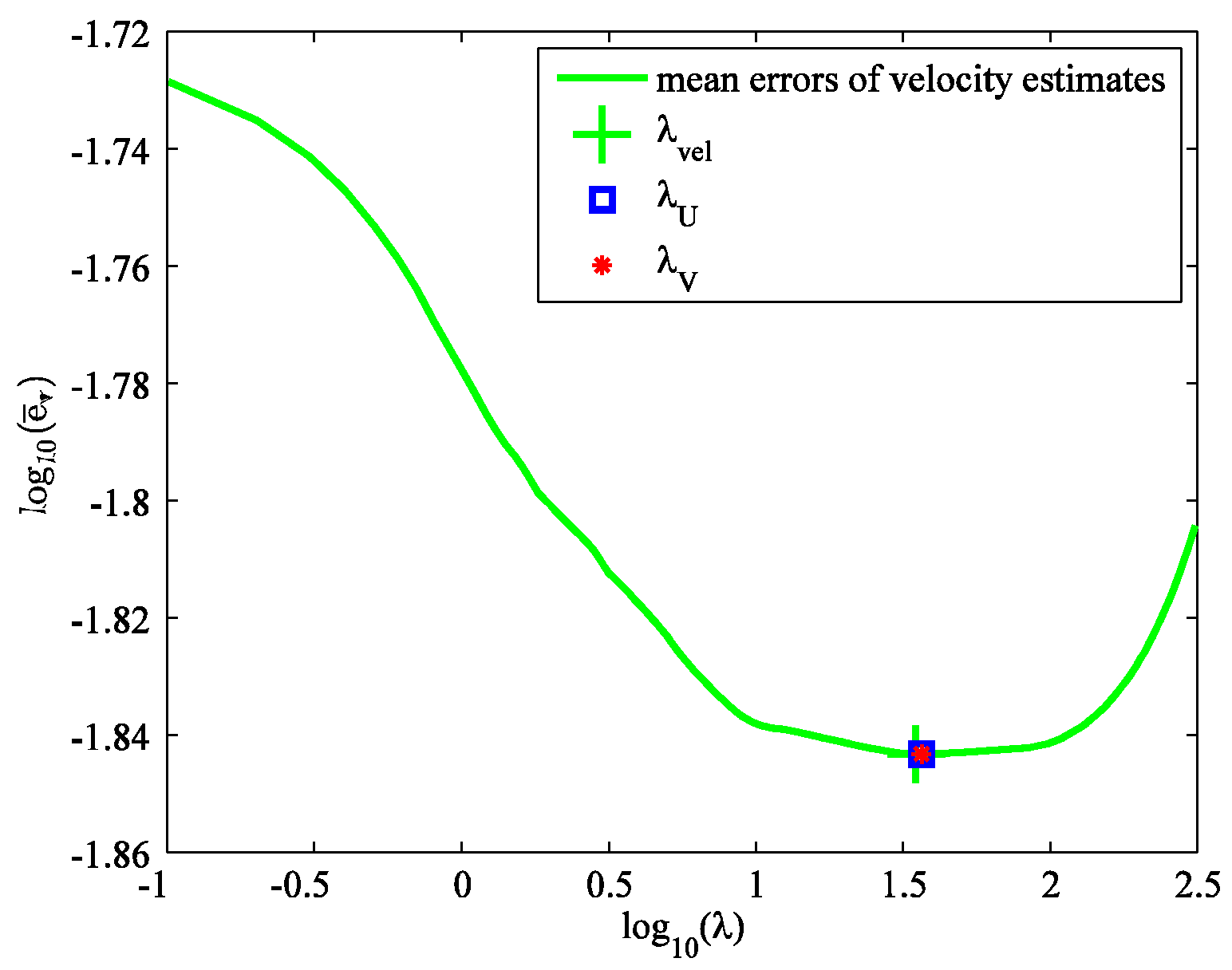
3.1. SURE Method
3.2. GCV Method
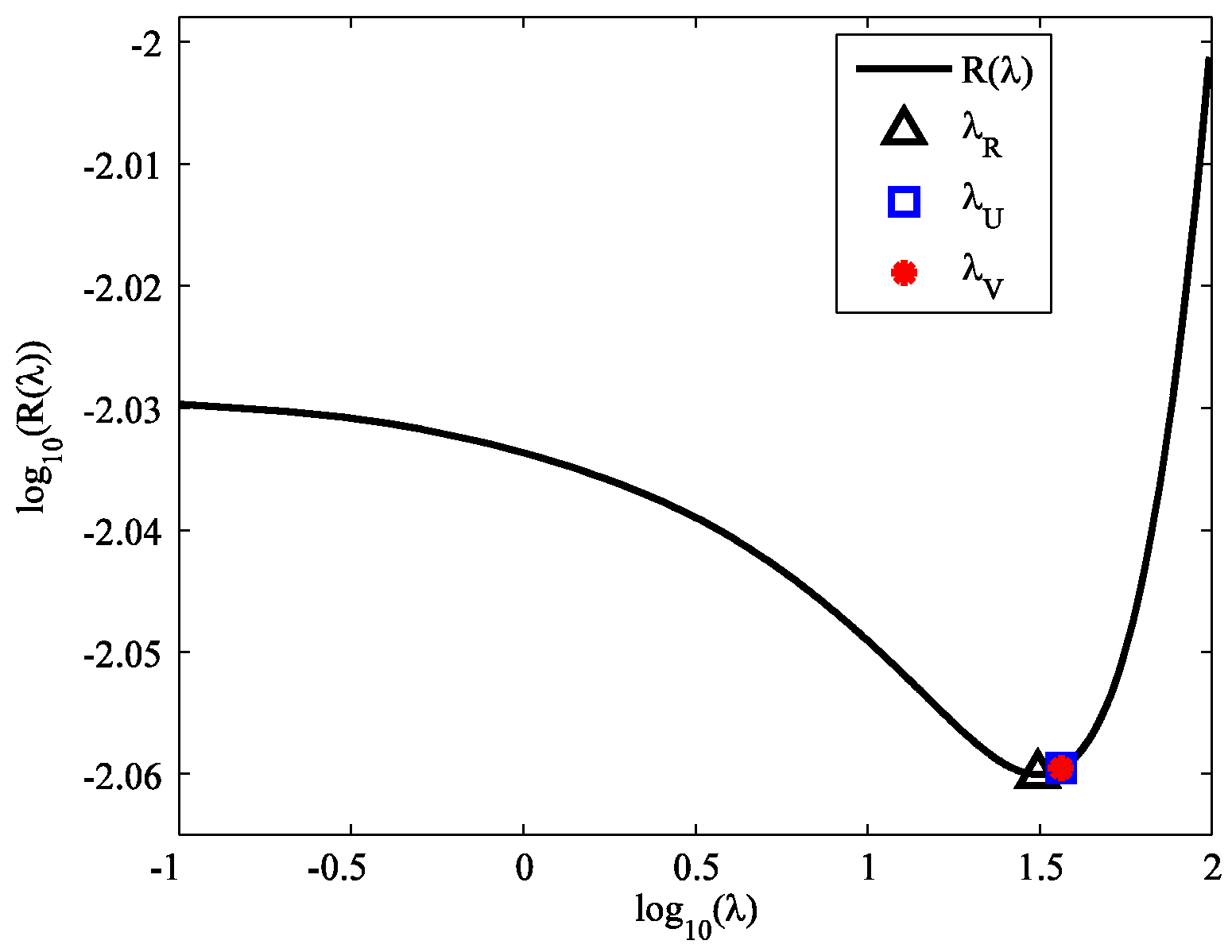
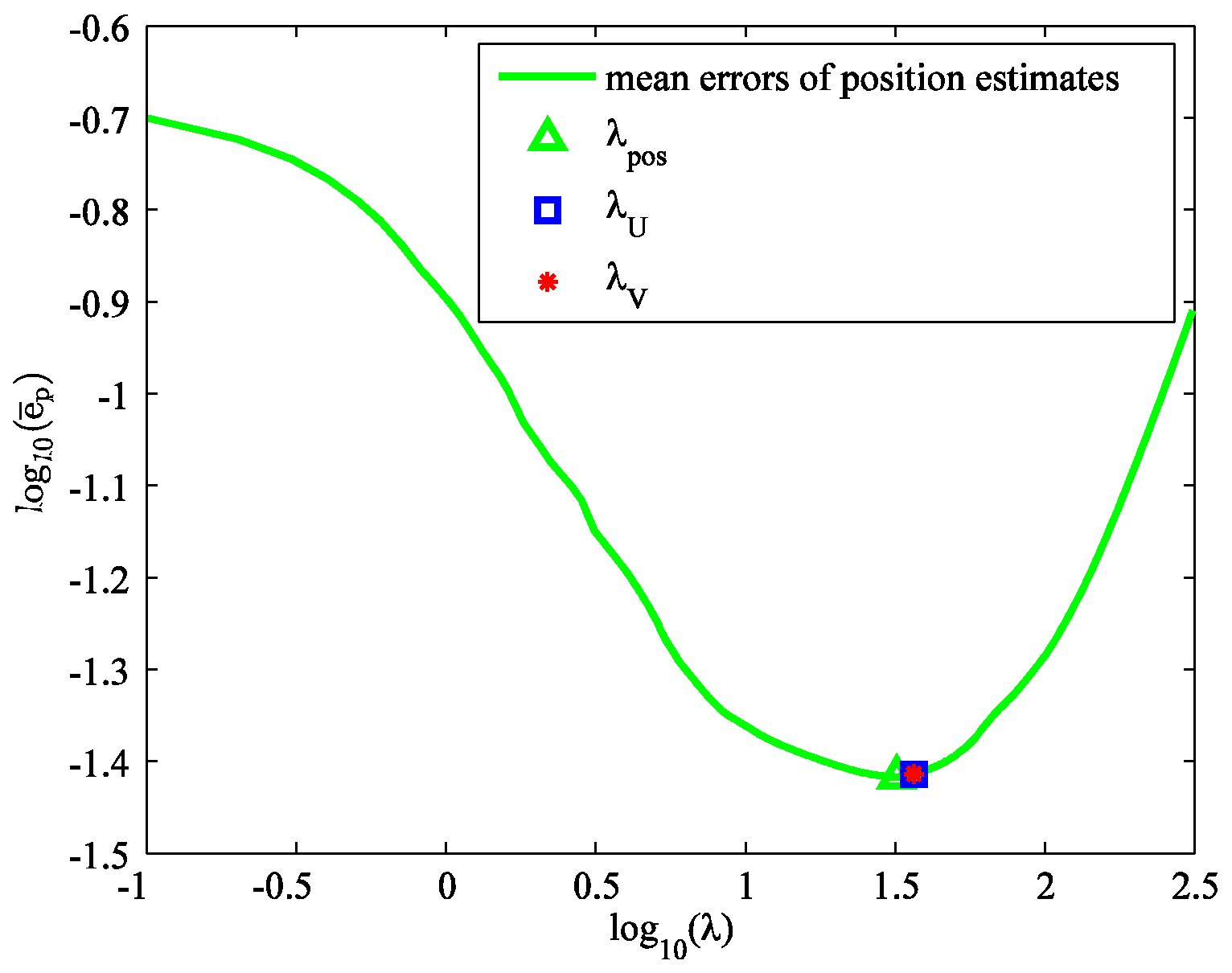
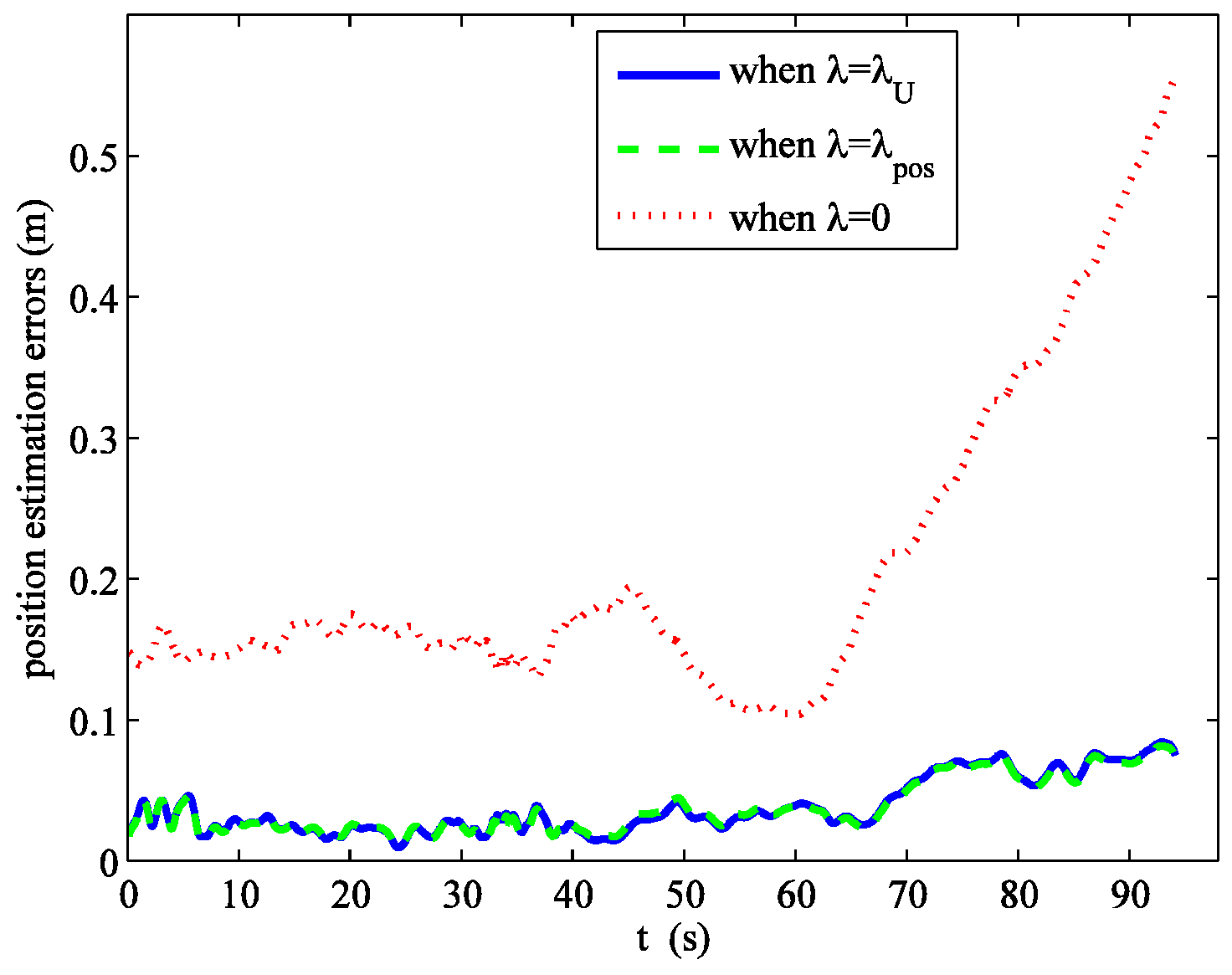
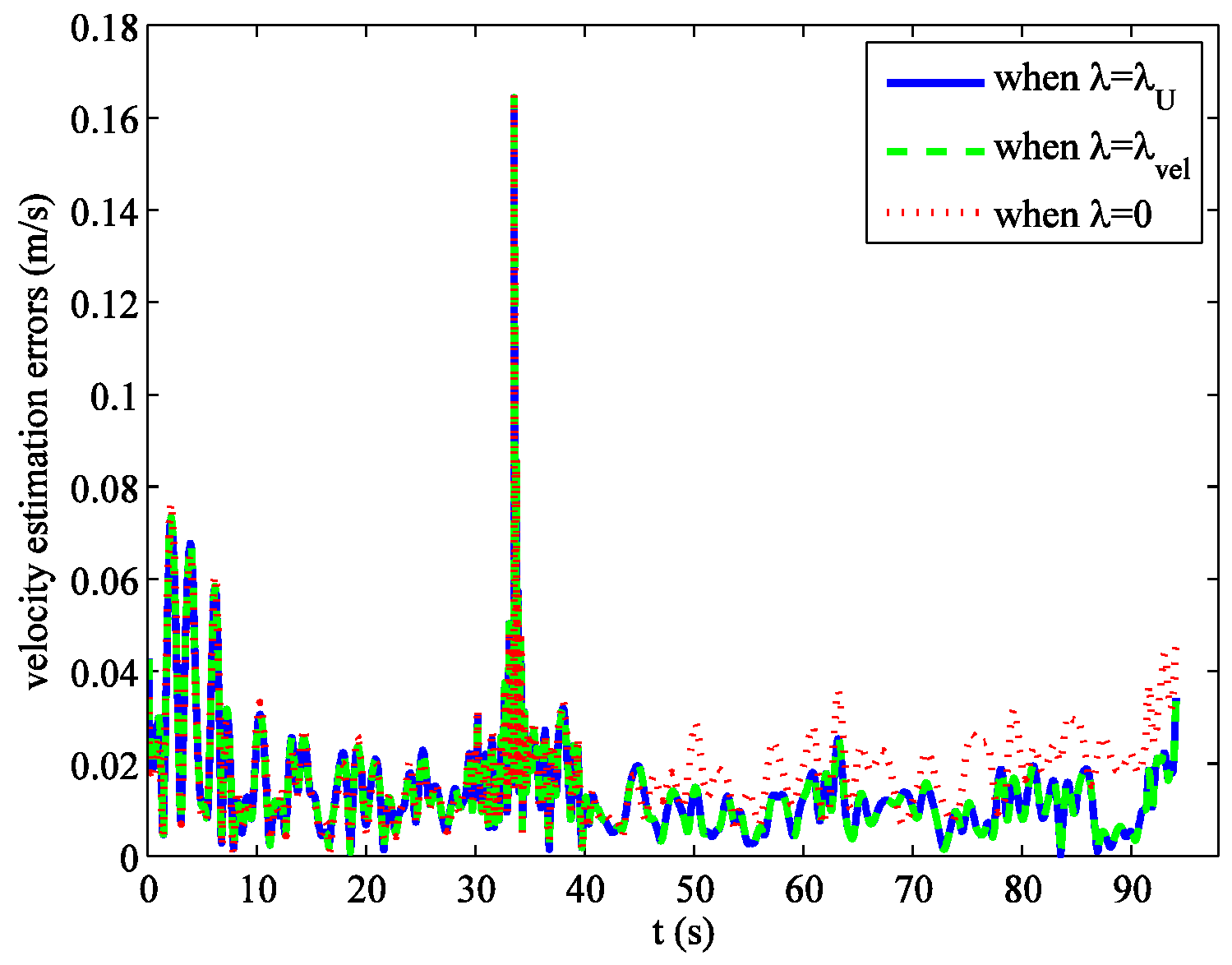
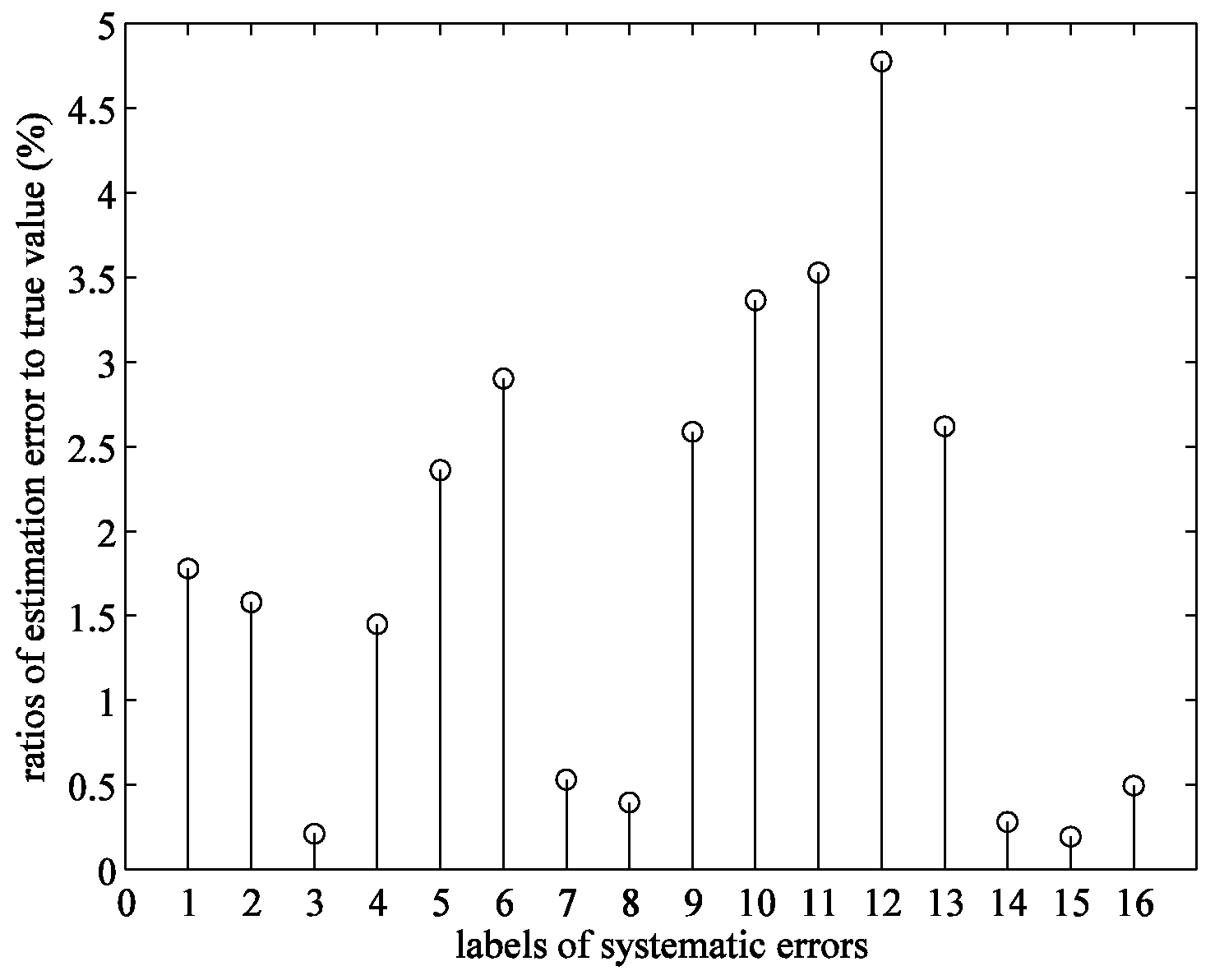
4. Simulation Example
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wu, Y.; Zhu, J. A fusion method for estimate of trajectory. J. Sci. China Ser. E-Technol. Sci. 1999, 42, 150–156. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, J. Reduced parameter model on trajectory tracking data with applications. J. Sci. China Ser. E-Technol. Sci. 1999, 42, 190–199. [Google Scholar] [CrossRef]
- Zhu, J. Data fusion techniques for incomplete measurement of trajectory. Chin. Sci. Bull. 2001, 46, 627–629. [Google Scholar] [CrossRef]
- Wang, Z.; Yi, D.; Duan, X.; Yao, J.; Gu, D. Measurement Data Modeling and Parameter Estimation; CRC Press: Boca Raton, FL, USA, 2011; ISBN 978-1-4398-5378-8. [Google Scholar]
- Guo, J.; Zhao, H. Accurate algorithm for trajectory determination of launch vehicle in ascent phase. J. Astronautics 2015, 36, 1018–1023. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, W.Z.; Zhang, J.J. Sparse signal recovery by accelerated lq (0 <q <1) thresholding algorithm. Int. J. Comput. Math. 2017, 94, 2481–2491. [Google Scholar] [CrossRef]
- Shah, J.; Qureshi, I.; Deng, Y.; Kadir, K. Reconstruction of sparse signals and compressively sampled images based on smooth l1-norm approximation. J. Signal Process. Syst. 2017, 88, 333–344. [Google Scholar] [CrossRef]
- Bevacqua, M.T.; Isernia, T. Shape reconstruction via equivalence principle, constrained inverse source problems and sparsity promotion. Prog. Electromagn. Res. 2017, 158, 37–48. [Google Scholar] [CrossRef]
- Sun, S.; Kooij, B.J.; Yarovoy, A.G. Linearized 3-D electromagnetic contrast source inversion and its applications to half-space configurations. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3475–3487. [Google Scholar] [CrossRef]
- Bevacqua, M.T.; Isernia, T. A boundary indicator for aspect limited sensing of hidden dielectric objects. IEEE Geosci. Remote Sens. Lett. 2018, 15, 838–842. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, J.; Xie, M. Trajectory estimation with multi-range-rate system based on sparse representation and spline model optimization. Chin. J. Aeronaut. 2010, 23, 84–90. [Google Scholar] [CrossRef]
- Hansen, P.C. Analysis of discrete ill-posed problems by means of the L-curve. SIAM Rev. 1992, 34, 561–580. [Google Scholar] [CrossRef]
- Reginska, T. A regularization parameter in discrete ill-posed problem. SIAM J. Sci. Comput. 1996, 17, 740–749. [Google Scholar] [CrossRef]
- Batu, O.; Cetin, M. Parameter selection in sparsity-driven SAR imaging. IEEE Trans. Aerosp. Electr. Syst. 2011, 47, 3040–3050. [Google Scholar] [CrossRef]
- Ramani, S.; Blu, T.; Unser, M. Monte-carlo sure: A black-box optimization of regularization parameters for general denoising algorithms. IEEE Trans. Image Proc. 2008, 17, 1540–1554. [Google Scholar] [CrossRef] [PubMed]
- Ramani, S.; Liu, Z.; Rosen, J.; Nielsen, J.-F.; Fessler, J.A. Regularization parameter selection for nonlinear iterative image restoration and MRI reconstruction using GCV and SURE based methods. IEEE Trans. Image Proc. 2012, 21, 3659–3672. [Google Scholar] [CrossRef] [PubMed]
- Xue, F.; Yagola, A.G.; Liu, J.; Meng, G. Recursive SURE for iterative reweighted least square algorithms. Inverse Probl. Sci. Eng. 2016, 24, 625–646. [Google Scholar] [CrossRef]
- Craven, P.; Wahba, G. Smoothing noisy data with spline functions. Numer. Math. 1979, 31, 377–403. [Google Scholar] [CrossRef]
- Jansen, M. Generalized cross validation in variable selection with and without shrinkage. J. Stat. Plan. Inf. 2015, 159, 90–104. [Google Scholar] [CrossRef]
- Fenu, C.; Reichel, L.; Rodriguez, G. GCV for Tikhonov regularization via global Golub-Kahan decomposition. Numer. Linear Algebra Appl. 2016, 23, 467–484. [Google Scholar] [CrossRef]
- Hanke, M. Limitations of the L-curve method in ill-posed problem. BIT Numer. Math. 1996, 36, 287–301. [Google Scholar] [CrossRef]
- Vogel, C.R. Computational Methods for Inverse Problems; SIAM: Philadelphia, PA, USA, 2002; ISBN 0-89871-507-5. [Google Scholar]
- Li, X.R.; Jilkov, V.P. Survey of maneuvering target tracking. PartII: Motion models of ballistic and space targets. IEEE Trans. Aerosp. Elec. Sys. 2010, 46, 96–119. [Google Scholar] [CrossRef]
- Kelley, C.T. Iterative Methods for Optimization; SIAM: Philadelphia, PA, USA, 1995. [Google Scholar]
- Stein, C.M. Estimation of the mean of a multivariate normal distribution. Ann. Stat. 1981, 9, 1135–1151. [Google Scholar] [CrossRef]
- Hough, M.E. Nonlinear recursive filter for boost trajectories. J. Guid. Control Dyn. 2001, 24, 991–997. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Gong, L. Sensor Alignment for Ballistic Trajectory Estimation via Sparse Regularization. Information 2018, 9, 255. https://doi.org/10.3390/info9100255
Li D, Gong L. Sensor Alignment for Ballistic Trajectory Estimation via Sparse Regularization. Information. 2018; 9(10):255. https://doi.org/10.3390/info9100255
Chicago/Turabian StyleLi, Dong, and Lei Gong. 2018. "Sensor Alignment for Ballistic Trajectory Estimation via Sparse Regularization" Information 9, no. 10: 255. https://doi.org/10.3390/info9100255
APA StyleLi, D., & Gong, L. (2018). Sensor Alignment for Ballistic Trajectory Estimation via Sparse Regularization. Information, 9(10), 255. https://doi.org/10.3390/info9100255




