A New Anomaly Detection System for School Electricity Consumption Data †
Abstract
1. Introduction
- Investigated other two models which are not described in [8].
- Presented the design of the data detection and visualization system.
- Evaluated the anomaly detection models and the system.
2. Background
2.1. Anomaly Detection
- Supervised techniques build models for both anomalous data and normal data. An unseen data instance is classified as normal or an anomaly by comparing which model it belongs to.
- Semi-supervised techniques only build a model for normal data. An unseen data instance is classified as normal if it fits the model sufficiently well. Otherwise, the data instance is classified as anomalies.
- Unsupervised techniques do not need any training dataset. These approaches are based on the assumption that anomalies are much rarer than normal data in a given data set.
- Point Anomalies: A point anomaly is a single independent data instance which does not conform to a well defined normal behavior in a data set.
- Contextual Anomalies: A contextual anomaly is a data instance that is considered as an anomaly in a specific context, but not otherwise.
- Collective Anomalies: A collective anomaly is a collection of related data instances that are anomalous with respect to an entire data set.
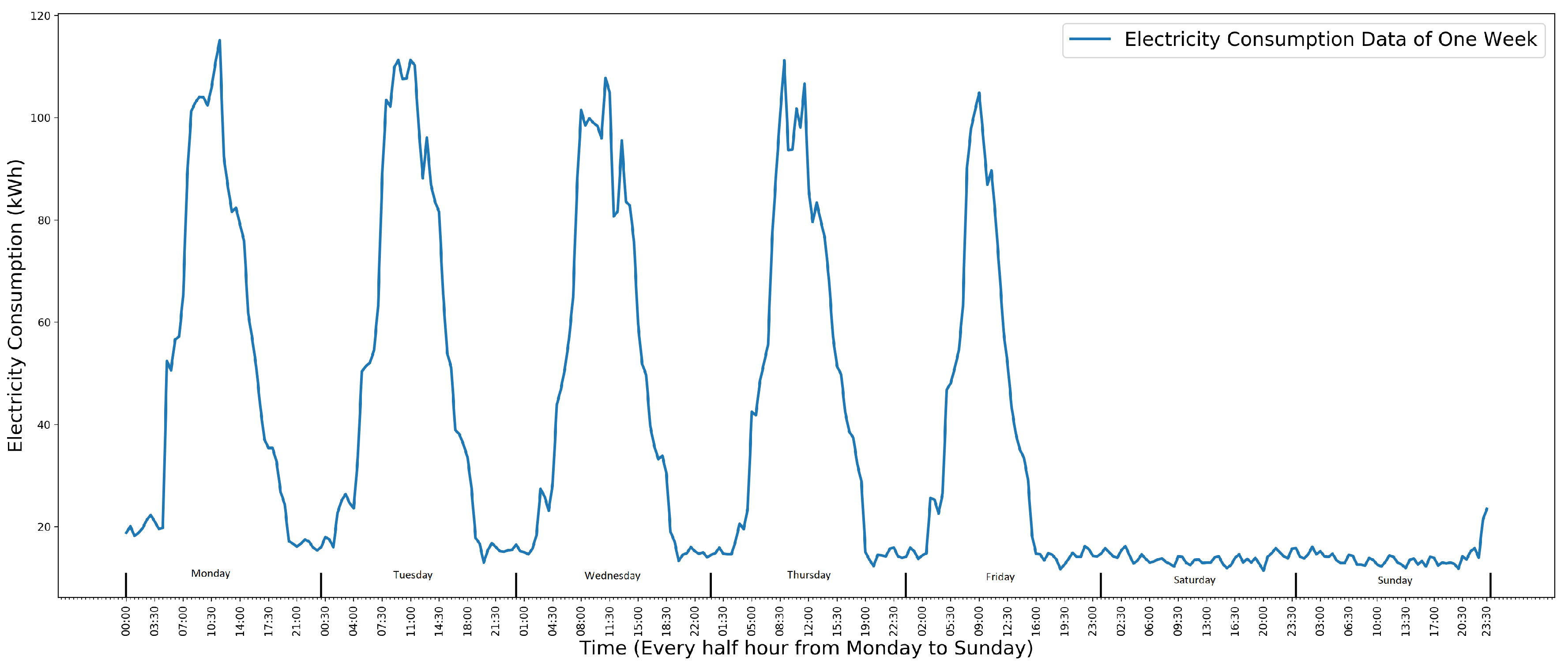
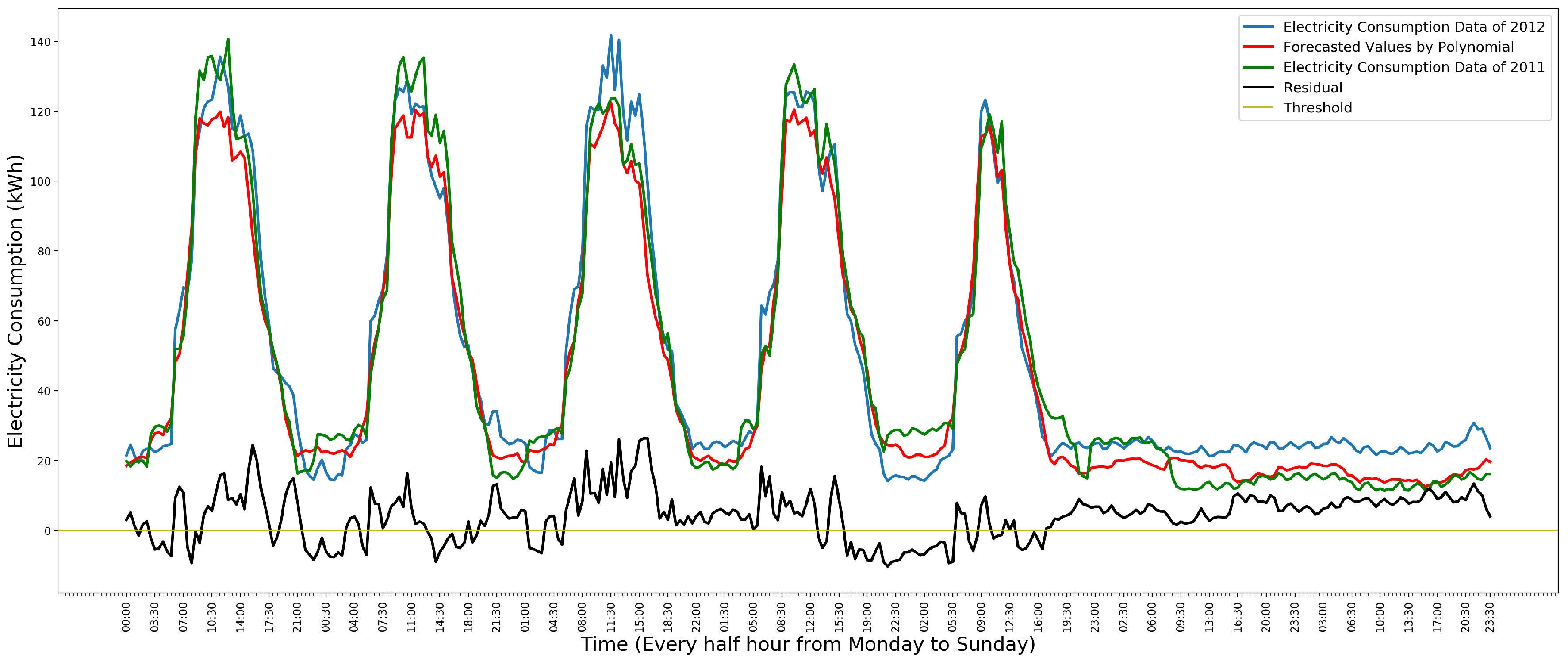
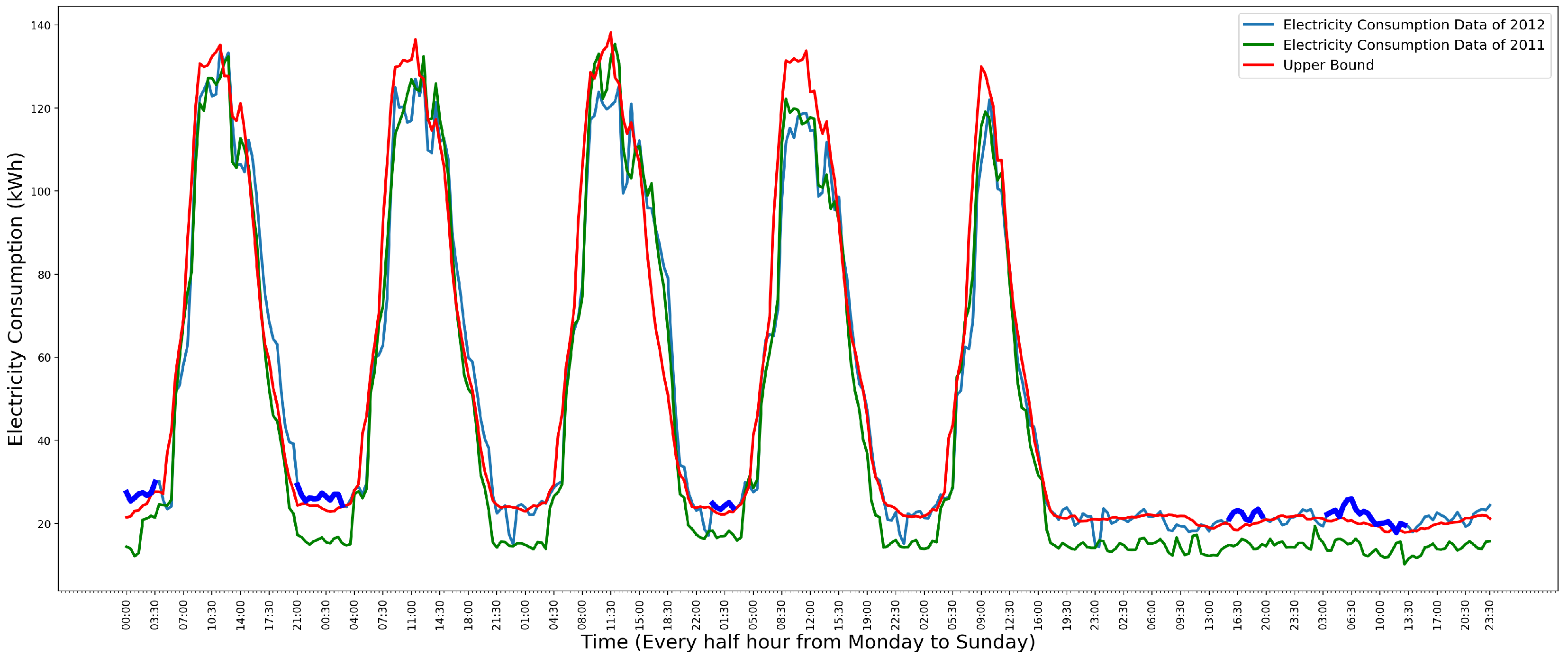
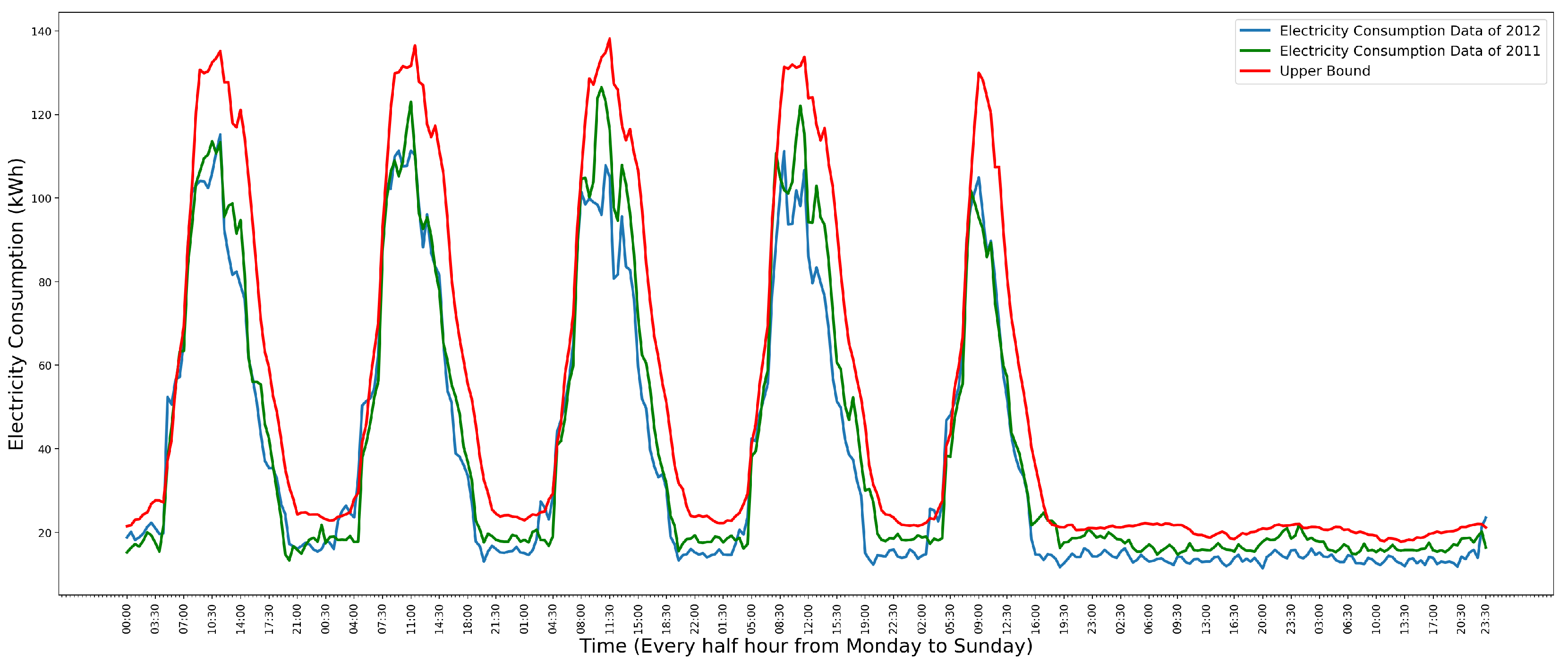
2.2. Time Series Data of School Electricity Consumption
- One single high data point anomaly. It is often used to identify an anomalous meter because it is usually caused by a meter that records a wrong reading.
- A collection of continuous anomalies. It is used to identify anomalous electricity facilities, such as heating being on at the wrong time.
2.3. Data Visualization
3. Anomaly Detection Models
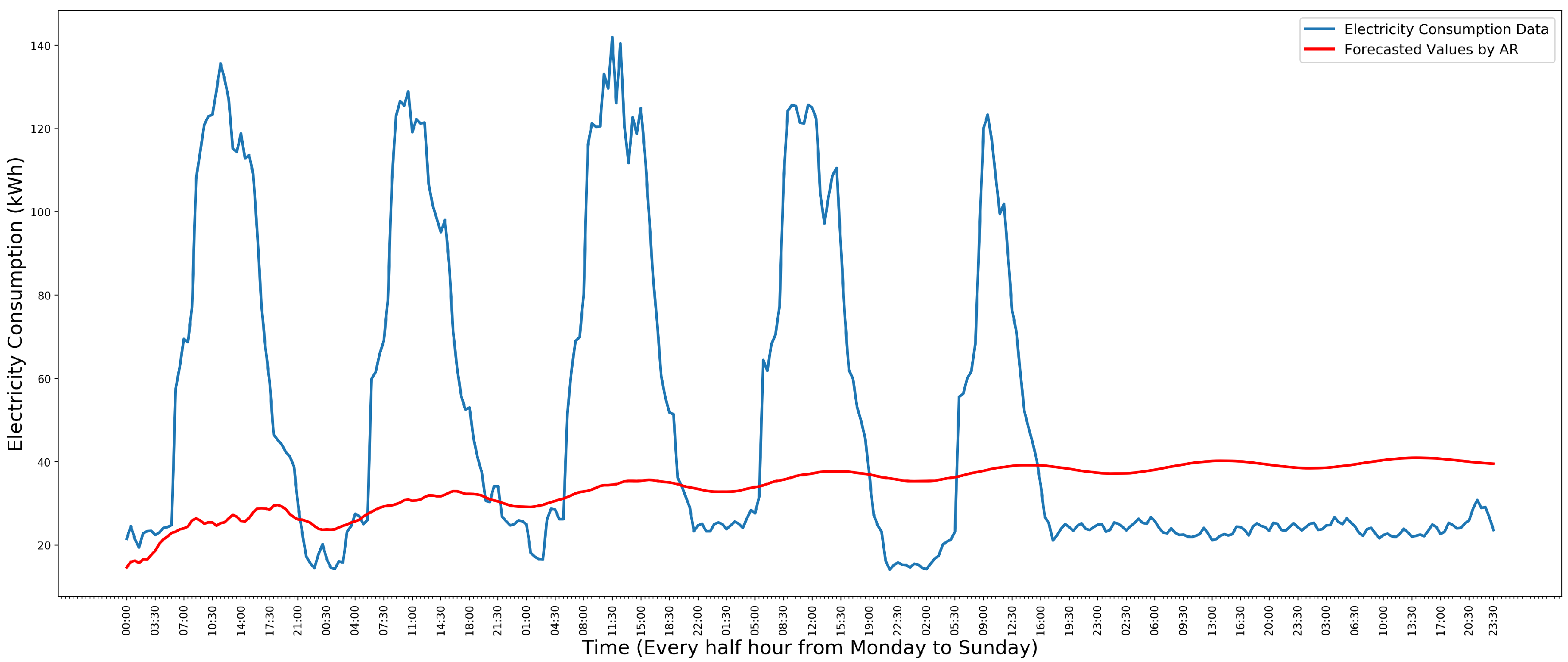
3.1. Autoregressive Model
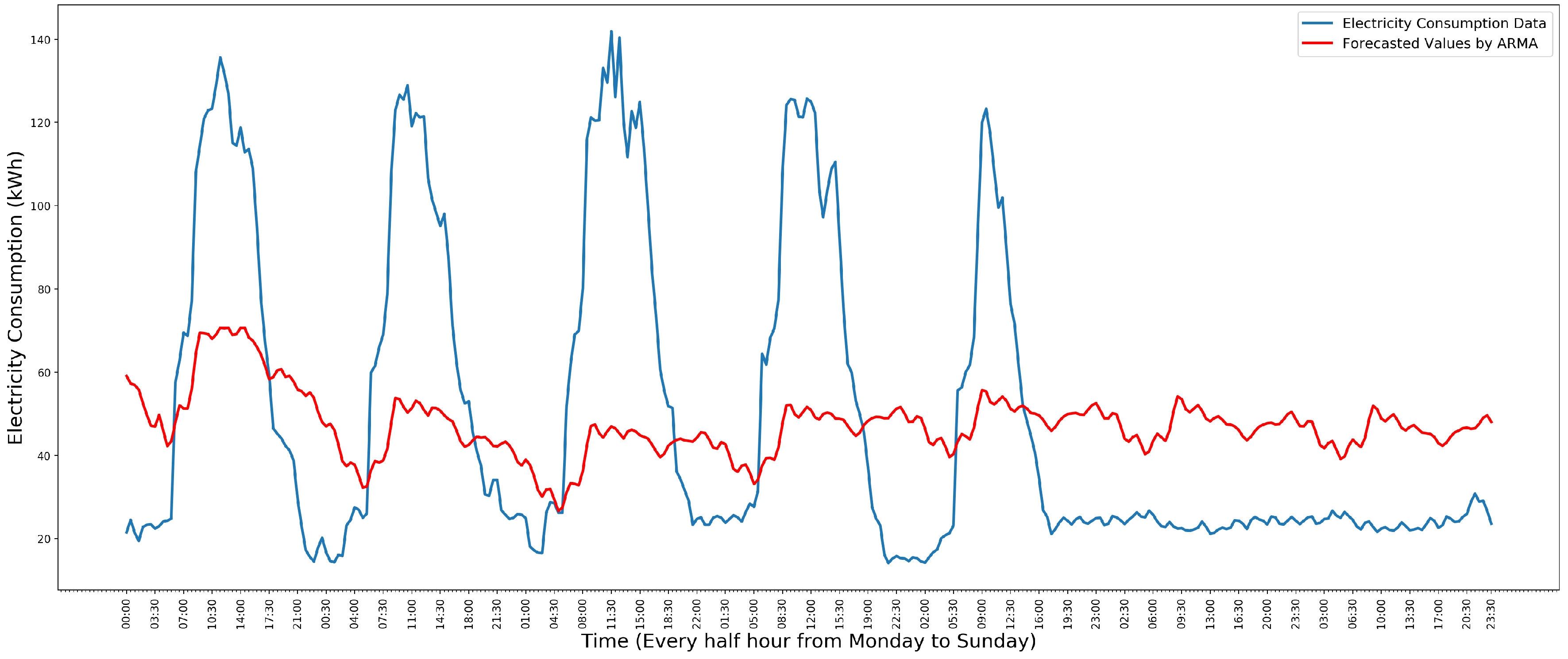
3.2. Autoregressive-Moving-Average Model
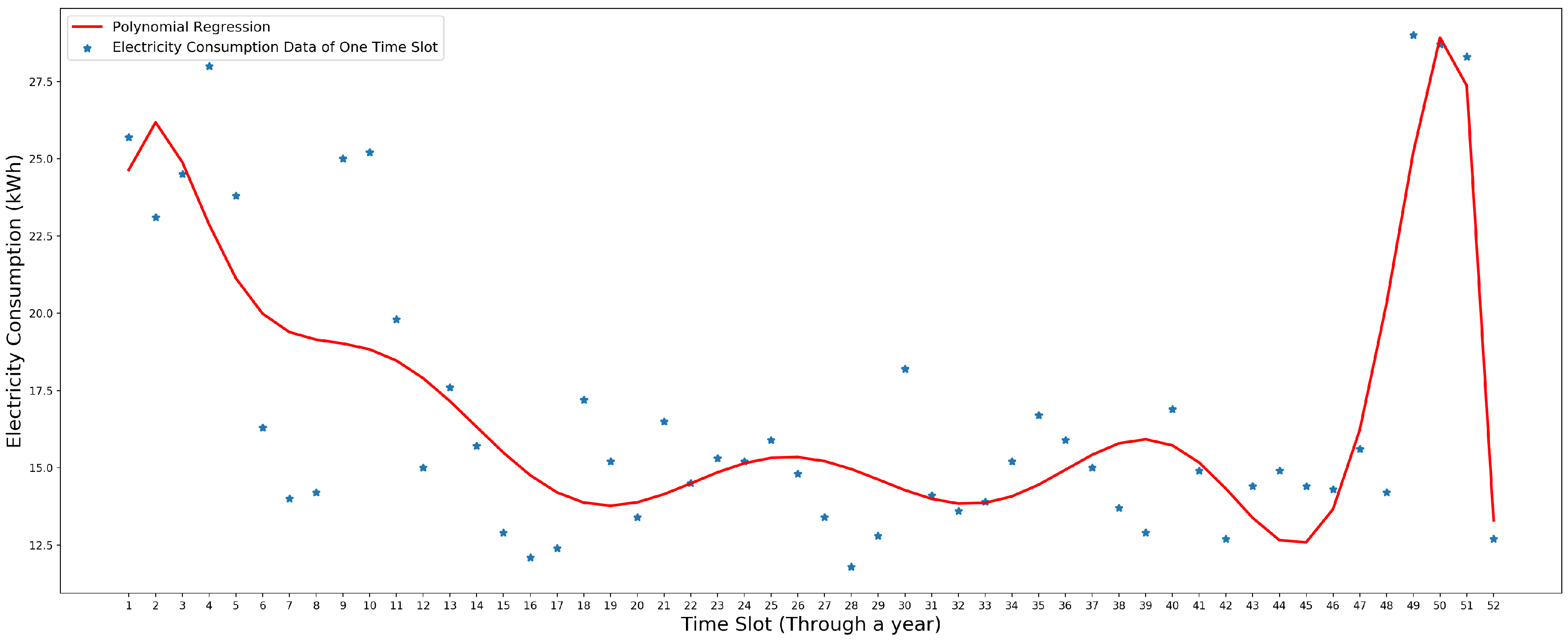
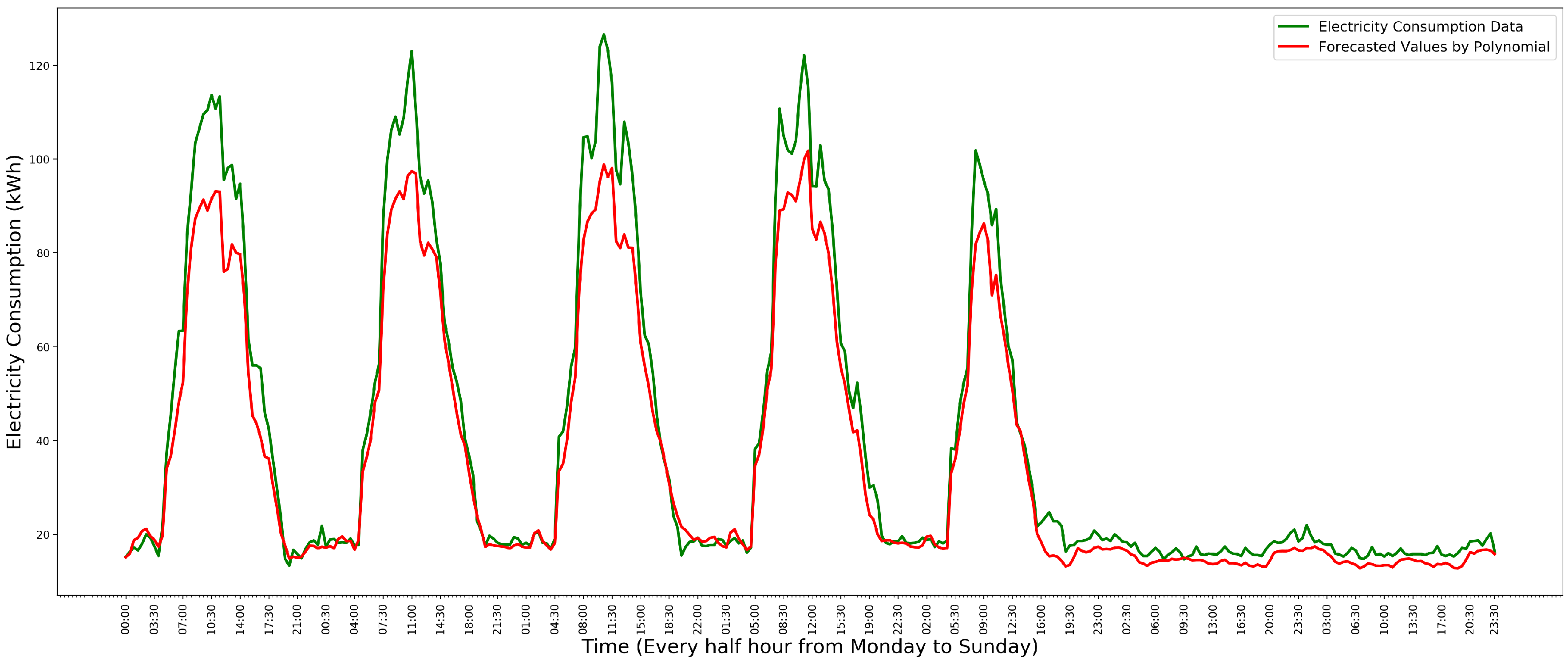
3.3. Polynomial Regression Model
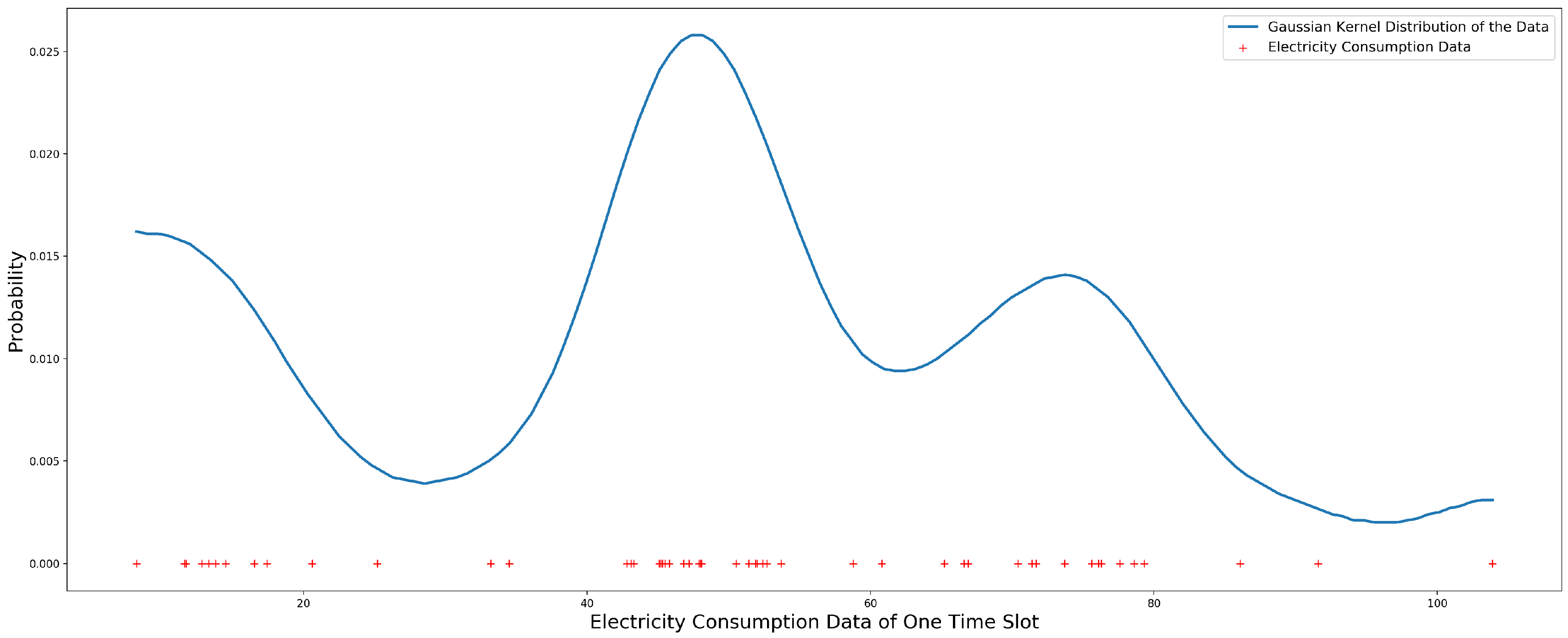
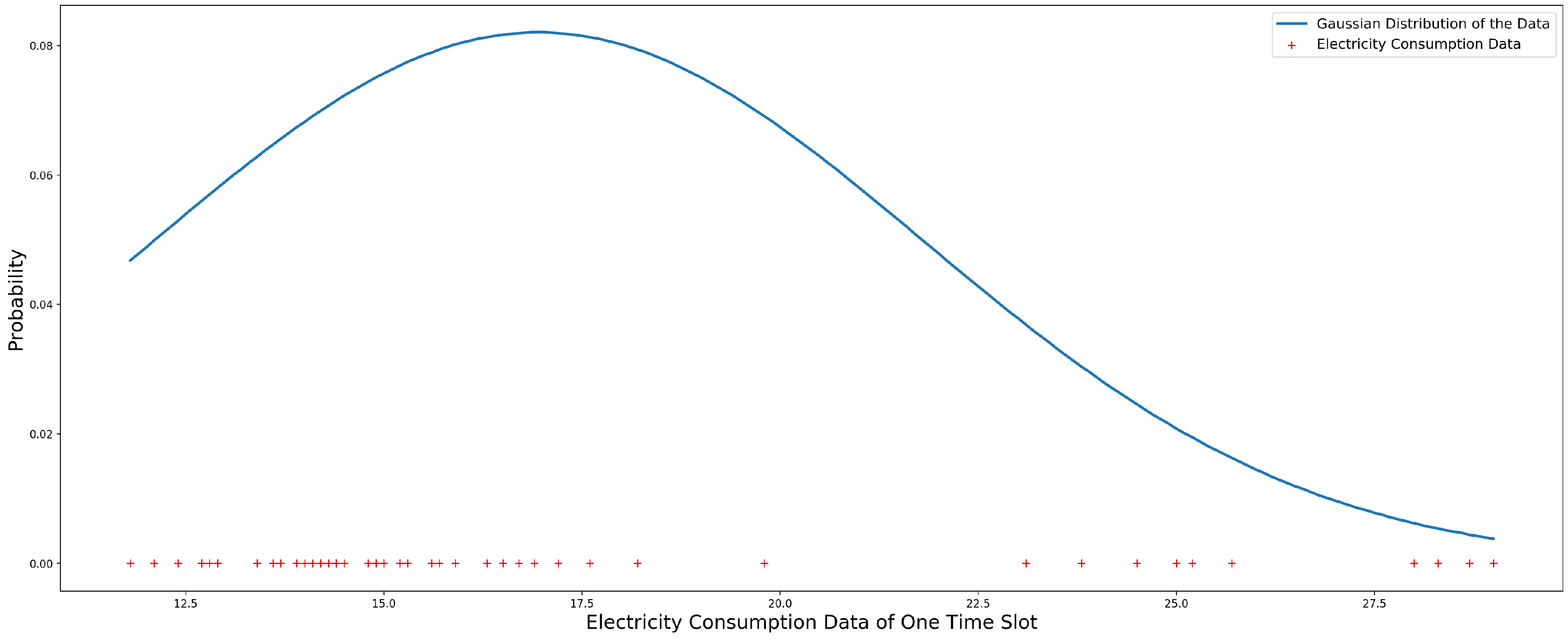
3.4. Gaussian Kernel Distribution Model
3.5. Gaussian Distribution Model
3.6. Model Selection
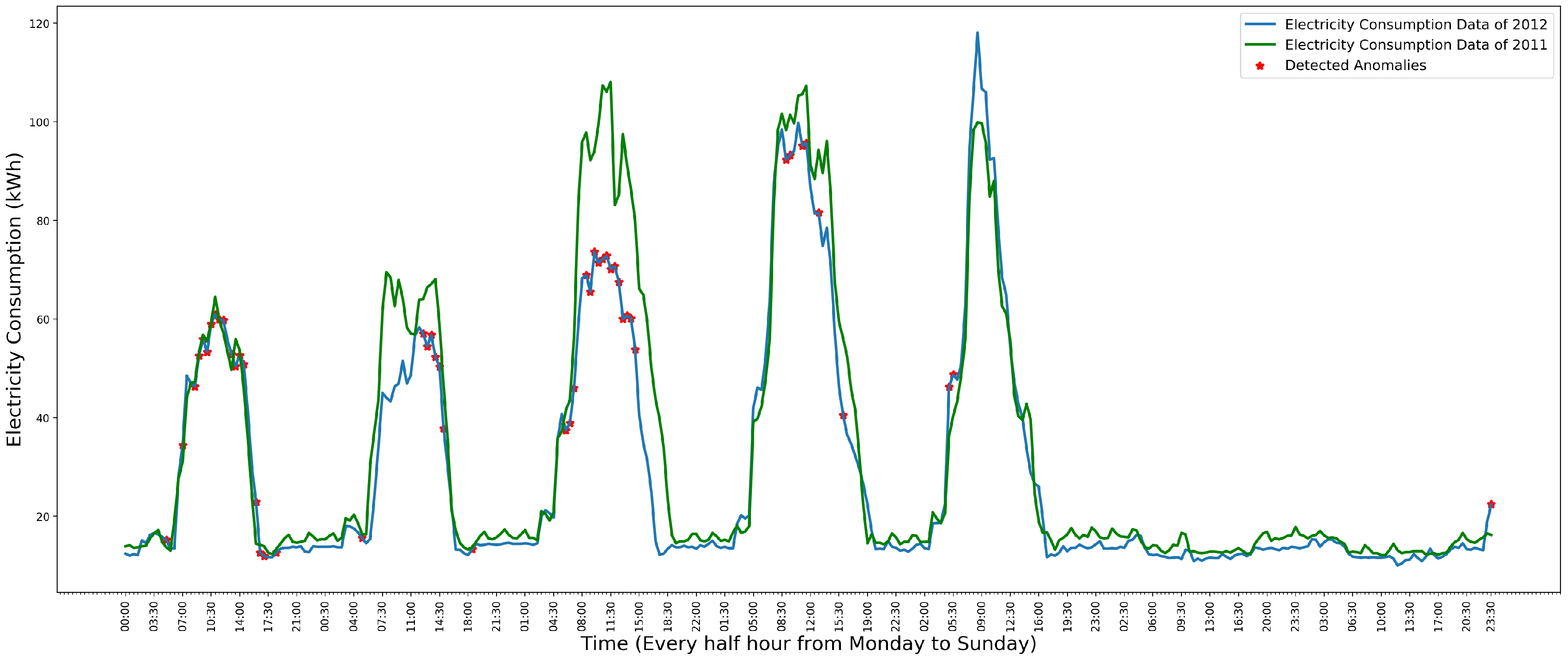
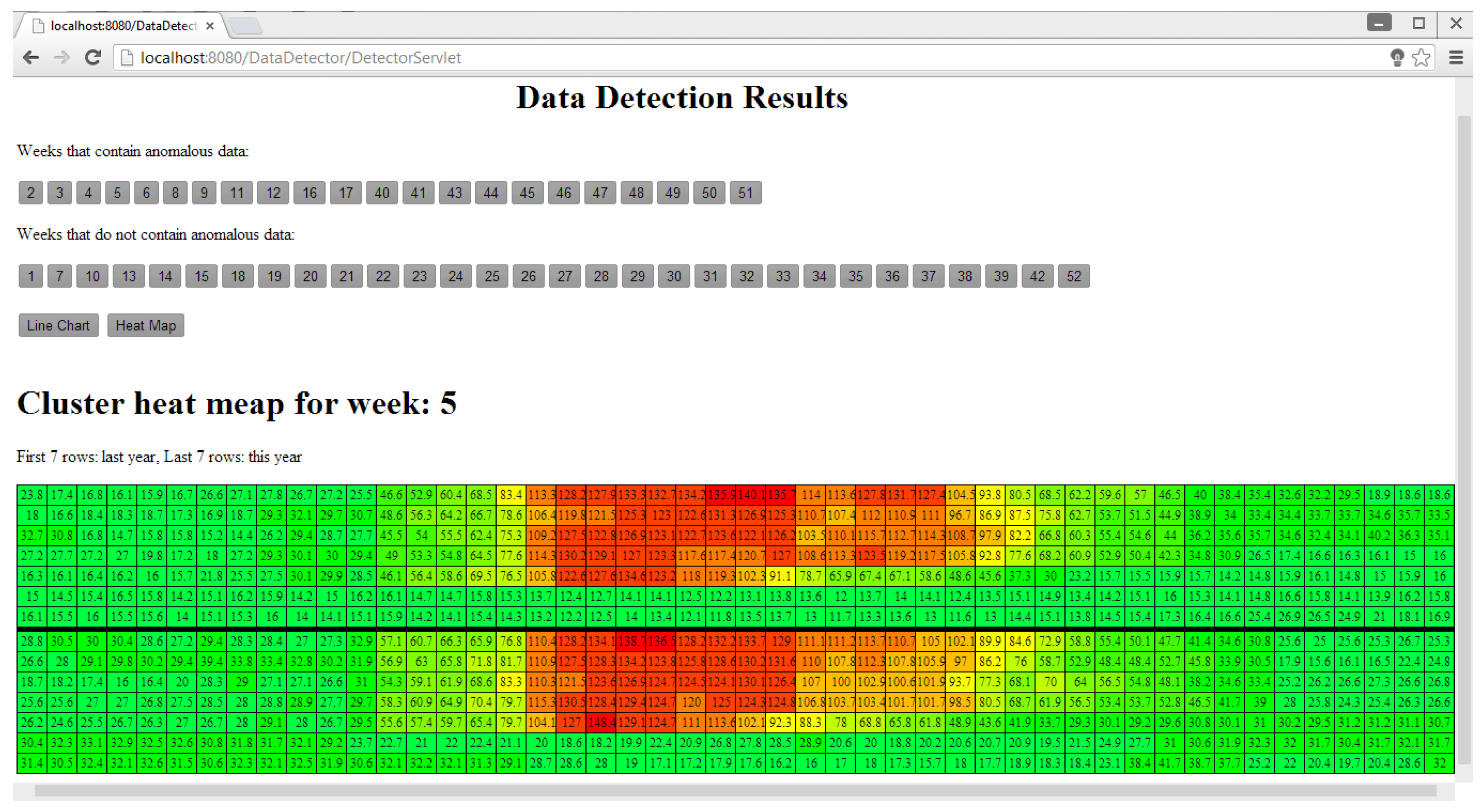
4. Anomaly Detection and Visualization System
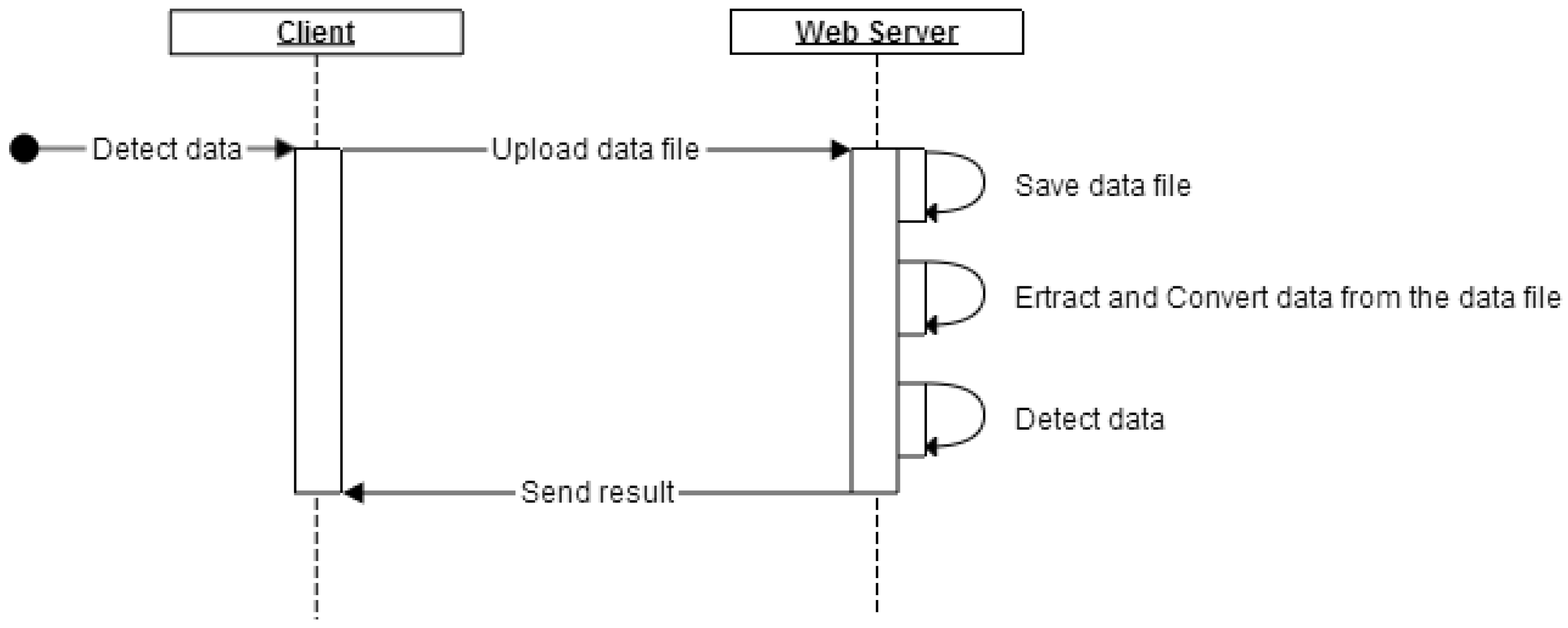
4.1. System Design
4.2. System Implementation
5. Evaluation
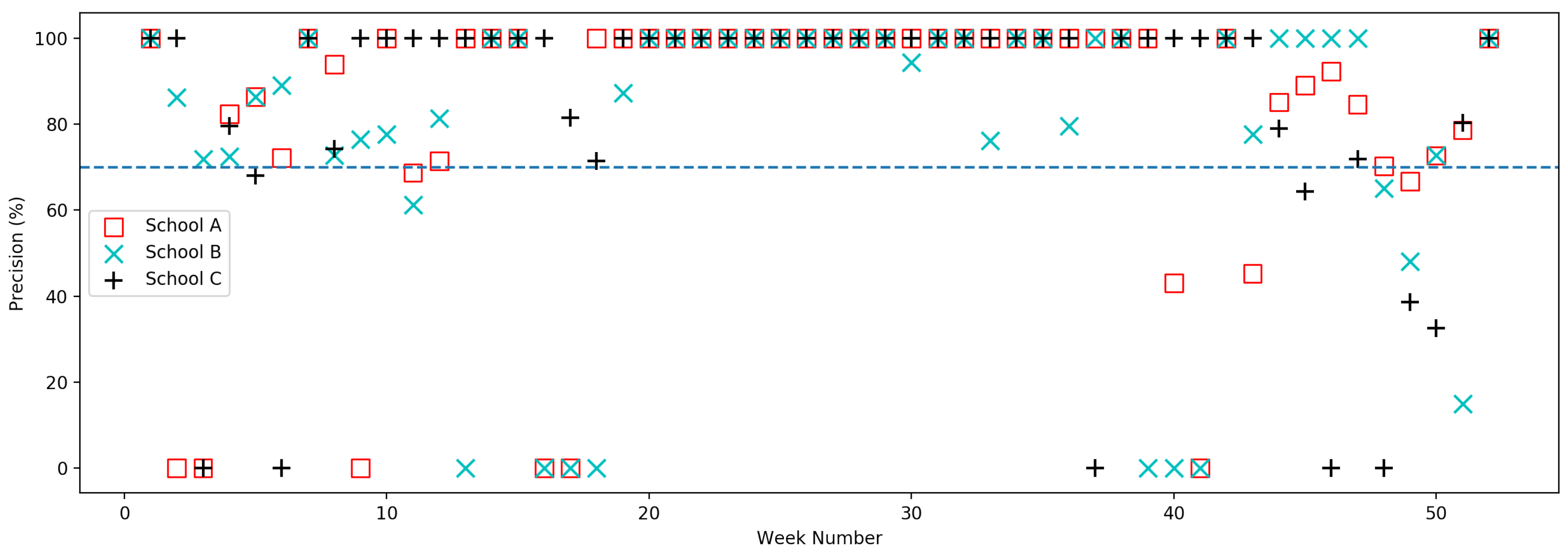
5.1. Model Evaluation
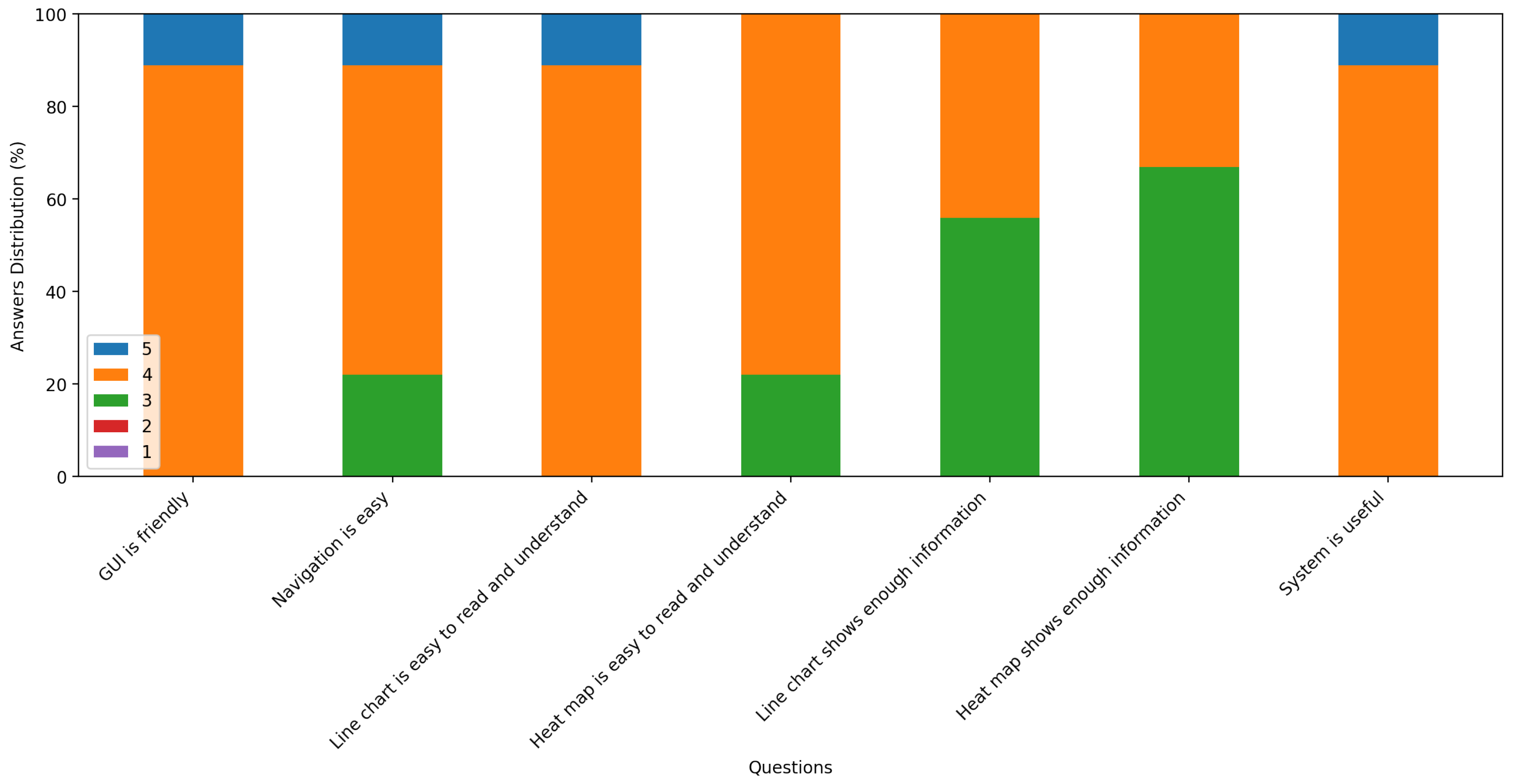
5.2. System Evaluation
- The system is easy to use.
- The visualization of anomaly detection is easy to read and understand.
- The system has improved their efficiency for identifying anomalies in school electricity consumption data.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Questionnaire
Appendix B. Tables of Precision Data
| Week | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Precision | 100% | 0 | 0 | 82.4% | 86.4% | 72.2% | 100% | 93.9% |
| Week | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Precision | 0 | 100% | 68.7% | 71.4% | 100% | 100% | 100% | 0 |
| Week | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Precision | 0 | 100% | 100% | 100% | 100% | 100% | 100% | 100% |
| Week | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
| Precision | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% |
| Week | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| Precision | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 43.1% |
| Week | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 |
| Precision | 0 | 100% | 45.3% | 85.1% | 89% | 92.3% | 84.6% | 70.2% |
| Week | 49 | 50 | 51 | 52 | ||||
| Precision | 66.7% | 72.7% | 78.6% | 100% |
| Week | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Precision | 100% | 86.2% | 71.9% | 72.4% | 86.4% | 89% | 100% | 72.7% |
| Week | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Precision | 76.5% | 77.6% | 61.2% | 81.4% | 0 | 100% | 100% | 0 |
| Week | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Precision | 0 | 0 | 87.2% | 100% | 100% | 100% | 100% | 100% |
| Week | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
| Precision | 100% | 100% | 100% | 100% | 100% | 94.3% | 100% | 100% |
| Week | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| Precision | 76.2% | 100% | 100% | 79.6% | 100% | 100% | 0 | 0 |
| Week | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 |
| Precision | 0 | 100% | 77.6% | 100% | 100% | 100% | 100% | 65% |
| Week | 49 | 50 | 51 | 52 | ||||
| Precision | 48% | 72.7% | 15% | 100% |
| Week | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Precision | 100% | 100% | 0 | 79.6% | 68.1% | 0 | 100% | 74.3% |
| Week | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Precision | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% |
| Week | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Precision | 81.5% | 71.4% | 100% | 100% | 100% | 100% | 100% | 100% |
| Week | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
| Precision | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% |
| Week | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| Precision | 100% | 100% | 100% | 100% | 0 | 100% | 100% | 100% |
| Week | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 |
| Precision | 100% | 100% | 100% | 78.9% | 64.4% | 0 | 71.8% | 0 |
| Week | 49 | 50 | 51 | 52 | ||||
| Precision | 38.6% | 32.6% | 80.3% | 100% |
References
- Perez-Lombard, L.; Ortiz, J.; Pout, C. A review on buildings energy consumption information. Energy Build. 2008, 40, 394–398. [Google Scholar] [CrossRef]
- Ardehali, M.M.; Smith, T.F.; House, J.M.; Klaassen, C.J. 4641 Building Energy Use and Control Problems: An Assessment of Case Studies. ASHRAE Trans. 2003, 109, 111–121. [Google Scholar]
- Heo, Y.; Choudhary, R.; Augenbroe, G. Calibration of building energy models for retrofit analysis under uncertainty. Energy Build. 2012, 47, 550–560. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. (CSUR) 2009, 41, 15. [Google Scholar] [CrossRef]
- Catterson, V.M.; McArthur, S.D.; Moss, G. Online conditional anomaly detection in multivariate data for transformer monitoring. IEEE Trans. Power Deliv. 2010, 25, 2556–2564. [Google Scholar] [CrossRef]
- McArthur, S.D.; Booth, C.D.; McDonald, J.; McFadyen, I.T. An agent-based anomaly detection architecture for condition monitoring. IEEE Trans. Power Syst. 2005, 20, 1675–1682. [Google Scholar] [CrossRef]
- Jakkula, V.; Cook, D. Outlier detection in smart environment structured power datasets. In Proceedings of the 2010 Sixth International Conference on Intelligent Environments (IE), Kuala Lumpur, Malaysia, 19–21 July 2010; pp. 29–33. [Google Scholar]
- Cui, W.; Hao, W. Anomaly Detection and Visualization of School Electricity Consumption Data. In Proceedings of the 2017 IEEE International Conference on Big Data Analysis (ICBDA), Beijing, China, 10–12 March 2017. [Google Scholar]
- Abraham, B.; Chuang, A. Outlier detection and time series modeling. Technometrics 1989, 31, 241–248. [Google Scholar] [CrossRef]
- Jansson, D.; Rosén, O.; Medvedev, A. Parametric and nonparametric analysis of eye-tracking data by anomaly detection. IEEE Trans. Control Syst. Technol. 2015, 23, 1578–1586. [Google Scholar] [CrossRef]
- Veracini, T.; Matteoli, S.; Diani, M.; Corsini, G. Fully unsupervised learning of Gaussian mixtures for anomaly detection in hyperspectral imagery. In Proceedings of the Ninth International Conference on Intelligent Systems Design and Applications (ISDA’09), Pisa, Italy, 30 November–2 December 2009; pp. 596–601. [Google Scholar]
- Feng, C.; Li, T.; Chana, D. Multi-level anomaly detection in industrial control systems via package signatures and lstm networks. In Proceedings of the 2017 47th Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN), Denver, CO, USA, 26–29 June 2017; pp. 261–272. [Google Scholar]
- Kumar, V. Parallel and distributed computing for cybersecurity. IEEE Distrib. Syst. Online 2005, 6. [Google Scholar] [CrossRef]
- Yaffee, R.A.; McGee, M. An Introduction to Time Series Analysis and Forecasting: With Applications of SAS® and SPSS®; Academic Press: New York, NY, USA, 2000. [Google Scholar]
- Krause, J.; Perer, A.; Bertini, E. INFUSE: Interactive feature selection for predictive modeling of high dimensional data. IEEE Trans. Vis. Comput. Graph. 2014, 20, 1614–1623. [Google Scholar] [CrossRef] [PubMed]
- Janetzko, H.; Stoffel, F.; Mittelstädt, S.; Keim, D.A. Anomaly detection for visual analytics of power consumption data. Comput. Graph. 2014, 38, 27–37. [Google Scholar] [CrossRef]
- Wilkinson, L.; Friendly, M. The history of the cluster heat map. Am. Stat. 2009, 63. [Google Scholar] [CrossRef]
- Chatfield, C. The Analysis of Time Series: An Introduction; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Keim, D.; Andrienko, G.; Fekete, J.D.; Gorg, C.; Kohlhammer, J.; Melançon, G. Visual analytics: Definition, process, and challenges. Lect. Notes Comput. Sci. 2008, 4950, 154–176. [Google Scholar]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, W.; Wang, H. A New Anomaly Detection System for School Electricity Consumption Data. Information 2017, 8, 151. https://doi.org/10.3390/info8040151
Cui W, Wang H. A New Anomaly Detection System for School Electricity Consumption Data. Information. 2017; 8(4):151. https://doi.org/10.3390/info8040151
Chicago/Turabian StyleCui, Wenqiang, and Hao Wang. 2017. "A New Anomaly Detection System for School Electricity Consumption Data" Information 8, no. 4: 151. https://doi.org/10.3390/info8040151
APA StyleCui, W., & Wang, H. (2017). A New Anomaly Detection System for School Electricity Consumption Data. Information, 8(4), 151. https://doi.org/10.3390/info8040151






