Abstract
We consider the simultaneous wireless information and power transfer in two-phase decode-and-forward two-way relaying networks, where a relay harvests the energy from the signal to be relayed through either power splitting or time splitting. Here, we formulate the resource allocation problems optimizing the time-phase and signal splitting ratios to maximize the sum rate of the two communicating devices. The joint optimization problems are shown to be convex for both the power splitting and time splitting approaches after some transformation if required to be solvable with an existing solver. To lower the computational complexity, we also present the suboptimal methods optimizing the splitting ratio for the fixed time-phase and derive a closed-form solution for the suboptimal method based on the power splitting. The results demonstrate that the power splitting approaches outperform their time splitting counterparts and the suboptimal power splitting approach provides a performance close to the optimal one while reducing the complexity significantly.
1. Introduction
The Internet-of-Things (IoT) is envisioned to make operation of our today life more convenient and productive by connecting things to collect data, make intelligent decisions, and perform autonomous controls without human intervention [1,2]. One of the major concerns in developing IoT systems is the energy consumption, not only in the data centers processing big data [3,4], but also in the end-devices sensing and exchanging data [1,5]. The devices should be even sustainable without a battery or with a small battery when they are deployed in either hazardous or vast areas due to the high cost of battery replacements. In this context, wireless power transfer through radio frequency signals has received huge attention as a way of charging the devices without battery replacements [5,6] and traditional wireless and mobile communication networks [7,8,9,10] are now being reformed by incorporating the energy harvesting capability at the devices.
In particular, various relaying protocols have been rebuilt to support energy harvesting devices in cooperative networks [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26], where relays can be categorized into either energy harvesting nodes or energy transmission nodes. Energy harvesting relays are as low in complexity as communicating devices and harvest the energy in helping the data exchange of the devices in general [11,12,13,14,15,16,17,18,19,23,24,25,26]. On the other hand, energy transmission relays are as highly complex as base stations so that the relays transfer the power and information to the communicating devices [20,21,22]; the relays even employ massive antennas to leverage the efficiency in the power and information transfer at a high cost in implementation [27,28]. This paper focuses on the former case in which there is no infrastructure relay and one of neighboring peer devices takes the role of signal relaying by spending the energy harvested by means of simultaneous wireless power and information transfer (SWIPT).
1.1. Related Works
This subsection discusses the relevant literature on SWIPT in cooperative networks, where the relays harvest energy and then transmit a signal. To accomplish SWIPT practically, the received signal should be split into two branches for energy harvesting and information decoding. This is performed either by power splitting (PS) or by time splitting (TS) at a single antenna receiver, although their variants exist [29]. These splitting methods are investigated in cooperative networks with one-way relaying (OWR) protocols [11,16,17,18,19,24,26] and with two-way relaying (TWR) protocols [12,13,15,23,25]. Here, amplify-and-forward (AF) relays are adopted in [11,12,13,15,24] for a lower complexity with the simple relay operation amplifying the received signal without information decoding, while decode-and-forward (DF) relays are adopted in [16,17,18,19,23,25] for a better performance with the complicated relay operation regenerating the relay signal after decoding the received signal.
To be more specific, for the OWR protocol, the performance of the PS-SWIPT and TS-SWIPT methods is studied with an AF relay in terms of the outage probability and ergodic capacity [11]; with a DF relay in terms of the ergodic capacity, outage capacity [16], maximum achievable rate [17], and outage probability [26]. The performance of the PS-SWIPT for the OWR protocol is also studied with a full-duplex DF relay [19] and with the AF relay when the direct link is available [24]. In addition, the optimization of the SWIPT parameters is also studied for the OWR with a DF relay by using statistical information [18].
For the TWR protocol, the SWIPT methods are combined with the spectrally efficient two-phase protocols composed of multiple access (MAC) and broadcasting (BC) phases [12,13,23,25]; an exception is observed in [15], which incorporates the PS-SWIPT and the TS-SWIPT into the four-phase TWR for an easier modification in spite of a large loss in the spectral efficiency. As in the OWR protocol, the outage probability and ergodic capacity are analyzed for the AF-TWR protocol employing the PS-SWIPT [12]. A source node selection method is devised for wireless power transfer in the AF-TWR protocol employing the TS-SWIPT [13]. In addition, the outage probability of the DF-TWR protocol with the PS-SWIPT and the TS-SWIPT is studied without resource allocation in cognitive radio environments [23] and with outage-optimal resource allocation in non-cognitive radio environment [25]. Some studies on the TWR with energy harvesting nodes are also observed in [14,20,22], but they are irrelevant since the SWIPT is not considered due to a different energy harvesting scenario [14] and an infrastructure relay transmitting the power is considered for the AF-TWR in [20,22].
1.2. Motivation and Contribution
The SWIPT methods are less studied for the TWR than for the OWR, and their initial studies for the TWR focus on the AF relays for low-complexity implementations [12,13]. In addition, the studies focus on the achievable performance when the SWIPT methods are introduced to the TWR protocols [23], although the traditional TWR protocols without energy harvesting are studied in various aspects from performance analysis to the resource allocation [30,31,32,33]. To leverage the performance at the given resources, resource allocation methods are essential. Therefore, they should be studied also for the TWR protocols employing the SWIPT methods. In such a case, the DF-TWR is preferable to the AF-TWR since the former not only outperforms the latter without resource allocation but also provides an additional degree of freedom in resource allocation by allowing unequal time durations for the MAC and BC phases; the time durations for two phases should be kept equal for the AF-TWR to relay the non-regenerative signal.
In this context, the PS-SWIPT and the TS-SWIPT have been introduced to the DF-TWR protocol recently and several resource allocation problems are addressed to optimize the outage probability by adapting the time-phase ratio and the SWIPT parameters [25]. The study reveals that the PS-SWIPT approach outperforms the TS-SWIPT in the outage probability and an appropriate choice of the time-phase ratio leverages the outage performance significantly by balancing the performance in two directions.
This paper revisits the DF-TWR network, employing two SWIPT methods in [25], but aims at maximizing the sum rate of the network instead of minimizing the outage probability. We formulate the problem optimizing the time-phase ratio of the DF-TWR and the splitting ratio of the SWIPT method for each of the PS-SWIPT and TS-SWIPT methods. The joint optimization problems are transformed to convex optimization problems after appropriate transformation if required so that they can be solved with an existing solver at some reasonable complexity. To reduce the computational complexity further, we also present the suboptimal methods adapting the splitting ratio for the fixed time-phase ratio and derive a closed-form solution readily available for the PS-SWIPT method.
The remainder of the paper is organized as follows: Section 2 describes the system model of the DF-TWR with the PS-SWIPT and the TS-SWIPT and provides the rate performance of the DF-TWR achievable with each SWIPT method. Section 3 formulates the resource allocation problems for the two SWIPT methods and provides the methods of finding the optimal and suboptimal solutions. Numerical results are provided in Section 4 for the two SWIPT methods with different resource allocation methods. Section 5 draws concluding remarks.
Notation: Vectors and matrices are expressed by boldface lowercase and uppercase letters, respectively, where denotes the length-n column vector with all zero entries and denotes the identity matrix. Functions and denote the maximum and minimum of x and y, respectively, while denotes the capacity at signal-to-noise ratio x. Distribution denotes the complex Gaussian with mean and variance . An optimization problem is stated as , where is a scalar-valued function called the objective function, x is the decision variable, is the constraint set (feasible set), and max and s.t. are abbreviations for maximize and subject to, respectively. An optimal solution of the optimization problem is expressed as . The approximate upper bound on the computational time is denoted by , which implies that, for some positive constants c and k, for all .
2. System Model and Rate Performance
2.1. System Model
We consider a three-device TWR network in Figure 1a, where a relay device cooperates in the information exchange of two communicating devices and . All devices operate in half-duplex and are equipped with a single antenna. The channel between and is denoted by for under the assumption of flat fading and channel reciprocity.
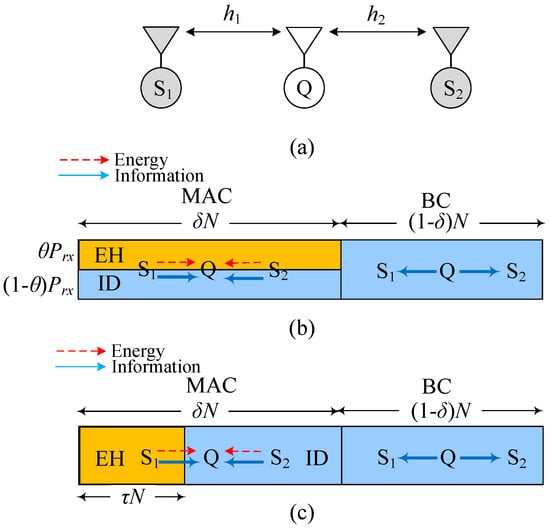
Figure 1.
DF-TWR network: (a) System configuration (b) DF-TWR with PS-SWIPT (c) DF-TWR with TS-SWIPT.
Figure 1b,c illustrate the SWIPT methods for the DF-TWR protocol when devices and exchange their messages and with each other. For the DF-TWR, a data frame is divided into MAC and BC phases of and durations, respectively, where N is the number of symbols comprising the data frame and is the time-phase (TP) ratio of the MAC phase in the data frame. In the MAC phase, and transmit their symbol vectors and containing the messages, as in [25], to the relay simultaneously. The relay harvests the energy as well as decodes the messages and by splitting the received signal in the MAC phase. The signal splitting is accomplished either in the power domain with PS ratio , as in Figure 1b, or in the time domain with TS ratio , as shown in Figure 1c, where and . The harvested energy is then given by
where is the energy harvesting efficiency, is the transmit power of for , and the background noise is ignored. On the other hand, the received signal vector for the information decoding in the MAC phase can be stated as
where is the vector of the background noise composed of the baseband equivalent antenna noise and the noise introduced by the conversion from the RF signal to the baseband signal [25].
In the BC phase, the relay transmits the network coded symbol vector [30,33] of the decoded messages and by consuming the energy harvested in the MAC phase. This paper does not take into account the energy consumption in the decoding process so that the transmit power of the relay is given by . The signal received at in the BC phase is then given by
where is the background noise vector at for .
2.2. Achievable Rate Region
Let be the rate delivered for the ith data flow from to , . The achievable rate region of the rates for the DF-TWR is given by [14,25]
where and are the maximum achievable rates in the MAC and BC phases, respectively, of the ith data flow for whilst is the maximum sum rate achievable in the MAC phase.
For the DF-TWR, the maximum achievable rate from to is derived from (2) as
where is the SNR from to , and the factors and represent the MAC-phase data fraction in a data frame for the PS-SWIPT and the TS-SWIPT, respectively. The maximum sum rate in the MAC phase is also obtained as
which is achievable by applying the successive interference cancellation to (2). The achievable sum rate for the MAC phase is explained in detail in [34] and is also summarized for the DF-TWR in [14,33]. On the other hand, the maximum achievable rate in the BC phase for the ith data flow is given by
for from (3). Since and for the PS-SWIPT and for the TS-SWIPT from (1), we have
where for .
3. Rate-Optimal Resource Allocation
We aim at maximizing the sum rate by optimizing the parameters for the SWIPT and the DF-TWR based on the instantaneous channel state information (CSI) . We provide optimal and suboptimal resource allocation methods for the PS-SWIPT and their counterparts for the TS-SWIPT.
3.1. Resource Allocation for the PS-SWIPT
For the PS-SWIPT, we optimize the PS ratio and TP ratio to maximize the sum rate. The problem is formulated with (4) as
by applying , , and , for the PS-SWIPT given in (5), (6), and (8), respectively. The problem has the linear objective function, the linear constraints and the convex constraints (10) and (12) with linear functions in the left hand side (LHS) and a concave function in the right hand side (RHS). However, the constraints (11) are not convex due to the factor in .
By introducing a new variable , we transform (9)–(12) into
which is convex with the convex constraints (14)–(16); the RHS of the constraints is the perspective of a concave function and is thus concave [35]. Therefore, the problem (13)–(16) can be solved with an existing convex optimization solver.
As a suboptimal approach, we fix the TP ratio as and find the optimal PS ratio to maximize the sum rate. The problem (9)–(12) with the fixed TP ratio becomes
The RHS of (18) is concave with respect to since the minimum operation preserves the concavity [35] and is a concave function while the RHS of (19) is also concave with concave function . Therefore, the constraints (18) and (19) are convex so that there exists a unique which maximizes .
With satisfying and satisfying , we can express according to the minimum value as
where , , and . From (20) representing (18) and (19), the optimal solution of (17) can be expressed as
where and the last equality comes from the fact that is a monotonically increasing function.
The solution of (23) is derived in Appendix A as
where
is the intersection of and for ,
is the intersection of and for , and
is the maximum point of for all .
Remark 1.
The original problem (9)–(12) for the PS-SWIPT can be solved by an exhaustive search at computational complexity with a searching step ϵ for two decision variables. After transformation, the problem (13)–(16) can be solved at complexity by applying interior-point methods in solving the convex optimization problem [36]. The suboptimal method with and has complexity since the closed-form solution is readily available.
3.2. Resource Allocation for the TS-SWIPT
For the TS-SWIPT, we optimize the TS ratio and the TP ratio to maximize the sum rate of the DF-TWR. The optimization problem is formulated as
from (4) by using , , and given in (5), (6), and (8), respectively, for the TS-SWIPT. The problem (28)–(31) has the linear objective function (28), linear constraints (29) and (31), and convex constraint (30). The convexity of (30) is guaranteed since the LHS is linear and the RHS is concave with the perspective of a concave function [35]. Therefore, the problem (28)–(31) is a convex optimization problem that can be solved with an existing convex optimization tool.
As in the PS-SWIPT, a suboptimal solution for the TS-SWIPT can be obtained by fixing for an appropriately choosing constant and finding the optimal TS ratio in (28)–(31). As another suboptimal approach, we may set (or equivalently, ) in (28)–(31) for equal time duration in data reception and transmission. Although the closed-form solution for the aforementioned suboptimal problems is not tractable, the solution can be obtained by an existing convex optimization tool at less computational time than that for the original problem for the TS-SWIPT.
4. Numerical Results
We evaluate the performance of the SWIPT methods in the DF-TWR network when the relay is positioned on a straight line, connecting and of distance D. The distance between and the relay is denoted by for , which satisfies with m. The transmission power of the sources is equal as and the noise power is set to dBm. The path loss and Rayleigh fading are included in the channels as for , where represents the path loss exponent. The energy harvesting efficiency is assumed to be in all the figures.
Figure 2 provides the constellation of the optimized TP and PS ratios obtained by solving the problem (9)–(12) for 500 channel realizations when and . The optimized values are shown in the subfigures with different transmit power as , 20, and 30 dBm. Figure 3 provides the constellation of the optimized TP and TS ratios obtained by solving the problem (28)–(31) under the same configuration with Figure 2. The parameter values optimizing the sum rate are observed to have a different tendency from those optimizing the outage probability [25] in that the TP ratio tends to have values around for both the PS-SWIPT and TS-SWIPT. When the transmit power is as small as dBm, the splitting ratio (PS ratio for the PS-SWIPT and TS ratio for the TS-SWIPT) tends to have a value close to 1 since the energy harvested in the MAC phase dominates the performance. As the transmit power increases, the splitting ratio varies in a large degree to balance the harvested energy and the reliably deliverable information rate for each channel realization.
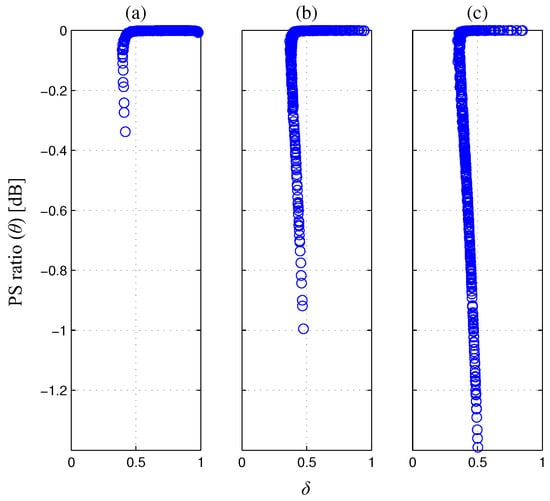
Figure 2.
Optimized TP and PS ratios for the PS-SWIPT: (a) dBm; (b) dBm; (c) dBm.
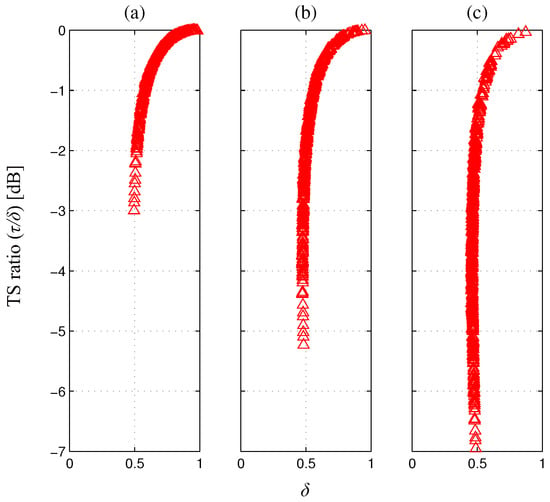
Figure 3.
Optimized TP and TS ratios for the TS-SWIPT: (a) dBm; (b) dBm; (c) P = 30 dBm.
Figure 4 compares the sum rate of the PS-SWIPT with different resource allocation methods when dBm and . The abscissa is the normalized distance between and . The results of “Opt” and “Sub (Tool)” are obtained by employing the convex optimization solver YALMIP [37] to find the solution of the joint optimization problem (13)–(16) and the suboptimal problem (17)–(19), respectively, the results of “Sub (Anal)” are obtained with the closed-form solution (24) for the suboptimal problem (17)–(19), and the results of “Equal” are obtained with . It should be mentioned that the performance obtained with the analytically derived solution is indistinguishable from that obtained with the convex optimization solver for the suboptimal problem. The joint resource allocation method shows the best performance, but the suboptimal method with the closed-form solution provides a performance close to the optimal one. Therefore, the suboptimal method is favorable to avoid the time-consuming computation in solving the joint optimization problems with the convex optimization solver. The sum rate decreases steeply as the relay moves toward the center location due to the energy harvesting relay which suffers from a large loss in the harvested energy as the distance increases. This observation is the opposite of that in the traditional DF-TWR without the SWIPT which provides the best performance at the center location of the relay.
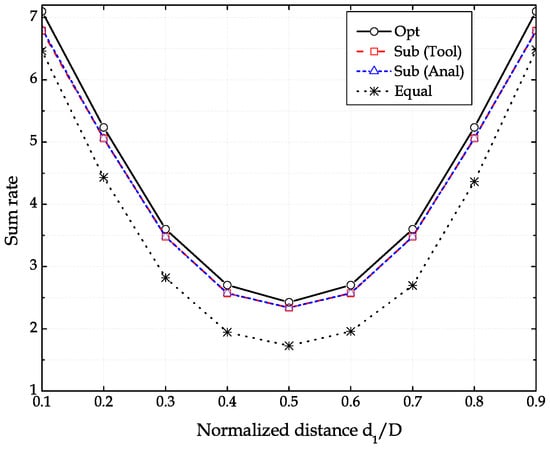
Figure 4.
Sum rate of the PS-SWIPT with different resource allocation methods as a function of when dBm and .
Figure 5 compares the sum rate of the TS-SWIPT with different resource allocation methods under the same conditions with Figure 4. In the figure, “Opt” denotes the performance obtained by solving the joint optimization problem (28)–(31) and “Equal” denotes the performance with . The suboptimal methods “Sub1” and “Sub2” denote the performance obtained by optimizing in (28)–(31), after fixing from the observation in Figure 3 and for the equal data portions in the MAC and BC, respectively. The solutions for “Opt”, “Sub1”, and “Sub2” are obtained by employing the convex optimization solver YALMIP [37]. The best performance is achieved by the joint optimization method The suboptimal method “Sub1” with provides a performance closer to than the suboptimal method “Sub1” with . This observation results from the fact that the BC phase dominates the performance by using the harvested energy so that the suboptimal method “Sub1” with asymmetric time allocation as and for the MAC and BC phases is more desirable than the suboptimal method `Sub2’ with symmetric time allocation as and .
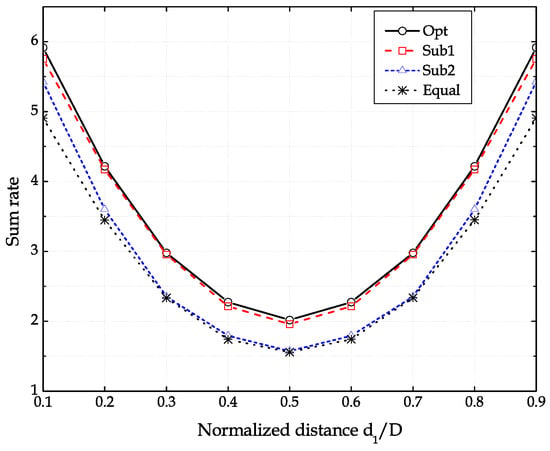
Figure 5.
Sum rate of the TS-SWIPT with different resource allocation methods as a function of when dBm and .
Figure 6 compares the sum rate of the two SWIPT methods as a function of the normalized distance when dBm. The optimal and suboptimal resource allocation methods are compared in the channels with different path exponents of and , where the suboptimal methods optimize the splitting ratio after fixing for both SWIPT methods. The results show that the sum rate performance is improved significantly as the path loss exponent decreases from 3 to since the harvested energy increases significantly. The PS-SWIPT methods outperform the TS-SWIPT methods in the sum rate as observed in the outage probability in [25]. In addition, the optimal and suboptimal methods exhibit very close performances for each SWIPT method.
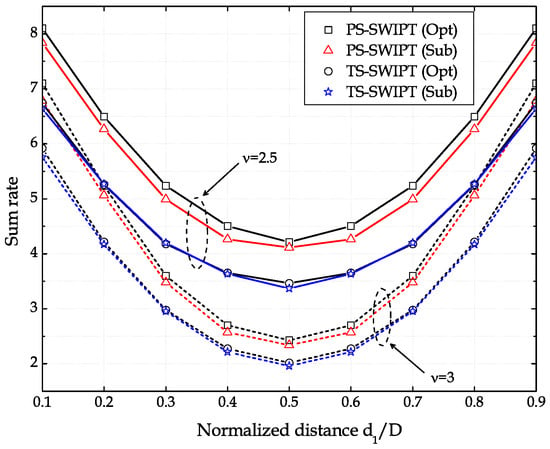
Figure 6.
Sum rate of the PS-SWIPT and the TS-SWIPT as a function of when dBm.
Figure 7 compares the sum rate of the SWIPT methods as the transmit power varies when and m. Again, the resource allocation methods for the PS-SWIPT outperform their counterparts for the TS-SWIPT. As the transmit power increases, the gain achieved with the resource allocation becomes more prominent for both the SWIPT methods.
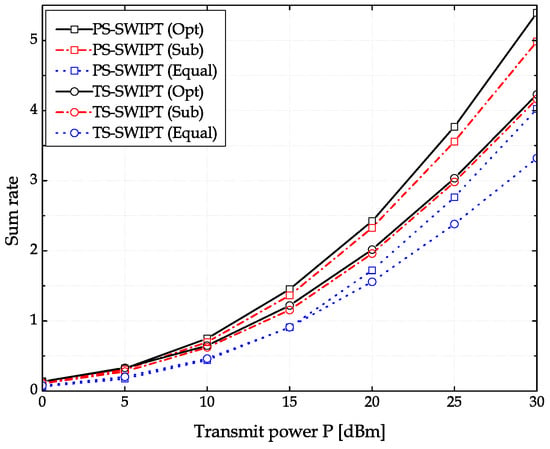
Figure 7.
Sum rate of the PS-SWIPT and the TS-SWIPT as a function of dBm when and .
5. Conclusions
The SWIPT performed by power splitting (PS) and time splitting (TS) is studied for the DF-TWR network to maximize the sum rate by optimizing the splitting ratio and the time-phase ratio of the DF-TWR. The joint optimization problem for each SWIPT method is shown to be convex with an appropriate transformation to that it can be solved by an existing convex optimization solver. To lower the computational complexity further, we also propose the suboptimal methods optimizing the splitting ratio for the given time-phase and derive a closed-form solution for the PS-SWIPT. It is observed that the PS-SWIPT outperforms the TS-SWIPT in both optimal and suboptimal methods and the suboptimal method provides a performance close to the optimal one for each SWIPT method. Therefore, the PS-SWIPT with the suboptimal closed-form solution is favorable to the DF-TWR in the aspects of complexity and performance.
As a future work, it would be interesting to extend the sum rate optimization problem to the problem of adapting not only the SWIPT parameter but also the transmit power of the devices under the constraints of the total power consumption and the battery capacity limit at the relay. In addition, the optimization problem in this paper can be extended to a scenario of supporting more than two devices, where the devices share all the data via multi-way relay communications [38]. Multi-way relay communications with K devices can be implemented efficiently with one MAC phase and BC phases for transmission of the network coded symbols similar to the TWR, for which the SWIPT parameters are optimized to maximize the overall performance.
Acknowledgments
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. NRF-2015R1A2A2A01005390).
Author Contributions
T.P. Do and Y.H. Kim designed the system model and formulated the problem; T.P. Do and Y. Jeong programmed the optimization problem and performed the simulations; Y.H. Kim solved the optimization problem and wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
We first prove that (24) is the solution of (23) when , or equivalently when , , and . Note that in (22) is a continuous function in with which consists of an increasing function for , a concave function for , and a decreasing function for . On the other hand, is a decreasing linear function in with and . Therefore, there is a unique intersection between and in . Since for , the unique intersection occurs in . In the following, we present the optimal PS ratio whether or .
Case (1) : If , we have a unique such that , which is given by in (25). Since is a monotonically decreasing function for while is a monotonically increasing function for and for , is maximized when . Therefore, the optimal PS ratio is given by in this case.
Case (2) : This case happens when and is obtained by solving , or equivalently
for . Since and , we have a unique solution for (A1) in which is given by
Note that is concave with the maximum point at
If , the maximum of in occurs at since and are decreasing functions of . If , the maximum of occurs at . If , the maximum of occurs at . Therefore, the optimal PS ratio can be expressed as
which corresponds to (24) when .
The proof for is straightforward by following the approach similar to that for .
References
- Al-Fuqaha, A.; Guizani, M.; Mohammadi, M.; Aledhari, M.; Ayyash, M. Internet of Things: A survey on enabling technologies, protocols, and applications. IEEE Commun. Surv. Tutor. 2015, 17, 2347–2376. [Google Scholar] [CrossRef]
- Baler, T.; Asim, M.; Tawfik, H.; Aldawsari, B.; Buyya, R. An energy-aware service composition algorithm for multiple cloud-based IoT applications. J. Netw. Comput. Appl. 2017. [Google Scholar] [CrossRef]
- Baker, T.; Al-Dawsaria, B.; Tawfik, H.; Reid, D.; Ngoko, Y. GreeDi: Anenergy efficient routing algorithm for big data on cloud. Ad Hoc Netw. 2015. [Google Scholar] [CrossRef]
- Aldawsari, B.; Baker, T.; England, D. Trusted energy-efficient cloud-based services brokerage platform. Int. J. Intell. Comput. Res. 2015, 6, 630–639. [Google Scholar] [CrossRef]
- Lu, X.; Wang, P.; Niyato, D.; Kim, D.I.; Han, Z. Wireless networks with RF energy harvesting: A contemporary survey. IEEE Commun. Surv. Tutor. 2015, 17, 757–789. [Google Scholar] [CrossRef]
- Jayakody, D.N.K.; Thompson, J.; Chatzinotas, S.; Durrani, S. Wireless Information and Power Transfer: A New Green Communications Paradigm; Springer-Verlag: New York, NY, USA, 2017. [Google Scholar]
- Chen, L.; Chen, W.; Wang, B.; Zhang, X.; Chen, H.; Yang, D. System-level simulation methodology and platform for mobile cellular systems. IEEE Commun. Mag. 2011, 49, 149–155. [Google Scholar]
- Wang, J.; YuWen, O.; Chen, H.; Li, S. Power allocation between pilot and data symbols for MIMO systems with MMSE detection under MMSE channel estimation. EURASIP J. Wirel. Commun. Netw. 2011, 2011, 785437. [Google Scholar] [CrossRef]
- Wang, C.; Chen, H.; Yin, Q.; Feng, A.; Molisch, A.F. Multi-user two-way relay networks with distributed beamforming. IEEE Trans. Wirel. Commun. 2011, 10, 3460–3471. [Google Scholar] [CrossRef]
- Li, Y.; Yin, Q.; Sun, L.; Chen, H.; Wang, H. A channel quality metric in opportunistic selection with outdated CSI over Nakagami-m fading channels. IEEE Trans. Veh. Technol. 2012, 61, 1427–1432. [Google Scholar] [CrossRef]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kenedy, R.A. Relaying protocols for wireless energy harvesting and information processing. IEEE Trans. Wirel. Commun. 2013, 12, 3622–3636. [Google Scholar] [CrossRef]
- Chen, Z.; Xia, B.; Liu, H. Wireless information and power transfer in two-way amplify-and-forward relaying channels. In Proceedings of the IEEE Global Conference Signal and Information Processing, Atlanta, GA, USA, 3–5 December 2014; pp. 168–172. [Google Scholar]
- Liu, Y.; Wang, L.; Elkashlan, M.; Duong, T.Q.; Nallanathan, A. Two-way relaying networks with wireless power transfer: Policies design and throughput analysis. In Proceedings of the IEEE Global Communication Conference, Austin, TX, USA, 8–12 December 2014; pp. 4030–4035. [Google Scholar]
- Tutuncuoglu, K.; Varan, B.; Yener, A. Throughput maximization for two-way relay channels with energy harvesting nodes: The impact of relaying strategies. IEEE Trans. Commun. 2015, 63, 2081–2093. [Google Scholar] [CrossRef]
- Fang, Z.; Yuan, X.; Wang, X. Distributed energy beamforming for simultaneous wireless information and power transfer in the two-way relay channel. IEEE Signal Process. Lett. 2015, 22, 656–660. [Google Scholar] [CrossRef]
- Gu, Y.; Aïssa, S. RF-based energy harvesting in decode-and-forward relaying systems: Ergodic and outage capacities. IEEE Trans. Wirel. Commun. 2015, 14, 6425–6434. [Google Scholar] [CrossRef]
- Ju, M.C.; Kang, K.M.; Hwang, K.S.; Jeong, C. Maximum transmission rate of PSR/TSR protocols in wireless energy harvesting DF-based relay networks. IEEE J. Sel. Areas Commun. 2015, 35, 2701–2717. [Google Scholar] [CrossRef]
- Mishra, D.; De, S.; Chiasserini, C.F. Joint optimization schemes for cooperative wireless information and power transfer over Rician channels. IEEE Trans. Commun. 2016, 64, 554–571. [Google Scholar] [CrossRef]
- Liu, H.; Kim, K.J.; Kwak, K.S.; Poor, H.V. Power splitting based SWIPT with decode and forward full-duplex relaying. IEEE Trans. Wirel. Commun. 2016, 15, 7561–7577. [Google Scholar] [CrossRef]
- Salem, A.; Hamdi, K.A. Wireless power transfer in multi-pair two-way AF relaying networks. IEEE Trans. Commun. 2016, 64, 4578–4591. [Google Scholar] [CrossRef]
- Sacarelo, G.; Thi Le, T.V.; Kim, Y.H. Resource allocation for wireless powered multi-pair massive antenna relaying with zero-forcing beamforming. IEEE Commun. Lett. 2016, 20, 2316–2319. [Google Scholar] [CrossRef]
- Wang, S.; Xia, M.; Wu, Y. Multipair two-way relay network with harvest-then-transmit users: Resolving pairwise uplink-downlink coupling. IEEE J. Sel. Top. Signal Proc. 2016, 10, 1506–1521. [Google Scholar] [CrossRef]
- Nguyen, D.K.; Jayakody, D.N.K.; Chatzinotas, S.; Thompson, J.S.; Li, J. Wireless energy harvesting assisted two-way cognitive relay networks: Protocol design and performance analysis. IEEE Access 2017. [Google Scholar] [CrossRef]
- Lee, H.; Song, C.; Choi, S.H.; Lee, I. Outage probability analysis and power splitter designs for SWIPT relaying systems with direct link. IEEE Commun. Lett. 2017, 21, 648–651. [Google Scholar] [CrossRef]
- Do, T.P.; Song, I.; Kim, Y.H. Simultaneous wireless transfer of power and information in a decode-and-forward two-way relaying network. IEEE Trans. Wirel. Commun. 2017, 16, 1579–1692. [Google Scholar] [CrossRef]
- Rajaram, A.; Jayakody, D.N.K.; Srinivasan, K.; Chen, B.; Sharma, V. Opportunistic wireless power transfer scheme for multiple access relay networks. IEEE Access 2017. [Google Scholar] [CrossRef]
- Ciuonzo, D.; Rossi, P.S.; Dey, S. Massive MIMO channel-aware decision fusion. IEEE Trans. Signal Process. 2015, 63, 604–619. [Google Scholar] [CrossRef]
- Shirazinia, A.; Dey, S.; Ciuonzo, D.; Rossi, P.S. Massive MIMO for decentralized estimation of a correlated source. IEEE Trans. Signal Process. 2016, 64, 2499–2512. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, R.; Ho, C.K. Wireless information and power transfer: Architecture design and rate-energy tradeoff. IEEE Trans. Commun. 2013, 61, 4754–4767. [Google Scholar] [CrossRef]
- Shim, Y.; Park, H. A closed-form expression of optimal time for two-way relay using DF MABC protocol. IEEE Commun. Lett. 2014, 18, 721–724. [Google Scholar] [CrossRef]
- Pang, L.; Zhang, Y.; Li, J.; Ma, Y.; Wang, J. Power allocation and relay selection for two-way relaying systems by exploiting physical layer network coding. IEEE Trans. Veh. Technol. 2014, 63, 2723–2730. [Google Scholar] [CrossRef]
- Kim, S.H.; Jung, B.C.; Sung, D.K. Transmit power optimization for two-way relay channels with physical layer network coding. IEEE Commun. Lett. 2015, 19, 151–154. [Google Scholar] [CrossRef]
- Do, T.P.; Kim, Y.H. Outage-optimal power and time allocation for rate-aware two-way relaying with a decode-and-forward protocol. IEEE Trans. Veh. Technol. 2016, 65, 9673–9686. [Google Scholar] [CrossRef]
- Tse, D. Fundamentals of Wireless Communications; Cambridge University Press: Cambrige, UK, 2005; pp. 228–232. ISBN 978-0-521-84527-4. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004; pp. 89–91. ISBN 978-0-521-83378-3. [Google Scholar]
- Potra, F.A.; Wright, S.J. Interior-point methods. J. Comput. Appl. Math. 2000, 124, 281–302. [Google Scholar] [CrossRef]
- Löfberg, J. YALMIP : A Toolbox for Modeling and Optimization in MATLAB. In Proceedings of the CACSD Conference, New Orleans, LA, USA, 2–4 September 2004; pp. 284–289. [Google Scholar]
- Xue, J.; Sellathurai, M.; Ratnarajah, T.; Ding, Z. Performance analysis for multi-way relaying in Rician fading channels. IEEE Trans. Commun. 2015, 63, 4050–4062. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).