Decentralized State-Observer-Based Traffic Density Estimation of Large-Scale Urban Freeway Network by Dynamic Model
Abstract
:1. Introduction
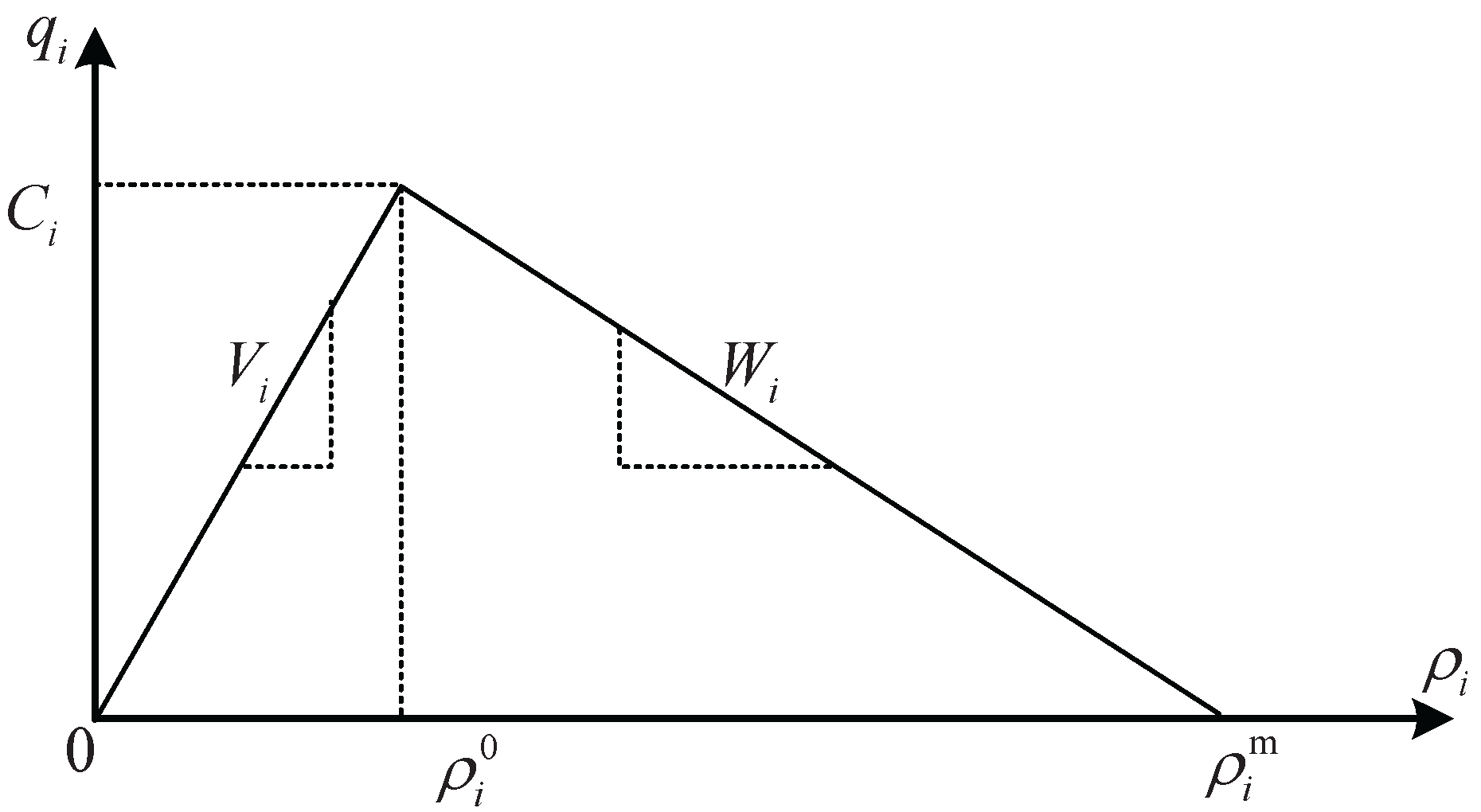
2. Preliminaries and Problem Formula
3. Decentralized State Observer Design
4. Experimental Results and Analysis
4.1. Data Collection and Parameter Settings
4.2. Traffic Sensor Placement
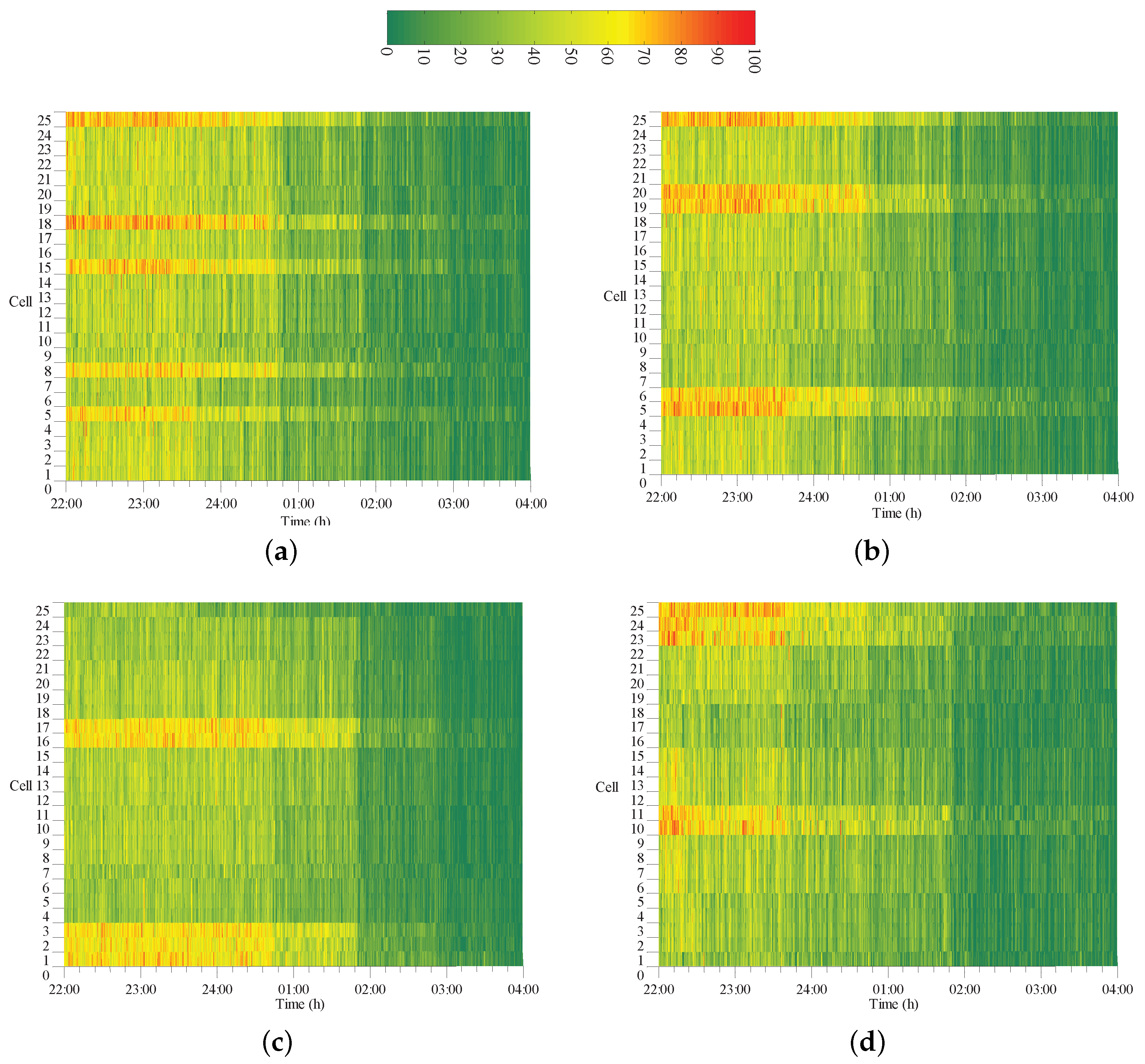
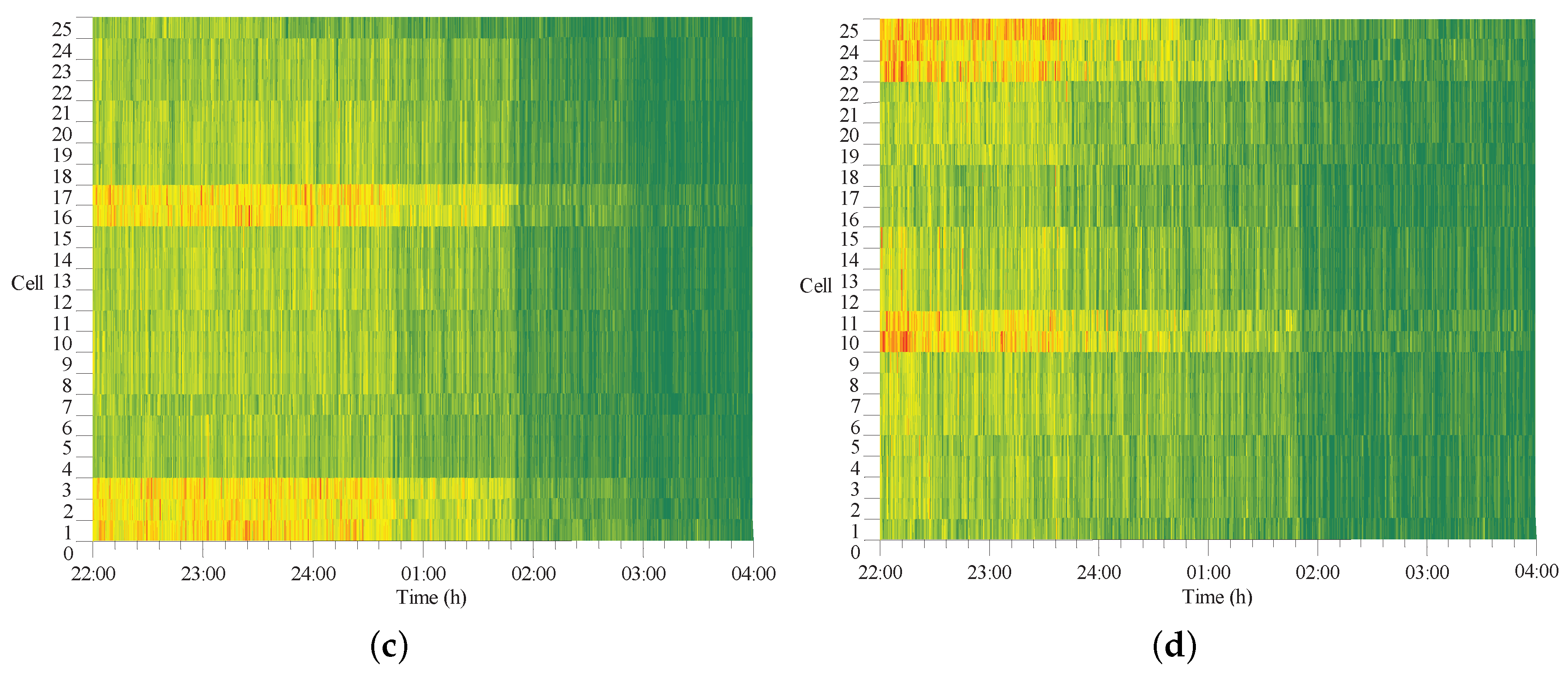
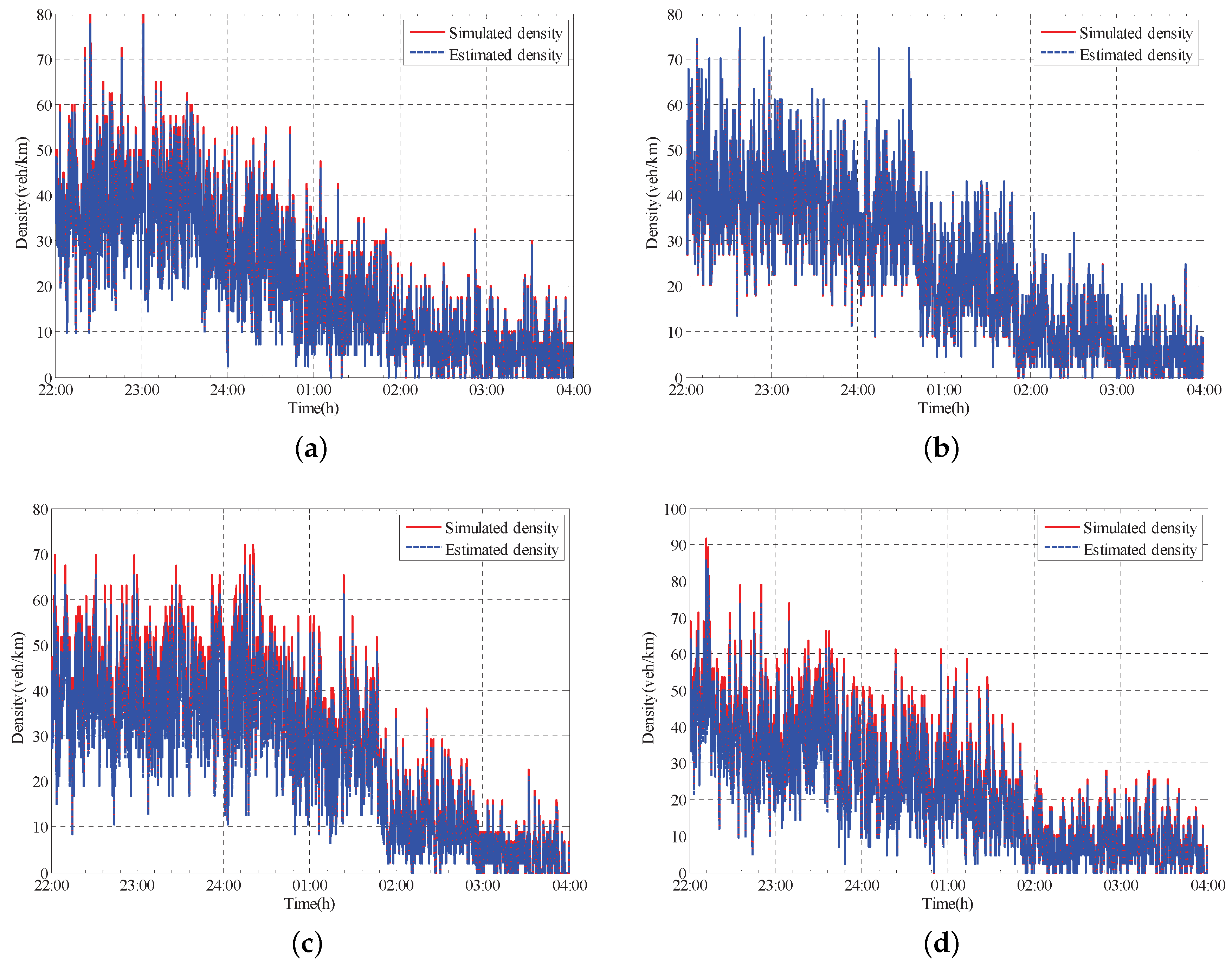
4.3. Analysis of Results
5. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Number | Length | Number | Length | Number | Length | Number | Length |
|---|---|---|---|---|---|---|---|
| 1 | 215 m | 26 | 661 m | 51 | 318 m | 76 | 133 m |
| 2 | 700 m | 27 | 112 m | 52 | 232 m | 77 | 337 m |
| 3 | 170 m | 28 | 726 m | 53 | 260 m | 78 | 368 m |
| 4 | 382 m | 29 | 607 m | 54 | 185 m | 79 | 158 m |
| 5 | 182 m | 30 | 356 m | 55 | 185 m | 80 | 330 m |
| 6 | 456 m | 31 | 445 m | 56 | 270 m | 81 | 358 m |
| 7 | 423 m | 32 | 445 m | 57 | 296 m | 82 | 283 m |
| 8 | 288 m | 33 | 406 m | 58 | 301 m | 83 | 347 m |
| 9 | 370 m | 34 | 277 m | 59 | 336 m | 84 | 306 m |
| 10 | 204 m | 35 | 505 m | 60 | 160 m | 85 | 391 m |
| 11 | 339 m | 36 | 467 m | 61 | 136 m | 86 | 288 m |
| 12 | 132 m | 37 | 477 m | 62 | 108 m | 87 | 370 m |
| 13 | 240 m | 38 | 160 m | 63 | 100 m | 88 | 305 m |
| 14 | 450 m | 39 | 418 m | 64 | 96 m | 89 | 125 m |
| 15 | 236 m | 40 | 421 m | 65 | 265 m | 90 | 651 m |
| 16 | 123 m | 41 | 415 m | 66 | 135 m | 91 | 127 m |
| 17 | 753 m | 42 | 130 m | 67 | 185 m | 92 | 426 m |
| 18 | 508 m | 43 | 270 m | 68 | 393 m | 93 | 146 m |
| 19 | 508 m | 44 | 336 m | 69 | 475 m | 94 | 231 m |
| 20 | 198 m | 45 | 336 m | 70 | 363 m | 95 | 308 m |
| 21 | 608 m | 46 | 211 m | 71 | 195 m | 96 | 421 m |
| 22 | 150 m | 47 | 290 m | 72 | 237 m | 97 | 240 m |
| 23 | 845 m | 48 | 316 m | 73 | 396 m | 98 | 329 m |
| 24 | 278 m | 49 | 561 m | 74 | 429 m | 99 | 317 m |
| 25 | 435 m | 50 | 411 m | 75 | 168 m | 100 | 223 m |
Appendix B
References
- Daganzo, C.F. The cell transmission model: A dynamic representation of highway traffic consistent with the hydrodynamic theory. Transp. Res. Part B 1994, 28, 269–287. [Google Scholar] [CrossRef]
- Daganzo, C.F. The cell transmission model, part II: Network traffic. Transp. Res. Part B 1995, 29, 79–93. [Google Scholar] [CrossRef]
- Muñoz, L.; Sun, X.; Horowitz, R.; Luis, A. Traffic density estimation with the cell transmission model. In Proceedings of the American Control Conference (ACC), Denver, CO, USA, 4–6 June 2003; Volume 5, pp. 3750–3755. [Google Scholar]
- Muñoz, L.; Sun, X.; Sun, D.; Gomes, G.; Horowitz, R. Methodological calibration of the cell transmission model. In Proceedings of the IEEE American Control Conference (ACC), Boston, MA, USA, 30 June–2 July 2004; Volume 1, pp. 798–803. [Google Scholar]
- Alvarez-Icaza, L.; Muñoz, L.; Sun, X.; Horowitz, R. Adaptive observer for traffic density estimation. In Proceedings of the IEEE American Control Conference (ACC), Boston, MA, USA, 30 June–2 July 2004; Volume 3, pp. 2705–2710. [Google Scholar]
- Canudas de Wit, C.; Ojeda, L.L.; Kibangou, A.Y. Graph constrained-CTM observer design for the Grenoble south ring. In Proceedings of the 13th IFAC Symposium on Control in Transportation Systems, Sofia, Bulgaria, 12–14 September 2012; Volume 45, pp. 197–202. [Google Scholar]
- Morbidi, F.; Ojeda, L.L.; Canudas de Wit, C.; Bellicot, I. A new robust approach for highway traffic density estimation. In Proceedings of the IEEE European Control Conference (ECC), Strasbourg, France, 24–27 June 2014; pp. 2575–2580. [Google Scholar]
- Chen, Y.; Guo, Y.; Wang, Y.; Li, W. Modeling freeway network by using dynamic graph hybrid automata and estimating its states by designing state observer. In Proceedings of the Chinese Automation Congress (CAC), Wuhan, China, 27–29 November 2015; pp. 237–242. [Google Scholar]
- Chen, Y.; Guo, Y.; Wang, Y. Modeling and Density Estimation of an Urban Freeway Network Based on Dynamic Graph Hybrid Automata. Sensors 2017, 17, 716. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Papageorgiou, M. Real-time freeway traffic state estimation based on extended Kalman filter: A general approach. Transp. Res. Part B 2005, 39, 141–167. [Google Scholar] [CrossRef]
- Herrera, J.C.; Bayen, A.M. Incorporation of Lagrangian measurements in freeway traffic state estimation. Transp. Res. Part B 2010, 44, 460–481. [Google Scholar] [CrossRef]
- Dörfler, F.; Pasqualetti, F.; Bullo, F. Continuous-time distributed observers with discrete communication. IEEE J. Sel. Top. Signal Process. 2013, 7, 296–304. [Google Scholar] [CrossRef]
- Silva, M.P.D.; Bottura, C.P. Decentralized Observer for A Class of Nonlinear Norm Bounded Systems. In Proceedings of the International Conference on Chaos and Nonlinear Dynamics, São José Dos Campos, Brazil, 26–30 July 2010; pp. 1–2. [Google Scholar]
- Dhbaibi, S.; Tlili, A.S.; Benhadj Braiek, N. Decentralized observer based feedback control for interconnected nonlinear systems: Application to a multi-machine power systems. J. Autom. Syst. Eng. 2008, 2, 1–17. [Google Scholar]
- Zhu, Y.; Pagilla, P.R. Decentralized output feedback control of a class of large scale interconnected systems. IMA J. Math. Control Inf. Adv. Access 2006, 17, 1–13. [Google Scholar] [CrossRef]
- Tlili, A.S.; Braiek, N.B. Decentralized observer based guaranteed cost control for nonlinear interconnected systems. Int. J. Control Autom. 2009, 2, 19–34. [Google Scholar]
- Contreras, S.; Kachroo, P.; Agarwal, S. Observability and sensor placement problem on highway segments: A traffic dynamics-based approach. IEEE Trans. Intell. Transp. Syst. 2016, 17, 848–858. [Google Scholar] [CrossRef]
- Agarwal, S.; Kachroo, P.; Contreras, S. A dynamic network modeling-based approach for traffic observability problem. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1168–1178. [Google Scholar] [CrossRef]
- Coclite, G.M.; Piccoli, B. Traffic flow on a road network. SIAM J. Math. Anal. 2005, 36, 1862–1886. [Google Scholar] [CrossRef]
- Contreras, S.; Agarwal, S.; Kachroo, P. Quality of Traffic Observability on Highways with Lagrangian Sensors. IEEE Trans. Autom. Sci. Eng. 2017, 1–11. [Google Scholar] [CrossRef]
- Yakubovich, V.A. The S-procedure in Nonlinear Control Theory. Vestnik Leningr. Univ. 1971, 1, 62–67. [Google Scholar]
- Boyd, S.; El Ghaoui, L.; Ferron, E.; Balakrishnan, V. Linear Matrix Inequalities in Systems and Control Theory; SIAM: Philadelphia, PA, USA, 1994; pp. 7–35. [Google Scholar]


| Cell | V | W | C | ||
|---|---|---|---|---|---|
| 2, 9 | 63 | 18 | 6230 | 105 | 535 |
| 11 | 66 | 18 | 6505 | 95 | 580 |
| 25 | 60 | 18 | 5980 | 95 | 585 |
| 36, 40 | 61 | 17 | 6200 | 102 | 550 |
| 57 | 63 | 19 | 6135 | 99 | 568 |
| 59 | 61 | 17 | 6158 | 103 | 505 |
| 73 | 66 | 18 | 6250 | 105 | 560 |
| 99, 100 | 65 | 20 | 6000 | 102 | 550 |
| Others | 75 | 19 | 6500 | 115 | 582 |
| Subsystem | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| MSE | 0.1295 | 0.1326 | 0.1332 | 0.1293 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Chen, Y.; Zhang, C. Decentralized State-Observer-Based Traffic Density Estimation of Large-Scale Urban Freeway Network by Dynamic Model. Information 2017, 8, 95. https://doi.org/10.3390/info8030095
Guo Y, Chen Y, Zhang C. Decentralized State-Observer-Based Traffic Density Estimation of Large-Scale Urban Freeway Network by Dynamic Model. Information. 2017; 8(3):95. https://doi.org/10.3390/info8030095
Chicago/Turabian StyleGuo, Yuqi, Yangzhou Chen, and Chiyuan Zhang. 2017. "Decentralized State-Observer-Based Traffic Density Estimation of Large-Scale Urban Freeway Network by Dynamic Model" Information 8, no. 3: 95. https://doi.org/10.3390/info8030095
APA StyleGuo, Y., Chen, Y., & Zhang, C. (2017). Decentralized State-Observer-Based Traffic Density Estimation of Large-Scale Urban Freeway Network by Dynamic Model. Information, 8(3), 95. https://doi.org/10.3390/info8030095





