A Filter Structure for Arbitrary Re-Sampling Ratio Conversion of a Discrete Signal
Abstract
:1. Introduction
- The modified Farrow filter is simple to use for sampling rate conversion of a discrete signal in an arbitrary ratio between the original discrete signal and the converted sampling rate signal. In the conversion algorithm, because the modified Farrow structure depends only on the conversion ratio, a minimal amount of calculation information is needed. Thus, the modified Farrow filter can greatly simplify the calculation complexity of sampling rate conversion theory.
- For a specific order number of the modified Farrow structure, its sampling points must be increased to improve the sampling rate accuracy. To the existing theory, our approach is a simplification of a complex signal to the modified Farrow filter.
- Our proposed method is more accurate than the existing methods in the literature. For a complex signal, such as an existing harmonic distortion, the determined sampling rate accuracy is higher when using the FFR to perform the sampling rate problem of a discrete signal.
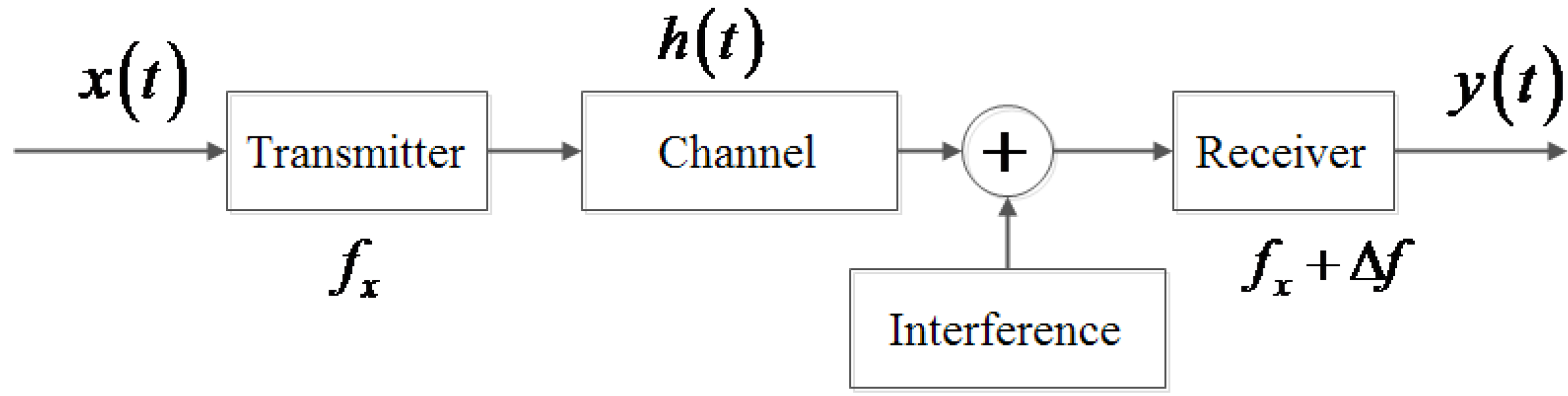
2. Frequency Deviation Estimation
2.1. Problem Statement
2.2. FFR Estimation
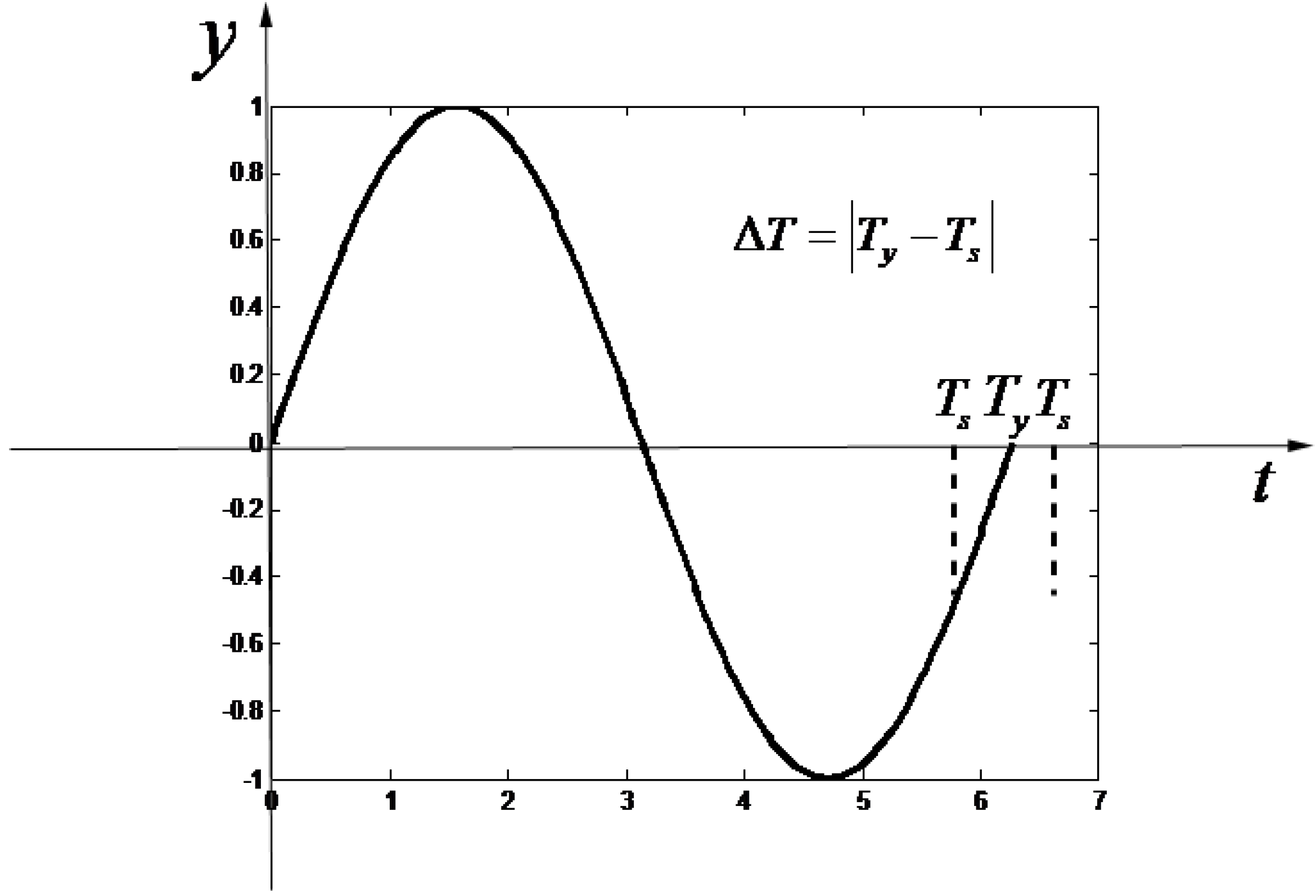
2.3. Signal Frequency Correction
2.4. Performance Analysis of the Frequency Deviation Estimation
3. Sampling Rate Conversion Algorithm
3.1. The Modified Farrow Filter
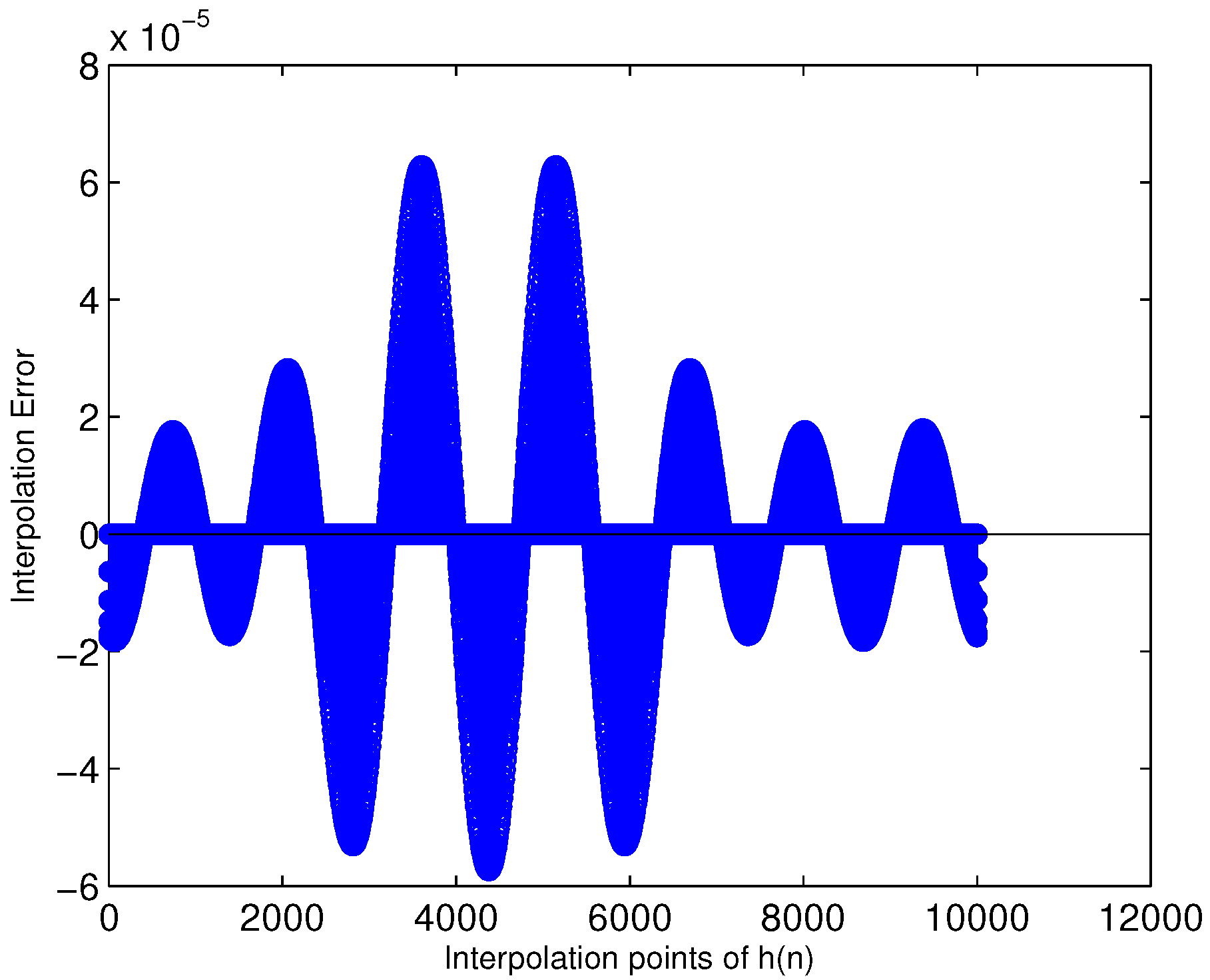
3.2. The Interpolation Arithmetic of the Modified Farrow Filter
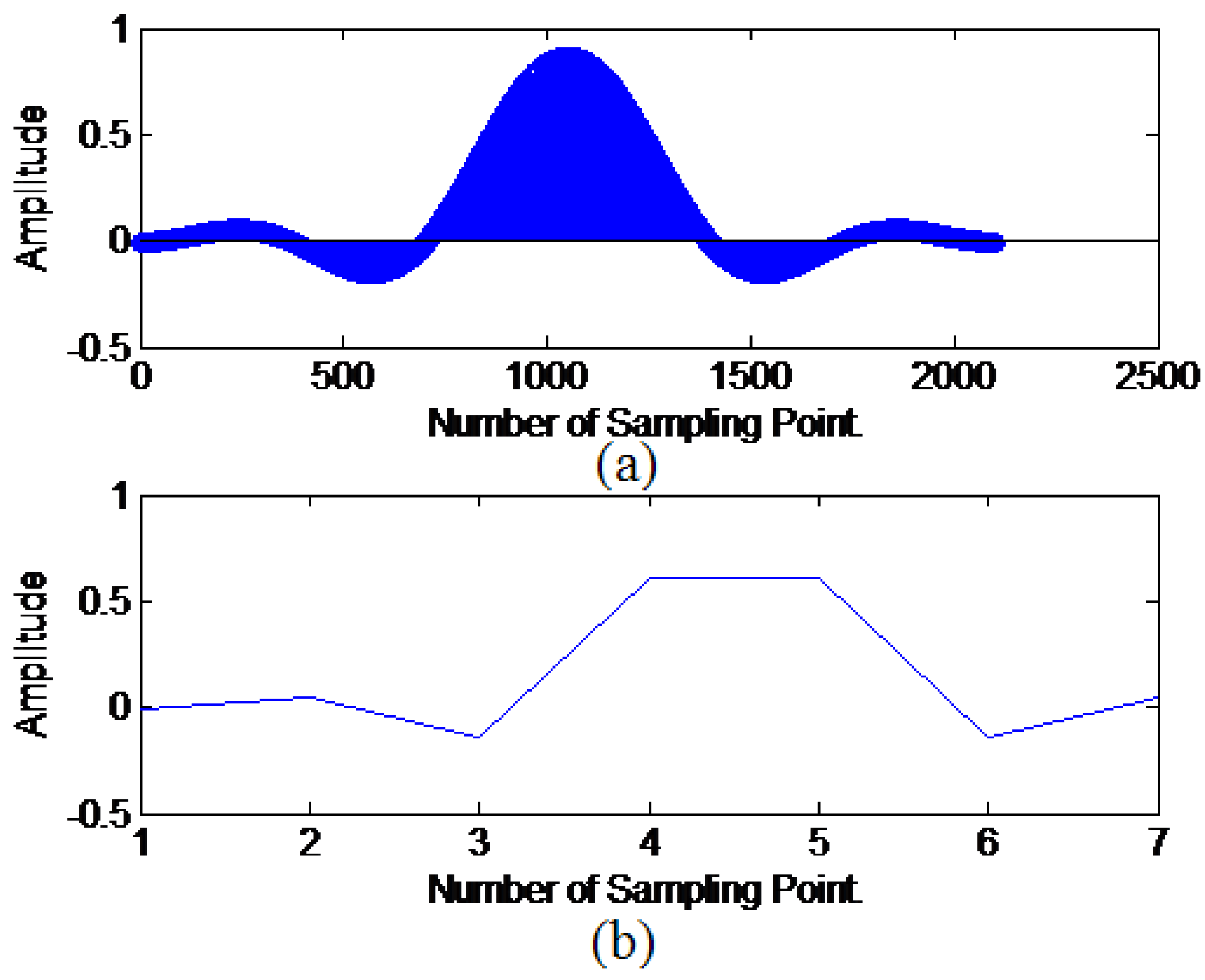
3.3. SRC of Discrete Signal
4. Experimental Results
4.1. Results of the Frequency Estimation
- a signal without harmonic components and noise
- a signal consisting of three times, five times, and seven times harmonics
- a signal consisting of a harmonic and 20 dB of Gaussian white noise. The results obtained using the FFR estimation method are shown in Table 1.
4.2. Design of the Modified Farrow Filter
4.3. Simulation Results for SRC
4.4. Comparison Results
4.4.1. Frequency Deviation Estimation
4.4.2. Sampling Rate Conversion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Vaidyanathan, P.P. Generalizations of the sampling theorem: Seven decades after Nyquist. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2001, 48, 1094–1109. [Google Scholar] [CrossRef]
- Nyquist, H. Certain topics in telegraph transmission theory. Trans. Am. Inst. Electr. Eng. 1928, 47, 617–644. [Google Scholar] [CrossRef]
- Shannon, C.E. Communications in the presence of noise. Proc. IRE 1949, 37, 10–21. [Google Scholar] [CrossRef]
- Tavares, G.; Tavares, L.; Petrolino, A. An improved feedforward frequency offset estimator. IEEE Trans. Signal Process. 2008, 56, 2155–2160. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y. An islanding detection method for inverter-based distributed generators based on the reactive power disturbance. IEEE Trans. Power Electron. 2016, 31, 3559–3574. [Google Scholar] [CrossRef]
- Gupta, P.; Bhatia, R.S.; Jain, D.K. Active ROCOF Relay for Islanding Detection. IEEE Trans. Power Deliv. 2017, 32, 420–429. [Google Scholar] [CrossRef]
- Narayanan, K.; Siddiqui, S.A.; Fozdar, M. Hybrid islanding detection method and priority-based load shedding for distribution networks in the presence of DG units. IET Gener. Transm. Distrib. 2017, 11, 586–595. [Google Scholar]
- Viterbi, A.J. Principles of Coherent Communication; McGraw-Hill: New York, NY, USA, 1966; Volume 966, pp. 40–42. [Google Scholar]
- Fitz, M.P. Further results in the fast estimation of a single frequency. IEEE Trans. Commun. 1994, 42, 862–864. [Google Scholar] [CrossRef]
- Mengali, U.; Morelli, M. Data-aided frequency estimation for burst digital transmission. IEEE Trans. Commun. 1997, 45, 23–25. [Google Scholar] [CrossRef]
- Kay, S. A fast and accurate single frequency estimator. IEEE Trans. Acoustics Speech Signal Process. 1989, 37, 1987–1990. [Google Scholar] [CrossRef]
- Tretter, S. Estimating the frequency of a noisy sinusoid by linear regression (Corresp.). IEEE Trans. Inf. Theory 1985, 31, 832–835. [Google Scholar] [CrossRef]
- Brown, T.; Wang, M.M. An iterative algorithm for single-frequency estimation. IEEE Trans. Signal Process. 2002, 50, 2671–2682. [Google Scholar] [CrossRef]
- Gedalyahu, K.; Ronen, T.; Eldar Yonina, C. Multichannel sampling of pulse streams at the rate of innovation. IEEE Trans. Signal Process. 2011, 59, 1491–1504. [Google Scholar] [CrossRef]
- Harris, F. Performance and design of Farrow filter used for arbitrary resampling. Proceedings of 13th International Conference on Digital Signal Processing, Santorini, Greece, 2–4 July 1997; Volume 2, pp. 595–599. [Google Scholar]
- Farrow, C.W. A continuously variable digital delay element. In Proceedings of the IEEE International Symposium on Circuits and Systems, Espoo, Finland, 7–9 June 1988; pp. 2641–2645. [Google Scholar]
- Mitra, S.K.; Kuo, Y. Digital Signal Processing: A Computer-Based Approach; McGraw-Hill: New York, NY, USA, 2006; Volume 2. [Google Scholar]
- Blok, M. Farrow structure implementation of fractional delay filter optimal in Chebyshev sense. In Proceedings of the Photonics Applications in Astronomy, Communications, Industry, and High-Energy Physics Experiments IV, Wilga, Poland, 29 May–4 June 2006; p. 61594k. [Google Scholar]
- Wang, T.; Li, C. Sample rate conversion technology in software defined radio. In Proceedings of the IEEE Conference on Electrical and Computer Engineering, CCECE’06, Ottawa, ON, Canada, 7–10 May 2006; pp. 1355–1358. [Google Scholar]
- Horridge, J.P.; Frazer, G.J. Accurate arbitrary resampling with exact delay for radar applications. In Proceedings of the IEEE 2008 International Conference on Radar, Adelaide, Australia, 2–5 September 2008; pp. 123–127. [Google Scholar]
- Blok, M. Fractional delay filter design for sample rate conversion. In Proceedings of the 2012 Federated Conference on IEEE Computer Science and Information Systems (FedCSIS), Wroclaw, Poland, 9–12 September 2012; pp. 701–706. [Google Scholar]
- Andria, G.; Savino, M.; Trotta, A. Windows and interpolation algorithms to improve electrical measurement accuracy. IEEE Trans. Instrum. Meas. 1989, 38, 856–863. [Google Scholar] [CrossRef]
- Rajamani, K.; Yhean-Sen, L.; Farrow, C.W. An efficient algorithm for sample rate conversion from CD to DAT. IEEE Signal Process. Lett. 2000, 7, 288–290. [Google Scholar] [CrossRef]
- Evangelista, G. Design of digital systems for arbitrary sampling rate conversion. Signal Process. 2003, 83, 377–387. [Google Scholar] [CrossRef]
- Psiaki, M.L. Block acquisition of weak GPS signals in a software receiver. In Proceedings of the 14th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2001), Salt Lake City, UT, USA, 11–14 September 2001. [Google Scholar]
- Gupta, P.; Bhatia, R.S.; Jain, D.K. Average absolute frequency deviation value based active islanding detection technique. IEEE Trans. Smart Grid 2015, 6, 26–35. [Google Scholar] [CrossRef]
- Rife, D.C.; Boorstyn, R.R. Single tone parameter estimation from discrete-time observations. IEEE Trans. Inf. Theory 1974, 20, 591–598. [Google Scholar] [CrossRef]
- Aboutanios, E.; Mulgrew, B. Iterative frequency estimation by interpolation on Fourier coefficients. IEEE Trans. Signal Process. 2005, 53, 1237–1242. [Google Scholar] [CrossRef]
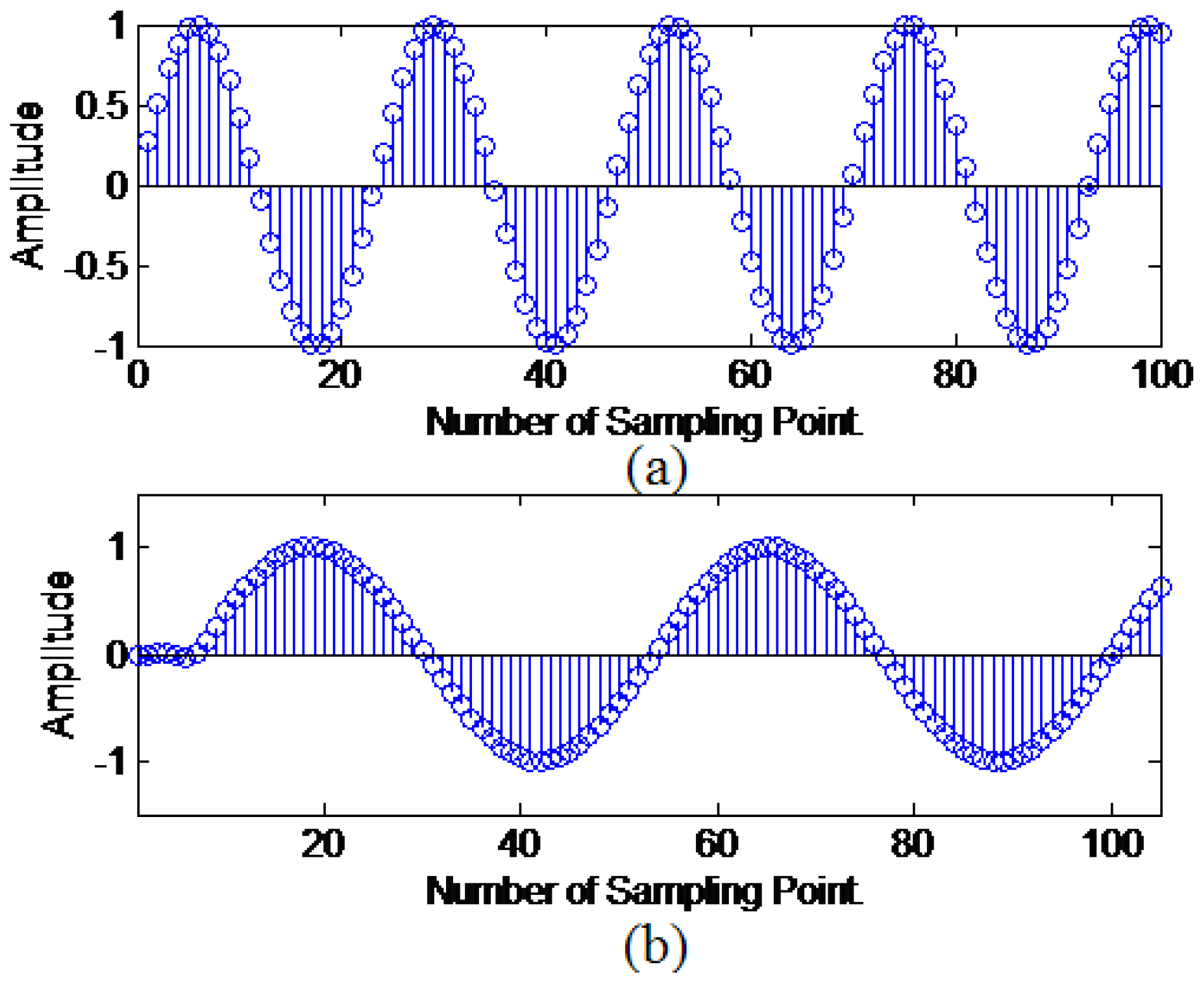

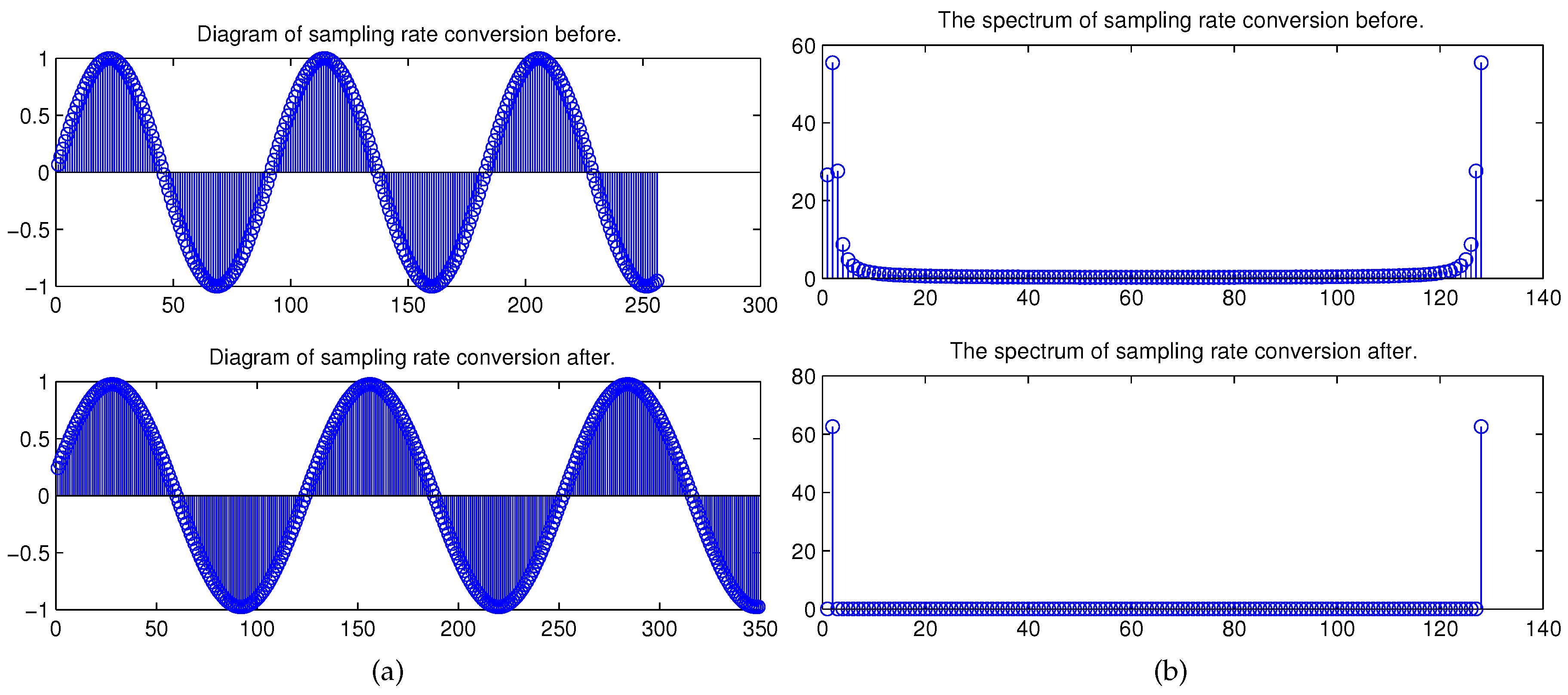

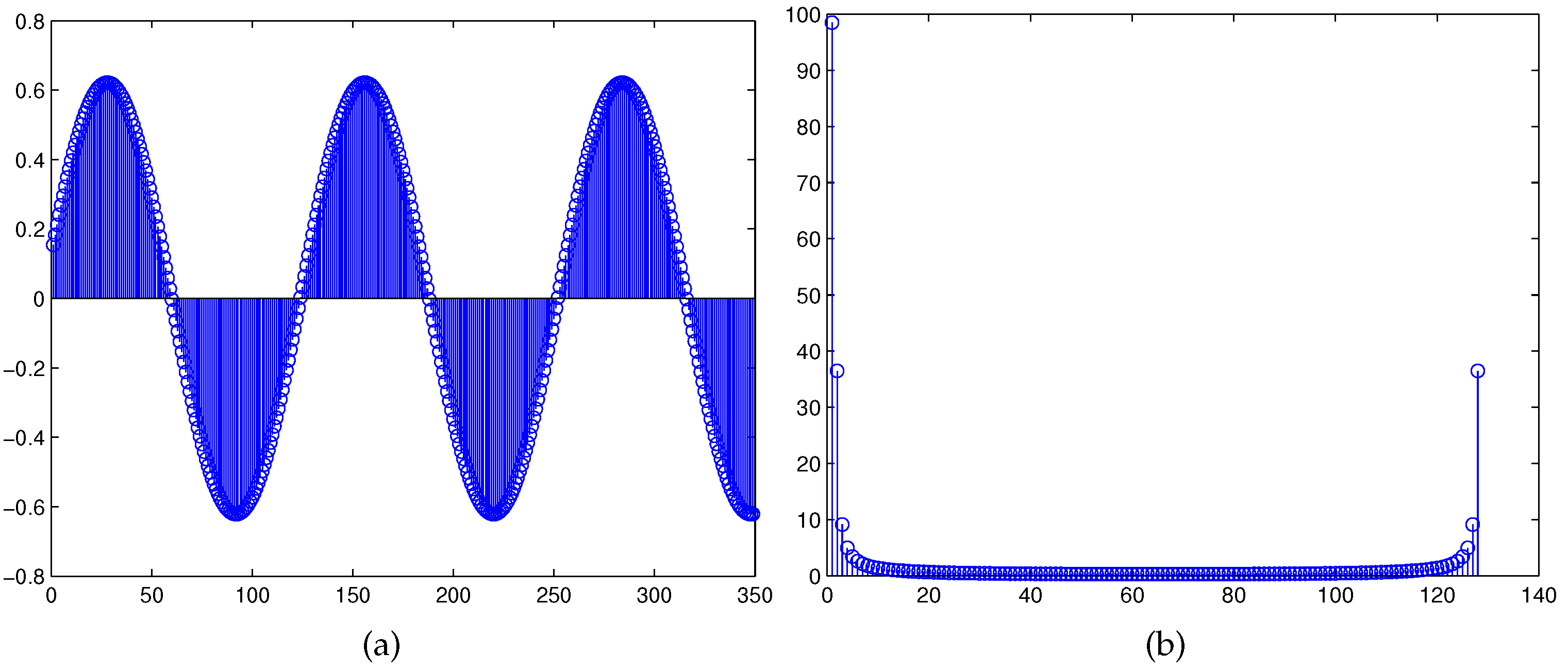
| Loop Number | Frequency Estimation | Containing Harmonic | Containing Harmonic and Noise |
|---|---|---|---|
| 1 | 50.200796 | 50.205414 | 50.329538 |
| 2 | 50.20000 | 50.200000 | 50.200333 |
| 3 | 50.20000 | 50.200000 | 50.200000 |
| 4 | 50.20000 | 50.200000 | 50.200000 |
| 5 | 50.20000 | 50.200000 | 50.200000 |
| The Results of the Sampling Signal for before the sampling rate conversion (SRC) | The Results for after the SRC |
|---|---|
| 0 | 0.00485602103592 |
| 0 | 0.00473329018826 |
| 0.00000000000001 | 0.00435523550826 |
| 0.00000000000001 | 0.00377333106918 |
| 0.00000000000001 | 0.00243896125486 |
| 0.00000000000001 | 0.00038573119211 |
| 0.00000000000001 | 0.00019852719739 |
| 0 | 0.00013465731865 |
| 62.82496056620225 | 62.56533184922048 |
| 20.86262463928692 | 20.77828756114954 |
| 12.42215235579411 | 12.37393682470713 |
| 8.76973611504727 | 8.73749834116767 |
| 0 | 0.00070606042704 |
| 0.00000000000001 | 0.00026219741259 |
| 0 | 0.00016016198162 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Zhu, C. A Filter Structure for Arbitrary Re-Sampling Ratio Conversion of a Discrete Signal. Information 2017, 8, 53. https://doi.org/10.3390/info8020053
Zhang H, Zhu C. A Filter Structure for Arbitrary Re-Sampling Ratio Conversion of a Discrete Signal. Information. 2017; 8(2):53. https://doi.org/10.3390/info8020053
Chicago/Turabian StyleZhang, Hong, and Changjian Zhu. 2017. "A Filter Structure for Arbitrary Re-Sampling Ratio Conversion of a Discrete Signal" Information 8, no. 2: 53. https://doi.org/10.3390/info8020053
APA StyleZhang, H., & Zhu, C. (2017). A Filter Structure for Arbitrary Re-Sampling Ratio Conversion of a Discrete Signal. Information, 8(2), 53. https://doi.org/10.3390/info8020053






