Automated Prostate Gland Segmentation Based on an Unsupervised Fuzzy C-Means Clustering Technique Using Multispectral T1w and T2w MR Imaging
Abstract
:1. Introduction
2. Background
3. Patients and Methods
3.1. Patient Dataset Description
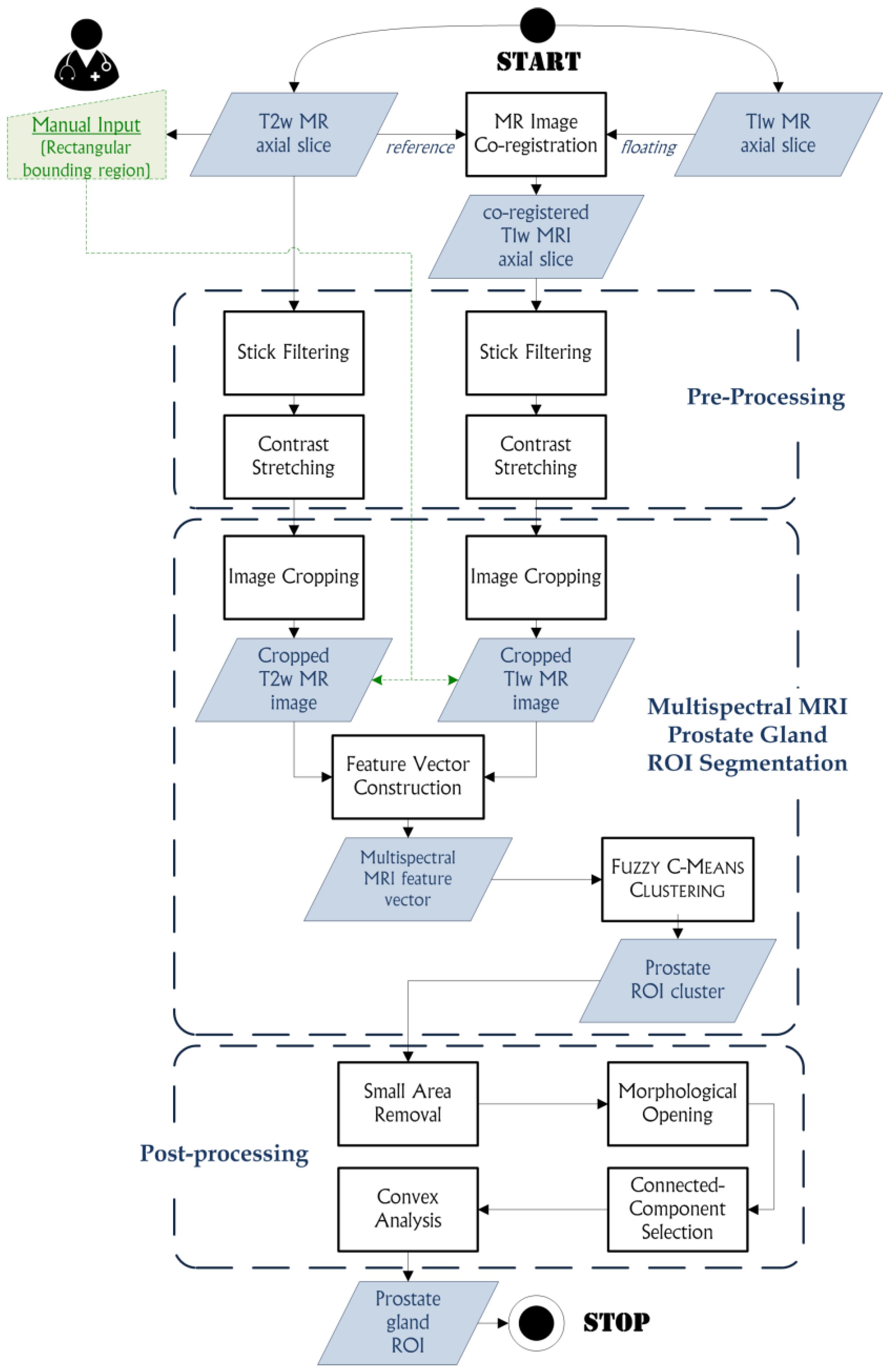
3.2. The Proposed Method
3.2.1. MR Image Co-Registration
3.2.2. Pre-Processing
- original T1w and T2w MR images;
- T1w and T2w MR images pre-processed with stick filtering (length , thickness );
- T1w and T2w MR images filtered with 3 × 3 and 5 × 5 Gaussian kernels;
- T1w and T2w MR images filtered with 3 × 3 and 5 × 5 average kernels.
3.2.3. Multispectral MRI Prostate Gland ROI Segmentation Based on the FCM Algorithm
- is the fuzzification constant (weighting exponent: ) that controls the fuzziness of the classification process. If , the FCM algorithm approximates hard version. In general, the higher the value the greater will be the fuzziness degree (the most common value is ).
- is the fuzzy C-partition of the set ().
- is the squared distance between the elements and , computed through an induced norm on (usually the Euclidean norm).
| Algorithm 1. Pseudo-code of the Fuzzy C-Means clustering algorithm used for prostate gland ROI segmentation on multispectral MRI anatomical data. |
|
3.2.4. Post-Processing
- A small area removal operation is employed to delete any unwanted connected-components, whose area is less than 500 pixels, which are included into the ROI cluster. These small regions can have similar gray levels to the prostate ROI and were classified into the same cluster by the FCM clustering algorithm. The areas less than 500 pixels certainly do not represent the prostate ROI, since the prostate gland in MRI slices is always characterized by a greater area, regardless of the used acquisition protocol. Thus, these small areas can be removed from the prostate ROI cluster to avoid a wrong connected-component selection in the next processing steps.
- A morphological opening, using a 5 × 5 pixel square structuring element, is a good compromise between precision in the actual detected contours and capability for unlinking poorly connected regions to the prostate ROI.
- Connected-component selection, using a flood-fill algorithm [73], determines the connected-component that is the nearest to the cropped image center, since the prostate is always located at the central zone of the cropped image.
- Convex analysis of the ROI shape since the prostate gland appearance is always convex. A convex hull algorithm [74] is suitable to envelope the segmented ROI into the smallest convex polygon that contains it, so considering possible adjacent regions excluded by the FCM clustering output. Finally, a morphological opening operation with a circular structuring element, is performed for smoothing prostate ROI boundaries. The used circular structuring element with 3 pixel radius allows for smoother and more realistic ROI boundaries without deteriorating significantly the output yielded by the FCM clustering. Accordingly, the value of the radius does not affect the segmentation results and it is not dependent on image resolution.
3.3. Segmentation Evaluation Metrics
3.3.1. Volume-Based Metrics
3.3.2. Spatial Overlap-Based Metrics
- Dice similarity coefficient () is the most used statistic in validating medical volume segmentations:
- Jaccard index () is another similarity measure, which is the ratio between the cardinality of the intersection and the cardinality of the union calculated on the two segmentation results:As can be seen in Equation (15), is strongly related to . Moreover is always larger than except at extrema , where they take equal values.
- Sensitivity, also called True Positive Ratio (), measures the portion of positive (foreground) pixels correctly detected by the proposed segmentation method with respect to the gold-standard segmentation:
- Specificity, also called True Negative Ratio (), indicates the portion of negative (background) pixels correctly identified by the automatic segmentation against the gold-standard segmentation:
- False Positive Ratio () denotes the presence of false positives compared to the reference region:
- False Negative Ratio () is analogously defined as:
3.3.3. Spatial Distance-Based Metrics
- Mean absolute distance () quantifies the average error in the segmentation process:
- Maximum distance () measures the maximum difference between the two ROI boundaries:
- Hausdorff distance () is a max-min distance between the point sets A and T defined by:where is called the directed Hausdorff distance and is the Euclidean distance ( norm) in .
4. Experimental Results
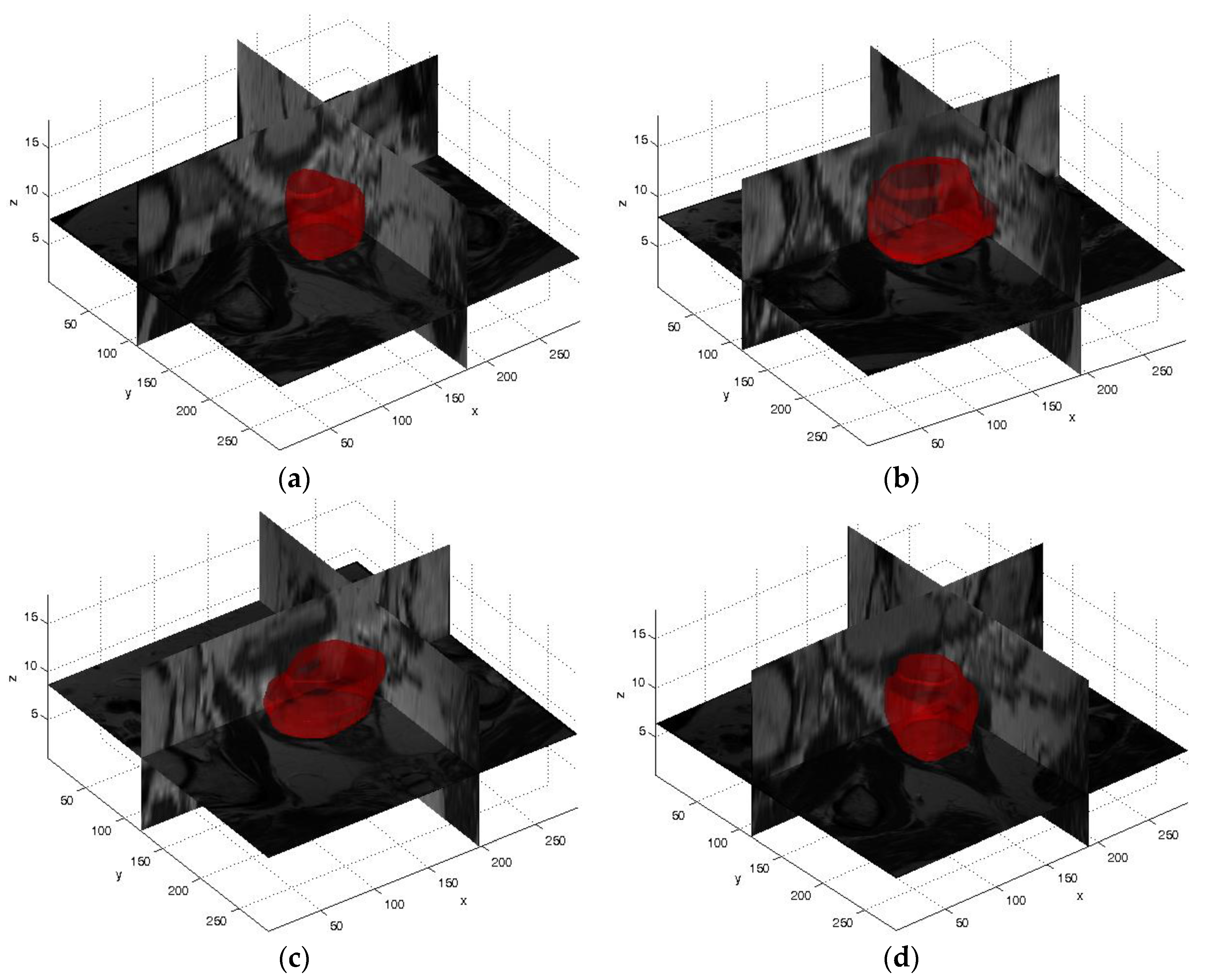
4.1. Volume Measurements and Volume-Based Metrics Prostate Segmentation Results
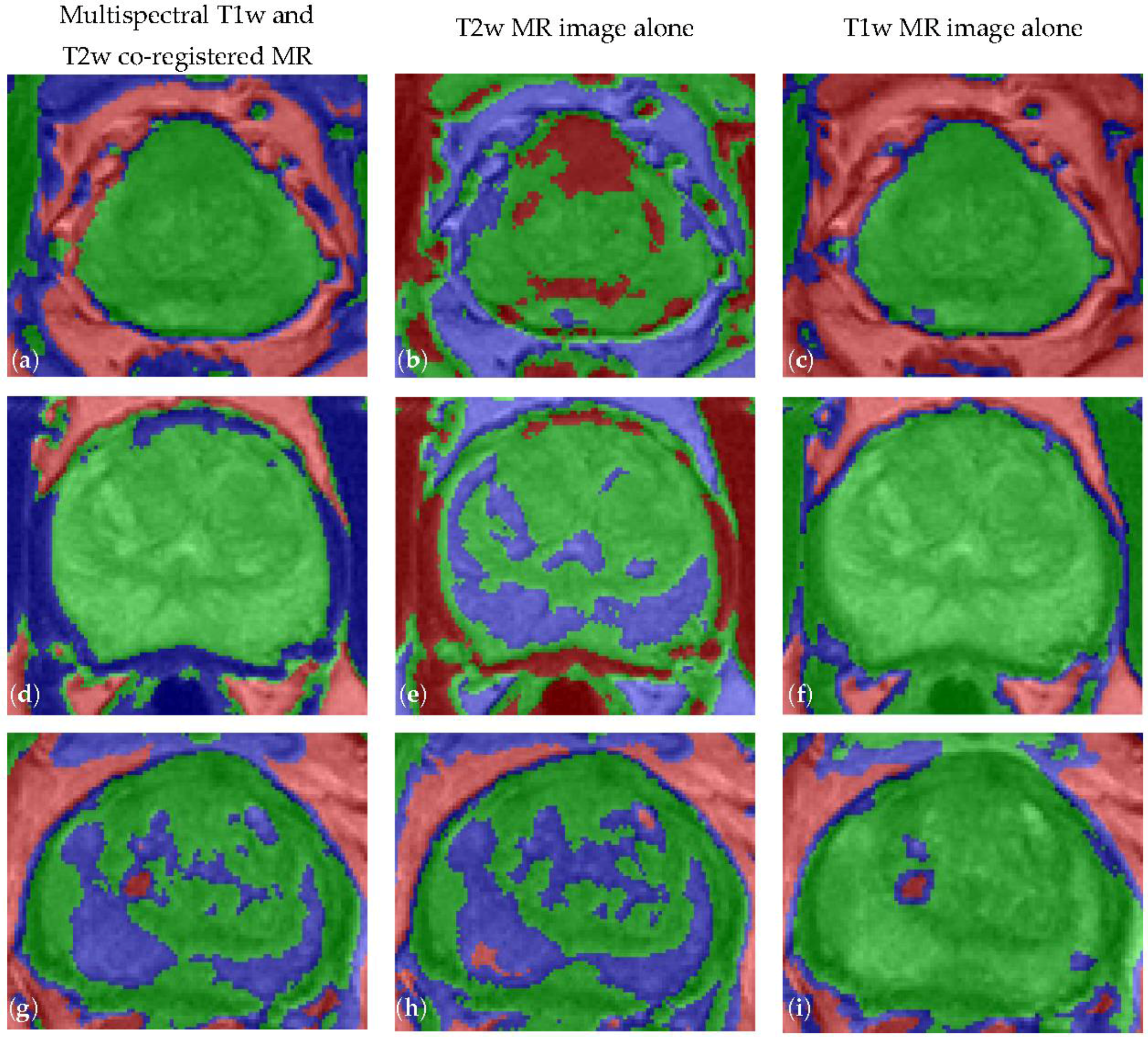
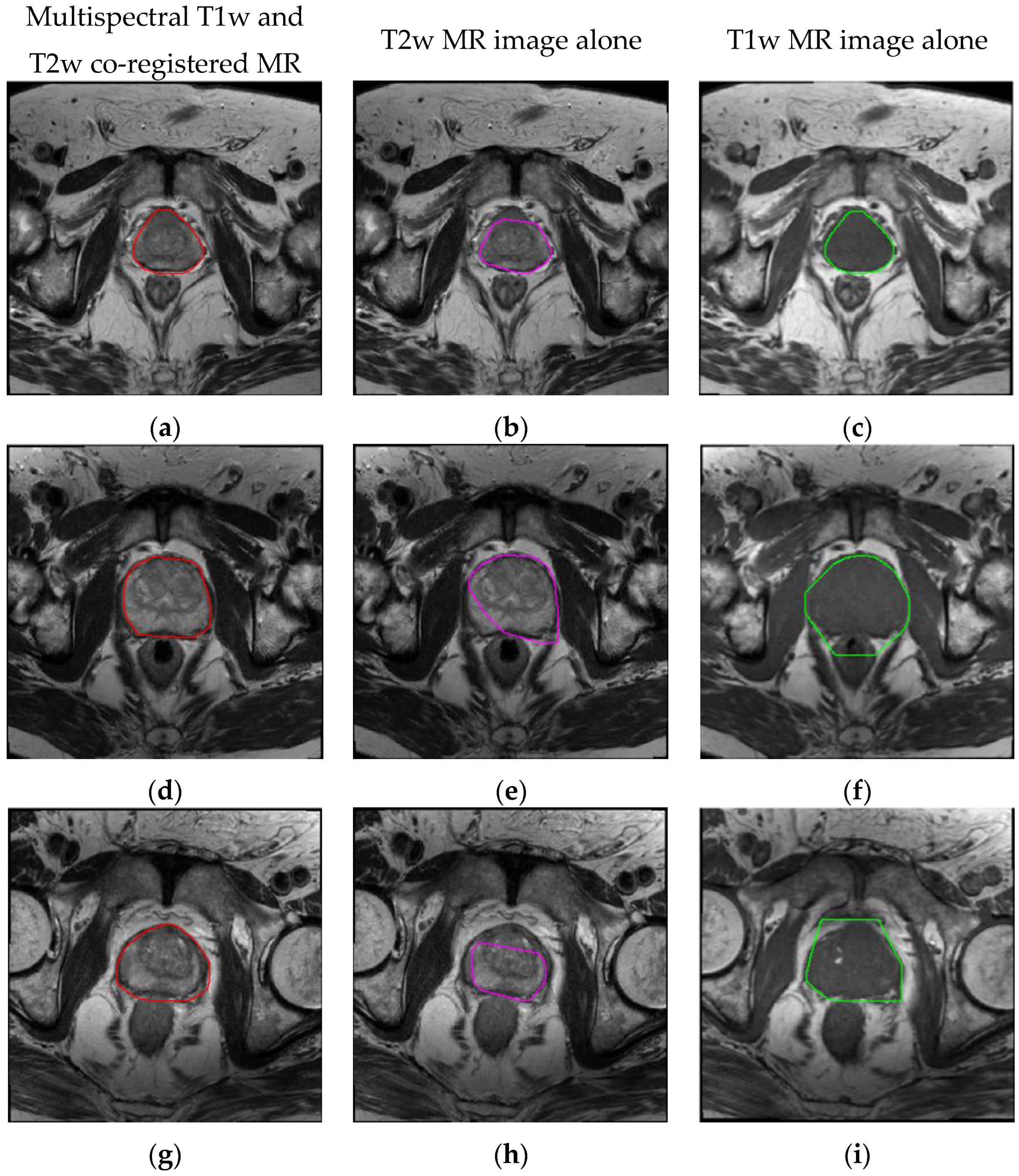
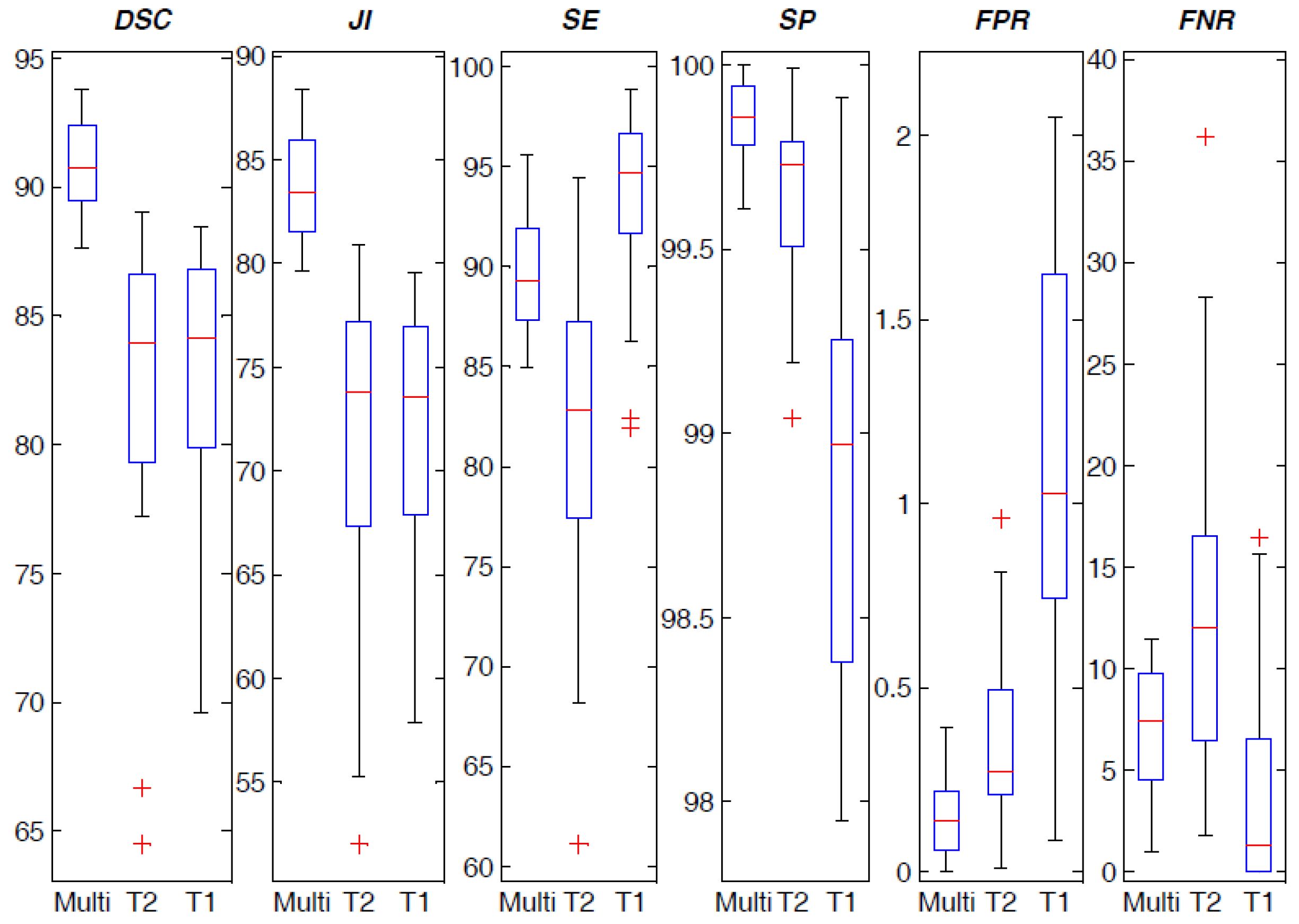
4.2. Spatial Overlap-based Metrics Prostate Segmentation Results
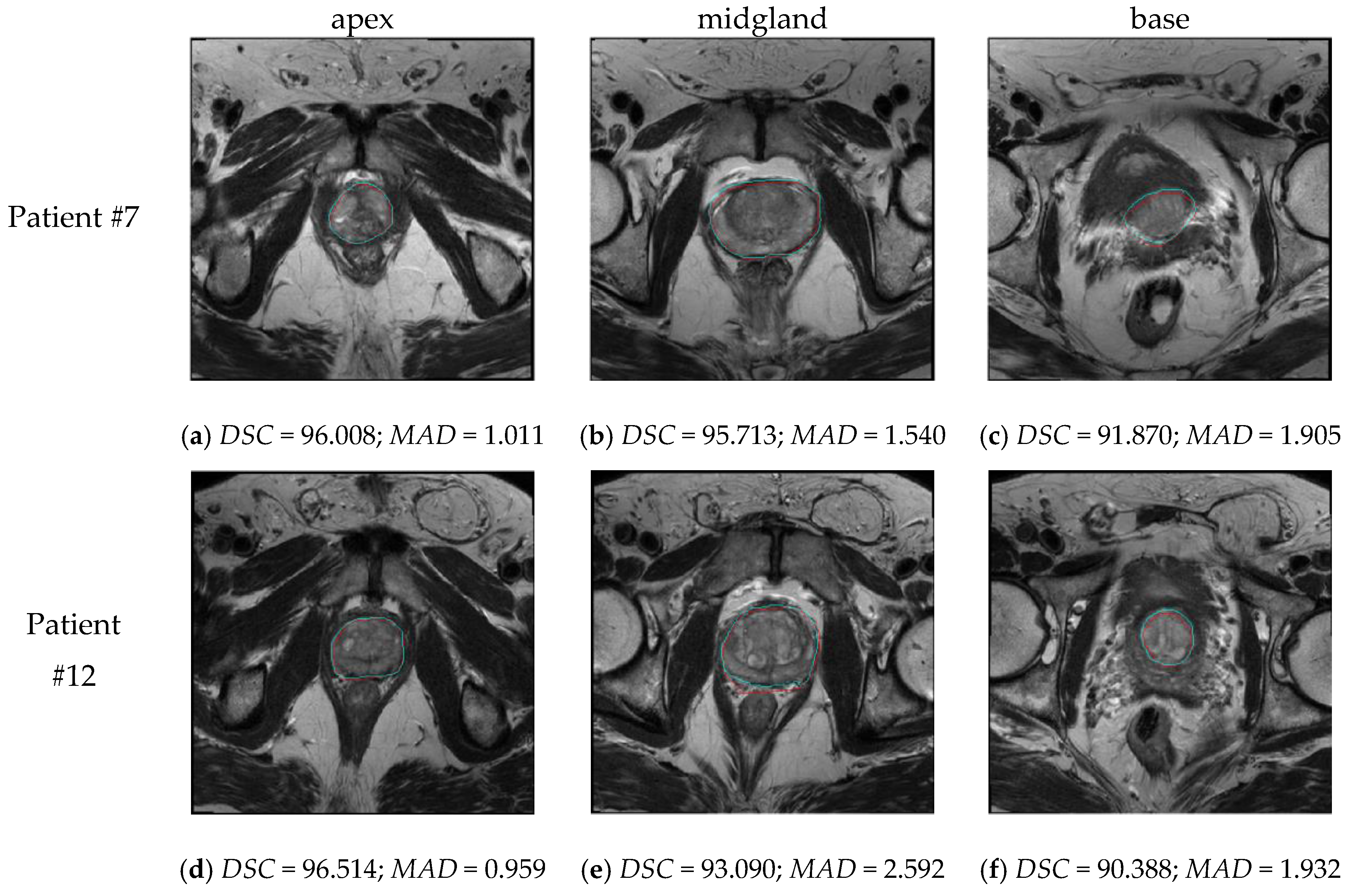
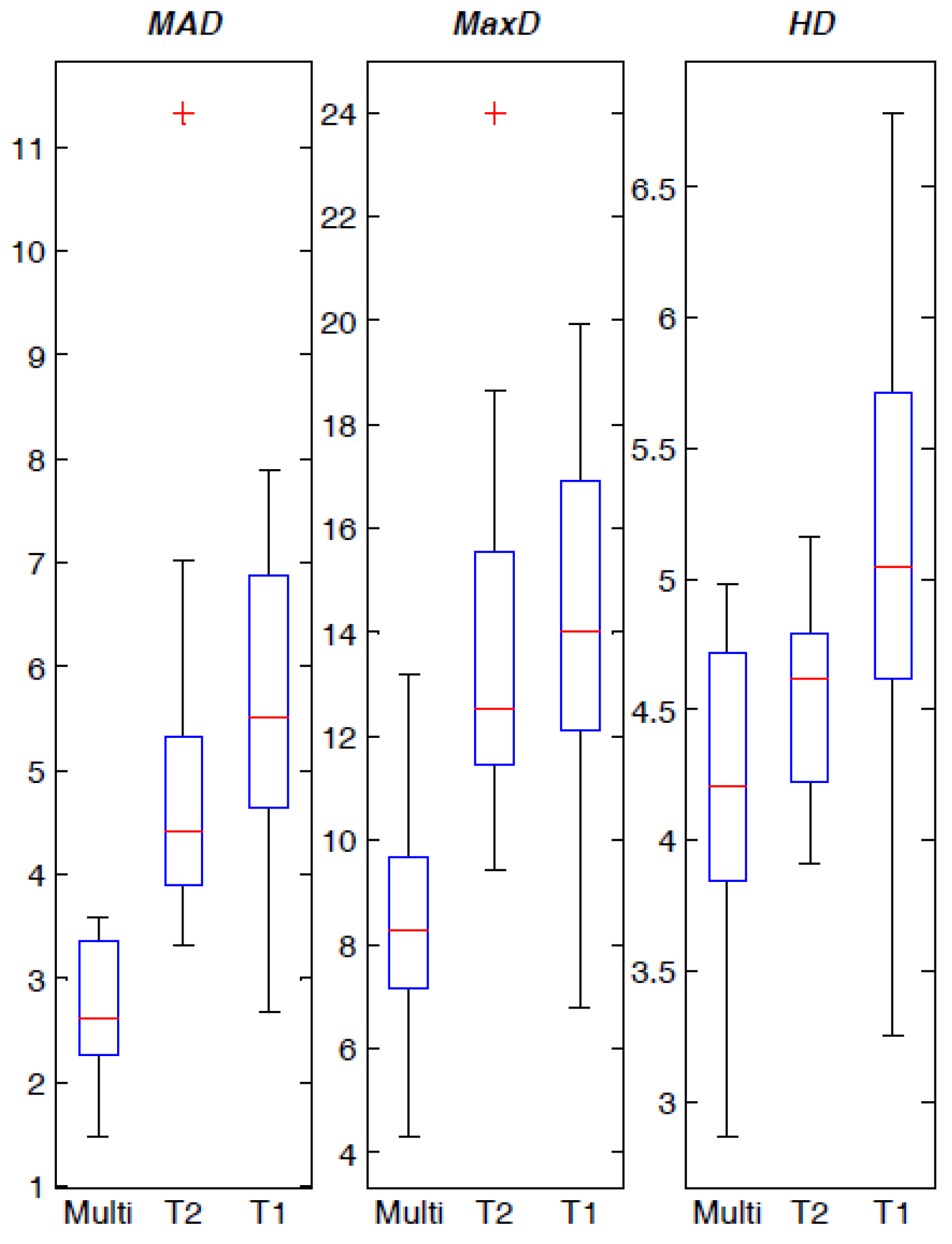
4.3. Spatial Distance-Based Metrics Prostate Segmentation Results
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- American Cancer Society, Cancer Facts and Figures 2016. Available online: http://www.cancer.org/acs/groups/content/@research/documents/document/acspc-047079.pdf (accessed on 23 January 2017).
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer statistics, 2016. CA Cancer J. Clin. 2016, 66, 7–30. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Langer, D.L.; Haider, M.A.; Yang, Y.; Wernick, M.N.; Yetik, I.S. Prostate cancer segmentation with simultaneous estimation of Markov random field parameters and class. IEEE Trans. Med. Imaging 2009, 28, 906–915. [Google Scholar] [CrossRef] [PubMed]
- Roethke, M.; Anastasiadis, A.G.; Lichy, M.; Werner, M.; Wagner, P.; Kruck, S.; Claussen, C.D.; Stenzl, A.; Schlemmer, H.P.; Schilling, D. MRI-guided prostate biopsy detects clinically significant cancer: Analysis of a cohort of 100 patients after previous negative TRUS biopsy. World J. Urol. 2012, 30, 213–218. [Google Scholar] [CrossRef] [PubMed]
- Heidenreich, A.; Aus, G.; Bolla, M.; Joniau, S.; Matveev, V.B.; Schmid, H.P.; Zattoni, F. EAU guidelines on prostate cancer. Eur. Urol. 2008, 53, 68–80. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, H.U.; Kirkham, A.; Arya, M.; Illing, R.; Freeman, A.; Allen, C.; Emberton, M. Is it time to consider a role for MRI before prostate biopsy? Nat. Rev. Clin. Oncol. 2009, 6, 197–206. [Google Scholar] [CrossRef] [PubMed]
- Klein, S.; van der Heide, U.A.; Lips, I.M.; van Vulpen, M.; Staring, M.; Pluim, J.P. Automatic segmentation of the prostate in 3D MR images by atlas matching using localized mutual information. Med. Phys. 2008, 35, 1407–1417. [Google Scholar] [CrossRef] [PubMed]
- Villeirs, G.M.; De Meerleer, G.O. Magnetic resonance imaging (MRI) anatomy of the prostate and application of MRI in radiotherapy planning. Eur. J. Radiol. 2007, 63, 361–368. [Google Scholar] [CrossRef] [PubMed]
- Hambrock, T.; Vos, P.C.; Hulsbergen-van de Kaa, C.A.; Barentsz, J.O.; Huisman, H.J. Prostate cancer: Computer-aided diagnosis with multiparametric 3-T MR imaging–effect on observer performance. Radiology 2013, 266, 521–530. [Google Scholar] [CrossRef] [PubMed]
- Ghose, S.; Oliver, A.; Martí, R.; Lladó, X.; Vilanova, J.C.; Freixenet, J.; Mitra, J.; Sidibé, D.; Meriaudeau, F. A survey of prostate segmentation methodologies in ultrasound, magnetic resonance and computed tomography images. Comput. Meth. Prog. Biomed. 2012, 108, 262–287. [Google Scholar] [CrossRef] [PubMed]
- Chilali, O.; Ouzzane, A.; Diaf, M.; Betrouni, N. A survey of prostate modeling for image analysis. Comput. Biol. Med. 2014, 53, 190–202. [Google Scholar] [CrossRef] [PubMed]
- Lemaître, G.; Martí, R.; Freixenet, J.; Vilanova, J.C.; Walker, P.M.; Meriaudeau, F. Computer-aided detection and diagnosis for prostate cancer based on mono and multi-parametric MRI: A review. Comput. Biol. Med. 2015, 60, 8–31. [Google Scholar] [CrossRef] [PubMed]
- Fabijańska, A. A novel approach for quantification of time-intensity curves in a DCE-MRI image series with an application to prostate cancer. Comput. Biol. Med. 2016, 73, 119–130. [Google Scholar] [CrossRef] [PubMed]
- Haider, M.A.; van der Kwast, T.H.; Tanguay, J.; Evans, A.J.; Hashmi, A.T.; Lockwood, G.; Trachtenberg, J. Combined T2-weighted and diffusion-weighted MRI for localization of prostate cancer. AJR Am. J. Roentgenol. 2007, 189, 323–328. [Google Scholar] [CrossRef] [PubMed]
- Matulewicz, L.; Jansen, J.F.; Bokacheva, L.; Vargas, H.A.; Akin, O.; Fine, S.W.; Shukla-Dave, A.; Eastham, J.A.; Hricak, H.; Koutcher, J.A.; et al. Anatomic segmentation improves prostate cancer detection with artificial neural networks analysis of 1H magnetic resonance spectroscopic imaging. J. Magn. Reson. Imaging 2014, 40, 1414–1421. [Google Scholar] [CrossRef] [PubMed]
- Fütterer, J.J.; Heijmink, S.W.; Scheenen, T.W.; Veltman, J.; Huisman, H.J.; Vos, P.; Hulsbergen-van de Kaa, A.C.; Witjes, J.A.; Krabbe, P.F.M.; Heerschap, A.; et al. Prostate cancer localization with dynamic contrast-enhanced MR imaging and proton MR spectroscopic imaging. Radiology 2006, 241, 449–458. [Google Scholar] [CrossRef] [PubMed]
- Rosenkrantz, A.B.; Lim, R.P.; Haghighi, M.; Somberg, M.B.; Babb, J.S.; Taneja, S.S. Comparison of interreader reproducibility of the prostate imaging reporting and data system and Likert scales for evaluation of multiparametric prostate MRI. AJR Am. J. Roentgenol. 2013, 201, W612–W618. [Google Scholar] [CrossRef] [PubMed]
- Toth, R.; Bloch, B.N.; Genega, E.M.; Rofsky, N.M.; Lenkinski, R.E.; Rosen, M.A.; Kalyanpur, A.; Pungavkar, S.; Madabhushi, A. Accurate prostate volume estimation using multifeature active shape models on T2-weighted MRI. Acad. Radiol. 2011, 18, 745–754. [Google Scholar] [CrossRef] [PubMed]
- Caivano, R.; Cirillo, P.; Balestra, A.; Lotumolo, A.; Fortunato, G.; Macarini, L.; Zandolino, A.; Vita, G.; Cammarota, A. Prostate cancer in magnetic resonance imaging: Diagnostic utilities of spectroscopic sequences. J. Med. Imaging Radiat. Oncol. 2012, 56, 606–616. [Google Scholar] [CrossRef] [PubMed]
- Rouvière, O.; Hartman, R.P.; Lyonnet, D. Prostate MR imaging at high-field strength: Evolution or revolution? Eur. Radiol. 2006, 16, 276–284. [Google Scholar] [CrossRef] [PubMed]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Choi, Y.J.; Kim, J.K.; Kim, N.; Kim, K.W.; Choi, E.K.; Cho, K.S. Functional MR imaging of prostate cancer. Radiographics 2007, 27, 63–75. [Google Scholar] [CrossRef] [PubMed]
- Studholme, C.; Drapaca, C.; Iordanova, B.; Cardenas, V. Deformation-based mapping of volume change from serial brain MRI in the presence of local tissue contrast change. IEEE Trans. Med. Imaging 2006, 25, 626–639. [Google Scholar] [CrossRef] [PubMed]
- Rueckert, D.; Sonoda, L.I.; Hayes, C.; Hill, D.L.; Leach, M.O.; Hawkes, D.J. Nonrigid registration using free-form deformations: Application to breast MR images. IEEE Trans. Med. Imaging 1999, 18, 712–721. [Google Scholar] [CrossRef] [PubMed]
- Warfield, S.K.; Zou, K.H.; Wells, W.M. Simultaneous truth and performance level estimation (STAPLE): An algorithm for the validation of image segmentation. IEEE Trans. Med. Imaging 2004, 23, 903–921. [Google Scholar] [CrossRef] [PubMed]
- Vincent, G.; Guillard, G.; Bowes, M. Fully automatic segmentation of the prostate using active appearance models. In Proceedings of the 15th International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI) Grand Challenge: Prostate MR Image Segmentation 2012, Nice, France, 1–5 October 2012; p. 7. [Google Scholar]
- Heimann, T.; Meinzer, H.P. Statistical shape models for 3D medical image segmentation: A review. Med. Image Anal. 2009, 13, 543–563. [Google Scholar] [CrossRef] [PubMed]
- Litjens, G.; Toth, R.; van de Ven, W.; Hoeks, C.; Kerkstra, S.; van Ginneken, B.; Vincent, G.; Guillard, G.; Birbeck, N.; Zhang, J.; et al. Evaluation of prostate segmentation algorithms for MRI: The PROMISE12 challenge. Med. Image Anal. 2014, 18, 359–373. [Google Scholar] [CrossRef] [PubMed]
- Cootes, T.F.; Twining, C.J.; Petrovic, V.S.; Schestowitz, R.; Taylor, C.J. Groupwise construction of appearance models using piece-wise affine deformations. In Proceedings of the 16th British Machine Vision Conference (BMVC), Oxford, UK, 5–8 September 2005; Clocksin, W.F., Fitzgibbon, A.W., Torr, P.H.S., Eds.; Volume 2, pp. 879–888. [Google Scholar]
- Gao, Y.; Sandhu, R.; Fichtinger, G.; Tannenbaum, A.R. A coupled global registration and segmentation framework with application to magnetic resonance prostate imagery. IEEE Trans. Med. Imaging 2010, 29, 1781–1794. [Google Scholar] [CrossRef] [PubMed]
- Sandhu, R.; Dambreville, S.; Tannenbaum, A. Particle filtering for registration of 2D and 3D point sets with stochastic dynamics. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2008), Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Tsai, A.; Yezzi, A.; Wells, W.; Tempany, C.; Tucker, D.; Fan, A.; Grimson, W.E.; Willsky, A. A shape-based approach to the segmentation of medical imagery using level sets. IEEE Trans. Med. Imaging 2003, 22, 137–154. [Google Scholar] [CrossRef] [PubMed]
- Chan, T.F.; Vese, L.A. Active contours without edges. IEEE Trans. Med. Imaging 2001, 10, 266–277. [Google Scholar] [CrossRef] [PubMed]
- Martin, S.; Daanen, V.; Troccaz, J. Atlas-based prostate segmentation using an hybrid registration. Int. J. Comput. Assist. Radiol. Surg. 2008, 3, 485–492. [Google Scholar] [CrossRef]
- Hellier, P.; Barillot, C. Coupling dense and landmark-based approaches for nonrigid registration. IEEE Trans. Med. Imaging 2003, 22, 217–227. [Google Scholar] [CrossRef] [PubMed]
- Rangarajan, A.; Chui, H.; Bookstein, F.L. The softassign procrustes matching algorithm. In Information Processing in Medical Imaging, Proceedings of the 15th International Conference, IPMI'97, Poultney, VT, USA, 9–13 June 1997; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1997; Volume 1230, pp. 29–42. [Google Scholar]
- Cootes, T.F.; Hill, A.; Taylor, C.J.; Haslam, J. Use of active shape models for locating structures in medical images. Image Vis. Comput. 1994, 12, 355–365. [Google Scholar] [CrossRef]
- Martin, S.; Troccaz, J.; Daanen, V. Automated segmentation of the prostate in 3D MR images using a probabilistic atlas and a spatially constrained deformable model. Med. Phys. 2010, 37, 1579–1590. [Google Scholar] [CrossRef] [PubMed]
- Cootes, T.F.; Taylor, C.J.; Cooper, D.H.; Graham, J. Active shape models-their training and application. Comput. Vis. Image Underst. 1995, 61, 38–59. [Google Scholar] [CrossRef]
- Toth, R.; Tiwari, P.; Rosen, M.; Reed, G.; Kurhanewicz, J.; Kalyanpur, A.; Pungavkar, S.; Madabhushi, A. A magnetic resonance spectroscopy driven initialization scheme for active shape model based prostate segmentation. Med. Image Anal. 2011, 15, 214–225. [Google Scholar] [CrossRef] [PubMed]
- Cosío, F.A. Automatic initialization of an active shape model of the prostate. Med. Image Anal. 2008, 12, 469–483. [Google Scholar] [CrossRef] [PubMed]
- Hricak, H.; Dooms, G.C.; McNeal, J.E.; Mark, A.S.; Marotti, M.; Avallone, A.; Pelzer, M.; Proctor, E.C.; Tanagho, E.A. MR imaging of the prostate gland: Normal anatomy. AJR Am. J. Roentgenol. 1987, 148, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Makni, N.; Iancu, A.; Colot, O.; Puech, P.; Mordon, S.; Betrouni, N. Zonal segmentation of prostate using multispectral magnetic resonance images. Med. Phys. 2011, 38, 6093–6105. [Google Scholar] [CrossRef] [PubMed]
- Masson, M.H.; Denœux, T. ECM: An evidential version of the fuzzy c-means algorithm. Pattern Recognit. 2008, 41, 1384–1397. [Google Scholar] [CrossRef]
- Litjens, G.; Debats, O.; van de Ven, W.; Karssemeijer, N.; Huisman, H. A pattern recognition approach to zonal segmentation of the prostate on MRI. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2012, Proceedings of the 15th International Conference on Medical Image Computing and Computer Assisted Intervention, Nice, France, 1–5 October 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 413–420. [Google Scholar]
- Huang, H.C.; Chuang, Y.Y.; Chen, C.S. Multiple Kernel Fuzzy Clustering. IEEE Trans. Fuzzy Syst. 2012, 20, 120–134. [Google Scholar] [CrossRef]
- Pasquier, D.; Lacornerie, T.; Vermandel, M.; Rousseau, J.; Lartigau, E.; Betrouni, N. Automatic segmentation of pelvic structures from magnetic resonance images for prostate cancer radiotherapy. Int. J. Radiat. Oncol. Biol. Phys. 2007, 68, 592–600. [Google Scholar] [CrossRef] [PubMed]
- Kurhanewicz, J.; Vigneron, D.; Carroll, P.; Coakley, F. Multiparametric magnetic resonance imaging in prostate cancer: Present and future. Curr. Opin. Urol. 2008, 18, 71–77. [Google Scholar] [CrossRef] [PubMed]
- Barentsz, J.O.; Weinreb, J.C.; Verma, S.; Thoeny, H.C.; Tempany, C.M.; Shtern, F.; Padhani, A.R.; Margolis, D.; Macura, K.J.; Haider, M.A.; et al. Synopsis of the PI-RADS v2 guidelines for multiparametric prostate magnetic resonance imaging and recommendations for use. Eur. Urol. 2016, 69, 41–49. [Google Scholar] [CrossRef] [PubMed]
- Lagendijk, J.J.W.; Raaymakers, B.W.; Van den Berg, C.A.T.; Moerland, M.A.; Philippens, M.E.; van Vulpen, M. MR guidance in radiotherapy. Phys. Med. Biol. 2014, 59, R349–R369. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Abdelnour-Nocera, J.; Wells, S.; Pan, N. Usability practice in medical imaging application development. In HCI and Usability for e-Inclusion; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5889, pp. 405–415. [Google Scholar]
- Boykov, Y.Y.; Jolly, M.P. Interactive graph cuts for optimal boundary & region segmentation of objects in N-D images. In Proceedings of the Eighth IEEE International Conference on Computer Vision (ICCV), Vancouver, BC, Canada, 7–14 July 2001; Volume 1, pp. 105–112. [Google Scholar]
- Boykov, Y.Y.; Jolly, M.P. Interactive organ segmentation using graph cuts. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2000, Proceedings of the Third International Conference on Medical Image Computing and Computer Assisted Intervention, Pittsburgh, PA, USA, 11–14 October 2000; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1935, pp. 276–286. [Google Scholar]
- Pluim, J.P.W.; Maintz, J.B.A.; Viergever, M.A. Mutual-information-based registration of medical images: A survey. IEEE Trans. Med. Imaging 2003, 22, 986–1004. [Google Scholar] [CrossRef] [PubMed]
- Mattes, D.; Haynor, D.R.; Vesselle, H.; Lewellen, T.; Eubank, W. Non-rigid multimodality image registration. In Medical Imaging 2001: Image Processing, Proceedings of the SPIE 4322, San Diego, CA, USA, 17 February 2001; SPIE: Bellingham, WA, USA, 2001; pp. 1609–1620. [Google Scholar]
- Styner, M.; Brechbuhler, C.; Szckely, G.; Gerig, G. Parametric estimate of intensity inhomogeneities applied to MRI. IEEE Trans. Med. Imaging 2000, 19, 153–165. [Google Scholar] [CrossRef] [PubMed]
- Rundo, L.; Tangherloni, A.; Militello, C.; Gilardi, M.C.; Mauri, G. Multimodal medical image registration using particle swarm optimization: A review. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence (IEEE SSCI 2016)—Swarm Intelligence Symposium (SIS), Athens, Greece, 6–9 December 2016; pp. 1–8. [Google Scholar]
- Czerwinski, R.N.; Jones, D.L.; O’Brien, W.D. Line and boundary detection in speckle images. IEEE Trans. Image Process. 1998, 7, 1700–1714. [Google Scholar] [CrossRef] [PubMed]
- Czerwinski, R.N.; Jones, D.L.; O’Brien, W.D. Detection of lines and boundaries in speckle images-application to medical ultrasound. IEEE Trans. Med. Imaging 1999, 18, 126–136. [Google Scholar] [CrossRef] [PubMed]
- Edelstein, W.A.; Glover, G.H.; Hardy, C.J.; Redington, R.W. The intrinsic signal-to-noise ratio in NMR imaging. Magn. Reson. Med. 1986, 3, 604–618. [Google Scholar] [CrossRef] [PubMed]
- Macovski, A. Noise in MRI. Magn. Reson. Med. 1996, 36, 494–497. [Google Scholar] [CrossRef] [PubMed]
- Pizurica, A.; Wink, A.M.; Vansteenkiste, E.; Philips, W.; Roerdink, B.J. A review of wavelet denoising in MRI and ultrasound brain imaging. Curr. Med. Imaging Rev. 2006, 2, 247–260. [Google Scholar] [CrossRef]
- Papoulis, A.; Pillai, S.U. Probability, Random Variables and Stochastic Processes, 4th ed.; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Xiao, C.Y.; Zhang, S.; Cheng, S.; Chen, Y.Z. A novel method for speckle reduction and edge enhancement in ultrasonic images. In Electronic Imaging and Multimedia Technology IV, Proceedings of the SPIE 5637, Beijing, China, 8 November 2004; SPIE: Bellingham, WA, USA, 2005. [Google Scholar]
- Firbank, M.J.; Coulthard, A.; Harrison, R.M.; Williams, E.D. A comparison of two methods for measuring the signal to noise ratio on MR images. Phys. Med. Biol. 1999, 44. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics), 1st ed.; Springer: Secaucus, NJ, USA, 2006. [Google Scholar]
- Wang, S.; Summers, R.M. Machine learning and radiology. Med. Image Anal. 2012, 16, 933–951. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Xue, S.; Zhang, X.; Han, Y. A neural network-based interval pattern matcher. Information 2015, 6, 388–398. [Google Scholar] [CrossRef]
- Militello, C.; Vitabile, S.; Rundo, L.; Russo, G.; Midiri, M.; Gilardi, M.C. A fully automatic 2d segmentation method for uterine fibroid in MRgFUS treatment evaluation. Comput. Biol. Med. 2015, 62, 277–292. [Google Scholar] [CrossRef] [PubMed]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.; Wu, A.Y. An efficient k-means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 881–892. [Google Scholar] [CrossRef]
- Zhang, D.Q.; Chen, S.C. A novel kernelized fuzzy c-means algorithm with application in medical image segmentation. Artif. Intell. Med. 2004, 32, 37–50. [Google Scholar] [CrossRef] [PubMed]
- Soille, P. Morphological Image Analysis: Principles and Applications, 2nd ed.; Springer: Secaucus, NJ, USA, 2003. [Google Scholar]
- Breen, E.J.; Jones, R.; Talbot, H. Mathematical morphology: A useful set of tools for image analysis. Stat. Comput. 2000, 10, 105–120. [Google Scholar] [CrossRef]
- Zimmer, Y.; Tepper, R.; Akselrod, S. An improved method to compute the convex hull of a shape in a binary image. Pattern Recognit. 1997, 30, 397–402. [Google Scholar] [CrossRef]
- Taha, A.A.; Hanbury, A. Metrics for evaluating 3D medical image segmentation: Analysis, selection, and tool. BMC Med. Imaging 2015, 15, 1–28. [Google Scholar] [CrossRef] [PubMed]
- Fenster, A.; Chiu, B. Evaluation of segmentation algorithms for medical imaging. In Proceedings of the 27th Annual International Conference of the Engineering in Medicine and Biology Society, Shanghai, China, 1–4 September 2005; pp. 7186–7189. [Google Scholar]
- Zhang, Y.J. A review of recent evaluation methods for image segmentation. In Proceedings of the Sixth IEEE International Symposium on Signal Processing and Its Applications (ISSPA), Kuala Lumpur, Malaysia, 13–16 August 2001; Volume 1, pp. 148–151. [Google Scholar]
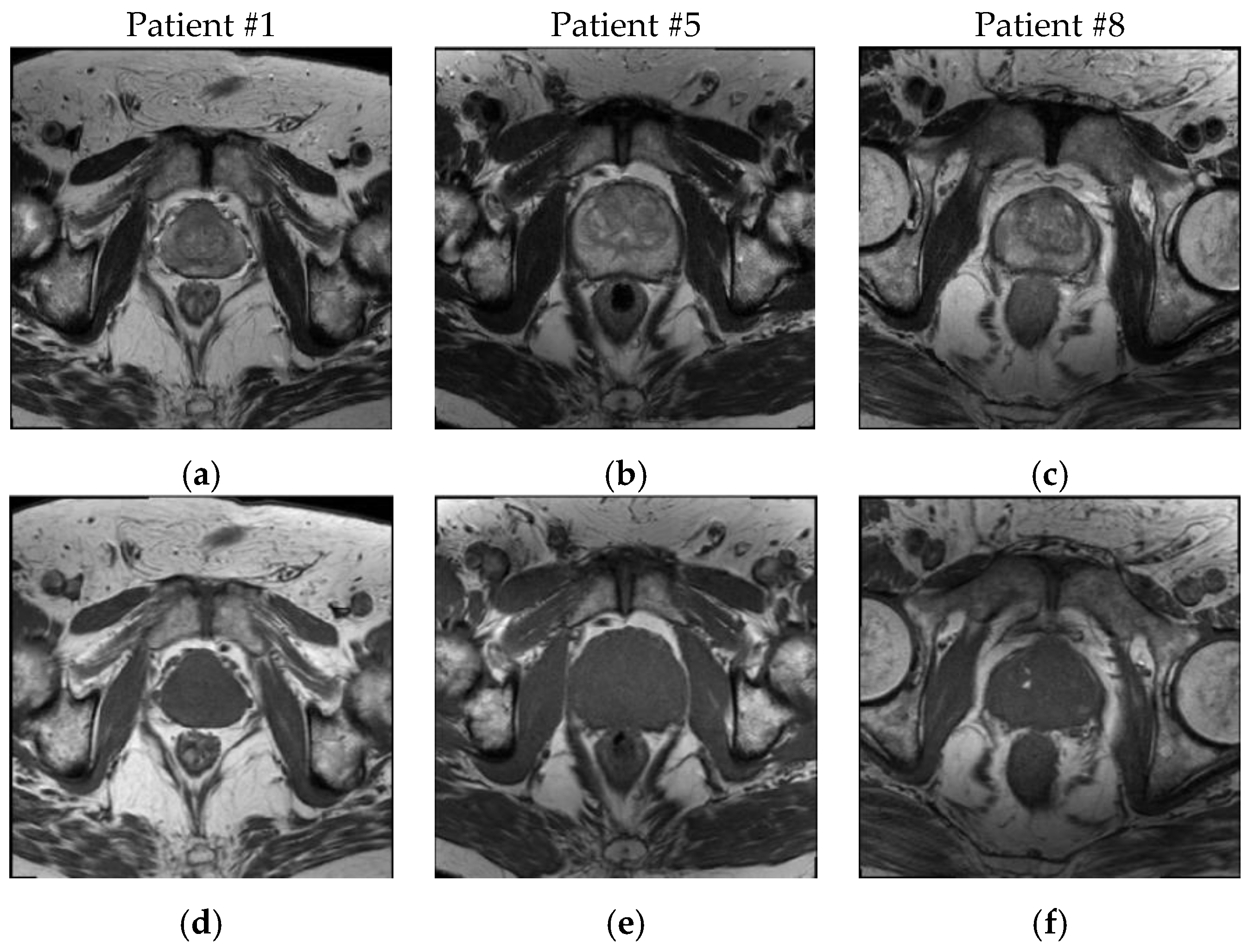
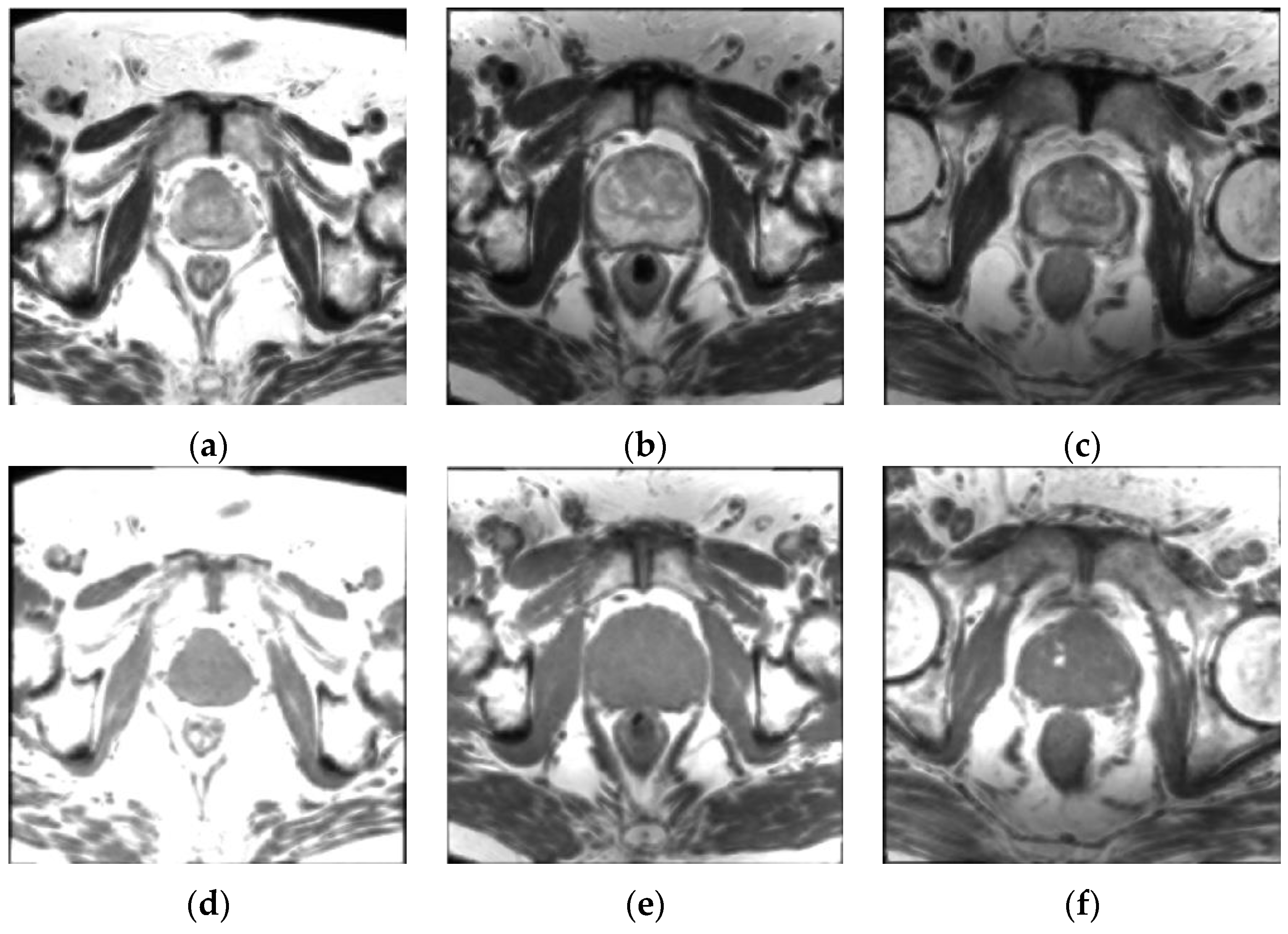
| MRI Sequence | TR (ms) | TE (ms) | Matrix Size (pixels) | Pixel Spacing (mm) | Slice Thickness (mm) | Interslice Spacing (mm) | Slice Number |
|---|---|---|---|---|---|---|---|
| T1w | 515.3 | 10 | 256 × 256 | 0.703 | 3 | 4 | 18 |
| T2w | 3035.6 | 80 | 288 × 288 | 0.625 | 3 | 4 | 18 |
| MRI Sequence | Original | Stick Filtering | 3 × 3 Gaussian Filter | 5 × 5 Gaussian Filter | 3 × 3 Average Filter | 5 × 5 Average Filter |
|---|---|---|---|---|---|---|
| T1w | 4.2133 | 5.2598 | 4.4069 | 4.4081 | 4.7523 | 4.9061 |
| T2w | 3.7856 | 5.0183 | 4.0032 | 4.0044 | 4.3479 | 4.8739 |
| Patient | Automatic Volume Measurement (cm3) | Manual Volume Measurement (cm3) | AVD (cm3) | VS (%) |
|---|---|---|---|---|
| #1 | 22.713 | 23.673 | 4.06 | 97.93 |
| #2 | 46.420 | 51.608 | 10.05 | 94.71 |
| #3 | 52.644 | 47.888 | 9.93 | 95.27 |
| #4 | 37.552 | 35.898 | 4.61 | 97.75 |
| #5 | 63.261 | 64.045 | 1.22 | 99.38 |
| #6 | 37.586 | 35.323 | 6.41 | 96.90 |
| #7 | 47.077 | 49.133 | 4.18 | 97.86 |
| #8 | 33.533 | 35.469 | 5.46 | 97.19 |
| #9 | 20.683 | 23.231 | 10.97 | 94.20 |
| #10 | 40.602 | 42.688 | 4.89 | 97.50 |
| #11 | 36.209 | 34.895 | 3.77 | 98.15 |
| #12 | 44.398 | 49.336 | 10.01 | 94.73 |
| #13 | 39.427 | 41.355 | 4.66 | 97.61 |
| #14 | 91.419 | 100.111 | 8.68 | 95.46 |
| #15 | 75.225 | 74.678 | 0.73 | 99.64 |
| #16 | 23.852 | 23.714 | 0.58 | 99.71 |
| #17 | 47.755 | 51.667 | 7.57 | 96.07 |
| #18 | 49.738 | 51.545 | 3.51 | 98.22 |
| #19 | 85.152 | 89.584 | 4.95 | 97.46 |
| #20 | 55.416 | 57.603 | 3.80 | 98.06 |
| #21 | 45.941 | 49.533 | 7.25 | 96.24 |
| Average | 47.46 | 49.19 | 5.59 | 97.14 |
| Stand. Dev. | 18.70 | 20.03 | 3.08 | 1.61 |
| MRI Data | DSC | JI | Sensitivity | Specificity | FPR | FNR |
|---|---|---|---|---|---|---|
| Multispectral | 90.77 ± 1.75 | 83.63 ± 2.65 | 89.56 ± 3.02 | 99.85 ± 0.11 | 0.15 ± 0.11 | 6.89 ± 3.02 |
| T2w alone | 81.90 ± 6.49 | 71.39 ± 7.56 | 82.21 ± 8.28 | 99.63 ± 0.25 | 0.37 ± 0.25 | 12.58 ± 8.49 |
| T1w alone | 82.55 ± 4.93 | 71.78 ± 6.15 | 93.27 ± 4.87 | 98.85 ± 0.58 | 1.15 ± 0.58 | 3.58 ± 4.95 |
| MRI Data | MAD (pixels) | MaxD (pixels) | HD (pixels) |
|---|---|---|---|
| Multispectral | 2.676 ± 0.616 | 8.485 ± 2.091 | 4.259 ± 0.548 |
| T2w alone | 4.941 ± 1.780 | 13.779 ± 3.430 | 4.535 ± 0.335 |
| T1w alone | 5.566 ± 1.618 | 14.358 ± 3.722 | 5.177 ± 0.857 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rundo, L.; Militello, C.; Russo, G.; Garufi, A.; Vitabile, S.; Gilardi, M.C.; Mauri, G. Automated Prostate Gland Segmentation Based on an Unsupervised Fuzzy C-Means Clustering Technique Using Multispectral T1w and T2w MR Imaging. Information 2017, 8, 49. https://doi.org/10.3390/info8020049
Rundo L, Militello C, Russo G, Garufi A, Vitabile S, Gilardi MC, Mauri G. Automated Prostate Gland Segmentation Based on an Unsupervised Fuzzy C-Means Clustering Technique Using Multispectral T1w and T2w MR Imaging. Information. 2017; 8(2):49. https://doi.org/10.3390/info8020049
Chicago/Turabian StyleRundo, Leonardo, Carmelo Militello, Giorgio Russo, Antonio Garufi, Salvatore Vitabile, Maria Carla Gilardi, and Giancarlo Mauri. 2017. "Automated Prostate Gland Segmentation Based on an Unsupervised Fuzzy C-Means Clustering Technique Using Multispectral T1w and T2w MR Imaging" Information 8, no. 2: 49. https://doi.org/10.3390/info8020049
APA StyleRundo, L., Militello, C., Russo, G., Garufi, A., Vitabile, S., Gilardi, M. C., & Mauri, G. (2017). Automated Prostate Gland Segmentation Based on an Unsupervised Fuzzy C-Means Clustering Technique Using Multispectral T1w and T2w MR Imaging. Information, 8(2), 49. https://doi.org/10.3390/info8020049









