Aesthetic Local Search of Wind Farm Layouts
Abstract
:1. Introduction
2. Technical Background
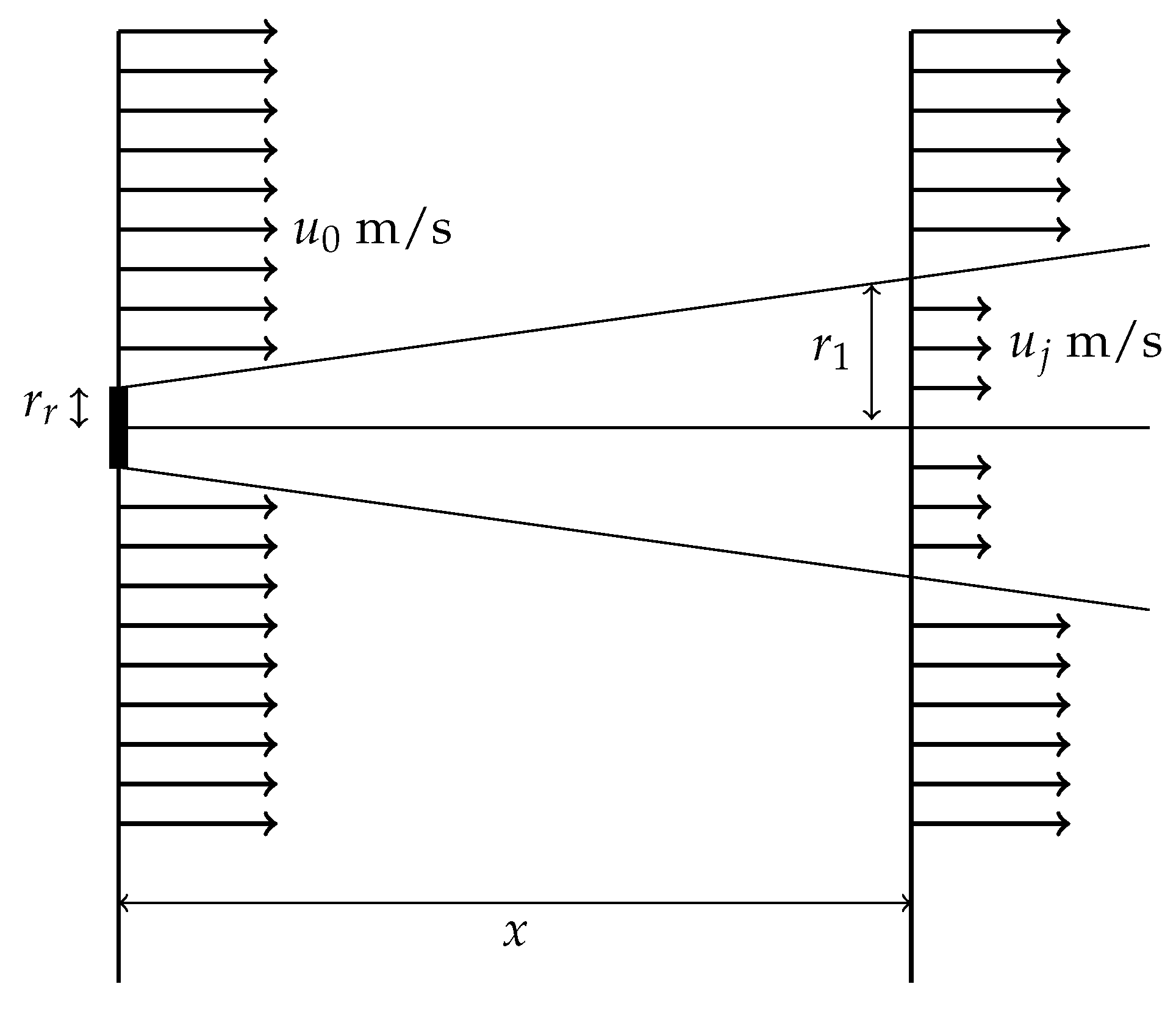
2.1. Jensen Wake Model
2.2. Objective Function
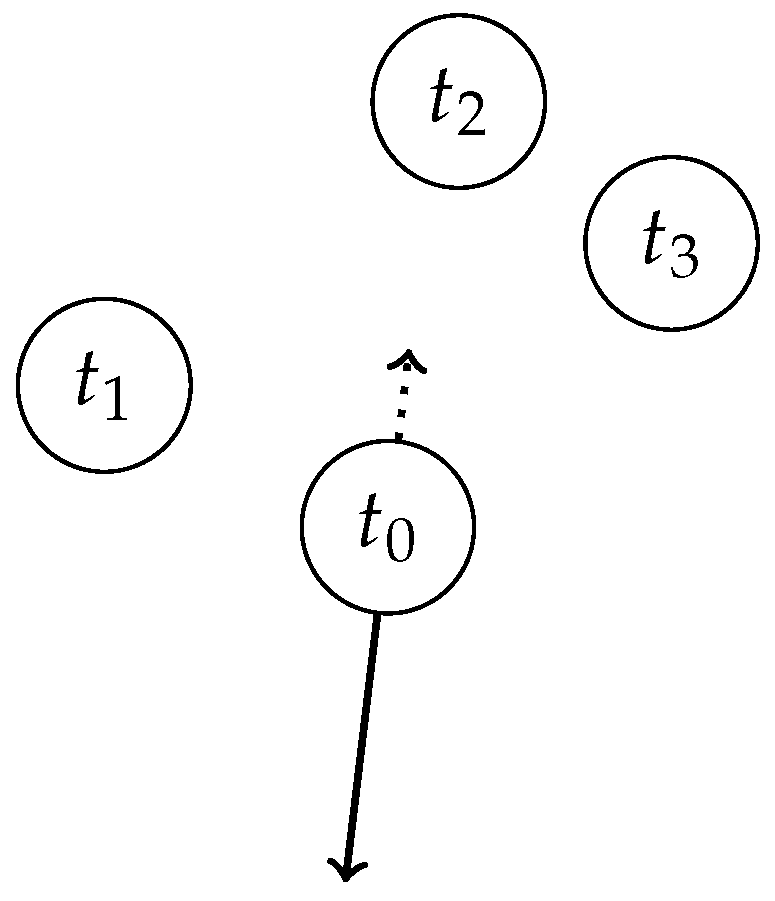
2.3. Turbine Displacement Algorithm
2.4. BlockCopy Local Search Algorithm
2.5. Harmony Pattern Metric
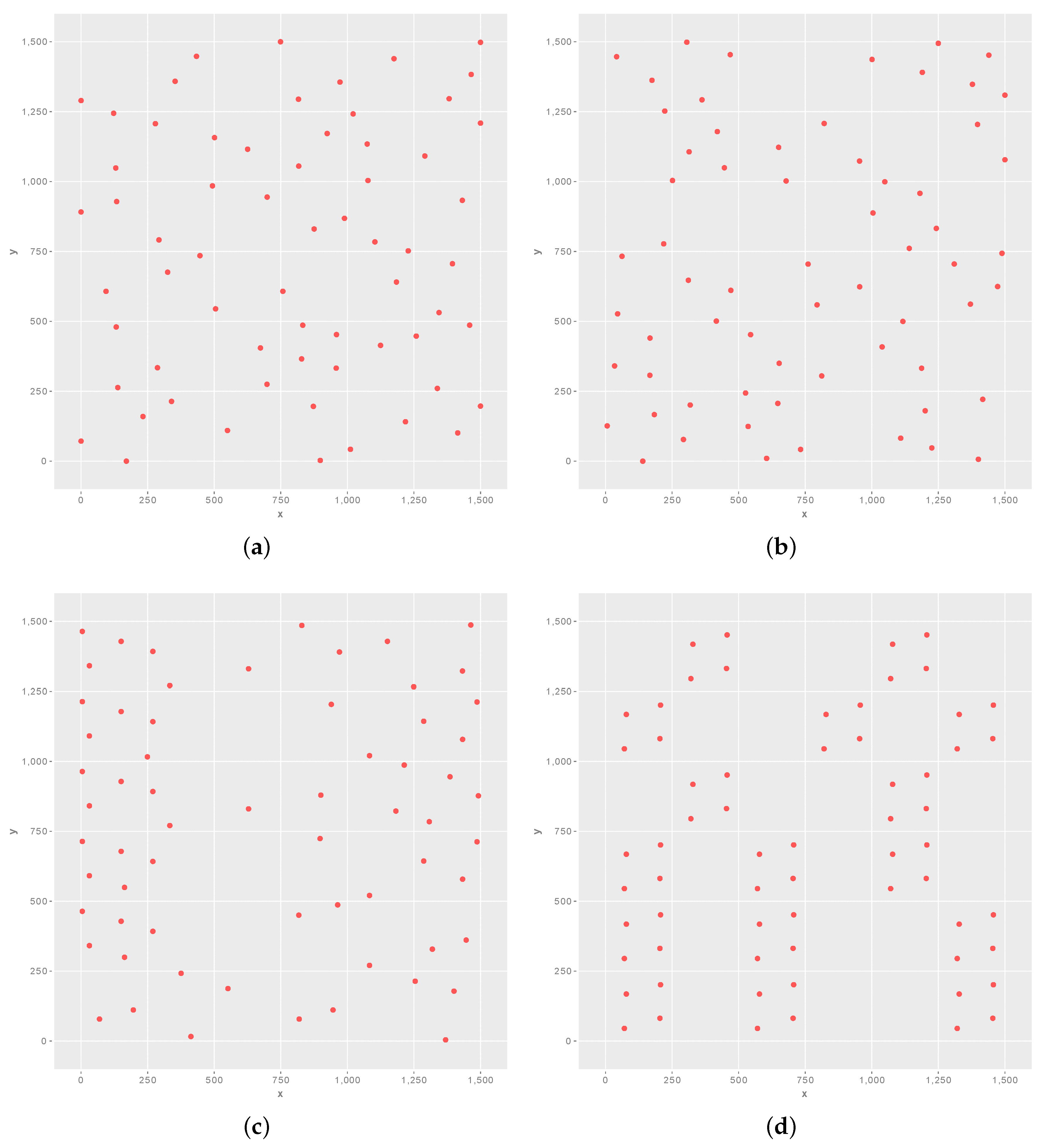
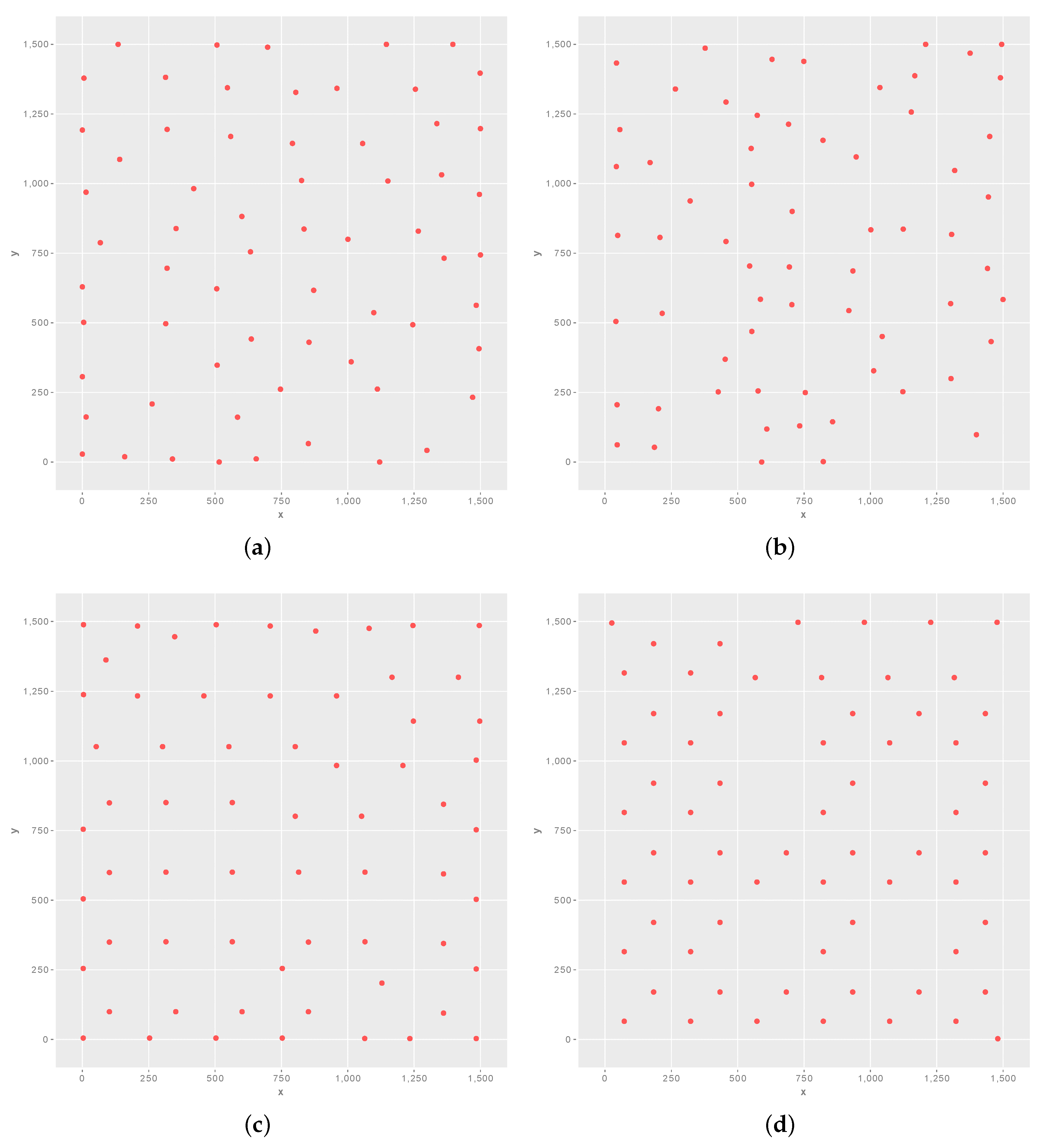
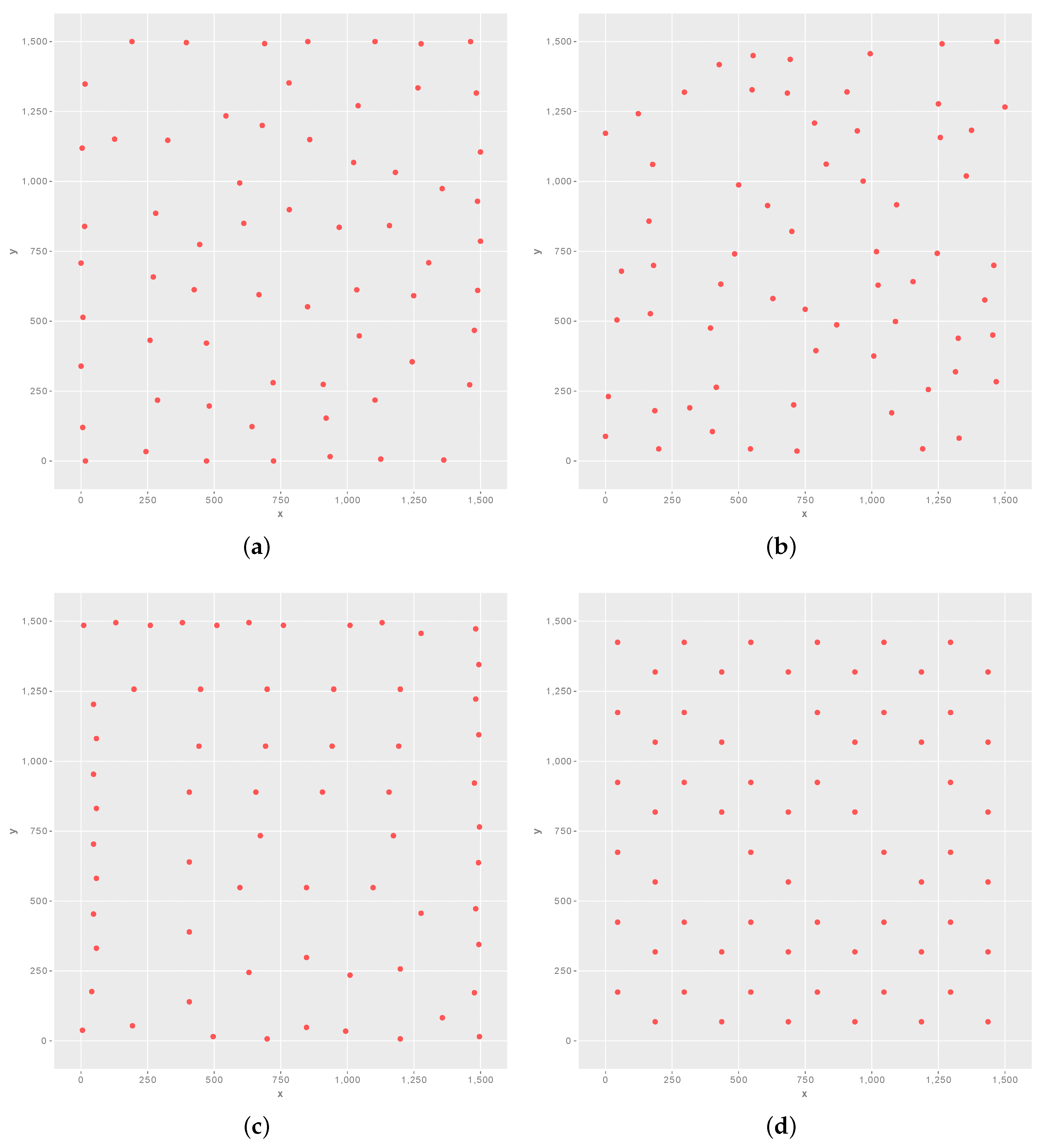
3. Optimising Wind Farm Layouts for Both Energy Efficiency and Harmony
4. Experiments
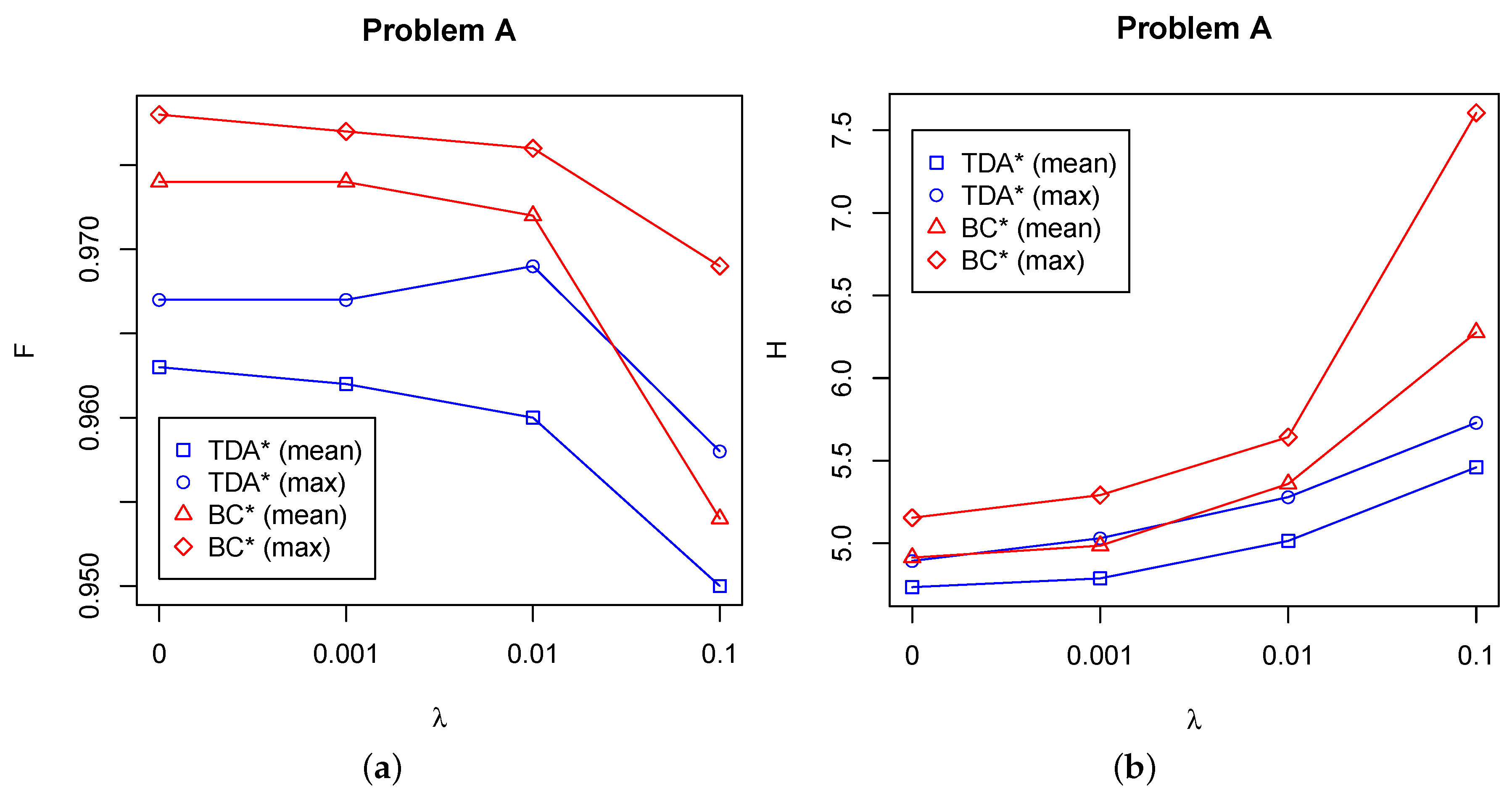
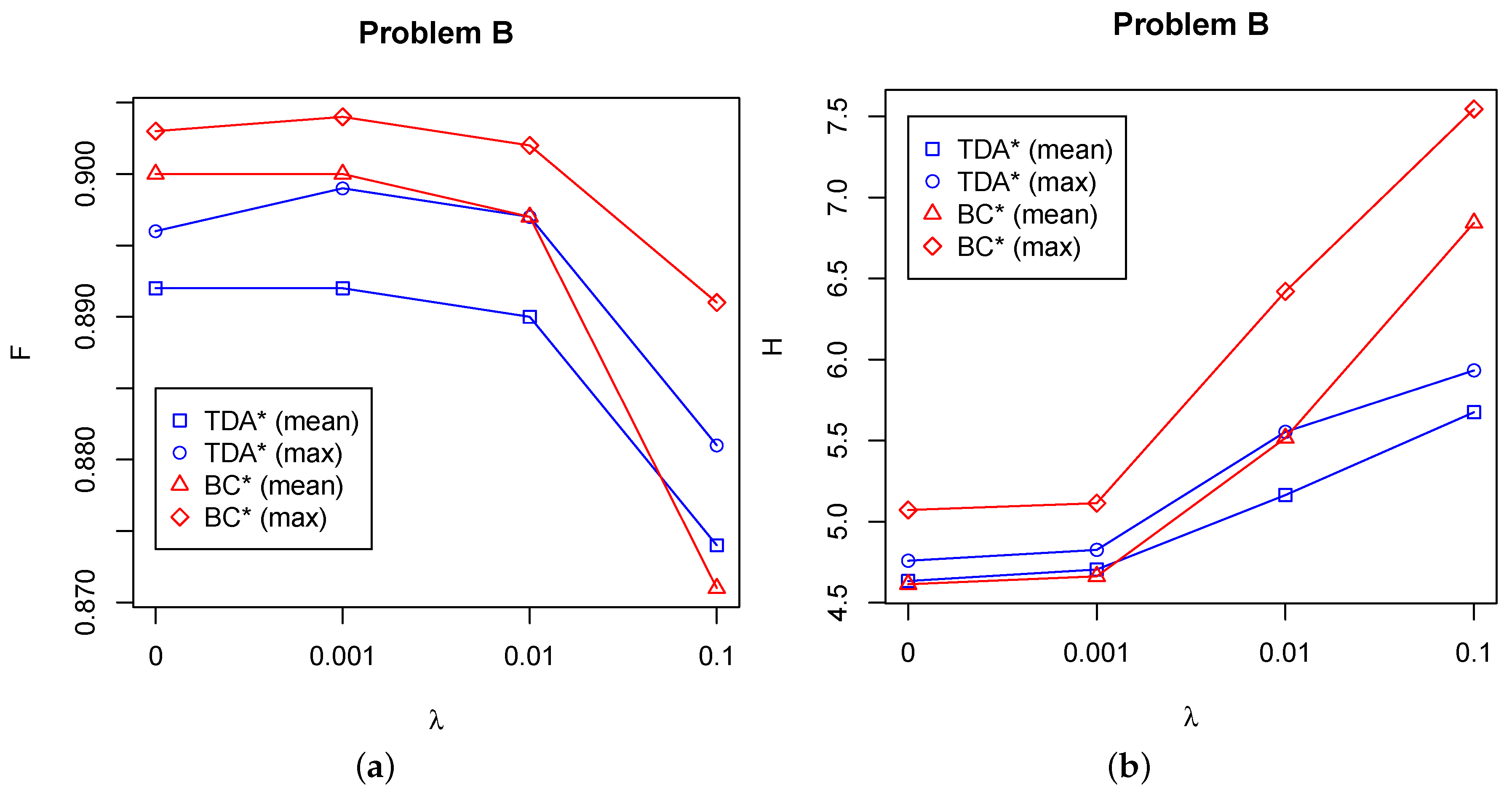
5. Results
- {(TDA, ), (TDA, ), (TDA, )}
- {(BC, ), (BC, ), (BC, )}
- {(TD, ), (BC, )} (Problem B only)
- {(BC, ), (BC, ), (TDA, )}
- {(TDA, ), (TDA, ), (BC, )}
- {(TDA, ), (BC, ), (TDA, )}
- {(TDA, )}
- {(BC, )}
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Global Wind Energy Council. Global Wind Energy Outlook 2014; Global Wind Energy Council: Brussels, Belgium, 2014. [Google Scholar]
- London Array Brochure. Online PDF Brochure. Available online: http://www.londonarray.com/wp-content/uploads/London-Array-Brochure.pdf (accessed on 9 November 2015).
- Watts, J. Winds of Change Blow through China as Spending on Renewable Energy Soars. The Guardian. 2012. Available online: http://www.theguardian.com/world/2012/mar/19/china-windfarms-renewable-energy (accessed on 23 March 2017).
- Dai, K.; Bergot, A.; Liang, C.; Xiang, W.N.; Huang, Z. Environmental issues associated with wind energy—A review. Renew. Energy 2015, 75, 911–921. [Google Scholar] [CrossRef]
- Piorkowski, M.D.; Farnsworth, A.J.; Fry, M.; Rohrbaugh, R.W.; Fitzpatrick, J.W.; Rosenberg, K.V. Research priorities for wind energy and migratory wildlife. J. Wildl. Manag. 2012, 76, 451–456. [Google Scholar] [CrossRef]
- Tabassum-Abbasi; Premalatha, M.; Abbasi, T.; Abbasi, S. Wind energy: Increasing deployment, rising environmental concerns. Renew. Sustain. Energy Rev. 2014, 31, 270–288. [Google Scholar]
- Tsoutsos, T.; Gouskos, Z.; Karterakis, S.; Peroulaki, E. Aesthetic Impact from Wind Parks; Technical Report; Technical University of Crete: Chania, Greece, 2006. [Google Scholar]
- Mosetti, G.; Poloni, C.; Diviacco, B. Optimization of wind turbine positioning in large wind farms by means of a genetic algorithm. J. Wind Eng. Ind. Aerodyn. 1994, 51, 105–116. [Google Scholar] [CrossRef]
- Wagner, M.; Day, J.; Neumann, F. A fast and effective local search algorithm for optimizing the placement of wind turbines. Renew. Energy 2013, 51, 64–70. [Google Scholar] [CrossRef]
- Rodrigues, S.M.F.; Bauer, P.; Pierik, J. Modular Approach for the Optimal Wind Turbine Micro Siting Problem Through CMA-ES Algorithm. In Proceedings of the 15th Annual Conference Companion on Genetic and Evolutionary Computation, Amsterdam, The Netherlands, 6–10 July 2013; pp. 1561–1568. [Google Scholar]
- Guirguis, D.; Romero, D.A.; Amon, C.H. Toward efficient optimization of wind farm layouts: Utilizing exact gradient information. Appl. Energy 2016, 179, 110–123. [Google Scholar] [CrossRef]
- Mayo, M.; Zhen, C. BlockCopy-based operators for evolving efficient wind farm layouts. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation, Vancouver, BC, Canada, 24–29 July 2016; pp. 1085–1092. [Google Scholar]
- Mayo, M.; Daoud, M. Informed mutation of wind farm layouts to maximise energy harvest. Renew. Energy 2016, 89, 437–448. [Google Scholar] [CrossRef]
- Neubert, A.; Shah, A.; Schlez, W. Maximum Yield from Symmetrical Wind Farm Layouts. In Proceedings of the 10th German Wind Energy Conference, DEWEK, Bremen, Germany, 17–18 November 2010. [Google Scholar]
- Al-Yahyai, S.; Charabi, Y.; Gastli, A. Geometrical approach for wind farm symmetrical layout design optimization. In Proceedings of the 2015 IEEE 8th GCC Conference and Exhibition (GCCCE), Muscat, Oman, 1–4 February 2015; pp. 1–6. [Google Scholar]
- Mayo, M.; Daoud, M.; Zheng, C. Randomising block sizes for BlockCopy-based wind farm layout optimisation. In Proceedings of the 20th Asia Pacific Symposium on Intelligent and Evolutionary Systems, Canberra, Australia, 16–18 November 2016; pp. 277–289. [Google Scholar]
- Salingaros, N. Life and complexity in architecture from a thermodynamic analogy. Phys. Essays 1997, 10. [Google Scholar] [CrossRef]
- Klinger, A.; Salingaros, N. A pattern measure. Environ. Plan. B Plan. Des. 2000, 27, 537–547. [Google Scholar] [CrossRef]
- Jensen, N. A Note on Wind Generator Interaction; Technical Report; Risø DTU National Laboratory for Sustainable Energy: Roskilde, Denmark, 1983. [Google Scholar]
- Katic, I.; Høstrup, J.; Jensen, N. A simple model for cluster efficiency. In Proceedings of the Europe and Wind Energy Association Conference and Exhibition, Rome, Italy, 7–9 October 1986. [Google Scholar]
- Samorani, M. The Wind Farm Layout Optimization Problem. In Handbook of Wind Power Systems; Pardolas, P., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 21–38. [Google Scholar]
- Shakoor, R.; Hassan, M.; Raheem, A.; Wu, Y. Wake effect modelling: A review of wind farm layout optimization using Jensen’s model. Renew. Sustain. Energy Rev. 2016, 58, 1048–1059. [Google Scholar] [CrossRef]
- Song, Z.; Zhang, Z.; Chen, X. The decision model of 3-dimensional wind farm layout design. Renew. Energy 2016, 85, 248–258. [Google Scholar] [CrossRef]
- Wilson, D.; Cussat-Blanc, S.; Veeramachaneni, K.; O’Reilly, U.; Luga, H. A Continuous Development Model for Wind Farm Layout Optimization. In Proceedings of the 2014 Conference on Genetic and Evolutionary Computation, Vancouver, BC, Canada, 12–16 July 2014; pp. 745–752. [Google Scholar]
- Den Heijer, E.; Eiben, A. Comparing Aesthetic Measures for Evolutionary Art. In Applications of Evolutionary Computation; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6025, pp. 311–320. [Google Scholar]
- Galanter, P. Computational Aesthetic Evaluation: Past and Future. In Computers and Creativity; McCormack, J., d’Inverno, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Chapter 11; pp. 255–293. [Google Scholar]
- Chen, L.; MacDonald, E. Considering Landowner Participation in Wind Farm Layout Optimization. J. Mech. Des. 2012, 134, 084506. [Google Scholar] [CrossRef]
- Feng, J.; Shen, W. Modelling wind for wind farm layout optimisation using joint distribution of wind speed and wind direction. Energies 2015, 8, 3075–3092. [Google Scholar] [CrossRef]
- Feng, J.; Shen, W.Z. Solving the wind farm layout optimization problem using random search algorithm. Renew. Energy 2015, 78, 182–192. [Google Scholar] [CrossRef]
- Marchesotti, L.; Murray, N.; Perronnin, F. Discovering beautiful image attributes for aesthetic image analysis. Int. J. Comput. Vis. 2015, 113, 246–266. [Google Scholar] [CrossRef]
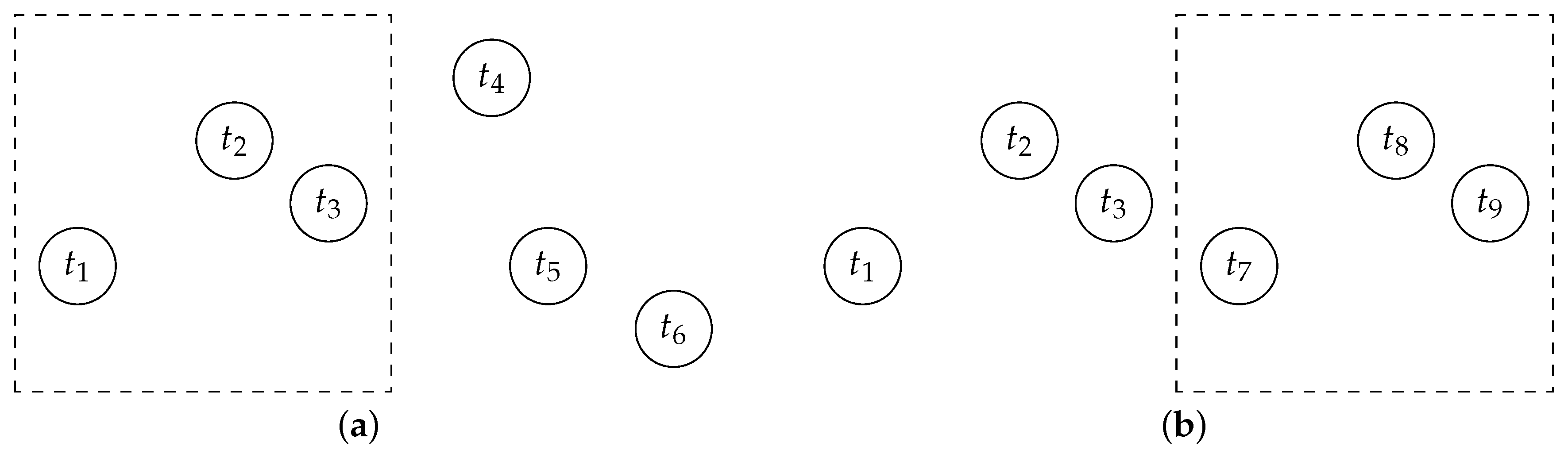


| Harmony | Description |
|---|---|
| Symmetry about the x axis. | |
| Symmetry about the y axis. | |
| Symmetry about the diagonal. | |
| Symmetry about the diagonal. | |
| rotational symmetry. | |
| rotational symmetry. | |
| Translational symmetry with another pattern. | |
| Translation plus reflectional symmetry with another pattern. | |
| Translation plus rotational ( or ) symmetry with another pattern. |
| Problem | Direction(s) | Expected Speed(s) | #Wind Scenarios |
|---|---|---|---|
| A | {} | {12 m/s} | 1 |
| B | {} | {12 m/s} | 36 |
| C | {} | {8 m/s, 12 m/s, 17 m/s} | 108 |
| Direction | m/s | m/s | m/s |
|---|---|---|---|
| 0∘ to 260∘ | 0.00404 | 0.00865 | 0.0115 |
| 270∘ | 0.00404 | 0.0107 | 0.0127 |
| 280∘ | 0.00404 | 0.0121 | 0.0156 |
| 290∘ | 0.00404 | 0.0141 | 0.0185 |
| 300∘ | 0.00404 | 0.0138 | 0.0300 |
| 310∘ | 0.00404 | 0.0190 | 0.0352 |
| 320∘ | 0.00404 | 0.0138 | 0.0300 |
| 330∘ | 0.00404 | 0.0141 | 0.0185 |
| 340∘ | 0.00404 | 0.0121 | 0.0156 |
| 350∘ | 0.00404 | 0.0107 | 0.0127 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mayo, M.; Daoud, M. Aesthetic Local Search of Wind Farm Layouts. Information 2017, 8, 39. https://doi.org/10.3390/info8020039
Mayo M, Daoud M. Aesthetic Local Search of Wind Farm Layouts. Information. 2017; 8(2):39. https://doi.org/10.3390/info8020039
Chicago/Turabian StyleMayo, Michael, and Maisa Daoud. 2017. "Aesthetic Local Search of Wind Farm Layouts" Information 8, no. 2: 39. https://doi.org/10.3390/info8020039
APA StyleMayo, M., & Daoud, M. (2017). Aesthetic Local Search of Wind Farm Layouts. Information, 8(2), 39. https://doi.org/10.3390/info8020039






