Abstract
Day-to-day information is increasingly being implemented in transit networks worldwide. Feeder bus service (FBS) plays a vital role in a public transit network by providing feeder access to hubs and rails. As a feeder service, a space-time path for frequent passengers is decided by its dynamic strategy procedure, in which a day-to-day information self-learning mechanism is identified and analyzed from our survey data. We formulate a frequency-based assignment model considering day-to-day evolution under oversaturated conditions, which takes into account the residual capacity of bus and the comfort feelings of sitting or standing. The core of our proposed model is to allocate the passengers on each segment belonging to their own paths according to multi-utilities transformed from the time values and parametric demands, such as frequency, bus capacity, seat comfort, and stop layout. The assignment method, albeit general, allows us to formulate an equivalent optimization problem in terms of interaction between the FBS’ operation and frequent passengers’ rational behaviors. Finally, a real application case is generated to test the ability of the modeling framework capturing the theoretical consequents, serving the passengers’ dynamic externalities.
1. Introduction
Intelligent information systems have been widely used in public transit. Advanced traveler information systems (ATIS), such as automatic vehicle location (AVL) and auto fare collection (AFC), enable transit agencies to implement data analysis techniques and provide travelers with real-time information (RTI) aimed to support their travel decisions. However, the resulting performance is not invariable, but changes day-to-day as a consequence of actual experience or information. In this paper, therefore, a day-to-day information self-learning mechanism is investigated.
High-frequency public transit has been popular for passengers or travelers. Especially, in the context of transit networks, the popularization of seamless connecting is taken into full consideration for operation plans and all individuals. The more comprehensive the public transit system being developed is, the better FBS and feeder connecting service need to be provided. This is the major direction of sophisticated and comprehensive urban transit service. For instance, urban rail transit (URT) is in the period of flourishing development in China. At the same time, the feeder bus service plays a vital role at estimating the level of service (LOS) and systematizing public transit, providing convenience to URT. By increasing the accessibility and shortcut between FBS and rail transit, the schedule coordination can make a great contribution to the seamless transfer and in reducing the delays or times to users.
Passenger flow assignment is a vital component of transportation systems. The assignment results can be applied to support transportation system management, such as operation planning, regular passenger flow forecasting, and station passenger crowd regulation, or evacuation strategies. However, a congestion condition usually produces some annoyance in waiting for buses and establishes some decrease in on-board comfort up to a maximum threshold, since some passengers who are not allowed to board have to wait for the next FBS under oversaturated conditions. An oversaturated condition means the total number of waiting passengers wanting to board could hardly be loaded by their desired vehicles, which derives from the vehicle’s explicit capacity constraint. In general, the phenomena of oversaturated or undersaturated conditions are proposed to explain congestion severity. Obviously, the congestion leads to the disequilibrium between FBS and feeder connecting services for their plans, respectively, which will cause the frequent passengers’ inconvenience, especially.
Before passengers depart, they could not acquire full transportation information about congestion conditions. As a result, the passengers’ bounded-rationality would optimize their travel strategies (including departure time or arriving time, travel paths, and so on), which have been adjusted based on their experience. The passengers’ bounded-rationality refers to people who regard their travel strategies as the best choices depending on their own confined information (e.g., from radio or other’s talk). However, the strategies may be appropriate for some certain paths or desired times, in which those passengers with those cognitive expressions can be defined as bounded-rationality ones.
A day-to-day assignment model is applied to describe the evolution of passengers’ traveling decisions based on the accustomed FBS schedule and self-learning adjustment to avoid congestion to attend to one’s comfort. FBS transit networks usually provide different access stops and buses for passengers traveling on a given origin-destination pair. A multi-path choice is decided by sophisticated passengers’ experience from four components: (a) in-vehicle time, (b) waiting time, (c) delay time, and (d) a line change penalty.
This paper develops a stochastic user equilibrium (SUE) between a frequency-based feeder bus service and passengers’ day-to-day self-learning evolution behavior. In this context, we present a frequency-based travel path choice model that can be self-optimized, considering different congestion effects.
The assignment approach considering congestion on public transport can be modeled by using an implicit or explicit approach [1]. The implicit model is derived from road traffic flow assignment and the congestion effect is similar for all passengers boarding or waiting. The major drawback of these models is the approximation of congestion and all-or-nothing assignment methods resulting in large errors. In other words, the congestion would create a negative effect to all users [2,3]. Those approaches used to lead to overlapping problems [4]. Daganzo and Sheffi [5] suggested the use of probit-based models to overcome this problem. Another logit-like form would have been approved with proving process. In order to overcome those disadvantages, the explicit approach is presented based on the vehicle’s capacity constraint. Passengers’ boarding characteristics and queuing rules have been captured in recent studies [6,7,8].
An assignment model is proposed under explicit constraints considering schedules and individual vehicle capacities [7]. Assuming passengers using their travel strategies, the hyperpath in [9,10] can be added with different penalties depending each one’s desired time (arrival or departure times). The traditional diachronic-graphs method introduces volume-delay functions leading to a distortion of the cost pattern. With the problem overcome, Papola et al. [8] extend to the case of scheduled services allowing for explicit capacity constraints and first-in-first-out (FIFO) queue representation. Under the scheduled runs’ capacities, saw-tooth temporal profiles of the waiting times that concentrate passengers are yielded. A stochastic dynamic transit assignment model is established considering seat capacities [11,12]. The explicit seating layout must produce a differentiation of comfortable feelings between standing and sitting. Each type probability of passengers obtaining a seat can produce the utility from capturing the stochastic nature.
A schedule-based dynamic assignment model is developed for transit networks, which takes into account congestion through explicit vehicle capacity constraints. According to passengers’ experience (especially failure-to-board experience due to congestion), the assignment method jointly simulates their learning mechanism adjusting the departure time, stop, and run choices on the basis of mixed pre-trip/en-route choice behavior [1]. A schedule-based model is presented in a congested, dynamic, and schedule-based transit network [6]. Based on the first-in-first-out discipline, the passenger demand is loaded onto the network and produces dynamic queuing delays, which are calculated minimum paths. Wu et al. [13] propose a day-to-day dynamic evolution model with the consideration of bounded rationality (BR) proposed, which can better captures travelers’ characteristics in path-finding within an urban railway network.
There are two types of transit assignment: one based on network unreliability and one that does not consider reliability at all. The first type is used when the system is established and does not develop steadily from cultivating habitual passengers. The second type, on the other hand, is the relatively mature system, which is typical of assignment models with heterogeneous information evolution.
As for the typical transit assignment, a stochastic model explicitly considers the effect of seat availability on route choice, as well as departure time choice. The priorities of on-board passengers are assumed over newly-boarding passengers and further suppose that (a) passengers who are traveling further and (b) passengers who have stood for a longer time have a higher motivation in chasing any free seats [14]. Moreover, based on the queuing theory on bus networks, interactions are considered between transit route choice and congestion effects [15].
Providing new lines to a transit network, or increasing the frequency of an existing line, may not improve the system performance in terms of expected total travel cost [16]. An analytical schedule-based transit assignment model, considering both supply uncertainties and travel strategies, was developed, which takes into account the explicit transit capacities and the first-come-first-serve concept when loading passengers [17]. The crowding cost was included as a component of individuals’ route choices over railway systems [18].
With estimation and prediction of travel time presented, an extensive survey of all of the necessary concepts when modeling travel time is performed [19]. An initial individual path utility model is proposed directly from a sample of choices of the user [20]. A macroscopic transit assignment model, which explicitly considers real-time prediction of on-board passenger numbers and crowding of PT services, was presented [21]. A more effective model is proposed on the basis of individual traveler preferences, which are obtained by the use of new information technology tracking users and registering their choices [22].
Referring to reliability-based transit assignment, three types of the reliability are introduced: travel time reliability of the community administration, schedule reliability of the operator, and direct boarding waiting-time reliability of the passengers, which are qualified by the Monte Carlo simulation approach with a stochastic user equilibrium transit assignment mode [23]. In addition, a novel dynamic transit assignment model, which takes into account the demand and supply uncertainties, is related to the stochastic process of passengers’ arrival and boarding at transit stops, and modeled by the renewal theory and M/G/1 queues theory [24]. A multi-modal transport network assignment model is proposed considering that demand and supply are uncertain because of adverse weather conditions [25]. The variability of in-vehicle congestion and the risk-averse behaviors of passengers are described in the frequency-based transit assignment model [26].
An and Lo [27] formulate the Transit Network Design Problem (TNDP) under demand uncertainty for optimal system flows by considering the combination of two services types: (i) rapid transit lines (RTL) or regular services and (ii) demand responsive or flexible services. Defining the notion of service reliability (SR), they propose a two-phase model to separate the otherwise intertwined decisions over the deployment of these two service types [27].
Most previous works focus on the day-to-day evolution process and traffic assignment model of urban road traffic networks. However, what is the correlation between the travelers’ day-to-day evolution and the frequency settings of the FBS, and how do we reveal that the traveler autonomous choice behaviors are given little attention in the previous works. In addition, most works are based on urban road traffic and private traffic, while one paid little attention to the behavior of the daily evolution of urban public transport passengers. The urban public transport systems (public traffic and urban transit traffic) have their own complex features, in which demand-supply interaction is derived from the congestion (the failed-to-sit, and even failed-to-board) and frequency settings, thus affecting the day-to-day information evolution of the passengers.
Therefore, the main contributions of the present study are to model the day-to-day information evolution with the consideration of congested performance, and gain insights into the process of passenger flow evolution on an FBS over time. This daily information evolution characteristic in the route choice can be clarified and encourage high-quality service. To discover this complex characteristic in the passenger flow sequence, FBS paths involve sequential segment decision-making that relies on passenger-accumulated knowledge and the prior-estimated available information, which is evolved from a day-to-day information self-learning process. It is the motivation of this paper to introduce a day-to-day information evolution model to improve an FBS.
Our paper presents recent developments in the theory of assignment approaches applied to FBS operation, which is mainly concerned with Chinese buses in Section 1. Section 2 establishes the essential assumptions and defines the core mechanism of our proposed model, in which the time lost in each stage of a round-trip is derived. In Section 3, the fundamental time values from the previous section are used to find the expression of utility items, which is able to estimate the passengers’ path choices. Section 4 describes its solution algorithms, and Section 5 reports on our numerical test. Finally, Section 6 is the conclusion.
2. Model Formulation
2.1. Day-to-Day Information Learning Mechanism
FBS networks constitute a series of stops where the passengers can board, alight from, or change the line. Rational passengers would choose their desired time (e.g., desired departure or arrival times), which defines that passengers arriving at the desired stop are able to board the bus and avoid the congestion or heavy delays. According to the information type provided (e.g., by ATIS) and passenger experience (especially failure-to-board, as well as board-to-keep-standing experience due to congestion), frequent passengers would optimize their traveling strategies through a day-to-day information self-learning process. With investigating the effects of congestion, we find that frequent passengers are particularly sensitive to congestion. Since the frequent passengers are mainly involved in home-origin or work-destination scenarios, they are very used to the trip paths and wish greatly to acquire the desired departure time (DDT), as well as the desired arrival time (DAT). Additionally, it is rational and reasonable for them to estimate the level of service on FBS.
Generally, path choice is obtained from the perceived balance between the desired utilities (provided by some information) and the latest memory (e.g., from yesterday). Forecasted path utilities can be defined from the day-to-day learning mechanism:
where represents the perceived utilities on path at day , and are the actual utilities on path at day . K is the set of path k, namely, . Namely, is equal to the weighted average of the previous day’s perceived utilities and the actual utilities for path . Furthermore, the parameter represents the weight of the actual utilities in updating the perceived utilities. A small implies those passengers’ trip behaviors are strongly habitual or path-changing may be not be a reality, while a large means that passengers find out the accustomed paths are filled with inconvenience or more rational choices exist. The threshold can estimate the choice of the passengers. If , the passengers will not change their frequent paths because of habituation; otherwise, .
Passengers’ pre-trip choice of departure time t with in a departure time choice set defined for the passenger desired time can be written as
Referring to as the passengers’ memory influencing their decision on the departure time at present, the day-to-day variation can be expressed as
where is the perceived utility for a passenger of departing at time t of day n with desired time on path , and represent the different weights for arriving before and after the desired time , the parameter is the weight of the perceived utility , whose meaning is almost the same as . The value is similar changing-threshold, whose meaning is the same to in Equation (1).
Following [28,29], the arrival rules of feeder service vehicles fit the normal distribution. Equation (4) can, therefore, describe the weight parameter , which estimates the availability of passengers’ departing time t according to desired time . In this equation, is the mean headway deviation of feeder service vehicles, whose value may be acquired as 3 min [30]. Furthermore, the parameters and are derived from based on the deduction below:
2.2. Basic Elements and Assumptions
Our study describes the passengers’ travel utilities under a day-to-day evolution process, considering the service characteristics of both frequency and oversaturated conditions. Figure 1 illustrates the main components of total travel time included from the model concept of the FBS system. Therefore, the basic elements of this model are specified as follows:
- FBS is the only method provided for passengers to access some other connecting transits (e.g., rail and metro).
- This model only analyzes one feeder bus service utility for various different conditions (e.g., oversaturated, undersaturated, or traffic jam).
- All of the passengers who arrive by FBS are planning to transfer to a multi-modal station, i.e., the multi-modal station is not their travel destination [30].
- The feelings of passengers are attributed to the estimation of the LOS of traveling time in the vehicle, i.e., the seat layout and bus size makes a significant contribution to passengers’ utilities [11].

Figure 1.
Components of total travel time.
According to these assumptions, the following sections introduce the different utilities according to passengers’ waiting, delay, travel, and so on, which derive from the concept of the proposed model.
2.3. Running Time
We consider a linear single-directional corridor of length including total available paths k. The round-trip or cycle time, , is defined as the total travel time during one FBS cycle, given both the service time and slack time at termini. Let be the running time along the path, the delay at intersections (due to traffic lights), the queuing time at bus stops, and the waiting time at the origin of the path; then the round-trip time is:
When the FBS shares the right-of-way with no interactions with other modes on a dedicated road corridor, apart from the implicit delay due to traffic lights, the running time can be expressed as Equation (6), where is the constant running (cruising) speed, and denotes, implicitly, the free-flow travel times:
In a real scenario, the feeder bus departing from the stop would drive into the mixed traffic flow, obstructing other multi-mode vehicles. Taking a certain path k for illustration, we model the real running time as a function of both traffic flow and bus frequency by applying the well-known Bureau of Public Roads (BPR) formula. The formula is transformed as Equation (7):
where and are parameters, is an equivalency translation to the car criterion depending on the bus length , and is the capacity of the road of path k. is the traffic flow(veh/h), and denotes the bus frequency(veh/h). The factor X means is equal to the volume-to-capacity ratio, which is also applied to Equation (11). Furthermore, the equivalency factor is 1.65 for a small bus (8 m), 2.19 for standard buses (12 m), 2.60 for rigid long buses (15 m), and 3.00 for articulated buses (18 m).
2.4. Queuing Time
The queuing time can be divided into two main parts deriving from the stops and intersections, both of which include the acceleration and deceleration delay. Initially, the delay due to deceleration and acceleration at bus stops is expressed as
The delay time is inversely proportional to the acceleration rate and the acceleration rate of a bus. Next, the feeder bus has slowed its speed, stopping at the bus stop in order to connect the queuing passengers. The boarding time of the FBS depends on various multi-modes of door layout or a specified boarding policy (e.g., boarding at one front door and alighting at another rear door, see Equation (9); or both boarding and alighting at arbitrary doors, explained by Equation(9)) under its capacity constraint until all waiting passengers are loaded. The estimation of the boarding time requires the alternative situations: one is that the boarding queues interact with alighting ones from the same doors, which may occur at some congested location; on the other hand, both boarding and alighting flows are divided into exclusive corridors without any interactions, alternatively. Considering two regular situations, the boarding time can be represented by Equation (9):
where is the time to open and close the doors, and are the average boarding and alighting times per passenger, and are the numbers of passengers boarding and alighting a bus for one stop, the factors and are the proportion of passengers boarding and alighting under some certain oversaturated condition, whose meaning is given in Appendix B (Table B1). Furthermore, boarding or alighting times, as well as boarding policies are explained in more detail in [31].
The queuing time at a stop is a measure of the external congestion caused by bus jams. In addition, the bus jams are derived from all berths occupied by some popular vehicles loading numerous passengers, i.e., the queuing time is related with those queuing passengers. According to the simulation model [32,33,34], conforms exponentially to the bus frequency. Some research on the empirical estimation is developed in [35,36,37], observing the impact of relaying bus berths. The regression model is simplified in Equation (10), observed when we find the bus length is not so important for the concept of the queuing time .
where the parameters are estimated factors, both and are explained as follows:
Equation (10) is a generalization of the models developed by Tirachini [34,35] and can be used to assess the optimal bus size and bus stop design under congested bus stop operations. The case of split bus stops (a large stopping area consisting of two subgroups with one, two, or three berths each) can be accommodated by establishing a rule for the assignment of buses to the stopping areas (e.g., 50% of buses assigned to each stopping area). Parameters for Equation (10) are presented in Table B2.
In addition to its inclusion in the economic effect, as well as the frequency and demand, the number of berths is taken into account during the queuing delay. The more berths a stop layout is constructed with, the shorter the queuing delay will be, in the case that empirical applications have been made and accepted in Beijing’s public transportation. If the boarding or alighting process would occupy more time, the high demand contributes positively to a longer queuing time.
2.5. Delay Time
Next, we will introduce the delay time caused by the red light at an intersection (or crossroad). The queuing delay is an important parameter depending whether it is given priority under a different number of intersections along its own path. However, the queuing delay is difficult to estimate because of its randomness or various queue modes [36]. Many basic signal theories [36,37,38] have demonstrated classic deterministic queuing models that can describe the FBS running delays on its own path. The diagram of Figure 2 indicates that the FBS encountering an intersection experiences three processes, including deceleration, queuing time, and acceleration, which conform a queue type D/D/1.The first D denotes that the time between arrivals to the queue is deterministic type; the second D describes the deterministic service time distribution; lastly, the 1 indicates only one server at the station. Equation (11) can be derived to calculate the average uniform delay incurred every signal cycle by the FBS crossing one intersection. The formulation of Equation (11) is identical to what has been suggested as an analytical steady-state approach, like the Highway Capacity Manual (HCM) or the Canadian Capacity Guide for Signalized Intersections:
where is the queuing time caused by the intersection, C denotes the traffic signal cycle length (s), X = v/c = volume-to-capacity ratio, and g is the effective green interval duration (s).
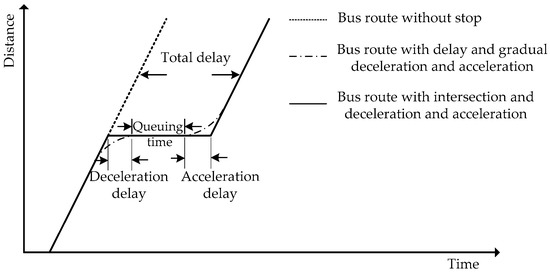
Figure 2.
An intersection of queuing time for FBS.
The queuing time and delay time can be summarized with Equations (10) and (11) according with the number of stops and intersections , which are described in Equation (12). Due to its lengthiness, Equation (12) is not decomposed:
3. Path Utilities for Passengers
3.1. In-FBS Congested Cost
Passengers’ utilities (explained at Section 2.1) are divided into necessary time cost, congestion utility , and waiting utility . The congestion utility has been developed in some literature. Numerous approaches to transit assignment considering seat capacities have been developed. A “fail-to-sit” probability is introduced at boarding points with travel costs without relying on a first-come-first-serve (FCFS) principle for many crowded buses in European countries [11]. A schedule-based equilibrium model is proposed assuming passengers use their own individual strategies [7]. For instance, the on-board passengers have priority to obtain seats and queuing rules are limited under a FCFS principle. The seat capacity is incorporated into the hyperpath-based transit assignment model and considered a different discomfort cost for the seated and standing passengers [39]. This model has been further applied in Paris in large-scale URT [40]. Therefore, the cost of passengers’ standing or seating in a FBS is different, which is derived from either oversaturated or undersaturated conditions. The in-vehicle congested cost is mainly decided by the number of passengers, described in Equation (13):
where denotes the assigned passenger flow belonging to the path k, is the number of the seats of a given bus, and A and B are the converting parameters, whose suggested values are A = 1 and B = 1.
3.2. Waiting Utilities
A different number of demands would influence what different passengers perceive at the waiting process. It might be too complex to apply into the proposed model if all different scenarios are classified relying on the demands. Thus, a certain scale of value scenario almost covers passenger demand conditions even though it is separated into only two scenarios (high and low demand) in the model. In order to apply our proposed assignment model to a certain scale of value scenario, we separated the passenger demand into two groups: a percentage of high demand (possible under oversaturated conditions) and a percentage of low demand (scarcely fail to board), which are derived from the Equation (14):
The waiting utilities under a specific periodical segment are described as Equation (15):
where is the headway of the path k, derived from the reciprocal of the frequency . In addition, and is the penalty coefficient of low and high demand respectively.
3.3. The Total Utilities
The final Equation (21) for passengers’ total utilities is to switch the accumulated time to a utility-based criterion:
where the parameters are the weighted factors switching the accumulated time to a utility-based criterion. Finally, after deriving the expressions for passengers’ utilities, the total utility minimization problem is formulated as Equations (22) and (23):
Subject to the following real constraints,
where Equation (24) is a frequency constraint that ensures that a minimum policy frequency (set to have a minimum level of service, if desired) and the maximum feasible frequency are feasible. Equation (25) states the FBS berths layout may be 1, 2, or 3, which means a more complex berth layout will not be taken into account. is the assigned passenger flow of route belonging to the flow (Equation (26) on path , and the value of may be null (Equation (27)). The factor is used to investigate stochastic properties of the optimal formulation of Equation (18), so we henceforth assume to be non-negative. The higher the value , the more the passengers’ understanding of the path’s utility. The recommended value is in the range of [15,25] for our case study after our observing experiments.
The final Equations (22) and (23) are given in Equation (28) (see Appendix A for details):
The logit assignment model is applied, leading to the proportion of demand on the path based on the utility . Then the feasible path flow and the actual utility are updated. Therefore, with the time going on, the passengers will form a typical and accustomed time series analyzed to describe the complexities of traveler choice behavior.
4. Solution Algorithm
The investigated subject includes dynamic aspects: the user’s updating process of the travel time perceived, experience of the traveling path, and information acquired. In order to take into account these dynamics, the model proposed in this work is a day-to-day model. Path choice is simulated along several days. A traversal search algorithm is adopted to solve the transit assignment problem. This solution is applied at the path level based on the day-to-day information evolution. The main steps of our proposed algorithm are described in the form of a flowchart in Figure 3.
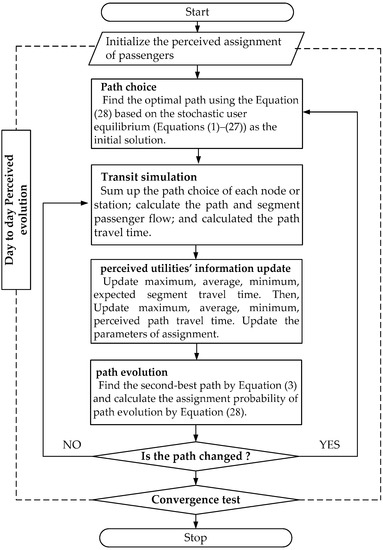
Figure 3.
Solution algorithm.
Step 0: (Initialization): Initialize the previous distribution of passenger flow. Input the data structures, including default parameters, feeder bus operation parameters, and day-to-day information evolution regulation.
Step 1: (Path choice): Find the optimal path using Equation (28) based on the stochastic user equilibrium (Equations (1)–(27)) as the initial solution.
Step 2: (Transit simulation): Sum up the path choice of each node or station; calculate the path and segment passenger flow; and calculate the path travel time.
Step 3: (Perceived utilities’ information update): Update maximum, average, minimum, and expected segment travel times. Then, update maximum, average, minimum, and perceived path travel times. Update the parameters of assignment.
Step 4: (Path evolution): Find the second-best path by Equation (3) and calculate the assignment probability of path evolution by Equation (28). If the path is changed based on the combination between perceived and actual utilities, Step 1 is entered into again; otherwise, shift into Step 2.
5. Numerical Test
The ability of the proposed model to capture day-to-day information evolution of the oversaturated effect was tested by an application on a realistic case study, whose numerical results are discussed, providing a day-to-day self-learning mechanism. The application case is abstracted from three FBS lines at Xizhimen District in Beijing, China. There are a total of eight stops along their respective lines. Suppose the traffic capacity of the three lines are 1200 veh/h, with the volume-to-capacity ratio X = 0.6. There exist three intersections belonging to their lines, shown in Figure 4. The actual path diagram is translated into the topological structure of the network, shown in Figure 5.
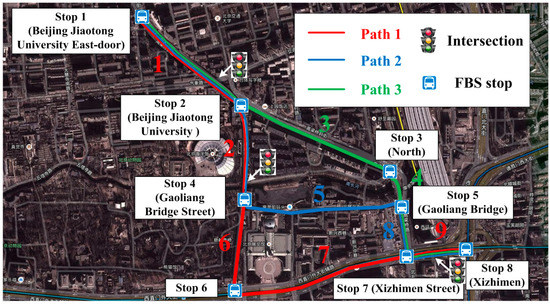
Figure 4.
Graphical path for FBS lines and stops (Beijing Xizhimen District).
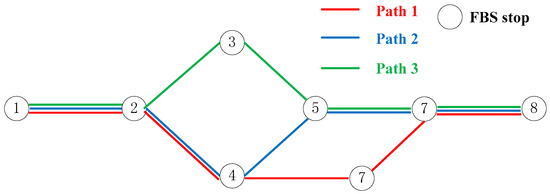
Figure 5.
Topological structure of the network.
With the origin and destination assumed as stop 1 and stop 8, alternatively, unidirectional passenger assignment is tested relying on the series of time stamps. Based on the former context, the similar capacities of three lines are 1200 veh/h, which can be applied into BPR functions (Equation (7)). The acceleration and deceleration delays are the same, whose approximate value is two seconds, alternatively. Coincidently, there are five stops along the three lines based on the different paths.
The form of FBS in Beijing is the standard bus (Sb = 12 m), which can load 80 pax/veh. The frequency of FBS is 10 bus/h, which means that the headway is almost 6 min. The factor in Equation (28) is 20 based on the numerical experiments, because it might be consistent with our empirical survey. Table 1 provides all parameters of our proposed model. Based on the statistical data of behavioral habits during a period, the passengers are frequent travelers served by FBS with strong habits. With typical information according to which the regular timetable changed, detailed data were captured throughout September 2015. The observed assignment conditions were recorded belonging to different segments of three paths, certainly, which were analyzed depending on the scheduled time buckets. We found that the passengers served by FBS were not disturbed strongly by the changed departure and arrival times. This was reflected at the whole average times of the own paths within the day-to-day evolution. Thus, we can primarily estimate the values and , and even conclude that the passengers are frequent travelers served by FBS with strong habits, the latter of which is assistant proof of appropriate values (less than 50%). Thus, and being less than 50% indicates their insensitivity of updating the perceived utilities deriving from the day-to-day information evolution [6]. For the sake of simplifying assumptions and calculation convenience, fundamental elements of uniform passenger arrival conditions will be shown in Table 2 and the total eight stops’ layout is constructed similarly with two berths. Additionally, the specified boarding and alighting policy is provided by Equation (9), referring to boarding at the front door and alighting at the behind door. Then, the accumulative total flow of boarding and alighting passengers for one hour can be obtained, as expressed in Figure 6. The three lines share nine communal composed segments, the lengths of which are measured in Table 3. Thus, the preliminary results can be calculated easily from the basic algorithm of Equations (1)–(27), such as the departure and arrival times in Table 4.

Table 1.
Model parameters following appearing orders.

Table 2.
Average arrival and leave rate at each stop (unit: people/min).
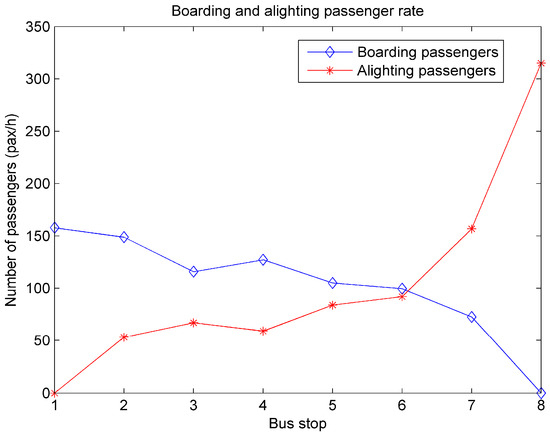
Figure 6.
Boarding and alighting passenger volume.

Table 3.
Length of Segment .

Table 4.
Time stamps of FBS at each stop for the three lines illustrated as an example.
Suppose that the three buses belonging to their own lines leave the terminal, stop 1, at the same time 17:00:00. The running time (Equation (7)), the deceleration and acceleration time (Equation (8)), as well as the intersection delay time (Equation (11)) at segment 1 can be taken as , and . Thus, the arrival time of stop 2 is 17:02:01, which adds to the boarding time (Equation (9)) and the queuing time (Equation (10)) with is equal to the departure time 17:02:12. Subsequently, a complete cycle can be tested for the sustaining buses tracking the scheduled stops. Then we can amplify each segment by the respective calculated utility, expressed in Table 5. Thus, the passenger flow of each cell (segment 1–9) can be elaborated and divided from the origin-destination matrix (Table C1, see Appendix C).

Table 5.
The passenger assignment of each segment for three paths based on a SUE (accumulative total flow/h).
If there is a smaller threshold estimating whether the path is changed or not, the assignment evaluation process tends to convergence. It should be noted that the SUE result is selected as the initial reference scheme for evaluation comparison. First, the dependency of the final assignment on the process of day-to-day evaluation is shown (from two days to eight days). The changing rating of passengers’ travel utilities is set as 10%, which is mainly used in Step 3 (perceived utilities’ information update) as the upper threshold of changing passengers’ travel utilities each day. In all results, the model converges to a stable scheme of 10 days. From Table 6, the utilities threshold seems to have no effect on the final assignment. Certain stability results are summarized and the convergence of the route-swapping process is illustrated using a three-route example. In the day-to-day evaluation model, the experience of demands is accumulated with a self-learning rate. When the self-learning rate is high, a path choice result might not remain stable and may not even converge for a long period. To the contrary, if the rate drops excessively, the model would require long and tardy evaluation duration. This means that the parameters in the learning model play a core role in the path choice and assignment. In other words, the convergence depends on the parameters set of , related to the self-leaning mechanism. This indicates that the assignment results are insensitive to the given parameters in the day-to-day evaluation model.

Table 6.
Path flow and travel time according to the day-to-day evaluation.
Second, considering results obtained through the numerical experiments presented above, some qualitative findings might be clarified. On one hand, the path-changing behavior is characterized by a specific converged assignment, shown as Table 6. A possible hypothesis of assignment is the long-tailed distribution. In further study, more investigations about the assignment that are able to represent the day-to-day information self-learning mechanism should be carried out. Moreover, having sufficient duration necessary to meet the demands in order to consider their perceived predilection has to be investigated further. The self-learning process leading to a path-changing decision is influenced by multiple factors; for instance, the availability and the class of information provided. The amount of time necessary to complete the learning process was studied in the numerical test above but greater understanding is required in order to identify factors that influence the length of the learning process. Therefore, more experiments should be developed.
A frequency-based assignment model enables us to estimate how passengers’ choice evolves during the varying operational time and optimal multi-factors, especially under oversaturated conditions. For example, we can see that running time plays an important role in deciding the strategy. Furthermore, the higher a FBS’s frequency is, the greater a path appeals to frequent travelers, even though the logical performance is not presented following the simulation results.
6. Conclusions
In this paper, we have introduced a time-valuing utility assignment model based on the frequency of the day-to-day information self-learning evolution oversaturated condition for FBS. The disaggregated origin destination demand and multiple travel paths are decided with the aim of optimizing the passengers’ utilities. The influence of FBS congestion is highlighted as we analyze the probability of fail-to-board and keep-standing under the bus’ capacity and seat layout.
The influence of bus crowding is highlighted as we analyze its impact on both the design of the bus service and the congestion level on the road. The consideration of crowding utilities as increasing the discomfort of FBS users pushes towards having a regular day-to-day evolution, which in turn may affect both bus and traffic flow on shared roads. The number of seats in buses is introduced as a decision variable for the first time in a microeconomic FBS model; the number of seats is the result of the trade-off between passengers’ comfort (that drives the number of seats up) and vehicle capacity (which might be increased by removing seats). The model is applied to the Xizhimen District in Beijing, and results discussed under daily information evolution in the route choice can be clarified in order to encourage high-quality service.
FBS paths involve sequential segment decision-making that rely on passenger accumulated knowledge and the prior-estimated available information, which evolves from the day-to-day information self-learning process. In the sphere of frequency-based assignment modeling of an FBS all operational parameters under explicit bus capacity are synthesized. Demand-supply interaction is defined from the congested performance, in which the failed-to-sit state, and even the failed-to-board state, is evaluated, decreasing the LOS attributes. The higher frequency path cultivates the frequent travelers’ customs for acquainted commuting behaviors, reducing fails. One parametric case as evidence is raised that a theoretical simulation is combined with a frequency-based assignment model under day-to-day information evolution. However, the essential long-term data collection is scarce, which will be completed in further research. As a problem of the dynamic assignment approaches, a new solution algorithm will be put forward towards an open issue, which will be achieved in future work.
Acknowledgments
This research is supported by the National Basic Research Program of China (No. 2012CB725403), and Fundamental Research Funds for the Central Universities (3122016D031).
Author Contributions
Zhichao Cao wrote the manuscript; Silin Zhang, Zhenzhou Yuan, and Zhichao Cao provided relevant information, discussed the data, and corrected the manuscript; and Zhichao Cao revised the manuscript. All authors have read and approved the final manuscript. All authors would also like to thank Dewei Li for his advice on this paper.
Conflicts of Interest
There is no conflict of interest related to the content of this paper.
Appendix A. The Derivation Process of the Logit Model
We will provide the proof on the objective function (Equation (23)) defining the logit model. The first order random condition of Equation (23) is the equilibrium formulation (A1).
where and are Lagrange multipliers corresponding to Equation (26) and (27), respectively, designated by . To determine the optima of in , we construct the Lagrangian as:
Based on Fisk’s theory [40,41], Equating the partial derivatives of to zero will give the conditions that a stationary point of , subject to Equations (26) and (27) being satisfied. Since does not exist when , a solution will only be valid if all components of are strictly positive. Setting the derivatives of to zero we find:
Using Equations (A1)–(A3) into Equation (26), this can be simplified to:
Appendix B. Boarding and Alighting Behaviors Estimation
If there are multiple doors provided for passengers’ to choose for boarding and alighting, the accurate threshold of the dwell time of a bus should be determined by the time slice when the last person gets on or off the bus. At the same time, the multi-doors lead to various boarding (or alighting) rules that have produced complicated and dynamic boarding (or alighting) percentages. Certainly, we have some empirical reasons to consider that the waiting queues are not distributed homogeneously at all doors. On one hand, some doors may be obstructed by some people carrying large luggage or faltering men (or women). On the other hand, rational passengers are willing to take more chances to obtain seats or avoid a failed-to-board state. As illustrated in the statistics from the No. 87 and 651 buses in Beijing, we can see that passengers can board (or alight) from arbitrary doors at the original (or terminal) station, hence, some certain percentage values of either 98% or 2% occur under defined rules. Many people have more preference for rear doors, which is shown as Table B1.

Table B1.
Boarding and alighting behaviors for multi-policy.
| The Number of Doors | 1 | 2 | 3 | |||
|---|---|---|---|---|---|---|
| The doors’ positions | only | Front | Behind | Front | Middle | Behind |
| Alighting Percentage (%) | 100 | 98 | 2 | 3 | 96 | 1 |
| Boarding Percentage (%) | 100 | 2 | 98 | 38 | 2 | 60 |
To estimate the queuing delay of buses, we use the bus stop simulator IRENE [34], which can determine the capacity, queuing delay, dwell time, berth usage, and other indicators of the performance of a bus stop as a function of a number of inputs such as the boarding and alighting demand, the number of berths, bus size, and frequency. For a more detailed description of the program see Son [38].
Regarding inputs, the following conditions are made:
Bus size: Four different bus sizes are considered in accordance with standard commercial vehicle sizes: 8 m, 12 m, 15 m, and 18 m long buses.
Number of berths: Three configurations are simulated, with one, two, and three contiguous berths. For a split bus stop with two stopping areas with two berths each, we assume that half of the buses are assigned to each stopping area.
Berth length: Each berth is assumed to be 1.5 times the bus length, which is the minimum distance necessary for buses to maneuver and overtake a preceding bus if necessary. The attributes directly reflected on the values .
Bus saturation flow: This parameter depends on the length of the bus and influences the queuing delay. We assume a basic saturation flow of s = 2086 passengers per hour per lane [37] and apply the following equivalency factors depending on the size of the bus, yielding estimated saturation flows of 1262, 951, 823, and 694 veh/h for 8 m, 12 m, 15 m, and 18 m buses, respectively.
A total of 265 simulations were run encompassing all bus sizes and bus stop designs previously described for a range of frequencies from 20 to 220 veh/h and dwell times between 10 and 65 s. Buses are assumed to arrive at a constant rate at stops (no bus bunching) and bus stops are isolated from traffic lights. The fitting parametric is given as Table B2.

Table B2.
Queuing delay parameters for Equation (10).
| Parameter | ||||||||
|---|---|---|---|---|---|---|---|---|
| Estimate | 0.25 | 5.28 | 1.9 | 2.1 | 25 | 1.1 | 0.37 | 0.63 |
Appendix C. Origin-Destination Matrix
The origin-destination matrix obtained with data investigation in presented in Table C1, with 25 unidirectional trips in the evening peak (17:00:00–18:00:00), from which three intersections are shared under oversaturated conditions.

Table C1.
Origin–destination matrix.
| O/D | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 53 | 27 | 13 | 15 | 38 | 9 | 3 |
| 2 | 0 | 40 | 46 | 21 | 18 | 16 | 8 | |
| 3 | 0 | 0 | 29 | 0 | 31 | 56 | ||
| 4 | 0 | 19 | 36 | 47 | 25 | |||
| 5 | 0 | 0 | 20 | 85 | ||||
| 6 | 0 | 34 | 66 | |||||
| 7 | 0 | 73 | ||||||
| 8 | 0 |
References
- Nuzzolo, A.; Crisalli, U.; Rosati, L. A schedule-based assignment model with explicit capacity constraints for congested transit networks. Transp. Res. C 2012, 20, 16–33. [Google Scholar] [CrossRef]
- Tong, C.O.; Wong, S.C. A stochastic transit assignment model using a dynamic schedule-based network. Transp. Res. B 1999, 33, 107–121. [Google Scholar] [CrossRef]
- Nielsen, O.A. A stochastic transit assignment model considering differences in passengers utility functions. Transp. Res. B 2000, 34, 377–402. [Google Scholar] [CrossRef]
- Daskin, M.S.; Sheffi, Y. Urban transportation networks: Equilibrium analysis with mathematical programming methods. Transp. Sci. 1985, 19, 463–466. [Google Scholar] [CrossRef]
- Daganzo, C.F.; Sheffi, Y. On stochastic models of traffic assignment. Transp. Sci. 1977, 11, 253–274. [Google Scholar] [CrossRef]
- Poon, M.H.; Wong, S.C.; Tong, C.O. A dynamic schedule-based model for congested transit networks. Transp. Res. B 2004, 38, 343–368. [Google Scholar] [CrossRef]
- Hamdouch, Y.; Lawphongpanich, S. Schedule-based transit assignment model with travel strategies and capacity constraints. Transp. Res. B 2008, 42, 663–684. [Google Scholar] [CrossRef]
- Papola, N.; Filippi, F.; Gentile, G.; Meschini, L. Schedule-based transit assignment: New dynamic equilibrium model with vehicle capacity constraints. In Schedule-Based Modeling of Transportation Networks; Springer: New York, NY, USA, 2009; pp. 1–26. [Google Scholar]
- Nguyen, S.; Pallottino, S. Equilibrium traffic assignment for large scale transit networks. Eur. J. Oper. Res. 1988, 37, 176–186. [Google Scholar] [CrossRef]
- Spiess, H.; Florian, M. Optimal strategies: A new assignment model for transit networks. Transp. Res. B 1989, 23, 83–102. [Google Scholar] [CrossRef]
- Schmöcker, J.D.; Fonzone, A.; Shimamoto, H.; Kurauchi, F.; Bell, M.G. Frequency-based transit assignment considering seat capacities. Transp. Res. B 2011, 45, 392–408. [Google Scholar] [CrossRef]
- Sumalee, A.; Pan, T.; Zhong, R.; Uno, N.; Indra-Payoong, N. Dynamic stochastic journey time estimation and reliability analysis using stochastic cell transmission model: Algorithm and case studies. Transp. Res. C 2013, 35, 263–285. [Google Scholar] [CrossRef]
- Wu, J.; Sun, H.; Wang, D.Z.; Zhong, M.; Han, L.; Gao, Z. Bounded-rationality based day-to-day evolution model for travel behavior analysis of urban railway network. Transp. Res. C 2013, 31, 73–82. [Google Scholar] [CrossRef]
- Sumalee, A.; Tan, Z.; Lam, W.H. Dynamic stochastic transit assignment with explicit seat allocation model. Transp. Res. B 2009, 43, 895–912. [Google Scholar] [CrossRef]
- Trozzi, V.; Gentile, G.; Bell, M.; Kaparias, I. Dynamic user equilibrium in public transport networks with passenger congestion and hyperpaths. Transp. Res. B 2013, 57, 266–285. [Google Scholar] [CrossRef]
- Szeto, W.Y.; Jiang, Y. Transit assignment: Approach-based formulation, extragradient method, and paradox. Transp. Res. B 2014, 62, 51–76. [Google Scholar] [CrossRef]
- Hamdouch, Y.; Szeto, W.Y.; Jiang, Y. A new schedule-based transit assignment model with travel strategies and supply uncertainties. Transp. Res. B 2014, 67, 35–67. [Google Scholar] [CrossRef]
- Pel, A.J.; Bel, N.H.; Pieters, M. Including passengers’ response to crowding in the Dutch national train passenger assignment model. Transp. Res. A 2014, 66, 111–126. [Google Scholar] [CrossRef]
- Mori, U.; Mendiburu, A.; Álvarez, M.; Lozano, J.A. A review of travel time estimation and forecasting for Advanced Traveller Information Systems. Transp. A 2015, 11, 119–157. [Google Scholar] [CrossRef]
- Nuzzolo, A.; Comi, A. Advanced public transport and intelligent transport systems: New modelling challenges. Transp. A 2016, 12, 674–699. [Google Scholar] [CrossRef]
- Nuzzolo, A.; Crisalli, U.; Comi, A.; Rosati, L. A mesoscopic transit assignment model including real-time predictive information on crowding. J. Intell. Transp. Syst. 2016, 20, 316–333. [Google Scholar] [CrossRef]
- Nuzzolo, A.; Comi, A. Individual utility-based path suggestions in transit trip planners. IET Intell. Transp. Syst. 2016, 10, 219–226. [Google Scholar] [CrossRef]
- Yin, Y.; Lam, W.H.; Miller, M.A. A simulation-based reliability assessment approach for congested transit network. J. Adv. Transp. 2004, 38, 27–44. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Lam, W.H.K. Dynamic transit assignment model for congested transit networks with uncertainties. In Proceedings of the 88th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 11–15 January 2009.
- Sumalee, A.; Uchida, K.; Lam, W.H. Stochastic multi-modal transport network under demand uncertainties and adverse weather condition. Transp. Res. C 2011, 19, 338–350. [Google Scholar] [CrossRef]
- Szeto, W.Y.; Jiang, Y.; Wong, K.I.; Solayappan, M. Reliability-based stochastic transit assignment with capacity constraints: Formulation and solution method. Transp. Res. C 2013, 35, 286–304. [Google Scholar] [CrossRef]
- An, K.; Lo, H.K. Robust transit network design with stochastic demand considering development density. Transp. Res. B 2015, 81, 737–754. [Google Scholar] [CrossRef]
- Taylor, M.A.P. Travel Time Variability—The Case of Two Public Modes. Transp. Sci. 1982, 16, 507–521. [Google Scholar] [CrossRef]
- Knoppers, P.; Muller, T. Optimized Transfer Opportunities in Public Transport. Transp. Sci. 1995, 29, 101–105. [Google Scholar] [CrossRef]
- Hsu, S.C. Determinants of passenger transfer waiting time at multi-modal connecting stations. Transp. Res. E 2010, 46, 404–413. [Google Scholar] [CrossRef]
- Gibson, J.; Baela, I.; Willumsen, L. Bus-stops, congestion and congested bus-stops. Traffic Eng. Control 1989, 30, 291–302. [Google Scholar]
- Chang, T.H.; Lin, J.T. Optimal signal timing for an oversaturated intersection. Transp. Res. B 2000, 34, 471–491. [Google Scholar] [CrossRef]
- Chang, T.H.; Sun, G.Y. Modeling and optimization of an oversaturated signalized network. Transp. Res. B 2004, 38, 687–707. [Google Scholar] [CrossRef]
- Tirachini, A. The economics and engineering of bus stops: Spacing, design and congestion. Transp. Res. A 2014, 59, 37–57. [Google Scholar] [CrossRef]
- Tirachini, A.; Hensher, D.A.; Rose, J.M. Multimodal pricing and optimal design of urban public transport: The interplay between traffic congestion and bus crowding. Transp. Res. B 2014, 61, 33–54. [Google Scholar] [CrossRef]
- Dion, F.; Rakha, H.; Kang, Y.S. Comparison of delay estimates at under-saturated and over-saturated pre-timed signalized intersections. Transp. Res. B 2004, 38, 99–122. [Google Scholar] [CrossRef]
- Akçelik, R.; Rouphail, N.M. Estimation of delays at traffic signals for variable demand conditions. Transp. Res. B 1993, 27, 109–131. [Google Scholar] [CrossRef]
- Son, Y.T. Queueing delay models for two-lane highway work zones. Transp. Res. B 1999, 33, 459–471. [Google Scholar] [CrossRef]
- Leurent, F. On seat capacity in traffic assignment to a transit network. J. Adv. Transp. 2012, 46, 112–138. [Google Scholar] [CrossRef]
- Leurent, F. On seat congestion, passenger comfort and route choice in urban transit: A network equilibrium assignment model with application to Paris. In Proceedings of the Annual Meeting of the Transportation Research Board Session Transit Capacity and Quality of Service, Washington, DC, USA, 11–15 January 2009.
- Fisk, C. Some developments in equilibrium traffic assignment. Transp. Res. B 1980, 14, 243–255. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).