Joint Modulation Classification and User Number Detection for Multiuser MIMO-STBC Systems

Abstract

The research on non-cooperative multiuser multiple-input multiple-output with space-time block code (MIMO-STBC) communication systems is a challenging and important task. However, to our knowledge, there is little report of this topic. Being two key research issues in this area, modulation classification and user number detection are studied in this paper. We consider both problems jointly as a multiple hypothesis testing problem. Based on this idea, we propose a joint modulation classification and user number detection algorithm for the multiuser MIMO-STBC systems. The proposed method does not require prior knowledge of the propagation channel or noise power, and thus might be suitable for the non-cooperative scenario. Simulations validate the effectiveness of the proposed method.

1. Introduction

Multiple-input multiple-output (MIMO) in conjunction with space-time block code (STBC) is a key technology to improve rate, reliability, and decoding complexity [1,2] in modern wireless communication systems. The blind identification of MIMO signals is a challenging task, which has recently attracted an increasing amount of attention. One essential step is the blind estimation of communication parameters, such as the channel matrix, the modulation type, and so on, which has found application in military and commercial scenarios.

Blind estimation of communication parameters for single-user MIMO systems has been summarized in [3,4]. These methods are devoted to the blind estimation of STBC type, modulation, transmitting antenna number, and so on. In addition, the authors in [5] have shown that some communication parameters are deeply interrelated and can be jointly estimated. However, there is little literature regarding the blind estimation of communication parameters for multiuser MIMO systems. In [6,7], the authors propose three semi-blind multiuser MIMO-Orthogonal STBC (OSTBC) channel estimation methods based on capon, multiple signal classification (MUSIC), and alternating projection techniques, severally. Although these methods perform well for multiuser MIMO-OSTBC systems, they require the transmitter to send training sequence, which is not suitable for the non-cooperative scenery. In [8], the authors propose a blind zero-forcing (ZF) detector for multiuser MIMO-OSTBC systems based on quadratic programming (QP), which does not require a training sequence. However, it does require prior knowledge of user number and modulation type. Thus, it must estimate the user number and modulation type blindly in practical non-cooperative scenarios.

In this paper, we propose a joint modulation classification and user number detection algorithm for the multiuser MIMO-STBC system. The proposed algorithm considers the modulation classification and user number detection task as a multiple hypothesis testing problem. The cost function is derived based on the maximum likelihood and information theoretic criteria. The noise power is estimated by averaging the eigenvalues of the noise subspace, and the virtual channel matrix is estimated by the subspace-Joint Approximate Diagonalization of Eigen-matrices (SJADE) algorithm [9]. The user number and modulation are recognized by choosing the candidate that minimizes the likelihood function (LF)-minimum description length (MDL) cost function. Simulations validate that the proposed algorithm can recognize the user number and modulation type simultaneously and have perfect performance at a high SNR.

Notations 1.

Hereinafter, lower case and non-bold letters denote scalars, lower case and bold letters denote vectors, and uppercase and bold letters denote matrices. Superscripts ${(\cdot )}^{*}$, ${(\cdot )}^T$, ${(\cdot )}^H$ stand for complex conjugate, transpose, and Hermitian transpose, respectively. The symbol ${\Vert \Vert }_F$ denotes a Frobenius norm. The operators $\Re e(\cdot )$, $\Im m(\cdot )$, $E[\cdot ]$ and $\arg (\cdot )$ represent the real part, imaginary part, expectation, and phase extraction, respectively. The operator “underline” for any matrix $M$ is defined as $\underset{\_}{M}\triangleq \left[\begin{array}{c}vec\left\{\Re e\left(M\right)\right\}\\ vec\left\{\Im m\left(M\right)\right\}\end{array}\right]$ and the operator $vec(\cdot )$ denotes the vectorization. Notation $\triangleq$ is used for definition, and $\mathrm{diag}\{\cdot \}$ and $\mathrm{bdiag}\{\cdot \}$ denote the dialogue matrix and block dialogue matrix, respectively.

2. System Model

In a single-user MIMO-STBC communication system, a signal vector $s={\left[s_1,\cdots ,s_n\right]}^T$ composed of $n$ symbols is encoded into an $n_t\times l$ transmitting matrix $C(s)$ [1,2]:

$$\mathcal{C}(s)={\displaystyle \sum _{k=1}^n(A_k\Re e(s_k)+B_k\Im m(s_k))}$$

(1)

where $n_t$ and $l$ denote the number of transmitting antennas and the length of a block, $A_k$ and $B_k$ denote space-time coding matrices, respectively. The transmitted symbols are assumed to be independent and identically distributed (i.i.d.) and belong to the same constellation $ℳ$.

In this paper, we focus on multiuser MIMO-STBC systems, and the channel is assumed to be quasi-static and frequency-flat. In addition, the receiver is assumed to be perfectly synchronized with the transmitter. In this case, the communication model is expressed as [6,7]

$$Y={\displaystyle \sum _{p=1}^P{H}_p\mathcal{C}(s_p)}+N$$

(2)

where the $n_r\times l$ matrix $Y$ refers to a block of the received samples, $H_p$ is the channel matrix from the $p\mathrm{-t}\mathrm{h}$ user to the receiver, the $n_r\times l$ matrix $N$ denotes the complex additive white Gaussian noise, with mean zero and variance ${\sigma }^2$ for each complex dimension.

3. Proposed Algorithm

3.1. LF-MDL Based Function

Using the vectorization operator in Equation (2), we can obtain the following:

$$\begin{array}{ll}y\triangleq \underset{\_}{Y^T}=& {\displaystyle \sum _{p=1}^{P}A(H_p){\tilde{s}}_p}+n\\ & =A(H)\tilde{s}+n\end{array}$$

(3)

where

$$A(H_p)=\left[\begin{array}{ccccc}{\left(H_p{A}_1\right)}^T& {\left(H_p{B}_1\right)}^T& \cdots & {\left(H_p{A}_n\right)}^T& {\left(H_p{B}_n\right)}^T\end{array}\right]$$

(4)

$${\tilde{s}}_p\triangleq {\left[\begin{array}{ccccc}\Re e(s_{p1})& \Im m(s_{p1})& \cdots & \Re e(s_{pn})& \Im m(s_{pn})\end{array}\right]}^T$$

(5)

$$A(H)=\left[\begin{array}{cccc}A(H_1)& A(H_2)& \cdots & A(H_P)\end{array}\right]$$

(6)

$$\tilde{s}={\left[\begin{array}{cccc}{{\tilde{s}}_1}^T& {{\tilde{s}}_2}^T& \cdots & {{\tilde{s}}_p}^T\end{array}\right]}^T$$

(7)

$$n\triangleq \underset{\_}{N^T}.$$

(8)

Then, the recognition of user number and modulation based on the LF and the information theoretic method (MDL; [10]) can be expressed as

$$\begin{array}{cc}\left[\begin{array}{cc}\widehat{P},& \widehat{ℳ}\end{array}\right]\hfill & =\arg \underset{P\in {\mathrm{\Theta }}_1,ℳ\in {\mathrm{\Theta }}_2}{\min }\left\{-\log (\mathrm{\Lambda }[y|\mathcal{C},ℳ,P,H,{\sigma }^2])+p(z)\right\}\hfill \\ & =\arg \underset{P\in {\mathrm{\Theta }}_1,ℳ\in {\mathrm{\Theta }}_2}{\min }\{-{\displaystyle \sum _{v=1}^{N_b}\log (\mathrm{\Lambda }[y(v)|\mathcal{C},ℳ,P,H,{\sigma }^2])}\hfill \\ & \hfill +\frac{1}{2}\left(2n_r{n}_{t}P+1\right)\log N_b\}\end{array}$$

(9)

where ${\mathrm{\Theta }}_1$ and ${\mathrm{\Theta }}_2$ denote the set of all possible user number and modulation candidates, $v$ denotes the index of STBC block, and $N_b$ is the total number of the received STBC blocks.

Considering that the transmitted symbols are i.i.d. and that the noise $n(v)$ is jointly Gaussian distributed [11], the LF can be expressed as

$$\begin{array}{l}\log \left(\mathrm{\Lambda }\left[y|\mathcal{C},ℳ,P,H,{\sigma }^2\right]\right)=-N_b\log \left(M^{nP}{\left(\pi {\sigma }^2\right)}^{n_{r}l}\right)\\ +{\displaystyle \sum _{v=1}^{N_b}\log \left({\displaystyle \sum _{s(v)\in {ℳ}^{nP}}\exp \left[-\frac{||y(v)-A(H)\tilde{s}(v)|{|}_F^2}{{\sigma }^2}\right]}\right)}\end{array}$$

(10)

where $M$ is the number of states of the constellation $ℳ$.

However, in the practical non-cooperative scenery, the receiver side does not have prior knowledge of ${\sigma }^2$ and $A(H)$. Thus, we have to first estimate them, and then use this estimate in the LF.

3.2. Estimation of the Noise Power

To estimate the noise power, we have to first calculate the covariance of the $y$:

$$R=E\left(y{y}^T\right)=A(H)E\left(\tilde{s}{\tilde{s}}^T\right)A^T(H)+E\left(n{n}^T\right).$$

(11)

Utilizing the property of $s$ and $n$, Equation (11) can be rewritten as

$$R=\frac{1}{2}A(H)I_{2nP}{A}^T(H)+\frac{{\sigma }^2}{2}{I}_{2n_{r}l}.$$

(12)

Assume ${\lambda }_i(i=1,\cdots ,2n_{r}l)$ is the i-th largest eigenvalue of the covariance matrix $R$, then the noise subspace is constituted by the eigenvectors corresponding to the $2n_{r}l-2nP$ smallest eigenvalues [11]. Thus, the ${\sigma }^2$ can be estimated by

$$\frac{{\widehat{\sigma }}^2}{2}=\frac{1}{2n_{r}l-2nP}{\displaystyle \sum _{i=2nP+1}^{2n_{r}l}{\lambda }_i}.$$

(13)

3.3. Estimation of the Virtual Channel Matrix

As channel matrix $H$ is implicated as being contained in the LF, we can estimate the virtual channel matrix $A(H)$ instead of estimating $H$ directly. First, we employ the subspace-JADE (SJADE) algorithm in [9] to provide an initial estimate of the virtual channel matrix $A(H)$. Then, we use the modulation assumption to remove the partial phase ambiguity for the estimated $A(H)$. The details of each step are presented in the following subsections.

3.3.1. Pre-Estimate the Virtual Channel

As the real part and imaginary part of the $s$ may be dependent on each other, we cannot use the traditional ICA algorithm to estimate the virtual channel. Thus, we have to employ the independent subspace analysis (ISA) algorithm to estimate the virtual channel. Here, we choose the SJADE algorithm. However, it should be noted that there are remaining ambiguities between the estimated sources and the true sources for the ISA algorithm.

3.3.2. Remove Partial Remaining Ambiguity

For the SJADE algorithm, the original sources can be recovered up to block permutation and subspace ambiguities, i.e.,

$$\widehat{\tilde{s}}=\tilde{D}\tilde{P}\tilde{s}$$

(14)

where $\tilde{D}=\mathrm{bdiag}\left\{\begin{array}{cccc}{\tilde{E}}_1& {\tilde{E}}_2& \cdots & {\tilde{E}}_{nP}\end{array}\right\}$, ${\tilde{E}}_i=\left[\begin{array}{cc}\cos {\theta }_i& -\sin {\theta }_i\\ \sin {\theta }_i& \cos {\theta }_i\end{array}\right]$ denotes the subspace ambiguity, and $\tilde{P}$ is the block permutation matrix.

It is obvious that the LF is not sensitive to the block permutation ambiguity since it only changes the order of the summation in the LF.

By using the Q power-law estimator in [12], we can estimate the ${\theta }_i$ to an unknown ambiguity factor $e^{j2\pi {\rho }_i/q}$:

$${\widehat{\theta }}_i=\frac{1}{q}\arg \left(E\left({\left(s^{*}\right)}^q\right){\displaystyle \sum _{v=1}^{N_b}{\left({\widehat{s}}_i(v)\right)}^q}\right)$$

(15)

where $\widehat{s}=\left(I_{nP}\otimes [\begin{array}{cc}1& 1\mathrm{j}\end{array}]\right)\widehat{\tilde{s}}$, ${\widehat{s}}_i$ is the $i\mathrm{th}$ element of the $\widehat{s}$, ${\rho }_i$ is an integer, and $q$ depends on the modulation. For PAM, $q=2$; for M-PSK, $q=M$; for QAM, $q=4$.

Then, $\tilde{D}={\tilde{D}}_1{\tilde{D}}_2$, where ${\tilde{D}}_1=\mathrm{bdiag}\left\{\begin{array}{cccc}{\widehat{\tilde{E}}}_1& {\widehat{\tilde{E}}}_2& \cdots & {\widehat{\tilde{E}}}_{nP}\end{array}\right\}$, ${\widehat{\tilde{E}}}_i=\left[\begin{array}{cc}\cos {\widehat{\theta }}_i& -\sin {\widehat{\theta }}_i\\ \sin {\widehat{\theta }}_i& \cos {\widehat{\theta }}_i\end{array}\right]$, ${\tilde{D}}_2=\mathrm{bdiag}\left\{\begin{array}{cccc}{\widehat{\tilde{F}}}_1& {\widehat{\tilde{F}}}_2& \cdots & {\widehat{\tilde{F}}}_{nP}\end{array}\right\}$, and ${\widehat{\tilde{F}}}_i=\left[\begin{array}{cc}\cos (2\pi {\rho }_i/q)& -\sin (2\pi {\rho }_i/q)\\ \sin (2\pi {\rho }_i/q)& \cos (2\pi {\rho }_i/q)\end{array}\right]$.

Since both $s$ and $s^{\prime }=Fs$ belong to the same modulation type, the LF is not sensitive to the remaining ambiguity ${\tilde{D}}_2$. Thus,

$$\begin{array}{cc}& {\displaystyle \sum _{s(v)\in {ℳ}^{nP}}\exp \left[-\frac{||y(v)-A(H)\tilde{s}(v)|{|}_F^2}{{\sigma }^2}\right]}\hfill \\ =& {\displaystyle \sum _{s(v)\in {ℳ}^{nP}}\exp \left[-\frac{||y(v)-A(\widehat{H}){\tilde{D}}_1{\tilde{D}}_2\tilde{s}(v)|{|}_F^2}{{\widehat{\sigma }}^2}\right]}\hfill \\ =& {\displaystyle \sum _{s^{\prime }(v)\in {ℳ}^{nP}}\exp \left[-\frac{||y(v)-A(\widehat{H}){\tilde{D}}_1{\tilde{s}}^{\prime }(v)|{|}_F^2}{{\widehat{\sigma }}^2}\right]}\hfill \\ =& {\displaystyle \sum _{s(v)\in {ℳ}^{nP}}\exp \left[-\frac{||y(v)-A(\widehat{H}){\tilde{D}}_1\tilde{s}(v)|{|}_F^2}{{\widehat{\sigma }}^2}\right]}\hfill \end{array}$$

(16)

where $F=\mathrm{diag}\left\{\begin{array}{cccc}{e}^{j2\pi {\rho }_1/q}& e^{j2\pi {\rho }_2/q}& \cdots & e^{j2\pi {\rho }_{nP}/q}\end{array}\right\}$, ${\tilde{s}}^{\prime }={\tilde{D}}_2\tilde{s}$ and $A(\widehat{H})$ denotes the estimated virtual channel matrix.

Therefore, the estimated virtual channel can be used to calculate the LF. The LF can be further expressed as

$$\begin{array}{ll}& \log \left(\mathrm{\Lambda }\left[y|\mathcal{C},ℳ,P,H,{\sigma }^2\right]\right)\\ =& \log \left(\mathrm{\Lambda }\left[y|\mathcal{C},ℳ,P,A(\widehat{H}),{\tilde{D}}_1,{\widehat{\sigma }}^2\right]\right)\\ =& -N_b\log \left(M^{nP}{\left(\pi {\widehat{\sigma }}^2\right)}^{n_{r}l}\right)\\ & +{\displaystyle \sum _{v=1}^{N_b}\log \left({\displaystyle \sum _{s(v)\in {ℳ}^{nP}}\exp \left[-\frac{||y(v)-A(\widehat{H}){\tilde{D}}_1\tilde{s}(v)|{|}_F^2}{{\widehat{\sigma }}^2}\right]}\right)}\end{array}$$

(17)

In summary, the proposed algorithm (Algorithm 1) is implemented as follows:

Algorithm 1 Joint Modulation Classification and User Number Detection

Step 1: Reconstruct the received samples with Equation (3) and compute the covariance of $y$ with (11). Step 2: For all pairs of $P\in {\mathrm{\Theta }}_1,ℳ\in {\mathrm{\Theta }}_2$ (1) Estimate the noise power with Equation (13). (2) Estimate the virtual channel with the SJADE algorithm in [9]. (3) Remove the partial remaining ambiguity with Equation (15). (4) Compute the value of LF with (17). (5) Compute the value of LF-MDL based function $-\mathrm{LF}+\frac{1}{2}\left(2n_r{n}_{t}P+1\right)\log N_b$. End for Step 3: Choose the one which minimizes the LF-MDL based function as the recognized user number and modulation.

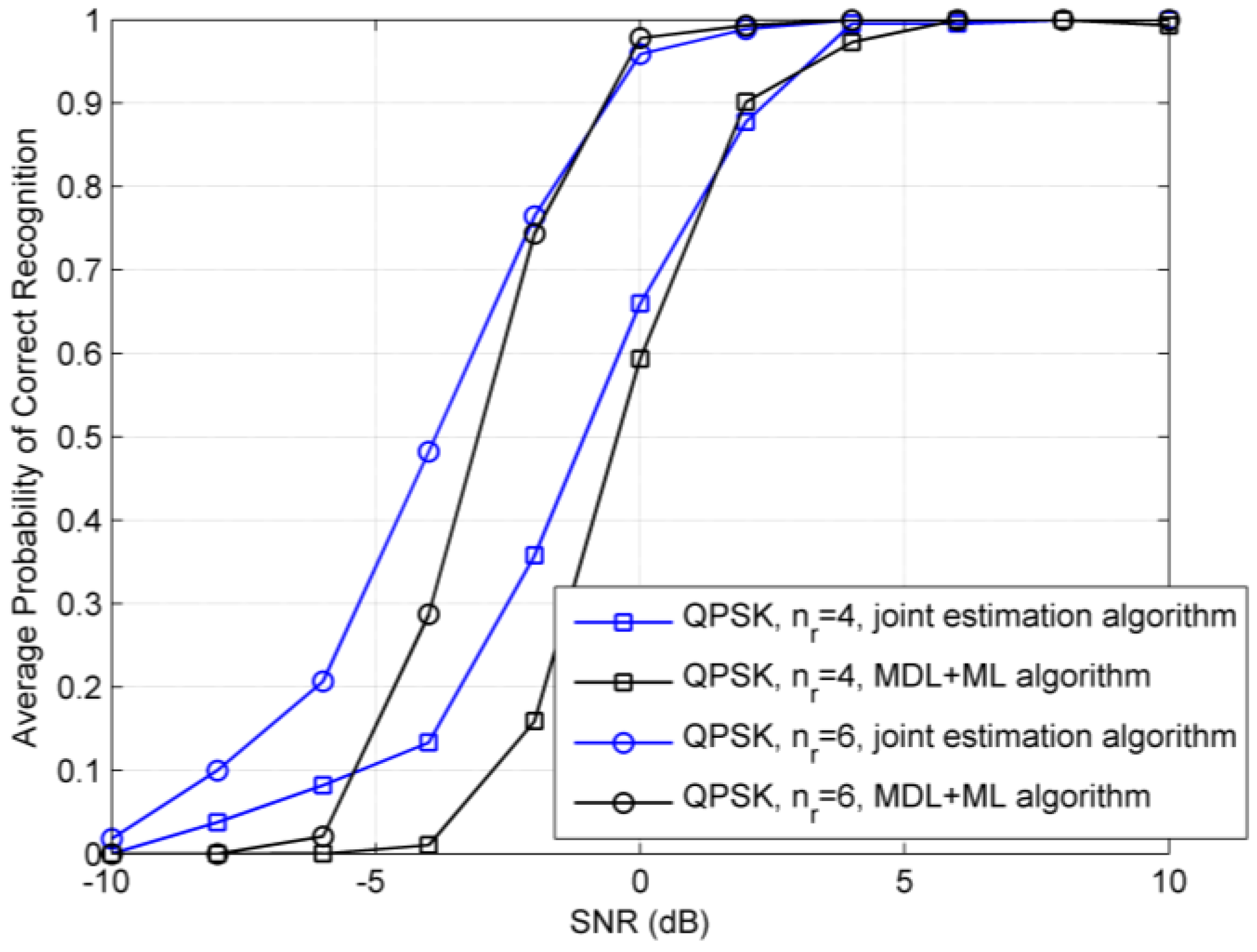
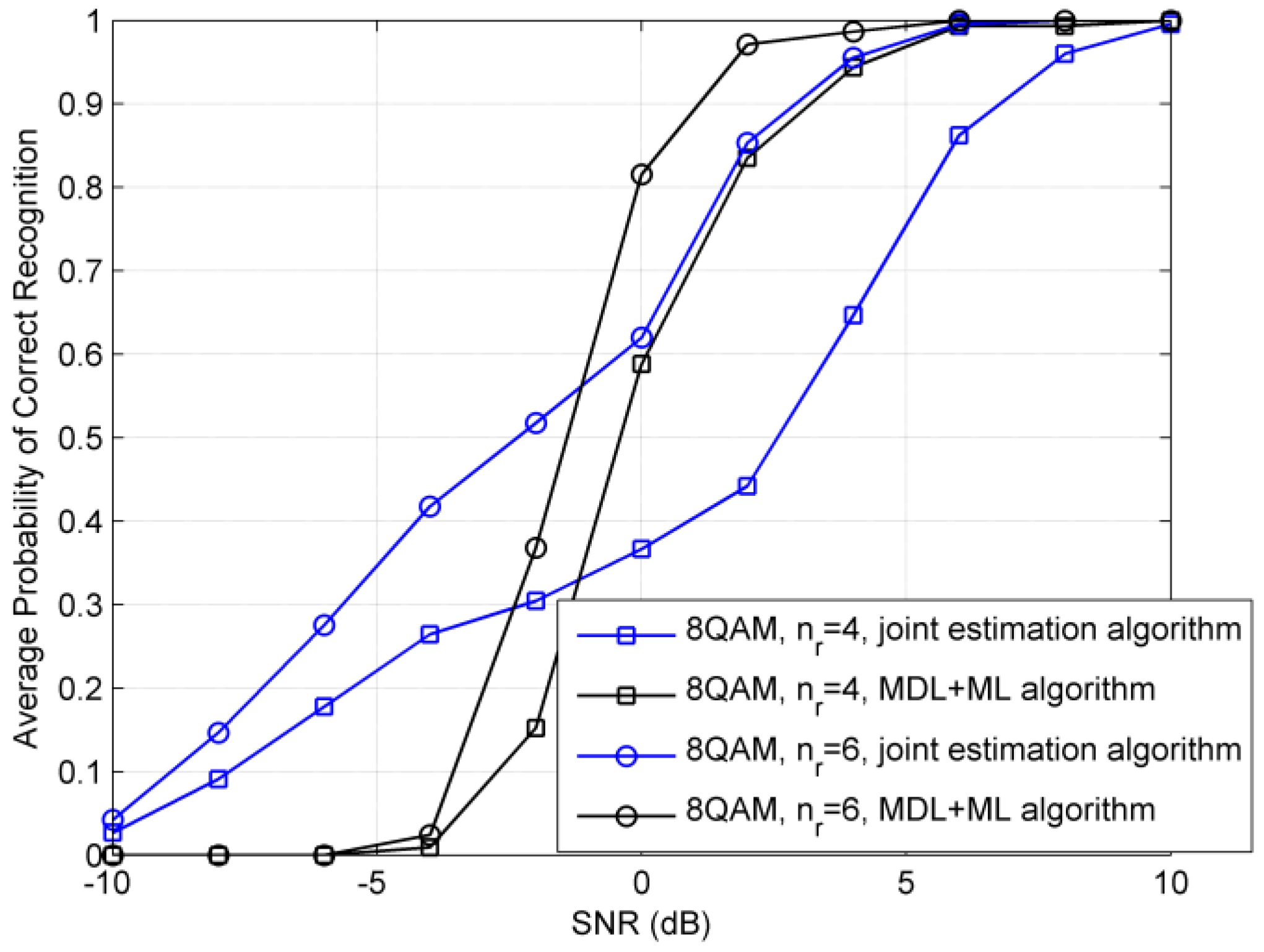
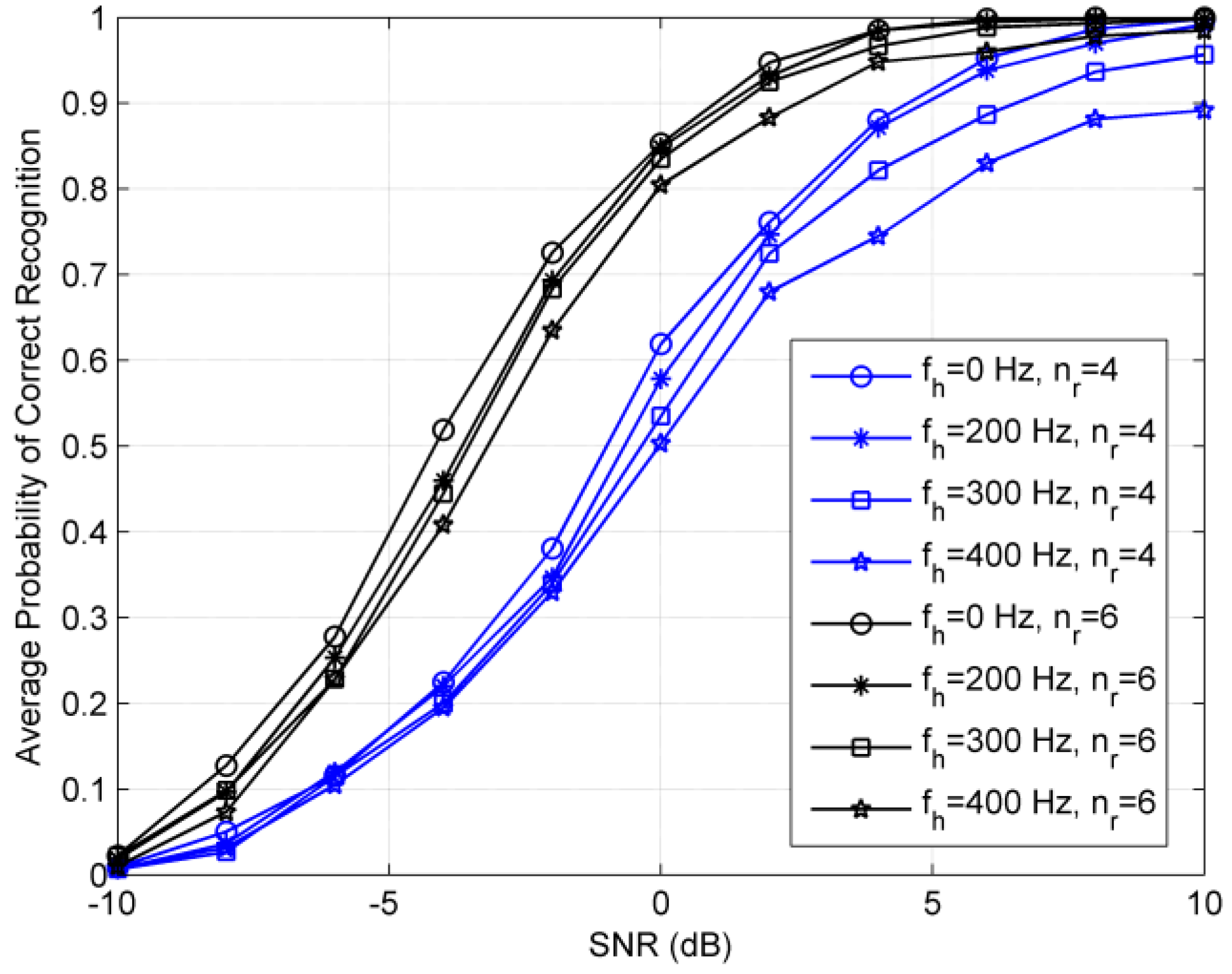
4. Simulation Results

In this section, the proposed method is validated by simulations. Simulations are carried out under the following conditions: (1) the multiuser MIMO-Alamouti system and a user number of 2; (2) the Rayleigh fading channel; (3) the number of receive antenna $n_r$ fixed at 4 and 6, severally; (4) temporally and spatially zero-mean white Gaussian additive noise; (5) a SNR varying from −10 dB to 10 dB; (6) a sample size of 500. The set of user number candidate is ${\mathrm{\Theta }}_1=\left\{\begin{array}{cc}1& 2\end{array}\right\}$, and the set of modulation candidate is ${\mathrm{\Theta }}_2=\{\begin{array}{ccc}\mathrm{QPSK},& 8\mathrm{PSK},& 8\mathrm{QAM}\}\end{array}$. For each modulation type, 200 Monte–Carlo trials are performed to approximate the average probability of correct recognition (APCR), where the correct recognition is defined as correctly determining both the user number and the modulation type. Moreover, we compare the proposed joint estimation method with a combined approach, where the user number is estimated by MDL [10] and the modulation is classified by maximizing the LF function (17).

Figure 1 presents the APCR for the proposed joint estimation algorithm and the combined approach, when QPSK is employed. This shows that the proposed joint estimation algorithm has better performance than the combined approach in most cases. The joint estimation algorithm can achieve perfect recognition at SNR = 4 dB, when $n_r$ is 4 and 6, severally. In addition, the performance of correct recognition is improved for two approaches with an increase in $n_r$. The performance of the joint estimation algorithm with $n_r=6$ is about 2–3 dB better compared with the case where $n_r=4$.

Figure 2 presents the APCR for the two approaches when 8PSK is employed. In this case, the proposed joint estimation algorithm can achieve perfect recognition at SNR = 4 dB and SNR = 2 dB, when $n_r$ is 4 and 6, respectively. Similarly, the proposed joint estimation algorithm has better performance than the combined approach in most cases. In addition, the performance of correct recognition is improved for the two approaches with an increase in $n_r$. The performance of the joint estimation algorithm with $n_r=6$ is about 2–3 dB better than the case where $n_r=4$. Compared with Figure 1, it can be seen that the performance of the proposed joint estimation algorithm for 8PSK is better than QPSK, which is due to the fact that the value of the LF-MDL-based function for 8PSK is markedly different from QPSK and 8QAM.

Figure 3 presents the APCR for the two approaches when 8QAM is employed. In this case, the proposed joint estimation algorithm has better performance than the combined approach when SNR ≤ −2 dB. In addition, the joint estimation algorithm can achieve perfect recognition at SNR = 10 dB and SNR = 6 dB, when $n_r$ is 4 and 6, respectively. Compared with Figure 1 and Figure 2, it can be seen that the performance of the proposed joint estimation algorithm is worst for 8QAM. Similarly, the performance of correct recognition is improved for 8QAM with an increase in $n_r$.

Figure 4 presents the APCR for the proposed joint estimation algorithm in the case of a fast fading Rayleigh channel with Jake’s Doppler spectrum, where the APCR is derived by averaging the cases of QPSK, 8PSK, and 8QAM. The sample period is fixed to 10⁻⁵ s. It shows that, the fast fading decreases the APCR. Moreover, the faster of the fading speed, the worse of the APCR. This is due to the fact that our joint estimation algorithm is designed for the quasi-static channel, which mismatches the fast fading channel.

5. Conclusions

In this paper, we propose a modulation classification and user number detection algorithm for multiuser MIMO-STBC systems. The proposed algorithm first estimates the noise power and the virtual channel matrix, and then recognizes the user number and modulation type jointly using the estimated noise power and the virtual channel matrix. Simulations verified that the proposed algorithm can correctly recognize the user number and modulation type at a high SNR when the channel fading is not very fast. Our future work will focus on cases where the channel is time-variant.