Methods of Generating Key Sequences Based on Parameters of Handwritten Passwords and Signatures
Abstract
:1. Introduction
2. Building a Template Database for Open and Hidden Biometric Images for Investigation
3. Analysis of Test Persons’ Handwritten Passwords and Signatures and Features Space
- Discard the first and last values for all dots with zero pressure.
- Perform one-dimensional Fourier transform for x(t), y(t), and p(t).
- Perform the inverse transform of these functions, taking into account that the output dimension should correspond to the nearest minimum integer multiple of the 2nd power.
3.1. The Distances between the Dots (Readings) of the Signature
- 4.
- Calculate the step: , where N is the number of dots resulting from the inverse Fourier transform, and Rd is the desirable matrix dimension that is a multiple of the second power.
3.2. Signature Appearance Characteristics
- The proportion of the length and the width of the signature.
- The center of the signature described by Cx, Cy, and Cp coordinates.
- An angle of slope for the signature. The angle of slope is a cosine of a mean angle of slope for a polygonal path of the signature to the X axis.
- An angle of slope between the centers of halves of the signature. After the center of the signature Cx has been found, the set (X,Y,Z) = {(xi,yi,pi)} should be divided into two subsets L = {(xi,yi,pi)|𝑥𝑖 > Cx} and R = {(xi,yi,pi)|𝑥𝑖 > Cx}. Further, the centers of the obtained sets L and R should be found:
3.3. Daubechies Wavelet Transform Coefficients
- Periodic addition, which means the beginning of the sequence is put at the end of the numerical series.
- Mirroring data at the ends of the sequence.
- The calculation of special scaling and wavelet functions that are applied to the beginning and the end of the sequence, presupposed by Gram–Schmidt orthogonalization.
3.4. Fourier Wavelet Transform Coefficients
- Time normalization (resampling, described above).
- Fourier series function decomposition.
- Harmonics amplitude normalization based on power.
3.5. Correlation Coefficients between Functions of the Signature
4. A Fuzzy Extractor Method
4.1. On the Presenting of Attribute Values in the Form of a Bit Sequence
4.2. Evaluation of Feature Informativeness Individually for each Subject
5. A Simulation Model of the Cryptographic Key Generation System
- a number of recording attributes (when the procedure of estimating the information content for the attribute is used);
- a number of signature (handwritten password) instances;
- an encryption algorithm;
- a block size (for Hadamard codes);
- the error-correcting ability (for BCH codes).
6. Results and Their Comparison with Early Achieved Results
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| IV | the procedure of estimation of informative value (stability) of features |
| NoI | number of signature instances when forming the open string |
| KL | the length of generated key in bits |
| Code | error correction code name |
| FAR1 | the probability of FAR for biometric unknown (secret) image |
| FAR2 | the probability of FAR for biometric known image |
| CI | confidence interval of FRR, FAR1, and FAR2 probabilities |
References
- Managing Cyber Risks in an Interconnected World. Key Findings from The Global State of Information Security Survey 2015. PricewaterhouseCoopers. Available online: http://www.pwc.ru/ru_RU/ru/riskassurance/publications/assets/managing-cyberrisks.pdf (accessed on 20 October 2016). (In Russian)
- Turnaround and Transformation in Cybersecurity. Key Findings from the Global State of Information Security Survey 2016. PricewaterhouseCoopers. Available online: http://www.pwc.ru/ru/riskassurance/publications/assets/gsiss2016-report.pdf (accessed on 20 October 2016).
- Center for Strategic and international Studies, Net Losses: Estimating the Global Cost of Cybercrime, June 2014. Available online: http://csis.org/files/attachments/140609_rp_economic_impact_cybercrime_report.pdf (accessed on 20 October 2016).
- Lozhnikov, P.S.; Sulavko, A.E.; Samotuga, A.E. Personal Identification and the Assessment of the Psychophysiological State While Writing a Signature. Information 2015, 6, 454–466. [Google Scholar] [CrossRef]
- Epifantsev, B.N.; Lozhnikov, P.S.; Kovalchuk, A.S. Hidden identification for operators of information-processing systems by heart rate variability in the course of professional activity. In Proceedings of the Dynamics of Systems, Mechanisms and Machines (Dynamics), Omsk, Russia, 11–13 November 2014; pp. 1–4.
- Lozhnikov, P.S.; Sulavko, A.E.; Volkov, D.A. Application of noise tolerant code to biometric data to verify the authenticity of transmitting information. In Proceedings of the Control and Communications (SIBCON), Omsk, Russia, 21–23 May 2015; pp. 1–3.
- Dodis, Y.; Reyzin, L.; Smith, A. Fuzzy Extractors: How to Generate Strong Keys from Biometrics and Other Noisy Data. In Advances in Cryptology—EUROCRYPT; Springer: Berlin/Heidelberg, Germany, 2004; pp. 79–100. [Google Scholar]
- Epifantsev, B.N. Hidden Identification of Psycho-Physiological State of the Human Operator in the Course of Professional Activity; SibADI Publisher: Omsk, Russia, 2013; p. 198. (In Russian) [Google Scholar]
- Lam, C.F.; Kamins, D. Signature verification through spectral analysis. Patter Recognit. 1989, 22, 39–44. [Google Scholar] [CrossRef]
- Graps, A. An Introduction to Wavelets. IEEE Comput. Sci. Eng. 1995, 2, 50–61. [Google Scholar] [CrossRef]
- Patil, P.; Hegadi, R. Offline Handwritten Signatures Classification Using Wavelet Packets and Level Similarity Based Scoring. Int. J. Eng. Technol. 2013, 5, 421–426. [Google Scholar]
- Ismail, A.; Ramadan, M.; El danaf, T.; Samak, A. Signature Recognition using Multi Scale Fourier Descriptor and Wavelet Transform. Int. J. Comput. Sci. Inf. Secur. 2010, 7, 14–19. [Google Scholar]
- McCabe, A. Neural network-based handwritten signature verification. J. Comput. 2008, 3, 9–22. [Google Scholar] [CrossRef]
- Deng, P.S.; Liao, H.-Y.M.; Ho, C.W.; Tyan, H.-R. Wavelet-based offline handwritten signature verification. Comput. Vis. Image Underst. 1999, 76, 173–190. [Google Scholar] [CrossRef]
- Fahmy, M. Online handwritten signature verification system based on DWT features extraction and neural network classification. Ain Shams Eng. J. 2010, 1, 59–70. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Morelos-Zaragoza, R. The Art of Error Correcting Coding; John Wiley & Sons: Hoboken, NJ, USA, 2006; p. 320. [Google Scholar]
- Solovjeva, F.I. Introduction to Coding Theory; Novosibirsk State University Publisher: Novosibirsk, Russia, 2006; p. 127. (In Russian) [Google Scholar]
- Eremenko, A.V.; Sulavko, A.E. Research of Algorithm for Generating Cryptographic Keys from Biometric Information of Users of Computer Systems; Information Technology; New Technologies Publisher: Moscow, Russia, 2013; pp. 47–51. (In Russian) [Google Scholar]
- Scotti, F.; Cimato, S.; Gamassi, M.; Piuri, V.; Sassi, R. Privacy-Aware Biometrics: Design and Implementation of a Multimodal Verification System. In Proceedings of the Annual Computer Security Applications Conference, Anaheim, CA, USA, 8–12 December 2008; pp. 130–139.
- Santos, M.F.; Aguilar, J.F.; Garcia, J.O. Cryptographic key generation using handwritten signature. In Proceedings of SPIE 6202, Biometric Technology for Human Identification III, Orlando, FL, USA, 17 April 2006; pp. 225–231.
- Yip, K.W.; Goh, A.; Ling, D.N.C.; Jin, A.T.B. Generation of replaceable cryptographic keys from dynamic handwritten signatures. In Proceedings of the ICB 2006 International Conference, Hong Kong, China, 5–7 January 2006; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3832, pp. 509–515. [Google Scholar]
- Hao, F.; Chan, C.W. Private key generation from on-line handwritten signatures. Inf. Manag. Comput. Secur. 2002, 10, 159–164. [Google Scholar]
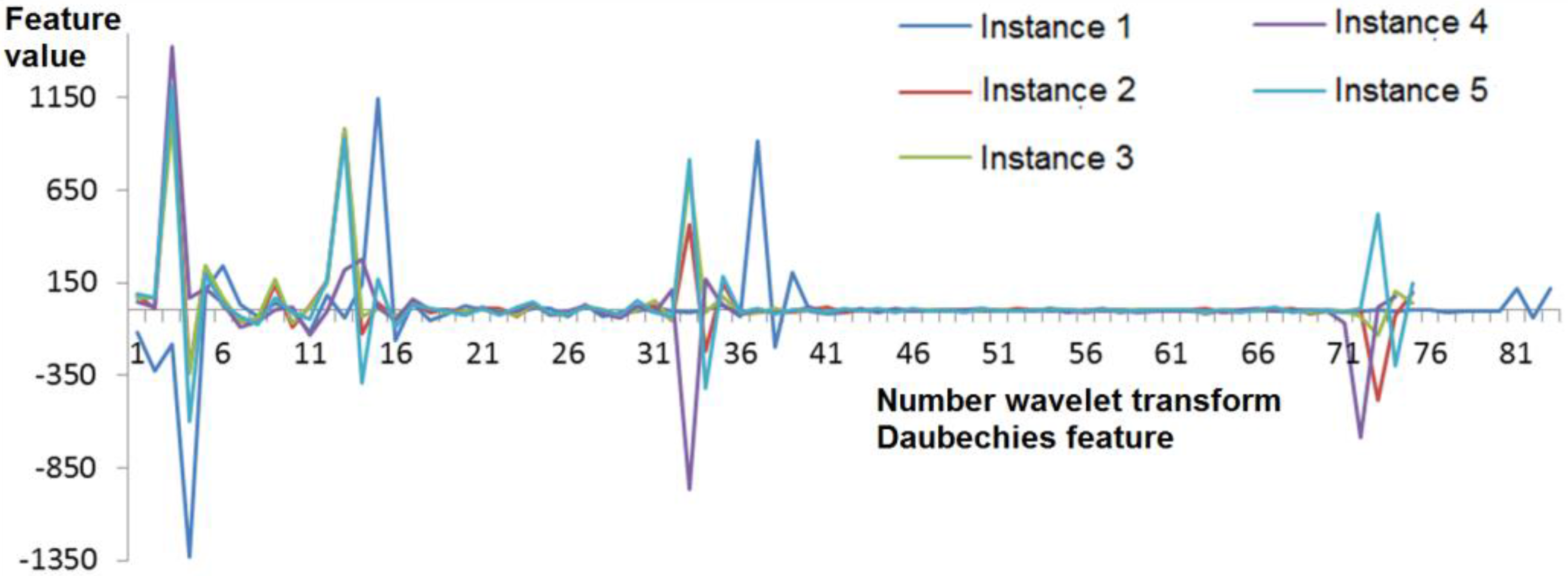
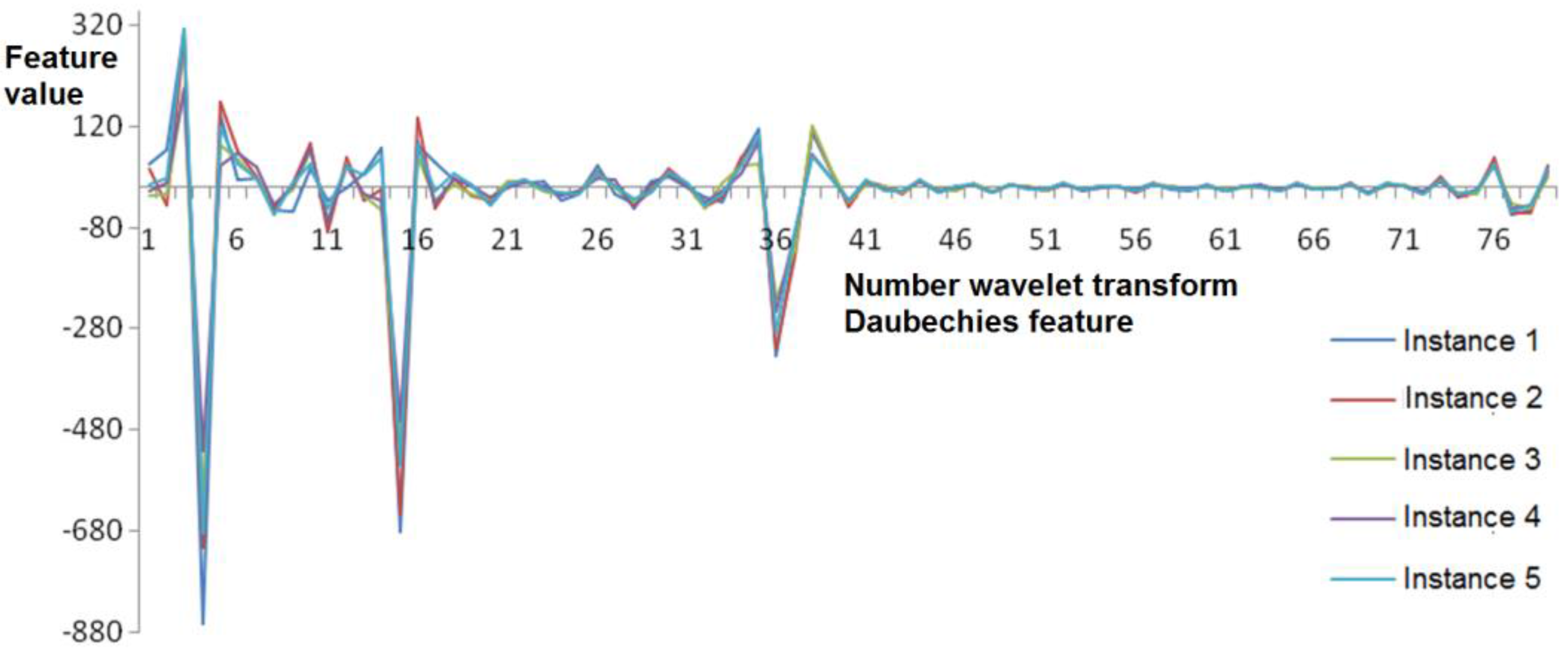
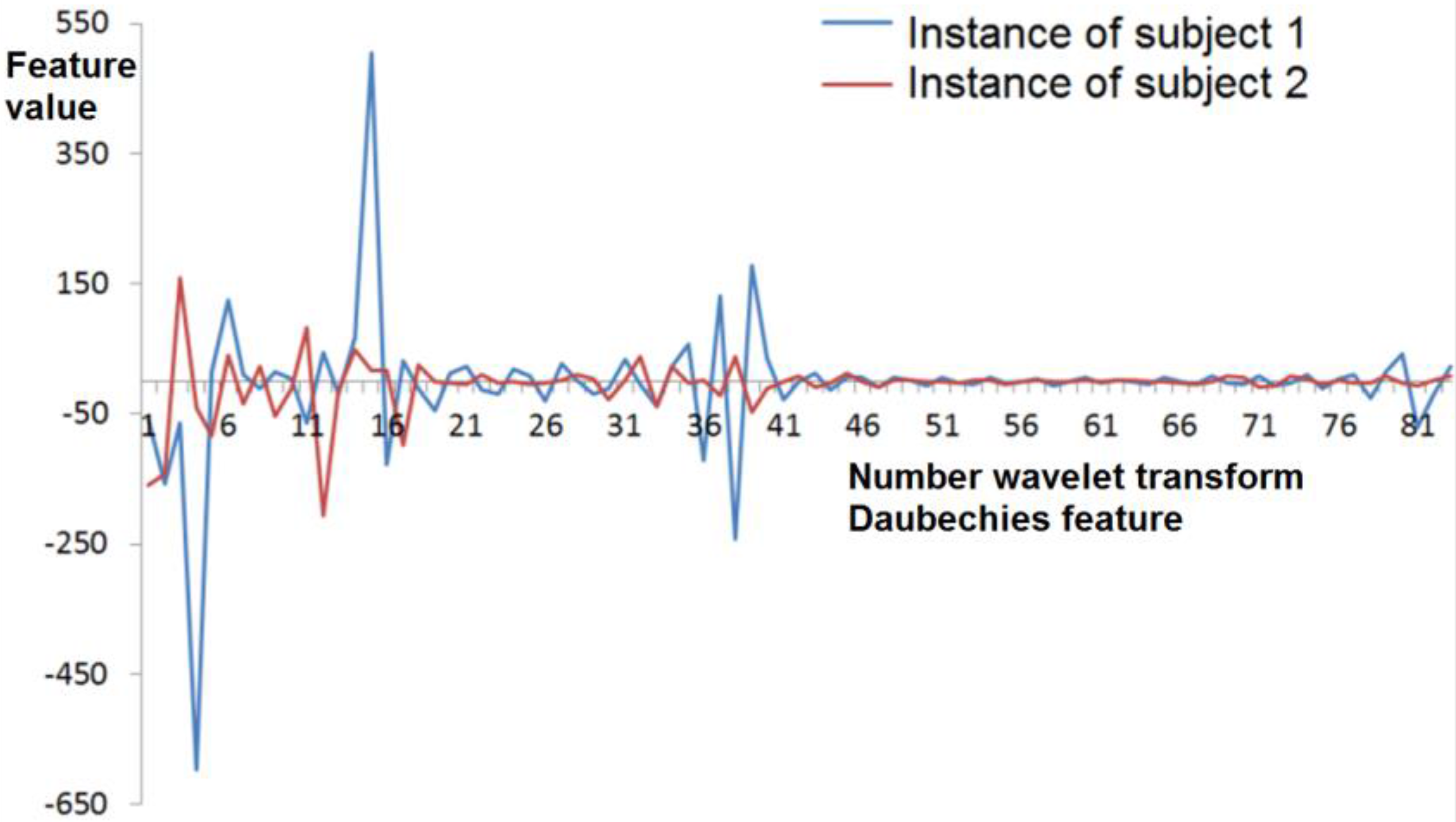
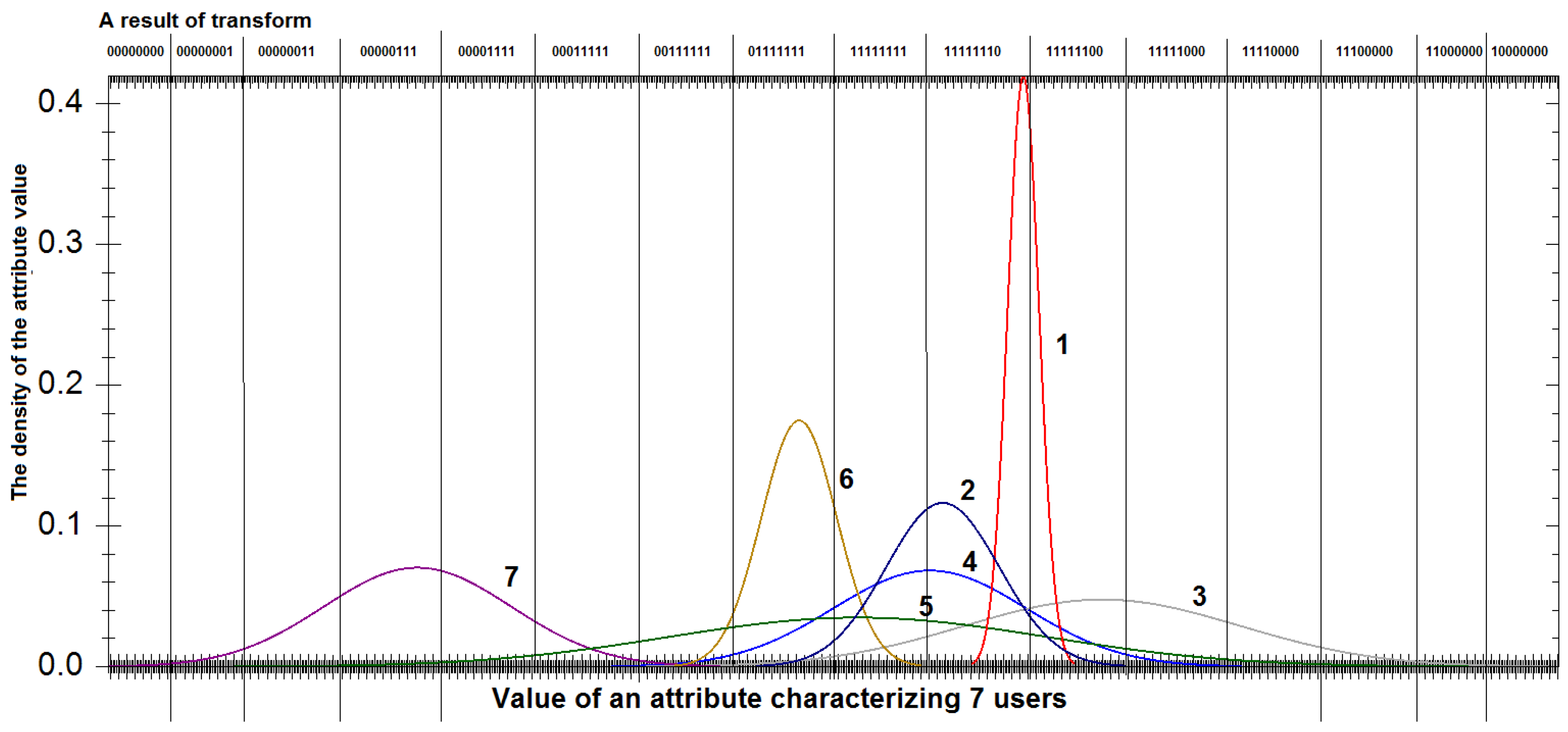
| No. | Attributes Group | Short Description | Number of Features |
|---|---|---|---|
| 1.1 | Distances in 3d | Distances between some signature dots are normalized on the signature length in three-dimensional space (the third dimension is pen pressure on the tablet) | 120 |
| 1.2 | Distances in 2d | Distances between some signature dots are normalized on the signature length in two-dimensional space (the tablet surface without taking into account the pressure) | 120 |
| 2 | Static | Some characteristics of the static signature image | 5 |
| 3.1 | Daubechies D4 | Daubechies wavelet transform coefficient D4 | 74–392 |
| 3.2 | Daubechies D6 | Daubechies wavelet transform coefficient D6 | 68–369 |
| 3.3 | Daubechies D8 | Daubechies wavelet transform coefficient D8 | 68–369 |
| 3.4 | Daubechies D10 | Daubechies wavelet transform coefficient D10 | 58–369 |
| 4.1 | Fourier v(t) | The first 16 amplitudes (the most low frequency) of function v(t) harmonics | 16 |
| 4.2 | Fourier p(t) | The first 16 amplitudes (the most low frequency) of function p(t) harmonics | 16 |
| 5 | Correlation between x(t), y(t), p(t), x’(t), y’(t), p’(t) | Correlation coefficients between pairs of signature x(t), y(t), p(t) functions and their derivatives—x’(t), y’(t), p’(t) functions | 15 |
| Attributes | IV | NoI | KL | Code | FRR | FAR1 | FAR2 | CI |
|---|---|---|---|---|---|---|---|---|
| Fourier v(t) and p(t) + correlation between x(t), y(t), p(t), x’(t), y’(t), p’(t) | + | 25 | 32 | BCH | 0.314 | 0.255 | 0.263 | 0.05/0.05/0.05 |
| Fourier v(t) and p(t) + correlation between x(t), y(t), p(t), x’(t), y’(t), p’(t) | + | 25 | 32 | BCH | 0.31 | 0.315 | 0.325 | 0.05/0.05/0.05 |
| Fourier v(t) and p(t) + correlation between x(t), y(t), p(t), x’(t), y’(t), p’(t) + static | + | 25 | 48 | BCH | 0.225 | 0.001 | 0.005 | 0.05/0.001/0.001 |
| Fourier v(t) and p(t) + correlation between x(t), y(t), p(t), x’(t), y’(t), p’(t) + static | + | 25 | 48 | BCH | 0.225 | 0.004 | 0.044 | 0.05/0.002/0.01 |
| Fourier v(t) and p(t) + correlation between x(t), y(t), p(t), x’(t), y’(t), p’(t) + static | − | 25 | 48 | BCH | 0.351 | 0.095 | 0.109 | 0.05/0.01/0.01 |
| Fourier v(t) and p(t) + correlation between x(t), y(t), p(t), x’(t), y’(t), p’(t) + static | − | 25 | 48 | BCH | 0.357 | 0.215 | 0.251 | 0.05/0.05/0.05 |
| Distances in 3d | − | 30 | 64 | BCH | 0.305 | 0.212 | 0.315 | 0.05/0.05/0.05 |
| Distances in 2d | − | 30 | 64 | BCH | 0.226 | 0.237 | 0.338 | 0.05/0.05/0.05 |
| Daubechies D4 | + | 20 | 168 | Hadamard | 0.343 | 0.33 | 0.35 | 0.05/0.05/0.05 |
| Daubechies D6 | + | 20 | 180 | Hadamard | 0.34 | 0.323 | 0.325 | 0.05/0.05/0.05 |
| Daubechies D8 | + | 20 | 172 | Hadamard | 0.36 | 0.34 | 0.345 | 0.05/0.05/0.05 |
| Daubechies D10 | + | 20 | 160 | Hadamard | 0.349 | 0.33 | 0.34 | 0.05/0.05/0.05 |
| Daubechies D4 | + | 20 | 160 | BCH | 0.11 | 0.105 | 0.11 | 0.01/0.01/0.01 |
| Daubechies D6 | + | 20 | 168 | BCH | 0.105 | 0.095 | 0.013 | 0.01/0.01/0.01 |
| Daubechies D8 | + | 20 | 160 | BCH | 0.115 | 0.11 | 0.122 | 0.01/0.01/0.01 |
| Daubechies D10 | + | 20 | 152 | BCH | 0.121 | 0.115 | 0.129 | 0.01/0.01/0.01 |
| Daubechies D4 + distances in 2d and 3d + static + Fourier v(t) and p(t) + correlation between x(t), y(t), p(t), x’(t), y’(t), p’(t) | + | 30 | 256 | BCH | 0.055 | 0.016 | 0.016 | 0.01/0.01/0.01 |
| Daubechies D6 + distances in 2d and 3d + static + Fourier v(t) and p(t) + correlation between x(t), y(t), p(t), x’(t), y’(t), p’(t) | + | 30 | 264 | BCH | 0.045 | 0.015 | 0.015 | 0.01/0.002/0.002 |
| Daubechies D8 + distances in 2d and 3d + static + Fourier v(t) and p(t) + correlation between x(t), y(t), p(t), x’(t), y’(t), p’(t) | + | 30 | 248 | BCH | 0.075 | 0.017 | 0.018 | 0.01/0.002/0.002 |
| Daubechies D10 + distances in 2d and 3d + static + Fourier v(t) and p(t) + correlation between x(t), y(t), p(t), x’(t), y’(t), p’(t) | + | 30 | 248 | BCH | 0.08 | 0.019 | 0.02 | 0.01/0.002/0.002 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lozhnikov, P.; Sulavko, A.; Eremenko, A.; Volkov, D. Methods of Generating Key Sequences Based on Parameters of Handwritten Passwords and Signatures. Information 2016, 7, 59. https://doi.org/10.3390/info7040059
Lozhnikov P, Sulavko A, Eremenko A, Volkov D. Methods of Generating Key Sequences Based on Parameters of Handwritten Passwords and Signatures. Information. 2016; 7(4):59. https://doi.org/10.3390/info7040059
Chicago/Turabian StyleLozhnikov, Pavel, Alexey Sulavko, Alexander Eremenko, and Danil Volkov. 2016. "Methods of Generating Key Sequences Based on Parameters of Handwritten Passwords and Signatures" Information 7, no. 4: 59. https://doi.org/10.3390/info7040059
APA StyleLozhnikov, P., Sulavko, A., Eremenko, A., & Volkov, D. (2016). Methods of Generating Key Sequences Based on Parameters of Handwritten Passwords and Signatures. Information, 7(4), 59. https://doi.org/10.3390/info7040059






