Super-Activation as a Unique Feature of Secure Communication in Malicious Environments

Abstract

The wiretap channel models secure communication between two users in the presence of an eavesdropper who must be kept ignorant of transmitted messages. This communication scenario is studied for arbitrarily varying channels (AVCs), in which the legitimate users know only that the true channel realization comes from a pre-specified uncertainty set and that it varies from channel use to channel use in an arbitrary and unknown manner. This concept not only captures the case of channel uncertainty, but also models scenarios in which malevolent adversaries influence or jam the transmission of the legitimate users. For secure communication over orthogonal arbitrarily varying wiretap channels (AVWCs) it has been shown that the phenomenon of super-activation occurs; that is, there are orthogonal AVWCs, each having zero secrecy capacity, which allow for transmission with positive rate if they are used together. It is shown that for such orthogonal AVWCs super-activation is generic in the sense that whenever super-activation is possible, it is possible for all AVWCs in a certain neighborhood as well. As a consequence, a super-activated AVWC is robust and continuous in the uncertainty set, although a single AVWC might not be. Moreover, it is shown that the question of super-activation and the continuity of the secrecy capacity solely depends on the legitimate link. Accordingly, the single-user AVC is subsequently studied and it is shown that in this case, super-activation for non-secure message transmission is not possible making it a unique feature of secure communication over AVWCs. However, the capacity for message transmission of the single-user AVC is shown to be super-additive including a complete characterization. Such knowledge is important for medium access control and in particular resource allocation as it determines the overall performance of a system.

1. Introduction

The architecture of today’s communication systems is designed such that data encryption and error correction are clearly separated. Data encryption is based on cryptographic principles and usually implemented at higher layers which abstracts out the underlying communication channel as an ideal bit pipe. The error correction is performed at the physical layer by adding redundancy into the message bits in order to combat the noisy channel. Such separation based approaches have been the typical solution in current communication systems.

In recent years there has been a growing interest in complementary approaches that realize security directly at the physical layer. Such information theoretic approaches to security establish data confidentiality and reliable communication jointly at the physical layer by exploiting the noisy and imperfect nature of the communication channel. This line of thinking goes back to Wyner, who introduced the so-called wiretap channel in [1]. This area of research provides a promising approach to achieve secrecy and to embed secure communication into wireless networks. Not surprisingly, it has drawn considerable attention recently [2,3,4,5,6,7] and has also been identified by operators of communication systems and national agencies as a key technique to secure future communication systems [8,9,10].

These studies are in particular relevant for wireless communication systems as the open nature of the wireless medium makes such systems inherently vulnerable for eavesdropping: Transmitted signals are received not only by intended users, but also easily eavesdropped upon by non-legitimate receivers. A common assumption of many studies is that all channels to the intended receivers and also to the non-legitimate eavesdroppers are known perfectly to all users. However, practical systems will always be limited in the availability of channel state information (CSI) due to nature of the wireless medium but also due to practical limitations such as estimation/feedback inaccuracy. In addition to that, the assumption of knowing the eavesdropper’s channel is often hard to justify in practice since malevolent eavesdroppers will not share any information about their channels to make eavesdropping even harder. Accordingly, such approaches to security must incorporate imperfect CSI assumptions to yield practically meaningful insights. A recent survey on secure communication under channel uncertainty and adversarial attacks can be found in [11].

In this paper, we model the uncertainty in CSI by assuming arbitrarily varying channels (AVCs) [12,13,14]. This concept assumes that the actual channel realization is unknown; rather, it is only known that this realization is from a known uncertainty set and that it may vary in an arbitrary and unknown manner from channel use to channel use. The concept of AVCs provides a very general and powerful framework as it not only models the case of channel uncertainty, but also captures scenarios with malevolent adversaries who maliciously influence or jam the legitimate transmission.

Secure communication over AVCs is then modeled by the arbitrarily varying wiretap channel (AVWC) which has been studied in [15,16,17,18,19,20,21,22]. It has been shown that it makes a substantial difference whether unassisted or common randomness (CR) assisted codes are used by the transmitter and the legitimate receiver. Specifically, if the AVC to the legitimate receiver possesses the so-called symmetrizability property, then the unassisted secrecy capacity is zero, while the CR-assisted secrecy capacity may be positive. A complete characterization of how unassisted and CR-assisted secrecy capacity relate to each other is given in [16,21]. However, a single-letter characterization of the secrecy capacity itself remains open. Only a multi-letter description of the CR-assisted secrecy capacity has been recently established in [20].

Wireless communication systems are usually composed of orthogonal sub-systems such as those that arise via orthogonal frequency division multiplexing (OFDM) or time division multiplexing (TDM). And the important issue in such systems is how the available resources should be allocated to these orthogonal sub-systems. Common sense tells us that the overall capacity of such a system is given by the sum of the capacities of all orthogonal sub-systems. The inherent world view of the additivity of classical resources is also reflected by Shannon who conjectured in [23] the additivity of the zero error capacity for orthogonal discrete memoryless channels (DMCs). This was later restated by Lovász in ([24], Problem 2) and recently further highlighted in [25].

To this end, let us consider a system consisting of two orthogonal ordinary DMCs ${\mathrm{W}}_1$ and ${\mathrm{W}}_2$. If both channels are accessed in an orthogonal way by using independent encoders and decoders, we obtain $C({\mathrm{W}}_1)+C({\mathrm{W}}_2)$ as an achievable transmission rate, where $C(·)$ denotes the capacity of the corresponding channel.

An interesting question is: Are there gains in capacity to be had by bonding the orthogonal channels and jointly accessing the resulting system ${\mathrm{W}}_1\otimes {\mathrm{W}}_2$ by using a joint encoder and decoder? From the operational definition of the capacity it is clear that we have

$$C({\mathrm{W}}_1\otimes {\mathrm{W}}_2)\ge C({\mathrm{W}}_1)+C({\mathrm{W}}_2)$$

(1)

since a joint use of both channels can only increase the capacity. However, it is known that the capacity of ordinary DMCs is additive under the average error criterion so that Equation (1) is actually satisfied with equality, i.e.,

$$C({\mathrm{W}}_1\otimes {\mathrm{W}}_2)=C({\mathrm{W}}_1)+C({\mathrm{W}}_2).$$

(2)

This means that joint encoding and decoding over orthogonal channels does not provide any gains in capacity and the overall capacity of an OFDM system is indeed given by the sum of the capacities of all orthogonal sub-channels.

Although this verifies what one usually would expect for the capacity of orthogonal channels, the question of additivity of the capacity function is in general by no means obvious or trivial to answer. As already mentioned, Shannon for example asked this question in 1956 for the zero error capacity [23]. He conjectured that the zero error capacity $C_0$ is additive, thus possessing the same behavior as ordinary DMCs: $C_0({\mathrm{W}}_1\otimes {\mathrm{W}}_2)=C_0({\mathrm{W}}_1)+C_0({\mathrm{W}}_2)$; similar to Equation (2). This problem was subsequently studied by Haemers [26] and later by Alon [27] who explicitly constructed counter-examples. Thus, there exist channels for which the zero error capacity is strictly greater when encoding and decoding are done jointly instead of independently. This means that the zero error capacity is super-additive and there exist channels for which “≥” in Equation (1) can actually be replaced by “>” so that

$$C_0({\mathrm{W}}_1\otimes {\mathrm{W}}_2)>C_0({\mathrm{W}}_1)+C_0({\mathrm{W}}_2)$$

holds. To date, only certain explicit examples are known that possess this property of super-additivity. A general characterization of which channels are super-additive or what further properties such channels possess remains open. In 1970 it was Ahlswede who showed that the capacity of the AVC under the maximum error criterion includes the characterization of the zero error capacity as a special case [28]. This is only one example demonstrating that Shannon’s question of additivity of the zero error capacity considerably influenced the research in discrete mathematics and graph theory, cf. for example ([29], Chapter 41). Thus, Shannon’s zero error capacity is closely related to AVCs, making it worth studying this question also from an AVC perspective.

The extreme case of non-additivity in Equation (1) occurs when for a system consisting of two orthogonal “useless” channels, i.e., having zero capacity $C({\mathrm{W}}_1)=C({\mathrm{W}}_2)=0$, it holds that $C({\mathrm{W}}_1\otimes {\mathrm{W}}_2)>0$. This phenomenon is called super-activation: Two channels each with zero capacity can be used together to super-activate the whole system giving it a positive capacity. This phenomenon has been observed and studied in particular in the area of quantum information theory [30,31].

Very recently the phenomenon of super-activation has been observed for classical communication as well. Super-activation can occur for secure communication over AVCs and there exist orthogonal “useless” AVWCs, i.e., having zero secrecy capacity, whose overall secrecy capacity is strictly positive [17]. This phenomenon of super-activation and its resulting secrecy capacity have then been completely characterized in [21].

In this paper we further explore the phenomenon of super-activation for AVWCs and its contributions are as follows. After introducing the system model in Section 2, we show that super-activation is not an isolated phenomenon in the sense that whenever two AVWCs can be super-activated, this is also true for all AVWCs in a certain neighborhood. As a consequence, we show that the secrecy capacity of a super-activated AVWC is continuous in the underlying uncertainty set, although this might not be the case for one of the AVWCs itself. Furthermore, we show that the question of whether super-activation is possible or not depends only on the legitimate channel, making it independent of the eavesdropper channel. This is the content of Section 3.

From a super-activation and continuity perspective, the legitimate AVC is more important than the eavesdropper AVC. Accordingly, we subsequently study these issues for the single-user AVC in detail in Section 4. Surprisingly, this has not been done so far to the best of our knowledge and we show that super-activation is not possible for public message transmission, making this a unique phenomenon of secure communication over AVWCs. However, we show that the single-user AVC indeed possesses the property of super-additivity which means that a joint use of orthogonal AVCs can provide gains in capacity. With this we provide a complete characterization of super-additivity and super-activation for the capacity of a single-user AVC. Finally, a discussion is given in Section 5.

Notation

Discrete random variables are denoted by capital letters and their realizations and ranges by lower case and script letters, respectively; all logarithms and information quantities are taken to the base 2; $X-Y-Z$ denotes a Markov chain of random variables X, Y, and Z in this order; $\mathcal{P}(\mathcal{X})$ is the set of all probability distributions on $\mathcal{X}$; the mutual information between the input random variable X and the output random variable Y of a channel W is denoted by $I(X;Y)=I(P_X,W)$, where the latter notation is interchangeably used to emphasize the dependence on the input distribution $P_X$ and the channel.

2. Arbitrarily Varying Wiretap Channels

In this section we introduce the problem of secure communication over arbitrarily varying channels [12,13,14]. Such channel conditions appear for example in fast fading environments but also, more importantly, in scenarios in which malevolent adversaries actively influence or jam the legitimate transmission. This is the AVWC [15,16,17,18,19,20,21,22] which is depicted in Figure 1.

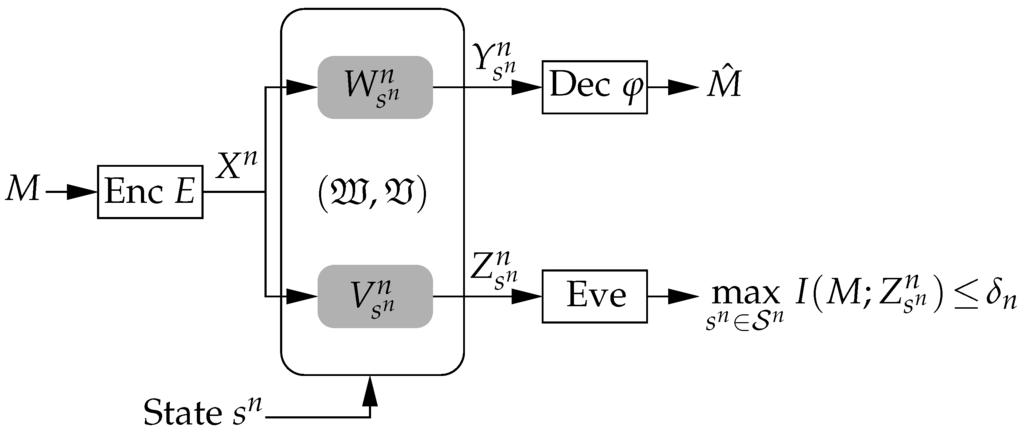
Figure 1. Arbitrarily varying wiretap channel. The transmitter encodes the message M into the codeword $X^n=E(M)$ and transmits it over the AVWC to the legitimate receiver, which has to decode its intended message $\widehat{M}=\phi (Y_{s^n}^n)$ for any state sequence $s^n\in {\mathcal{S}}^n$. At the same time, the eavesdropper must be kept ignorant of M by requiring ${max}_{s^n\in {\mathcal{S}}^n}I(M;Z_{s^n}^n)\le {\delta }_n$.

2.1. System Model

The channel state may vary in an unknown and arbitrary manner from channel use to channel use and this uncertainty in CSI is modeled with the help of a finite state set $\mathcal{S}$. Then the communication links to the legitimate receiver and the eavesdropper are given by stochastic matrices $W:\mathcal{X}\times \mathcal{S}\to \mathcal{P}(\mathcal{Y})$ and $V:\mathcal{X}\times \mathcal{S}\to \mathcal{P}(\mathcal{Z})$ with $\mathcal{X}$ the finite input alphabet and $\mathcal{Y}$ and $\mathcal{Z}$ the finite output alphabets at the legitimate receiver and eavesdropper respectively. We interchangeably also write $W_s:\mathcal{X}\to \mathcal{P}(\mathcal{Y})$ and $V_s:\mathcal{X}\to \mathcal{P}(\mathcal{Z})$ with $s\in \mathcal{S}$.

For a fixed state sequence $s^n=(s_1,s_2,...,s_n)\in {\mathcal{S}}^n$ of length n, the discrete memoryless channel to the legitimate receiver is given by $W_{s^n}^n(y^n|x^n)=W^n(y^n|x^n,s^n)={\prod }_{i=1}^{n}W(y_i|x_i,s_i)$ for all input and output sequences $x^n\in {\mathcal{X}}^n$ and $y^n\in {\mathcal{Y}}^n$.

Definition 1. 

The arbitrarily varying channel (AVC) $\mathfrak{W}$ to the legitimate receiver is defined as the family of channels for all state sequences $s^n\in {\mathcal{S}}^n$ as

$$\mathfrak{W}=\left\{W_{s^n}^n:s^n\in {\mathcal{S}}^n\right\}.$$

We further need the definition of an averaged channel which is defined for any probability distribution $q\in \mathcal{P}(\mathcal{S})$ as

$${\overline{W}}_q(y|x)=\sum _{s\in \mathcal{S}}W(y|x,s)q(s)$$

(3)

for all $x\in \mathcal{X}$ and $y\in \mathcal{Y}$. An important property of an AVC is the so-called concept of symmetrizability as introduced next.

Definition 2. 

An AVC $\mathfrak{W}$ is called symmetrizable if there exists a channel (stochastic matrix) $\sigma :\mathcal{X}\to \mathcal{P}(\mathcal{S})$ such that

$$\sum _{s\in \mathcal{S}}W(y|x,s)\sigma (s|x^{\prime })=\sum _{s\in \mathcal{S}}W(y|x^{\prime },s)\sigma (s|x)$$

(4)

holds for all $x,x^{\prime }\in \mathcal{X}$ and $y\in \mathcal{Y}$.

Roughly speaking, symmetrizability means that the AVC can “simulate” a valid channel input which makes it impossible for the receiver to decide on the correct codeword sent by the transmitter. This can be seen by writing the left hand side of Equation (4) as $\tilde{W}(y|x,x^{\prime })={\sum }_{s\in \mathcal{S}}W(y|x,s)\sigma (s|x^{\prime })$. Now symmetrizability means that this channel is symmetric in both inputs x and $x^{\prime }$, i.e., $\tilde{W}(y|x,x^{\prime })=\tilde{W}(y|x^{\prime },x)$.

In a similar way we can define the channel to the eavesdropper. For fixed $s^n\in {\mathcal{S}}^n$ the discrete memoryless channel is given by $V_{s^n}^n(z^n|x^n)=V^n(z^n|x^n,s^n)={\prod }_{i=1}^{n}V(z_i|x_i,s_i)$. We also set $\mathfrak{V}=\{V_{s^n}^n:s^n\in {\mathcal{S}}^n\}$ and ${\overline{V}}_q(z|x)={\sum }_{s\in \mathcal{S}}V(z|x,s)q(s)$ for $q\in \mathcal{P}(\mathcal{S})$.

Definition 3. 

The arbitrarily varying wiretap channel (AVWC) $(\mathfrak{W},\mathfrak{V})$ is given by its marginal AVCs $\mathfrak{W}$ and $\mathfrak{V}$ with common input as

$$(\mathfrak{W},\mathfrak{V})=\left(\{W_{s^n}^n:s^n\in {\mathcal{S}}^n\},\{V_{s^n}^n:s^n\in {\mathcal{S}}^n\}\right).$$

Finally, we need a concept to measure the distance between two channels. As in [22] we define the distance between two channels $W_1,W_2:\mathcal{X}\to \mathcal{P}(\mathcal{Y})$ based on the total variation distance as

$$d(W_1,W_2)=\underset{x\in \mathcal{X}}{max}\sum _{y\in \mathcal{Y}}|W_1(y|x)-W_2(y|x)|.$$

(5)

Now, this generalizes to a distance between two AVCs as follows. For two AVWCs ${\mathfrak{W}}_1$ and ${\mathfrak{W}}_2$ with finite state sets ${\mathcal{S}}_1$ and ${\mathcal{S}}_2$ we define uncertainty sets ${\mathcal{W}}_1=\{W_{s_1}:s_1\in {\mathcal{S}}_1\}$ and ${\mathcal{W}}_2=\{W_{s_2}:s_2\in {\mathcal{S}}_2\}$. Then the distance between these two sets of channels is

$$\begin{array}{cc}\hfill d_1({\mathcal{W}}_1,{\mathcal{W}}_2)& =\underset{s_2\in {\mathcal{S}}_2}{max}\underset{s_1\in {\mathcal{S}}_1}{min}d(W_{s_1},W_{s_2})\hfill \\ \hfill d_2({\mathcal{W}}_1,{\mathcal{W}}_2)& =\underset{s_1\in {\mathcal{S}}_1}{max}\underset{s_2\in {\mathcal{S}}_2}{min}d(W_{s_1},W_{s_2})\hfill \end{array}$$

so that the distance between the AVCs ${\mathfrak{W}}_1$ and ${\mathfrak{W}}_2$ is given as

$$D({\mathfrak{W}}_1,{\mathfrak{W}}_2)=max\left\{d_1({\mathcal{W}}_1,{\mathcal{W}}_2),d_2({\mathcal{W}}_1,{\mathcal{W}}_2)\right\}.$$

Roughly speaking, the distance $D({\mathfrak{W}}_1,{\mathfrak{W}}_2)$ between two AVCs ${\mathfrak{W}}_1$ and ${\mathfrak{W}}_2$ is given by the largest distance in Equation (5) between all possible channel realizations in the corresponding state sets.

The distance $D({\mathfrak{V}}_1,{\mathfrak{V}}_2)$ between two eavesdropper AVCs is defined accordingly so that the distance between two AVWCs $({\mathfrak{W}}_1,{\mathfrak{V}}_1)$ and $({\mathfrak{W}}_2,{\mathfrak{V}}_2)$ is finally given by

$$D(({\mathfrak{W}}_1,{\mathfrak{V}}_1),({\mathfrak{W}}_2,{\mathfrak{V}}_2))=max\left\{D({\mathfrak{W}}_1,{\mathfrak{W}}_2),D({\mathfrak{V}}_1,{\mathfrak{V}}_2)\right\}.$$

2.2. Code Concepts

For communication over AVCs it makes a substantial difference whether unassisted (deterministic) or more sophisticated code concepts based on common randomness (CR) are used. Indeed, the unassisted capacity of an AVC can be zero, while the corresponding CR-assisted capacity is positive [12,13,14].

2.2.1. Unassisted Codes

Unassisted codes refer to codes whose encoder and decoder are pre-specified and fixed prior to the transmission as shown in Figure 1.

Definition 4. 

An unassisted $(n,M_n)$-code$\mathcal{C}$ consists of a stochastic encoder at the transmitter

$$E:\mathcal{M}\to \mathcal{P}({\mathcal{X}}^n)$$

(6)

with a set of messages $\mathcal{M}=\{1,...,M_n\}$ and a deterministic decoder at the legitimate receiver

$$\phi :{\mathcal{Y}}^n\to \mathcal{M}.$$

(7)

Remark 1. 

Since the encoder in Equation (6) and the decoder in Equation (7) are fixed prior to the transmission of the message, they must be universally valid for all possible state sequences $s^n\in {\mathcal{S}}^n$ simultaneously.

The average probability of error of such a code for a given state sequence $s^n\in {\mathcal{S}}^n$ is given by

$${\overline{e}}_n(s^n)=\frac{1}{\left|\mathcal{M}\right|}\sum _{m\in \mathcal{M}}\sum _{x^n\in {\mathcal{X}}^n}\sum _{y^n:\phi (y^n)\ne m}{W}^n(y^n|x^n,s^n)E(x^n|m).$$

The confidentiality of the message is ensured by requiring ${max}_{s^n\in {\mathcal{S}}^n}I(M;Z_{s^n}^n)\le {\delta }_n$ for some ${\delta }_n>0$ with M the random variable uniformly distributed over the set of messages $\mathcal{M}$ and $Z_{s^n}^n=(Z_{s_1},Z_{s_2},...,Z_{s_n})$ the output at the eavesdropper for state sequence $s^n\in {\mathcal{S}}^n$. This criterion is termed strong secrecy [32,33] and the reasoning is to control the total amount of information leaked to the eavesdropper. This yields the following definition.

Definition 5. 

A rate $R_S>0$ is an achievable secrecy rate for the AVWC $(\mathfrak{W},\mathfrak{V})$ if for all $\tau >0$ there exists an $n(\tau )\in \mathbb{N}$, positive null sequences ${\left\{{\lambda }_n\right\}}_{n\in \mathbb{N}}$, ${\left\{{\delta }_n\right\}}_{n\in \mathbb{N}}$, and a sequence of $(n,M_n)$-codes ${\left\{{\mathcal{C}}_n\right\}}_{n\in \mathbb{N}}$ such that for all $n\ge n(\tau )$ we have $\frac{1}{n}log{M}_n\ge R_S-\tau$,

$$\underset{s^n\in {\mathcal{S}}^n}{max}{\overline{e}}_n(s^n)\le {\lambda }_n,$$

and

$$\underset{s^n\in {\mathcal{S}}^n}{max}I(M;Z_{s^n}^n)\le {\delta }_n.$$

The unassisted secrecy capacity $C_S(\mathfrak{W},\mathfrak{V})$ of the AVWC $(\mathfrak{W},\mathfrak{V})$ is given by the maximum of all achievable rates $R_S$.

Unfortunately, it has been shown that unassisted codes with a pre-specified encoder and decoder will not work for symmetrizable channels, cf. Definition 2. Thus the unassisted capacity will be zero [14] and more sophisticated code concepts based on CR are needed.

2.2.2. CR-Assisted Codes

CR is a powerful coordination resource and can be realized for example based on a common synchronization procedure or a satellite signal. It is modeled by a random variable Γ which takes values in a finite set ${\mathcal{G}}_n$ according to a distribution $P_{\Gamma }\in \mathcal{P}({\mathcal{G}}_n)$. This enables the transmitter and the receiver to choose their encoder in Equation (6) and decoder in Equation (7) according to the actual realization $\gamma \in {\mathcal{G}}_n$ as shown in Figure 2.

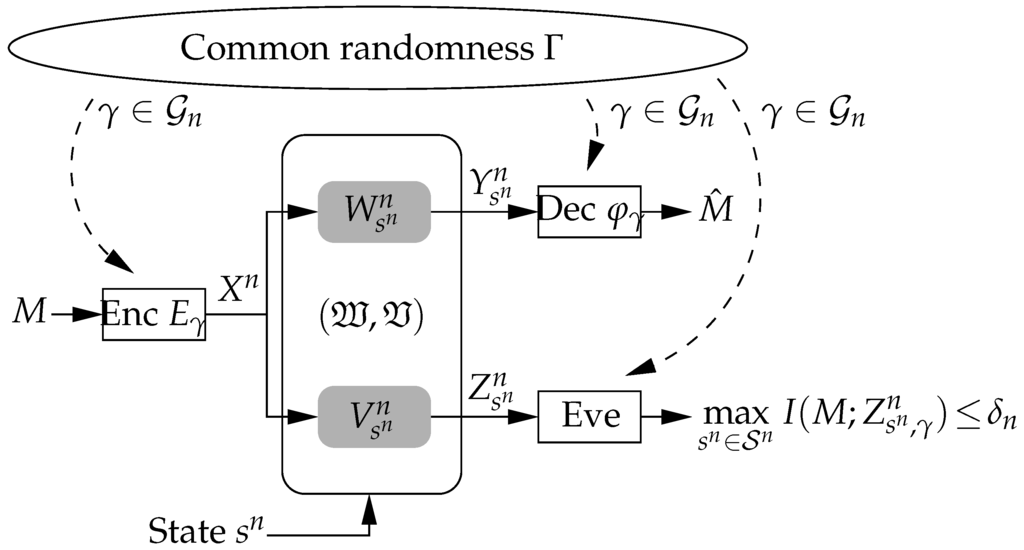
Figure 2. CR is available to all users including the eavesdropper. The transmitter and receiver can adapt their encoder and decoder according to the actual CR realization $\gamma \in {\mathcal{G}}_n$.

Definition 6. 

A CR-assisted $(n,M_n,{\mathcal{G}}_n,P_{\Gamma })$-code${\mathcal{C}}_{\mathbf{CR}}$ is given by a family of unassisted codes

$$\left\{\mathcal{C}(\gamma ):\gamma \in {\mathcal{G}}_n\right\}$$

together with a random variable Γ taking values in ${\mathcal{G}}_n$ with $|{\mathcal{G}}_n|<\infty$ according to $P_{\Gamma }\in \mathcal{P}({\mathcal{G}}_n)$.

The reliability and secrecy constraints extend to CR-assisted codes in a natural way: The mean average probability of error is

$$\begin{array}{c}\hfill {\overline{e}}_{\text{CR}}=\underset{s^n\in {\mathcal{S}}^n}{max}\frac{1}{\left|\mathcal{M}\right|}\sum _{m\in \mathcal{M}}\sum _{\gamma \in {\mathcal{G}}_n}\sum _{x^n\in {\mathcal{X}}^n}\sum _{y^n:{\phi }_{\gamma }(y^n)\ne m}{W}^n(y^n|x^n,s^n)E_{\gamma }(x^n|m)P_{\Gamma }(\gamma )\end{array}$$

where $E_{\gamma }$ and ${\phi }_{\gamma }$ indicate that the encoder and decoder are chosen according to the CR realization $\gamma \in {\mathcal{G}}_n$. Accordingly, the secrecy criterion becomes

$$\underset{s^n\in {\mathcal{S}}^n}{max}\sum _{\gamma \in {\mathcal{G}}_n}I(M;Z_{s^n,\gamma }^n)P_{\Gamma }(\gamma )\le {\delta }_n$$

(8)

where $Z_{s^n,\gamma }^n$ indicates that the observed output at the eavesdropper depends on the chosen encoder $E_{\gamma }$, $\gamma \in {\mathcal{G}}_n$.

Remark 2. 

Note that the secrecy criterion Equation (8) can further be strengthened by requiring

$$\underset{s^n\in {\mathcal{S}}^n}{max}\underset{\gamma \in {\mathcal{G}}_n}{max}I(M;Z_{s^n,\gamma }^n)\le {\delta }_n,$$

i.e., the average over all CR in Equation (8) is replaced by the maximum. Surprisingly, this strengthening comes at no cost and does not decrease the secrecy capacity, cf. [20]. The stronger criterion has the advantage that it protects the message even in the scenario in which the eavesdropper is aware of the CR realization $\gamma \in {\mathcal{G}}_n$, cf. Figure 2.

Then the definitions of a CR-assisted achievable secrecy rate and the CR-assisted secrecy capacity $C_{S,\text{CR}}(\mathfrak{W},\mathfrak{V})$ of the AVWC $(\mathfrak{W},\mathfrak{V})$ follow accordingly.

2.3. Capacity Results

There has been some work done in order to understand the secrecy capacity of the AVWC [15,16,17,18,19,20,21,22] which is briefly reviewed in the following. If CR is available, the transmitter and the legitimate receiver can coordinate their choice of encoder and decoder. This scenario has been studied in [15,16,17,18,20,22], but despite these efforts a single-letter characterization remains unknown to date (if it exists at all). Only a multi-letter description has been found in [20].

Theorem 1 

([20]). A multi-letter description of the CR-assisted secrecy capacity $C_{S,\text{CR}}(\mathfrak{W},\mathfrak{V})$ of the AVWC $(\mathfrak{W},\mathfrak{V})$ is

$$\begin{array}{c}\hfill C_{S,\text{CR}}(\mathfrak{W},\mathfrak{V})=\underset{n\to \infty }{lim}\frac{1}{n}\underset{U-X^n-({\overline{Y}}_q^n,Z_{s^n}^n)}{max}\left(\underset{q\in \mathcal{P}(\mathcal{S})}{min}I(U;{\overline{Y}}_q^n)-\underset{s^n\in {\mathcal{S}}^n}{max}I(U;Z_{s^n}^n)\right)\end{array}$$

with ${\overline{Y}}_q^n$ the random variable associated with the output of the averaged channel ${\overline{W}}_q^n={\sum }_{s^n\in {\mathcal{S}}^n}{q}^n(s^n)W_{s^n}$, $q\in \mathcal{P}(\mathcal{S})$.

If CR is not available to the transmitter and legitimate receiver, unassisted codes must be used and the corresponding unassisted secrecy capacity has been completely characterized in terms of its CR-assisted secrecy capacity [16,21].

Theorem 2 

([16,21]). The unassisted secrecy capacity $C_S(\mathfrak{W},\mathfrak{V})$ of the AVWC $(\mathfrak{W},\mathfrak{V})$ possesses the following symmetrizability properties:

• If $\mathfrak{W}$ is symmetrizable, then $C_S(\mathfrak{W},\mathfrak{V})=0$.
• If $\mathfrak{W}$ is non-symmetrizable, then $C_S(\mathfrak{W},\mathfrak{V})=C_{S,\text{CR}}(\mathfrak{W},\mathfrak{V})$.

The unassisted secrecy capacity displays a dichotomous behavior similar to the capacity of the single-user AVC: The unassisted secrecy capacity $C_S(\mathfrak{W},\mathfrak{V})$ either equals its CR-assisted secrecy capacity $C_{S,\text{CR}}(\mathfrak{W},\mathfrak{V})$ or else is zero.

From Theorem 2 we see that it is only the symmetrizability of the legitimate AVC $\mathfrak{W}$ that controls whether the unassisted secrecy capacity is zero or positive. However, it does not specify the sensitivity, meaning how rapidly the AVC $\mathfrak{W}$ can change from symmetrizable to non-symmetrizable. This is addressed by the next result.

Theorem 3 

([21]). If the unassisted secrecy capacity $C_S(\mathfrak{W},\mathfrak{V})$ of the AVWC $(\mathfrak{W},\mathfrak{V})$ satisfies $C_S(\mathfrak{W},\mathfrak{V})>0$, then there is an $ϵ>0$ such that for all AVWCs $({\mathfrak{W}}^{\prime },{\mathfrak{V}}^{\prime })$ satisfying $D((\mathfrak{W},\mathfrak{V}),({\mathfrak{W}}^{\prime },{\mathfrak{V}}^{\prime }))\le ϵ$ we have $C_S({\mathfrak{W}}^{\prime },{\mathfrak{V}}^{\prime })>0$.

This result shows the stability of positivity of the unassisted secrecy capacity: Wherever it is positive, i.e., $C_S(\mathfrak{W},\mathfrak{V})>0$, it remains positive in a certain neighborhood, i.e., $C_S({\mathfrak{W}}^{\prime },{\mathfrak{V}}^{\prime })>0$ for $D((\mathfrak{W},\mathfrak{V}),({\mathfrak{W}}^{\prime },{\mathfrak{V}}^{\prime }))\le ϵ$. Thus, if the AVC $\mathfrak{W}$ is non-symmetrizable, small changes in the uncertainty set will not make it symmetrizable.

To further explore the question of continuity for the AVWC, we need the function

$$\begin{array}{c}\hfill F(\mathfrak{W})=\underset{\sigma :\mathcal{X}\to \mathcal{P}(\mathcal{S})}{min}\left(\underset{x\ne x^{\prime }}{max}\sum _{y\in \mathcal{Y}}|\sum _{s\in \mathcal{S}}W(y|x^{\prime },s)\sigma (s|x)-\sum _{s\in \mathcal{S}}W(y|x,s)\sigma (s|x^{\prime })|\right).\end{array}$$

(9)

This function generalizes ideas from the concept of symmetrizability, cf. Definition 2. It is a continuous function of the legitimate AVC $\mathfrak{W}$ and the AVC $\mathfrak{W}$ is symmetrizable if and only if $F(\mathfrak{W})=0$. This yields a characterization of when the unassisted secrecy capacity $C_S(\mathfrak{W},\mathfrak{V})$ is discontinuous: The AVC $\mathfrak{W}$ changes from non-symmetrizable to symmetrizable and the capacity breaks down to zero.

That the unassisted secrecy capacity is indeed discontinuous has been observed in [22] for the first time by constructing a simple example of dimensions $\left|\mathcal{X}\right|=2$, $\left|\mathcal{Y}\right|=3$, and $\left|\mathcal{S}\right|=2$. It is noteworthy that a state set consisting of two different states only is already sufficient to get a discontinuous behavior. From an adversarial point of view this means that two different strategies for the adversary suffice to break down the system. On the other hand, reducing the state set to have only one element, i.e., $\left|\mathcal{S}\right|=1$, the AVWC becomes a compound wiretap channel [34,35,36] (as the state remains constant for the entire duration of transmission) and the corresponding secrecy capacity becomes continuous [22]. Subsequently, the discontinuous behavior was then completely characterized in [21].

Theorem 4 

([21]). The unassisted secrecy capacity $C_S(\mathfrak{W},\mathfrak{V})$ of the AVWC $(\mathfrak{W},\mathfrak{V})$ possesses the following discontinuity properties:

• The AVWC $(\mathfrak{W},\mathfrak{V})$ is a discontinuity point of $C_S(\mathfrak{W},\mathfrak{V})$ if and only if the following holds: First, $C_{S,\text{CR}}(\mathfrak{W},\mathfrak{V})>0$, and second, $F(\mathfrak{W})=0$ but for every $ϵ>0$ there is a finite ${\mathfrak{W}}^{\prime }$ with $D(\mathfrak{W},{\mathfrak{W}}^{\prime })\le ϵ$ and $F({\mathfrak{W}}^{\prime })>0$.
• If $C_S(\mathfrak{W},\mathfrak{V})$ is discontinuous in the point $(\mathfrak{W},\mathfrak{V})$ then it is discontinuous for all ${\mathfrak{V}}^{\prime }$ for which $C_{S,\text{CR}}(\mathfrak{W},{\mathfrak{V}}^{\prime })>0$.

This result has the following important consequence: Since the second condition relates the question of discontinuity to the function $F(\mathfrak{W})$ and therewith solely to the symmetrizability of the legitimate AVC $\mathfrak{W}$, the unassisted secrecy capacity $C_S(\mathfrak{W},\mathfrak{V})$ is always a continuous function of the eavesdropper AVC $\mathfrak{V}$, while the discontinuity comes from the legitimate AVC $\mathfrak{W}$ only.

3. Super-Activation and Robustness

Medium access control and in particular resource allocation is one of the most important issues for wireless communication systems as it determines the overall performance of a system. For example, the overall capacity of an OFDM system is given by the sum of the capacities of all orthogonal sub-channels. To this end, a system consisting of two orthogonal ordinary DMCs, where both are “useless” in the sense of having zero capacity, the capacity of the whole system is zero as well. This reflects the world view of classical additivity of resources in the sense that “$0+0=0$.”

Recently, it was shown in [17] that the additivity of basic resources does not hold anymore for secure communication over AVCs. Specifically, it was demonstrated that two orthogonal AVWCs which are themselves useless can be used jointly to allow for secure transmission with positive rate, i.e., “$0+0>0$.” This phenomenon of super-activation was then further studied in [21], which in particular provides a characterization of when super-activation is possible.

3.1. Secure Communication over Orthogonal AVWCs

To continue this line of research, we now introduce the corresponding system model in detail.

For finite state sets ${\mathcal{S}}_i$, input alphabets ${\mathcal{X}}_i$, and output alphabets ${\mathcal{Y}}_i$ and ${\mathcal{Z}}_i$, $i=1,2$, we define two AVWCs $({\mathfrak{W}}_1,{\mathfrak{V}}_1)$ and $({\mathfrak{W}}_2,{\mathfrak{V}}_2)$ exactly as in Section 2.1, cf. Definitions 1 and 3. Then the parallel use of both AVWCs $({\mathfrak{W}}_1,{\mathfrak{V}}_1)$ and $({\mathfrak{W}}_2,{\mathfrak{V}}_2)$ creates a combined AVWC

$$\begin{array}{cc}\hfill (\tilde{\mathfrak{W}},\tilde{\mathfrak{V}})& =({\mathfrak{W}}_1,{\mathfrak{V}}_1)\otimes ({\mathfrak{W}}_2,{\mathfrak{V}}_2)\hfill \\ & =({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2,{\mathfrak{V}}_1\otimes {\mathfrak{V}}_2),\hfill \end{array}$$

where the notation ⊗ indicates the orthogonal use of $({\mathfrak{W}}_1,{\mathfrak{V}}_1)$ and $({\mathfrak{W}}_2,{\mathfrak{V}}_2)$. Now, for given state sequences ${\mathit{s}}^n=(s_1^n,s_2^n)\in {\mathcal{S}}_1^n\times {\mathcal{S}}_2^n$, the discrete memoryless channel to the legitimate receiver is

$$\begin{array}{cc}\hfill {\tilde{W}}^n({\mathit{y}}^n|{\mathit{x}}^n,{\mathit{s}}^n)& =W_{1,s_1^n}^n(y_1^n|x_1^n)W_{2,s_2^n}^n(y_2^n|x_2^n)\hfill \\ & =W_1^n(y_1^n|x_1^n,s_1^n)W_2^n(y_2^n|x_2^n,s_2^n)\hfill \\ & =\prod _{i=1}^n{W}_1(y_{1,i}|x_{1,i},s_{1,i})\prod _{i=1}^n{W}_2(y_{2,i}|x_{2,i},s_{2,i})\hfill \end{array}$$

(10)

with ${\mathit{x}}^n=(x_1^n,x_2^n)\in {\mathcal{X}}_1^n\times {\mathcal{X}}_2^n$ and ${\mathit{y}}^n=(y_1^n,y_2^n)\in {\mathcal{Y}}_1^n\times {\mathcal{Y}}_2^n$. Accordingly, the AVC $\tilde{\mathfrak{W}}$ is then given by

$$\begin{array}{cc}\hfill \tilde{\mathfrak{W}}& =\left\{{\tilde{W}}_{{\mathit{s}}^n}^n:{\mathit{s}}^n\in {\mathcal{S}}_1^n\times {\mathcal{S}}_2^n\right\}\hfill \\ & =\left\{W_{1,s_1^n}^n{W}_{2,s_2^n}^n:s_1^n\in {\mathcal{S}}_1^n,s_2^n\in {\mathcal{S}}_2^n\right\}\hfill \end{array}$$

(11)

and the AVWC $(\tilde{\mathfrak{W}},\tilde{\mathfrak{V}})$ by

$$(\tilde{\mathfrak{W}},\tilde{\mathfrak{V}})=\left(\{{\tilde{W}}_{{\mathit{s}}^n}^n:{\mathit{s}}^n\in {\mathcal{S}}_1^n\times {\mathcal{S}}_2^n\},\{{\tilde{V}}_{{\mathit{s}}^n}^n:{\mathit{s}}^n\in {\mathcal{S}}_1^n\times {\mathcal{S}}_2^n\}\right)$$

with $\tilde{\mathfrak{V}}$ the AVC to the eavesdropper defined accordingly as in Equation (11).

Note that a parallel use of both AVWCs $({\mathfrak{W}}_1,{\mathfrak{V}}_1)$ and $({\mathfrak{W}}_2,{\mathfrak{V}}_2)$ means that for each $({\mathfrak{W}}_i,{\mathfrak{V}}_i)$ we have individual encoders $E_i:{\mathcal{M}}_i\to \mathcal{P}({\mathcal{X}}_i^n)$ and decoders ${\phi }_i:{\mathcal{Y}}_i^n\to {\mathcal{M}}_i$, $i=1,2$, according to Definitions 4 and 6. On the other hand, a joint use of both AVWCs results in a joint encoder $E:\mathcal{M}\to \mathcal{P}({\mathcal{X}}_1^n\times {\mathcal{X}}_2^n)$ and a joint decoder $\phi :{\mathcal{Y}}_1^n\times {\mathcal{Y}}_2^n\to \mathcal{M}$.

3.2. Super-Activation of Orthogonal AVWCs

For orthogonal AVWCs as described above, the phenomenon of super-activation has been completely characterized in [21].

Theorem 5 

([21]). Let $({\mathfrak{W}}_1,{\mathfrak{V}}_1)$ and $({\mathfrak{W}}_2,{\mathfrak{V}}_2)$ be two orthogonal AVWCs. Then the following properties hold:

• If $C_S({\mathfrak{W}}_1,{\mathfrak{V}}_1)=C_S({\mathfrak{W}}_2,{\mathfrak{V}}_2)=0$, then

  $$C_S({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2,{\mathfrak{V}}_1\otimes {\mathfrak{V}}_2)>0$$

  if and only if ${\mathfrak{W}}_1\otimes {\mathfrak{W}}_2$ is non-symmetrizable and $C_{S,\text{CR}}({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2,{\mathfrak{V}}_1\otimes {\mathfrak{V}}_2)>0$. If $({\mathfrak{W}}_1,{\mathfrak{V}}_1)$ and $({\mathfrak{W}}_2,{\mathfrak{V}}_2)$ can be super-activated it holds that

  $$C_S({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2,{\mathfrak{V}}_1\otimes {\mathfrak{V}}_2)=C_{S,\text{CR}}({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2,{\mathfrak{V}}_1\otimes {\mathfrak{V}}_2).$$
• If $C_{S,\text{CR}}$ shows no super-activation for $({\mathfrak{W}}_1,{\mathfrak{V}}_1)$ and $({\mathfrak{W}}_2,{\mathfrak{V}}_2)$, then super-activation of $C_S$ can only happen if ${\mathfrak{W}}_1$ is non-symmetrizable and ${\mathfrak{W}}_2$ is symmetrizable and $C_{S,\text{CR}}({\mathfrak{W}}_1,{\mathfrak{V}}_1)=0$ and $C_{S,\text{CR}}({\mathfrak{W}}_2,{\mathfrak{V}}_2)>0$. The statement is independent of the specific labeling.
• There exist AVWCs that exhibit the behavior described by the second property.

To give some intuition into why super-activation can happen, let us consider the following scenario: Assume there are two orthogonal AVWCs each having zero unassisted secrecy capacity. To this end, assume that one of the unassisted secrecy capacities is zero because the corresponding legitimate AVC is symmetrizable and the other capacity is zero because the eavesdropper AVC is “stronger” than the legitimate AVC. Since the latter legitimate AVC supports a positive rate (although non-secure), it can be used to transmit information to the legitimate receiver (and eavesdropper) to generate CR. Then the legitimate users can use CR-assisted codes to achieve a positive CR-assisted secrecy rate.

Theorem 5 provides a complete characterization of when super-activation can happen. In the following, we want to further explore this phenomenon. To this end, we first show that super-activation is generic in the sense that whenever two orthogonal AVWCs can be super-activated, it is possible for all AVWCs in a certain neighborhood as well.

Theorem 6. 

Let $({\mathfrak{W}}_1,{\mathfrak{V}}_1)$ and $({\mathfrak{W}}_2,{\mathfrak{V}}_2)$ be two useless AVWCs that can be super-activated, i.e., $C_S({\mathfrak{W}}_1,{\mathfrak{V}}_1)=C_S({\mathfrak{W}}_2,{\mathfrak{V}}_2)=0$ and $C_S({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2,{\mathfrak{V}}_1\otimes {\mathfrak{V}}_2)>0$. Then there exists an $ϵ>0$ such that for all useless AVWCs $({\mathfrak{W}}_1^{\prime },{\mathfrak{V}}_1^{\prime })$ and $({\mathfrak{W}}_2^{\prime },{\mathfrak{V}}_2^{\prime })$ with

$$D(({\mathfrak{W}}_i,{\mathfrak{V}}_i),({\mathfrak{W}}_i^{\prime },{\mathfrak{V}}_i^{\prime }))<ϵ,i=1,2,$$

we have

$$C_S({\mathfrak{W}}_1^{\prime }\otimes {\mathfrak{W}}_2^{\prime },{\mathfrak{V}}_1^{\prime }\otimes {\mathfrak{V}}_2^{\prime })>0,$$

i.e., all channels in the neighborhood of $({\mathfrak{W}}_1,{\mathfrak{V}}_1)$ and $({\mathfrak{W}}_2,{\mathfrak{V}}_2)$ can be super-activated as well.

Proof. 

Let $({\mathfrak{W}}_1,{\mathfrak{V}}_1)$ and $({\mathfrak{W}}_2,{\mathfrak{V}}_2)$ be two useless orthogonal AVWCs that can be super-activated and let $({\mathfrak{W}}_1^{\prime },{\mathfrak{V}}_1^{\prime })$ and $({\mathfrak{W}}_2^{\prime },{\mathfrak{V}}_2^{\prime })$ be two useless AVWCs with $D(({\mathfrak{W}}_i,{\mathfrak{V}}_i),({\mathfrak{W}}_i^{\prime },{\mathfrak{V}}_i^{\prime }))<ϵ$, $i=1,2$. Then it holds that

$$\begin{array}{cc}& \sum _{y_1\in {\mathcal{Y}}_1}\sum _{y_2\in {\mathcal{Y}}_2}|W_1(y_1|x_1,s_1)W_2(y_2|x_2,s_2)-W_1^{\prime }(y_1|x_1,s_1^{\prime })W_2^{\prime }(y_2|x_2,s_2^{\prime })|\hfill \\ & =\sum _{y_1\in {\mathcal{Y}}_1}\sum _{y_2\in {\mathcal{Y}}_2}|W_1(y_1|x_1,s_1)W_2(y_2|x_2,s_2)-W_1^{\prime }(y_1|x_1,s_1^{\prime })W_2(y_2|x_2,s_2)\hfill \\ & +W_1^{\prime }(y_1|x_1,s_1^{\prime })W_2(y_2|x_2,s_2)-W_1^{\prime }(y_1|x_1,s_1^{\prime })W_2^{\prime }(y_2|x_2,s_2^{\prime })|\hfill \\ & \le \sum _{y_1\in {\mathcal{Y}}_1}\sum _{y_2\in {\mathcal{Y}}_2}\left|\left(W_1(y_1|x_1,s_1)-W_1^{\prime }(y_1|x_1,s_1^{\prime })\right)W_2(y_2|x_2,s_2)\right|\hfill \\ & +\sum _{y_1\in {\mathcal{Y}}_1}\sum _{y_2\in {\mathcal{Y}}_2}\left|\left(W_2(y_2|x_2,s_2)-W_2^{\prime }(y_2|x_2,s_2^{\prime })\right)W_1^{\prime }(y_1|x_1,s_1^{\prime })\right|\hfill \\ & =\sum _{y_1\in {\mathcal{Y}}_1}|W_1(y_1|x_1,s_1)-W_1^{\prime }(y_1|x_1,s_1^{\prime })|+\sum _{y_2\in {\mathcal{Y}}_2}|W_2(y_2|x_2,s_2)-W_2^{\prime }(y_2|x_2,s_2^{\prime })|.\hfill \end{array}$$

Since $D(({\mathfrak{W}}_i,{\mathfrak{V}}_i),({\mathfrak{W}}_i^{\prime },{\mathfrak{V}}_i^{\prime }))<ϵ$, $i=1,2$, by assumption, we have

$$D(({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2,{\mathfrak{V}}_1\otimes {\mathfrak{V}}_2)),({\mathfrak{W}}_1^{\prime }\otimes {\mathfrak{W}}_2^{\prime },{\mathfrak{V}}_1^{\prime }\otimes {\mathfrak{V}}_2^{\prime })<2ϵ.$$

(12)

Now we can apply the stability result in Theorem 3. From this we know that for all AVWCs $(\tilde{\mathfrak{W}},\tilde{\mathfrak{V}})$ with $\tilde{W}:{\mathcal{X}}_1\times {\mathcal{X}}_2\times {\mathcal{S}}_1\times {\mathcal{S}}_2\to \mathcal{P}({\mathcal{Y}}_1\times {\mathcal{Y}}_2)$ and $\tilde{V}:{\mathcal{X}}_1\times {\mathcal{X}}_2\times {\mathcal{S}}_1\times {\mathcal{S}}_2\to \mathcal{P}({\mathcal{Z}}_1\times {\mathcal{Z}}_2)$ and

$$D(({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2,{\mathfrak{V}}_1\otimes {\mathfrak{V}}_2),(\tilde{\mathfrak{W}},\tilde{\mathfrak{V}}))<\widetilde{ϵ}$$

we have

$$C_S(\tilde{\mathfrak{W}},\tilde{\mathfrak{V}})>0.$$

Now we choose ϵ in Equation (12) small such that $2ϵ<\widetilde{ϵ}$ holds. With this we obtain the desired positivity for all AVWCs $({\mathfrak{W}}_1^{\prime },{\mathfrak{V}}_1^{\prime })$ and $({\mathfrak{W}}_2^{\prime },{\mathfrak{V}}_2^{\prime })$ for which Equation (12) is satisfied. This completes the proof. ☐

This result shows that super-activation is not an isolated phenomenon of orthogonal AVWCs. In fact, whenever super-activation is possible for two AVWCs, it occurs for all AVWCs that are sufficiently close to them.

Corollary 1. 

Let $({\mathfrak{W}}_1,{\mathfrak{V}}_1)$ and $({\mathfrak{W}}_2,{\mathfrak{V}}_2)$ be two useless orthogonal AVWCs that can be super-activated. Then $({\mathfrak{W}}_2,{\mathfrak{V}}_2)$ super-activates all AVWCs $({\mathfrak{W}}_1^{\prime },{\mathfrak{V}}_1^{\prime })$ that are close enough to $({\mathfrak{W}}_1,{\mathfrak{V}}_1)$.

Proof. 

The result follows immediately from Theorem 6. Note that we can even choose $ϵ=\widetilde{ϵ}$ in this case to obtain the desired result. ☐

The previous result of Theorem 6 can even be strengthened. This formulation is more involved than the previous one, but the advantage is that it reveals the following behavior: The AVC to the legitimate receiver is much more important than the AVC to the eavesdropper in terms of super-activation. Specifically, there is no need of an explicit requirement on the distance between the eavesdropper channels. We obtain the following result.

Theorem 7. 

Let $({\mathfrak{W}}_1,{\mathfrak{V}}_1)$ and $({\mathfrak{W}}_2,{\mathfrak{V}}_2)$ be two useless orthogonal AVWCs that can be super-activated. Then there exists an $ϵ>0$ such that all useless orthogonal AVWCs $({\mathfrak{W}}_1^{\prime },{\mathfrak{V}}_1^{\prime })$ and $({\mathfrak{W}}_2^{\prime },{\mathfrak{V}}_2^{\prime })$ that satisfy

$$\begin{array}{c}\hfill D({\mathfrak{W}}_1,{\mathfrak{W}}_1^{\prime })<ϵ,D({\mathfrak{W}}_2,{\mathfrak{W}}_2^{\prime })<ϵ,\end{array}$$

and

$$C_{S,\text{CR}}({\mathfrak{W}}_1^{\prime }\otimes {\mathfrak{W}}_2^{\prime },{\mathfrak{V}}_1^{\prime }\otimes {\mathfrak{V}}_2^{\prime })>0,$$

can be super-activated as well.

Proof. 

We know that the combined AVC ${\mathfrak{W}}_1\otimes {\mathfrak{W}}_2$ is non-symmetrizable, since otherwise super-activation would not be possible, cf. Theorem 5. Similarly as in the proof of Theorem 6 we can then show that $D({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2,{\mathfrak{W}}_1^{\prime }\otimes {\mathfrak{W}}_2^{\prime })<2ϵ$ holds. Next we consider the function $F({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)$, cf. Equation (9). Since ${\mathfrak{W}}_1\otimes {\mathfrak{W}}_2$ is non-symmetrizable, we have $F({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)>0$. In addition, since the function F depends in a continuous way on the channel, for all AVCs $\tilde{\mathfrak{W}}$ with $\tilde{W}:{\mathcal{X}}_1\times {\mathcal{X}}_2\times {\mathcal{S}}_1\times {\mathcal{S}}_2\to \mathcal{P}({\mathcal{Y}}_1\times {\mathcal{Y}}_2)$ and $D({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2,\tilde{\mathfrak{W}})<\widetilde{ϵ}$ we always have $F(\tilde{\mathfrak{W}})>0$. Here we have to choose $\widetilde{ϵ}>0$ sufficiently small depending on ${\mathfrak{W}}_1\otimes {\mathfrak{W}}_2$. Since $F(\tilde{\mathfrak{W}})>0$, the AVC $\tilde{\mathfrak{W}}$ is non-symmetrizable and from Theorem 2 it follows that

$$C_S({\mathfrak{W}}_1^{\prime }\otimes {\mathfrak{W}}_2^{\prime },{\mathfrak{V}}_1^{\prime }\otimes {\mathfrak{V}}_2^{\prime })=C_{S,\text{CR}}({\mathfrak{W}}_1^{\prime }\otimes {\mathfrak{W}}_2^{\prime },{\mathfrak{V}}_1^{\prime }\otimes {\mathfrak{V}}_2^{\prime })>0$$

which proves that these AVWCs can be super-activated. This completes the proof. ☐

In the following we briefly present an example in which super-activation is possible for all orthogonal AVWCs in a certain neighborhood. This example is based on an example given in ([22], Section V-C). This constructs suitable AVWCs, whose unassisted secrecy capacities are zero in a certain neighborhood, but who all can be super-activated to allow for secure communication at a positive rate.

Example 1. 

First, we construct an AVWC $({\mathfrak{W}}^{*},{\mathfrak{V}}^{*})$ with $\left|\mathcal{X}\right|=2$, $\left|\mathcal{Y}\right|=3$, $\left|\mathcal{Z}\right|=2$, and $\left|\mathcal{S}\right|=2$ for which in a set of AVWCs $(\mathfrak{W},\mathfrak{V})$ around this channel we always have $C_{S,\text{CR}}({\mathfrak{W}}^{*},{\mathfrak{V}}^{*})>0$ and $C_S(\mathfrak{W},\mathfrak{V})=C_S({\mathfrak{W}}^{*},{\mathfrak{V}}^{*})=0$. To do so, we define the legitimate AVC as ${\mathfrak{W}}^{*}=\{W_1^{*},W_2^{*}\}$ with

$$\begin{array}{c}\hfill W_1^{*}=\left(\begin{array}{ccc}\frac{1}{2}& \frac{1}{2}& 0\\ \frac{1}{4}& 0& \frac{3}{4}\end{array}\right)\text{and}{W}_2^{*}=\left(\begin{array}{ccc}0& 0& 1\\ 0& 1& 0\end{array}\right)\end{array}$$

and the eavesdropper AVC as ${\mathfrak{V}}^{*}=\{V^{*},V^{*}\}$ with

$$\begin{array}{c}\hfill V^{*}=\left(\begin{array}{cc}\frac{1}{2}& \frac{1}{2}\\ \frac{1}{2}& \frac{1}{2}\end{array}\right).\end{array}$$

(13)

With this choice, the eavesdropper channel is fixed, while the legitimate channel allows appropriate variations. In particular, it is easy to show that ${\mathfrak{W}}^{*}$ is symmetrizable so that $C_S({\mathfrak{W}}^{*},{\mathfrak{V}}^{*})=0$ but $C_{S,\text{CR}}({\mathfrak{W}}^{*},{\mathfrak{V}}^{*})>0$, cf. ([22], Section V-C). Further, for all AVWCs $(\mathfrak{W},\mathfrak{V})$ with $D({\mathfrak{W}}^{*},\mathfrak{W})<ϵ$ for some $ϵ>0$ it holds that $C_S({\mathfrak{W}}^{*},{\mathfrak{V}}^{*})=0$ but $C_{S,\text{CR}}({\mathfrak{W}}^{*},{\mathfrak{V}}^{*})>0$, cf. ([22], Theorem 6), which means that all AVWCs in a certain neighborhood have zero unassisted secrecy capacity. Now we can find another orthogonal AVWC $(\tilde{\mathfrak{W}},\tilde{\mathfrak{V}})$ that super-activates the original AVWC $({\mathfrak{W}}^{*},{\mathfrak{V}}^{*})$, but also all other AVWCs $(\mathfrak{W},\mathfrak{V})$ with $D({\mathfrak{W}}^{*},\mathfrak{W})<ϵ$, cf. Corollary 1 and Theorem 7.

Remark 3. 

The previous considerations show that bonding of orthogonal resources can increase the performance significantly. Such bonding gains do not only appear if both unassisted secrecy capacities are equal to zero (super-activation), but also if only one of these is zero while the other one is positive (super-additivity). This follows by an easy adaptation of the discussion above.

Next we want to show that bonding of orthogonal resources reveals further effects and properties that are practically relevant. This is discussed in the following result.

Theorem 8. 

Let $({\mathfrak{W}}_1,{\mathfrak{V}}_1)$ and $({\mathfrak{W}}_2,{\mathfrak{V}}_2)$ be two useless orthogonal AVWCs that can be super-activated. Then the unassisted secrecy capacity $C_S({\mathfrak{W}}_1^{\prime }\otimes {\mathfrak{W}}_2^{\prime },{\mathfrak{V}}_1^{\prime }\otimes {\mathfrak{V}}_2^{\prime })$ depends in a continuous way on the channels $({\mathfrak{W}}_1^{\prime },{\mathfrak{V}}_1^{\prime })$ and $({\mathfrak{W}}_2^{\prime },{\mathfrak{V}}_2^{\prime })$ with $D({\mathfrak{W}}_i,{\mathfrak{W}}_i^{\prime })<ϵ$, $i=1,2$. Here, ϵ depends only on the orthogonal AVCs ${\mathfrak{W}}_1$ and ${\mathfrak{W}}_2$.

Proof. 

Since the AVWCs $({\mathfrak{W}}_1,{\mathfrak{V}}_1)$ and $({\mathfrak{W}}_2,{\mathfrak{V}}_2)$ can be super-activated, we know that $C_S({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2,{\mathfrak{V}}_1\otimes {\mathfrak{V}}_2)>0$. Then we know that this is also true for all AVWCs $(\tilde{\mathfrak{W}},\tilde{\mathfrak{V}})$ with $\tilde{W}:{\mathcal{X}}_1\times {\mathcal{X}}_2\times {\mathcal{S}}_1\times {\mathcal{S}}_2\to \mathcal{P}({\mathcal{Y}}_1\times {\mathcal{Y}}_2)$ and $\tilde{V}:{\mathcal{X}}_1\times {\mathcal{X}}_2\times {\mathcal{S}}_1\times {\mathcal{S}}_2\to \mathcal{P}({\mathcal{Z}}_1\times {\mathcal{Z}}_2)$ that are sufficiently close to $({\mathfrak{W}}_1,{\mathfrak{V}}_1)$ and $({\mathfrak{W}}_2,{\mathfrak{V}}_2)$, cf. Theorem 3, so that

$$C_S(\tilde{\mathfrak{W}},\tilde{\mathfrak{V}})=C_{S,\text{CR}}(\tilde{\mathfrak{W}},\tilde{\mathfrak{V}})$$

holds. Since $C_{S,\text{CR}}(\tilde{\mathfrak{W}},\tilde{\mathfrak{V}})$ is a continuous function, cf. [20,22], the desired result follows then from Theorem 6.

Remark 4. 

The unassisted secrecy capacity $C_S({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2,{\mathfrak{V}}_1\otimes {\mathfrak{V}}_2)$ need not necessarily be continuous in $({\mathfrak{W}}_1,{\mathfrak{V}}_1)$ or $({\mathfrak{W}}_2,{\mathfrak{V}}_2)$. In particular, there are examples with a discontinuous behavior as discussed above.

Remark 5. 

We see that bonding of orthogonal resources can also lead to a more robust system which is continuous. On the other hand, for a single AVC such continuous behavior cannot be guaranteed in general.

In the following we briefly present an example that demonstrates these effects. This example is based on an example in ([22], Section V-A). This constructs suitable AVWCs, whose unassisted secrecy capacity is continuous after super-activation although the unassisted secrecy capacity of one AVWC itself has a discontinuity point.

Example 2. 

First, we construct an AVWC $(\mathfrak{W}(\lambda ),\mathfrak{V})$ for $0\le \lambda \le 1$ with $\left|\mathcal{X}\right|=2$, $\left|\mathcal{Y}\right|=3$, $\left|\mathcal{Z}\right|=2$, and $\left|\mathcal{S}\right|=2$, whose unassisted secrecy capacity has a discontinuity point. To do so, for $0\le \lambda \le 1$ we define the legitimate AVC as $\mathfrak{W}(\lambda )=\{W_1(\lambda ),W_2(\lambda )\}$ with

$$\begin{array}{c}\hfill W_1(\lambda )=\left(\begin{array}{ccc}1& 0& 0\\ 0& \lambda & 1-\lambda \end{array}\right)\text{and}{W}_2(\lambda )=\left(\begin{array}{ccc}\lambda & 0& 1-\lambda \\ 0& 1& 0\end{array}\right)\end{array}$$

and the eavesdropper AVC as $\mathfrak{V}=\{V^{*},V^{*}\}$ with $V^{*}$ the useless channel as in (13) of Example 1. It can be shown that the unassisted secrecy capacity of the AVWC $(\mathfrak{W}(\lambda ),\mathfrak{V})$ has a discontinuity point at $\lambda =0$, i.e., we have $C_S(\mathfrak{W}(0),\mathfrak{V})=0$, but ${lim}_{\lambda \searrow 0}{C}_S(\mathfrak{W}(0),\mathfrak{V})>0$, cf. ([22], Theorem 4). Now we can find another orthogonal AVWC $(\tilde{\mathfrak{W}},\tilde{\mathfrak{V}})$ that super-activates the original AVWC $(\mathfrak{W}(\lambda ),\mathfrak{V})$. Then we know from Theorem 8 that the unassisted secrecy capacity of this super-activated AVWC is continuous.

4. Communication over Orthogonal AVCs

The previous results and in particular Theorem 7 have shown that super-activation of AVWCs is robust in the eavesdropper AVC. Specifically, it is sufficient to require the eavesdropper AVC to be such that the CR-assisted secrecy capacity of the corresponding AVWC is positive. Then this capacity is continuous in the eavesdropper AVC. As a consequence, the phenomenon of super-activation depends particularly on the legitimate AVC. Accordingly, it is interesting to drop the eavesdropper and the security requirement for a while and study reliable message transmission over single-user AVCs in more detail.

4.1. Capacity Results

The single-user AVC is given as in Section 2.1 by considering only the legitimate AVC between the transmitter and legitimate receiver. Reliable message transmission for the single-user AVC has been well studied and its capacity has been established for both unassisted [13,14] and CR-assisted [12] codes.

Theorem 9 

([12]). The CR-assisted capacity $C_{\text{CR}}(\mathfrak{W})$ of the AVC $\mathfrak{W}$ is

$$C_{\text{CR}}(\mathfrak{W})=\underset{P_X\in \mathcal{P}(\mathcal{X})}{max}\underset{q\in \mathcal{P}(\mathcal{S})}{inf}I(X;{\overline{Y}}_q)$$

(14)

where ${\overline{Y}}_q$ denotes the random variable associated with the output of the averaged channel ${\overline{W}}_q$, $q\in \mathcal{P}(\mathcal{S})$, cf. Equation (3).

The unassisted capacity is then completely characterized in terms of its CR-assisted capacity.

Theorem 10 

([13,14]). The unassisted capacity $C(\mathfrak{W})$ of the AVC $\mathfrak{W}$ is

$$\begin{array}{c}\hfill C(\mathfrak{W})=\left\{\begin{array}{cc}{C}_{\text{CR}}(\mathfrak{W})\hfill & \text{if}\mathfrak{W}\text{is}\text{non-symmetrizable}\hfill \\ 0\hfill & \text{if}\mathfrak{W}\text{is}\text{symmetrizable}.\hfill \end{array}\right.\end{array}$$

To the best of our knowledge, reliable message transmission over orthogonal AVCs has not been studied previously. This is surprising as this is already implicitly addressed by Shannon’s question of the additivity of the zero error capacity [23]. Specifically, Ahlswede showed in [28] that the capacity of the AVC under the maximum error criterion includes the characterization of the zero error capacity as a special case. To this end, Alon’s example in [27] for the super-additivity of the capacity of reliable message transmission over orthogonal AVCs under the maximum error criterion can be seen as the first contribution towards understanding the behavior of the capacity of orthogonal AVCs. In the following, we completely characterize the behavior of the capacity of orthogonal AVCs for the average error criterion.

4.2. Additivity of CR-Assisted Capacity

We start with the CR-assisted capacity and show that it is additive. This means that the CR-assisted capacity of two orthogonal AVCs is the sum of its CR-assisted capacities.

Theorem 11. 

Let ${\mathfrak{W}}_1$ and ${\mathfrak{W}}_2$ be two orthogonal AVCs. Then the CR-assisted capacity is additive, i.e.,

$$C_{\text{CR}}({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)=C_{\text{CR}}({\mathfrak{W}}_1)+C_{\text{CR}}({\mathfrak{W}}_2).$$

(15)

Proof. 

From the definition of capacity it follows immediately that

$$C_{\text{CR}}({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)\ge C_{\text{CR}}({\mathfrak{W}}_1)+C_{\text{CR}}({\mathfrak{W}}_2)$$

(16)

is satisfied since joint encoding and decoding over both AVCs can only increase the capacity compared to an individual encoding and decoding for both channels. Thus, to show equality in Equation (15) it remains to prove that the reversed inequality is also true, i.e., $C_{\text{CR}}({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)\le C_{\text{CR}}({\mathfrak{W}}_1)+C_{\text{CR}}({\mathfrak{W}}_2)$.

For the following argumentation it is beneficial to write the CR-assisted capacity in Equation (14) as

$$\begin{array}{cc}\hfill C_{\text{CR}}(\mathfrak{W})& =\underset{P_X\in \mathcal{P}(\mathcal{X})}{max}\underset{q\in \mathcal{P}(\mathcal{S})}{inf}I(X;{\overline{Y}}_q)\hfill \\ & =\underset{P_X\in \mathcal{P}(\mathcal{X})}{max}\underset{q\in \mathcal{P}(\mathcal{S})}{min}I(P_X,{\overline{W}}_q)\hfill \end{array}$$

as the mutual information term is completely determined by the input distribution $P_X\in \mathcal{P}(\mathcal{X})$ and the averaged channel ${\overline{W}}_q$, $q\in \mathcal{P}(\mathcal{S})$, cf. Equation (3).

With this notation, the CR-assisted capacity of the combined AVC ${\mathfrak{W}}_1\otimes {\mathfrak{W}}_2$, cf. also Equations (10) and (11), is given by

$$C_{\text{CR}}({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)=\underset{P_{X_1{X}_2}\in \mathcal{P}({\mathcal{X}}_1\times {\mathcal{X}}_2)}{max}\underset{q_{12}\in \mathcal{P}({\mathcal{S}}_1\times {\mathcal{S}}_2)}{min}I(P_{X_1{X}_2},{\overline{W}}_{q_{12}})$$

(17)

where ${\overline{W}}_{q_{12}}$, $q_{12}\in \mathcal{P}({\mathcal{S}}_1\times {\mathcal{S}}_2)$, denotes the corresponding averaged channel.

Now, this mutual information quantity in Equation (17) is continuous, concave in $P_{X_1{X}_2}$, and convex in ${\overline{W}}_{q_{12}}$ so that the order of max and min can be exchanged to obtain

$$\begin{array}{cc}\hfill C_{\text{CR}}({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)& =\underset{q_{12}\in \mathcal{P}({\mathcal{S}}_1\times {\mathcal{S}}_2)}{min}\underset{P_{X_1{X}_2}\in \mathcal{P}({\mathcal{X}}_1\times {\mathcal{X}}_2)}{max}I(P_{X_1{X}_2},{\overline{W}}_{q_{12}})\hfill \\ & \le \underset{P_{X_1{X}_2}\in \mathcal{P}({\mathcal{X}}_1\times {\mathcal{X}}_2)}{max}I(P_{X_1{X}_2},{\overline{W}}_{{\widehat{q}}_1\otimes {\widehat{q}}_2})\hfill \end{array}$$

for some arbitrary but fixed ${\widehat{q}}_1\in \mathcal{P}({\mathcal{S}}_1)$ and ${\widehat{q}}_2\in \mathcal{P}({\mathcal{S}}_2)$. In addition, we have

$$\begin{array}{cc}& {\overline{W}}_{{\widehat{q}}_1\otimes {\widehat{q}}_2}(y_1,y_2|x_1,x_2)\hfill \\ & =\left(\sum _{s_1\in {\mathcal{S}}_1}{\widehat{q}}_1(s_1)W_{1,s_1}(y_1|x_1)\right)\left(\sum _{s_2\in {\mathcal{S}}_2}{\widehat{q}}_2(s_2)W_{2,s_2}(y_2|x_2)\right)\hfill \\ & ={\overline{W}}_{1,{\widehat{q}}_1}(y_1|x_1){\overline{W}}_{2,{\widehat{q}}_2}(y_2|x_2)\hfill \end{array}$$

so that

$${\overline{W}}_{{\widehat{q}}_1\otimes {\widehat{q}}_2}={\overline{W}}_{1,{\widehat{q}}_1}\otimes {\overline{W}}_{2,{\widehat{q}}_2}.$$

Since for ordinary DMCs under the average error criterion we have additivity, it holds that

$$\begin{array}{cc}& \underset{P_{X_1{X}_2}\in \mathcal{P}({\mathcal{X}}_1\times {\mathcal{X}}_2)}{max}I(P_{X_1{X}_2},{\overline{W}}_{{\widehat{q}}_1\otimes {\widehat{q}}_2})=\underset{P_{X_1}\in \mathcal{P}({\mathcal{X}}_1)}{max}I(P_{X_1},{\overline{W}}_{1,{\widehat{q}}_1})+\underset{P_{X_2}\in \mathcal{P}({\mathcal{X}}_2)}{max}I(P_{X_2},{\overline{W}}_{2,{\widehat{q}}_2}).\hfill \end{array}$$

Since ${\widehat{q}}_1\in \mathcal{P}({\mathcal{S}}_1)$ and ${\widehat{q}}_2\in \mathcal{P}({\mathcal{S}}_2)$ are arbitrary, we obtain

$$\begin{array}{cc}\hfill C_{\text{CR}}({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)& \le \underset{{\widehat{q}}_1\in \mathcal{P}({\mathcal{S}}_1),{\widehat{q}}_2\in \mathcal{P}({\mathcal{S}}_2)}{min}\left(\underset{P_{X_1}\in \mathcal{P}({\mathcal{X}}_1)}{max}I(P_{X_1},{\overline{W}}_{1,{\widehat{q}}_1})+\underset{P_{X_2}\in \mathcal{P}({\mathcal{X}}_2)}{max}I(P_{X_2},{\overline{W}}_{2,{\widehat{q}}_2})\right)\hfill \\ & =\underset{{\widehat{q}}_1\in \mathcal{P}({\mathcal{S}}_1)}{min}\underset{P_{X_1}\in \mathcal{P}({\mathcal{X}}_1)}{max}I(P_{X_1},{\overline{W}}_{1,{\widehat{q}}_1})+\underset{{\widehat{q}}_2\in \mathcal{P}({\mathcal{S}}_2)}{min}\underset{P_{X_2}\in \mathcal{P}({\mathcal{X}}_2)}{max}I(P_{X_2},{\overline{W}}_{2,{\widehat{q}}_2})\hfill \\ & =C_{\text{CR}}({\mathfrak{W}}_1)+C_{\text{CR}}({\mathfrak{W}}_2)\hfill \end{array}$$

(18)

where the last step follows again from the fact that the mutual information is concave in the input distribution and convex in the channel which allows an exchange of min and max.

Now the inequalities in Equations (16) and (18) establish the desired additivity of the CR-assisted capacity, thereby proving the result. ☐

This result shows that the CR-assisted capacity is always additive and therewith confirms Shannon’s conviction of the additivity of the capacity. The consequence is that joint encoding and decoding for both AVCs does not yield any gains in terms of CR-assisted capacity.

4.3. Super-Additivity of Unassisted Capacity

Next, we consider the unassisted capacity of two orthogonal AVCs.

Proposition 1. 

Let ${\mathfrak{W}}_1$ and ${\mathfrak{W}}_2$ be two orthogonal AVCs. If the unassisted capacities satisfy $C({\mathfrak{W}}_1)>0$ and $C({\mathfrak{W}}_2)>0$, then the unassisted capacity is additive, i.e.,

$$C({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)=C({\mathfrak{W}}_1)+C({\mathfrak{W}}_2).$$

(19)

Proof. 

From the additivity of the CR-assisted capacity, cf. Theorem 11, we have

$$\begin{array}{cc}\hfill C({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)& \le C_{\text{CR}}({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)\hfill \\ & =C_{\text{CR}}({\mathfrak{W}}_1)+C_{\text{CR}}({\mathfrak{W}}_2)\hfill \\ & =C({\mathfrak{W}}_1)+C({\mathfrak{W}}_2)\hfill \end{array}$$

(20)

where the last equality follows from Theorem 10. On the other hand we have

$$\begin{array}{cc}\hfill C({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)& \ge C({\mathfrak{W}}_1)+C({\mathfrak{W}}_2)\hfill \\ & =C_{\text{CR}}({\mathfrak{W}}_1)+C_{\text{CR}}({\mathfrak{W}}_2)\hfill \\ & =C_{\text{CR}}({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)\hfill \\ & =C({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)\hfill \end{array}$$

(21)

where the first equality is again due to Theorem 10 since $C({\mathfrak{W}}_1)>0$ and $C({\mathfrak{W}}_2)>0$, and the second equality follows from Theorem 11. Equations (20) and (21) yield the desired equality in Equation (19), thereby proving the result. ☐

Proposition 2. 

Let ${\mathfrak{W}}_1$ and ${\mathfrak{W}}_2$ be two orthogonal AVCs. If the unassisted capacities satisfy $C({\mathfrak{W}}_1)=C({\mathfrak{W}}_2)=0$, then the unassisted capacity is additive, i.e.,

$$C({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)=C({\mathfrak{W}}_1)+C({\mathfrak{W}}_2).$$

Proof. 

If $C({\mathfrak{W}}_1)=C({\mathfrak{W}}_2)=0$, then both AVCs are symmetrizable according to Definition 2. This means there exist stochastic matrices ${\sigma }_i:{\mathcal{X}}_i\to \mathcal{P}({\mathcal{S}}_i)$, $i=1,2$, such that

$$\sum _{s_i\in {\mathcal{S}}_i}{W}_i(y_i|x_i,s_i){\sigma }_i(s_i|x_i^{\prime })=\sum _{s_i\in {\mathcal{S}}_i}{W}_i(y_i|x_i^{\prime },s_i){\sigma }_i(s_i|x_i)$$

holds for all $x_i,x_i^{\prime }\in {\mathcal{X}}_i$ and $y_i\in {\mathcal{Y}}_i$, $i=1,2$.

Then, the AVC ${\mathfrak{W}}_1\otimes {\mathfrak{W}}_2$ is symmetrizable as well and

$$\begin{array}{cc}& \sum _{s_1\in {\mathcal{S}}_1}\sum _{s_2\in {\mathcal{S}}_2}{W}_1(y_1|x_1,s_1)W_2(y_2|x_2,s_2){\sigma }_1(s_1|x_1^{\prime }){\sigma }_2(s_2|x_2^{\prime })\hfill \\ & =\left(\sum _{s_1\in {\mathcal{S}}_1}{W}_1(y_1|x_1,s_1){\sigma }_1(s_1|x_1^{\prime })\right)\left(\sum _{s_2\in {\mathcal{S}}_2}{W}_2(y_2|x_2,s_2){\sigma }_2(s_2|x_2^{\prime })\right)\hfill \\ & =\left(\sum _{s_1\in {\mathcal{S}}_1}{W}_1(y_1|x_1^{\prime },s_1){\sigma }_1(s_1|x_1)\right)\left(\sum _{s_2\in {\mathcal{S}}_2}{W}_2(y_2|x_2^{\prime },s_2){\sigma }_2(s_2|x_2)\right)\hfill \\ & =\sum _{s_1\in {\mathcal{S}}_1}\sum _{s_2\in {\mathcal{S}}_2}{W}_1(y_1|x_1^{\prime },s_1)W_2(y_2|x_2^{\prime },s_2){\sigma }_1(s_1|x_1){\sigma }_2(s_2|x_2)\hfill \end{array}$$

holds for all $x_i,x_i^{\prime }\in {\mathcal{X}}_i$ and $y_i\in {\mathcal{Y}}_i$, $i=1,2$. This implies that $C({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)=0$ as well which shows the additivity for this case as well as completing the proof. ☐

These two results show that when the unassisted capacities are both positive or both zero, the overall unassisted capacity is additive. In addition, from Proposition 2 it follows immediately that super-activation is not possible for reliable message transmission over orthogonal AVCs.

Corollary 2. 

Let ${\mathfrak{W}}_1$ and ${\mathfrak{W}}_2$ be two orthogonal AVCs. If the unassisted capacities satisfy $C({\mathfrak{W}}_1)=C({\mathfrak{W}}_2)=0$, then super-activation is not possible for the combined AVC ${\mathfrak{W}}_1\otimes {\mathfrak{W}}_2$.

Finally, the following result solves the remaining case for which the unassisted capacity is actually super-additive.

Theorem 12. 

Let ${\mathfrak{W}}_1$ and ${\mathfrak{W}}_2$ be two orthogonal AVCs. The unassisted capacity $C({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)$ is super-additive, i.e.,

$$C({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)>C({\mathfrak{W}}_1)+C({\mathfrak{W}}_2),$$

(22)

if and only if either of ${\mathfrak{W}}_1$ or ${\mathfrak{W}}_2$ is symmetrizable and has a positive CR-assisted capacity.

Without loss of generality, let ${\mathfrak{W}}_1$ be symmetrizable; then

$$\begin{array}{cc}\hfill C({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)& =C_{\text{CR}}({\mathfrak{W}}_1)+C({\mathfrak{W}}_2)\hfill \\ & >C({\mathfrak{W}}_1)+C({\mathfrak{W}}_2)=C({\mathfrak{W}}_2).\hfill \end{array}$$

Proof. 

First we show that if ${\mathfrak{W}}_1$ is symmetrizable and $C_{\text{CR}}({\mathfrak{W}}_1)>0$, then the unassisted capacity $C({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)$ is super-additive. To do so, we use the idea of Ahlswede’s de-randomization [13]. Although CR is not available, CR-assisted codes can still be used if the transmitter is able to inform the receiver prior to the actual message transmission about which realization of encoder and decoder has to be used. From [13] we know that the amount of information that needs to be transmitted prior to transmission for this task is polynomial in the block length and therewith negligible for increasing block length.

Since ${\mathfrak{W}}_2$ is non-symmetrizable, we have $C_{\text{CR}}({\mathfrak{W}}_2)>0$ and therefore also $C({\mathfrak{W}}_2)>0$. This allows us to use the second AVC to transmit information to the receiver to make CR available for the first AVC ${\mathfrak{W}}_1$. Then CR-assisted codes can be used for ${\mathfrak{W}}_1$ so that

$$\begin{array}{cc}\hfill C({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)& \ge C_{\text{CR}}({\mathfrak{W}}_1)+C({\mathfrak{W}}_2)\hfill \\ & =C_{\text{CR}}({\mathfrak{W}}_1)+C_{\text{CR}}({\mathfrak{W}}_2)\hfill \\ & =C_{\text{CR}}({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)\hfill \end{array}$$

is achievable. Since $C({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)\le C_{\text{CR}}({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)$ is obviously true, we have equality which means that we actually achieve

$$\begin{array}{cc}\hfill C({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)& =C_{\text{CR}}({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)\hfill \end{array}$$

which shows the super-additivity of $C({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)$.

Next we show the other direction: If $C({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)$ is super-additive, i.e.,

$$C({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)>C({\mathfrak{W}}_1)+C({\mathfrak{W}}_2),$$

(23)

then either ${\mathfrak{W}}_1$ or ${\mathfrak{W}}_2$ must be symmetrizable so that $C({\mathfrak{W}}_1)=0$ or $C({\mathfrak{W}}_2)=0$.

Assume both unassisted capacities are strictly positive. Then from Theorem 10 it follows that $C({\mathfrak{W}}_1)=C_{\text{CR}}({\mathfrak{W}}_1)$ and $C({\mathfrak{W}}_2)=C_{\text{CR}}({\mathfrak{W}}_2)$ so that Equation (23) becomes

$$\begin{array}{cc}\hfill C({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)& >C_{\text{CR}}({\mathfrak{W}}_1)+C_{\text{CR}}({\mathfrak{W}}_2)\hfill \\ & =C_{\text{CR}}({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)\hfill \end{array}$$

where the last step follows from the additivity of the CR-assisted capacity, cf. Theorem 11. This contradicts $C({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)\le C_{\text{CR}}({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)$ which always holds. Accordingly, without loss of generality, we must have $C({\mathfrak{W}}_1)=0$. However, $C_{\text{CR}}({\mathfrak{W}}_1)>0$ must be true, since otherwise we would have

$$\begin{array}{c}\hfill C({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)>0+C_{\text{CR}}({\mathfrak{W}}_2)=C_{\text{CR}}({\mathfrak{W}}_1\otimes {\mathfrak{W}}_2)\end{array}$$

which would be a contradiction. Thus, it must hold that $C_{\text{CR}}({\mathfrak{W}}_1)>0$ and $C({\mathfrak{W}}_1)=0$ so that ${\mathfrak{W}}_1$ is symmetrizable, proving the desired result. ☐

This result shows that the capacity of reliable message transmission over orthogonal AVCs is super-additive under certain circumstances. This breaks with the world view of classical additivity of resources.

Note that Example 1 discussed in Section 3.2 provides an AVC with $\left|\mathcal{S}\right|=2$, which exactly displays the behavior characterized above. Interestingly, if the state set is reduced to $\left|\mathcal{S}\right|=1$, such a behavior is not possible anymore.

5. Discussion

In this paper, we have studied communication under arbitrarily varying channel conditions. For the case of public message transmission over orthogonal AVCs we have completely characterized the behavior of the unassisted and CR-assisted capacity. While the CR-assisted capacity is additive, the unassisted capacity is super-additive, which means that there are orthogonal AVCs for which joint encoding and decoding results in a higher capacity than individual encoding and decoding.

If secrecy requirements are imposed on the message transmission, the capacity behavior for orthogonal AVWCs becomes even more involved. In this case, the phenomenon of super-activation occurs. A joint use of two completely useless AVWCs, i.e., with zero unassisted secrecy capacity, can result in a combined AVWC whose unassisted secrecy capacity is non-zero. From a practical point of view this has important consequences for medium access control and in particular for resource allocation.

The problem of reliable communication over AVCs is closely related to Shannon’s zero error capacity problem, as the latter turns out to be a special case of the capacity of the AVC under the maximum error criterion. Shannon conjectured in 1956 that the zero error capacity is additive. Accordingly, the phenomena of super-additivity and super-activation for AVCs and AVWCs respectively are remarkable as these properties show the non-additivity of the capacity of the AVC.

The phenomenon of super-activation has substantial consequences for jamming strategies of potential adversaries. Let us assume that there are two orthogonal AVWCs that can be super-activated. Further assume that for each AVWC an adversary has a suitable jamming strategy to drive the unassisted secrecy capacity to zero. In more detail, for each AVWC the adversary can choose a corresponding state sequence that symmetrizes the legitimate AVC, prohibiting any reliable communication between transmitter and legitimate receiver. Now, joint encoding and decoding allows super-activation of the combined AVWC to make the communication robust: They can now transmit at a positive secrecy rate. This means that for the adversary there is no suitable jamming strategy for the combined AVWC although there is one for each AVWC individually. As there are no restrictions on the strategy space of the adversary, this includes even the case of a product strategy consisting of both individually working jamming strategies.

Super-activation is not an isolated phenomenon. We have shown that whenever orthogonal AVWCs can be super-activated, this is also true for all AVWCs in a certain neighborhood. As a consequence the overall system becomes stable as well. If a super-activated AVWC allows for secure communication with a positive rate, then this is true for all AVWCs sufficiently close to this super-activated AVWC.

Finally we want to note that this also has a game-theoretic interpretation of a “game against nature” [37]. The legitimate users (player) and the adversary (nature) play a two-player zero-sum game [38,39] with the secure communication rate as the payoff function. In this game, the set of state sequences corresponds to nature’s action space, and nature’s intention is to establish the worst possible communication conditions by selecting the state sequence such that the legitimate AVC becomes symmetrizable. The set of input distributions corresponds to the action space of the player and, clearly, the aim is to maximize the secure communication rate. Within this game against nature framework, the player and nature move simultaneously without knowing the other’s choice which leads to the $maxmin$ expressions in the corresponding secrecy capacity results.