Batch Attribute-Based Encryption for Secure Clouds

Abstract

Cloud storage is widely used by organizations due to its advantage of allowing universal access with low cost. Attribute-based encryption (ABE) is a kind of public key encryption suitable for cloud storage. The secret key of each user and the ciphertext are associated with an access policy and an attribute set, respectively; in addition to holding a secret key, one can decrypt a ciphertext only if the associated attributes match the predetermined access policy, which allows one to enforce fine-grained access control on outsourced files. One issue in existing ABE schemes is that they are designed for the users of a single organization. When one wants to share the data with the users of different organizations, the owner needs to encrypt the messages to the receivers of one organization and then repeats this process for another organization. This situation is deteriorated with more and more mobile devices using cloud services, as the ABE encryption process is time consuming and may exhaust the power supplies of the mobile devices quickly. In this paper, we propose a batch attribute-based encryption (BABE) approach to address this problem in a provably-secure way. With our approach, the data owner can outsource data in batches to the users of different organizations simultaneously. The data owner is allowed to decide the receiving organizations and the attributes required for decryption. Theoretical and experimental analyses show that our approach is more efficient than traditional encryption implementations in computation and communication.

1. Introduction

In cloud computing, if a file owner would like to share his file with others, he just stores his data on a cloud server, then his friends/colleagues, including himself, can access the data by visiting the server from any place where there is an Internet connection. In this way, cloud storage makes it possible for people to exploit almost unlimited computation, storage space and information services anytime and anywhere without suffering from complicated local maintenance and management. Due to these advantages, cloud computing is becoming an indispensable part of organizations and individuals.

The security concern of the data owner is believed to be the main obstacle for wide adoption of cloud storage. Especially, the user who do not have access right may collude with the server for illegal access. Encryption is a standard way to protect data security. Public encryption is preferable in organization-oriented applications. In this scenario, one organization can have a cloud account associated with a public key, and anyone can securely upload files to this account by encrypting the files under the public key. Only the one who owes the corresponding secret key of the public key can decrypt the encrypted file, which prevents illegal access from the cloud server or other non-authorized ones. However, the traditional public key cryptosystems suffer from complicated key management in this scenario, since it is unknown who will be allowed to access a specific encrypted file when the system is set up or the file is encrypted. Attribute-based encryption (ABE) [1] is the up-to-date cryptographic concept to address this problem. In this case, the encryptor can specify the attributes required for decryption, and the access policy can be made for the secret key of each requestor. A requestor can decrypt a ciphertext only if the labeled attributes meet the access policy associated with the secret key of the requestor.

An issue in deploying ABE is that all known ABE encryption/decryption operations are time and resource consuming. Furthermore, the existing ABE schemes only allow encryption for the receivers of a single organization. Consider a scenario where the scientists from different universities jointly work on a project. In this case, if a scientist wants to share his or her research progress with the scientists of other universities, then he or she needs to encrypt the files to these organizations repetitively. In [2], an approach is proposed to speed up the decryption with the help of a semi-honest third party. However, to the best of our knowledge, no known work in the public literature has been done to speed up the ABE encryption in our motivating scenario. This situation inspires our work in this paper.

1.1. Our Contribution

In this paper, we investigate the acceleration of ABE encryption where one encrypts for the requestors of different organizations. Our contributions are summarized as follows.

We propose a batch attribute-based encryption (BABE) framework. In this framework, when the different ABE systems are set up, the users of different systems get their keys from the authority of the corresponding system, and these keys are associated with the access policies of the corresponding organizations. One data owner can simultaneously encrypt his or her data for the receivers from different systems in a batch way. The data owner can freely choose the receiving organizations and define separate attributes for the receivers of different organizations. One can decrypt only if his/her organization has been chosen and his/her attributes meet the access policy for his organization.

Following the BABE framework, we propose a concrete BABE scheme. The security of the scheme is formally proven under a well-established computational assumption. Even if an adversary colludes with the cloud server and all non-authorized users, he or she cannot get any useful information of the encrypted message. We conduct experiments in typical system parameters. The experimental results show that our BABE scheme is more efficient than existing ABE implementations. These features render our BABE an efficient solution to securing one-to-many organization-oriented sensitive data sharing in clouds.

1.2. Related Work

Due to its versatility, ABE has attracted extensive research [1,3,4,5]. The ABE concept was introduced by Sahai and Waters [1]. There are two types of ABE systems, i.e., ciphertext-policy ABE (CP-ABE) and key-policy ABE (KP-ABE). In CP-ABE, the secret key of each user is associated with his/her attributes. When one encrypts for the users of the system, he or she specifies an access policy, which is a collection of attribute sets. Only the user whose attributes match the policy can decrypt. Similarly, in KP-ABE, the secret key of a user is associated with an access policy, and each ciphertext is labeled with a set of attributes. One can decrypt a ciphertext only if the labeled attributes meet the policy associated with the user’s secret key. Yu et al. [6] proposed a KP-ABE scheme to achieve flexible access control over outsourced data.

In a regular ABE system, a single authority generates the secrets of all of the users in the system. This incurs the so-called single-point problem, that is all of the parties have to fully trust the single authority, who can read all of the messages encrypted for any users. Furthermore, no new user can join the system if the authority is occasionally unavailable. To mitigate this drawback, the notion of multi-authority ABE (MA-ABE) has been proposed. In this notion, multiple authorities jointly generate the secret keys for the users in the system. No single authority can read the messages encrypted for the users. New users can still be enrolled if some of the authorities are available. An encryptor can choose, for each authority, a number $d_k$ and a set of attributes; he or she can then encrypt a message, such that a user can decrypt only if he or she has at least $d_k$ of the given attributes from each authority k [7]. Chase and Chow improved the MA-ABE in [8] by exchanging a shared secret among the authorities during the system setup process. Their scheme is time consuming and needs heavy communication and computation. Yang et al. [9] designed an access control framework for multi-authority systems and proposed a secure multi-authority access control scheme for cloud storage. Li et al. [10] proposed an MA-ABE scheme for mobile cloud computing by introducing a cloud-based semi-trusted-authority between the mobile user and the attribute authorities.

ABE schemes require time-consuming computations in encryption and decryption, which prevent them from being widely deployed in cloud computing applications for enforcing fine-grained access control. Several works have been proposed to speed up ABE. Attrapadung et al. proposed ABE schemes [11,12] that only need a constant number of bilinear maps in decryption, albeit with the constraint of a bound on the maximum number of attributes. Hohenberger and Waters [2] introduced a method that needs a constant number of bilinear maps in decryption without the bound constraint on the attribute number. In contrast, no public work has been reported to accelerate the encryption process in ABE.

Fiat proposed the first batch signature scheme [13]. Since then, a large body of references has focused on the batch verification of signatures [14,15,16,17]. It is unclear whether these technologies can be employed to accelerate ABE encryption in our motivating scenario. Still in a single system-oriented setting, multi-receiver encryption and signcryption [18] have been proposed to reduce the encryption complexity. Baek, Safavi-Naini and Susilo proposed an efficient multi-receiver identity-based encryption scheme [19] in multi-cast encryption applications. All of these schemes are considered in a single organization-oriented scenario. A trivial application of these schemes to multiple organizations needs to repeat the basic encryption operation for each organization, which implies growing overheads linear with the number of organizations. In this paper, we propose to encrypt for the different organizations in a batch way and to provide a more efficient solution to the motivating applications.

1.3. Paper Organization

The rest of this paper is organized as follows. Section 2 presents a BABE framework and the adversary model. We propose a concrete BABE scheme in Section 3, together with detailed security and efficiency analyses. Section 4 concludes the paper.

2. Modeling BABE

2.1. The System Framework

We propose a BABE framework for cloud storage, as illustrated in Figure 1. The framework consists of four types of parties: the data owner, the cloud server, the data requestor/consumer and the authority. The data owner would like to share his or her data with the data requestors managed by different authorities. Each authority generates a secret key for the data requestor in its management domain according to the consumer’s attributes (or the corresponding access policies). The data owner encrypts his or her file for the data requestors of different organizations, i.e., the users managed by different authorities, by specifying the intended authorities and the attributes that the data requestors should have in the according authorities’ management domains. Then, the data owner uploads the encrypted data to the cloud storage server. When a data requestor requests for the cloud server, the server responds with the corresponding ciphertext. The requestor can decrypt if the attributes labeled with the ciphertext meet the access policy associated with the secret key of the requestor; else, the requestor should get no useful information of the original data.

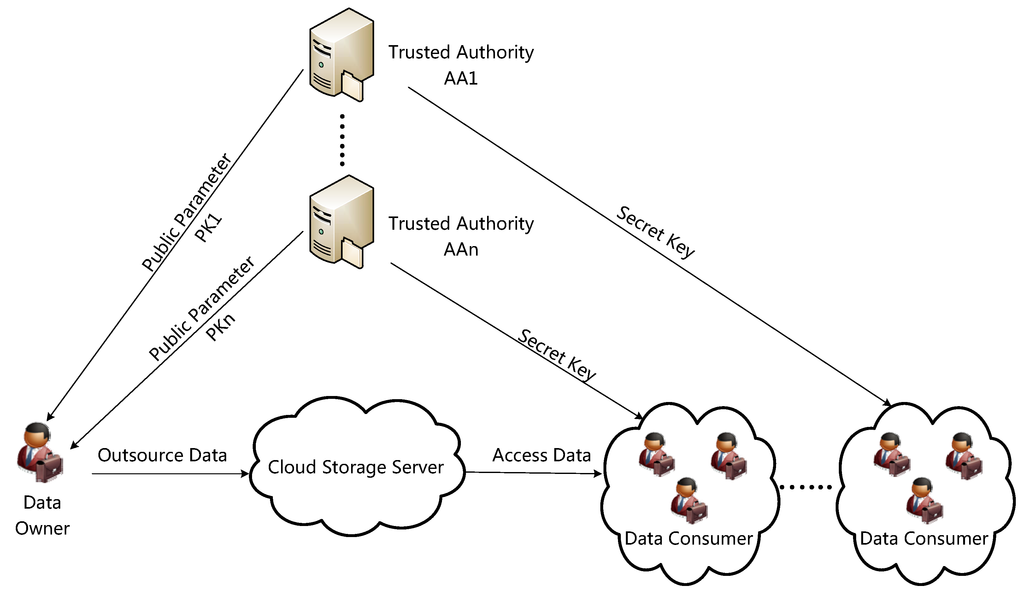
Figure 1. Batch attribute-based encryption (BABE) framework.

Figure 1. Batch attribute-based encryption (BABE) framework.

2.2. Defining BABE

A BABE scheme consists of four polynomial-time algorithms: Setup, Encrypt, KeyGeneration and Decrypt. Let $\mathbb{I}$ represent the collection of underlying ABE subsystems indexed from one to $\left|\mathbb{I}\right|$. Denote that the i-th underlying ABE subsystem has master public key $P{K}_i$ and master secret key $M{K}_i$ for $i\in \mathbb{I}$. The algorithms work as follows.

• Setup($\lambda ,U_i$)→($P{K}_i,M{K}_i$). This is a randomized algorithm run by an authority $A{A}_i$. It takes as inputs the security parameter λ and an attribute universe $U_i$, which defines the set of allowed attributes in different underlying ABE subsystems. The authority $A{A}_i$ outputs the public parameters $P{K}_i$ and the mater keys $M{K}_i$.
• Encrypt($\overrightarrow{PK},\overrightarrow{M},\overrightarrow{S}$)→$\overrightarrow{CT}$. Assume that the data owner wants to share data $M_i$ with the data requestors of the systems $i\in \psi \subseteq \mathbb{I}$. This is a randomized algorithm that takes as inputs the public parameters vector $\overrightarrow{PK}$, a message vector $\overrightarrow{M}$, which contain different messages $M_i$, and a series of attribute sets $\overrightarrow{S}$, which contains attribute sets $S_i,i\in \psi$. It outputs $\left|\psi \right|$ ciphertext $C{T}_i,i\in \psi$ associated with the attribute sets $S_i,i\in \psi$.
• KeyGen($M{K}_i,A_i$)→ SK. Assume that a data requestor belongs to the i-th subsystem. Then, $M{K}_i$ is used to generate the secret key $SK$. This is a randomized algorithm that takes as inputs the master secret key $M{K}_i$ and an access structure $A_i$ and outputs a secret key $SK$.
• Decrypt ($SK,C{T}_i$)$\to M_i$. The decryption algorithm takes as inputs a secret key $SK$ associated with the access structure $A_i$ and a ciphertext $C{T}_i$ associated with attribute set $S_i$. It outputs the message $M_i$ if $S_i$ satisfies $A_i$ or the error message ⊥ otherwise.

2.3. The Adversary Model

For sensitive files stored on the cloud, we mainly consider the secrecy of the files. In this scenario, both the cloud server and users may be potential attackers. Specifically, the cloud server (or the staff who manages the cloud server) may be curious and access the private files of the users without being known by the users. Furthermore, some unauthorized users may collude, even with the cloud server, to illegally access the files. However, we have to make a minimum trust assumption that the cloud server will honestly follow the scheme to execute the procedures and return the service to the users. Else, the scheme will not work and makes no sense in practice. We require that the attacker in such a situation cannot get any useful information of the outsourced data.

Now we formally define the security model of a BABE scheme. Let $U_i$ be the attribute universe of the i-th underlying ABE scheme. All of the underlying ABE schemes share the security parameter λ. Each underlying ABE scheme is managed by an authority $A{A}_i$. $\mathbb{I}$ is the index set of the underlying ABE schemes. Formally, we define the security model for BABE via a game between a challenger and an adversary.

Initialize. 

The adversary declares the different underlying ABE schemes upon which he or she wants to be challenged, indexed by $\psi \subseteq \mathbb{I}$. The adversary also declares the attribute set $S_i^{*},i\in \psi$ of different ABE schemes upon which he or she wished to be challenged upon.

Setup. 

The challenger runs the Setup algorithm to set up the BABE system and sends the public parameters, $P{K}_i,i\in \mathbb{I}$, to the adversary.

Phase 1. 

For the i-th underlying ABE subsystem, the challenger initializes for $i\in \mathbb{I}$ an empty table $T_i$, an empty set $D_i$ and an integer counter $j_i=0$. The adversary can repeatedly make the following queries:

Create($A_i$): 

The challenger sets $j_i=j_i+1$. It runs the key generation algorithm on $A_i$ to obtain the secret key $SK$ and stores it in table $T_i$, forming the entry $(j_i,A_i,SK)$.

Corrupt($\kappa ,i$): 

The adversary queries for the secret key corresponding to the κ-th entry in Table i. If there exists such an entry in table $T_i$, the challenger obtains the entry ($\kappa ,A_i,SK$), sets $D_i=D_i\bigcup \left\{A_i\right\}$ and returns the secret key $SK$ to the adversary. Else, it returns ⊥.

Challenge. 

The adversary submits two equal-length messages, vector $\overrightarrow{M_0}$ and $\overrightarrow{M_1}$, with each vector having $\left|\psi \right|$ message $M_{0,i},i\in \psi$ and $M_{1,i},i\in \psi$. In addition, the adversary gives a set of attributes $S_i^{*},i\in \psi$, such that for all $A_i\in D_i,i\in \psi$, the set $S_i^{*},i\in \psi$ does not satisfy the access structure $A_i,i\in \psi$. The challenger chooses $b\in \{0,1\}$ randomly and encrypts $\overrightarrow{M_b}$ under $S_i^{*},i\in \psi$. The resulting ciphertext $C{T}_i^{*},i\in \psi$ is given to the adversary.

Phase 2. 

Phase 1 is repeated with the restriction that the adversary cannot obtain any secret key that can be used to decrypt the challenge ciphertext. This means that it cannot issue a Corrupt query that would result in an access structure $A_i$ that $S_i^{*}$ satisfies being added to $D_i\in \psi$. Of course, the adversary cannot issue a decryption query on the challenge ciphertext $C{T}_i^{*},i\in \psi$.

Guess. 

The adversary outputs a guess bit $b^{\prime }$ of b. The output of the experiment is one if and only if $b=b^{\prime }$.

The advantage of the adversary $\mathcal{A}$ in this game is defined as $Pr[b^{\prime }=b]-\frac{1}{2}$.

Definition 1. A BABE scheme is secure if all polynomial time adversaries have at most a negligible advantage in the above game.

3. The Proposed BABE Scheme

3.1. Mathematical Background

We briefly review the basic mathematical concepts used in our schemes.

Definition 2. (Access structure [20]). Consider a set of parties $P=\{P_1,P_2,\cdots ,P_n\}$. A collection $\mathbb{A}\subseteq 2^{\{P_1,P_2,\cdots ,P_n\}}$ is said to be monotone if for $\forall B,C$, we have that $B\in \mathbb{A}$ and $B\subseteq C$, then $C\in \mathbb{A}$. An access structure (respectively, monotone access structure) is a collection (respectively, monotone collection) $\mathbb{A}$ of non-empty subsets of $\{P_1,P_2,\cdots ,P_n\}$, i.e., $\mathbb{A}\subseteq 2^P\backslash \varnothing$. The authorized sets represent the sets in $\mathbb{A}$, and the sets not in $\mathbb{A}$ are called the unauthorized sets.

Definition 3. (Linear secret sharing scheme [20]). Let P be a set of parties. Let W be an $l\times m$ matrix. Let f be a function that maps a row to a party. A secret sharing scheme Π for access structure $\mathbb{A}$ over a set of parties P is a linear secret-sharing scheme (LSSS) in ${\mathbb{Z}}_p$ and is represented by $(W,f)$ if it consists of two efficient algorithms:

Share$(W,f)$: 

This takes as input $s\in {\mathbb{Z}}_p$, which is to be shared. It chooses $r_2,r_3,\cdots ,r_n$, and let $\overrightarrow{v}=(s,r_2,\cdots ,r_n)$. It outputs $W\overrightarrow{v}$ as the vector of the shares. The share ${\omega }_i=W_i\overrightarrow{v}$ belongs to party $f\left(i\right)$, where $W_i$ is the i-th row of W.

Recon$(W,f)$: 

This takes as input an access set $S\in A$. Let $I=\left\{i\right|f\left(i\right)\in S\}$. It outputs a set of constants ${(i,{\mu }_i)}_{i\in I}$, such that ${\sum }_{i\in I}{\mu }_i·{\omega }_i=s$.

In a KP-ABE scheme, a ciphertext is associated with a set of attributes S, and each secret key corresponds to an access structure $\mathbb{A}$. One can decrypt if the attribute set S is authorized in the access structure $\mathbb{A}$$(i.e.,S\in \mathbb{A})$.

Our scheme is built on bilinear groups briefly defined as follows.

Definition 4. (Bilinear group). Let G and $G_T$ be two multiplicative cyclic groups of prime order p. Let g be a generator of G and e be a bilinear map, $e:G\times G\to G_T$. The bilinear map e has the following properties:

(1)

Bilinearity: for all $g,h\in G$ and $a,b\in {\mathbb{Z}}_p$, we have $e(g^a,h^b)=e{(g,h)}^{ab}$.

(2)

Non-degeneracy: $e(g,g)\ne 1$.

We say that G is a bilinear group if the group operation in G and the bilinear map $e:G\times G\to G_T$ are both efficiently computable. Notice that the map e is symmetric since $e(g^a,h^b)=e{(g,h)}^{ab}=e(g^b,h^a)$.

3.2. The Proposal

We first give an outline of our BABE scheme. The scheme is proposed to accelerate the encryption process when one needs to encrypt for the users from different organizations in a cloud storage setting where ABE is used to enforce fine-grained access control. The data owner chooses the data he or she wants to share with the data requestors of the different systems. Then, he or she encrypts the data and sends the encrypted data to the cloud server. Authorized data requestors will be able to decrypt the encrypted data by using the secret key given by the corresponding authority. Using the traditional approach, the owner needs to encrypt each data item for the receivers of the different organizations repetitively, which is inefficient in practice. We suggest to encrypt in a batch way and propose a BABE scheme managing to solve this problem.

For $i\in \mathbb{I}$, we describe different subsystems with different universes $U_i$ of different attributes. The attributes are indexed by integers $1,\cdots ,|U_i|$. We use $|U_i|$ to represent the number of the attribute universe $U_i$. The number of the attributes may be different in distinct subsystems.

Setup. 

This algorithm, run by the authority $A{A}_i$, takes as inputs a system parameter λ and an attribute universe $U_i$. It generates a bilinear group G of prime order p, with generator $g\in G$. It selects random values $h_{i,1},\cdots h_{i,|U_i|}\in G$. It further chooses a distinct ${\alpha }_i\in {\mathbb{Z}}_p$ for each i. Finally, for each i, it outputs the public key and master secret key as:

$$P{K}_i=(G,p,g,e{(g,g)}^{{\alpha }_i},h_{i,1},\cdots ,h_{i,\left|U\right|}),M{K}_i=(P{K}_i,{\alpha }_i)$$

Encrypt. 

The data owner chooses the organizations that he or she wants to communicate with, denoted by $\psi \subseteq \mathbb{I}$. Then, he or she asks the authority $A{A}_i$,$i\in \psi$ for the public key $P{K}_i$ and chooses a series of attributes $\overrightarrow{S}$, where $S_i,i\in \psi$, a series of messages $\overrightarrow{M}\in G_T$. The data owner chooses a random $s\in {\mathbb{Z}}_p$. The ciphertext component used by i-th subsystem is $C{T}_i=(S_i,C_i,C^{\prime },C_{i,x})$ where:

$$C_i=M_i·e{(g,g)}^{{\alpha }_{i}s},C^{\prime }=g^s,{\{C_x=h_{i,x}^s\}}_{x\in S_i}$$

After the encryption, the data owner sends the encrypted data to the cloud server.

KeyGen. 

For each i, the authority $A{A}_i$ takes as inputs the master secret key $M{K}_i$ and an LSSS access structure $A_i$ represented by $(W,f)$. Let W be an $l\times m$ matrix. The function f is associated with the rows of W. Let β denote the set of distinct attributes appearing in the access structure matrix W, i.e., $\beta =\{d:\exists \tau \in [1,l],f(\tau )=d\}$. This algorithm chooses a random vector $\overrightarrow{v}=({\alpha }_i,y_2,\cdots ,y_m)\in Z_n$. Here, these values will be used to share the master secret ${\alpha }_i$, and $y_2,\cdots ,y_m$ are random numbers. For $\tau =1$ to l, it calculates ${\lambda }_{\tau }=\overrightarrow{v}·W_{\tau }$, where $W_{\tau }$ is the vector corresponding to the τ-th row of W. The algorithm chooses random integers $r_1$, $\cdots r_l\in {\mathbb{Z}}_p$.It outputs the secret key $SK$ as:

$$\begin{array}{c}(D_1=g^{{\lambda }_1}·h_{i,f\left(1\right)}^{r_1},R_1=g^{r_1},\forall d\in \beta \backslash f\left(1\right),Q_{1,d}=h_{i,d}^{r_1})\\ ⋮\\ (D_l=g^{{\lambda }_l}·h_{i,f\left(l\right)}^{r_l},R_l=g^{r_l},\forall d\in \beta \backslash f\left(l\right),Q_{l,d}=h_{i,d}^{r_l})\end{array}$$

In the above, $\beta \backslash x$ means the set β excluding x.

Decrypt. 

The data requestor requests the encrypted data from the cloud server. The requestor runs the decryption algorithm with his/her secret key $(SK=P{K}_i,(D_1,R_1,Q_{1,d}),\cdots ,(D_l,R_l,Q_{l,d}))$ for access structure ($W,f$) and the ciphertext $C{T}_i=(S_i,C_i,C^{\prime },{\left\{C_x\right\}}_{x\in S_i})$ for set $S_i$. Let W be an $l\times m$ matrix. The function f is associated with some rows of W. If $S_i$ does not satisfy the access structure, the decryption algorithm outputs ⊥.

If $S_i$ satisfies the access structure, we let I$\subseteq \{1,2,\cdots l\}$ be a set of indices and ${\left\{{\omega }_{\tau }\right\}}_{\tau \in I}\in {\mathbb{Z}}_p$ be a set of constants, such that $f\left(\tau \right)\in S_i$ and ${\Sigma }_{\tau \in I}{\omega }_{\tau }·W_{\tau }=(1,0,0\cdots 0)$ for all $\tau \in I$. Note that ${\omega }_{\tau }$ can be found in polynomial time.

We represent the attributes satisfying the access structure as $\gamma =\{x:\exists \tau \in I,f(\tau )=x\}$. I is the set of indices corresponding to the rows used to decrypt the ciphertext, and γ is the set of distinct attributes associated with these rows. In fact, there are multiple I’s that satisfy the constraints above. Typically, the smaller the size of I, the better. Observe that $\gamma \subseteq S_i$, where $S_i$ is the attribute set used to encrypt the ciphertext $M_i$ and $\gamma \subseteq \beta$, the set of attributes used to create the secret key.

To recover the value $e{(g,g)}^{{\alpha }_{i}s}$, we define a function v, which transforms a set of attributes into an element of G in the way $v\left(\gamma \right)={\prod }_{x\in \gamma }{h}_{i,x}$. For each $\tau \in I$, the data requestor computes the value $D_{\tau }^{\prime }=D_{\tau }·{\prod }_{x\in \gamma /f\left(\tau \right)}{Q}_{\tau ,x}=g^{{\lambda }_{\tau }}f{\left(\gamma \right)}^{r_{\tau }}$. For the ciphertext, the data requestor computes the value $L={\prod }_{x\in \gamma }{C}_x={\prod }_{x\in \gamma }{h}_{i,x}^s=f{\left(\gamma \right)}^s$.

Finally, the data requestor recovers the value $e{(g,g)}^{{\alpha }_{i}s}$ by computing:

$$\begin{array}{ccc}& & e(C^{\prime },\prod _{\tau \in I}{D}_{\tau }^{{}^{\prime }{\omega }_{\tau }})/e(\prod _{\tau \in I}{R}_{\tau }^{{\omega }_{\tau }},L)\hfill \\ & & =e(g^s,\prod _{\tau \in I}{g}^{{\lambda }_{\tau }{\omega }_{\tau }}v{\left(\gamma \right)}^{r_{\tau }{\omega }_{\tau }})/e(\prod _{\tau \in I}{g}^{r_{\tau }{\omega }_{\tau }},v{\left(\gamma \right)}^s)\hfill \\ & & =e{(g,g)}^{{\alpha }_{i}s}·e{(g,v\left(\gamma \right))}^{s{\sum }_{\tau \in I}{r}_{\tau }{\omega }_{\tau }}/e{(g,v\left(\gamma \right))}^{s{\sum }_{\tau \in I}{r}_{\tau }{\omega }_{\tau }}\hfill \\ & & =e{(g,g)}^{{\alpha }_{i}s}\hfill \end{array}$$

Note that $C_i=M_i·e{(g,g)}^{{\alpha }_{i}s}$. Hence, the data requestor can obtain $M_i$ from $C_i$. From the computation process, it can be seen that the decryption algorithm requires only two pairing operations.

3.3. Security Analysis

The security of the proposal is based on the hardness of the q-decision bilinear Diffie–Hellman exponent (q-DBDHE) problem defined below.

Definition 5 (q-Decision bilinear Diffie–Hellman exponent [21]). In $(G,G_T)$, the q-DBDHE problem states that, given:

$$(g,g^x,g^{\left(x^2\right)},\cdots g^{\left(x^q\right)},g^{\left(x^{q+2}\right)},\cdots g^{\left(x^{2q}\right)},h,T)$$

where $x\in {\mathbb{Z}}_p,g,h\in G$ and $T\in G_T$, decide whether $T=e{(g,h)}^{x^{(q+1})}$ or T is a random element of $G_T$.

The q-DBDHE assumption states that any probabilistic polynomial time (PPT) algorithm has only negligible advantage in solving the above q-DBDHE problem, where the advantage is defined as $\left|Pr\right[T=e{(g,h)}^{x^{(q+1)}}]-Pr[T=R]|$.

The security of the proposed BABE scheme is guaranteed by the following claim.

Theorem 1. (Security). The BABE scheme is selectively secure against chosen plaintext attacks under the $\left|U\right|-DBDHE$ assumption in G.

Proof. Let $\left|U\right|$ be the maximum of all of the $|U_i|$’s for security parameter λ. Assume that each attribute is indexed by a unique integer between one and $|U_i|$. Suppose there exists a PPT adversary $\mathcal{A}$ who can distinguish the encrypted message vectors with non-negligible probability under the selective security experiment [22]. Then, we show that there exists a PPT adversary $\mathcal{B}$ that can break the $\left|U\right|-DBDHE$ assumption in G, which contradicts the hardness of the $\left|U\right|-DBDHE$ problem.

Init: $\mathcal{A}$ chooses the underlying ABE schemes on which he or she wants to be challenged. For each sub-system, $\mathcal{A}$ outputs the attribute set $S_i^{*},i\in [1,n]$ for the challenge ciphertext.

Setup: The challenger $\mathcal{B}$ is given the tuple:

$$(G,p,g,g^s,g^a,g^{\left(a^2\right)},\cdots g^{\left(a^{\left|U\right|}\right)},g^{\left(a^{\left|U\right|+2}\right)},\cdots g^{\left(a^{2\left|U\right|}\right)},T)$$

for security parameter λ. The challenger is required to solve the $\left|U\right|-DBDHE$ challenge, i.e., to answer whether $T=e{(g,g)}^{a^{\left|U\right|+1}s}$ or a random element in $G_T$. The challenger randomly chooses ${\alpha }_i^{\prime },z_{i,1},\cdots ,z_{i,|U_i|}\in {\mathbb{Z}}_p,i\in [1,n]$ and sets $e{(g,g)}^{{\alpha }_i}=e{(g,g)}^{{\alpha }_i^{\prime }}·e(g^a,g^{a^{\left|U\right|}})$, which means that ${\alpha }_i={\alpha }_i^{\prime }+a^{\left|U\right|+1}$. For $x\in [1,|U\left|\right]$, compute:

$$\begin{array}{ccc}& & h_{i,x}=g^{z_{i,x}},x\in S_i^{*}\hfill \\ & & h_{i,x}=g^{z_{i,x}}{g}^{a^x},x\notin S_i^{*}\hfill \end{array}$$

The public parameter $P{K}_i$ for the i-th subsystem is $(G,p,g,e{(g,g)}^{{\alpha }_i},h_{i,1},\cdots ,h_{i,|U_i|})$ and is sent to the adversary $\mathcal{A}$.

Phase 1: For system i, the challenger $\mathcal{B}$ initializes an empty table $T_i$, an empty set $D_i$ and a counter $j_i$ = 0. The adversary $\mathcal{A}$ can query the challenger $\mathcal{B}$, and the challenger $\mathcal{B}$ responds as follows:

(1). Create($A_i$): The challenger $\mathcal{B}$ sets $j_i=j_i+1$. The access structure $A_i$ is represented by ($W,f$), where W is an $l\times m$ matrix. Let $K_i$ be the set of the rows in which the attributes are in $S_i^{*}$ and $K_i^{\prime }$ be the rows in which the attributes are not in $S_i^{*}(i.e.,K_i^{\prime }=[1,l]/K_i)$. Define an m-element vector $\overrightarrow{v}$ over ${\mathbb{Z}}_p$ with the first element of $\overrightarrow{v}$ being one, for all $\tau \in K_i$, $\overrightarrow{v}{W}_{\tau }=0$. $W_{\tau }$ is the vector row τ of the matrix W. Note that when $S_i$ does not satisfy W, it must be the case that $(1,0,\cdots ,0)$ is not in the span of rows $W_{\tau }$ for $\tau \in K_i$. With the property of LSSS, the vector $\overrightarrow{v}$ can be found in polynomial time. In addition, in order to share the secret ${\alpha }_i$, $\mathcal{B}$ generates a secret key with the vector ${\alpha }_i\overrightarrow{v}$ by noting $v_1=1$. $\mathcal{B}$ computes $\left({\alpha }_i\overrightarrow{v}\right)W_{\tau }$ regarding share ${\lambda }_{\tau }$ for $\tau \in [1,l]$.

The challenger $\mathcal{B}$ randomly chooses $r_1^{\prime },$,⋯,$r_l^{\prime }\in Z_q$ and $y_2,\cdots ,y_m\in {\mathbb{Z}}_p$ to construct a new vector $\overrightarrow{v_{new}}=(0,y_2,y_3,\cdots ,y_m)$. Then, it computes ${\lambda }_{\tau }^{\prime }=\overrightarrow{v_{new}}{W}_{\tau }$ for $\tau \in [1,l]$.

For $\tau \in K_i$, compute $D_{\tau }^{\prime }=g^{{\lambda }_{\tau }^{\prime }}·h_{i,f\left(\tau \right)}^{r_{\tau }^{\prime }},R_{\tau }^{\prime }=g^{r_{\tau }^{\prime }},Q_{\tau ,x}^{\prime }=h_{i,x}^{r_{\tau }^{\prime }},\forall x\in \beta \backslash f\left(\tau \right)$.

For $\tau \in K_i^{\prime }$, compute $c_{\tau }=\overrightarrow{v}{W}_{\tau }$. Set that ${\lambda }_{\tau }=c_{\tau }·{\alpha }_i=c_{\tau }({\alpha }_i^{\prime }+a^{\left|U\right|+1})$. Set $R_{\tau }=g^{-c_{\tau }{a}^{\left|U\right|+1-f\left(\tau \right)}}$, which means $r_{\tau }=-c_{\tau }{a}^{\left|U\right|+1-f\left(\tau \right)}$. Then, set $R_{\tau }^{\prime }=g^{-c_{\tau }{a}^{\left|U\right|+1-f\left(\tau \right)}}{g}^{r_{\tau }^{\prime }}$, and compute:

$$\begin{array}{ccc}& & D_{\tau }^{\prime }=g^{c_{\tau }{\alpha }_i^{\prime }}·R_{\tau }^{z_{i,\tau }}·g^{{\lambda }_{\tau }^{\prime }}·h_{i,f\left(\tau \right)}^{r_{\tau }^{\prime }}\hfill \\ & & =g^{c_{\tau }{\alpha }_i^{\prime }}·g^{-z_{i,\tau }{c}_{\tau }{a}^{\left|U\right|+1-f\left(\tau \right)}}·g^{{\lambda }_{\tau }^{\prime }}·h_{i,f\left(\tau \right)}^{r_{\tau }^{\prime }}\hfill \\ & & =g^{c_{\tau }{\alpha }_i^{\prime }}·g^{-z_{i,\tau }{c}_{\tau }{a}^{\left|U\right|+1-f\left(\tau \right)}}·g^{{\lambda }_{\tau }^{\prime }}·h_{i,f\left(\tau \right)}^{r_{\tau }^{\prime }}·g^{c_{\tau }{a}^{\left|U\right|+1}}·g^{-c_{\tau }{a}^{\left|U\right|+1}}\hfill \\ & & =g^{c_{\tau }{\alpha }_i}·{\left(g^{z_{\tau }}\right)}^{r_{\tau }}·\left(g^{a^{f\left(\tau \right)}}\right)·g^{{\lambda }_{\tau }^{\prime }}·h_{i,f\left(\tau \right)}^{r_{\tau }^{\prime }}\hfill \\ & & =g^{c_{\tau }{\alpha }_i}·h_{i,f\left(\tau \right)}^{r_{\tau }}·g^{{\lambda }_{\tau }^{\prime }}·h_{i,f\left(\tau \right)}^{r_{\tau }^{\prime }}\hfill \end{array}$$

Next, for all $x\in \beta \backslash f\left(\tau \right)$, $Q_{\tau ,x}^{\prime }=h_{i,x}^{r_{\tau }+r_{\tau }^{\prime }}$ is computed as follows:

$$\begin{array}{ccc}& & h_{i,x}^{r_{\tau }+r_{\tau }^{\prime }}={g^{z_{i,x}}}^{(r_{\tau }+r_{\tau }^{\prime })}=g^{-z_{i,x}{c}_{\tau }a\left(\right|U|+1)-f\left(\tau \right)}{g}^{z_{i,x}{r}_{\tau }^{\prime }},x\in S_i^{*}\hfill \\ & & h_{i,x}^{r_{\tau }+r_{\tau }^{\prime }}={g^{z_{i,x}}}^{(r_{\tau }+r_{\tau }^{\prime })}{\left(g^{a^x}\right)}^{(r_{\tau }+r_{\tau }^{\prime })}=g^{-z_{i,x}{c}_{\tau }a\left(\right|U|+1)-f\left(\tau \right)}{g}^{-c_{\tau }a\left(\right|U|+1)-f\left(\tau \right)+x}·{\left(g^{z_{i,x}}{g}^{a^x}\right)}^{r_{\tau }^{\prime }},x\notin S_i^{*}\hfill \end{array}$$

After the process above, the keys are valid with access policy ($W,f$). From the view of $\mathcal{A}$, their distribution is identical to that of the keys generated by the KeyGen algorithm. Hence, the secret keys requested by the adversary is perfectly simulated.

(2). Corrupt($\kappa ,i$): The challenger $\mathcal{B}$ obtains the entry ($\kappa ;A_i;SK$) if the κ-th entry appears in table $T_i$. Set $D_i=D_i\bigcup \left\{A_i\right\}$. It then sends $SK$ to adversary $\mathcal{A}$. If no such entry exists, then return ⊥.

Challenge: $\mathcal{A}$ outputs two equal-length message vectors $\overrightarrow{M_0},\overrightarrow{M_1}$, each of which contains n messages in the message space of the corresponding subsystem. The challenger $\mathcal{B}$ chooses a random bit b. It constructs and sends to $\mathcal{A}$ the challenge ciphertext:

$$C{T}_i^{*}=(C_i^{*}=M_b·T·e(g^{{\alpha }_i^{\prime }},g^s),C^{\prime }=g^s,\forall x\in S^{*},C_{i,x}^{*}={\left(g^s\right)}^{z_{i,x}})$$

Phase 2: $\mathcal{B}$ responds to $\mathcal{A}$’s queries in the same manner as in Phase 1, except that it refuses to answer any Corrupt query that would result in an access structure $A_i$, which $S_i$ satisfies.

Guess: Finally, $\mathcal{A}$ outputs a bit $b^{\prime }$. If $b=b^{\prime }$, then $\mathcal{B}$ outputs that $T=e{(g,g)}^{a^{\left|U\right|+1}s}$, else it outputs that T is a random element.

3.4. Efficiency Analysis

In this section, we analyze the performance of our BABE scheme. It can be seen that our approach is more efficient than encrypting data for different organizations one by one using the underlying Hohenberger-Waters ABE (HW-ABE) [2] scheme. In the encryption process, the number of exponentiations grows with the number of attributes. Comparing to the plain implementation of the HW-ABE scheme, our approach is more efficient because $C^{\prime }$ is the same for all of the ciphertexts. Hence, it can be calculated once and then be reused. Assume that the data owner wants to share data with the users of n organizations simultaneously, and the average number of the attributes used in encryption is m. Our scheme needs $(m+1)n+1$ exponentiations, while the HW-ABE scheme needs $(m+2)n$ exponentiations. From the comparison, the improved efficiency is dominated by the average number of the attributes used by the data owner. We can save $n-1$ exponentiations in the encryption process. The computation overhead for the data requestors is also very small. They need only two pairings and a number of multiplications. This is the same as the HW-ABE scheme [2].

We encoded our BABE and performed experiments on a PC with a 2.80 GHz CPU and 3 GB RAM, using the C programming language in the GMP (https://gmplib.org/) and PBC (https://crypto.stanford.edu/pbc/) library. For the encryption algorithms: (1) we generated n different 1024 bit-long random numbers as exponents; (2) we implemented the batch algorithm and normal algorithm, respectively. We executed Steps 1 and 2 100 times to eliminate experimental noise. We set the values of n ranging from 10 to 100 to see the performance improvement due to the batch algorithms.

Figure 2 show the time to compute n ciphertext in the HW-ABE and BABE with the average attribute number $m=4$ or $m=8$. It can be seen that the time consumed in both BABE and HW-ABE grows linearly with the number of messages to be encrypted. However, the batch encryption takes about 15% less time for $m=4$ or $10\%$ less time for $m=8$ than the normal encryption, which confirms the theoretical analysis.

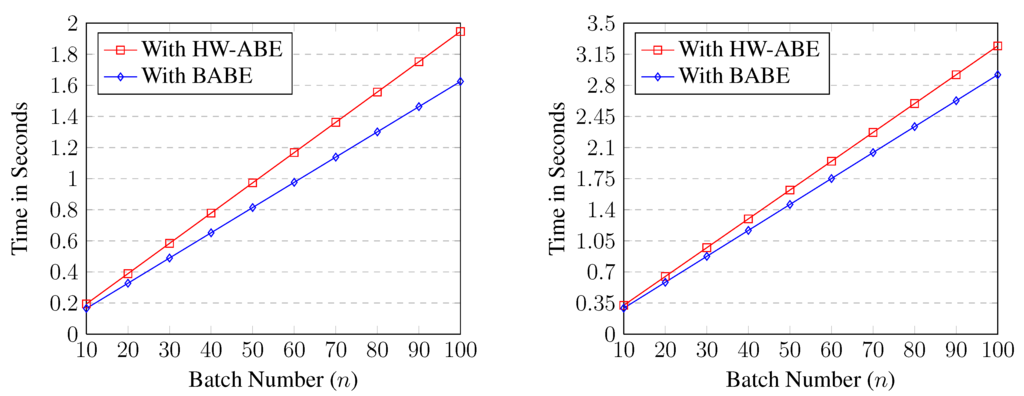
Figure 2. The encryption performance comparison for producing multiple ciphertexts with BABE/HW-ABE ($m=4,m=8$).

Figure 2. The encryption performance comparison for producing multiple ciphertexts with BABE/HW-ABE ($m=4,m=8$).

4. Conclusions

In this paper, we proposed BABE to accelerate the ABE encryption for the users of multiple organizations. Our approach makes the data owner able to share his or her data with the data requestors of different systems simultaneously. We formally proved the security of our scheme and compared it to previous work. The analyses and comparisons show that our scheme has desirable high performance. It is efficient to secure data to be outsourced to clouds.