Bayesian Angular Superresolution Algorithm for Real-Aperture Imaging in Forward-Looking Radar
Abstract
:1. Introduction
2. Signal Model of the Real Aperture Image
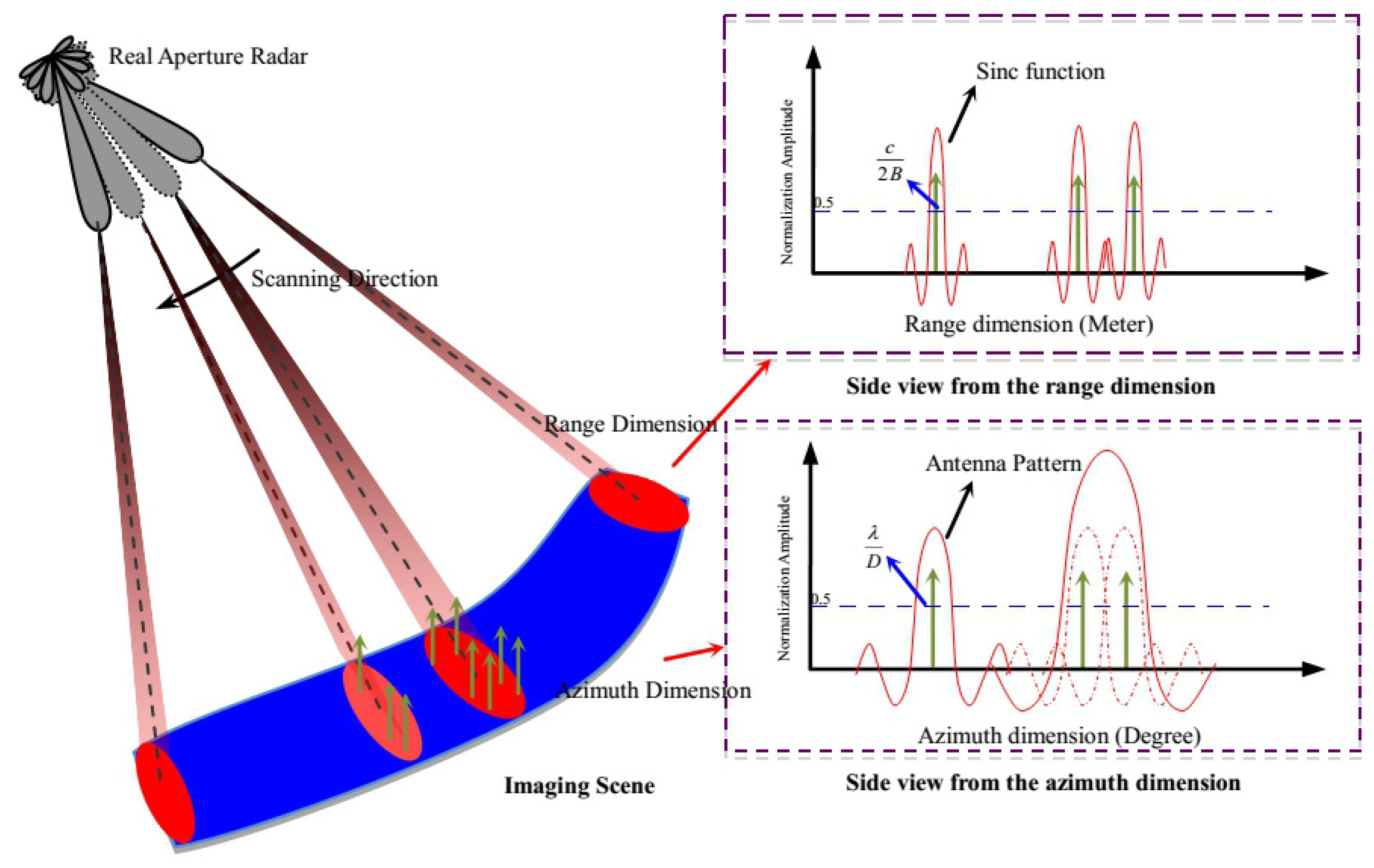
3. Angular Superresolution for Real Aperture Radar
3.1. Tikhonov Regularization
3.2. Richardson-Lucy Superresolution Algorithm
3.3. Proposed MAP Deconvolution Algorithm
4. Results and Discussion
4.1. Point Target Simulation
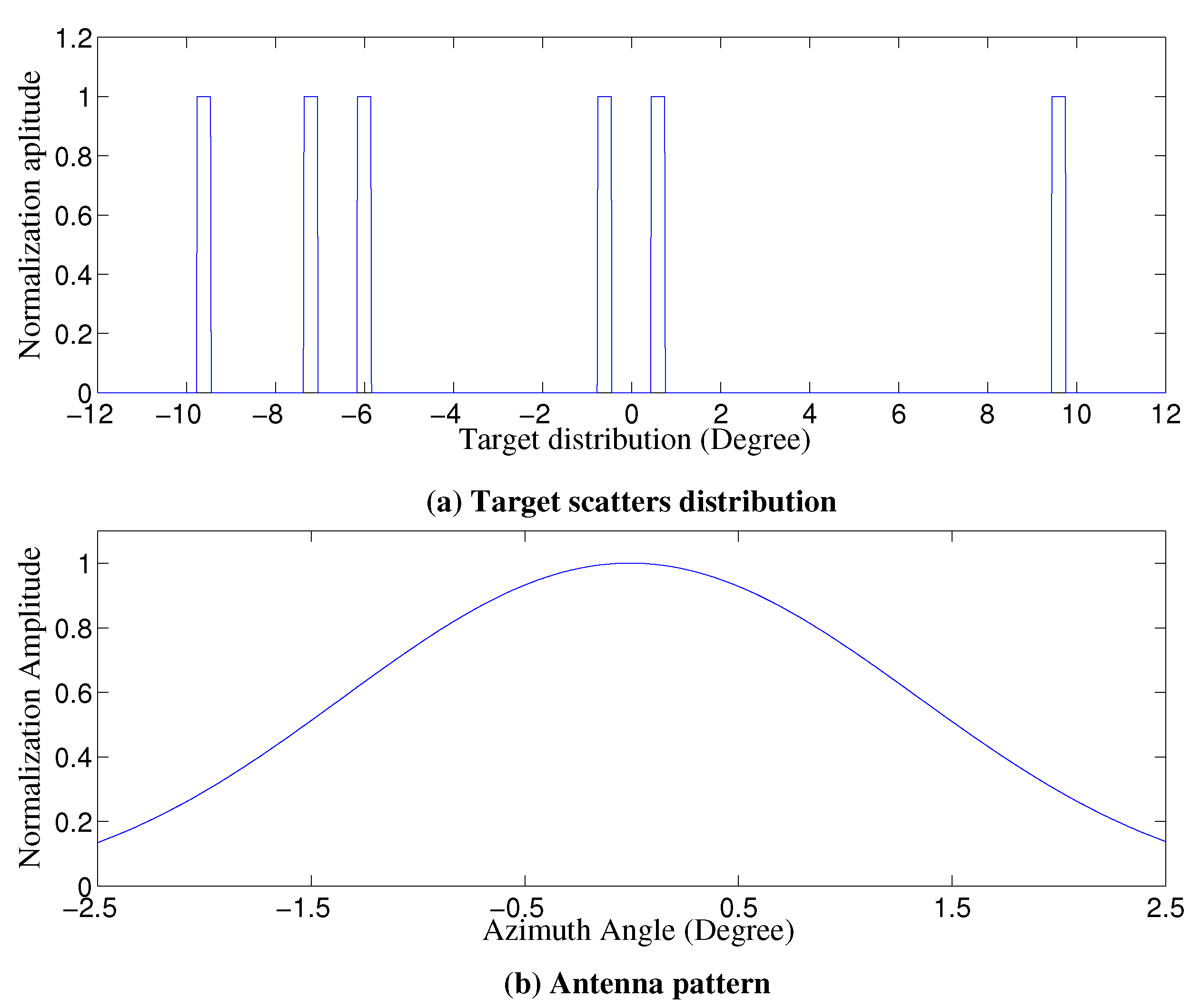
| Parameter | Value | Units |
|---|---|---|
| Carrier frequency | 9.6 | GHz |
| Band width | 30 | MHz |
| Antenna scanning velocity | 30 | °/s |
| Antenna scanning area | ° | |
| Pulse repetition frequency | 2000 | Hz |
| Working distance | 10 | km |
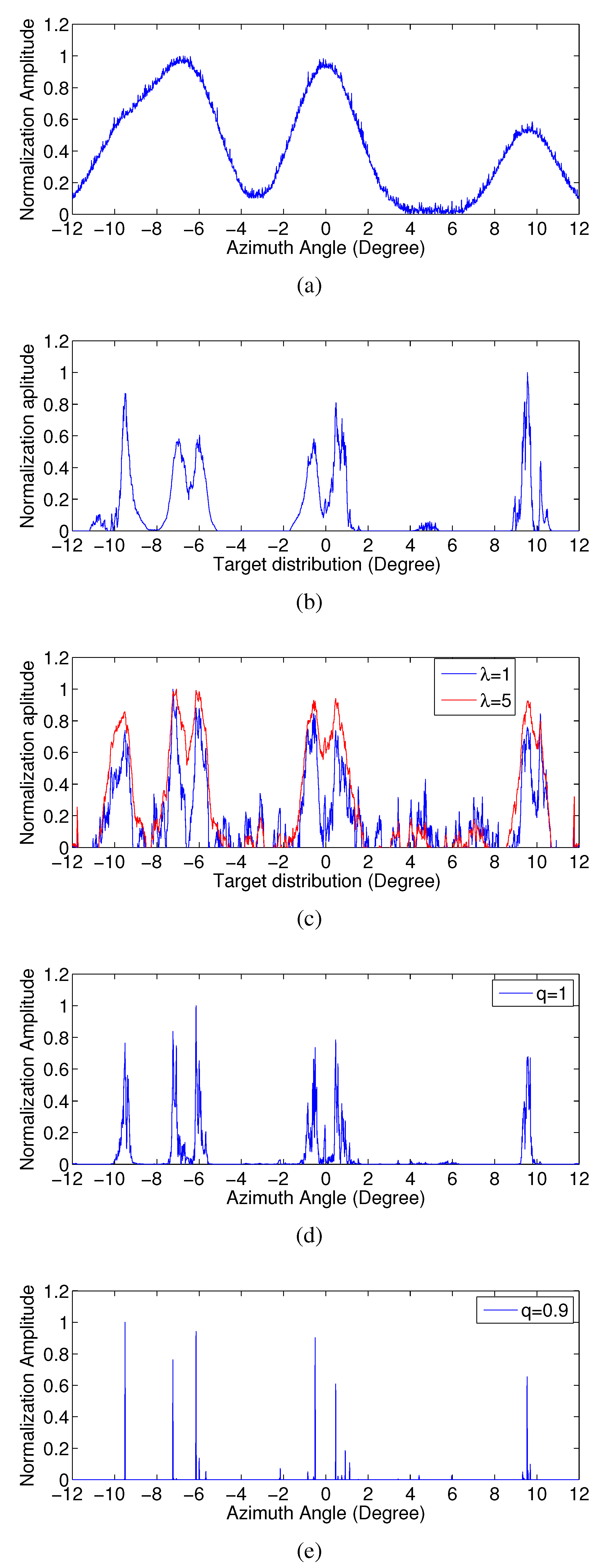
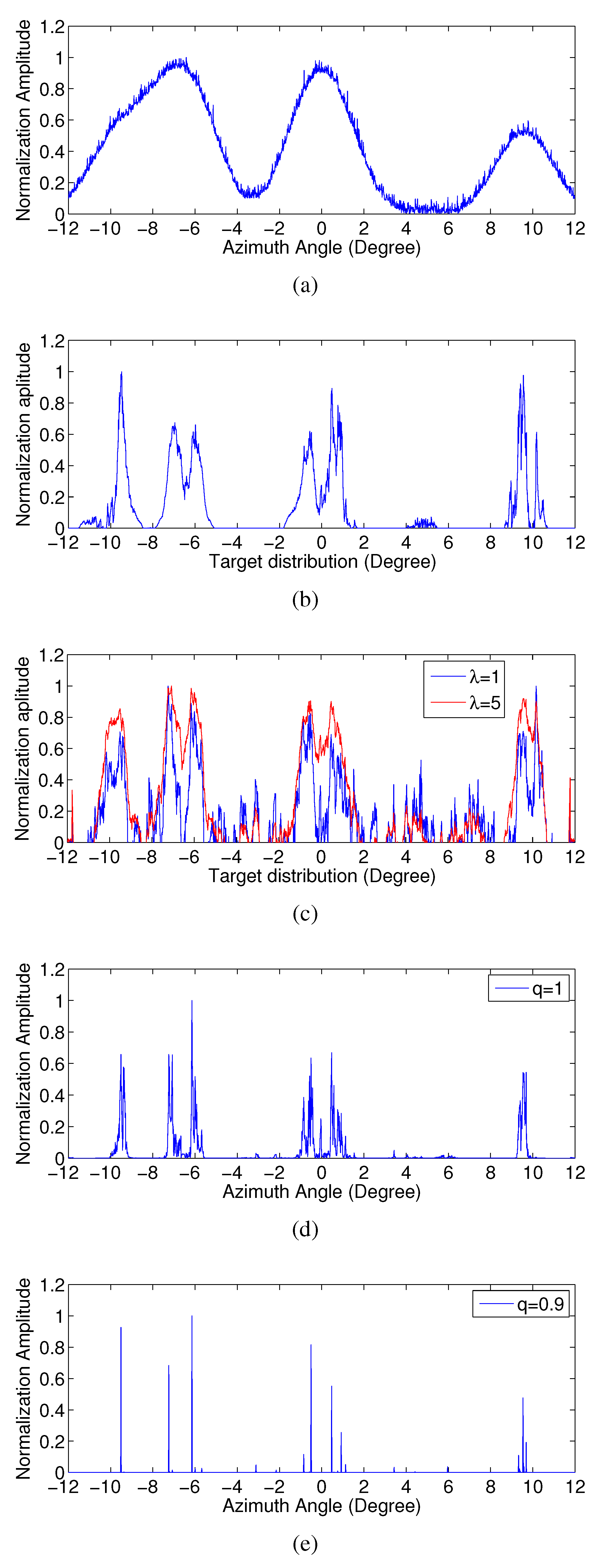
4.2. Scene Simulation
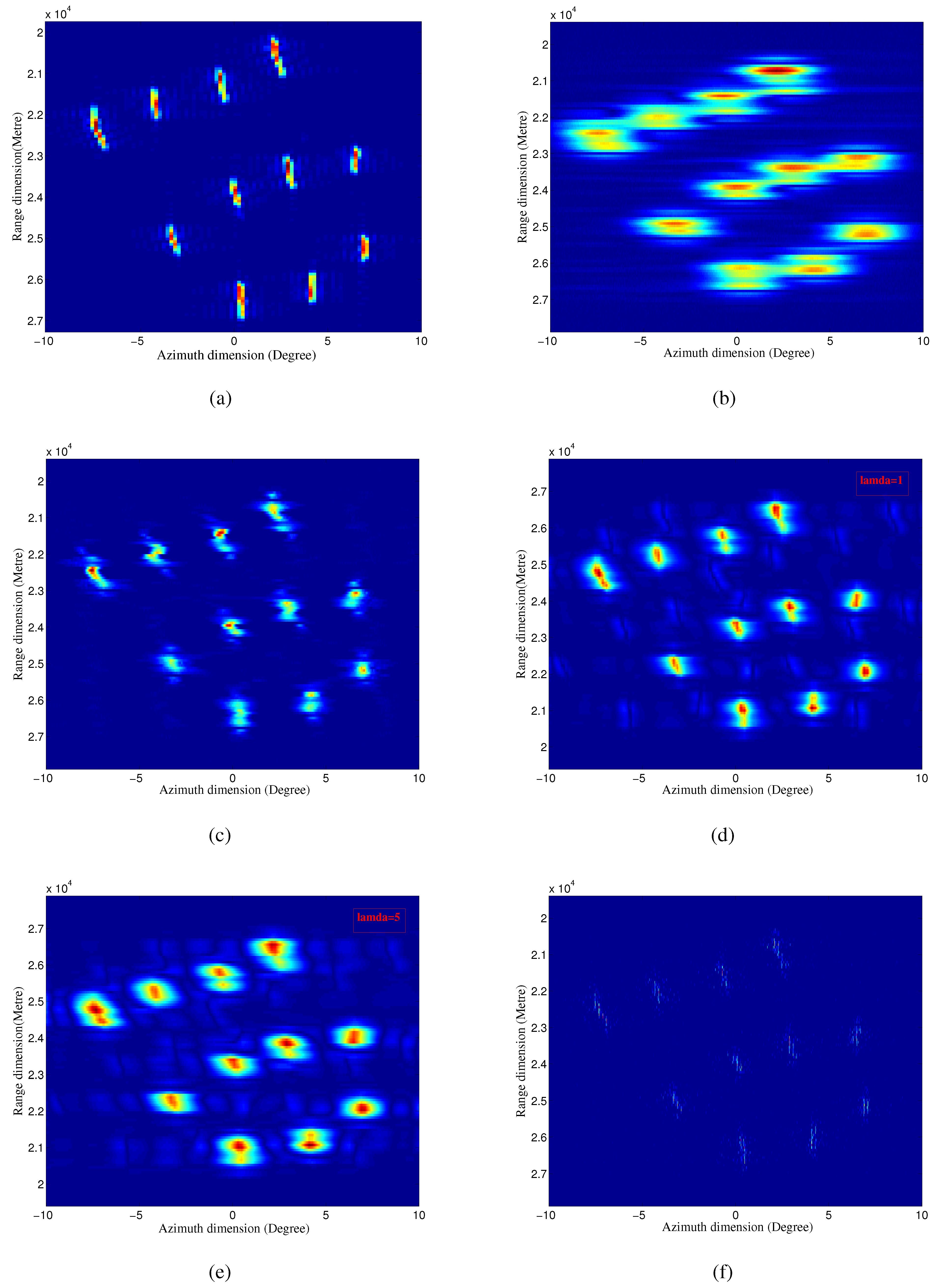
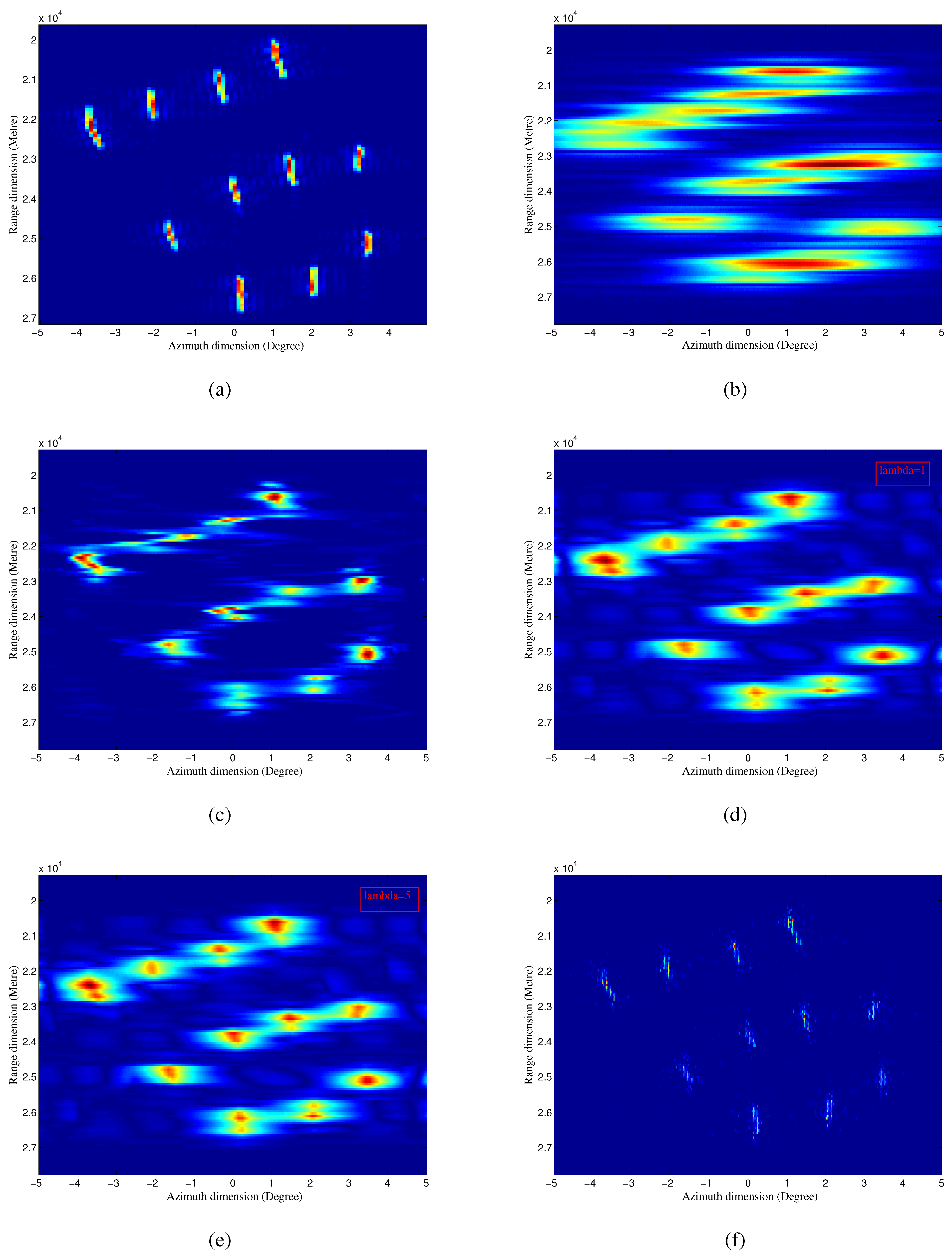
4.3. Real Measured Data
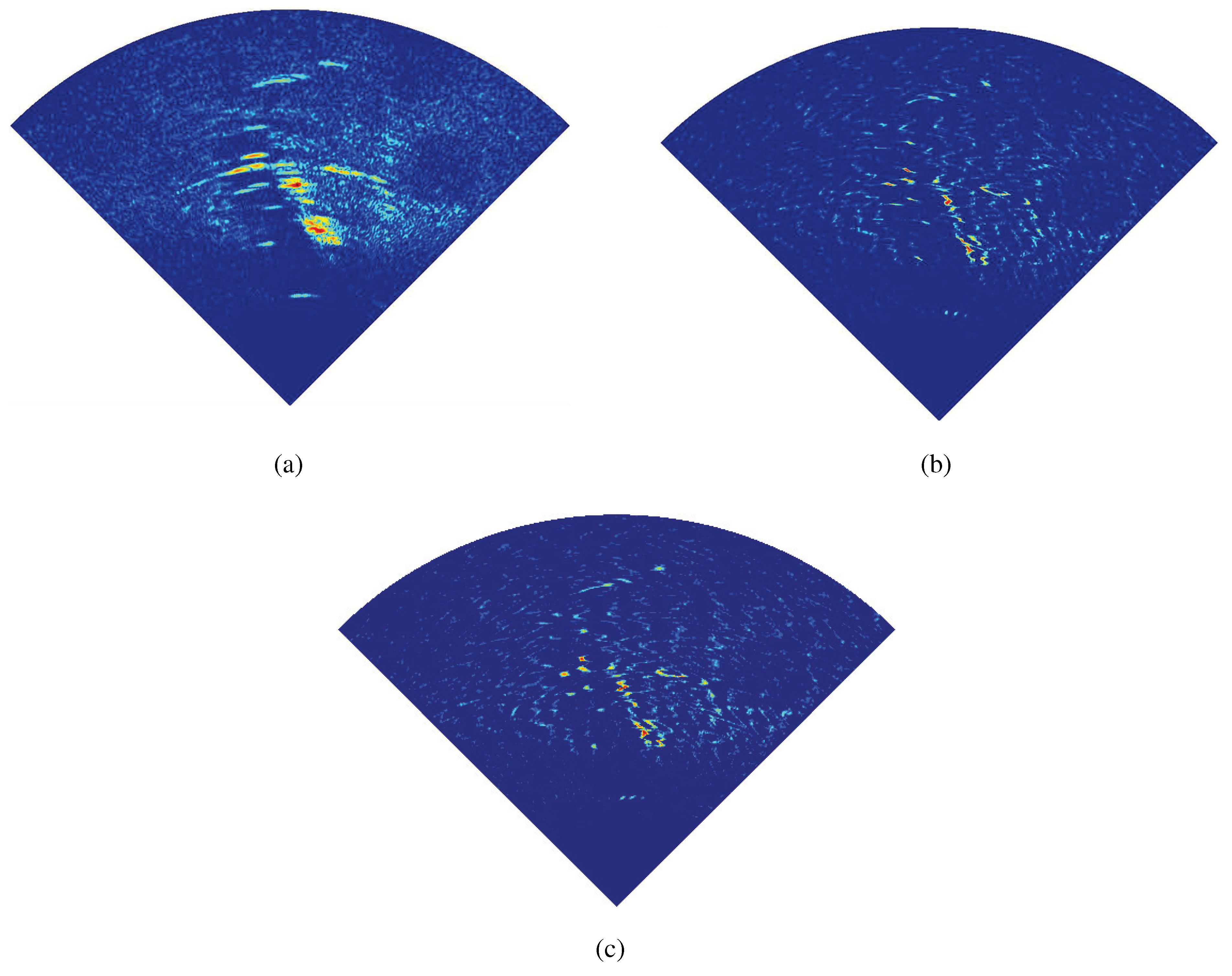
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Skolnik, M.I. Introduction to radar. Radar Handb. 1962, 2. Available online: http://www.turma-aguia.com/davi/skolnik/Skolnik_chapter_1.pdf (accessed on 10 October 2015). [Google Scholar]
- Wehner, D.R. High Resolution Radar; Artech House: Norwood, MA, USA, 1987; p. 484. [Google Scholar]
- Senmoto, S.; Childers, D. Signal resolution via digital inverse filtering. IEEE Trans. Aerosp. Electron. Syst. 1972, 5, 633–640. [Google Scholar] [CrossRef]
- Richards, M.A. Iterative noncoherent angular superresolution [radar]. In Proceedings of the 1988 IEEE National Radar Conference, Ann Arbor, MI, USA, 20–21 April 1988.
- Migliaccio, M.; Gambardella, A. Microwave radiometer spatial resolution enhancement. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1159–1169. [Google Scholar] [CrossRef]
- Gambardella, A.; Migliaccio, M. On the superresolution of microwave scanning radiometer measurements. IEEE Geosci. Remote Sens. Lett. 2008, 5, 796–800. [Google Scholar] [CrossRef]
- Bose, R.; Freedman, A.; Steinberg, B.D. Sequence CLEAN: A modified deconvolution technique for microwave images of contiguous targets. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 89–97. [Google Scholar] [CrossRef]
- Pérez-Martínez, F.; García-Fominaya, J.; Calvo-Gallego, J. A shift-and-convolution technique for high-resolution radar images. IEEE Sens. J. 2005, 5, 1090–1098. [Google Scholar] [CrossRef]
- Ly, C.; Dropkin, H.; Manitius, A.Z. Extension of the MUSIC algorithm to millimeter-wave (MMW) real-beam radar scanning antennas. In Proceedings of Radar Sensor Technology and Data Visualization, Orlando, FL, USA, 1 April 2002.
- Uttam, S.; Goodman, N.A. Superresolution of Coherent Sources in Real-Beam Data. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1557–1566. [Google Scholar] [CrossRef]
- Yardibi, T.; Li, J.; Stoica, P.; Xue, M.; Baggeroer, A.B. Source localization and sensing: A nonparametric iterative adaptive approach based on weighted least squares. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 425–443. [Google Scholar] [CrossRef]
- Roberts, W.; Stoica, P.; Li, J.; Yardibi, T.; Sadjadi, F.A. Iterative adaptive approaches to MIMO radar imaging. IEEE J. Sel. Top. Signal Process. 2010, 4, 5–20. [Google Scholar] [CrossRef]
- Stoica, P.; Li, J.; Ling, J. Missing data recovery via a nonparametric iterative adaptive approach. IEEE Signal Process. Lett. 2009, 16, 241–244. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Li, W.; Huang, Y.; Yang, J. Angular superresolution for real beam radar with iterative adaptive approach. In Proceedings of 2013 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, Austrilia, 21–26 July 2013.
- Zhang, Y.; Zhang, Y.; Huang, Y.; Yang, J.; Zha, Y.; Wu, J.; Yang, H. ML iterative superresolution approach for real-beam radar. In Proceedings of 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014.
- Lenti, F.; Nunziata, F.; Migliaccio, M.; Rodriguez, G. Two-Dimensional TSVD to enhance the spatial resolution of radiometer data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2450–2458. [Google Scholar] [CrossRef]
- Lenti, F.; Nunziata, F.; Estatico, C.; Migliaccio, M. On the spatial resolution enhancement of microwave radiometer data in Banach spaces. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1834–1842. [Google Scholar] [CrossRef]
- Schiavulli, D.; Nunziata, F.; Pugliano, G.; Migliaccio, M. Reconstruction of the normalized radar cross section field from GNSS-R delay-Doppler map. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1573–1583. [Google Scholar] [CrossRef]
- Schiavulli, D.; Lenti, F.; Nunziata, F.; Pugliano, G.; Migliaccio, M. Landweber method in Hilbert and Banach spaces to reconstruct the NRCS field from GNSS-R measurements. Int. J. Remote Sens. 2014, 35, 3782–3796. [Google Scholar] [CrossRef]
- Tan, X.; Roberts, W.; Li, J.; Stoica, P. Sparse learning via iterative minimization with application to MIMO radar imaging. IEEE Trans. Signal Process. 2011, 59, 1088–1101. [Google Scholar] [CrossRef]
- Xu, G.; Xing, M.; Zhang, L.; Liu, Y.; Li, Y. Bayesian inverse synthetic aperture radar imaging. IEEE Geosci. and Remote Sens. Lett. 2011, 8, 1150–1154. [Google Scholar] [CrossRef]
- Zha, Y.; Huang, Y.; Yang, J.; Wu, J.; Zhang, Y.; Yang, H. An improved Richardson-Lucy algorithm for radar angular super-resolution. In Proceedings of 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014.
- Golub, G.H.; Hansen, P.C.; O’Leary, D.P. Tikhonov regularization and total least squares. SIAM J. Matrix Anal. Appl. 1999, 21, 185–194. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Chartrand, R. Exact reconstruction of sparse signals via nonconvex minimization. IEEE Signal Process. Lett. 2007, 14, 707–710. [Google Scholar] [CrossRef]
- Vu, D.; Xue, M.; Tan, X.; Li, J. A Bayesian approach to SAR imaging. Digit. Signal Process. 2013, 23, 852–858. [Google Scholar] [CrossRef]
- Kuruoglu, E.E.; Zerubia, J. Modeling SAR images with a generalization of the Rayleigh distribution. IEEE Trans. Image Process. 2004, 13, 527–533. [Google Scholar] [CrossRef] [PubMed]
- Anastassopoulos, V.; Lampropoulos, G.A.; Drosopoulos, A.; Rey, M. High resolution radar clutter statistics. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 43–60. [Google Scholar] [CrossRef]
- Migliaccio, M.; Ferrara, G.; Gambardella, A.; Nunziata, F.; Sorrentino, A. A physically consistent speckle model for marine SLC SAR images. IEEE J. Ocean. Eng. 2007, 32, 839–847. [Google Scholar] [CrossRef]
- Snyder, D.L.; Helstrom, C.W.; Lanterman, A.D.; Faisal, M.; White, R.L. Compensation for readout noise in CCD images. J. Opt. Soc. Am. A 1995, 12, 272–283. [Google Scholar] [CrossRef]
- Dey, N.; Blanc-Feraud, L.; Zimmer, C.; Roux, P.; Kam, Z.; Olivo-Marin, J.C.; Zerubia, J. Richardson-Lucy algorithm with total variation regularization for 3D confocal microscope deconvolution. Microsc. Res. Tech. 2006, 69, 260–266. [Google Scholar] [CrossRef] [PubMed]
- Ward, K.D.; Watts, S.; Tough, R.J. Sea Clutter: Scattering, the K Distribution and Radar Performance; IET: Stevenage, UK, 2006. [Google Scholar]
- Oliver, C.; Quegan, S. Understanding Synthetic Aperture Radar Images; SciTech Publishing: Stevenage, UK, 2004. [Google Scholar]
- Dey, S.; Dey, T.; Kundu, D. Two-Parameter Rayleigh Distribution: Different Methods of Estimation. Am. J. Math. Manag. Sci. 2014, 33, 55–74. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zha, Y.; Zhang, Y.; Huang, Y.; Yang, J. Bayesian Angular Superresolution Algorithm for Real-Aperture Imaging in Forward-Looking Radar. Information 2015, 6, 650-668. https://doi.org/10.3390/info6040650
Zha Y, Zhang Y, Huang Y, Yang J. Bayesian Angular Superresolution Algorithm for Real-Aperture Imaging in Forward-Looking Radar. Information. 2015; 6(4):650-668. https://doi.org/10.3390/info6040650
Chicago/Turabian StyleZha, Yuebo, Yin Zhang, Yulin Huang, and Jianyu Yang. 2015. "Bayesian Angular Superresolution Algorithm for Real-Aperture Imaging in Forward-Looking Radar" Information 6, no. 4: 650-668. https://doi.org/10.3390/info6040650
APA StyleZha, Y., Zhang, Y., Huang, Y., & Yang, J. (2015). Bayesian Angular Superresolution Algorithm for Real-Aperture Imaging in Forward-Looking Radar. Information, 6(4), 650-668. https://doi.org/10.3390/info6040650






