Applying the Upper Integral to the Biometric Score Fusion Problem in the Identification Model

Abstract

This paper presents a new biometric score fusion approach in an identification system using the upper integral with respect to Sugeno’s fuzzy measure. First, the proposed method considers each individual matcher as a fuzzy set in order to handle uncertainty and imperfection in matching scores. Then, the corresponding fuzzy entropy estimates the reliability of the information provided by each biometric matcher. Next, the fuzzy densities are generated based on rank information and training accuracy. Finally, the results are aggregated using the upper fuzzy integral. Experimental results compared with other fusion methods demonstrate the good performance of the proposed approach.

1. Introduction

Biometric systems refer to the identification of human beings by their physical or behavioral traits [1]. These traits have the advantage that they are unique and permanent, unlike conventional techniques, such as passwords and badges, which can be used fraudulently by others. Depending on the application context, biometric systems can operate in two modes, namely verification and identification [2]. In the verification mode, the system validates a query biometric by comparing only the captured biometric data with the biometric template of a specific identity stored in the database. In the identification mode, the user’s biometric input is compared to the templates of all persons enrolled in the database. Therefore, the identification task is significantly more challenging than verification [3].

Biometric systems based on a single biometric trait have several inherent problems, such as large intra-class variations, sensitivity to noise and non-universality [4]. Multibiometric systems, which combine multiple sources of biometric information, have been developed in order to overcome most of those weaknesses and to achieve better recognition performance [5]. Information from different biometric traits can be integrated at the feature extraction level (integrating the features of different biometrics), matching score level (combining the genuine and imposter scores) or decision level (combining the decisions) [5]. Compared to the feature-level and decision-level fusion, the matching score-level fusion is the most popular because it offers the best compromise in terms of the information content and the ease in fusion [6].

Several fusion methods at the matching score level have been proposed in the literature. These methods can be divided into three large groups [5,6]. The first group of methods are density based: the densities of genuine and impostor matching scores are firstly estimated, and the fusion is carried out by statistical tests (e.g., the likelihood ratio test with the Gaussian mixture model [6]). The second group of methods is transformation based: the matching scores are firstly transformed to a common domain and then combined by a simple fusion rules (e.g., sum rule-based fusion preceded by min-max normalization [4]). The third group of methods is classifier based: scores from multiple matchers are concatenated into new feature vectors, which are used to train a new classifier (e.g., SVM-based fusion [7]). However, most of these fusion methods have been implicitly designed for the verification scenario and cannot be directly applied to the identification scenario [3,8]. For instance, in [3], the authors have shown that likelihood ratio-based score fusion, which has originally designed for verification systems, is applicable to multibiometric identification systems only under certain assumptions.

Generally, combining information from multiple sources can give better classification accuracy of a multibiometric system. However, researchers have shown that fusing different matching scores does not necessarily give better performance than the best individual biometric system [9,10,11]. The performance in this case is highly dependent on the imprecise, uncertain and incomplete nature of the matching scores output by biometric sources. This is due to the noise present in the sensor during the acquisition of the biometric signal and the errors made by the feature extraction and matching processes [4]. In such cases, fusion methods have to deal with imprecise and conflicting information. Fuzzy set theory [12] provides numerous methodologies for the modeling and management of uncertainty. One of these methods, which is very useful in information fusion, is the fuzzy integral. This latter one is known to be one of the most powerful and flexible nonlinear function that can capture interactions among the various sources of information [13].

The idea of using the fuzzy integral in multibiometric systems is not new. Several researchers have attempted to use the fuzzy integral in multibiometric systems [14,15,16]. However, the Choquet fuzzy integral [17] and the Sugeno fuzzy integral [18] are often used. Recently, another fuzzy integral proposed by Wang et al. [19], namely the upper integral, has been successfully applied to classifier combination in a number of contexts [20,21,22]. To the authors’ knowledge, it has never been used for multibiometric systems. Hence, we focus in our study on using the upper integral in multibiometric identification systems.

In a previous work [23], we introduced a general framework of a multibiometric identification system based on fusion at the matching score level using fuzzy set theory. The output of each biometric matcher is modeled as a fuzzy set in order to handle uncertainty and imperfection in matching scores. Then, the fuzzy entropy estimates the reliability of the information provided by each biometric matcher. However, the results are aggregated with a simple fuzzy combination rule. In this paper, we propose using the upper integral as an aggregation operator. This novel approach provides a possibility to use all matching scores received by all users enrolled in the system, unlike most fusion approaches in multibiometric identification systems. Moreover, it can clearly express the interaction among biometric matchers and provides a measure of importance for any subset of matchers.

The rest of this paper is organized as follows. Section 2 presents the concepts of the upper fuzzy integral and the fuzzy measure. The proposed fusion method based on the upper integral is described in Section 3. Section 4 gives the experimental results. Finally, some conclusions end this paper.

2. Fuzzy Measure and Upper Integral

In this section, we introduce some mathematical concepts of the fuzzy measure and the upper integral that are suitable for a multibiometric identification system.

2.1. Fuzzy Measure

Let X be an arbitrary set and $P\left(X\right)$ denote the power set of X or the set of all subsets of X. A set function $\mu :P\left(X\right)\to [0,1]$ is a fuzzy measure if it satisfies the following three axioms:

(1)

Boundary conditions: $\mu \left(\text{∅}\right)=0$, $\mu \left(X\right)=1$.

(2)

Monotonicity: $\mu \left(A\right)\le \mu \left(B\right)$ if $A\subseteq B$ and $A,B\in P\left(X\right)$.

(3)

Continuity: ${lim}_{i\to \infty }\mu \left(A_i\right)=\mu \left({lim}_{i\to \infty }{A}_i\right)$ if $A_i\in P\left(X\right)$ and $\left\{A_i\right\}$ are monotone (an increasing sequence of measurable sets).

In general, the fuzzy measure of a union of two disjoint subsets cannot be directly computed from the fuzzy measures of the subsets. Sugeno [24] has proposed the decomposable so-called λ-fuzzy measure satisfying the following additional property:

$$\mu (A\cup B)=\mu \left(A\right)+\mu \left(B\right)+\lambda \mu \left(A\right)\mu \left(B\right)$$

(1)

for all $A,B\in P\left(X\right)$ with $A\cap B=\varnothing$ and for some $\lambda >-1$.

Let $X=\{x_1,x_2,\cdots ,x_K\}$ be a finite set, and let ${\mu }^k=\mu \left(\left\{x_k\right\}\right)$. The values ${\mu }^k$ are called the densities of the measure. The value of the constant λ can be determined from the equation $\mu \left(X\right)=1$, which is equivalent to solving the following equation:

$$\lambda +1=\prod _{k=1}^K(1+\lambda {\mu }^k)$$

(2)

2.2. Upper Integral

Let $X=\{x_1,x_2,\cdots ,x_K\}$ be a nonempty set, $P\left(X\right)$ be the power set of X, $\mu :P\left(X\right)\to [0,+\infty )$ be a set function denoting the fuzzy measure and $f:X\to [0,+\infty )$ be a function. The upper integral of f with respect to a set function μ, denoted by $\left(U\right)\int fd\mu$, is described as:

$$\left(U\right)\int fd\mu =\text{sup}\left\{\sum _{i=1}^{2^K-1}{a}_i\mu \left(A_i\right)|\sum _{i=1}^{2^K-1}{a}_i{\chi }_{A_i}=f\right\}$$

(3)

where ${\chi }_{A_i}$ is the characteristic function of set $A_i$, $a_i\ge 0$, and $A_i={\bigcup }_{k:b_k=1}\left\{x_k\right\}$ if i is expressed in binary digits as $b_K{b}_{K-1}\cdots b_1$ for every $i=1,2,\cdots ,2^K-1$.

When set function μ and function f are given, the value of the upper integral $\left(U\right)\int fd\mu$ is the solution of the following linear programming problem [19,25], where $a_1,a_2,\cdots ,a_{2^K-1}$ are unknown parameters:

$$\begin{array}{ccc}\text{Maximum}\hfill & & {\displaystyle z=\sum _{i=1}^{2^K-1}{a}_i{\mu }_i}\hfill \\ \text{Subject}\text{to}\hfill & & {\displaystyle \sum _{i=1}^{2^K-1}{a}_i{\chi }_{A_i}\left(x_k\right)=f\left(x_k\right),k=1,2,\cdots ,K}\hfill \\ & & a_i\ge 0,i=1,2,\cdots ,2^K-1\hfill \end{array}$$

where ${\mu }_i=\mu \left(A_i\right)$ for $i=1,2,\cdots ,2^K-1$.

Note that when μ is a λ-fuzzy measure, the values of $\mu \left(A_i\right)$ can be computed recursively as follows:

$$\left\{\begin{array}{c}\mu \left(A_i\right)={\mu }^k\text{if}{\left(i\right)}_2\equiv \overline{0_K{0}_{K-1}\dots 0_{k+1}}{\mathbf{1}}_k\overline{0_{k-1}\dots 0_1},\hfill \\ \mu \left(A_i\right)=\mu \left(A_k\right)+\mu \left(A_{i-2^{k-1}}\right)+\lambda \mu \left(A_k\right)\mu \left(A_{i-2^{k-1}}\right)\text{if}{\left(i\right)}_2\equiv \overline{b_K{b}_{K-1}\dots b_{k+1}}{\mathbf{1}}_k\overline{0_{k-1}\dots 0_1}\hfill \end{array}\right.$$

(4)

where $b_K{b}_{K-1}\dots b_k\dots b_1$ is the binary expression of i.

3. Proposed Method

3.1. The Fusion Model Based on the Upper Integral

Let $X=\{x_1,x_2,\cdots ,x_K\}$ be a set of biometric matchers in the multibiometric system and N be the number of users enrolled in the system. Each of these users has his own reference model. To simplify the notation, we assume that there is only a single reference model associated with each user for each biometric modality. A way to work at the score level is the use of a score matrix that contains the matching scores output by each biometric matchers. Let $s_n^k$ denote the generic matching score output by the k-th biometric matcher for the n-th user in the database, $n=1,2,\cdots ,N$; $k=1,2,\cdots ,K$. For a given query, all outputs of biometric matchers can be organized in the score matrix S defined as:

$$\mathrm{S}=\left(\begin{array}{ccc}{s}_1^1& \cdots & s_N^1\\ ⋮& \ddots & ⋮\\ s_1^K& \cdots & s_N^K\end{array}\right)$$

(5)

According to [23], the output of each biometric matcher can be modeled as a fuzzy set using membership functions. Therefore, we can rewrite the score matrix S in the following way:

$$\mathrm{S}=\left(\begin{array}{ccc}{\xi }_1\left(s_1^1\right)& \cdots & {\xi }_1\left(s_N^1\right)\\ ⋮& \ddots & ⋮\\ {\xi }_K\left(s_1^K\right)& \cdots & {\xi }_K\left(s_N^K\right)\end{array}\right)$$

(6)

where ${\xi }_k$ is the fuzzy membership function of the k-th biometric matcher. The membership value ${\xi }_k\left(s_n^k\right)$ varies from zero to one, where the case that ${\xi }_k\left(s_n^k\right)=1$ shows absolute certainty that the identity of the user is n, from the standpoint of the k-th biometric matcher, while ${\xi }_k\left(s_n^k\right)=0$ implies absolute certainty that the identity of the user is not n. In this study, each biometric matcher $x_k$ is represented by a piecewise-linear membership function defined as:

$${\xi }_k\left(y\right)=\left\{\begin{array}{cc}0& \text{if}y\le a,\hfill \\ {\displaystyle \frac{1}{4}\left(\frac{y-a}{b-a}\right)}& \text{if}a<y\le b,\hfill \\ {\displaystyle \frac{1}{4}+\frac{1}{4}\left(\frac{y-b}{c-b}\right)}& \text{if}b<y\le c,\hfill \\ {\displaystyle \frac{1}{2}+\frac{1}{4}\left(\frac{y-c}{d-c}\right)}& \text{if}c<y\le d,\hfill \\ {\displaystyle \frac{3}{4}+\frac{1}{4}\left(\frac{y-d}{e-d}\right)}& \text{if}d<y\le e,\hfill \\ 1& \text{if}y>e\hfill \end{array}\right.$$

(7)

where a and d are the minimum and the maximum value of the impostor score distributions, respectively, b and e are the minimum and the maximum value of the genuine score distributions, respectively, and $c\in (b,d)$. The values of these parameters are learned using a training dataset for each biometric matcher.

When a biometric matcher $x_k$ provides a reliable result, the fuzzy set $\{{\xi }_k\left(s_1^k\right),{\xi }_j\left(s_2^k\right),\cdots ,{\xi }_j\left(s_N^k\right)\}$ will be close to a binary set. On the contrary, when $x_k$ is unreliable, no opportunity should be significantly higher than the others. The fuzzy entropy of this fuzzy set is given by [26]:

$$H\left({\xi }_k\right)=Q\sum _{n=1}^{N}S\left({\xi }_k\left(s_n^k\right)\right)$$

(8)

where $S\left(y\right)=-ylog\left(y\right)-(1-y)log(1-y)$ and Q is a normalizing constant. In terms of fuzzy entropy, the set constructed with a reliable biometric matcher will have a low degree contrary to a set constructed with an unreliable biometric matcher. Thus:

$$w_k=\frac{{\displaystyle \sum _{i=1,i\ne k}^{K}H\left({\xi }_i\right)}}{{\displaystyle \sum _{i=1}^{K}H\left({\xi }_i\right)}}$$

(9)

is interpreted as the degree in which biometric matcher $x_k$ identifies the identity of the user correctly. Then, each fuzzy set will be weighted by $w_k$, and we can rewrite the score matrix S in the following way:

$$\mathrm{S}=\left(\begin{array}{ccc}{w}_1{\xi }_1\left(s_1^1\right)& \cdots & w_1{\xi }_1\left(s_N^1\right)\\ ⋮& \ddots & ⋮\\ w_K{\xi }_K\left(s_1^K\right)& \cdots & w_K{\xi }_K\left(s_N^K\right)\end{array}\right)$$

(10)

when a biometric matcher $x_k$ has a low uncertainty, $w_k$ is close to one, and it only slightly affects the corresponding fuzzy set.

Each column of the new score matrix S can be regarded as a function defined on the set X, $f_n:X⟶[0,1]$, $f_n\left(x_k\right)=w_k{\xi }_k\left(s_n^k\right)$, $k=1,2,\cdots ,K$, $n=1,2,\cdots ,N$. Thus, if we know the fuzzy densities, according to Equation (3), we can compute the integral value of each column of the new matrix S, and the subscript of the maximum of all integral value is the final identity. The next task is to determine the fuzzy densities.

3.2. Determining Fuzzy Densities

Besides the fusion technique, the critical issue in the fuzzy integral is how to determine the most appropriate fuzzy densities. Various methods have been developed to determine the fuzzy densities to a given problem [27,28,29,30,31,32]. However, many of these methods are based on accuracy or on both accuracy and uncertainty. In this work, we propose a new method for determining fuzzy densities using the training accuracy and dynamic information provided by each biometric matcher.

When a multibiometric system operates in the identification mode, the matching scores of each biometric matcher are arranged in descending order to form the ranking list in order to determine potential matching identities (a lower rank indicating a better match). Let $r_k^n$ be the rank output by the k-th matcher for the n-th template in the database, $k=1,\dots ,K$; $n=1,\dots ,N$. For a given query, we have also the rank matrix R defined as:

$$\mathrm{R}=\left(\begin{array}{ccc}{r}_1^1& \cdots & r_N^1\\ ⋮& \ddots & ⋮\\ r_1^K& \cdots & r_N^K\end{array}\right)$$

(11)

The fuzzy densities that we propose are based on the training accuracy and rank information as follows:

$${\mu }_n^k=p_k\times {\left(\frac{N+1-r_n^k}{N}\right)}^{{\displaystyle \underset{i=1}{\overset{K}{min}}{r}_n^i}},\mathrm{for}k=1,2,\cdots ,K;n=1,2,\cdots ,N$$

(12)

where $p_k$ is the training accuracy of the k-th biometric matcher. In this method, the fuzzy densities might be different for each user enrolled in the system and are also specific for the current query.

4. Experimental Results

We evaluated the performance of our method on the publicly-available benchmark database for score level fusion BSSR1 distributed by NIST (referenced as NIST-BSSR1 in the paper) [33]. This database contains three different partitions. The first partition is the NIST-Multimodal database, which contains two face scores and two fingerprint scores from 517 subjects. The second partition is the NIST-Fingerprint database, which contains two fingerprint scores from 6000 subjects. Finally, the third partition is the NIST-Face database, which contains two face scores from 3000 subjects. The face scores are generated by two commercial systems, which are labeled as Matcher C and Matcher G. One fingerprint score is obtained by comparing a pair of images of the left index finger, and another score is obtained by comparing a pair of images of the right index finger. For this database, there is no experimental protocol defined. In the experimental process, half of the imposter and the genuine scores are randomly selected to be in the training set to estimate the training accuracy and the parameters of the fuzzy membership functions. The remaining half of the scores is used to evaluate the fusion performance. The above training test partitioning is repeated 20 times, and the reported cumulative match characteristic (CMC) curves correspond to the mean identification rates over the 20 trials. In the identification system, the CMC is widely used as an accuracy performance measure. The CMC shows the ratio of correct identification versus the matching rank.

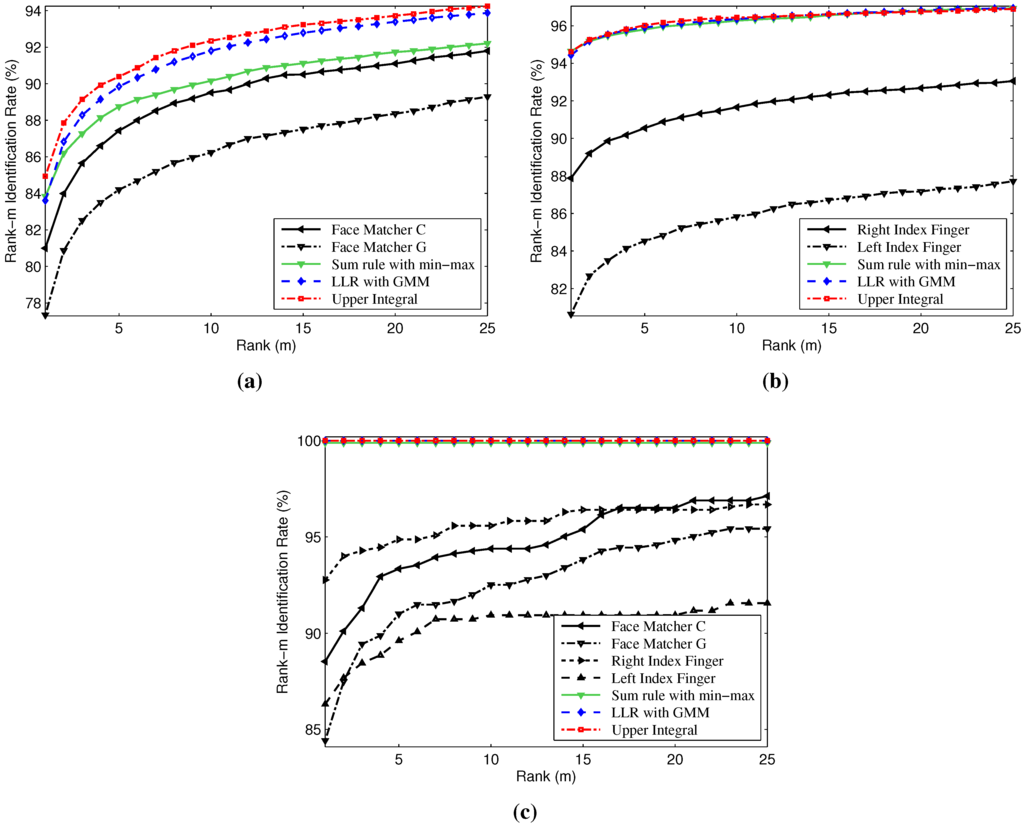
Figure 1. Cumulative match characteristic curves of the proposed method, individual matchers and other biometric score fusion methods on the (a) NIST-Face, (b) NIST-Fingerprint and (c) NIST-Multimodal databases.

Figure 1. Cumulative match characteristic curves of the proposed method, individual matchers and other biometric score fusion methods on the (a) NIST-Face, (b) NIST-Fingerprint and (c) NIST-Multimodal databases.

The goal of the multibiometric system is to increase precision and enhance reliability more than individual matchers. In order to demonstrate the effectiveness of our proposed method, Figure 1 shows the CMC curves of the individual matchers and the proposed method on the three partitions of the NIST-BSSR1 database. These results clearly show that our method provides a significantly better recognition rate than the individual matchers on all databases. The improvement of the rank-1 accuracy is approximately 3.88%, 6.62% and 7.24% compared to the best single matcher of the NIST-Face, NIST-Fingerprint and NIST-Multimodal databases, respectively.

In order to evaluate the efficiency of the proposed method, comparisons are made against well-established existing biometric score fusion methods, like the sum rule with min-max normalization method [4] and the likelihood ratio-based fusion with the Gaussian mixture model (LLR-GMM) [6]. Figure 1 shows also the CMC curves of these methods for the three partitions of the NIST-BSSR1 database. We can see from this figure that the recognition rates of sum rule and LLR-GMM fusion methods are comparable to our method on the NIST-Fingerprint and NIST-Multimodal databases (see Figure 1b,c), but they are inferior to our method on the NIST-Face database (see Figure 1a).

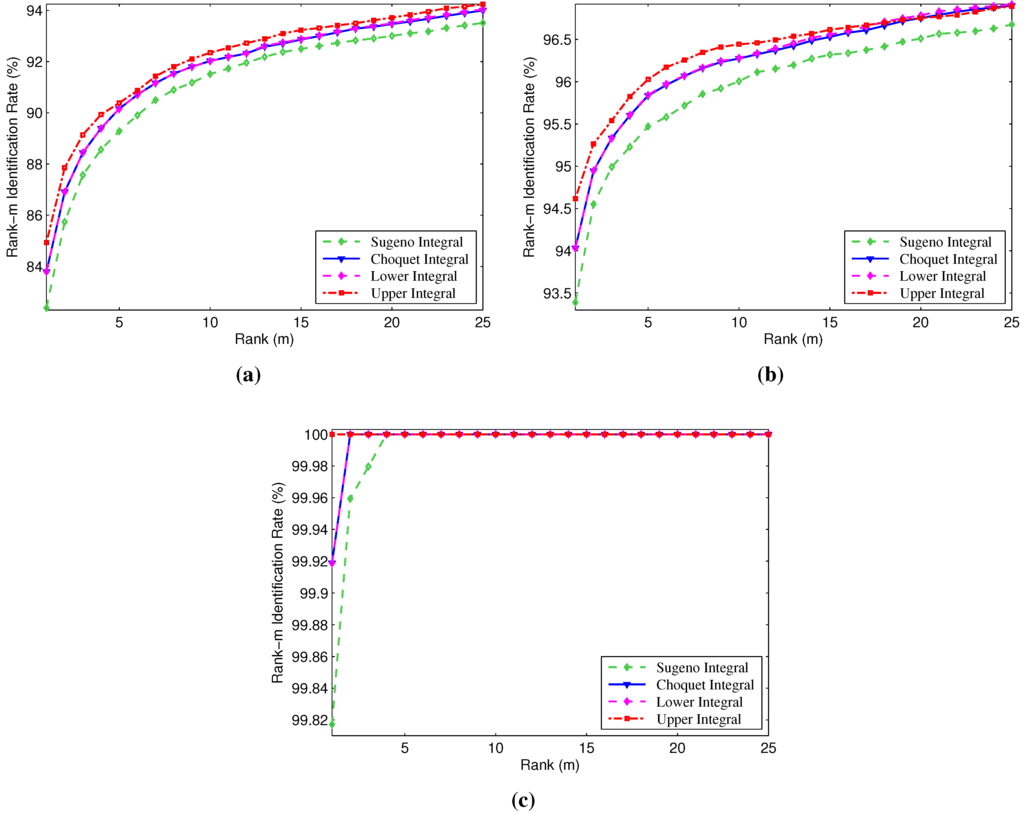
Figure 2. Cumulative match characteristic curves of the proposed method and other fuzzy integrals on the (a) NIST-Face, (b) NIST-Fingerprint and (c) NIST-Multimodal databases.

Figure 2. Cumulative match characteristic curves of the proposed method and other fuzzy integrals on the (a) NIST-Face, (b) NIST-Fingerprint and (c) NIST-Multimodal databases.

We also compared the performance of the proposed method with other fuzzy integrals, such as the Choquet integral [17], the Sugeno integral [18] and the lower integral [19], on the three partitions of the NIST-BSSR1 database. We note that for these fuzzy integrals, we utilize the same fusion technique as used in our method. From Figure 2, we notice that the proposed method outperforms slightly all other fuzzy integral fusion methods on all databases.

5. Conclusions

In this paper, we have proposed a new biometric score fusion method based on the upper integral with respect to Sugeno’s fuzzy measure in an identification model. In order to prove the efficiency of our fusion approach, we have used a publicly-available benchmark database for the biometric score fusion problem. Experimental results exhibit that our fusion approach achieves better performance than the best single matcher and other fusion methods.