Robust Sparse Representation for Incomplete and Noisy Data
Abstract
:1. Introduction
2. Sparse Representation for Classification
3. Incomplete Sparse Representation for Classification
3.1. Model of Incomplete Sparse Representation
3.2. Generic Formulation of ADMM
3.3. Algorithm for Incomplete Sparse Representation
| Algorithm 1. Solving Problem (11) via ADMM. |
| Input: the dictionary matrix constructed by all training samples, an incomplete test sample and the sampling index set . |
| Output:, , and . |
| Initialize: . |
| While not converged do |
| 1: Update according to (14). |
| 2: Update according to (16). |
| 3: Update according to (19). |
| 4: Update according to (20). |
| 5: Update according to (22). |
| 6: Update according to (23). |
| 7: Update as . |
| End while |
4. Convergence Analysis and Model Extension
5. Experiments
5.1. Datasets Description and Experimental Setting
5.2. Experimental Analysis
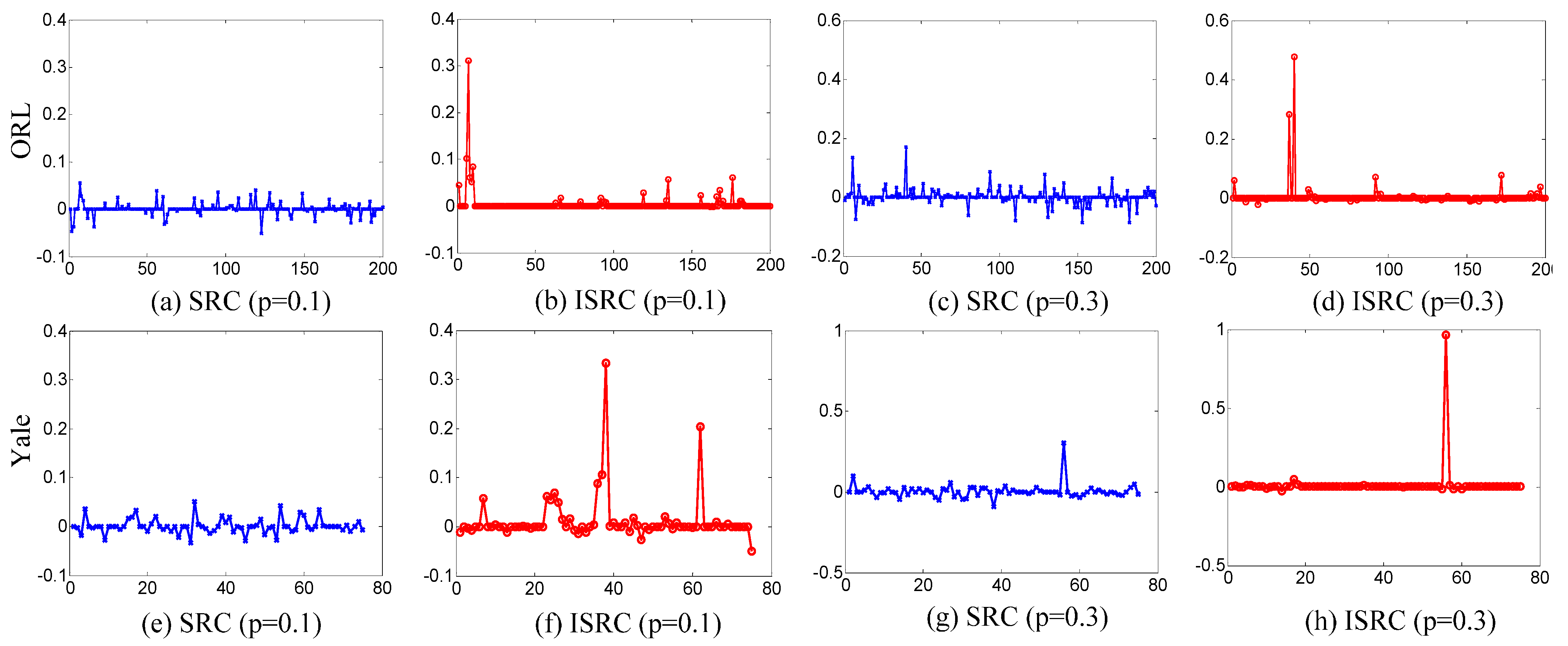
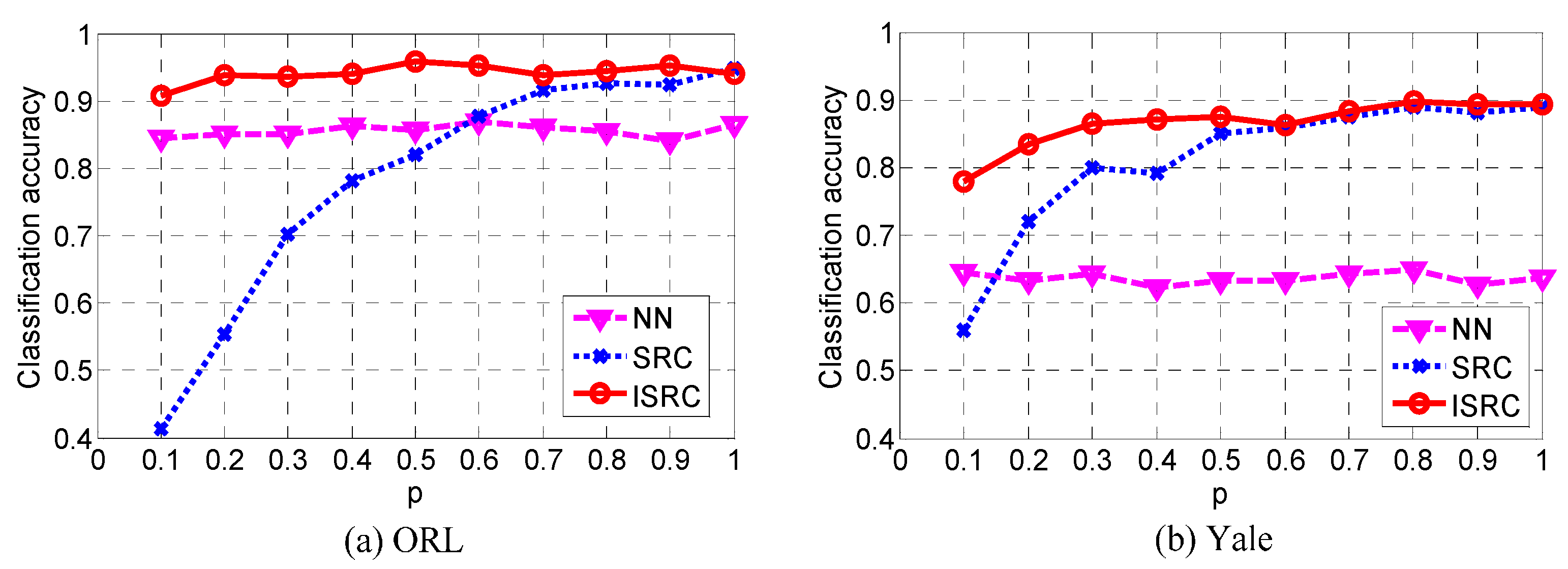
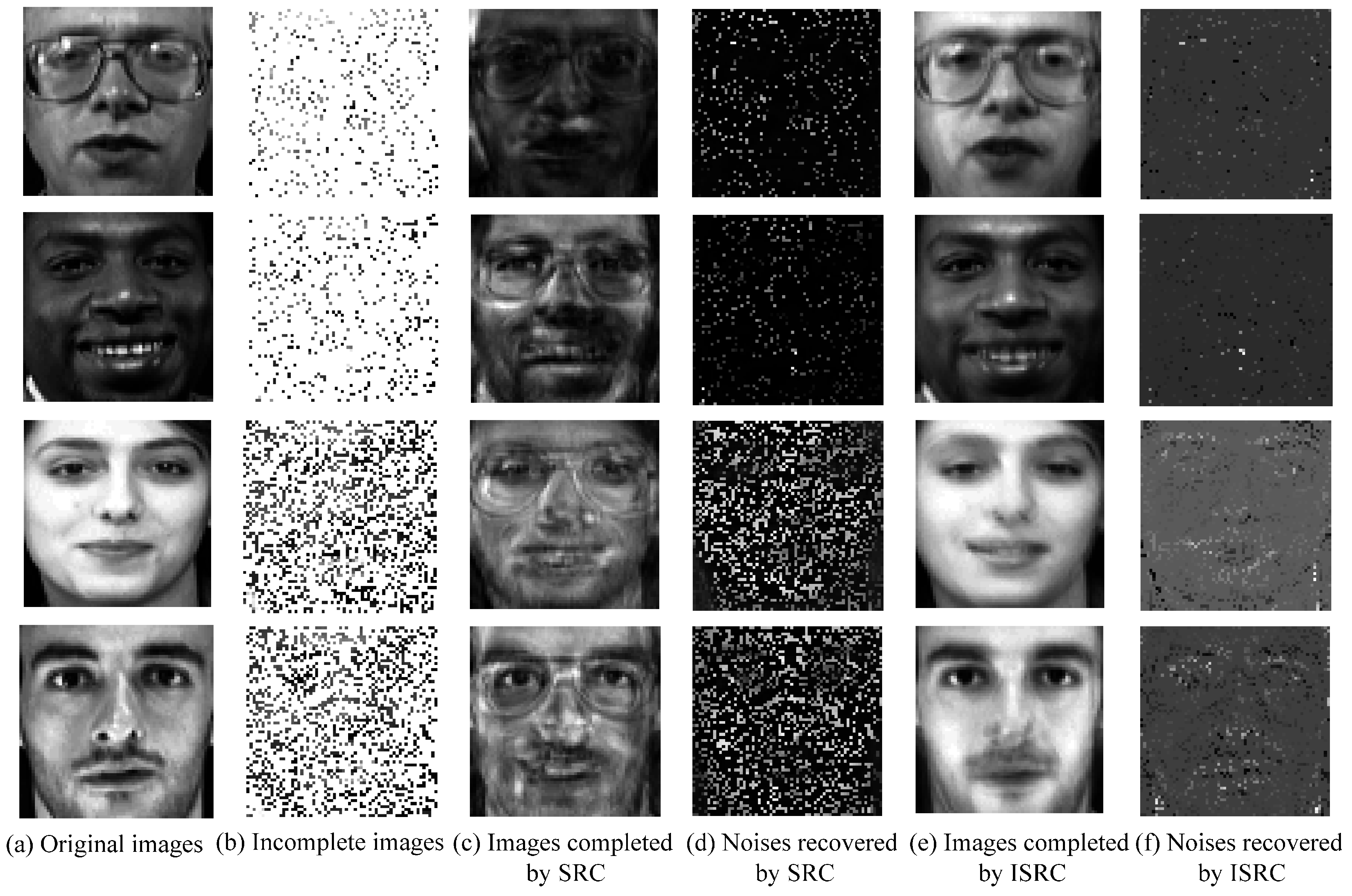

6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Donoho, D. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candès, E.J.; Michael, W. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Wright, J.; Yang, A.Y.; Ganesh, A.; Sastry, S.S.; Ma, Y. Robust face recognition via sparse representation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 210–227. [Google Scholar] [CrossRef] [PubMed]
- Qiao, L.; Chen, S.; Tan, X. Sparsity preserving discriminant analysis for single training image face recognition. Pattern Recogn. Lett. 2010, 31, 422–429. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, X.; Lei, B. Robust facial expression recognition via compressive sensing. Sensors 2012, 12, 3747–3761. [Google Scholar] [CrossRef] [PubMed]
- Wright, J.; Ma, Y.; Mairal, J.; Sapiro, G.; Huang, T.; Yan, S. Sparse representation for computer vision and pattern recognition. Proc. IEEE 2010, 98, 1031–1044. [Google Scholar] [CrossRef]
- Cheng, B.; Yang, J.; Yan, S.; Fu, Y.; Huang, T. Learning with L1-graph for image analysis. IEEE Trans. Image Process. 2010, 19, 858–866. [Google Scholar] [CrossRef] [PubMed]
- Yin, J.; Liu, Z.; Jin, Z.; Yang, W. Kernel sparse representation based classification. Neurocomputing 2012, 77, 120–128. [Google Scholar] [CrossRef]
- Huang, K.; Aviyente, S. Sparse representation for signal classification. Neural Inf. Proc. Syst. 2006, 19, 609–616. [Google Scholar]
- Zhang, H.; Zha, Z.J.; Yang, Y.; Yan, S.; Chua, T.S. Robust (semi) nonnegative graph embedding. IEEE Trans. Image Process. 2014, 23, 2996–3012. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zhang, S.; Zhao, X. Facial expression recognition via non-negative least-squares sparse coding. Information 2014, 5, 305–318. [Google Scholar] [CrossRef]
- Elhamifar, E.; Vidal, R. Sparse subspace clustering: Algorithm, theory, and applications. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2765–2781. [Google Scholar] [CrossRef] [PubMed]
- Candès, E.J.; Recht, B. Exact matrix completion via convex optimization. Found. Comput. Math. 2009, 9, 717–772. [Google Scholar] [CrossRef]
- Shi, J.; Yang, W.; Yong, L.; Zheng, X. Low-rank representation for incomplete data. Math. Probl. Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM 2011, 58. [Google Scholar] [CrossRef]
- ORL Database of Faces. Available online: http://www.cl.cam.ac.uk/research/dtg/attarchive/ facedatabase.html (accessed on 23 June 2015).
- Yale Face Database. Available online: http://vision.ucsd.edu/content/yale-face-database (accessed on 23 June 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Zheng, X.; Yang, W. Robust Sparse Representation for Incomplete and Noisy Data. Information 2015, 6, 287-299. https://doi.org/10.3390/info6030287
Shi J, Zheng X, Yang W. Robust Sparse Representation for Incomplete and Noisy Data. Information. 2015; 6(3):287-299. https://doi.org/10.3390/info6030287
Chicago/Turabian StyleShi, Jiarong, Xiuyun Zheng, and Wei Yang. 2015. "Robust Sparse Representation for Incomplete and Noisy Data" Information 6, no. 3: 287-299. https://doi.org/10.3390/info6030287
APA StyleShi, J., Zheng, X., & Yang, W. (2015). Robust Sparse Representation for Incomplete and Noisy Data. Information, 6(3), 287-299. https://doi.org/10.3390/info6030287





