Applying TRIZ and Fuzzy AHP Based on Lean Production to Develop an Innovative Design of a New Shape for Machine Tools

Abstract

Companies are facing cut throat competition and are forced to continuously perform better than their competitors. In order to enhance their position in the competitive world, organizations are improving at a faster pace. Industrial organizations must be used to the new ideals, such as innovation. Today, innovative design in the development of new products has become a core value in most companies, while innovation is recognized as the main driving force in the market. This work applies the Russian theory of inventive problem-solving, TRIZ and the fuzzy analytical hierarchy process (FAHP) to design a new shape for machine tools. TRIZ offers several concepts and tools to facilitate concept creation and problem-solving, while FAHP is employed as a decision support tool that can adequately represent qualitative and subjective assessments under the multiple criteria decision-making environment. In the machine tools industry, this is the first study to develop an innovative design under the concept of lean production. We used TRIZ to propose the relevant principles to the shape’s design with the innovative design consideration and also used FAHP to evaluate and select the best feasible alternative from independent factors based on a multiple criteria decision-making environment. To develop a scientific method based on the lean production concept in order to design a new product and improve the old designing process is the contribution of this research.

1. Introduction

The rapidly changing marketplace leads to companies seeking competitiveness for their products with respect to innovation, higher performance, lower prices and more functionality. Since companies’ resources are limited, the top-level management tends to set-up the main competiveness with minimum resources. Therefore, it is very important to establish a systematic approach for designing solutions in the early phases of design, since solutions in the early design stages play a critical role for the competitiveness of product development.

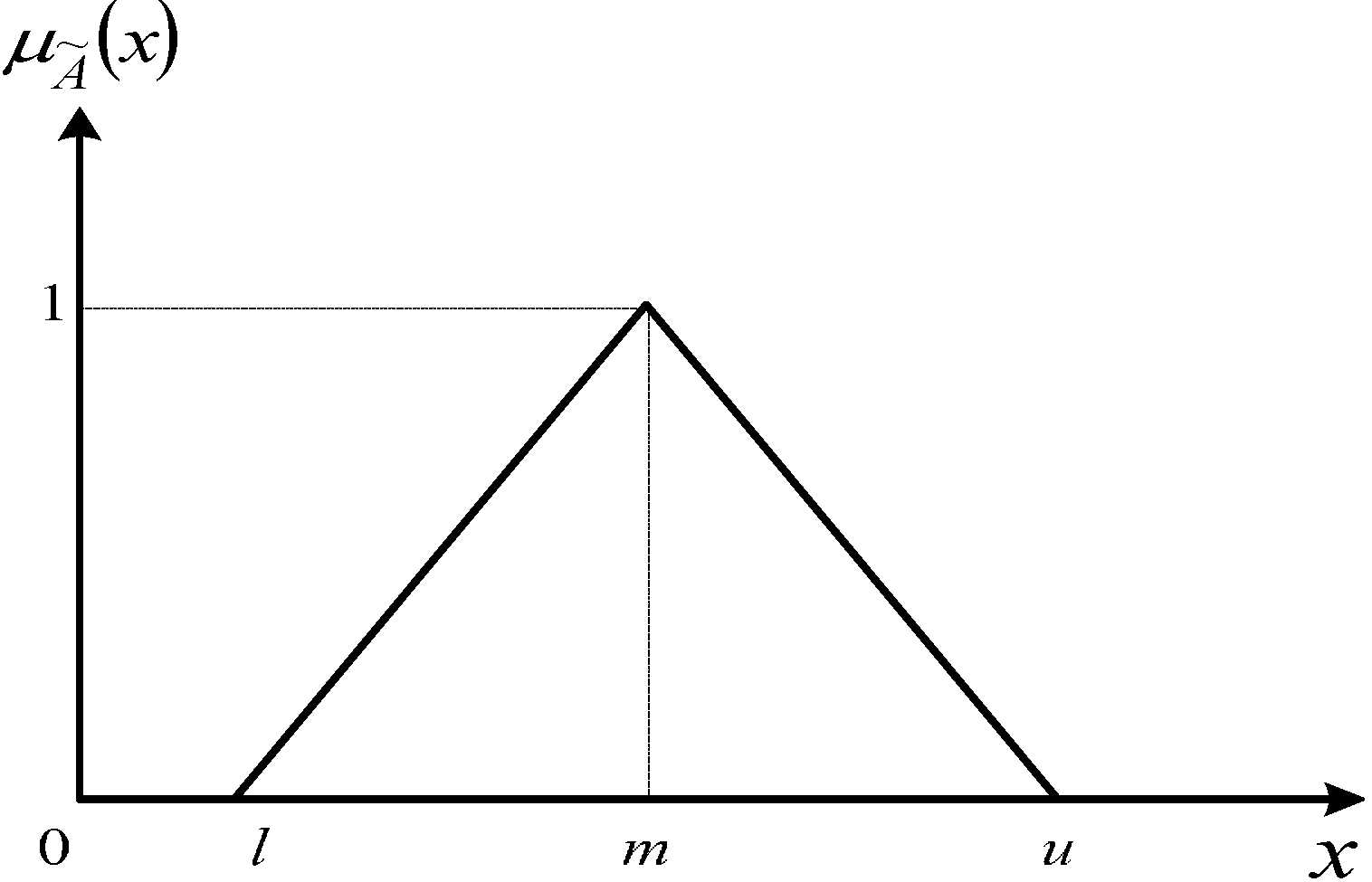
Innovation is a new idea, device or process. It can be viewed as the application of better solutions to meet new requirements, unarticulated needs or existing market needs. TRIZ is a knowledge-based method of inventive problem-solving. It can offer concepts and tools to facilitate the concept creation and problem-solving. On the other hand, lean production is a management philosophy and a systematic method for the elimination of waste within a manufacturing process. In practice, both the lean production concept and innovative design concept cannot be quantified precisely. However, fuzzy set theory can be employed to deal with the uncertainty due to imprecision or vagueness, and the AHP can be applied to solve multiple criteria decision-making problems. Hence, in this research, we apply the TRIZ and FAHP based on the lean production concept to design an innovative shape for machine tools to meet the requirement of the companies’ competitiveness.

Our review of the literature shows that TRIZ and fuzzy, as well as multiple-criteria decision-making (MCDM) are widely used to deal with many issues of enterprise. The applications of these tools are briefly discussed in the following. Rosli et al. [1] use an AHP-TRIZ innovation method to design an automotive door panel. Chen [2] takes an application of a hybrid dynamic MCDM to explore the key factors for the internal control of procurement circulation. Tompkins et al. [3] use the TRIZ method to derive the technology forecasting of CCD and CMOS digital imaging technology. Ding et al. [4] use the MCDM method to develop a model for optimal maintenance policy selection. Dong et al. [5] use an automatic method to reach consensus in a local context for AHP group decision-making. Ishizaka [6] applied fuzzy logic and AHP for supplier selection. Ishizaka and Nguyen [7] use the method of calibrated fuzzy AHP to develop a model for current bank account selection. A review of the literature [1,2,3,4,5,6,7] shows that most research in the applicability of TRIZ or FAHP is focused on the improvement of manufacturing, quality and procurement management of innovative designs. From the review of the literature, we know from Rosli et al. 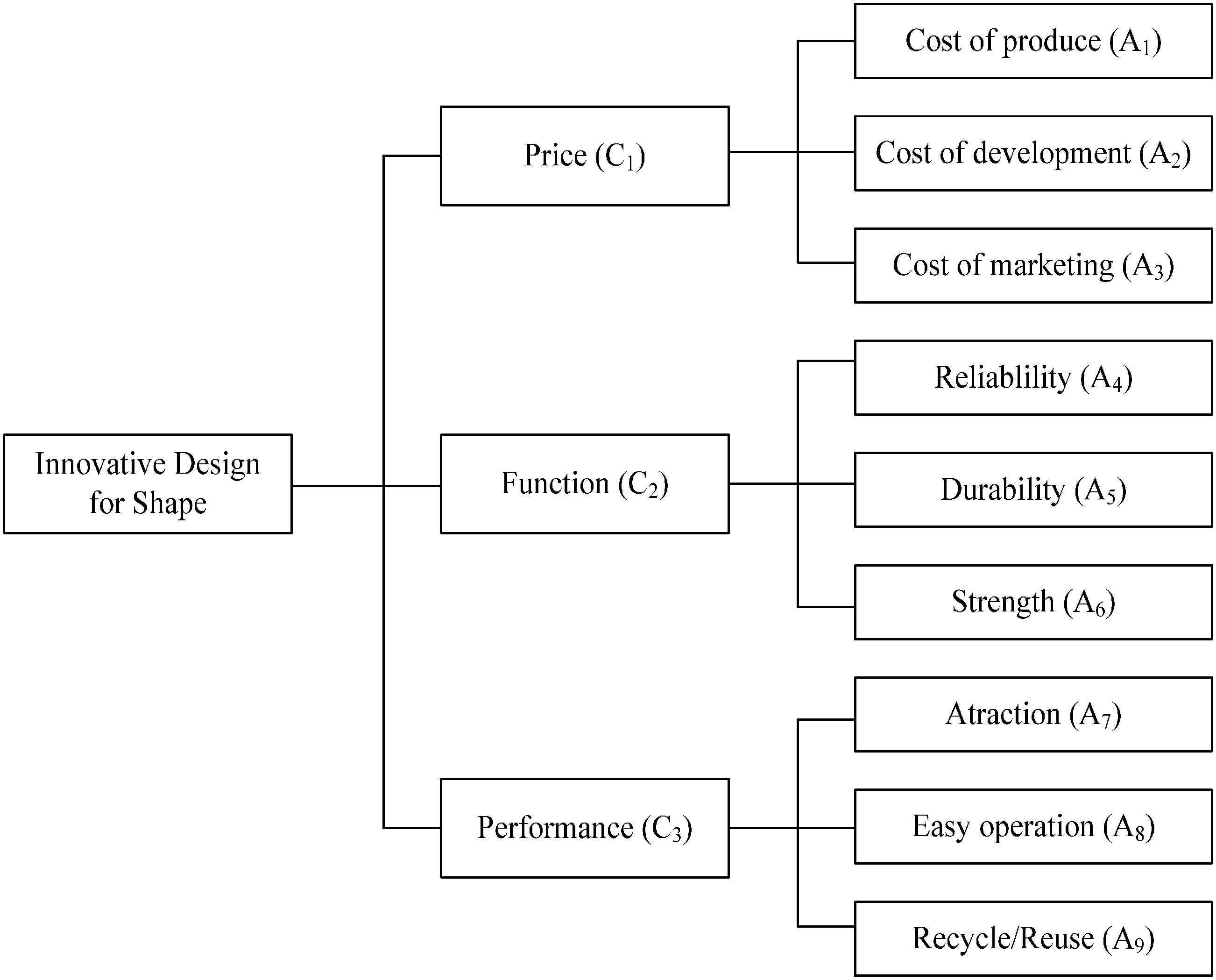[1] that the factors of AHP were independence and certainty. However, in our study, we assume that the innovative design concept and lean production concept are vague. We demonstrate how to apply the TRIZ and FAHP to make new innovative changes in the design for a new product under the concept of lean production. This study applies the contradiction matrix table, 40 innovative principles and 39 engineering parameters to tackle the trade-off between design contradictions and engineering parameters, while at the same time, the project team can acquire more inspiration and feasible solutions through the proposed approach. However, due to vagueness and uncertainty in the decision-makers’ judgments, we adopted a FAHP method as a decision support tool that can adequately represent qualitative and subjective assessments for the independent factors under the multiple criteria decision-making environment. Based on the TRIZ-FAHP synergy, the authors selected the top five criteria (cost of production, cost of development, reliability, costs of marketing, attractiveness) from the AHP method as the main objectives and in view of certain subjective and objective aspects to collect the relevant principles from the TRIZ matrix, in order to complete the innovative design of a new shape for machine tools.

This paper is composed of the following: Section 2 shows the introduction of the hybrid-method about TRIZ, and a FAHP method is illustrated. Section 3 provides an application of innovative design for a new shape of machine tools. Finally, the last section highlights the most relevant results of the authors’ work and proposes possible extensions.

2. Introduction of the Hybrid Method

The hybrid method starts by the TRIZ method, followed by the FAHP method, and is illustrated as follows:

2.1. The TRIZ

TRIZ is a knowledge-based systematic methodology of inventive problem-solving [8]. It is based on analytical logic and a systematic way of thinking. TRIZ depends on the premise that technology evolves and that the means to inventions are not a random process, since they are predictable and are governed by certain laws [9]. The main concepts of TRIZ are contradiction, ideality and the evolution patterns introduced by Altshuller [10], and at least one of these concepts is applied in any TRIZ problem-solving process. Gadd [11] has described it as a toolkit consisting of methods that cover all aspects of problem understanding and solving. This toolkit is regarded as the most complete and systematical organization for the invention and creative thinking methodology [12]. This approach provides a structure for the application of TRIZ tools and techniques. Although TRIZ has been described in various ways—as a methodology, a toolkit, a science [13], a philosophy [14], etc.—it provides a systematic approach for finding solutions to innovative technical systems and technical problems.

2.1.1. Contradiction

Contradictions are indicative of inventive problems arising from the obvious incompatibility of the desired features within a system. These problems were solved through resolving the contradictions. There are two main types of contradictions: technical and physical contradictions.

(1-1) Technical contradiction: This situation arises when an attempt to improve certain attributes or functions of a system leads to the deterioration of other attributes of that system. For instance, a bigger, more powerful engine, proposed for a car to increase its speed, would contribute more weight to the car, which thus limits how fast it could travel and, therefore, negates the expected benefit of increased speed.

(1-2) Physical contradiction: This issue arises when there are inconsistent requirements to the physical condition of the same system. For example, a system might have a function that is both beneficial and adverse or unpleasant. For instance, an umbrella’s large size helps with protection from rain, but may make it too bulky to carry around.

2.1.2. Ideality

Ideality comes from “the ideal machine”, which is an arbitrary system that has all of its parts performing at the greatest possible capacity, as introduced by Altshuller. Ideality is a measure of how close a system is to the best, i.e., it can possibly be the ideal machine or the ideal final result (IFR). The ideality of a system can be expressed in a mathematical formula as follows:

$$\text{Ideality}=\left(\frac{{\displaystyle \sum \text{Benefits}}}{{\displaystyle \sum \text{Costs}+{\displaystyle \sum \text{Harms}}}}\right)$$

(1)

The positive benefits are the functions provided by the system, while the harm aspects are its useless output and also the waste products of the system. One of the objectives of TRIZ is to increase ideality. As the above equation shows, this can be achieved by one aspect or a combination in order to find a means of increasing the benefits provided by the system and, thereby, reducing the costs of resource inputs towards providing those benefits or reducing the harmful functions that come with the benefits. Defining the IFR is important in innovation, since it indicates the direction in which the search for new and better systems should be carried out. Furthermore, it helps in understanding and identifying the optimum resources to use in delivering innovative solutions.

2.1.3. Patterns of evolution of systems

Altshuller discovered that technical systems normally follow certain regularities in their development. These regularities were translated into patterns of evolution and are beneficial for developing good solutions to problems and to predict how systems would evolve [15]. There are eight different trends that guide development, and each trend is further divided into lines of evolution. Savranksy [8] points out that it is possible to express the idea of technical evolution through the concept of ideality. It is desirable for evolution to bring an increase of the ideality of a system. Understanding this and other patterns of evolution can help in predicting technological development and identify features that are likely to be successful in newly launched products.

Several tools and techniques were developed by Altshuller and his colleagues in the development of TRIZ [16]. The ones that appear most prominently are listed as follows:

(1)

Forty inventive principles: conceptual solutions to technical and physical contradictions.

(2)

Seventy six standard solutions: for solving system problems without the need to identifying contradictions; they are usually applied to correct the undesired interactions between two parts of a system.

(3)

Contradiction matrix: The contradiction matrix contains 39 improving parameters (IP) and 39 worsening parameters (avoiding degradation parameters, ADP) with each cell entry giving the most often used inventive principles. In other words, the contradiction matrix can tell us which of the 40 principles have been used most frequently to solve a problem that involves a particular contradiction. The 39 × 39 matrix contains the zero to four most likely principles for solving design problems involving the 1482 most common contradiction types, as shown partially in Table 1.

(4)

Separation principles: for understanding and solving physical contradictions and indicating solutions from the inventive principles pertaining to the problem.

(5)

Effects database: this includes about 2500 concepts extracted from the body of engineering and scientific knowledge and is applied to problem-solving.

(6)

IFR and ideality: an arbitrary system that has all of its parts performing at the greatest possible capacity, as introduced by Altshuller [10]; the IFR serves as a beacon that guides the achievement of innovative solutions.

(7)

Fitting: This is the process of taking a step back from the IFR, which is a conceptual and unachievable ideal, into a realistic “robust” solution within the constraints of present real-life conditions.

(8)

Patterns of evolution of technical systems: for identifying directions of technology development, as explained earlier.

(9)

Function analysis: understanding the interactions between all of the components of the system, and identifying the problems arising from the interactions.

(10)

Analysis of system resources: This is the systematic search and analysis of resources within and outside the system to the benefit of the problem situation, so that the solutions identified are as close as possible to the ideal final result (IFR).

(11)

Substance field (Su-field) analysis: similar to function analysis; helps to outline the entire system and point to exact problems without adding unnecessary details.

(12)

Nine windows (also known as the inventive system thinking or a system operator or multi-screen diagram of thinking): used to understand the problem or a technical system in terms of the context (or environment) in which it exists and the details of the parts within the system itself; this contributes to understanding how the problem (its context and details) may change over time, which is useful for deriving potential solutions.

(13)

ARIZ (the algorithm for inventive problem-solving): a series of steps utilizing an array of TRIZ tools (some of which are explained above) to determine solutions and innovations; it is reported to be the most suitable for difficult and complicated problems.

(14)

Creativity tools: for overcoming psychological inertia or mental habits that prevent innovation, clarity of thought and thinking contextually; these tools include size-time-cost and the method of little men, otherwise known as “smart little people”.

Table 1. Partial cells of the contradiction matrix. ADP, avoiding degradation parameters; IP, improving parameters.

	ADP	1	2	3	4	…	11	…	39
IP
1
2
3
4
…
12				#15, #34, #10, #14
…
39

Table 1. Partial cells of the contradiction matrix. ADP, avoiding degradation parameters; IP, improving parameters.

	ADP	1	2	3	4	…	11	…	39
IP
1
2
3
4
…
12				#15, #34, #10, #14
…
39

A framework to structure the tools according to the fields of application is considered important to problem analysis and solving, which was provided by Moehrle [17]. These fields included the following:

• What is the current situation (current state)?
• What is the future situation supposed to look like (intended state)?
• Which goals are to be fulfilled and to what degree (goals)?
• How can the current state be transformed into the intended state (transformation)?
• Which resources are available and can be used (resources analysis)?

The tools were put into the groups for which they were thought to be the most relevant. The tools also include (adapted from Pannenbaecker [18] and Moehrle [17]): (1) function (and object) analysis, contradiction substance field analysis and evolution analysis; (2) strong solution (or the most ideal outcome achievable); (3) ideal final result (IFR) fitting; (4) inventive principles; (5) contradiction matrix (and inventive principles); (6) separation principles; (7) substance field analysis; (8) evolution analysis; (9) resource analysis; (10) effects database; and (11) resource analysis (system analysis, substance field analysis and performing a systematic search for resources).

Zlotinetal [19] classified the tools into three groups: analytical tools, knowledge-based tools and psychological operators. Analytical tools, such as Su-field analysis, functional analysis and ARIZ, contribute to defining, formulating and modeling a problem; knowledge-based tools, such as 40 inventive principles, 76 standard solutions and effects, provide recommendations for system transformation, while the psychological operators help to facilitate the creative and problem-solving process.

2.2. The FAHP

In this section, the fuzzy sets and fuzzy numbers are briefly introduced. The AHP and fuzzy AHP methods are then presented.

2.2.1. Fuzzy Sets and Fuzzy Numbers

Fuzzy set theory [20] was first introduced to deal with the uncertainty due to imprecision or vagueness. A fuzzy set $\tilde{A}=\left\{\right(x,{\mu }_{\tilde{A}}(x)\left)\right|x\in X\}$ is a set of ordered pairs, and X is a subset of real numbers R, where ${\mu }_{\tilde{A}}(x)$ is called the membership function, which assigns to each object, x, a grade of membership ranging from zero to one. Since its introduction, fuzzy set theory has been widely applied to address real-world problems in which decision-makers need to analyze and process information that is imprecise. A fuzzy number is a special case of a convex normalized fuzzy set [21]. It is possible to use different fuzzy numbers under various particular situations. Triangular and trapezoidal fuzzy numbers are usually adopted to deal with the vagueness of decisions related to the performance levels of alternative choices with respect to each criterion. When the two most promising values of a trapezoidal fuzzy number are the same number, it becomes a triangular fuzzy number (TFN). This means that a TFN is a special case of a trapezoidal fuzzy number. Because of its intuitive appeal and computational efficiency, the TFN is the most widely-used membership function for many applications. TFNs are usually employed to capture the vagueness of parameters related to the decision-making process. In order to reflect the fuzziness that surrounds the decision-makers when they conduct a pair-wise comparison matrix, TFN is expressed with boundaries instead of crisp numbers. A triangular fuzzy number, denoted as $\tilde{A}=\left(l,m,u\right)$, has the following membership function:

$${\mu }_{\tilde{A}}(x)=\{\begin{array}{cc}(x-l)/(m-l),& l\le x\le m\\ (u-x)/(u-m),& m\le x\le u\\ 0& otherwise\end{array}$$

(2)

A triangular fuzzy number $\tilde{A}$ is shown in Figure 1. The parameter m is the most promising value. The parameters l and u, respectively, are the smallest possible value and the largest possible value; they limit the field of possible evaluation. When l = m = u, the triangular fuzzy number becomes a non-fuzzy number. The triplet (l, m, u) can be used to describe a fuzzy event.

Figure 1. A triangular fuzzy number $\tilde{A}=\left(l,m,u\right)$.

Figure 1. A triangular fuzzy number $\tilde{A}=\left(l,m,u\right)$.

Consider two TFNs ${\tilde{A}}_1$ and ${\tilde{A}}_2$, ${\tilde{A}}_1$ = (l₁, m₁, u₁) and ${\tilde{A}}_2$ = (l₂, m₂, u₂). The main operational laws [22] for two triangular fuzzy numbers ${\tilde{A}}_1$ and ${\tilde{A}}_2$ are as follows:

• Addition of the fuzzy number:

  $${\tilde{A}}_1\oplus {\tilde{A}}_2=(l_1+l_2,m_1+m_2,u_1+u_2)$$

  (3)
• Multiplication of the fuzzy number:

  $${\tilde{A}}_1\otimes {\tilde{A}}_2\approx (l_1{l}_2,m_1{m}_2,u_1{u}_2)\text{ for }{l}_{\mathrm{i}}>0,m_{\mathrm{i}}>0,u_{\mathrm{i}}>0,i=1,2$$

  (4)
• Division of the fuzzy number:

  $${\tilde{A}}_1/{\tilde{A}}_2=(l_1/u_2,m_1/m_2,u_1/l_2)\text{ for }{l}_{\mathrm{i}}>0,m_{\mathrm{i}}>0,u_{\mathrm{i}}>0,i=1,2$$

  (5)
• Reciprocal of the fuzzy number:

  $${\tilde{A}}_1^{-1}\approx (1/u_1,1/m_1,1/l_1)\text{ for }{l}_1>0,m_1>0,u_1>0$$

  (6)

2.2.2. The AHP Method

The AHP was proposed by Saaty [23] to solve multiple criteria decision-making problems. The AHP includes three main steps.

First step: The complex problem is broken down into elements according to their common characteristics; this step produces a hierarchical model.

Second step: A series of pair-wise comparisons is made among the elements at the same level using the nine-point scale, which ranges from one to nine (see Table 2) and their reciprocal values. In this step, pair-wise comparison matrices are formulated for all evaluation criteria.

Table 2. The pair-wise comparison judgment.

Intensity of Importance	Definition	Explanation
1	Equal-importance	A is equal-importance to B
3	Weak-importance	A is weak-importance than B
5	Essential-importance	A is essential-importance than B
7	Demonstrated-importance	It is demonstrated-importance to A
9	Absolute-importance	A is absolute-importance than B
2, 4, 6, 8	Intermediate-values	Inverse comparisons

Table 2. The pair-wise comparison judgment.

Intensity of Importance	Definition	Explanation
1	Equal-importance	A is equal-importance to B
3	Weak-importance	A is weak-importance than B
5	Essential-importance	A is essential-importance than B
7	Demonstrated-importance	It is demonstrated-importance to A
9	Absolute-importance	A is absolute-importance than B
2, 4, 6, 8	Intermediate-values	Inverse comparisons

Third step: The relative weights of criteria are obtained by calculating the eigenvalues for pair-wise comparison matrices.

In the pure AHP, the relative importance of decision elements is evaluated from comparison judgments, which are represented as crisp values. The pure AHP method tends to be less effective when dealing with the uncertainty in the decision-making processes. This led to the development of fuzzy AHP methods.

2.2.3. The Fuzzy AHP Method

There are several fuzzy AHP methods. The earliest work of fuzzy AHP was proposed by Van Laarhoven and Pedrycz [24]. They applied the logarithmic least squares method to derive fuzzy weights and scores from the triangular fuzzy pair-wise comparison matrix. Since then, fuzzy AHP-related developments have been reported in the concomitant literature. Buckley et al. [25] used the comparison ratios based on trapezoidal fuzzy numbers to deal with the imprecision. They extended Saaty’s AHP [23] and used the geometric mean method to obtain fuzzy weights and scores. Chang [26] proposed an extent analysis approach based on triangular fuzzy numbers for pair-wise comparison. Buyukozkan et al. [27] made comparisons of different fuzzy AHP methods and pointed out the advantages, as well as the disadvantages of each method. In this study, the fuzzy AHP method, proposed by Buckley [25], was utilized. A brief description of this fuzzy AHP method is given as follows:

A matrix $\tilde{A}$ is constructed according to fuzzy pair-wise comparisons.

$$\tilde{A}=\left[\begin{array}{cccc}1& {\tilde{a}}_{12}& \mathrm{...}& {\tilde{a}}_{1n}\\ {\tilde{a}}_{21}& 1& \mathrm{...}& {\tilde{a}}_{2n}\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ {\tilde{a}}_{n1}& {\tilde{a}}_{n2}& \mathrm{...}& 1\end{array}\right]$$

(7)

where ${\tilde{a}}_{ij}$ = (l_ij, m_ij, u_ij) is the fuzzy comparison value of criterion i to criterion j.

The fuzzy weights of each criterion are calculated as:

$${\tilde{r}}_i={\left({\tilde{a}}_{i1}\otimes {\tilde{a}}_{i2}\otimes \mathrm{...}\otimes {\tilde{a}}_{in}\right)}^{1/n}\text{ for }i=1,2,\mathrm{...},n$$

(8)

$${\tilde{w}}_i=\frac{{\tilde{r}}_i}{{\tilde{r}}_1\oplus {\tilde{r}}_2\oplus \mathrm{...}\oplus {\tilde{r}}_n}\text{ for }i=1,2,\mathrm{...},n$$

(9)

where ${\tilde{r}}_i$ is the geometric mean of fuzzy comparison value of criterion i to each criterion and ${\tilde{w}}_i$ is the fuzzy weight of the i-th criterion.

The fuzzy weight vector $\tilde{W}$ is constructed as:

$$\tilde{W}={\left({\tilde{w}}_1,{\tilde{w}}_2,\mathrm{...},{\tilde{w}}_n\right)}^T$$

(10)

3. Application of Innovative Design for a New Shape of Machine Tools

The hybrid method in our work proposes applying the TRIZ and FAHP based on the lean production concept to design an innovative new shape of machine tools. The case study includes the problem description and design research. The problem description shows the existing issues of the cover shape of machine tools, and the designing research shows that 12 research steps are considered and carried out in this research; they are illustrated as follows:

3.1. Problem Description

Due to the fact that the current machine tools produced in our company cannot meet the rigid competitiveness in the marketplace, they need to be analyzed and redesigned to increase profit. The cover consists of a control panel, a water tank, an inside panel, an outside panel, a cover for the head and a cover for the tool magazine (Figure 2). The material of the cover is made of steel; the assembly panel is fastened with bolts and welding; and the assembly between the panel and plastic glass is glued with double-sided 3M tape. Finally, in order to prevent water leakage, it is necessary to apply sealing into the gaps between the panels. The cover of the machine tools has been designed and manufactured in the old designing process explained in Table 2. As a result, it cannot compete with the marketplace, because the production cost is too high and the shape of the machine tools is too old-fashioned. The innovative design system, i.e., a new model for a designing process, is a challenge not only for the designer, but also for the project team (Table 3). The innovative design of the cover can deal with this difficulty of delivery and can reduce the material cost. Initially, the designer observed the existing complex structure of the covers of the machine tools and converted the complex structures of the covers of the machine tools into an innovative design system by redesigning the shape, structure and used materials. The innovative design system applied problem-solving (TRIZ) and the FAHP method.

Figure 2. The main parts of the body panel.

Figure 2. The main parts of the body panel.

Table 3. The illustration of the process of design.

The Old Process of Design (Concept of Safety)	The New Process of Design (Concept of Lean)
(1) The cover of the machine tools was designed by a machine engineering firm (2) The shape of the cover was discussed with business managers (3) Modify the shape of the cover according to the opinions of business managers (4) Manufacturing by the vendor	(1) Find out the main goals for the project with project team members (2) Construct the hierarchy AHP to evaluate the relative weights to decide the priority solution; the project team leader then makes a decision (3) Design staff finds out the best solution to satisfy the strategies of the enterprises’ resources with the TRIZ theory (4) Designing staff design the shape of cover (5) Manufacturing

Table 3. The illustration of the process of design.

The Old Process of Design (Concept of Safety)	The New Process of Design (Concept of Lean)
(1) The cover of the machine tools was designed by a machine engineering firm (2) The shape of the cover was discussed with business managers (3) Modify the shape of the cover according to the opinions of business managers (4) Manufacturing by the vendor	(1) Find out the main goals for the project with project team members (2) Construct the hierarchy AHP to evaluate the relative weights to decide the priority solution; the project team leader then makes a decision (3) Design staff finds out the best solution to satisfy the strategies of the enterprises’ resources with the TRIZ theory (4) Designing staff design the shape of cover (5) Manufacturing

To validate the applicability of the proposed approach, this approach is implemented in an existing case of new shape design of machine tools. In this research, a machine tool manufacturer, located in Taiwan, was taken into consideration. The company is engaged in the production of a variety of machine tools for automobiles, airplanes and consumer electronics. The existing body panel of machine tools has the following issues:

(1)

The complex structures of the body panel of the machine tools make the cycle time longer and cannot meet the delivery requirements. In addition, this leads to higher production costs.

(2)

Too many elements of a body panel stocked in inventory make the inventory management inefficient.

(3)

The shape of the body panel is not attractive in comparison with other machine tools made abroad.

The company currently has a project with the innovation design company to design new shapes of machine tools. Taking into account the current business trends and competitiveness, the company is committed to coming up with a plan for new shape development. In this study, we applied the TRIZ-FAHP to implement the plan of shape development. The TRIZ and FAHP approach provides a methodology to select the best alternatives from the substitutes that are present in their domain based on certain subjective and objective aspects. The authors classified the criteria and sub-criteria that influenced their judgments and collected relevant data using the innovative design tool, the TRIZ [21].

3.2. Designing Research

In this study, a group of nine decision-makers, including design managers, business managers and plant managers, was formed. Questionnaires were provided to all parties to get their viewpoints. The questionnaire consisted of two parts: Part 1 included the pair-wise comparisons between the construct; Part 2 focused on the pair-wise comparisons between the criteria under each construct. The innovative design of a new shape was completed through 12 steps, and the content of each step is illustrated as follows:

Step 1: Analyze the Existing Manufacturing and Designing System

The old designing process is explained and compared with the new designing process in Table 3. The concept of the old designing process only considered the safety of workers, and the decision-making was from a few managers’ subjective ideas. Hence, it does not always match the demand of resources for enterprises and marketing, and the shapes of machine tools are usually not competitive in the marketplace. However, the new design process considers all of the demands of the enterprise and took into consideration the limited resources of the company. In fact, the old design process is based on the concept of safety, while the new design process is based on the concept of the enterprise’s limited resources and marketing. This new design process is based on the concept of marketing, which is the newest trend in the marketplace.

After analyzing the existing manufacturing problems, the designer sets the main goals for the innovative design of new shapes as follows:

(1)

Keep the delivery requirement (productivity).

(2)

Reduce the costs of direct labor and materials (cost).

(3)

Reduce the panel element and follow a module of thinking (quality, cost and delivery).

(4)

Increase the attractiveness of the shape (competitiveness).

Step 2: Identify the Attributes (Engineering Parameters) to Redesign the Manufacturing System

According to existing problems in the system, the designer discussed matters with the business manager and plant management and found that there were some manufacturing contradictions in the current manufacturing system. The designer also identified four major contradictions in the designing system (# XX represents the number of engineering parameters). The improving parameters and avoiding degradation parameters for each contradiction are illustrated as follows and given in Table 4.

Contradiction A:

Improving the shape (#12), avoiding the degradation of the stationary system weight (#2), stability of the object (#13), strength (#14), easy manufacturing (#32), easy operation (#33) and productivity (#39).

Contradiction B:

Improving the shape (#32), avoiding the degradation of the system strength (#14), durability of the nonmoving object (#16), reliability (#27), easy operation (#33) and productivity (#39).

Contradiction C:

Improving easy operation (#33), avoiding the degradation of the system strength (#14), durability of the nonmoving object (#16), reliability (#27), easy manufacturing (#32) and productivity (#39).

Contradiction D:

Improving the easy manufacturing (#32), avoiding the degradation of the system strength (#14), durability of the nonmoving object (#16), reliability (#27) and productivity (#39).

Table 4. Contradiction matrix for this case study.

	ADP	#2	#12	#13	#14	#16	#27	#32	#33	#39
IP
#12		#10, #15, #26, #3		#1, #18, #4, #33	#10, #14, #40, #30	x		#1, #17, #28, #32	#15, #26, #32	#10, #17, #26, #34
#32					#10, #1, #3, #32	#16, #35	x		#13, #16, #2, #5	#10, #1, #28, #35
#33					#40, #3, #28, #32	#1, #16, #25	#40, #17, #27, #8	#12, #5, #2		#1, #15, #28
#39			#10, #14, #40, #34		#10, #18, #28, #29	#10, #20, #16, #38	#10, #35, #1, #8	#24, #35, #28, #2	#10, #1, #28, #7

Table 4. Contradiction matrix for this case study.

	ADP	#2	#12	#13	#14	#16	#27	#32	#33	#39
IP
#12		#10, #15, #26, #3		#1, #18, #4, #33	#10, #14, #40, #30	x		#1, #17, #28, #32	#15, #26, #32	#10, #17, #26, #34
#32					#10, #1, #3, #32	#16, #35	x		#13, #16, #2, #5	#10, #1, #28, #35
#33					#40, #3, #28, #32	#1, #16, #25	#40, #17, #27, #8	#12, #5, #2		#1, #15, #28
#39			#10, #14, #40, #34		#10, #18, #28, #29	#10, #20, #16, #38	#10, #35, #1, #8	#24, #35, #28, #2	#10, #1, #28, #7

Step 3: Construct the Contradiction Matrix and Propose the Related Inventive Principles

From Step 2, the design engineer identified four major contradictions and then found the corresponding engineering parameters and inventive principles found. All of the proposed principles used to solve the contradictions are obtained from the web and integrated as follows: (1) segmentation; (2) taking out; (3) local quality; (4) asymmetry; (5) merging; (7) nested doll; (8) anti-weight; (10) preliminary action; (12) equipotentiality; (13) the other way around; (14) spheroidality-curvature; (15) dynamics; (16) partial or excessive actions; (17) another dimension; (18) mechanical vibration; (20) continuity of useful action; (24) intermediary; (25) self-service; (26) copying; (27) inexpensive short-living objects; (28) mechanics substitution; (29) pneumatics and hydraulics; (30) flexible shells and thin films; (32) color changes; (33) homogeneity; (34) discarding and recovering; (35) parameter changes; (38) strong oxidants; (40) composite materials. Additionally, the suggestions for improvement can be referenced from the web.

Step 4: Factor Selection Based on Delphi Method

The evaluation of new innovative design systems is conducted by applying AHP methodology in this research project. The top-level management proposes to the project team that the new innovative shape design project not only considers the innovative design rules (e.g., productivity, safety, precision, etc.), but also considers the factors of marketing strategy, such as performance, function and price for the newly designed product. This study uses the Delphi method to derive three determined constructs used in the industry and the nine critical success factors of the project from the project team experts. All of the constructs and criteria are CDI (Consensus Deviation Index) <0.1 and Cronbach a (reliability) >0.7. Due to the answers being from experts, the validity is accepted.

Step 5: Construct the Hierarchy of AHP

The goal of the AHP model is to choose the best alternative for a company. Figure 3 shows the AHP structure used in this study. The first-level criteria include performance, function and price. The sub-criteria of function include reliability, durability and strength. The sub-criteria of performance are attraction, easy operation and recycling. The sub-criteria of price are cost of product, cost of development and cost of marketing. Thus, the AHP approach breaks down a problem into smaller elements.

Figure 3. The hierarchical structure of AHP.

Figure 3. The hierarchical structure of AHP.

Step 6: Determining the Linguistic Variables and Fuzzy Conversion Scale

The decision-makers make pair-wise comparisons of the importance or preference between each pair of criteria. Consider a problem at a level with n elements; each set of pair-wise comparisons for a level requires n(n − 1)/2 judgments, which are further used to construct a positive fuzzy reciprocal comparison matrix. The comparison of one criterion over another can be done with the help of questionnaires, and it is in the form of linguistic variables. A linguistic variable is a variable whose values are words or sentences in a natural or artificial language [28]. In this paper, TFNs are used to represent subjective pair-wise comparisons of decision-makers, namely “just equal”, “equally important”, “weakly important”, “strongly important”, “very strongly important” and “absolutely important”. The triangular fuzzy conversion scales and linguistic scales [29] are used to convert such linguistic values into fuzzy scales, as is demonstrated in Figure 4 and Table 5.

Figure 4. Linguistic scale for relative importance. EI, equal importance; WMI, weakly more importance; SMI, strongly more importance; VSMI, very strong more importance; AMI, absolutely more importance.

Figure 4. Linguistic scale for relative importance. EI, equal importance; WMI, weakly more importance; SMI, strongly more importance; VSMI, very strong more importance; AMI, absolutely more importance.

Table 5. Linguistic scales and fuzzy scales for importance.

Linguistic Scales for Importance	Triangular Fuzzy Scale	Triangular Fuzzy Reciprocal Scale
Just equal	(1, 1, 1)	(1, 1, 1)
EI (equal importance)	(1/2, 1, 3/2)	(2/3, 1, 2)
WMI (weakly more importance)	(1, 3/2, 2)	(1/2, 2/3, 1)
SMI (strongly more importance)	(3/2, 2, 5/2)	(2/5, 1/2, 2/3)
VSMI (very strong more importance)	(2, 5/2, 3)	(1/3, 2/5, 1/2)
AMI (absolutely more importance)	(5/2, 3, 7/2)	(2/7, 1/3, 2/5)

Table 5. Linguistic scales and fuzzy scales for importance.

Linguistic Scales for Importance	Triangular Fuzzy Scale	Triangular Fuzzy Reciprocal Scale
Just equal	(1, 1, 1)	(1, 1, 1)
EI (equal importance)	(1/2, 1, 3/2)	(2/3, 1, 2)
WMI (weakly more importance)	(1, 3/2, 2)	(1/2, 2/3, 1)
SMI (strongly more importance)	(3/2, 2, 5/2)	(2/5, 1/2, 2/3)
VSMI (very strong more importance)	(2, 5/2, 3)	(1/3, 2/5, 1/2)
AMI (absolutely more importance)	(5/2, 3, 7/2)	(2/7, 1/3, 2/5)

Step 7: Establishing Comparison Matrices

Consider a problem at one level with n criteria, where the relative importance of criterion i to j is represented by triangular fuzzy numbers ${\tilde{a}}_{ij}=(l_{\text{ij}},m_{\text{ij}},u_{\text{ij}})$; one decision-maker considers criterion i is strongly important compared to criterion j; he/she may set ${\tilde{a}}_{ij}$ = (3/2, 2, 5/2). If criterion j is thought to be strongly important compared to criterion i, the pair-wise comparison between i and j could be presented by ${\tilde{a}}_{ij}$ = (2/5, 1/2, 2/3). As in the traditional AHP, the comparison matrix $\tilde{A}=\left\{{\tilde{a}}_{ij}\right\}$ can be constructed as:

$$\tilde{A}=\left[\begin{array}{cccc}1& {\tilde{a}}_{12}& \mathrm{...}& {\tilde{a}}_{1n}\\ {\tilde{a}}_{21}& 1& \mathrm{...}& {\tilde{a}}_{2n}\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ {\tilde{a}}_{n1}& {\tilde{a}}_{n2}& \mathrm{...}& 1\end{array}\right]=\left[\begin{array}{cccc}1& {\tilde{a}}_{12}& \mathrm{...}& {\tilde{a}}_{1n}\\ 1/{\tilde{a}}_{12}& 1& \mathrm{...}& {\tilde{a}}_{2n}\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\\ 1/{\tilde{a}}_{1n}& 1/{\tilde{a}}_{2n}& \mathrm{...}& 1\end{array}\right]$$

(11)

In this work, the comparison matrix of the construct for Expert 1 was established from the answers to the questionnaire with a 0–9 scale and is shown in Table 6.

Table 6. The comparison matrix of the construct for Expert 1.

	C1	C2	C3
C1	(1, 1, 1)	(2, 2.5, 3)	(1.5, 1.5, 2)
C2	(0.3333, 0.4, 0.5)	(1, 1, 1)	(0.5, 1, 1.5)
C3	(0.5, 0.6667, 1)	(0.6667, 1, 2)	(1, 1, 1)

Table 6. The comparison matrix of the construct for Expert 1.

	C1	C2	C3
C1	(1, 1, 1)	(2, 2.5, 3)	(1.5, 1.5, 2)
C2	(0.3333, 0.4, 0.5)	(1, 1, 1)	(0.5, 1, 1.5)
C3	(0.5, 0.6667, 1)	(0.6667, 1, 2)	(1, 1, 1)

Step 8: Calculating the Consistency Index and Consistency Ratio of the Comparison Matrix

To assure a certain quality level of a decision, the consistency of an evaluation has to be analyzed. Saaty [23] proposed a consistency index to measure consistency. This index can be used to indicate the consistency of the pair-wise comparison matrices. To investigate the consistency, the fuzzy comparison matrices need to be converted into crisp matrices [30]. The fuzzy mean and spread method [31] is utilized to de-fuzzify the fuzzy numbers. This method ranks fuzzy numbers according to the probabilities of fuzzy events. Assume that ${\tilde{a}}_{ij}$ = (l_ij, m_ij, u_ij) is a TFN with uniform distribution, its mean is calculated as:

$$x({\tilde{a}}_{ij})=(l_{\text{ij}}+m_{\text{ij}}+u_{\text{ij}})/3$$

(12)

After all of the elements in the comparison matrix are converted from triangular fuzzy numbers to crisp numbers, the consistence index, CI, for a comparison matrix can be computed with the use of the following equation:

$$CI=\frac{{\lambda }_{\text{max}}-n}{n-1}$$

(13)

where ${\lambda }_{\text{max}}$ is the largest eigenvalue of the comparison matrix and n is the dimension of the matrix. The consistency ratio (CR) [23] is defined as the ratio between the consistency of a given evaluation matrix and consistency of a random matrix:

$$CR=\frac{CI}{RI\left(n\right)}$$

(14)

where RI(n) is a random index [32] that depends on n, as shown in Table 7. Since all of the CR of a comparison matrix are equal or less than 0.1, it is acceptable. When the CR is unacceptable, the decision-maker is encouraged to repeat the pair-wise comparisons. In this step, the MATLAB package can be employed to calculate the eigenvalue of all comparison matrices.

Table 7. Random index (RI) of random matrices.

m	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
RI	0.00	0.00	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49	1.51	1.48	1.56	1.57	1.59

Table 7. Random index (RI) of random matrices.

m	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
RI	0.00	0.00	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49	1.51	1.48	1.56	1.57	1.59

Step 9: Constructing the Group Judgment Matrix

Each individual judgment matrix represents the opinion of one decision-maker. Aggregation is necessary to achieve a group consensus of decision-makers. In the conventional AHP, there are two basic approaches for aggregating the individual preferences into a group preference, namely aggregation of individual judgments (AIJ) and aggregation of individual priorities (AIP) [33]. The concepts and ideas employed in the conventional AHP can also be utilized in the fuzzy AHP. In the AIJ approach, the group judgment matrix is obtained from the individual judgment matrices. This means that the group judgment matrix is considered as the judgment matrix of a “new individual”, and the priorities of this individual are derived as a group solution. However, in the AIP approach, the group members act individually. Specifically, from the individual judgment matrices, we obtained the individual priorities, and from these, the group priorities are derived. AIJ is most often performed using the geometric mean operations; whereas AIP is typically performed using the arithmetic mean operations. Geometric mean operations are commonly used within the application of AHP for aggregating group decisions [34], and only the geometric mean satisfies the Pareto principle (unanimity condition) and homogeneity condition [35]. Hence, in this research, the AIJ approach is utilized for the aggregation of group decisions. Consider a group of K decision-makers involved in the research. They make pair-wise comparisons of n criteria. As a result of the pair-wise comparisons, we get a set of K matrixes ${\tilde{A}}_k=\left\{{\tilde{a}}_{ijk}\right\}$, where ${\tilde{a}}_{ijk}$ = (l_ijk, m_ijk, u_ijk) represents the relative importance of criterion i to j as assessed by the expert k. The triangular fuzzy numbers in the group judgment matrix can be obtained by using the following equation [36]:

$$\begin{gathered} l_{ij}=\underset{k=1,2,\mathrm{..}K}{\text{min}}\left(l_{ijk}\right) \\ {m}_{ij}=\sqrt[K]{{\displaystyle \prod _{k=1}^K{m}_{ijk}}} \\ {u}_{ij}=\underset{k=1,2,\mathrm{..}K}{\text{max}}\left(u_{ijk}\right) \end{gathered}$$

(15)

In this work, a group of nine decision-makers, including design managers, business managers and plant management, was established. The questionnaires were provided to obtain their viewpoints. The questionnaire consisted of two parts: Part 1 included the pair-wise comparisons between the construct; Part 2 focused on the pair-wise comparisons between the criteria under each construct. Subsequently, the fuzzy judgment matrices were formed based on the obtained pair-wise data comparisons from the original effective questionnaire using fuzzy numbers. By employing Equation (15), the geometric mean method was then applied to get the representative comparison matrix of the group. The group judgment matrix for the criteria and construct was derived from Microsoft Excel by following Equation (12). The matrix of the group acquired when making pairwise comparisons of the construct is shown in Table 8. In order to get the individual comparison matrices of the criteria, all criteria within a specific corresponding construct were compared. The representative matrices of the group were then obtained, and they are shown in Table 9, Table 10 and Table 11. The consistency test results of the individual comparison matrices and the representative matrices showed that they are all less than 0.1. Therefore, the consistency in each matrix is acceptable.

Table 8. The group judgment matrix of the criterion.

	C1	C2	C3
C1	(1, 1, 1)	(2.5, 2.6567, 3.5)	(1.5, 1.7599, 2.5)
C2	(0.3333, 0.3764, 0.5)	(1, 1, 1)	(1, 1.3104, 2)
C3	(0.5, 0.5682, 1)	(0.6667, 0.7631, 2)	(1, 1, 1)

Table 8. The group judgment matrix of the criterion.

	C1	C2	C3
C1	(1, 1, 1)	(2.5, 2.6567, 3.5)	(1.5, 1.7599, 2.5)
C2	(0.3333, 0.3764, 0.5)	(1, 1, 1)	(1, 1.3104, 2)
C3	(0.5, 0.5682, 1)	(0.6667, 0.7631, 2)	(1, 1, 1)

Table 9. The group judgment matrix of the attributes within the “price” criterion.

	A1	A2	A3
A1	(1, 1, 1)	(1.5, 1.6509, 2.5)	(1.5, 1.4805, 2.5)
A2	(0.5, 0.6057, 1)	(1, 1, 1)	(2, 2.3208, 3)
A3	(0.6667, 0.6754, 2)	(0.4, 0.4309, 0.6667)	(1, 1, 1)

Table 9. The group judgment matrix of the attributes within the “price” criterion.

	A1	A2	A3
A1	(1, 1, 1)	(1.5, 1.6509, 2.5)	(1.5, 1.4805, 2.5)
A2	(0.5, 0.6057, 1)	(1, 1, 1)	(2, 2.3208, 3)
A3	(0.6667, 0.6754, 2)	(0.4, 0.4309, 0.6667)	(1, 1, 1)

Table 10. The group judgment matrix of the attributes within the “function” criterion.

	A4	A5	A6
A4	(1, 1, 1)	(2, 2.1544, 3)	(2, 2.5, 3)
A5	(0.4, 0.4612, 0.6667)	(1, 1, 1)	(2, 2.2085, 3)
A6	(0.3333, 0.4, 0.5)	(0.4, 0.4528,0.6667)	(1, 1, 1)

Table 10. The group judgment matrix of the attributes within the “function” criterion.

	A4	A5	A6
A4	(1, 1, 1)	(2, 2.1544, 3)	(2, 2.5, 3)
A5	(0.4, 0.4612, 0.6667)	(1, 1, 1)	(2, 2.2085, 3)
A6	(0.3333, 0.4, 0.5)	(0.4, 0.4528,0.6667)	(1, 1, 1)

Table 11. The group judgment matrix of the attributes within the “performance” criterion.

	A7	A8	A9
A7	(1, 1, 1)	(1.5, 1.8171, 2.5)	(1, 1.3708, 2)
A8	(0.5, 0.5503, 1)	(1, 1, 1)	(1.5, 1.8172, 2.5)
A9	(0.6667, 0.7295, 2)	(0.5, 0.5503, 1)	(1, 1, 1)

Table 11. The group judgment matrix of the attributes within the “performance” criterion.

	A7	A8	A9
A7	(1, 1, 1)	(1.5, 1.8171, 2.5)	(1, 1.3708, 2)
A8	(0.5, 0.5503, 1)	(1, 1, 1)	(1.5, 1.8172, 2.5)
A9	(0.6667, 0.7295, 2)	(0.5, 0.5503, 1)	(1, 1, 1)

Step 10: Calculating the Local Weights and the Global Weights

The fuzzy AHP was then employed to identify the weights of criteria and the attributes. Taking the pair-wise comparison matrix of the construct in Table 8 as an illustration, the weights of the construct were acquired as follows: using Equations (3)–(7), we determined the TFN values of the geometric mean for the fuzzy comparison value of construct C1 to each construct, as seen in the following:

$${\tilde{r}}_1={\left({\tilde{c}}_{11}\otimes {\tilde{c}}_{12}\otimes {\tilde{c}}_{13}\right)}^{1/3}={\left(1_{*}{2.5}_{*}1.5\right)}^{1/3},{\left(1_{*}{2.6567}_{*}1.7599\right)}^{1/3},{\left(1_{*}{3.5}_{*}2.5\right)}^{1/3}=(1.5536,1.6722,2.0606)$$

Similarly, we obtained ${\tilde{r}}_2$ and ${\tilde{r}}_3$.

$${\tilde{r}}_2=({\left({0.3333}_{*}{1}_{*}1\right)}^{1/3},{\left({0.3764}_{*}{1}_{*}1.3104\right)}^{1/3},{\left({0.5}_{*}{1}_{*}2\right)}^{1/3})=(0.6933,0.7901,1)$$

$${\tilde{r}}_3=({\left({0.5}_{*}{0.6667}_{*}1\right)}^{1/3},{\left({0.5682}_{*}{0.7613}_{*}1\right)}^{1/3},{\left(1_{*}{2}_{*}1\right)}^{1/3})=(0.6934,0.7563,1.2599)$$

Subsequently, the weight of each criterion (${\tilde{w}}_i$) can be calculated as follows:

$$\begin{array}{l}{\tilde{w}}_{C1}={\tilde{r}}_1\otimes {\left({\tilde{r}}_1\oplus {\tilde{r}}_2\oplus {\tilde{r}}_3\right)}^{-1}\\ =(1.5536,1.6721,2.0606)*(1/(2.0606+1+1.2599),1/(1.6721+0.7901+0.7563),1/(1.5536+0.6933+0.6934\left)\right)\\ =(1.5536,1.6721,2.0606)*(0.2315,0.3107,0.3934)=(0.3597,0.5195,0.7008)\end{array}$$

Likewise,

$${\tilde{w}}_{C2}=(0.6933,0.7901,1)*(0.2315,0.3107,0.3401)=(0.1605,0.2455,0.3401)$$

$${\tilde{w}}_{C3}=(0.6934,0.7563,1.2599)*(0.2315,0.3107,0.3401)=(0.1605,0.2350,0.4285)$$

Thus, the fuzzy weight vector is as follows:

$$\tilde{W}={\left({\tilde{w}}_{C1},{\tilde{w}}_{C2},{\tilde{w}}_{C3}\right)}^T={\left(\right(0.3597,0.5195,0.7008),(0.1605,0.2455,0.3401),(0.1605,0.2350,0.4285\left)\right)}^T$$

The weight of each criterion is calculated by employing the de-fuzzification procedure proposed by Lee and Li [25].

Thus,

• WC₁ = (0.3597, 0.5195, 0.7008)/3
• WC₂ = (0.1605, 0.2455, 0.3401)/3
• WC₃ = (0.1605, 0.2350, 0.4285)/3
• (WC₁, WC₂, WC₃) = (0.5267, 0.2487, 0.2732,)

We, then, normalized the weight vector and obtained the relative weights of the three criteria.

WC = (0.5267/(0.5267 + 0.2487 + 0.2732), 0.2487/(0.5267 + 0.2487 + 0.2732),
0.2732/(0.5267 + 0.2487 + 0.2732)) = (0.5023, 0.2372, 0.2605)

The calculation results show that the weight of “price” is the largest. Hence, this construct plays the most important part in this project, followed by “performance”. Similarly, the weight vectors of criteria at the successive levels were determined. They are as shown below. The weight vector from Table 10 was calculated as:

(w_A1, w_A2, w_A3) = (0.2148, 0.1706, 0.1161)

The weight vector from Table 11 was calculated as:

(w_A4, w_A5, w_A6) = (0.1235, 0.0730, 0.0404)

The weight vector from Table 12 was calculated as:

(w_A7, w_A8, w_A9) = (0.1080, 0.0837, 0.0699)

In this work, the fuzzy AHP was then employed to identify the weights of the construct and criteria. Taking the pair-wise comparison matrix of the construct in Table 7 as an illustration, the weights of the construct were acquired as follows: the global weight of constructs is then calculated by multiplying the local weight of the criteria with the local weight of the construct in which it belongs. They are shown in Table 12. The three most important criteria that can affect the project overall are “cost of product (A₁)”, “cost of development (A₂)” and reliability (A₄)”. The importance weights of price (C₁), function (C₂) and performance (C₃) were 0.5023, 0.2372 and 0.2605, respectively. These results are logical when price and function are commonly considered to be more important than performance in the machine tools industry in Taiwan. The finding also reflects the characteristics of the Taiwan R&D system. Research and Development is weak in Taiwan’s machine tools industry. Due to the R&D system being weak in Taiwan, the top-level management always pays attention to price and function as the competitiveness factor in the marketplace.

Table 12. The computed global weights for the attributes.

Construct	Criteria	Local Weight	Global Weight
C1 0.5023	A1	0.4284	0.2148
	A2	0.3401	0.1706
	A3	0.2315	0.1161
C2 0.2372	A4	0.5215	0.1235
	A5	0.3080	0.0730
	A6	0.1705	0.0404
C3 0.2605	A7	0.4129	0.1080
	A8	0.3200	0.0837
	A9	0.2671	0.0699

Table 12. The computed global weights for the attributes.

Construct	Criteria	Local Weight	Global Weight
C1 0.5023	A1	0.4284	0.2148
	A2	0.3401	0.1706
	A3	0.2315	0.1161
C2 0.2372	A4	0.5215	0.1235
	A5	0.3080	0.0730
	A6	0.1705	0.0404
C3 0.2605	A7	0.4129	0.1080
	A8	0.3200	0.0837
	A9	0.2671	0.0699

Step 11: Determining the Relevant Principles of the TRIZ Matrix for New Innovative Design Shape

The global weights for criteria are listed in Table 12. The ranking of criteria is: cost of production > cost of development > reliability > …> strength, and so on. It was obviously shown that the cost of product was the most important criteria. According to the TRIZ-FAHP synergy and the limited resources of the enterprise, the authors selected the top five criteria (cost of production, cost of development, reliability, cost of marketing, attractiveness) from the FAHP method as the main design objectives, and in view of certain subjective and objective aspects, to collect the relevant principles from the TRIZ matrix, in order to complete the innovative shape design of machine tools (Figure 5). The relevant principles of the main designed objects are as follows:

(1) Segmentation; (2) merging; (3) anti-weight; (4) copying; (5) cheap short-living objects; (6) flexible shells and thin films.

Based on the relevant principles of the main design objects, we can find improvement suggestions from the web, adopting the improvement suggestions to design our innovative design for a new shape for the machine tools.

Figure 5. New innovative design shape for the machine tools.

Figure 5. New innovative design shape for the machine tools.

Step 12: Final Evaluation and Selection of the Best Designing System

The benefit of the new shape in comparison with the original shape is also illustrated in Table 13 and Table 14. Typically, the new shape can increase the economic effectiveness up to $3,530,000 NT per year. This economic effectiveness can be helpful for a small business or organization.

Table 13. Benefit comparisons with current and new shape machine tools (USD/unit).

Item	Before	After	Performance
Business	120 unit/year	130 unit/year	+8.3%
Cost	3000 USD	2850 USD	−5%
Production	42 days	35 days	−7 days

Table 13. Benefit comparisons with current and new shape machine tools (USD/unit).

Item	Before	After	Performance
Business	120 unit/year	130 unit/year	+8.3%
Cost	3000 USD	2850 USD	−5%
Production	42 days	35 days	−7 days

Table 14. The comparison of innovative shape design and original shape design.

Comparison Item	Innovative Design	Original Design	Note
Shape	attractive	general	Aesthetics design
Maintenance	easy	difficult	Module design for maintenance
Operation	easy	difficult	Analysis of human factor engineering
Manufacturing	easy	difficult	Module design for manufacturing
Environmental	easy	difficult	Change the glass to compound material Acrylonitrile-butadiene-sysrene (ABS) + Polymethylmethacrylate (PMMA)

Table 14. The comparison of innovative shape design and original shape design.

Comparison Item	Innovative Design	Original Design	Note
Shape	attractive	general	Aesthetics design
Maintenance	easy	difficult	Module design for maintenance
Operation	easy	difficult	Analysis of human factor engineering
Manufacturing	easy	difficult	Module design for manufacturing
Environmental	easy	difficult	Change the glass to compound material Acrylonitrile-butadiene-sysrene (ABS) + Polymethylmethacrylate (PMMA)

4. Conclusions

This is the first time, a TRIZ is used to propose the alternatives of a shape’s design under innovative design considerations and using a FAHP to evaluate and select the best feasible alternative under a multiple criteria decision-making environment in the machine tools industry. This work applied TRIZ-FAHP to develop the new shape of machine tools and demonstrates the development of innovative design for a new shape. If a design project includes a contradiction structure to be overcome, it is necessary to generate a novel solution from the systems point of view. For this purpose, an idea generation approach has been proposed in which the TRIZ contradiction matrix was adopted based on expert knowledge. The method enables the knowledge incorporated in TRIZ to be used in innovation design. The system of shape design is followed with an innovative approach, TRIZ. Although more than one design is probable, a multi-criteria decision-making, FAHP, is able to evaluate and suggest the most suitable design. The integration of an innovative design tool, TRIZ, and multi-criteria decision-making, FAHP, is used in this research and indicates that it is likely to be a reliable and promising form of hybrid method in new shape design. According to the TRIZ-FAHP synergy and the concept of lean production, the authors selected the top five criteria (cost of production, cost of development, reliability, cost of marketing, attractiveness) from the FAHP method as the main design objectives, and in view of certain subjective and objective aspects, to collect the relevant principles from the TRIZ matrix and to complete the innovative shape design of machine tools. From this case study, the benefits of this new innovative design shape, used with TRIZ-FAHP, are better than the old design for machine tools based on the concept of lean production.

In summary, we applied the TRIZ and FAHP to design an innovative new shape of machine tools for machine tools based on the concept of lean production. Our research has demonstrated that the use of an integrated hybrid-method of innovative design and multi-criteria decision-making tools for new shape design has enabled shape designers to improve the efficiency of the design task. Designing the best shape for a new product and expanding knowledge to the other industries is the contribution of our research.