Measures of Information
Abstract
:1. Introduction
- evidence from psychology indicates that humans have inherent difficulties in interpreting information;
- information has a geometry that constrains the possible approaches to truth;
- the interpretation of truth, like all concepts, is Ecosystem-dependent so we should expect different approaches to truth in different Ecosystems.
2. Summary of the Model for Information (MfI)
- how well does x represent what it is intended to represent?
- how useful is x in what an IE needs to achieve?
- properties: each slice has a set of properties and for each property there is one or more physical processes (called measurement) that takes the slice as input and generates the value of the property for the slice;
- entity: a type of slice corresponding to a substance;
- interaction: a physical process that relates the properties of two entities.
- the symbols that are used;
- the structure of IAs and the rules that apply to them;
- the ways in which concepts are connected;
- the ways in which IAs are created and parsed (embodying the rules for creating any compatible IA);
- the channels that are used to interact.
3. Interpretation and Connection Strategy
3.1. Connection Strategy
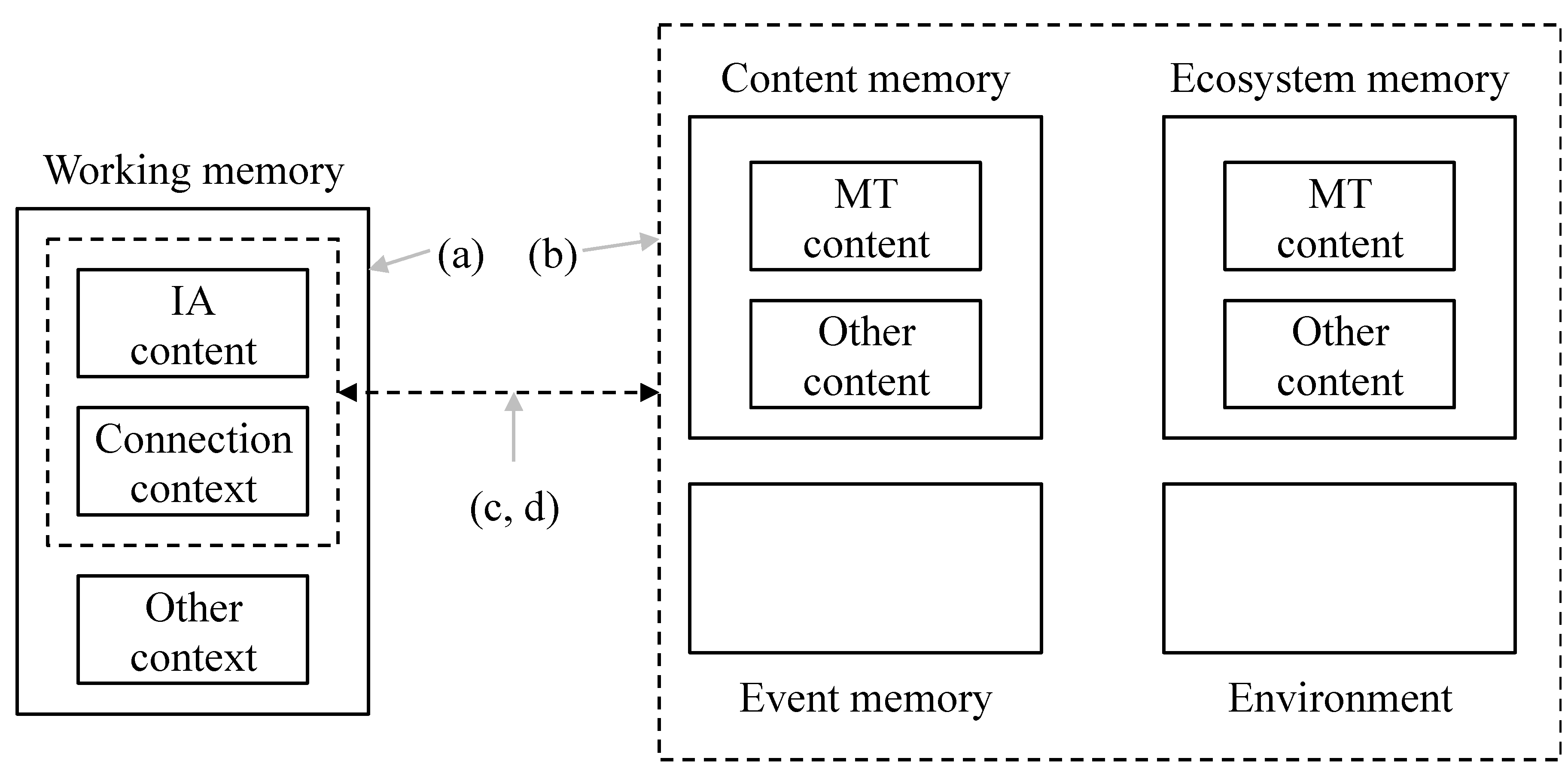
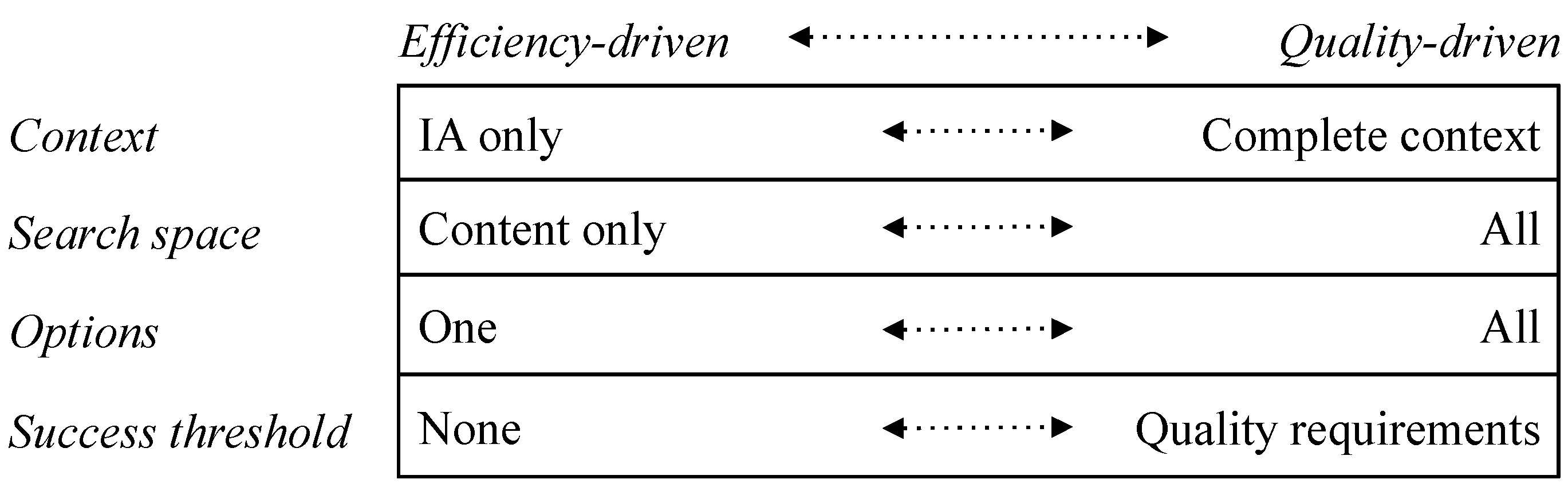
- (a)
- Context: as well as the IA under consideration, how much else of the external environment is taken into account?
- (b)
- Search space: there are choices about how widely to look. An IE can look in various subsets of content memory or event memory. It can look elsewhere in the Ecosystem or more generally in the environment.
- (c)
- Options: how many options will be entertained? Is the first good enough or are all of them needed?
- (d)
- Success threshold: when is a connection good enough to qualify for the interpretation? Is there any kind of quality threshold that must be met?
“…most of what you (your System 2) think and do originates in your System 1, but System 2 takes over when things get difficult, and it normally has the last word. … System 1 has biases, however, systematic errors that it is prone to make in specified circumstances.”
As a result, we cannot reliably trust our System 1 (but often do so without realising it).“System 1 is radically insensitive to both the quality and quantity of information that gives rise to impressions and intuitions.”
- the abstraction pattern of an IE (e.g., DNA, system architecture);
- the history of interactions of an IE (e.g., education, market success);
- the elements of an IA.
- questions and answers (in conversation);
- cross-examination (in the legal process);
- peer review (in the academic world);
- thought and introspection.
3.2. Derivation
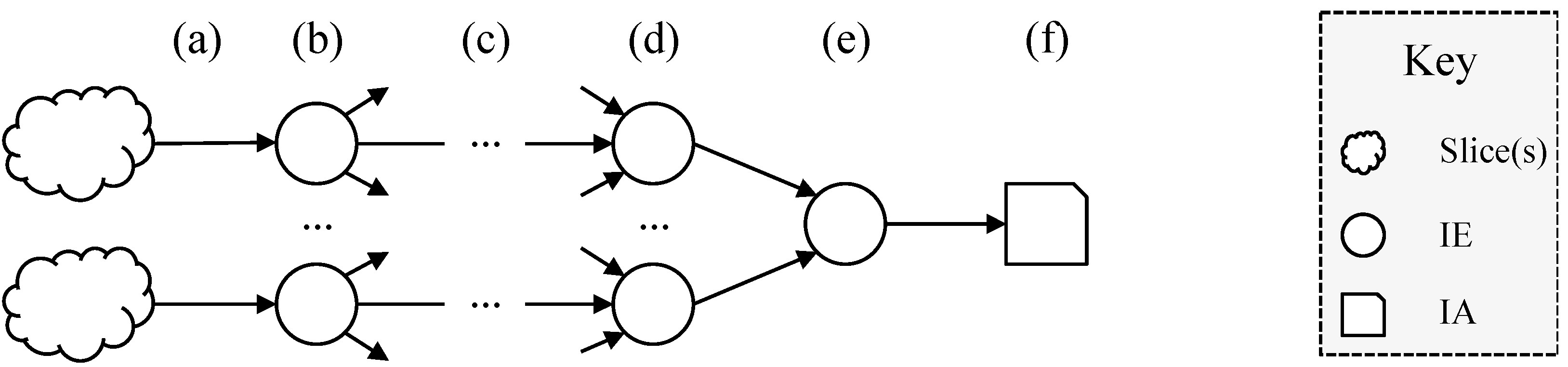
- (a)
- Measurement process: possibly at many different times and using many different measurement processes relating to different Ecosystems a number of properties of slices are measured;
- (b)
- Processing by an IE: each IE (potentially amongst many) senses and analyses the input and then creates one or more IAs;
- (c)
- Transmission: the IAs can be transmitted on various channels and in various modes (e.g., one-to-one or one-to-many);
- (d)
- Processing: intermediate IEs may convert between Ecosystems, combine IAs or process them in other ways;
- (e)
- Combination: one such IE produces the final IA (f).
- in IT, there are rigorous processes for designing, building and testing systems [10]—ensuring that the subsequent derivation of information is robust;
- in legal processes there are rules for handling evidence so that information presented in court has a reliable derivation;
- scientists pay considerable attention to the design of experiments so that measurement is as reliable as possible.
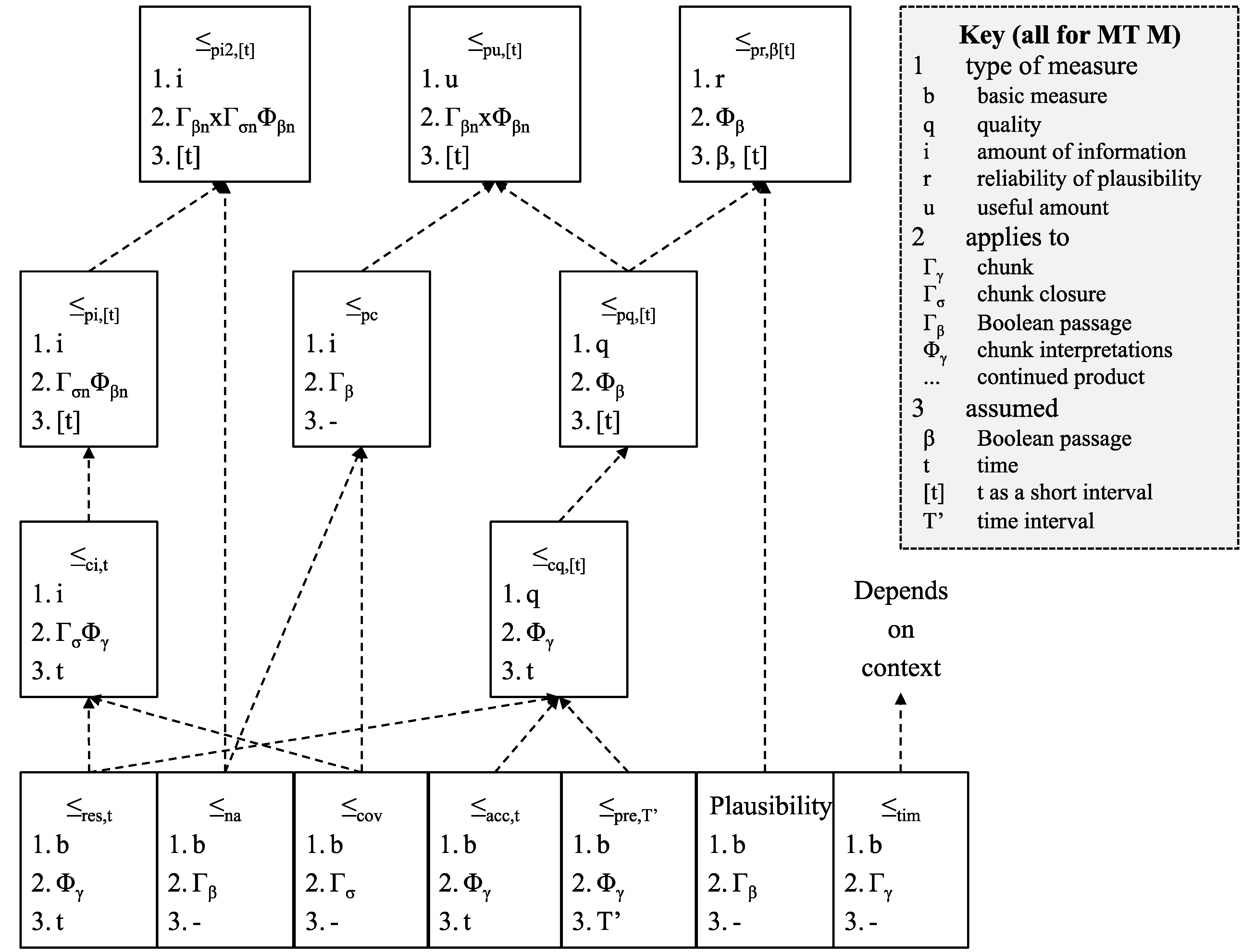
4. Measures
4.1. Definitions
- atom: the fundamental indivisible level of content in the Modelling Tool (note that this definition is different from the definition of “atom” in [11]);
- chunk: groups of atoms;
- assertion: the smallest piece of content that is a piece of information—containing two chunks in a manner that conforms to an assertion abstraction pattern;
- passage: a related sequence of assertions.
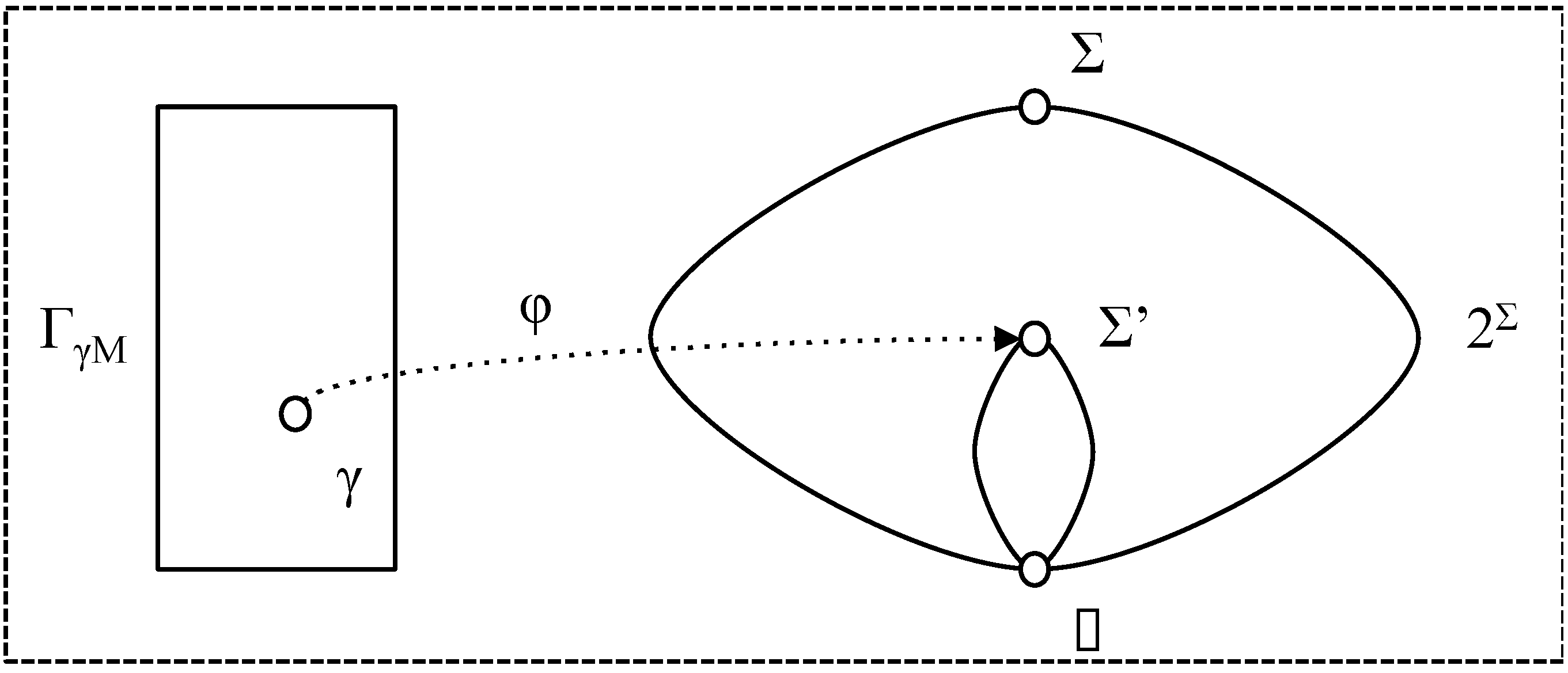
- M is a Modelling Tool (and all of the subsequent definitions are with respect to M);
- ΓΜ is the set of content in M;
- ΓγΜ is the set of chunk content in M and γ, δ ∈ ΓγΜ;
- ΓαΜ is the set of assertion content in M and α, β ∈ ΓαΜ where α = (γ, ρ, δ) and ρ is an assertion abstraction pattern;
- ΓπΜ is the set of passage content in M and π ∈ ΓπΜ;
- Ξ is the set of set theoretic relationships;
- Σ is the set of all slices;
- T is a set of discrete times and t ∈ T;
- φγ: ΓγΜ × T → 2Σ, is a chunk interpretation; Φγ is the set of all chunk interpretations (for M);
- φα: ΓαΜ × T → 2Σ × Ξ × 2Σ, is an assertion interpretation; Φα is the set of all assertion interpretations (for M);
- φπ: ΓπΜ × T → f (2Σ, …, 2Σ), is a passage interpretation where f is a Boolean expression (containing ANDs); Φπ is the set of all passage interpretations (for M);
- φeγ, φeα, φeπ are the corresponding the Ecosystem interpretations.
4.2. Chunks, Assertions, Passages and Interpretations
- the relations implicit in the assertion;
- synonyms (i.e., chunks for which the interpretation is the same);
- discrimination (i.e., chunks for which the interpretation is different).
- the φ-closure of γ, σφ(γ) = {δ ∈ ΓγΜ: φ (δ, t) = φ (γ, t)};
- the closure of γ, σ(γ) = {δ ∈ ΓγΜ: φe (δ, t) = φe (γ, t)};
- ΓσΜ = {σ(γ): γ ∈ ΓγΜ};
- φ is MT-closed if σ(γ) = σφ(γ) for all γ ∈ ΓγΜ;
- φ is MT-structured if φ maps to the same relation as φe for all passages;
- φ is MT-consistent if φ is MT-closed and MT-structured.
4.3. Boolean Passages
- α OR β;
- IF α THEN β.
4.4. Measures for Chunks—Accuracy
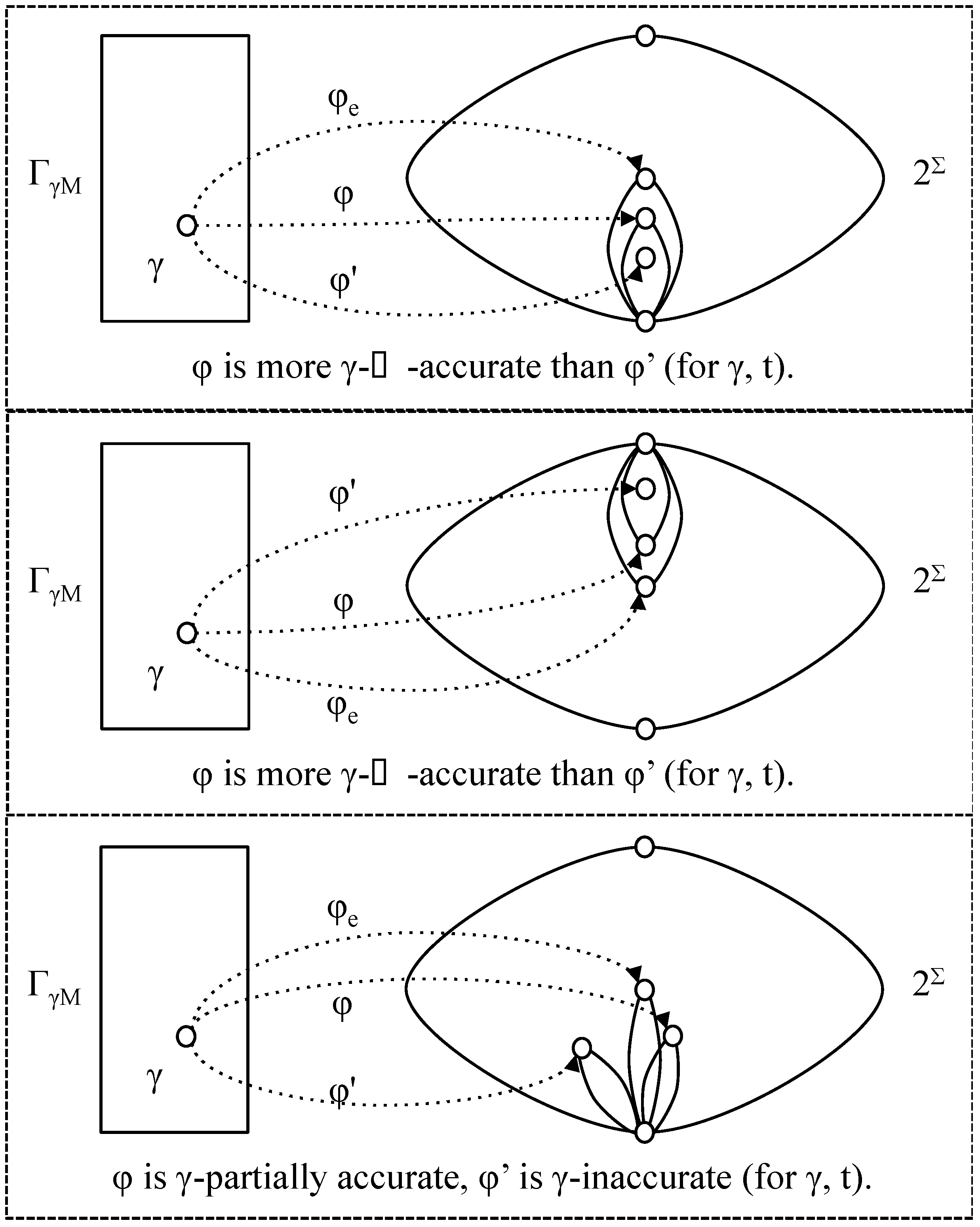
- φ is γ-accurate (with respect to t) if φ (γ, t) = φe (γ, t) ≠ ∅;
- φ is γ-inaccurate (with respect to t) if φ (γ, t) ∩ φe (λ, t) = ∅ ;
- φ is more γ-⊂-accurate than φ' (with respect to t) if φ' (γ, t) ⊂ φ (γ, t) ⊆ φe (γ, t);
- φ is more γ-⊃-accurate than φ' (with respect to t) if φe (γ, t) ⊆ φ (γ, t) ⊂ φ' (γ, t);
- φ is more γ-accurate than φ' (with respect to t) if it is more γ-⊂-accurate or more γ-⊃-accurate (note that it cannot be both);
- φ is γ-partially accurate (with respect to t) if φ (γ, t) ∩ φe (λ, t) ≠ ∅ and φ (γ, t) φe (λ, t) ≠ ∅.
- φ <acc,t φ' if φ' is more accurate than φ;
- φ =acc,t φ' if φ = φ';
- ≤acc,t, >acc,t, ≥acc,t correspondingly.
- φ <acc,t φ' and φ' ≤acc,t φ; then
- φ ≠acc,t φ' and there is some γ for which (depending on the type of relative accuracy) either
- φ (γ, t) ⊂ φ' (γ, t) ⊆ φe (γ, t), or
- φe (γ, t) ⊆ φ' (γ, t) ⊂ φ (γ, t).
4.5. Measures for Chunks—Precision
- the ∩T’-range of φ with respect to γ, ∩T’-ran (φ, γ) = {σ: σ ∈ φ (γ, t) ∀ t ∈ T’};
- the ∪T’-range of φ with respect to γ, ∪T’-ran (φ, γ) = {σ: ∃ t ∈ T’ such that σ ∈ φ (γ, t)};
- φ is γ-precise (with respect to T’) if ∩T’-ran (φ, γ) = ∪T’-ran (φ, γ);
- φ is γ-imprecise (with respect to T’) if ∩T’-ran (φ, γ) = ∅;
- φ is more γ-precise than φ' (with respect to T’) if
- ∩T’-ran (φ, γ) ⊃ ∩T’-ran (φ', γ) and ∪T’-ran (φ, γ) ⊆ ∪T’-ran (φ', γ), or
- ∩T’-ran (φ, γ) ⊇ ∩T’-ran (φ', γ) and ∪T’-ran (φ, γ) ⊂ ∪T’-ran (φ', γ);
- φ is as γ-precise as φ' (with respect to T’) if
- ∩T’-ran (φ, γ) ⊇ ∩T’-ran (φ', γ) and ∪T’-ran (φ, γ) ⊆ ∪T’-ran (φ', γ).
- φ <pre,T’ φ' if φ' is more precise than φ' for time period T’;
- φ =pre,T’ φ' if φ = φ';
- ≤pre,T’, >pre,T’, ≥pre,T’ correspondingly.
4.6. Measures for Chunks—Coverage
- γ >cov γ’ if γ has greater coverage than γ';
- ≥cov, ≤cov, <cov correspondingly.
- σ’(γ) = {δ ∈ ΓγΜ: γ ≤cov δ and δ ≤cov γ}
4.7. Measures for Chunks—Resolution
- φ resolves as well as φ' (with respect to t) if for all γ ∈ ΓγΜ, φ (γ, t) ⊆ φ' (γ, t); (note that this is a different definition from that in [1] but it expresses the concept more clearly).
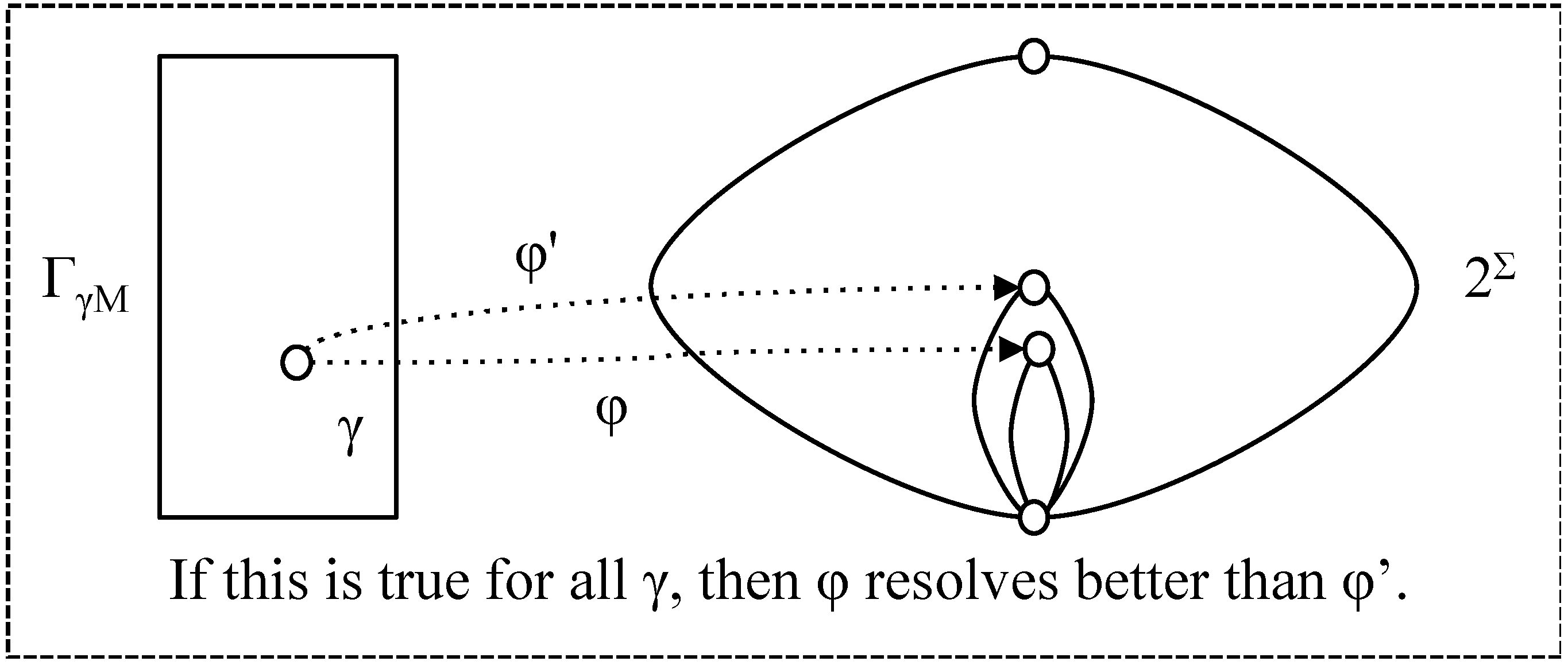
- φ ≤res,t φ' if φ resolves as well as φ' (for t);
- ≥res,t, <res,t, >res,t correspondingly.
4.8. Measures for Chunks—Timeliness
4.9. Measures for Chunks—Overall
- a ≤a a’ if a ≤a1 a’ and a ≤a2 a’ for a, a’ ∈ A;
- c ≤c c’ if a ≤a1 a’ and b ≤b b’ for c = (a, b), c’ = (a’, b’), a, a’ ∈ A, b, b’ ∈ B.
| Order | Definition | Assumes | Applies to |
| ≤acc,t | As above | Fixed t | Φγ |
| ≤pre,T’ | As above—precision applies to interpretations of all instances of a chunk in the time period in question | Range T’ | Φγ |
| ≤res,t | As above | Fixed t | Φγ |
| ≤cov | As above | - | Γσ |
| ≤tim | As above | - | T |
| ≤cq,t | sum (≤acc,t, ≤res,t) | Fixed t | Φγ |
| ≤ci,t | product (≤cov, ≤res,t) | Fixed t | ΓσΦγ = Γσ × Φγ |
4.10. Measures for Assertions
- φ (α, t) = (φ (γ, t), r, φ (δ, t)).
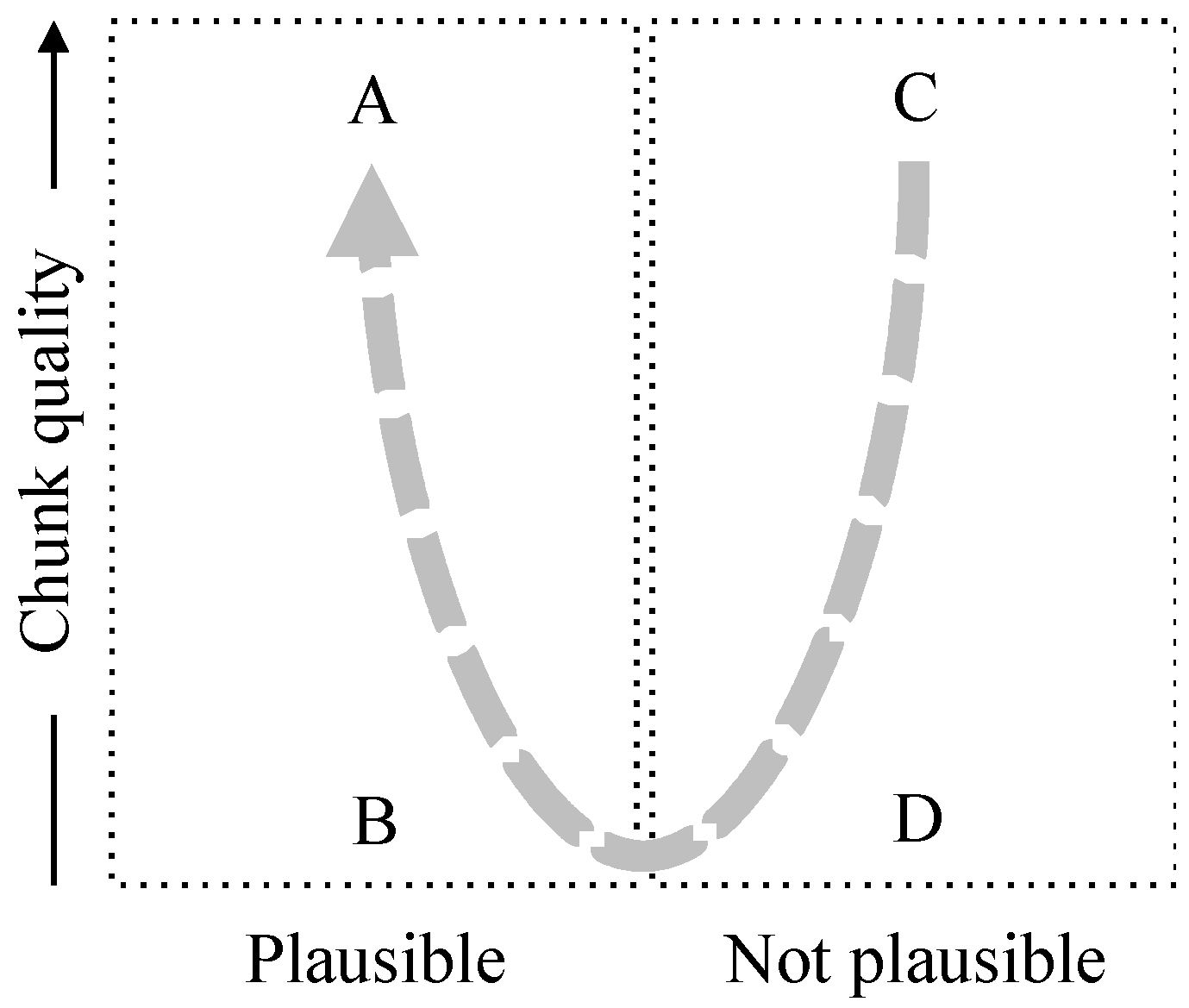
- α is (not) φ-plausible (with respect to t) if r (φ (γ, t), φ (δ, t)) is (not) satisfied;
- α is (not) plausible (with respect to t) if r (φe (γ, t), φe (δ, t)) is (not) satisfied.
| Order | Definition | Applies to |
| ≤cq,[t] | sum (≤pre,[t], ≤acc,t, ≤res,t) | Φγ |
| ≤aq,[t] | product (≤cq,[t], ≤cq,[t]) | Φγ × Φγ |
| ≤ai,[t] | product (≤ci,t, ≤ci,t) | ΓσΦγ × ΓσΦγ |
- P = ΓαΜ × Φα × T;
- Pαt0 = {φ ∈ Φα: α is not φ-plausible (with respect to t)} and similarly Pαt1 for which α is φ-plausible;
- Pαt = Pαt0 ∪Pαt1.
- if φ, φ' ∈ Pαt0, then φ ≤ar,α[t] φ' if φ ≥aq,[t] φ';
- if φ, φ' ∈ Pαt1, then φ ≤ar,α[t] φ' if φ ≤aq,[t] φ';
- if φ ∈ Pαt0 and φ' ∈ Pαt1, then φ <ar,α[t] φ'.
4.11. Measures for Boolean Passages
- β1 = f (α1i) is a passage and α1i = (γ1i, ρ1i, δ1i);
- β2 = f (α2j) is a passage and α2j = (γ2j, ρ2j, δ2j);
- β1 ≤na β2 if α1i∈ {α2j for all j} for all i.
| Order | Definition | Applies to |
| ≤na | As above | Γβ |
| ≤pcov | product (≤cov, …, ≤cov) | Γβ |
| ≤pc | sum (≤na, ≤pcov) | Γβ |
| ≤pq,[t] | product (≤cq,[t], …, ≤cq,[t]) | Φβ |
| ≤pi,[t] | product (≤ci,[t], …, ≤ci,[t]) | ΓσnΦβn = ΓσΦγ× … × ΓσΦγ |
| ≤pi2,[t] | product (≤na, ≤pi,[t]) | Γβn× ΓσnΦβn |
| ≤pu,[t] | product (≤pc, ≤pq,[t]) | Γβn× Φβn |
- if β11 ≥pcov β2 then β1 >pcov β2;
- if β11 <pcov β2 then β1 and β2 are not comparable;
- if β11 and β2 are not comparable then β1 and β2 are not comparable.
- if β11 ≤pq,[t] β2 then β1 <pq,[t] β2;
- if β11 >pq,[t] β2 then β1 and β2 are not comparable;
- if β11 and β2 are not comparable then β1 and β2 are not comparable.
- β = f (αi);
- αi = (γi, ρi, δi);
- φ (αi, t) = (φ (γi, t), ri, φ (δi, t)), where ri corresponds to ρi;
- β is (not) φ-plausible (with respect to t) if f (ri (φ (γi, t), φ (δi, t))) is (not) satisfied;
- β is (not) plausible (with respect to t) if f (ri (φe (γi, t), φe (δi, t))) is (not) satisfied.
- Q = ΓβΜ × Φβ × T;
- Qβt0 = {φ ∈ Φβ: β is not φ-plausible (with respect to t)} and similarly Qβt1;
- Qβt = Qβt0 ∪ Qβt1.
- if φ, φ' ∈ Qβt0, then φ ≤pr,β[t] φ' if φ ≥pq,[t] φ';
- if φ, φ' ∈ Qβt1, then φ ≤pr,β[t] φ' if φ ≤pq,[t] φ';
- if φ ∈ Qβt0 and φ' ∈ Qpt1, then φ <pr,β[t] φ'.
4.12. Restricting Measures
4.13. Summary of Orders
5. Truth and Truthlikeness
“Whether an informational theory could explain truth more satisfactorily than other current approaches” and
MfI allows truth to be examined from a number of different viewpoints and supplies some constraints (of the type that Floridi refers to). Truth is expressed using IAs and IAs are interpreted by IEs. So, truth (for an IE) is related to both an IA and its interpretation and the nature of truth cannot be disentangled from the quality of information. There are several implications of this.“if that is answered in the negative, whether an informational approach could at least help to clarify the theoretical constraints to be satisfied by other approaches.”
The “accepted examples” and “coherent traditions” he mentions correspond to Information Ecosystems.“I mean to suggest that some accepted examples of scientific practice—examples which include law, theory, application, and instrumentation together—provide models from which spring coherent traditions of scientific research.”
5.1. Measures of Information—Truth
- the law—“beyond reasonable doubt”;
- science—for example, the six-sigma criterion used in particle physics experiments like the test for the Higgs boson.
5.2. Measures of Information—Truthlikeness
- (1)
- “the room contains 150 people” is plausible;
- (2)
- “the room contains about 150 people” is also plausible;
- (3)
- “the room contains 151 people” is implausible but close (in some sense).
- P = ΓαΜ × Φα × T;
- pl: P → {0, 1} where “0” represents “not plausible” and “1” represents “plausible”;
- αi = (γ, ρ, δi) for 1 ≤ i ≤ n where the δi correspond to values for a single property and Α = {αi};
- Qt0 = {αi∈ ΓαΜ: pl (αi, φe, t) = 0} and similarly Qt1;
- Qt = Qt0 ∪ Qt1.
- α’1 >cov α’2 <cov α’3;
- α’1∈ Qt0;
- α’2, α’3∈ Qt1.
- α ∈ Qt0;
- α’1 >cov α >cov α’2 <cov α’3.
- α ∈ Qt1;
- α’2 <cov α <cov α’3.
6. The Amount of Information
6.1. The Bar-Hillel Carnap Paradox (BCP)
So the BCP leads to the following questions:“According to the classic quantitative theory of semantic information, there is more information in a contradiction than in a contingently true statement.”
- what does “more information” refer to?
- what is a contradiction?
- what does it mean in terms of MfI and the measures above?
6.2. The Scandal of Deduction
This is discussed further in [18,19]. When the scandal of deduction is viewed through the lens of MfI it prompts a number of questions including, for example, the following:“According to the received view, logical deduction never increases (semantic) information. This tenet clashes with the intuitive idea that deductive arguments are useful just because, by their means, we obtain information that we did not possess before.”
- “Logical deduction never increases (semantic) information”—for whom?
- What does increased information mean?
| α1 = “P” α2 = “P IMPLIES Q” α3 = “Q” | IE memory contains… | ||||
| - | α2 | α3 | α2, α3 | ||
| IA contains… | α1 | 1 | 2 | 3 | 4 |
| α1, α2 | 5 | 6 | 7 | 8 | |
- (a)
- the IE makes a connection with the content during recognition (depending on the connection strategy) but does not store the content in memory;
- (b)
- the content is stored in memory as a result of recognition (as a by-product of the Modelling Tool processing, again depending on connection strategy);
- (c)
- the content is stored in memory as a result of processing (again depending on the nature of the processing).
- the amount in the IA;
- how much is added to the memory of the IE and, in particular, whether either or both of the following are added (assuming that “P” is added in each case):
- ○
- “P IMPLIES Q”;
- ○
- “Q”.
| Option | Amount of information in IA | Possibility that “P IMPLIES Q” added | Possibility that “Q” added |
| 1 | Less | No | No |
| 2 | Less | No | c |
| 3 | Less | No | No |
| 4 | Less | No | No |
| 5 | More | a, b | a, b, c |
| 6 | More | No | a, b, c |
| 7 | More | a, b | No |
| 8 | More | No | No |
7. Conclusions
Acknowledgments
Conflicts of Interest
References
- Walton, P. A Model for Information. Information 2014, 5, 479–507. [Google Scholar] [CrossRef]
- Floridi, L. The Philosophy of Information; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Bar-Hillel, Y.; Carnap, R. An Outline of a Theory of Semantic Information. 1953. Reproduced in Language and Information: Selected Essays on Their Theory and Application; Addison-Wesley: Reading, MA, USA, 1964. [Google Scholar]
- Hintikka, J. Logic, Language-Games and Information: Kantian Themes in the Philosophy of Logic; Clarendon Press: Oxford, UK, 1973. [Google Scholar]
- Avgeriou, P.; Uwe, Z. Architectural patterns revisited: A pattern language. In Proceedings of 10th European Conference on Pattern Languages of Programs (EuroPlop 2005), Bavaria, Germany, July 2005.
- Burgin, M. Theory of Information: Fundamentality, Diversity and Unification; World Scientific Publishing: Singapore, 2010. [Google Scholar]
- Tulving, E. Episodic and semantic memory. In Organization of Memory; Tulving, E., Donaldson, W., Eds.; Academic Press: New York, NY, USA, 1972; pp. 381–403. [Google Scholar]
- Kahneman, D. Thinking, Fast and Slow; Macmillan: London, UK, 2011. [Google Scholar]
- Sieloff, C.G. “If only HP knew what HP knows”: The roots of knowledge management at Hewlett-Packard. J. Knowl. Manag. 1999, 3, 47–53. [Google Scholar] [CrossRef]
- Sommerville, I. Software Engineering; Addison-Wesley: Harlow, UK, 2010. [Google Scholar]
- Kohlas, J.; Schmid, J. An Algebraic Theory of Information: An Introduction and Survey. Information 2014, 5, 219–254. [Google Scholar] [CrossRef]
- Ryle, G.; Lewy, C.; Popper, K.R. Symposium: Why are the calculuses of logic and arithmetic applicable to reality? In Logic and Reality, Proceedings of the Symposia Read at the Joint Session of the Aristotelian Society and the Mind Association at Manchester, United Kingdom, 5–7 July 1946; pp. 20–60.
- Gottwald, S. Many-Valued Logic. The Stanford Encyclopedia of Philosophy. Zalta, E.N., Ed.; Spring 2014 ed. Available online: http://plato.stanford.edu/archives/spr2014/entries/logic-manyvalued/ (accessed on 26 January 2015).
- Kuhn, T.S. The Structure of Scientific Revolutions. Enlarged, 2nd ed.; University of Chicago Press: Chicago, IL, USA, 1970. [Google Scholar]
- Logan, R. What Is Information?: Why Is It Relativistic and What Is Its Relationship to Materiality, Meaning and Organization. Information 2012, 3, 68–91. [Google Scholar] [CrossRef]
- Brenner, J. Information: A Personal Synthesis. Information 2014, 5, 134–170. [Google Scholar] [CrossRef]
- D’Agostino, M. Semantic Information and the Trivialization of Logic: Floridi on the Scandal of Deduction. Information 2013, 4, 33–59. [Google Scholar] [CrossRef]
- D’Alfonso, S. On Quantifying Semantic Information. Information 2011, 2, 61–101. [Google Scholar] [CrossRef]
- Finger, M.; Reis, P. On the Predictability of Classical Propositional Logic. Information 2013, 4, 60–74. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Walton, P. Measures of Information. Information 2015, 6, 23-48. https://doi.org/10.3390/info6010023
Walton P. Measures of Information. Information. 2015; 6(1):23-48. https://doi.org/10.3390/info6010023
Chicago/Turabian StyleWalton, Paul. 2015. "Measures of Information" Information 6, no. 1: 23-48. https://doi.org/10.3390/info6010023
APA StyleWalton, P. (2015). Measures of Information. Information, 6(1), 23-48. https://doi.org/10.3390/info6010023





