Abstract
Adsorption is considered to be one of the most effective technologies widely used in global environmental protection areas. Modeling of experimental adsorption isotherm data is an essential way for predicting the mechanisms of adsorption, which will lead to an improvement in the area of adsorption science. In this paper, we employed three isotherm models, namely: Langmuir, Freundlich, and Dubinin-Radushkevich to correlate four sets of experimental adsorption isotherm data, which were obtained by batch tests in lab. The linearized and non-linearized isotherm models were compared and discussed. In order to determine the best fit isotherm model, the correlation coefficient (r2) and standard errors (S.E.) for each parameter were used to evaluate the data. The modeling results showed that non-linear Langmuir model could fit the data better than others, with relatively higher r2 values and smaller S.E. The linear Langmuir model had the highest value of r2, however, the maximum adsorption capacities estimated from linear Langmuir model were deviated from the experimental data.
1. Introduction
To date, the increasing release of phosphate-containing wastewater to natural water bodies has caused eutrophication, depopulated aquatic living species and deteriorated water quality [1], which has become a globally concerning problem. In order to avoid accelerating eutrophication, therefore, there is a need to control and reduce the level of phosphate in wastewater before their discharge to the environment.
Among a numbers of strategies, the adsorption-based process is considered to be efficient to remove various pollutants in water [2]. In this regard, a great deal of interest has been focused on the use of different types of materials as adsorbents for phosphate removal, such as activated carbon fiber [3], Fe-Zr binary oxide [4], pillared bentonites [5], hydrous zirconium oxide [6], and ferric oxides [7], etc. However, the efforts for exploiting new adsorbents, improving the removal efficiency of adsorbents and developing an ideal adsorption system have never been stopped. Recently, researchers found that functionalized mesoporous silica materials, such as Fe(III)-coordinated amino-functionalized SBA-15, have exhibit enhanced phosphate removal capacity, due to their large surface areas, accessible Fe(III) active sites as well as controllable pore sizes and arrangements [8,9].
The performance of an adsorbent can be studied by adsorption isotherm data, which can be obtained by a series of experimental tests in labs. Modeling the adsorption isotherm data is an essential way for predicting and comparing the adsorption performance, which is critical for optimization of the adsorption mechanism pathways, expression of the adsorbents capacities, and effective design of the adsorption systems [10]. Several two-parameter isotherm models are commonly used in modeling the adsorption data, such as Langmuir, Freundlich, Temkin, and Dubinin-Radushkevich et al. [11,12,13,14]. In general, the modeled adsorption isotherm is an invaluable non-linear curve describing the adsorption phenomenon at a constant temperature and pH; and the mathematical correlation which is depicted by the modeling analysis is important for operational design and applicable practice of the adsorption systems [15]. On the other hand, linear analysis of isotherm data into isotherm models is an alternative mathematical approach to predict the overall adsorption behavior. Over the past few decades, researchers found that it is easier to estimate the parameters by the linear analysis. Meanwhile, researchers also found that modeling of isotherm data by linear analysis might cause the discrepancy between the predictions and experimental data. In the endeavor to reliable prediction of adsorption parameters, many researchers have been advocated to investigate the applicability of linear or non-linear isotherm models in describing a number of adsorption systems, such as the adsorption of dyes, heavy metals and organic pollutants onto activated carbons and so on. Since new adsorption systems are continuously developed in water and wastewater treatment, further explorations on the identification and clarification of both linear and non-linear isotherm models in new adsorption systems are highly desirable.
In this paper, the adsorption isotherm data of a novel adsorption system, i.e., Fe(III)-coordinated amino-functionalized mesoporous silica materials for phosphate removal, have been modeled by both linearized and non-linearized methods. To establish the most appropriate adsorption equilibrium correlation, the accuracy in parameters prediction of both linear and non-linear isotherm models were compared and discussed. The results from modeling are expected to provide a certain theoretical basis for operational design and applicable practice of the adsorption systems of phosphate removal, which has drawn increasing attentions in the area of water environmental protection.
2. Experiments
2.1. The Experimental Isotherm Data
In this study, four sets of adsorption isotherm data were used for modeling [16]. As shown in Table 1, these adsorption data were experimentally obtained by a series of batch tests from four synthesized adsorbents (Fe(III)-coordinated amino-functionalized mesoporous MCM-41 with different amino loadings of 0%, 10%, 20% and 30%, denoted as M1, M2, M3, and M4, respectively) for adsorption of phosphate in solutions with different initial concentrations (C0 = 0.5, 1.0, 5.0, 10.0, 25.0, and 55.0 mg P/L). As for the equilibrium experiments, about 0.05 g adsorbent was added into 100 mL phosphate solution in a polypropylene bottle with various initial concentrations. After being shaken at 35 ºC for 2 h, the solutions were removed by filtering thru 0.45 μm syringe nylon-membrane filters, and the equilibrium phosphate concentrations (Ce, mg P/L) in the filtrates were analyzed by Autoanalyzer 3 (Bran and Luebbe Inc., Norderstedt, Germany). The amount of phosphate adsorbed at equilibrium (qe, mg P/g) was calculated by Equation (1):
where C0 and Ce (mg P/L) are the initial and equilibrium phosphate concentrations, respectively, V (L) is the volume of the solution and m (g) is the mass of the adsorbent.

Table 1.
Adsorption data of four adsorbents for phosphate removal in solution with different initial concentrations.
| C0\Samples | M1 | M2 | M3 | M4 | ||||
|---|---|---|---|---|---|---|---|---|
| Ce | qe | Ce | qe | Ce | qe | Ce | qe | |
| 0.5 | 0.49 | 0.021 | 0.061 | 0.93 | 0.037 | 0.98 | 0.052 | 0.95 |
| 1.0 | 0.78 | 0.39 | 0.023 | 1.91 | 0.013 | 1.92 | 0.017 | 1.94 |
| 5.0 | 3.67 | 1.91 | 0.35 | 8.56 | 0.036 | 9.26 | 0.034 | 9.26 |
| 10.0 | 9.03 | 3.88 | 2.45 | 17.18 | 0.15 | 19.49 | 0.33 | 18.97 |
| 25.0 | 23.98 | 4.82 | 16.43 | 19.74 | 5.74 | 42.22 | 4.12 | 44.95 |
| 55.0 | 53.25 | 5.01 | 44.40 | 20.91 | 29.54 | 44.30 | 26.09 | 52.14 |
2.2. Non-linear Forms of the Isotherm Models
Langmuir isotherm model is an empirical model assuming that adsorption can only occur at a finite number of definite localized sites, and the adsorbed layer is one molecule in thickness or monolayer adsorption. The non-linear expression of Langmuir isotherm model can be illustrated as Equation (2) [11]:
where Ce is the concentration of phosphate solution at equilibrium (mg P/L); qe is the corresponding adsorption capacity (mg P/g); qm (mg P/g) and KL (L/mg) are constants which are related to adsorption capacity and energy or net enthalpy of adsorption, respectively.
The Freundlich isotherm model is the earliest known relationship describing the non-ideal and reversible adsorption, which can be applied to multilayer adsorption, on the basis of an assumption concerning the energetic surface heterogeneity. The non-linear expression of Freundlich isotherm model can be illustrated as Equation (3) [12]:
where KF and n are the constants, which measure the adsorption capacity and intensity; respectively.
The Dubinin-Radushkevich isotherm model is another empirical model which initially formulated for the adsorption process following a pore filling mechanism. It is generally applied to express the adsorption process occurred onto both homogeneous and heterogeneous surfaces. The non-linear expression of Dubinin-Radushkevich isotherm model can be illustrated as Equations (4) and (5) [14]:
where qs (mg P/g) is a constant in the Dubinin-Radushkevich isotherm model which are related to adsorption capacity; KDR (mol2/kJ2) is a constant in related to the mean free energy of adsorption; R (J/mol K) is the gas constant; and T (K) is the absolute temperature.
2.3. Linear Forms of the Isotherm Models
Linear forms of the isotherms models are also widely adopted to determine the isotherm parameters or the most fitted model for the adsorption system due to the mathematical simplicity. The linear forms of the Langmuir, Freundlich and Dubinin-Radushkevichisotherms models are given in Table 2. The Langmuir isotherm model can be linearized into four different types, as displayed in Table 2 types I–IV. Among the four linear forms which will result in different parameter estimates, the type I is one of the most popular linear forms used in literatures, due to the minimal deviations from the fitted equation [17,18]. Hence by plotting Ce/qe against Ce it is possible to obtain the value of the Langmuir constant KL and qm; by plotting ln(qe) against ln(Ce), the Freundlich constant of KF and n can be determined; and by plotting ln(qe) against ε2, the Dubinin-Radushkevich constants of KD and qs can be obtained.

Table 2.
Linear forms of the isotherm models.
| Isotherm models | Linear form | |
|---|---|---|
| Langmuir | I | |
| II | ||
| III | ||
| IV | ||
| Freundlich | ||
| Dubinin-Radushkevich |
All the model parameters were evaluated by both non-linear regression and linear least-squares method using Origin 8.0 software. The standard errors (S.E.) for each parameter were used to measure the goodness-of-fit. Apart from S.E., the correlation coefficient (r2) was also used to determine the best-fitting isotherm to the experimental data, illustrated as Equation (6).
where qm is the constant obtained from the isotherm model, qe is the equilibrium capacity obtained from experimental data, and
is the average of qe.
3. Results and Discussion
3.1. Non-linear Fitting of the Isotherm Models
Figure 1 shows Langmuir, Freundlich and Dubinin-Radushkevich adsorption isotherms of the four adsorbents by nonlinear analysis; Table 3 shows the values of corresponding isotherm parameters, their correlation coefficients (r2) and related standard errors (S.E.) for each parameter. In Table 3 and Figure 1, high r2 are derived by fitting experimental data into the Langmuir isotherm model (r2 > 0.973) and the Dubinin-Radushkevich isotherm model (r2 > 0.946), as compared with the Freundlich isotherm model (r2 > 0.858). Meanwhile, the values of S.E. for each parameter obtained in Freundlich isotherm model are correspondingly higher than that of the other two models. These suggest that both Langmuir isotherm model and the Dubinin-Radushkevich isotherm model can generate a satisfactory fit to the experimental data, while Freundlich isotherm model cannot. As shown, the values of maximum adsorption capacity determined using Langmuir model was 5.92, 20.82, 44.36, and 52.53 mg P/g for M1, M2, M3, and M4, respectively. These values are near the experimental adsorbed amounts and correspond closely to the adsorption isotherm plateau, which indicates that the modeling of Langmuir for the adsorption system is acceptable. Moreover, the adsorption feature of the experimental system might be caused by the monolayer adsorption. The values of theoretical monolayer saturation capacity in the Dubinin-Radushkevich model obtained using non-linear regression are all lower than the experimental amounts corresponding to the adsorption isotherm plateau, indicating that the modeling of Dubinin-Radushkevich for the adsorption system is unacceptable. Therefore, by comparison, the order of the isotherm best fits the four sets of experimental data in this study is Langmuir > Dubinin-Radushkevich > Freundlich.
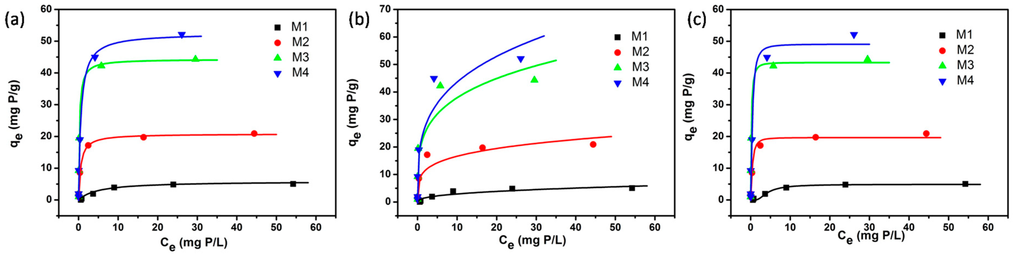
Figure 1.
Non-linear fitting of (a) Langmuir, (b) Freundlich, and (c) Dubinin-Radushkevich isotherm models for the four adsorbents (M1, M2, M3 and M4).

Table 3.
Langmuir, Freundlich and Dubinin-Radushkevich isotherm parameters obtained by nonlinear fitting for the four adsorbents (M1, M2, M3 and M4).
| Model/parameters | M1 | M2 | M3 | M4 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Value | S.E. | Value | S.E. | Value | S.E. | Value | S.E. | ||
| Langmuir | qm (mg P/g) | 5.92 | 0.51 | 20.82 | 0.62 | 44.36 | 2.38 | 52.53 | 3.24 |
| b (L/mg P) | 0.152 | 0.045 | 1.890 | 0.310 | 4.470 | 1.154 | 1.682 | 0.518 | |
| r2 | 0.973 | - | 0.993 | - | 0.979 | - | 0.978 | - | |
| Freundlich | KF | 1.18 | 0.45 | 9.91 | 1.96 | 21.61 | 4.17 | 22.88 | 4.32 |
| n | 2.541 | 0.729 | 4.440 | 1.259 | 4.103 | 1.096 | 3.572 | 0.853 | |
| r2 | 0.858 | - | 0.857 | - | 0.868 | - | 0.894 | - | |
| Dubinin-Radushkevich | qs (mg P/g) | 4.93 | 0.16 | 19.67 | 0.82 | 43.32 | 2.17 | 49.10 | 3.72 |
| KD (mol2/kJ2) | 2.79 | 0.37 | 0.074 | 0.014 | 0.032 | 0.005 | 0.080 | 0.024 | |
| r2 | 0.989 | - | 0.977 | - | 0.975 | - | 0.946 | - | |
3.2. Linear Fitting of the Isotherm Models
Figure 2 shows Langmuir, Freundlich andDubinin-Radushkevich adsorption isotherms of the four adsorbents by linear analysis; Table 4 summarizes the corresponding isotherm parameters, their correlation coefficients (r2) and related standard errors (S.E.) for each parameter. According to the r2 and related S.E. for each parameter in Table 4, the Langmuir model fitted the experimental data best by linear analysis, while the Freundlich fitted worst. These results are in good agreement with the results indicated by nonlinear analysis. However, the r2 (0.995, 0.999, 0.997 and 0.990 for M1, M2, M3, and M4, respectively) were all higher than the corresponding r2 obtained by nonlinear analysis methods. Moreover, although the r2 in Dubinin-Radushkevich model for M3 (0.980) is higher than that obtained by non-linear analysis (0.975), the r2 for the other three adsorbents are lower. In particularly, the r2 for M2 (0.688) is extremely lower than its corresponding r2 by non-linear analysis (0.977). Meanwhile, all the S.E. values are much higher than those determined in non-linear analysis. These indicate that the linear fitting of experimental data into Dubinin-Radushkevich model may cause great fluctuation of r2, and the predicted parameters may induce deviation.
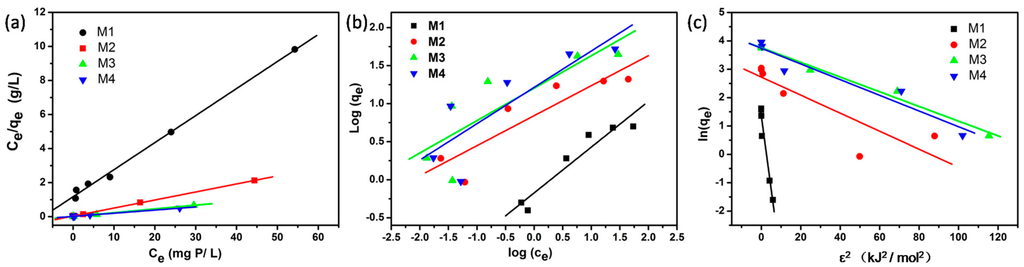
Figure 2.
Linear fitting plots of (a) Langmuir, (b) Freundlich, and (c) Dubinin-Radushkevich isotherm models for the four adsorbents (M1, M2, M3 and M4).

Table 4.
Langmuir, Freundlich and Dubinin-Radushkevich isotherm parameters obtained by linear fitting for the four adsorbents (M1, M2, M3 and M4).
| Model | M1 | M2 | M3 | M4 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Value | S.E. | Value | S.E. | Value | S.E. | Value | S.E. | ||
| Langmuir | qm (mg P/g) | 6.29 | 0.19 | 21.18 | 0.26 | 45.17 | 1.11 | 54.23 | 2.59 |
| b (L/mg P) | 0.135 | 0.018 | 1.352 | 0.442 | 1.815 | 1.01 | 0.985 | 0.524 | |
| r2 | 0.995 | - | 0.999 | - | 0.997 | - | 0.990 | - | |
| Freundlich | KF | 0.67 | 0.14 | 6.95 | 1.87 | 15.97 | 7.15 | 16.38 | 7.19 |
| n | 1.661 | 0.254 | 2.535 | 0.625 | 2.346 | 0.791 | 2.094 | 0.666 | |
| r2 | 0.916 | - | 0.806 | - | 0.701 | - | 0.714 | - | |
| Dubinin-Radushkevich | qs (mg P/g) | 3.87 | 0.63 | 15.25 | 5.82 | 42.99 | 4.83 | 42.14 | 10.74 |
| KD (mol2/kJ2) | 0.52 | 0.06 | 0.032 | 0.009 | 0.026 | 0.002 | 0.028 | 0.005 | |
| r2 | 0.946 | - | 0.688 | - | 0.980 | - | 0.900 | - | |
3.3. Comparison of Maximum Adsorption Capacities (qm)
Table 5 presents the comparison of maximum adsorption capacities (qm) of the adsorbents, which were calculated by both the linear and nonlinear Langmuir model, with other adsorbents in literatures.

Table 5.
Comparison of maximum adsorption capacities by linear and nonlinear isotherm studies.
| Adsorbents | Isotherm models | qm (mg P/g) | Da (mg P/g) | References |
|---|---|---|---|---|
| M1 | Nonlinear Langmuir | 5.92 | 0.91 | Present work |
| Linear Langmuir | 6.29 | 1.28 | ||
| M2 | Nonlinear Langmuir | 20.82 | 0.09 | Present work |
| Linear Langmuir | 21.18 | 0.27 | ||
| M3 | Nonlinear Langmuir | 44.36 | 0.06 | Present work |
| Linear Langmuir | 45.17 | 0.87 | ||
| M4 | Nonlinear Langmuir | 52.53 | 0.39 | Present work |
| Linear Langmuir | 54.23 | 2.09 | ||
| activated carbon fiber (ACF-NanoHFO) | Linear Langmuir | 12.86 | - | [3] |
| Fe-Zr binary oxide | Nonlinear Langmuir | 13.65 | - | [4] |
| aluminum pillared bentonites | Nonlinear Langmuir | 12.70 | - | [5] |
| Fe(III)-coordinated amino-functionalized SBA-15 | Linear Langmuir | 20.70 | - | [9] |
Da means the differences between the maximum adsorption capacities derived from linear or non-linear models and the experimental data.
It clearly shows that the values of qm increases in the order M4 > M3 > M2 > M1, and the qm of M4 exhibits a superior phosphate adsorption capacity, when compared to other reported adsorbents. The values of qm predicted by the linear Langmuir model (6.29, 21.18, 45.17, and 54.23 mg P/g for M1, M2, M3, and M4) are all higher than that calculated from nonlinear Langmuir model, and beyond the adsorption isotherm plateau of the experimental data. Moreover, the differences (Da) between the qm derived from linear Langmuir model and the experimental data are higher than that between the nonlinear Langmuir model and the experimental data, shown in Table 5. This indicates that, as for this adsorption system, i.e., Fe(III)-coordinated amino-functionalized mesoporous silica materials for phosphate removal, the results derived from linear fitting of the isotherm models can cause discrepancy.
4. Conclusions
The adsorption isotherm data of four different Fe(III)-coordinated amino-functionalized mesoporous silica adsorbents (M1, M2, M3, and M4) for phosphate removal were fitted to isotherm models by both non-linear regression and linear least-squares methods using Origin 8.0 software. The results showed that the Langmuir model could fit the data better than the Freundlich or Dubinin-Radushkevich models, and the determined parameters were acceptable. The values of maximum adsorption capacities estimated from Langmuir model (qm) increases in the order M4 > M3 > M2 > M1, and the qm of M4 exhibits a superior phosphate adsorption capacity than that of several other adsorbents in literatures. Although with higher r2 values, the qm of the four adsorbents estimated from linear Langmuir model were all higher than that from nonlinear Langmuir model, which were all beyond the experimental data with higher differences (Da). Therefore, it can be concluded that, as for the adsorption system of Fe(III)-coordinated amino-functionalized mesoporous silica materials for phosphate removal, the non-linear isotherm models are more powerful and viable in modeling the adsorption isotherm data.
Acknowledgements
This research was supported by Zhejiang Provincial Natural Science Foundation of China under Grant No. LQ14B070005.
Conflicts of Interest
The author declares no conflict of interest.
References
- Yuan, X.; Pan, G.; Chen, H.; Tian, B. Phosphorus fixation in lake sediments using LaCl3-modified clays. Ecol. Eng. 2009, 35, 1599–1602. [Google Scholar] [CrossRef]
- Eilbeck, W.J.; Mattock, G. Chemical Processes in Wastewater Treatment; Wiley: New York, NY, USA, 1987; pp. 12–96. [Google Scholar]
- Zhou, Q.; Wang, X.; Liu, J.; Zhang, L. Phosphorus removal from wastewater using nano-particulates of hydrated ferric oxide doped activated carbon fiber prepared by Sol-Gel method. Chem. Eng. J. 2012, 200, 619–626. [Google Scholar] [CrossRef]
- Long, F.; Gong, J.; Zeng, G.; Chen, L.; Wang, X.; Deng, J.; Niu, Q.; Zhang, H.; Zhang, X. Removal of phosphate from aqueous solution by magnetic Fe-Zr binary oxide. Chem. Eng. J. 2011, 171, 448–455. [Google Scholar] [CrossRef]
- Yan, L.; Xu, Y.; Yu, H.; Xin, X.; Wei, Q.; Du, B. Adsorption of phosphate from aqueous solution by hydroxy-aluminum, hydroxy-iron and hydroxy-iron-aluminum pillared bentonites. J. Hazard. Mater. 2010, 79, 244–250. [Google Scholar] [CrossRef]
- Rodrigues, L.; Maschio, L.; Coppio, L.; Thim, G.; da Silva, M. Adsorption of phosphate from aqueous solution by hydrous zirconium oxide. Environ. Technol. 2012, 33, 1345–1351. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.; Pham, A.N.; Xin, Y.; Waite, T.D. Effects of pH, floc age and organic compounds on the removal of phosphate by pre-polymerized hydrous ferric oxides. Sep. Purif. Technol. 2012, 91, 38–45. [Google Scholar] [CrossRef]
- Huang, W.; Li, D.; Zhu, Y.; Xu, K.; Li, J.; Han, B.; Zhang, Y. Fabrication of Fe-coordinated diamino-functionalized SBA-15 with hierarchical porosity for phosphate removal. Mater. Lett. 2013, 99, 154–157. [Google Scholar] [CrossRef]
- Huang, W.; Li, D.; Yang, J.; Liu, Z.; Zhu, Y.; Tao, Q.; Xu, K.; Li, J.; Zhang, Y. One-pot synthesis of Fe(III)-coordinated diamino-functionalized mesoporous silica: Effect of functionalization degrees on structures and phosphate adsorption. Microporous Mesoporous Mater. 2013, 170, 200–210. [Google Scholar] [CrossRef]
- Thompson, G.; Swain, J.; Kay, M.; Forster, C.F. The treatment of pulp and paper mill effluent: A review. Bioresour. Technol. 2001, 77, 275–286. [Google Scholar] [CrossRef] [PubMed]
- Langmuir, I. The constitution and fundamental properties of solids and liquids. J. Am. Chem. Soc. 1916, 38, 2221–2295. [Google Scholar] [CrossRef]
- Freundlich, H.M.F. Over the adsorption in solution. J. Phys. Chem. 1906, 57, 385–471. [Google Scholar]
- Temkin, M.I.; Pyzhev, V. Kinetics of Ammonia Synthesis on Promoted Iron Catalyst. Acta Physiochim. URSS 1940, 12, 217–222. [Google Scholar]
- Dubinin, M.M.; Radushkevich, L.V. The equation of the characteristic curve of the activated charcoal. Proc. Acad. Sci. USSR Phys. Chem. Sect. 1947, 55, 331–337. [Google Scholar]
- Foo, K.Y.; Hameed, B.H. Insights into the modeling of adsorption isotherm systems. Chem. Eng. J. 2010, 156, 2–10. [Google Scholar] [CrossRef]
- Huang, W.; Yang, J.; Zhang, Y. One-pot synthesis of mesoporous MCM-41 with different functionalization levels and their adsorption abilities to phosphate. Adv. Mater. Res. 2012, 476, 1969–1973. [Google Scholar] [CrossRef]
- Kinniburgh, D.G. General purpose adsorption isotherms. Environ. Sci. Technol. 1986, 20, 895–904. [Google Scholar] [CrossRef] [PubMed]
- Ho, Y.S. Isotherms for the sorption of lead onto peat: Comparison of linear and non-linear methods. Pol. J. Environ. Stud. 2005, 15, 81–86. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).