It from Qubit: How to Draw Quantum Contextuality †
Abstract
:1. Introduction
2. What Is a Dessin D’enfant?
2.1. The Fano Plane and Its Curve
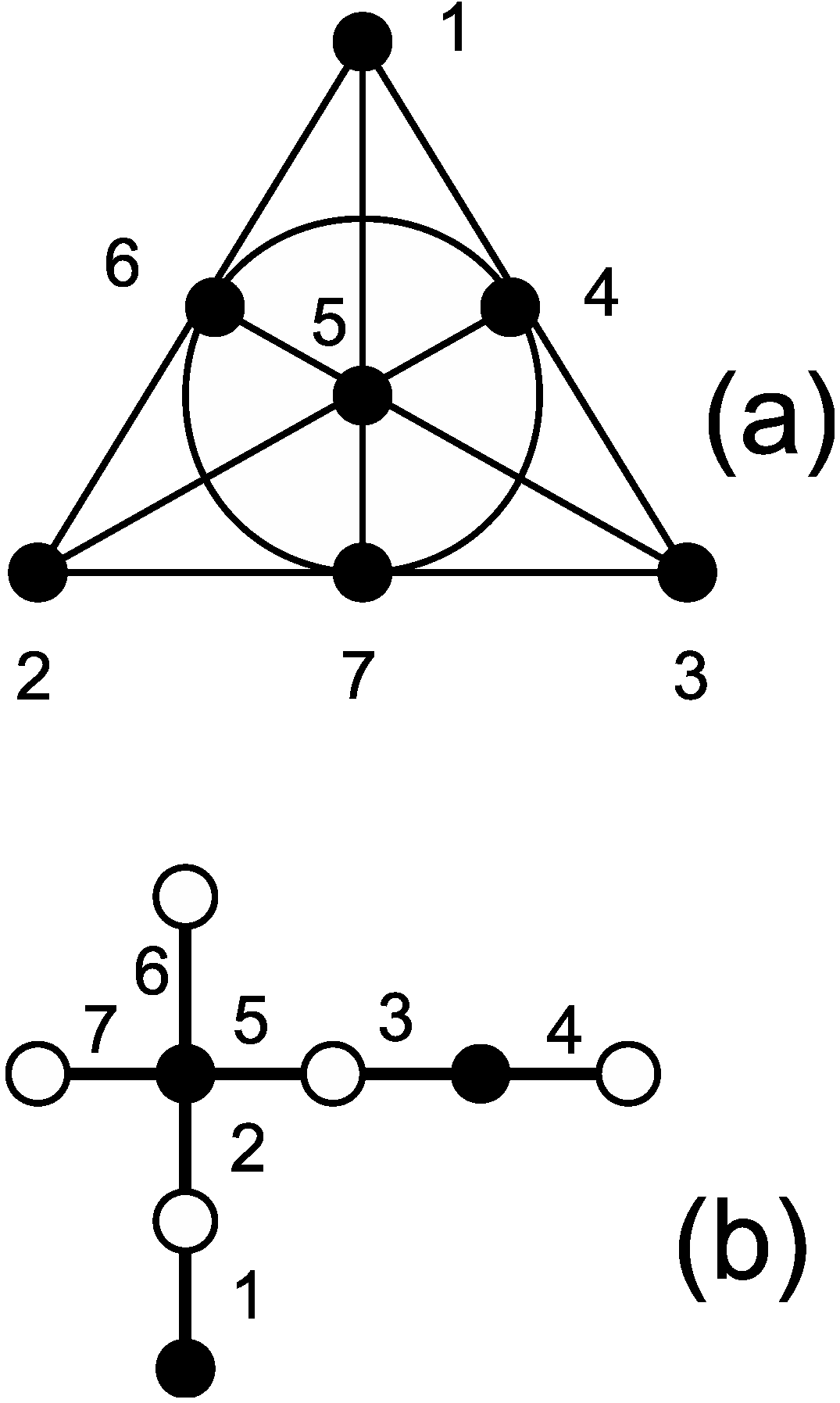
3. Dessins D’enfants, Non-Locality and Contextuality
3.1. A Dessin D’enfant for Bell’s Theorem

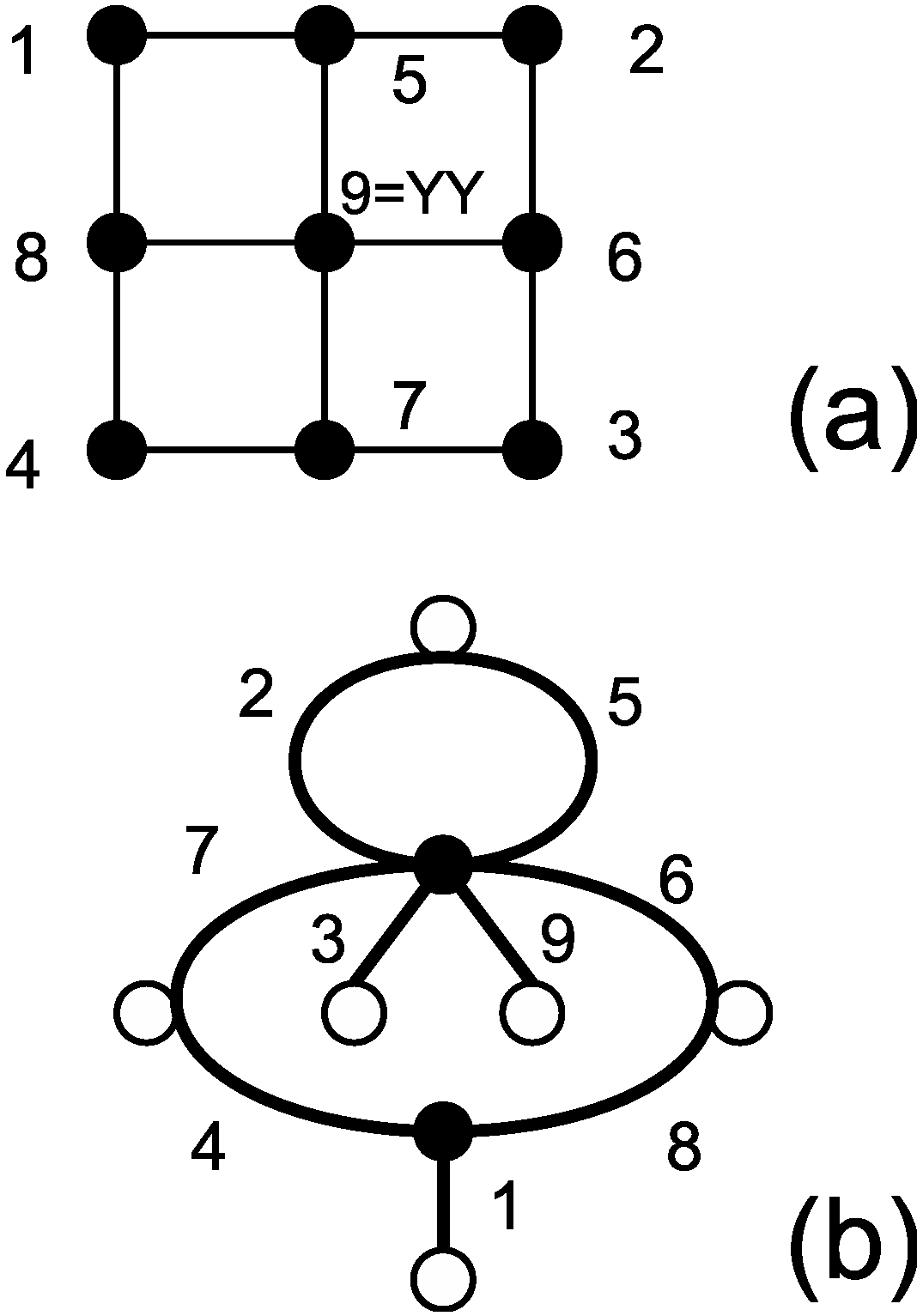
3.2. Mermin’s Square
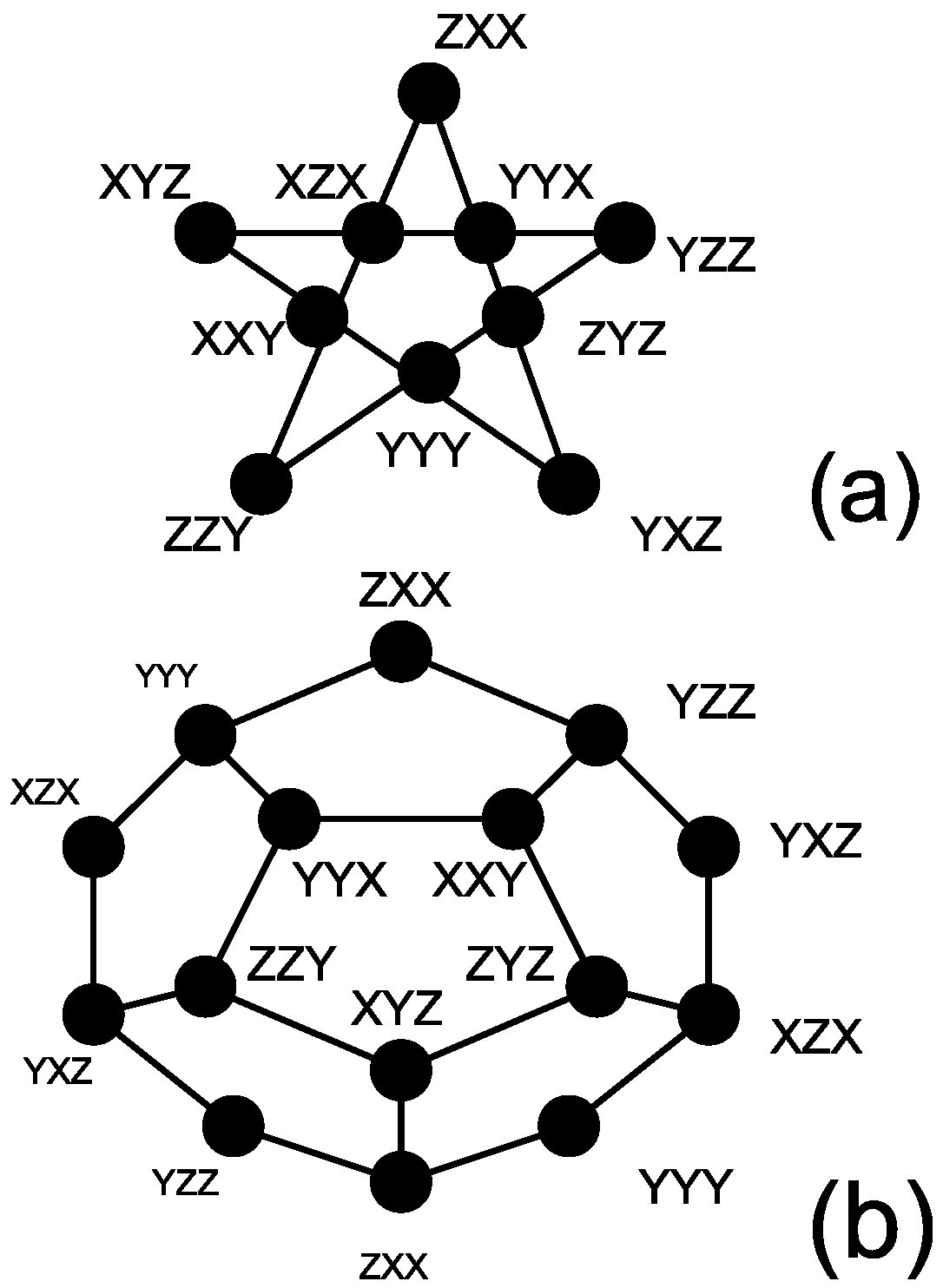
3.3. Mermin’s Pentagram
Acknowledgments
Conflicts of Interest
References
- Wheeler, J.A. Law without law. In Quantum Theory and Measurement; Wheeler, J.A., Zurek, W.H., Eds.; Princeton University Press: Princeton, MA, USA, 1983. [Google Scholar]
- Wheeler, J.A. Information, physics, quantum: The search for links. In Complexity, Entropy, and the Physics of Information; Zurek, W., Ed.; Addison-Wesley: Redwood, CA, USA, 1990. [Google Scholar]
- Bell, J.S. On the Einstein-Podolsky-Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar]
- Mermin, N.D. What’s wrong with these elements of reality. Phys. Today 1990, 43, 9–11. [Google Scholar] [CrossRef]
- Grothendieck, A. Sketch of a programme. In Geometric Galois Actions 1. Around Grothendieck’s Esquisse d’un Programme; Schneps, L., Lochak, P., Eds.; Cambridge University Press: Cambridge, UK, 1997; pp. 243–283. [Google Scholar]
- Planat, M.; Giorgetti, A.; Holweck, F.; Saniga, M. Quantum contextual finite geometries from dessins d’enfants. 2013; arXiv:1310.4267v2 [quant-ph]. [Google Scholar]
- Mermin, N.D. Hidden variables and two theorems of John Bell. Rev. Mod. Phys. 1993, 65. [Google Scholar] [CrossRef]
- Saniga, M.; Planat, M. Multiple qubits as symplectic polar spaces of order two. Adv. Studies Theor. Phys. 2007, 1, 1–4. [Google Scholar]
- Planat, M.; Saniga, M.; Holweck, F. Distinguished three-qubit ‘magicity’ via automorphisms of the split Cayley hexagon. Quant. Inf. Process. 2013, 12, 2535–2549. [Google Scholar] [CrossRef]
- Planat, M. On small proofs of the Bell-Kochen-Specker theorem for two, three and four qubits. Eur. Phys. J. Plus 2012, 127, 1–11. [Google Scholar] [CrossRef]
- Schneps, L.; Lochak, P. (Eds.) Geometric Galois Actions 2. The inverse Galois problem, Moduli Spaces and Mapping Class Groups; Cambridge University Press: Cambridge, UK, 1997.
- Schneps, L. (Ed.) The Grothendieck Theory of Dessins d’Enfants; Cambridge University Press: Cambridge, UK, 1994.
- Lando, S.K.; Zvonkin, A.K. Graphs on Surfaces and Their Applications; Springer: Berlin, Germany, 2004. [Google Scholar]
- Koch, R.M.; Ramgoolam, S. From matrix models and quantum fields to Hurwitz space and the absolute Galois group. 2010; arXiv:1002.1634v1 [hep-th]. [Google Scholar]
- Klein, F. The Icosahedron and the Solutions of Equations of the Fifth Degree; Dover: New York, NY, USA, 1956. [Google Scholar]
- Lévay, P.; Saniga, M.; Vrana, P. Three-qubit operators, the split Cayley hexagon of order two and black holes. Phys. Rev. D 2008, 78, 124022. [Google Scholar] [CrossRef]
- Peres, A. Quantum theory: Concepts and Methods; Kluwer: Dordrecht, The Netherlands, 1995. [Google Scholar]
- Flanagan, B.J. Are perceptual fields quantum fields? NeuroQuantology 2003, 1, 334–364. [Google Scholar] [CrossRef]
- Lovász, L. On the Shannon capacity of a graph. IEEE Trans. Inf. Theory 1979, 25, 1–7. [Google Scholar] [CrossRef]
- Cabello, A.; Severini, S.; Winter, A. (Non-)Contextuality of physical theories as an axiom. 2010; arXiv:1010.2163 [quant-ph]. [Google Scholar]
- Acín, A.; Fritz, T.; Leverrier, A.; Sainz, A.B. A combinatorial approach to nonlocality and contextuality. 2012; arXiv:1212.4084 [quant-ph]. [Google Scholar]
- Arkhipov, A. Extending and characterizing quantum magic games. 2012; arXiv:1209.3819 [quant-ph]. [Google Scholar]
© 2014 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Planat, M. It from Qubit: How to Draw Quantum Contextuality. Information 2014, 5, 209-218. https://doi.org/10.3390/info5020209
Planat M. It from Qubit: How to Draw Quantum Contextuality. Information. 2014; 5(2):209-218. https://doi.org/10.3390/info5020209
Chicago/Turabian StylePlanat, Michel. 2014. "It from Qubit: How to Draw Quantum Contextuality" Information 5, no. 2: 209-218. https://doi.org/10.3390/info5020209
APA StylePlanat, M. (2014). It from Qubit: How to Draw Quantum Contextuality. Information, 5(2), 209-218. https://doi.org/10.3390/info5020209



