Social Contagion and Cascade Behaviors on Twitter

Abstract

It has been found in a variety of face-to-face networks that diffusion of information, behaviors and sentiments extend up to two to four degrees of distance from the original source. This regularity has been popularized as the three degrees of influence phenomenon. Prior works have suggested a number of possible explanations to this pattern. In this paper, we study it in the context of an online network. We find similar results in this online setting to those already found offline. However, our approach suggests that two of the previously proposed explanations (increasing instability of connections at greater distances from the source and simple information decay) should not be central to explain the pattern.

1. Introduction

Studies on diffusion of communication [1], knowledge [2], behaviors [3,4,5], and sentiments [6,7,8] have consistently found that propagation vanishes beyond the third or fourth degree of separation from the original source. There are two parts in this remarkable empirical finding. On one hand, there is a claim about causation; on the other hand, there is an empirical observation about the social distance from a given subject at which a certain phenomenon is expected to be observed. Comprehensively, scholarly attention has been focused on the first part, namely, the homophily versus social contagion debate [9,10,11,12]. In this regard, recent findings based on experimental work have reinvigorated the social contagion explanation [13,14]. Nevertheless, the regularity with which the same pattern (roughly three degrees of separation) is observed in dissimilar phenomena is, in itself, a black box.

To the best of our knowledge, there are four proposed explanations for the declination of social contagion or diffusion. One is related with information decay. This could happen as a consequence of noisy communication or as a result of costly mechanisms to pass the message on. In the first case, the strength of diffusion decreases because the sender, the receptor or the message, introduces noise that increases after each new contact. In the second one, diffusion ceases spreading because the “technology” to produce it is resource-intensive (e.g., contagion of habits is time-consuming) and consequently subject to diminishing returns to scale as social distance between the original source and subjects susceptible to contagion increases. In both cases, the quality of the information declines while it travels along new ties and eventually it ceases to spread. A second explanation, network instability, is based on the dynamic of link formation. A common feature of social networks is that closer ties tend to be more stable than farther ones. Hence, an unintended consequence is that it reduces the capacity of the spreading mechanism to act on individuals at longer distances [9]. In this case, it is not the declination of the quality of the information what stops the diffusion, but the instability of the topology of the network that prevents the phenomenon to spread farther. A third alternative rests on an evolutionary argument of the limited attention that human subjects bestow on others, making influence by and over other individuals to be possible in relatively small groups. Thus, even when the strength of the phenomenon does not decline and the topology of the network is stable, the diffusion can cease because the phenomenon has reached individuals that are not susceptible to being influenced by it. Finally, there is an explanation based on competition. Individuals have limited attention capabilities and propagations coming from longer social distances have more substitutes and competition, diminishing contagion [15]. Thus, even in a world inhabited by fully-susceptible individuals, all contingent diffusion processes cannot succeed at the same time.

Which one of these mechanisms is the underlying explanation of the two to four degrees of separation observed in the social contagion literature? Suppose that we believe that the correct answer is, say, the first alternative. If we study a social phenomenon in which that alternative is not binding and we observe that the diffusion process is reaching significantly further social distances than those found to other phenomena; then, we will reinforce our prior belief. The contrary will also happen if the phenomenon follows the same pattern as other cases, despite the fact that our preferred explanation is not binding. In this paper, we study whether the propagation phenomenon observed in face-to-face networks is also observable in certain given online networks. However, at the same time, we choose a particular online behavior that, we claim, happens in conditions in which two of the above proposed explanations should not be binding or, at least, must be less so than in other phenomena. The behavior studied is the practice of retweeting.

We claim that the retweeting of tweets is a case in which the first two proposed explanations (information decay and network instability) are less restrictive than in other phenomena. Consequently, if one is the underlying cause of the decline of social contagion beyond a few degrees of social distance, we should expect that the social distances travelled by retweeted tweets should be consistently greater than three or four degrees. Our results did not show such a change in the pattern and, therefore, provide evidence against “information decay” and/or “network instability” as core explanations of the phenomenon.

2. Related Work

Twitter is a directed social graph on internet in which users share opinions and information (tweets) with whoever follows them. To follow another user means to receive his or her messages (tweets) in chronological order on your screen. Those tweets plus other tweets received from other users whom you also follow form your timeline. Each user can retweet (resend) tweets written by someone else just by pressing a button. As a result, a tweet can travel from user to user along the social graph. Through case studies, Boyd et al. [16] have studied the conversational aspects of retweeting. They map several conventions that Twitter users have adopted to post messages originally posted by others, including shortening retweets through deletion, attribution of authorship (i.e., adding “via @user” into their own messages), and retweeting tweets without altering them. Other works have tried to explain why some tweets are retweeted and others are not [17,18,19]. These studies have found that retweetability increases when tweets contains URLs or hashtags, when they have been written by greater connected users (users with more followers and friends), when authors have been already included on lists made by other users; when their accounts are relatively older ones; and when the topic is one in which the retweeter does not usually write about. None of those studies have focused their attention on the social distance at which sender and her retweeters are located in the topology of the followers-following networks. To the best of our knowledge, Goel et al. [20] is the only work that has previously looked at this aspect. They study diffusion networks in several online domains including tweets containing links to articles originally posted by one of five popular news sites (The New York Times, CNN, MSNBC, Yahoo! News and The Huffington Post) or links to YouTube videos. Although their work is focused on the diffusion of shared links rather than the diffusion of particular messages (as we do), their findings are consistent with those presented below.

The dynamic of retweets occurs over short periods of time after the original message was created [21], during that short period of time, the network of followers/following users is essentially fixed. Consequently, we propose that the practice of retweeting a tweet happens in a fundamentally stable environment in which some conditions for information decay are less restrictive. Consequently, retweeting is a good example of a next to costless diffusion process in a stable social graph. Information decay in the spreading mechanism and instability of the social graph, therefore, should not be seen as binding a restriction as they are in other settings and, therefore, we should expect the spread of retweeted tweets along Twitter’s social graph to reach greater social distances than those found in social phenomena where those restrictions are supposedly active.

Before we move forward, it is important to explain that there are at least two other alternative ways to measure social distances on Twitter. The first one is based only in the structural network of followers/followees. Measures of social distance based solely on the network of followers and followees without any consideration of the behavioral aspects of tweeters are not optimal for studying the spread of tweets. The overcrowding of spam bots and inactive twitter accounts could bias the results. Indeed, the company itself does not recommend the use of followers count as a measure of centrality, considering retweets as a better metric of influence [22]. The second one is the use of favorited tweets or FAVs tweets. Originally, favorited tweets were a private feature; as a consequence, diffusion of tweets could only reach one degree of social distance. During 2012, Twitter enabled reading followees’ activity, allowing this feature to extend to a longer distance. At the time of our data collection, this feature was new; hence results may be biased against the spread of diffusion. Moreover, the mechanism for collecting FAVs is slower than the one used to obtain retweets. For both these reasons, we decided to focus the inquiry on retweeting as the key behavior through which diffusion occurs on Twitter.

3. Method and Data Collection

We have taken a conservative approach to the process of information diffusion via retweets. Specifically, we have focused our attention on native mechanisms of retweeting, which means we will consider any tweet that Twitter API identifies as a retweeted tweet as such. We selected this operationalization to observe cases of pure contagion of information in which the costs of resending a message are at their minimal possible level. Recent work [16,23,24] has suggested broader definitions of retweeting behavior and it is a matter of future research to test whether the results presented here remain valid in those cases.

To study the social distance travelled by retweeted tweets, it is necessary to collect information about tweeters and retweeters and the follower/following graph linking them. To accomplish this task, Twitter provides three ways to gain access to large amounts of tweets and users’ accounts. These are: streaming API for real-time tweets, search API for past tweets and REST API for specific queries about tweets and users. The first does not have significant restrictions on the amount of queries; unlike the second and third. In particular, the REST API has a limit of 350 calls per hour. For large datasets, this rate limit can incur significant gaps between the time at which a tweet was written and the time at which information from the tweeter and retweeters is retrieved. Such a possibility can artificially introduce instability in the follower/following graph. For this reason, we complement the REST API calls with an external proxy service called Apigee [25] that allowed us to continue performing queries after the depletion of our API calls on the official Twitter service. Apigee is a free proxy server that allows indirect connections to Twitter API (and other social networks API) through whitelisted servers. Whitelisting was a feature of the first years of Twitter that allowed a higher rate limit. Despite being deprecated in 2011, the existing whitelisted servers, such as Apigee, were still working at the time of our data collection. This platform allows duplicating the original calls using a proxy server and, without authentication, getting an unlimited amount of calls to some resources. However, as a proxy server, the responses are slower than the original API, especially in the case of unauthenticated calls (at the time of this research apigee was still working, but it is important to mention that Twitter announced that starting from version 1.1 of its API all calls must be authenticated).

Data collection was carried out in four steps. Actual dates of data collection are detailed in Table 1. In Step 1, through Twitter Streaming API (at Spritzel 1% level), we downloaded samples of tweets. We had two alternatives. On one hand, we could select only retweeted tweets. This options faces a bias to popular tweets: in spite of the fact that most retweets are sent when little time has passed from the original message [20,21], popular tweets can be retweeted for longer periods. On the other hand, we could just collect tweets and in a later step verify whether each of them was or was not retweeted. The potential bias of this alternative is to truncate some diffusion trees. Our methodological decision was to follow the second choice, but through two samples covering different periods of time. The first sample was during a one-day window and the second one was during a ten-day period. As shown below (Table 2), there is no-significant difference between both samples in terms of proportion of retweets. This suggests that the potential bias was negligible.

Consequently, we obtained random samples of tweets in real-time periods of one day (1 June 2012) and ten days (22 August 2012 to 31 August 2012). We generated two datasets of 3,589,079 and 33,247,877 tweets, respectively (Table 1).

Table 1. Dates and steps used to collect and analyze retweeted tweets.

Steps	Dates	No. of tweets	Dates	No. of tweets
Step1: Streaming	30 June 2012	3 million	22–31 August 2012	33 million
Step2: Filtering	4–9 July 2012	13,946	5–18 September 2012	20,243
Step3:Computing social distance	9–10 July 2012	–	18 September–3 October 2012	–

Table 1. Dates and steps used to collect and analyze retweeted tweets.

Steps	Dates	No. of tweets	Dates	No. of tweets
Step1: Streaming	30 June 2012	3 million	22–31 August 2012	33 million
Step2: Filtering	4–9 July 2012	13,946	5–18 September 2012	20,243
Step3:Computing social distance	9–10 July 2012	–	18 September–3 October 2012	–

In Step 2, we worked with random subsamples of 400,000 tweets from each dataset for further analysis. The reason was to avoid taking months to recover the followers-following social graph. Taking a long period of time to recover the following-follower social graph is risky because the observed graph is more likely to have changed between the moment the original tweet was sent and the instance in which the underlying social graph was generated. This limitation is caused by the rate limit for calls that Twitter imposes on access to its REST API and the slower responses from Apigee. For each tweet, we collected information about the time at which it was created, its sender, location (if given) and other kinds of information.

In the third step, using Twitter REST API, we verified whether each tweet was retweeted and recorded its information including the list of its retweeters. From each sample of 400,000 tweets, we obtained subsamples of 13,946 (3.5%) and 20,278 (5%) retweeted tweets from the one-day and ten-day datasets, respectively. These proportions are consistent with those found in previous studies [17]. Results obtained from both samples are similar. Approximately, three fourths of retweeted tweets were retweeted once, 12.6% were retweeted twice and 11% three or more times (see Table 2). With that information, we recover the follower-following subgraphs connecting all Twitter’s accounts that participate in the diffusion of each retweeted tweet [26]. It is important to notice that this method to recover social distances over Twitter’s graph might overestimate the social distances in favor of longer paths. This may be because some accounts that did not participate in the diffusion of a tweet might provide shorter paths between the tweeter and some of his or her retweeters and those paths will be missed. As we will elucidate in the next section, when we mostly found short cascades, this bias reinforces our claim against the network instability and information decay as central explanations of the phenomenon.

In order to compare the pattern of retweeting in our dataset with those studied elsewhere [17,19], we fit a logit model to explain the probability of being retweeted based on a set of social features (number of followers, friends and statuses) and tweet features (having URLs, hashtags and/or mentions). Table 3 reports the odd-ratios estimated by the model. In general, the model qualitatively reproduces findings of previous studies: users with greater numbers of followers and followees have higher odds of being retweeted; the same happens for tweets with hashtags. Conversely, tweets containing mention of other users have a lower probability of being retweeted. Statuses (times that a given user have written tweets) does not seem to have any impact on retweeting probability. The only feature in which our sample departs from previous findings is in the use of URLs.

Table 2. Number of retweets.

No. of times retweeted	Over 400,000 obtained in a 1-day sample	Over 400,000 obtained in a 10-day sample
	(N = 13,946) (%)	(N = 20,278) (%)
1	76.40	75.83
2	12.63	12.64
3	4.46	4.35
4	2.05	2.03
5	1.13	1.16
6	0.62	0.68
7	0.38	0.46
8	0.32	0.37
9	0.24	0.25
10	0.12	0.23
11 to 99	1.65	2.01

Table 2. Number of retweets.

No. of times retweeted	Over 400,000 obtained in a 1-day sample	Over 400,000 obtained in a 10-day sample
	(N = 13,946) (%)	(N = 20,278) (%)
1	76.40	75.83
2	12.63	12.64
3	4.46	4.35
4	2.05	2.03
5	1.13	1.16
6	0.62	0.68
7	0.38	0.46
8	0.32	0.37
9	0.24	0.25
10	0.12	0.23
11 to 99	1.65	2.01

Table 3. Logit model for retweeted tweets. Odd-ratios and confidence intervals dependent variable: Retweeted tweet (1=Yes, 0= No).

Explanatory variables	Odd-Ratio	2.50%	97.50%
(Intercept)	0.0777794	0.07611414	0.07947813
Number of followers	1.0000087	1.00000748	1.00000988
Number of followees	1.0000224	1.00001758	1.00002721
Number of tweets (statuses) written by the user	1.0000001	0.99999962	1.00000052
Tweet has URLs	0.6617889	0.63148622	0.69322556
Tweet has mentions to other users	0.7396045	0.7175983	0.76224258
Tweet has hashtags	1.6323656	1.56797174	1.69894442

Table 3. Logit model for retweeted tweets. Odd-ratios and confidence intervals dependent variable: Retweeted tweet (1=Yes, 0= No).

Explanatory variables	Odd-Ratio	2.50%	97.50%
(Intercept)	0.0777794	0.07611414	0.07947813
Number of followers	1.0000087	1.00000748	1.00000988
Number of followees	1.0000224	1.00001758	1.00002721
Number of tweets (statuses) written by the user	1.0000001	0.99999962	1.00000052
Tweet has URLs	0.6617889	0.63148622	0.69322556
Tweet has mentions to other users	0.7396045	0.7175983	0.76224258
Tweet has hashtags	1.6323656	1.56797174	1.69894442

In the fourth and final step, we calculated the degree of separation between the tweet sender and the more distant retweeter (i.e., the eccentricity). From each list of retweeters of a tweet plus its original sender, we built the following-follower graph connecting them. This means that we recovered the complete topology for each retweeted tweet and obtained the distance between the original sender and its most distant retweeter. Results are shown in the next section.

4. Results and Discussion

A total of 13,946 and 20,278 social subgraphs of follower/following relationships were made (see some examples in Figure 1) and, for each one, we calculated the eccentricity of the tweeter’s tweet (i.e., the longest geodesic connecting each tweeter with the set of the retweeters of his/her tweet). Remarkably, the social distances traveled by retweeted tweets are in the same range found for other phenomena in literature on social contagion (see Table 4).

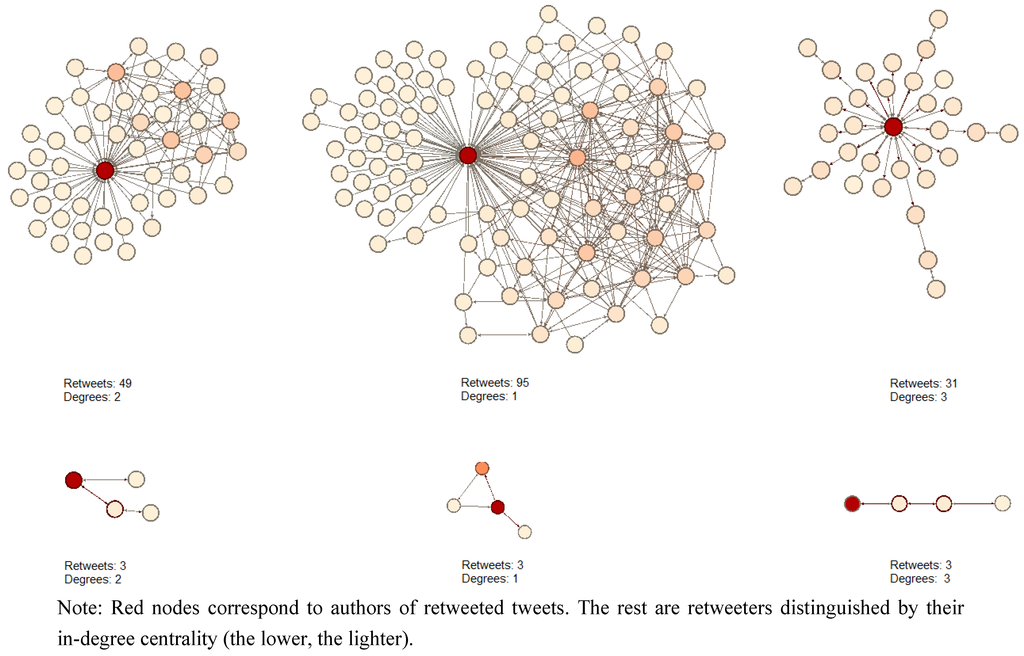
Figure 1. Examples of following/followers social graphs of retweeted tweets.

Figure 1. Examples of following/followers social graphs of retweeted tweets.

Table 4. Social distance traveled by retweeted tweets.

Social distance of retweets (%)	1-day sample	10-day sample
1 degree	86.25	83.24
2 degrees	6.92	7.11
3 degrees	1.12	1.38
4 degrees	0.21	0.31
5 to 9 degrees	0.19	0.14
Disconnected	4.62	7.81

Table 4. Social distance traveled by retweeted tweets.

Social distance of retweets (%)	1-day sample	10-day sample
1 degree	86.25	83.24
2 degrees	6.92	7.11
3 degrees	1.12	1.38
4 degrees	0.21	0.31
5 to 9 degrees	0.19	0.14
Disconnected	4.62	7.81

Despite the fact that our method to calculate social distances might overestimate them, we found that 94.5% and 91.7% of retweeted tweets in the 1-day and 10-day samples traveled short distances of three or less degrees of separation from the original source (Figure 2, Figure 3). In both cases, distances equal to or greater than four degrees were reached by less than 0.4% of retweeted tweets. The remaining portions correspond to retweets made by users not directly connected with the original sender (for example, users who retweeted tweets from lists or public timelines). Hence, even in cases with a significant number of retweets, we find that audiences remain fundamentally local.

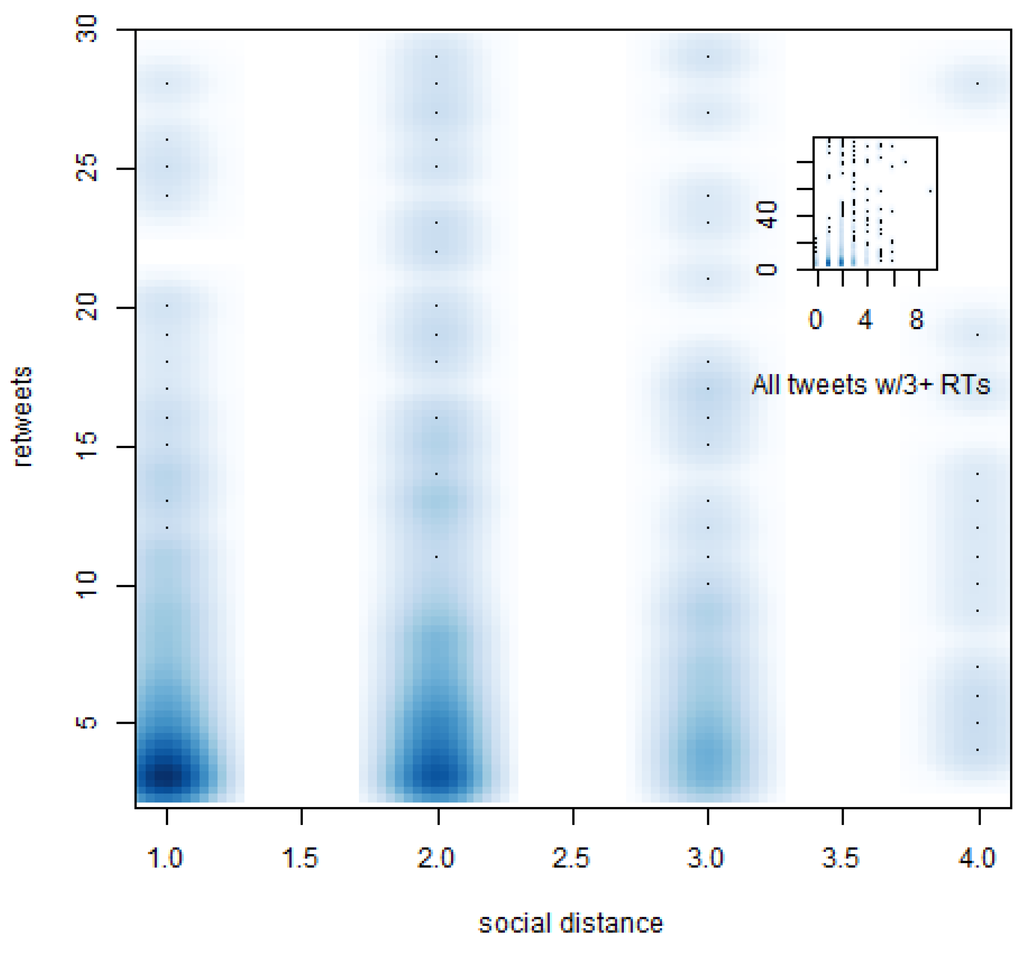
Figure 2. Density plot of social distance travelled by retweeted tweets by number of retweets (1-day sample).

Figure 2. Density plot of social distance travelled by retweeted tweets by number of retweets (1-day sample).

Figure 3. Density plot of social distance travelled by retweeted tweets by number of retweets (10-day sample).

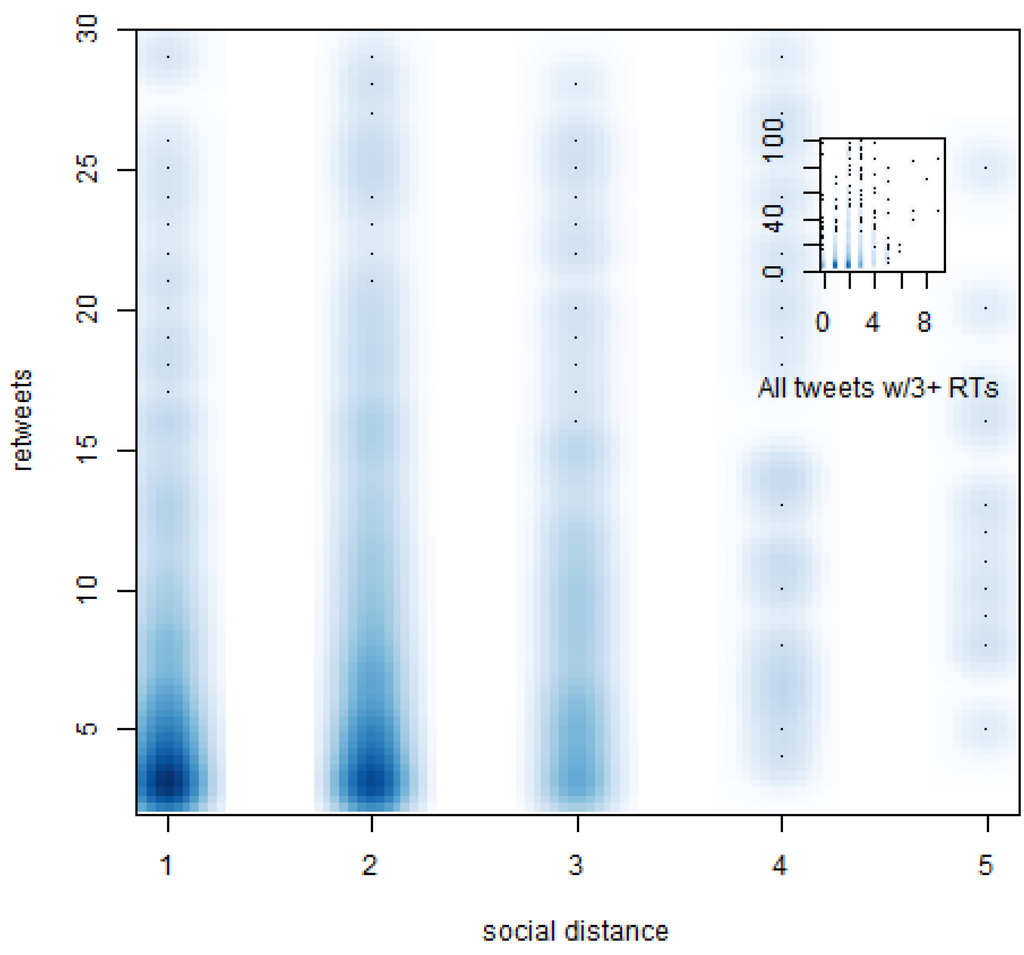
Figure 3. Density plot of social distance travelled by retweeted tweets by number of retweets (10-day sample).

From the perspective of a theory of diffusion of communication, our findings suggest that, at least in online social networks, propagation does not extend to greater distances even when the mechanism of diffusion does not become weaker at greater distances and the dynamic of link formation and destruction is held constant, such that the reachability of individuals located at greater distances does not change. Consequently, we are inclined to think that network instability and information decay should not be core explanations for the local features that diffusion shows in online domains.

However, is limited propagation a contagion-like or a homophily-like process? The decline in the diffusion process at further distances could simply be because dissimilar individuals are located at larger social distances from each other. Such a possibility would be consistent with our results and they would imply that the practice of retweeting is a case of homophily rather than social contagion. Nevertheless, recent work [18,27] offers contrary evidence, suggesting greater levels of anti-homophily in retweeting behaviors. That is an opened question for further research: To explain why—even in online social networks—diffusion usually stops within roughly three degrees of distance.