Abstract
A multi-layered perceptron type neural network is presented and analyzed in this paper. All neuronal parameters such as input, output, action potential and connection weight are encoded by quaternions, which are a class of hypercomplex number system. Local analytic condition is imposed on the activation function in updating neurons’ states in order to construct learning algorithm for this network. An error back-propagation algorithm is introduced for modifying the connection weights of the network.
1. Introduction
Processing multi-dimensional data is an important problem for artificial neural networks. A single neuron can take only one real value as its input, thus a network should be configured so that several neurons are used for accepting multi-dimensional data. This type of configuration is sometimes unnatural in applications of artificial neural networks to engineering problem, such as processing of acoustic signals or coordinates in the plane. Thus, complex number systems have been utilized to represent two-dimensional data elements as a single entity. Application of complex numbers to neural networks have been extensively investigated, as summarized in the references [1,2,3].
Though complex values can treat two-dimensional data elements as a single entity, what we should treat data with more than two-dimension in artificial neural networks? Although this problem can of course be solved by applying several real-valued or complex-valued neurons, it would be useful to introduce a number system with higher dimensions, the so-called hypercomplex number systems.
Quaternion is a four-dimensional hypercomplex number system introduced by Hamilton [4,5]. This number system has been extensively employed in several fields, such as modern mathematics, physics, control of satellites, computer graphics, etc. [6,7,8]. One of the benefits provided by quaternions is that affine transformations of geometric figures in three-dimensional spaces, especially spatial rotations, can be represented compactly and efficiently. Applying quaternions to the field of neural networks has been recently explored in an effort to naturally represent high-dimensional information, such as color and three-dimensional body coordinates, by a quaternionic neuron, rather than complex-valued or real-valued neurons.
Thus, there has been a growing number of studies concerning the use of quaternions in neural networks. Multilayer perceptron (MLP) models have been developed in [9,10,11,12,13,14]. The use of quaternion in MLP models has been applied to several engineering problems such as control problems [10], color image compression [12], color night vision [15,16], and predictions for the output of chaos circuits and winds in three-dimensional space [13,14]. Other types of network models has also been explored, such as the computational ability of a single quaternionic neuron [17] and the existence condition of an energy function in continuous-time and continuous-state recurrent networks [18]. There are several types of quaternionic Hopfield-type networks with discrete-time driven, such as bipolar state [19,20], continuous state [21,22], multistate by phase representation [23,24]. Learning schemes for these networks have also been proposed in [25].
One of the difficulties in constructing neural networks in the quaternionic domain is about the introduction of suitable functions for the activation function in updating the neurons’ states. A typical type of activation function is the so-called “split” type function, in which a real-valued function is appliedto update each component of a quaternionic value [10]. Real-valued sigmoidal function and hyperbolic function, which are analytic (differentiable) functions, are often used for this purpose. However, as an activation function, the split-type quaternionic function is not appropriate due to lack of analyticity. Thus, it is necessary to define other types of differential functions in order to construct learning schemes such as the error back-propagation algorithm. The Cauthy-Riemann-Fueter (CRF) equation defines the analytic condition for the quaternionic functions, which corresponds to the Cauthy-Riemann equation for the complex-valued functions. The functions satisfying the CRF equation turn out to be only linear functionsor constants; therefore it is impossible to introduce non-linearity into the updates of the neurons’ states.
Recently, another class of analyticity for the quaternionic functions has been developed [26,27,28]. Called “local analyticity”, this analytic condition is derived at a quaternionic point with its local coordinate, rather than in a quaternionic space with a global coordinate. The derivation of local analytic condition shows that a quaternion in the local coordinate system is isomorphic to the complex number system and thus it can be treated as a complex value. A neural network with an activation function with local analyticity has been first proposed and analyzed in [13,14] in terms of MLP-type network. It is shown that the performance for this network is superior to the network with a split-type activation function through several applications. Another application of analytic activation function to quaternionic neural networks has been investigated in terms of Hopfield-type network [22]. The local analytic condition is constructed based on [28], and the stability conditions are derived in the case of quaternionic tanh function being used for an activation function is deduced in this network, in which the complex-valued tanh function used in [29] can be used as a quaternionic function.
This paper presents an MLP-type quaternionic neural network with locally analytic activation function. All variables in this network, such as input, output, action potential and connection weights, are encoded by quaternions. A learning scheme, a quaternionic equivalent of error back-propagation algorithm, is presented and theoretically explored. The derivation of the learning scheme in this papera dopts the Wirtinger calculus [30], which has been invented in the field of complex analysis, where a quaternionic value and its conjugate are treated independent of each other. This calculus enables the derivations to be more straightforward of its description, than by using the conventional description, i.e., Cartesian representation.
2. Quaternionic Algebra
2.1. Definition of Quaternion
Quaternions forma class of hypercomplex numbers consistingofareal number and three imaginary numbers-i, j, and k. Formally, a quaternion number is defined as a vector x in a four-dimensional vector space,
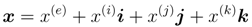 where x(e), x(i), x(j), and x(k) are real numbers. The division ring of quaternions, H, constitutes the four-dimensional vector space over the real numbers with bases 1, i, j, and k. Equation (1) can also be written using 4-tuple or 2-tuple notation as
where x(e), x(i), x(j), and x(k) are real numbers. The division ring of quaternions, H, constitutes the four-dimensional vector space over the real numbers with bases 1, i, j, and k. Equation (1) can also be written using 4-tuple or 2-tuple notation as
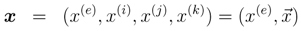 where
where 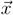 = { x(i), x(j), x(k)}. In this representation, x(e) is the scalar part of x, and
= { x(i), x(j), x(k)}. In this representation, x(e) is the scalar part of x, and 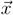 forms the vector part. The quaternion conjugate is defined as
forms the vector part. The quaternion conjugate is defined as
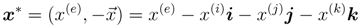
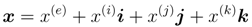
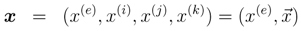
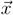 = { x(i), x(j), x(k)}. In this representation, x(e) is the scalar part of x, and
= { x(i), x(j), x(k)}. In this representation, x(e) is the scalar part of x, and  forms the vector part. The quaternion conjugate is defined as
forms the vector part. The quaternion conjugate is defined as
Quaternion bases satisfy the following identities,
 known as the Hamilton rule. From these rules, it follows immediately that multiplication of quaternions is not commutative.
known as the Hamilton rule. From these rules, it follows immediately that multiplication of quaternions is not commutative.
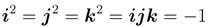
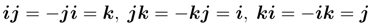
Next, we define the operations between quaternions p = (p(e), 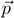 ) = (p(e), p(i), p(j), p(k)) and q = (q(e),
) = (p(e), p(i), p(j), p(k)) and q = (q(e), 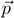 ) = (q(e), q(i), q(j), q(k)). The addition and subtraction of quaternions are defined in a similar manner as for complex-valued numbers or vectors, i.e.,
) = (q(e), q(i), q(j), q(k)). The addition and subtraction of quaternions are defined in a similar manner as for complex-valued numbers or vectors, i.e.,
 ) = (p(e), p(i), p(j), p(k)) and q = (q(e),
) = (p(e), p(i), p(j), p(k)) and q = (q(e),  ) = (q(e), q(i), q(j), q(k)). The addition and subtraction of quaternions are defined in a similar manner as for complex-valued numbers or vectors, i.e.,
) = (q(e), q(i), q(j), q(k)). The addition and subtraction of quaternions are defined in a similar manner as for complex-valued numbers or vectors, i.e.,
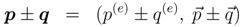
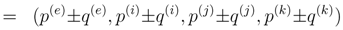
The product of p and q is determined by Equation (5) as
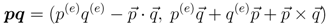 where
where 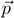 ·
· 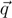 and
and 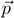 ×
× 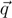 denote the dot and cross products, respectively, between three-dimensional vectors
denote the dot and cross products, respectively, between three-dimensional vectors 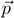 and
and 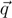 . The conjugate of the product is given as
. The conjugate of the product is given as
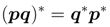
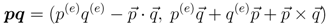
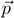 ·
· 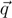 and
and 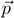 ×
× 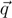 denote the dot and cross products, respectively, between three-dimensional vectors
denote the dot and cross products, respectively, between three-dimensional vectors 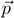 and
and 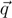 . The conjugate of the product is given as
. The conjugate of the product is given as
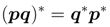
The quaternion norm of x, denoted by |x|, is defined as
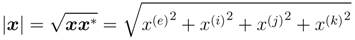
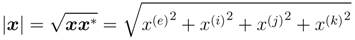
2.2. Quaternionic Analyticity
It is important to introduce an analytic function (or differentiable function) to serve as the activation function in the neural network. This section describes the required analyticity of the function in the quaternionic domain, in order to construct activation functions for quaternionic neural networks.
The condition for differentiability of the quaternionic function f is given by
The analytic condition for the quaternionic function, called the Cauchy-Riemann-Fueter (CRF) equation, yields:
This is an extension of the Cauchy-Riemann (CR) equations defined for the complex domain. However, only linear functions and constants satisfy the CRF equation [14,26,27].
An alternative approach to assure analyticity in the quaternionic domain has been explored in [26,27,28]. This approach is called local analyticity and is distinguished from the standard analyticity, i.e., global analyticity. In the following, we introduce local derivatives with Wirtinger representation and analytic conditions for quaternionic functions, with reference to [28].
A quaternion x can be alternatively represented as:
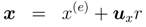
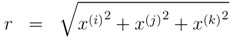
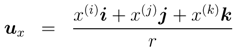
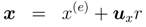
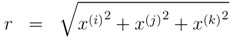
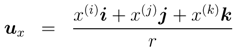
From the definition in Equation (15), we deduce that u2 x = −1. If ux holds a commutative property against a difference of x, then the system with ux can be regarded as locally isomorphic to the complex number system.
A quaternionic difference of x, denoted by dx =(dx(e), dx(i), dx(j), dx(k)), can be decomposed by using:
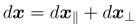 where,
where,
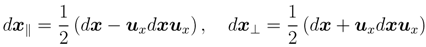
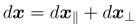
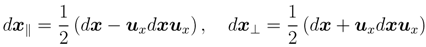
Then, the following relations hold:
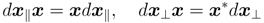 when we set dx⊥ = 0, i.e., dx + uxdxux = 0,which results in uxdx = dxux. This leads to ux × d
when we set dx⊥ = 0, i.e., dx + uxdxux = 0,which results in uxdx = dxux. This leads to ux × d 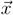 =0, because ux is a quaternion without a real part. Thus, ux and d
=0, because ux is a quaternion without a real part. Thus, ux and d 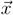 are parallel to each other. Then, d
are parallel to each other. Then, d 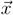 = uxδ can be obtained, where δ is a real-valued constant. From Equation (14), it follows that
= uxδ can be obtained, where δ is a real-valued constant. From Equation (14), it follows that
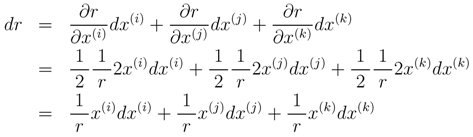
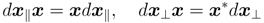
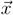 =0, because ux is a quaternion without a real part. Thus, ux and d
=0, because ux is a quaternion without a real part. Thus, ux and d 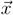 are parallel to each other. Then, d
are parallel to each other. Then, d 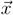 = uxδ can be obtained, where δ is a real-valued constant. From Equation (14), it follows that
= uxδ can be obtained, where δ is a real-valued constant. From Equation (14), it follows that
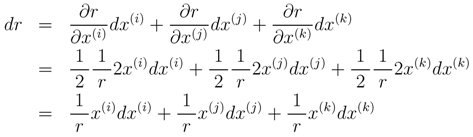
Then,
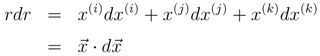
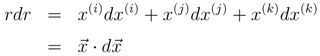
Considering 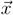 = uxr and d
= uxr and d 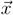 = uxδ, we obtain
= uxδ, we obtain
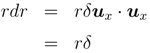
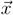 = uxr and d
= uxr and d 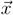 = uxδ, we obtain
= uxδ, we obtain
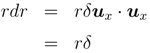
Hence, δ = dr is derived and d 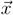 = uxdr is obtained. dx is represented as
= uxdr is obtained. dx is represented as 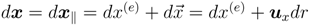 .
.
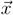 = uxdr is obtained. dx is represented as
= uxdr is obtained. dx is represented as 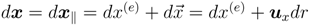 .
.Figure 1 shows a schematic coordinate system for defining a local complex plane. The component k is omitted (x(k) = 0) in this figure due to difficulties in representing a four-dimensional vector space. In this example, for a given quaternion x, its unit vector ux is defined in the i-j plane. Then, a complex plane is defined by spanning the components x(e)(real axis) and x(r) in the quaternionic space, and the analytic condition is constrained in this plane.
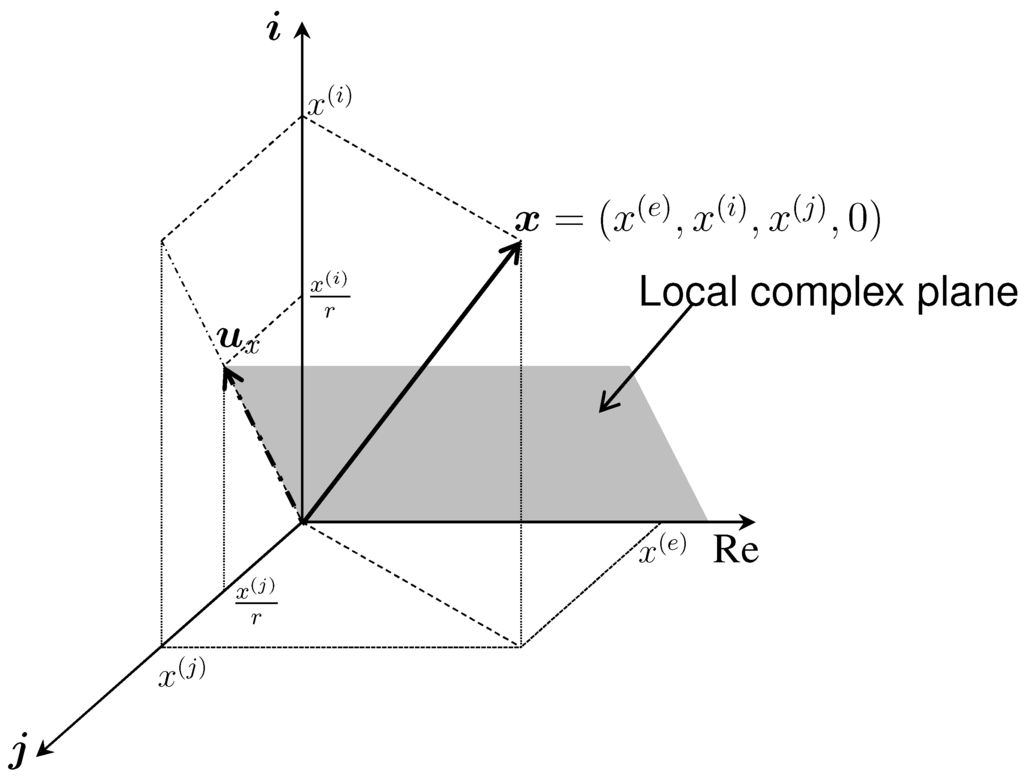
Figure 1.
A schematic illustration of local complex plane in a quaternionic space, where the component k is omitted for simplicity.
The local derivative operators are introduced, corresponding to the form of dx‖, as follows:
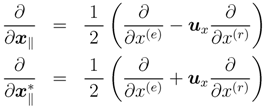 where
where
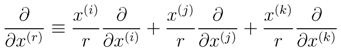 with the properties
with the properties
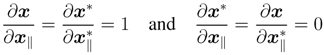
Note that the variables x and x∗ turn out to be independent of each other. These derivative operators are quaternionic equivalents to the well-known Wirtinger derivative in the complex domain [30].
F (x + dx) can be expanded using the above-mentioned representations as
 where,
where,
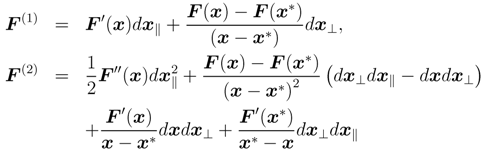
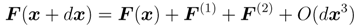
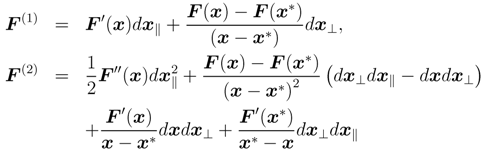
When dx⊥ = 0, the local derivative of F (x) is written as
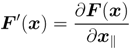 and the local analytic condition for the function F (x) is given by
and the local analytic condition for the function F (x) is given by
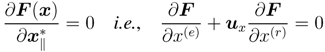 in the corresponding local complex plane. This result corresponds to the one presented in [27], where dx⊥ =0 always holds.
in the corresponding local complex plane. This result corresponds to the one presented in [27], where dx⊥ =0 always holds.
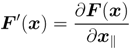
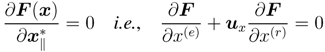
Moreover, if F is a function with the two arguments, x and x∗, it becomes:
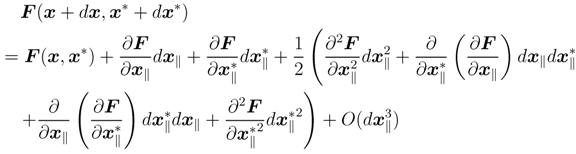 with x and x∗ being independent of each other. As a result, we can treat quaternionic functions in the same manner as complex-valued functions under the condition of local analyticity.
with x and x∗ being independent of each other. As a result, we can treat quaternionic functions in the same manner as complex-valued functions under the condition of local analyticity.
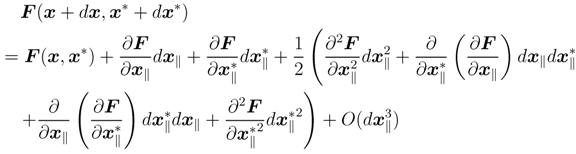
3. Quaternionic Multilayer Perceptron
3.1. Network Model
The structure of the network assumed in this paper is shown in Figure 2. This network is a so-called multilayer perceptron network with one hidden layer, and the parameters in the network are encoded by quaternionic values.
The numbers of neurons in the input, hidden and output layers are set to M, N and K, respectively. A set of quaternionic signals denoted by z is input to the neurons in the input layer of the network. The outputs of the neurons in the input layer are the same as input z’s. In the hidden layer, each neuron takes the weighted sum of the output signals from the input layer. The (connection) weight from the n-th neuron in the input layer to the m-th neuron in the hidden layer is denoted by vnm. The output of the neuron in the hidden layer, denoted by xn, is determined by
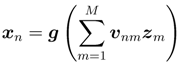 where g is a quaternionic activation function introducing non-linearity between the action potential and output in the neuron. This function satisfies the following condition:
where g is a quaternionic activation function introducing non-linearity between the action potential and output in the neuron. This function satisfies the following condition:
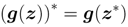
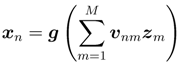
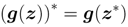
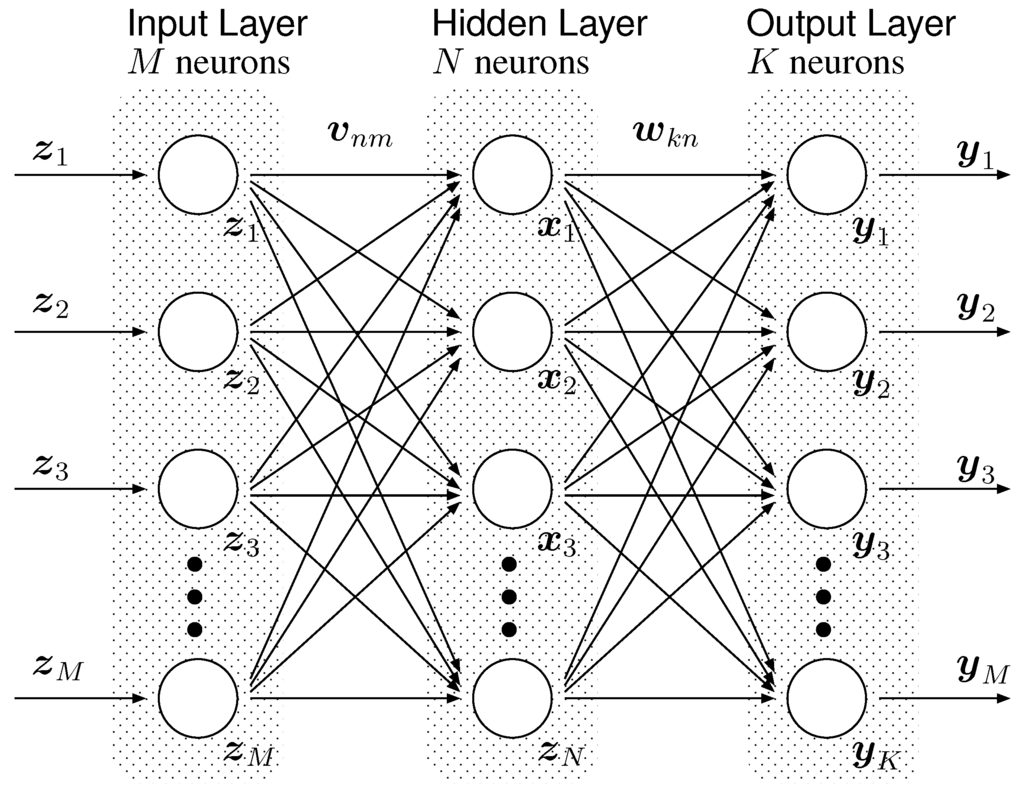
Figure 2.
The structure of the multilayer perceptron in this paper.
Processing the neurons’ outputs in the output layer can be defined in the same manner as in the hidden layer. The output of the neuron in the output layer, yk, is defined as
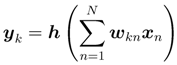 where the function h is a quaternionic activation function from the action potential to the output, and wkn is the connection weight between the n-th neuron in the hidden layer and the k-th neuron in the output layer. The function h also satisfies
where the function h is a quaternionic activation function from the action potential to the output, and wkn is the connection weight between the n-th neuron in the hidden layer and the k-th neuron in the output layer. The function h also satisfies
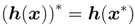
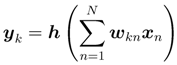
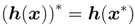
The connection weights should be modified by the so-called learning algorithms, in order to obtain the desired output signals with respect to the input signals. One of the learning algorithms for MLP-type networks is the error back-propagation (EBP) algorithm. The following section describes our derivation of this algorithm for the presented network.
3.2. Learning Algorithm
An EBP algorithm works so that the output error, calculated by the neurons’ outputs at the output layer and the desired output signals, is minimized. In the case of networks with three layers as shown in Figure 2, the connection weights between the hidden and output layers are first modified, and then the weights between the input and hidden layers are modified. In general (networks with n layers), EBP algorithms first modify the connection weights between the n-th layer (the output layer) and (n − 1)-th layer, and then between the (n − 1)-th layer and the (n − 2)-th layer, etc. This section only describes the three-layers case.
First, let dk be a quaternionic desired signal for the k-th output neuron when z’s are input to the network. The connection weights affect the output signals with respect to a set of input signals, thus the error E is regarded as a function with arguments wkn’s and wkn ∗’s. The output error E at the time t is then defined as
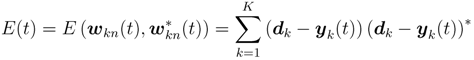
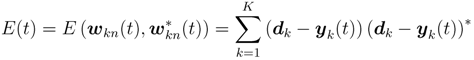
The output error should be real-valued so that it can be minimized.
Suppose that the connection weights are updated at the time (t + 1) by
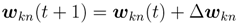 where Δwkn is a quantity in updating. Then, the output error at the time (t + 1) can be written as
where Δwkn is a quantity in updating. Then, the output error at the time (t + 1) can be written as
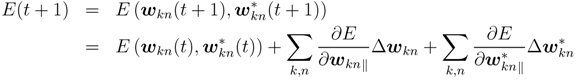
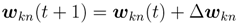
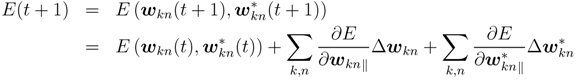
Note that the local analytic condition in quaternionic domain should be satisfied in calculating the derivatives. Thus, if we set Δwkn as
 where µ is a quaternionic constant, the temporal difference of the output error, ∆E, becomes
where µ is a quaternionic constant, the temporal difference of the output error, ∆E, becomes
If the real part of µ is positive, ∆E ≤ 0 holds. This indicates that the output error would decrease upon updating weights according to Equations (24) and (26). For calculating the updated quantity in Equation (26), the component ∂E/∂wkn∗‖ are expanded by using chain rule of derivative and ∂y/∂w∗‖= 0 from the local analytic condition is applied:
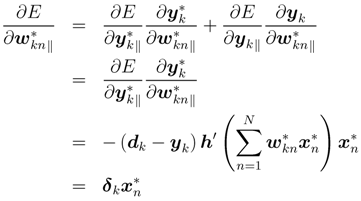 where h′ is the (local) derivative of the activation function h, and δk is defined as
where h′ is the (local) derivative of the activation function h, and δk is defined as 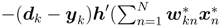 .
.
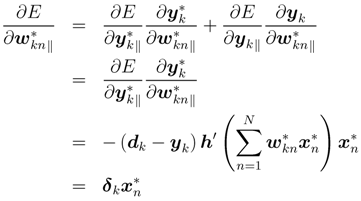
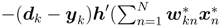 .
.Similarly, the updates for the connection weights v’s can be deduced. The output error function E isa function with arguments vnm’s and v∗nm’s, thus the output error at the time (t + 1) can be represented by
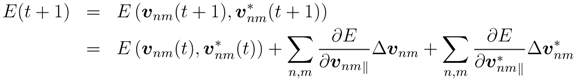
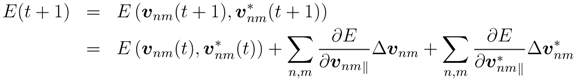
Hence, vnm is updated with the quantity ∆vnm,
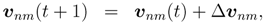
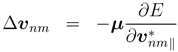
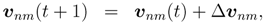
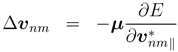
This leads to ∆E ≤ 0 under the condition of the real part of µ being positive. The component ∂E/∂*vnm‖ can be expanded by chain rules and local analytic conditions, ∂x/∂v*‖ = 0, ∂y/∂x*‖ = 0, and ∂x/∂v*‖ = 0 are applied:
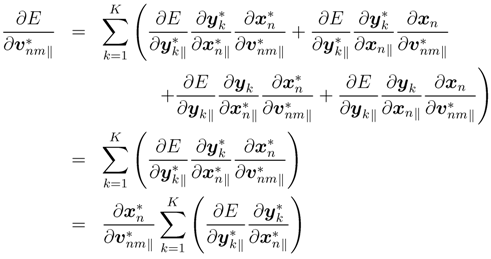
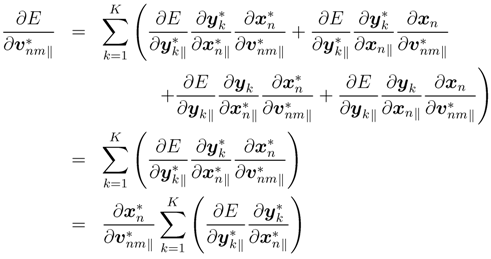
Using the derivatives 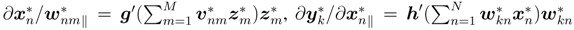 , and
, and 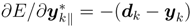 , we finally obtain
, we finally obtain
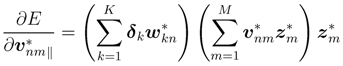
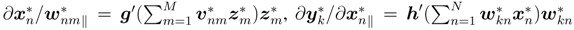 , and
, and 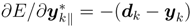 , we finally obtain
, we finally obtain
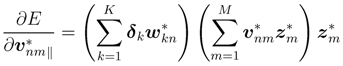
Once a set of network output {yk} is obtained for a set of net work input, the output error with respect to a target set {dk} can be calculated by Equation (23). Then, the connection weights between hidden and output layers are modified by Equations (24-28). The connection weights between input and hidden layers are finally modified by Equations (30-32).
3.3. Universal Approximation Capability
As an example of activation functions for neurons (g and h), the quaternionic tanh function [22] can be used. Other types of activation functions are also available, because complex-valued functions can be used for the presented network and the properties of several functions have been explored for the activation functions in [29]. It is important to consider the capability of the proposed quaternionic network with these activation functions, i.e., whether the proposed network can approximate given functions.
This concern is known as the universal approximation theorem [31,32]. In the real-valued MLPs with single hidden layer,the universality has been proven with a so-called sigmoidal function being used as an activation function of neurons. Other than sigmoidal functions, the bounded and differentiable functions are also available for activation functions.
This theorem is also discussed in the case of complex-valued networks [29]. The condition for boundedness in the real-valued MLPs is not required in some complex-valued MLPs. There are three types of activation functions discussed in [29], which are categorized by the properties of complex-valued functions, and for each of them, it is shown that universal approximation can be achieved.
The first type of complex-valued functions concerns the functions without anysingular points. These functions can be used as activation functions and the networks with this type of activation functions are shown as good approximators. Although some of the functions are not bounded, they can be used by introducing bounding operation for their regions. The second type concerns the functions having the bounded singular points, e.g., the discontinuous functions. These singularities can be removed and thus they can also be used for activation functions and can achieve their universality. The last type is for the functions with the so-called essential singularities, i.e., their singularities cannot be removed. These functions can also be used as activation functions, with the consideration of restricting the regions for them so that their regions never cover their singularities.
In the proposed quaternionic MLPs, for example, a quaternionic tanh function can be used as an activation function. This function is unbounded and may contain several kinds of singularities as in the case of complex-valued functions described above. Thus this quaternionic MLPs would face the same problem, i.e., the existence of singularities, but this can also be handled similarly as in the case of complex-valued MLPs for the removal or avoidance of such singularities. It could be possible to show the universality with handling singularities for the proposed MLPs according to the ways adopted in the complex-valued MLPs [29],but it remains as our future work.
4. Conclusions and Discussion
This paper has proposed a multilayer type neural network and an error back-propagation algorithm for its learning scheme in the quaternionic domain. The neurons in this network adopt locally analytic activation functions. The quaternionic functions with local analytic conditions are isomorphic to the complex functions, thus several activation functions, such as complex-valued tanh function, can be used extendedly in the quaternionic domain. The Wirtinger calculus, where a quaternion and its conjugate are treated as independent of each other, makes the derivation of the learning scheme clear and compact.
Analytic conditions for quaternionic functions are derived by defining a complex plane at a quaternionic point, which is a kind of reduction from quaternionic domain to complex domain. There exists another type of reduction in quaternionic domains, such as the commutative quaternion, which is a four-dimensional hypercomplex number system with commutativity in its multiplication [33,34,35,36]. A principal property is that a commutative quaternion can be decomposed and represented by two complex numbers with two linearly independent bases (called the decomposed form by idempotent bases). Commutative quaternions have been applied to neural networks only in terms of Hopfield-type network [24], but defining multilayer perceptron type networks can alsobe straightforward. Thus, it will be interesting to explore the relationship between commutative quaternion-based networks and networks with the local analyticity.
Showing the universality of the proposed network is also an important issue. Quaternionic functions, such as tanh function, may contain several kinds of singularities where the values of functions or their differentials are not defined in particular regions. In complex-valued networks with fully complex-valued function [29], the universality of the networks can be shown by dealing with these singularities, so that such singularities are removed or avoided by restricting the regions. It is expected to show the universality of the proposed network, in a similar way to the case of complex-valued networks.
Also, it is necessary to investigate the performances of the proposed network, though in this paper the experimental exploration could not be accomplished. The proposed network is similar to the networks proposed in [13,14], due to the introduction of local analytic function in quaternionic domain, thus the performances for both types of networks may have similar tendencies. Performance comparisons can also be conducted between the proposed network and the ones in [29], because both networks adopt the same representation in their constructions, i.e., Wirtinger calculus. A wide variety of activation functions have been investigated including the split-type function, phase-preserving function [37], and circular-type function [38]. Similar experiments should be conducted for the quaternionic networks.
Application of the presented network to engineering problems is also challenging. The processing of three or four dimensional vector data, such as color/multi-spectral image processing, predictions for three-dimensional protein structures, and controls of motion in three-dimensional space, will be the candidates from now on.
Acknowledgments
This study was financially supported by Japan Society for the Promotion of Science (Grant-in-Aids for Young Scientists (B) 24700227 and Scientific Research (C) 23500286).
References
- Hirose, A. Complex-Valued Neural Networks: Theories and Application; World Scientific Publishing: Singapore, 2003. [Google Scholar]
- Hirose, A. Complex-Valued Neural Networks; Springer-Verlag: Berlin, Germany, 2006. [Google Scholar]
- Nitta, T. Complex-Valued Neural Networks: Utilizing High-Dimensional Parameters; Information Science Reference: New York, NY, USA, 2009. [Google Scholar]
- Hamilton, W.R. Lectures on Quaternions; Hodges and Smith: Dublin, Ireland, 1853. [Google Scholar]
- Hankins, T.L. Sir William Rowan Hamilton; Johns Hopkins University Press: Baltimore, MD, USA, 1980. [Google Scholar]
- Mukundan, R. Quaternions: From classical mechanics to computer graphics, and beyond. In Proceedings of the 7th Asian Technology Conference in Mathematics, Melaka, Malaysia, 17-21 December 2002; pp. 97–105.
- Kuipers, J.B. Quaternions and Rotation Sequences: A Primer with Applications to Orbits, Aerospace and Virtual Reality; Princeton University Press: Princeton, NJ, USA, 1998. [Google Scholar]
- Hoggar, S.G. Mathematics for Computer Graphics; Cambridge University Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Nitta, T. An extension of the back-propagation algorithm to quaternions. In Proceedings of International Conference on Neural Information Processing (ICONIP’96), Hong Kong, China, 24-27 September 1996; 1, pp. 247–250.
- Arena, P.; Fortuna, L.; Muscato, G.; Xibilia, M. Multilayer perceptronsto approximate quaternion valued functions. Neural Netw. 1997, 10, 335–342. [Google Scholar] [CrossRef]
- Buchholz, S.; Sommer, G. Quaternionic spinor MLP. In Proceeding of 8th European Symposium on Artificial Neural Networks (ESANN 2000), Bruges, Belgium, 26-28 April 2000; pp. 377–382.
- Matsui, N.; Isokawa, T.; Kusamichi, H.; Peper, F.; Nishimura, H. Quaternion neural network with geometrical operators. J. Intell. Fuzzy Syst. 2004, 15, 149–164. [Google Scholar]
- Mandic, D.P.; Jahanchahi, C.; Took, C.C. A quaternion gradient operator and its applications. IEEE Signal Proc. Lett. 2011, 18, 47–50. [Google Scholar] [CrossRef]
- Ujang, B.C.; Took, C.C.; Mandic, D.P. Quaternion-valued nonlinear adaptive filtering. IEEE Trans. Neural Netw. 2011, 22, 1193–1206. [Google Scholar] [CrossRef]
- Kusamichi, H.; Isokawa, T.; Matsui, N.; Ogawa, Y.; Maeda, K. Anewschemeforcolornight vision by quaternion neural network. In Proceedings of the 2nd International Conferenceon Autonomous Robots and Agents (ICARA2004), Palmerston North, New Zealand, 13-15 December 2004; pp. 101–106.
- Isokawa, T.; Matsui, N.; Nishimura, H. Quaternionic neural networks: Fundamental properties and applications. In Complex-Valued Neural Networks: Utilizing High-Dimensional Parameters; Nitta, T., Ed.; Information Science Reference: New York, NY, USA, 2009; pp. 411–439, Chapter XVI. [Google Scholar]
- Nitta, T. A solution to the 4-bit parity problem with a single quaternary neuron. Neural Inf. Process. Lett. Rev. 2004, 5, 33–39. [Google Scholar]
- Yoshida, M.; Kuroe, Y.; Mori, T. Models of hopfield-type quaternion neural networks and their energy functions. Int. J. Neural Syst. 2005, 15, 129–135. [Google Scholar] [CrossRef]
- Isokawa, T.; Nishimura, H.; Kamiura, N.; Matsui, N. Fundamental properties of quaternionic hopfield neural network. In Proceedings of 2006 International Joint Conference on Neural Networks, Vancouver BC, USA, 30 October 2006; pp. 610–615.
- Isokawa, T.; Nishimura, H.; Kamiura, N.; Matsui, N. Associative memoryin quaternionic hopfield neural network. Int. J. Neural Syst. 2008, 18, 135–145. [Google Scholar] [CrossRef]
- Isokawa, T.; Nishimura, H.; Kamiura, N.; Matsui, N. Dynamics of discrete-time quaternionic hopfield neural networks. In Proceedings of 17th International Conference on Artificial Neural Networks, Porto, Portugal, 9-13 September 2007; pp. 848–857.
- Isokawa, T.; Nishimura, H.; Matsui, N. On the fundamental properties of fully quaternionic hopfield network. In Proceedings of IEEE World Congress on Computational Intelligence (WCCI2012), Brisbane, Australia, 10-15 June 2012; pp. 1246–1249.
- Isokawa, T.; Nishimura, H.; Saitoh, A.; Kamiura, N.; Matsui, N. On the scheme of quaternionic multistate hopfield neural network. In Proceedings of Joint 4th International Conference on Soft Computing and Intelligent Systems and 9th International Symposium on Advanced Intelligent Systems (SCIS&ISIS 2008), Nagoya, Japan, 17-21 September 2008; pp. 809–813.
- Isokawa, T.; Nishimura, H.; Matsui, N. Commutative quaternion and multistate hopfield neural networks. In Proceedings of IEEE World Congress on Computational Intelligence (WCCI2010), Barcelona, Spain, 18-23 July 2010; pp. 1281–1286.
- Isokawa, T.; Nishimura, H.; Matsui, N. An iterative learning schemefor multistate complex-valued and quaternionic hopfield neural networks. In Proceedings of International Joint Conference on Neural Networks (IJCNN2009), Atlanta, GA, USA, 14-19 June 2009; pp. 1365–1371.
- Leo, S.D.; Rotelli, P.P. Local hypercomplex analyticity. 1997. Available online: http://arxiv.org/abs/funct-an/9703002 (accessed on 20 November 2012).
- Leo, S.D.; Rotelli, P.P. Quaternonic analyticity. Appl. Math. Lett. 2003, 16, 1077–1081. [Google Scholar] [CrossRef]
- Schwartz, C. Calculus with a quaternionic variable. J. Math. Phys. 2009, 50, 013523:1–013523:11. [Google Scholar]
- Kim, T.; Adalı, T. Approximationby fully complex multilayer perceptrons. Neural Comput. 2003, 15, 1641–1666. [Google Scholar] [CrossRef]
- Wirtinger, W. Zur formalen theorie der funktionen von mehr komplexen veränderlichen. Math. Ann. 1927, 97, 357–375. [Google Scholar] [CrossRef]
- Cybenko, G. Approximations by superpositions of sigmoidal functions. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 1991, 4, 215–257. [Google Scholar]
- Segre, C. The real representations of complex elements and extension to bicomplex systems. Math. Ann. 1892, 40, 322–335. [Google Scholar]
- Catoni, F.; Cannata, R.; Zampetti, P. An Introduction to commutative quaternions. Adv. Appl. CliffordAlgebras 2006, 16, 1–28. [Google Scholar] [CrossRef]
- Davenport, C.M. A commutative hypercomplex algebra with associated function theory. In Clifford Algebra With Numeric and Symbolic Computation; Ablamowicz, R., Ed.; Birkhauser: Boston, MA, USA, 1996; pp. 213–227. [Google Scholar]
- Pei, S.C.; Chang, J.H.; Ding, J.J. Commutative reduced biquaternions and their Fourier Transformfor signal and image processing applications. IEEE Trans. Signal Proc. 2004, 52, 2012–2031. [Google Scholar] [CrossRef]
- Hirose, A. Continuous complex-valued back-propagation learning. Electron. Lett. 1992, 28, 1854–1855. [Google Scholar] [CrossRef]
- Georgiou, G.M.; Koutsougeras, C. Complex domain backpropagation. IEEE Trans. Circuits Syst. II 1992, 39, 330–334. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).