TFR-LRC: Rack-Optimized Locally Repairable Codes: Balancing Fault Tolerance, Repair Degree, and Topology Awareness in Distributed Storage Systems
Abstract
1. Introduction
- In this paper, we construct a new family of LRC, TFR-LRC, which can exhibit excellent repair performance in the case of multiple failures. TFR-LRC establishes a relationship between data blocks, local parity blocks, and global parity blocks by grouping all data blocks and global parity blocks within the structure and requiring each data block and global parity block to participate in the check of two local parity blocks. By this construction method, TFR-LRC can achieve the goal of tolerating any failures in the coding structure;
- In this paper, we design an algorithm for generating TFR-LRC coding matrix. The TFR-LRC structure constructed from this algorithm can perform excellently repair performance when multiple blocks fail without changing the structures of the traditional LRC, and obtain higher fault tolerance by increasing a little bit of repair degree;
- Unlike the existing schemes that use experiments to demonstrate coding fault tolerance, this paper rigorously proves that TFR-LRC has a fault tolerance of from a theoretical point of view, i.e., TFR-LRC can tolerate any failures within the structure. The existing LRC schemes can only tolerate any node failures, while TFR-LRC achieves the goal of improving the fault tolerance by sacrificing a little bit of repair degree.
2. Related Work
2.1. Data Repair
2.2. Locality in Erasure Coding
3. Motivation
| Algorithm 1 Generating a TFR-LRC matrix |
| Input: Number of data blocks k, Number of global parities g, Number of local parities l, Optional random seed seed. Output: A generation matrix satisfying specific conditions. 1: Begin 2: Set Lhalf = l/2 3: Set Q = 2 * (k + g) mod l 4: Set R = 2 * (k + g) % l 5: Set M = Lhalf—R 6: Initialize random number generator with seed 7: for i = 1 to k do 8: data block list = chr(ord(‘a’) + i) 9: if k is greater than the number of lowercase letters then 10: Other characters can be used to represent the block of data, but these characters cannot be uppercase letters or numbers. 11: end if 12: end for 13: duplicate data block list once 14: for i = 1 to g do 15: global blocks list = str(i) 16: end for 17: duplicate global block list once 18: Loop 19: if R = 0 then 20: Initialize a matrix of l rows and Q columns, all elements set to 0 21: Fill the first Lhalf rows of the matrix with these elements in order, with Q elements in each row. 22: Fill randomly another set of elements into the last Lhalf rows of the matrix, with Q elements in each row. 23: else 24: Initialize a matrix of l rows and columns, all elements set to 0. 25: Fill these elements into the first Lhalf rows of the matrix in order, where the first M rows are filled with Q elements and the remaining rows are filled with elements. 26: Fill randomly another set of elements into the last Lhalf rows of the matrix. 27: end if 28: if the matrix satisfies the condition then 29: Add a capital letter as a row number at the beginning of each row. 30: Return the matrix 31: end if 32: End Loop 33: End |
4. TFR-LRC
4.1. Definitions
4.2. The Core Idea of TFR-LRC
4.3. Matrix Generation Complexity Analysis
5. Fault Tolerance Analysis of TFR-LRC
- ;
- 2.
- .
6. Experiments and Analysis
6.1. Storage Cost
6.2. Fault Tolerance
6.3. Locality
6.4. ARD
7. Maintenance-Robust Deployment
7.1. Maintenance Area Deployment Problem Analysis
- (1)
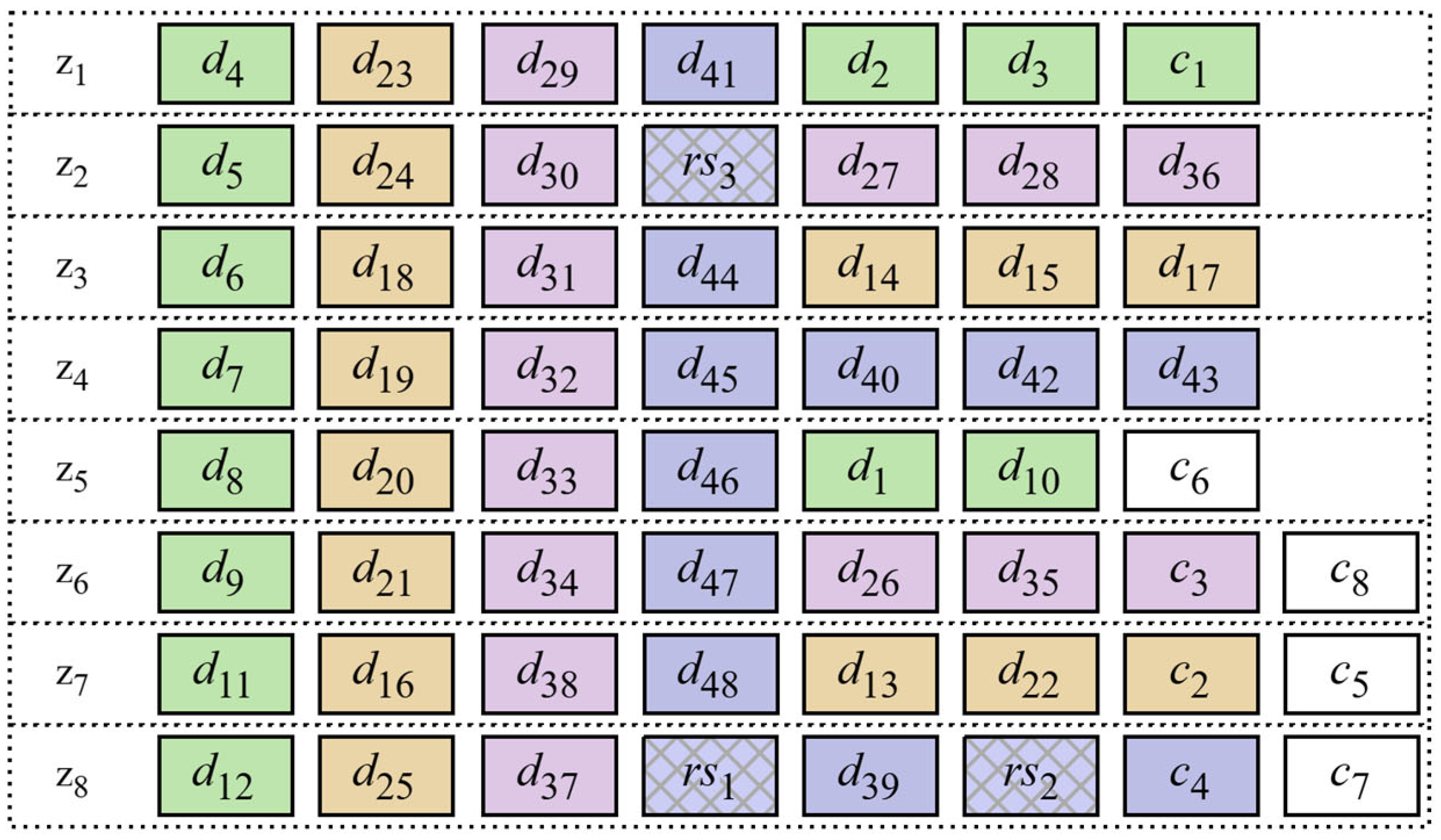
- Observe block distribution: Analyze the layout of blocks in the maintenance zone. appears in and , appears in and , appears in and , and appears in and .
- (2)
- Select optimal repair strategies: For blocks covered by local parities, apply local repair first. For blocks with unique local groups, choose the corresponding local parity for decoding. Since both and are verified by the local verification block , can be used to repair first, and then can be used to repair . Since the local blocks for verifying and are not repeated with other local blocks, can be used to repair , and can be used to repair .
- (3)
- Estimate repair cost: Assume direct block transfers without intra-rack coding. Based on the local repair strategies, repairing some blocks requires transmitting 13 blocks, while others require 12. The internal encoding of each rack is not considered here, that is, each block that helps to repair is directly transmitted to the destination rack. According to the description in step (2), the local repair scheme for each block in the region is shown in Figure 6. When using to repair , 13 blocks need to be transmitted; similarly, when using to repair , 13 blocks need to be transmitted; when using and to repair and , 23 blocks need to be transmitted.
- (4)
- Remove duplicate transfers: Identify blocks such as , , , , , , and that are transmitted more than once. Since repeated reads are unnecessary, the actual number of transmissions is reduced to 42. Right now: .5.
- (5)
- Compute total AMC: Aggregate the repair costs across all maintenance zones to obtain the overall AMC for this deployment scheme. According to steps (3) to (4), the final calculation is:.
7.2. Analysis and Evaluation of Degraded Read Experiments
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Reinsel, D.; Gantz, J.; Rydaing, J. Data Age 2025: The Digitization of the World from Edge to Core. IDC White Pap. 2018, 1, 1–29. [Google Scholar]
- Balaji, S.B.; Krishnan, M.N.; Vajha, M.; Ramkumar, V.; Sasidharan, B.; Kumar, P.V. Erasure coding for distributed storage: An overview. Sci. China Inf. Sci. 2018, 61, 100301. [Google Scholar] [CrossRef]
- Sathiamoorthy, M.; Asteris, M.; Papailiopoulos, D.; Dimakis, A.G.; Vadali, R.; Chen, S.; Borthakur, D. Xoring elephants: Novel erasure codes for big data. arXiv 2013, arXiv:1301.3791. [Google Scholar] [CrossRef]
- Calder, B.; Wang, J.; Ogus, A.; Nilakantan, N.; Skjolsvold, A.; McKelvie, S.; Xu, Y.; Srivastav, S.; Wu, J.; Simitci, H.; et al. Windows azure storage: A highly available cloud storage service with strong consistency. In Proceedings of the 23rd ACM Symposium on Operating Systems Principles (SOSP), Cascais, Portugal, 23–26 October 2011; pp. 143–157. [Google Scholar]
- Shvachko, K.; Kuang, H.; Radia, S.; Chansler, R. The hadoop distributed file system. In Proceedings of the IEEE 26th Symposium on Mass Storage Systems and Technologies (MSST), Incline Village, NV, USA, 3–7 May 2010; pp. 1–10. [Google Scholar]
- Weil, S.; Brandt, S.A.; Miller, E.L.; Long, D.D.; Maltzahn, C. Ceph: A scalable, high-performance distributed file system. In Proceedings of the 7th Conference on Operating Systems Design and Implementation (OSDI’06), Seattle, WA, USA, 6–8 November 2006; pp. 307–320. [Google Scholar]
- Ghemawat, S.; Gobioff, H.; Leung, S.T. The Google file system. In Proceedings of the 19th ACM Symposium on Operating Systems Principles (SOSP), Bolton Landing, NY, USA, 19–22 October 2003; pp. 29–43. [Google Scholar]
- Weatherspoon, H.; Kubiatowicz, J.D. Erasure coding vs. replication: A quantitative comparison. In Peer-to-Peer Systems; International Workshop on Peer-to-Peer Systems; Springer: Berlin/Heidelberg, Germany, 2002; pp. 328–337. [Google Scholar]
- Hu, Y.; Cheng, L.; Yao, Q.; Lee, P.P.; Wang, W.; Chen, W. Exploiting combined locality for Wide-Stripe erasure coding in distributed storage. In Proceedings of the 19th USENIX Conference on File and Storage Technologies (FAST 21), Olivia, MN, USA, 14 December 2020; pp. 233–248. [Google Scholar]
- Kadekodi, S.; Silas, S.; Clausen, D.; Merchant, A. Practical design considerations for wide locally recoverable codes (LRCs). ACM Trans. Storage 2023, 19, 1–26. [Google Scholar] [CrossRef]
- Wu, S.; Lin, G.; Lee, P.P.; Li, C.; Xu, Y. Optimal Wide Stripe Generation in Locally Repairable Codes via Staged Stripe Merging. In Proceedings of the 2024 IEEE 44th International Conference on Distributed Computing Systems (ICDCS), Jersey City, NJ, USA, 23–26 July 2024; IEEE: New York, NY, USA, 2024; pp. 450–460. [Google Scholar]
- Reed, I.S.; Solomon, G. Polynomial codes over certain finite fields. J. Soc. Ind. Appl. Math. 1960, 8, 300–304. [Google Scholar] [CrossRef]
- VastData. Available online: https://vastdata.com/providing-resilience-efficiently-part-ii/ (accessed on 15 January 2021).
- Huang, C.; Simitci, H.; Xu, Y.; Ogus, A.; Calder, B.; Gopalan, P.; Li, J.; Yekhanin, S. Erasure coding in windows azure storage. In Proceedings of the 2012 USENIX Annual Technical Conference (USENIX ATC 12), Boston, MA, USA, 13–15 June 2012; pp. 15–26. [Google Scholar]
- Cheng, K.; Wu, S.; Li, X.; Lee, P.P. Harmonizing Repair and Maintenance in LRC-Coded Storage. In Proceedings of the 2024 43rd International Symposium on Reliable Distributed Systems (SRDS), Charlotte, NC, USA, 30 September–3 October 2024; IEEE: New York, NY, USA, 2024; pp. 1–11. [Google Scholar]
- Shen, Z.; Cai, Y.; Cheng, K.; Lee, P.P.; Li, X.; Hu, Y.; Shu, J. A survey of the past, present, and future of erasure coding for storage systems. ACM Trans. Storage 2025, 21, 1–39. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, F.; Pei, X. Research on erasure code-based fault-tolerant technology for distributed storage. Chin. J. Comput. 2017, 40, 236–255. [Google Scholar]
- Muralidhar, S.; Lloyd, W.; Roy, S.; Hill, C.; Lin, E.; Liu, W.; Pan, S.; Shankar, S.; Sivakumar, V.; Tang, L.; et al. f4: Facebook’s warm BLOB storage system. In Proceedings of the 11th USENIX Symposium on Operating Systems Design and Implementation (OSDI 14), Broomfield, CO, USA, 6–8 October 2014; pp. 383–398. [Google Scholar]
- Kolosov, O.; Yadgar, G.; Liram, M.; Tamo, I.; Barg, A. On fault tolerance, locality, and optimality in locally repairable codes. ACM Trans. Storage (TOS) 2020, 16, 1–32. [Google Scholar] [CrossRef]
- Rashmi, K.V.; Shah, N.B.; Ramchandran, K. A piggybacking design framework for read-and download-efficient distributed storage codes. IEEE Trans. Inf. Theory 2017, 63, 5802–5820. [Google Scholar] [CrossRef]
- Pamies-Juarez, L.; Hollmann, H.D.L.; Oggier, F. Locally repairable codes with multiple repair alternatives. In Proceedings of the 2013 IEEE International Symposium on Information Theory, Istanbul, Turkey, 7–12 July 2013; IEEE: New York, NY, USA, 2013; pp. 892–896. [Google Scholar]
- Khan, O.; Burns, R.C.; Plank, J.S.; Plank, J.; Pierce, W.; Huang, C. Rethinking erasure codes for cloud file systems: Minimizing I/O for recovery and degraded reads. In Proceedings of the FAST’12: 10th USENIX Conference on File and Storage Technologies, San Jose, CA, USA, 14–17 February 2012. [Google Scholar]
- Ford, D.; Labelle, F.; Popovici, F.I.; Stokely, M.; Truong, V.A.; Barroso, L.; Grimes, C.; Quinlan, S. Availability in globally distributed storage systems. In Proceedings of the 9th USENIX Symposium on Operating Systems Design and Implementation (OSDI 10), Vancouver, BC, Canada, 4–6 October 2010. [Google Scholar]


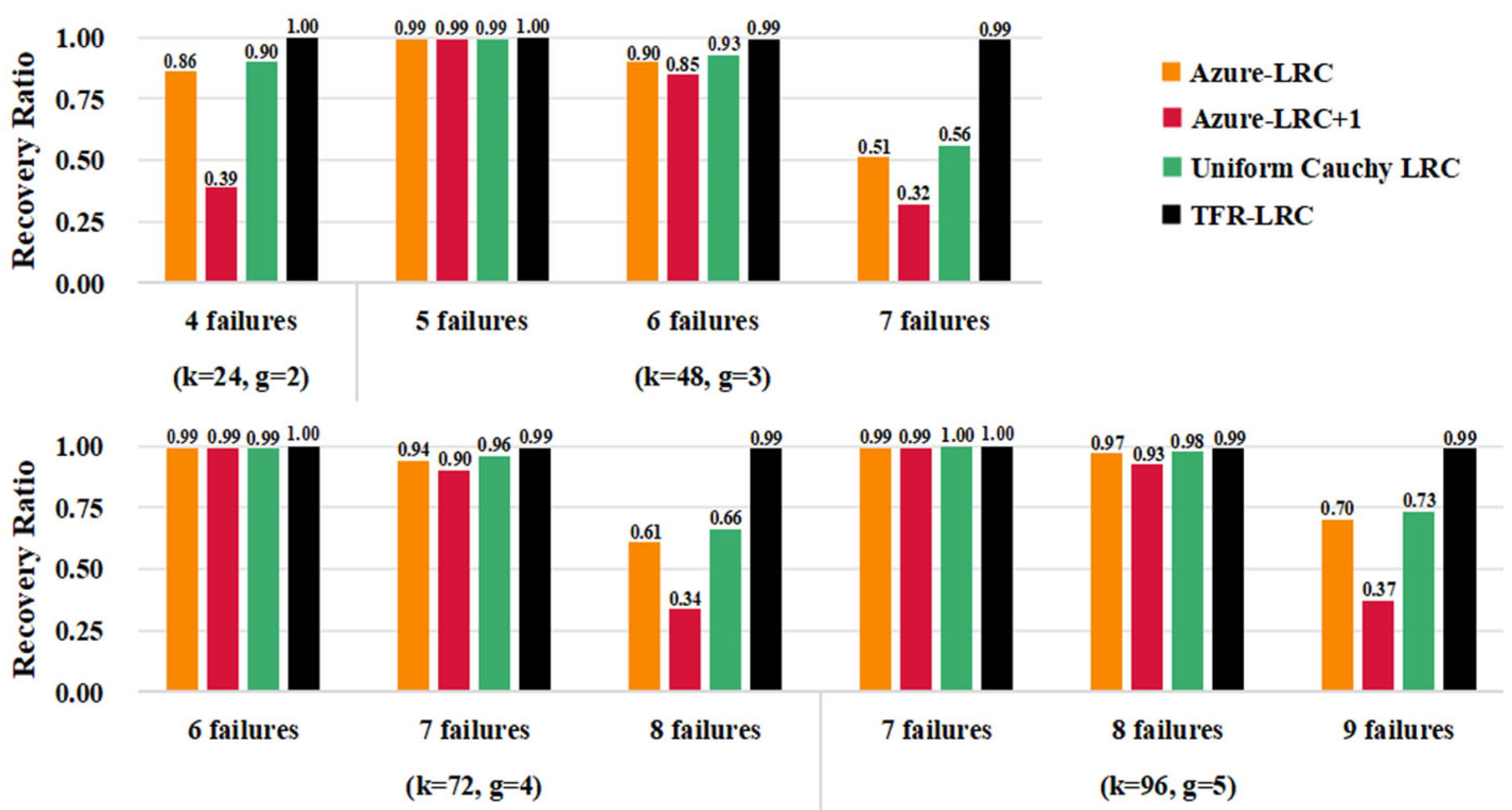





| 1 Failure | 2 Failures | |
|---|---|---|
| TFR-LRC(30, 24, 4, 2) | 13 | 18.75 |
| Uniform Cauchy LRC(28, 24, 2, 2) | 13 | 27.92 |
| 2 Failures | 3 Failures | 4 Failures | |
|---|---|---|---|
| TFR-LRC(30, 24, 4, 2) | 18.75 | 24 | 24 |
| Uniform Cauchy LRC(30, 24, 4, 2) | 16.86 | 22.15 | / |
| Storage Cost | Fault Tolerance | Locality | ARD (f = 1) | ARD (f = 2) | |
|---|---|---|---|---|---|
| Azure-LRC(28, 24, 2, 2) | 1.167× | 24 | 12.85 | 30.66 | |
| Azure-LRC+1(28, 24, 2, 2) | 1.167× | 24 | 21.64 | 43.46 | |
| Uniform Cauchy LRC(28, 24, 2, 2) | 1.167× | 13 | 13 | 27.92 | |
| TFR-LRC(30, 24, 4, 2) | 1.25× | 13 | 13 | 18.75 | |
| Azure-LRC(55, 48, 4, 3) | 1.146× | 48 | 13.96 | 35.49 | |
| Azure-LRC+1(55, 48, 4, 3) | 1.146× | 16 | 15.05 | 39.22 | |
| Uniform Cauchy LRC(55, 48, 4, 3) | 1.146× | 13 | 12.76 | 33.85 | |
| TFR-LRC(59, 48, 8, 3) | 1.229× | 13 | 12.10 | 21.75 | |
| Azure-LRC(80, 72, 4, 4) | 1.111× | 72 | 20.7 | 52.8 | |
| Azure-LRC+1(80, 72, 4, 4) | 1.111× | 24 | 22.75 | 59.38 | |
| Uniform Cauchy LRC(80, 72, 4, 4) | 1.111× | 19 | 19 | 49.22 | |
| TFR-LRC(84, 72, 8, 4) | 1.167× | 19 | 19 | 32.25 | |
| Azure-LRC(105, 96, 4, 5) | 1.094× | 96 | 27.42 | 70.68 | |
| Azure-LRC+1(105, 96, 4, 5) | 1.094× | 32 | 30.45 | 79.73 | |
| Uniform Cauchy LRC(105, 96, 4, 5) | 1.094× | 26 | 25.26 | 67.69 | |
| TFR-LRC(109, 96, 8, 5) | 1.135× | 26 | 25.26 | 42.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Cao, Y.; Shi, J. TFR-LRC: Rack-Optimized Locally Repairable Codes: Balancing Fault Tolerance, Repair Degree, and Topology Awareness in Distributed Storage Systems. Information 2025, 16, 803. https://doi.org/10.3390/info16090803
Wang Y, Cao Y, Shi J. TFR-LRC: Rack-Optimized Locally Repairable Codes: Balancing Fault Tolerance, Repair Degree, and Topology Awareness in Distributed Storage Systems. Information. 2025; 16(9):803. https://doi.org/10.3390/info16090803
Chicago/Turabian StyleWang, Yan, Yanghuang Cao, and Junhao Shi. 2025. "TFR-LRC: Rack-Optimized Locally Repairable Codes: Balancing Fault Tolerance, Repair Degree, and Topology Awareness in Distributed Storage Systems" Information 16, no. 9: 803. https://doi.org/10.3390/info16090803
APA StyleWang, Y., Cao, Y., & Shi, J. (2025). TFR-LRC: Rack-Optimized Locally Repairable Codes: Balancing Fault Tolerance, Repair Degree, and Topology Awareness in Distributed Storage Systems. Information, 16(9), 803. https://doi.org/10.3390/info16090803






