Abstract
The cross-sectional dimensions of structural elements in a structure are design elements that need to be carefully designed and are related to the stiffness of the structure. Various optimization processes are applied to determine the optimum cross-sectional dimensions of beams or columns in structures. By repeating the optimization processes for multiple load scenarios, it is possible to create a data set that shows the optimum design section properties. However, this step means repeating the same processes to produce the optimum cross-sectional dimensions. Artificial intelligence technology offers a short-cut solution to this by providing the opportunity to train itself with previously generated optimum cross-sectional dimensions and infer new cross-sectional dimensions. By processing the data, the artificial neural network can generate models that predict the cross-section for a new structural element. In this study, an optimization process is applied to a simple tubular column and an I-section beam, and the results are compiled to create a data set that presents the optimum section dimensions as a class. The harmony search (HS) algorithm, which is a metaheuristic method, was used in optimization. An artificial neural network (ANN) was created to predict the cross-sectional dimensions of the sample structural elements. The neural architecture search (NAS) method, which incorporates many metaheuristic algorithms designed to search for the best artificial neural network architecture, was applied. In this method, the best values of various parameters of the neural network, such as activation function, number of layers, and neurons, are searched for in the model with a tool called HyperNetExplorer. Model metrics were calculated to evaluate the prediction success of the developed model. An effective neural network architecture for column and beam elements is obtained.
1. Introduction
The load-bearing system elements are the main elements that determine the rigidity of a structure. Basic load-bearing system elements such as beams and columns are structural system parts that must be designed optimally within safe limits in the structure. In the design of such elements, the section dimensions that affect structural rigidity are taken into account. The element sections are designed in a way that will reduce the cost and provide carrying capacity. Another important factor in the design of structural system elements is the production process. The production process of structural elements is important in terms of maintaining standard dimensions and minimizing errors that will arise from workmanship. In recent years, considering such issues as cost, production, and workmanship, the section designs of system elements can be easily created using various optimization applications in a way that their load-carrying capacities are preserved. In the studies conducted in the literature on structural system elements, issues such as carbon emission, sustainability, structural weight, and cost have been considered as the objective function of optimization [1,2,3,4,5]. Optimization of structural systems is preferred to maximize the efficiency obtained from the design. However, repeating this process at the design stage is a time-consuming and analysis-requiring situation.
The developing world of science can offer effective solutions to many engineering problems using artificial intelligence technologies. These technologies include the ability of the human brain to make predictions and inferences based on knowledge by storing the knowledge that people gain through experience and more in their memory. Thanks to artificial intelligence, it is possible to store large amounts of data obtained from design optimization, which is difficult to keep in human memory, and to predict how a new design should be by taking this data into account. Artificial intelligence is divided into various subfields such as machine learning, deep learning, and natural language processing. Artificial neural networks are one of the methods developed to give a machine the ability to think like a human by imitating the neural networks in the human brain, which are among the sub-branches of artificial intelligence. It is a technique that has continued to develop from the mid-20th century to the present day. McCulloch and Pitts created a structure similar to neurons, which is seen as the first artificial neural network (ANN) model in 1943, based on the way the human brain works, and stated that knowledge can be acquired by neural networks [6,7,8,9]. After the first neurocomputer, named “SNARC”, was developed in 1951 [10,11], artificial neural networks have been the subject of many studies. In the field of civil engineering, artificial neural networks are a frequently used method. It has been examined by researchers for its application in various branches, such as hydraulics, transportation, structure, mechanics, and geotechnics, which are among the research areas of civil engineering. The literature describes the use of artificial neural networks for prediction in civil engineering problems, like evapotranspiration, water demand, ground acceleration in bridges, corrosion current density in concrete steel, shear strength, concrete thickness and steel reinforcement area, carbonation depth, seismic damage, soil mechanical properties, sensor error percentage in structural health monitoring, location of concrete surface defects, and concrete compressive strength [12,13,14,15,16,17,18,19,20,21,22,23].
Artificial neural networks (ANNs) play a good estimator role in obtaining parameters affecting the design, such as section dimensions, strength, manufacturing cost, and structural weight in structural system designs. They offer many advantages that facilitate the design of various structural models. ANNs have gained importance in the literature in estimating the design properties of various structural system elements, such as columns and beams, which are the subject of this study. A summary of the artificial neural network-based studies on structural system designs conducted in recent years is as follows: Naderpour et al. proposed an artificial neural network (ANN) model to estimate the shear resistance of FRP bar-reinforced concrete beams and observed that beam dimensions are the most important input parameter affecting the shear resistance [24]. Hashem et al. proposed an ANN model to estimate the structural weight in steel moment-resistant frame residential structures and determined that before the design process, the ANN model can produce sufficiently accurate estimations for the structural models obtained by varying the parameters [25]. Djerrad et al. proposed an ANN model to predict the properties such as tensile strength, strain, and compressive strength of circular hollow section steel pipes reinforced with aramid fiber-reinforced polymers (AFRP) and found that it showed remarkable predictive success, especially in the strength prediction of steel pipes [26]. Hisham et al. applied an artificial neural network model to predict the temperature change of circular reinforced concrete columns wrapped with fiber-reinforced polymers (FRP) exposed to fire and investigated the design effect of FRP usage under fire conditions [27]. Hong et al. used artificial neural networks for the ductile design of doubly reinforced concrete beams and proposed the prediction of multiple design parameters by an inverse design procedure [28]. Rabi et al. used an ANN-based model to predict the ultimate buckling resistance capacity of circular hollow section beams and columns and observed that it gave reliable results [29]. Peng and Xu used a data-driven ANN model for the forward and inverse design of bi-material composite triangular truss structures to predict important features for structure design and stated that the ANN model performed well [30].
Artificial neural networks are an artificial intelligence technique that requires various parameters in model production. For this method to provide better performance, the parameters affecting the neural network architecture can be optimized. This study aims to develop an artificial neural network model that estimates the best beam and column section properties under boundary conditions for an I-section beam and tubular column samples. For this purpose, beam and column sections under different load and stress combinations were optimized to minimize the cost using the harmony search (HS) algorithm developed by Geem et al. [31]. The optimum design parameters obtained from the optimization were converted into a data set. To minimize the labor cost and labor-related errors in column and beam production, standard production was targeted by classifying the section properties. The generated data set was used to create an artificial neural network model that estimates the section dimensions and thickness of a new structural system element under load and stress. As a new method that uses metaheuristic algorithms to increase the efficiency of artificial neural networks, the neural architecture search (NAS) [32] method was used. With this method, using a tool called HyperNetExplorer, optimum parameters were obtained by changing the hyperparameters such as the activation function, the number of neurons, and the number of layers, which affect the prediction success of the artificial neural network.
2. Materials and Methods
In this section, the harmony search algorithm used for the optimization of the section properties of column and beam elements, the artificial neural network (ANN) method used for developing the artificial intelligence model, the HyperNetExplorer tool, and the neural architecture search (NAS) method used for optimizing the ANN hyperparameters, genetic algorithm, the algorithms used to create machine learning models to compare the NAS method, the metrics for evaluating the classification problems and the model validation method are discussed.
2.1. Harmony Search Algorithm
Harmony search (HS) algorithm is a metaheuristic method developed by Geem et al. [31]. The basic principle of metaheuristic algorithms is to get inspiration from natural events and behaviors of living beings or spontaneous events in nature. There are many varieties based on different inspiration sources [33,34,35,36,37,38,39]. One of these is the HS algorithm, which is based on capturing harmony that appeals to the musical ear of people. It aims to find the best harmony for the feeling of appreciation that sounds create in people. While doing this, it can be inspired by likening a harmony to an old melody, taking a harmony from memory, or obtaining a new harmony by improvising from scratch. In the optimization process, the best harmony is reached by producing new harmonies. For the production of each harmony, the HMCR value, which is the algorithm-specific harmony memory consideration ratio, is examined. The harmony production equation is decided according to whether this value is greater or smaller than a randomly selected number. If the HMCR value is greater than the random number selected between 0 and 1, Equation (1) is used to generate new harmonies, and if it is smaller or equal, Equation (2) is used.
The and values in the equations indicate the minimum and maximum values that can be taken for the harmony, respectively, and indicates the new harmony vector. , given in Equation (2), indicates the nth harmony, and the FW value indicates the fret width number. Harmony production continues until all iterations are completed. Each new harmony produced is compared with the previous harmony according to the objective function of the problem, and it remains the same or is updated with the new one. When the iterations are completed, the best harmony is obtained.
2.2. Genetic Algorithm
A genetic algorithm is a metaheuristic algorithm developed by Holland [40], inspired by the principle of natural selection, whereby the strongest and most adaptable. It is essentially a method based on processes such as mating, reproduction, crossover, cloning, and mutation [41]. In the optimization process, the process starts with an initial population. The initial population changes over time and evolves into a population where the worst are rejected and the best solutions survive and reproduce. This situation stems from the principle that the genetic algorithm, due to its biological adaptation, only allows the strongest and most survivable individuals to reproduce. In each generation, solutions are expected to evolve into better ones, resulting in superior individuals in subsequent generations. In the optimization ranking of the population, new candidate solutions are expanded with suitable candidates, subjected to crossover, and undergo mutation based on their similarity [42]. The solution generation process used in genetic algorithms is shown in Equation (3).
In the equation, represents the new value of the qth variable, represents the mutation rate, and represent the lower and upper limits of the qth variable, and represents a random number between 0 and 1.
2.3. Design Parameters for Tubular Column Optimization
Tubular columns are structural elements with annular cross-sections, having an inner and outer centric diameter. In the optimization under compressive load, the cross-section dimensions are minimized to reduce the cost. A schematic view of a tubular column is shown in Figure 1.
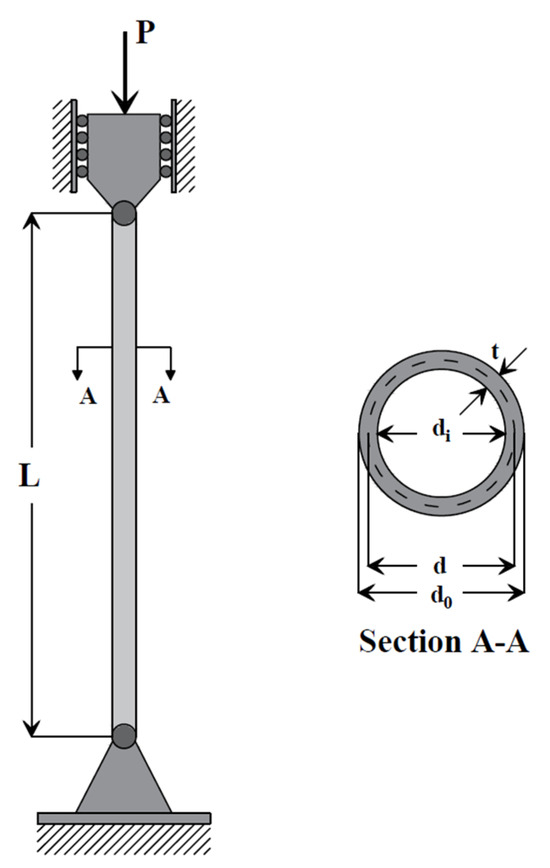
Figure 1.
Tubular column and cross-section detail [43].
In Figure 1, L represents the column length, and P represents the compressive load. In the image of the A-A section taken from the figure, t represents the section thickness, d0 represents the outer diameter, d represents the center diameter, and di represents the inner diameter. In the cost optimization to be carried out for the tubular column example, the objective function of the problem is given in Equation (4) [44].
The most appropriate design constraints for column design are axial load capacity and buckling. The condition considered in external load capacity is that the compressive stress does not exceed the yield strength. In the buckling constraint, unlike the external load, the modulus of elasticity (E) is also effective. The constraint based on external load () is shown in Equation (5) and the buckling constraint () is shown in Equation (6) [44].
In the equations, represents the yield strength of the material, and represents the modulus of elasticity.
2.4. Design Parameters for I-Beam Optimization
In the design of an I-section steel beam, the beam flange width and thickness, beam height, and web section thickness are important. In addition to the section dimensions, flange and web thicknesses should also be carefully designed for the durability of I-section beams under horizontal and vertical loads. A representative drawing of an example of an I-section steel beam is given in Figure 2.
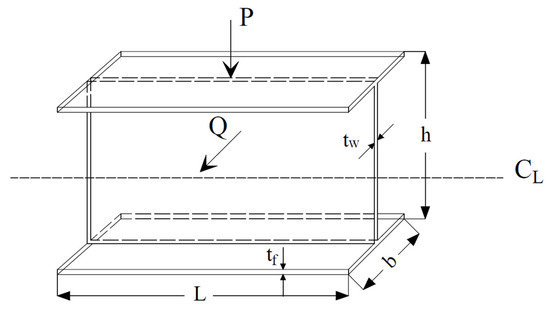
Figure 2.
I-section beam construction and design variables [45].
In Figure 2, vertical and horizontal loads are shown as P and Q, respectively. The beam flange width, b, beam flange thickness, tf, beam length, L, beam height, h, beam web thickness, tw, and centerline are expressed as CL. Deflection is one of the most important situations to be avoided in beams. It is desired to reduce deflection as much as possible. The displacement constraint for deflection () for an I-section beam is shown in Equation (7), and the objective function, including beam sections where inertia calculation is taken into account, is shown in Equation (8) [44].
In the equations, the moment of inertia of the beam is given by I, and the material elasticity modulus is given by E. The limitation of the section properties for the beam is determined by the designer, depending on the area where the design will be applied. The constraint taken as an example in this study is shown in Equations (9) and (10) as 300 cm2 for the beam section area and 6 kN/cm2 for the constraint moment stress, respectively [44].
2.5. Artificial Neural Networks
Artificial neural networks are an artificial intelligence technique developed with algorithms inspired by neural networks found in the human brain. Neural networks with parallel operation feature function according to the structure of the network and weights and consist of more than one processing element [46]. In its simplest form, a neural network has an architecture consisting of an input layer of neurons, one or two hidden layers, and an output layer, where neurons are connected linearly [47]. A simple artificial neural network is shown schematically in Figure 3.

Figure 3.
A schematic representation of an artificial neural network.
In artificial neural networks, data inputs are entered into the system by multiplying them by a certain weight. The strength of the connection between neurons represents these weights, expressed in numerical values. The inputs multiplied by the weights are added together by a sum function. In the next stage, the activation function comes into play, adjusts the weight and bias values, and enables the calculation of the neuron’s outputs. The artificial neural network model that defines the artificial neural network is shown in Figure 4.
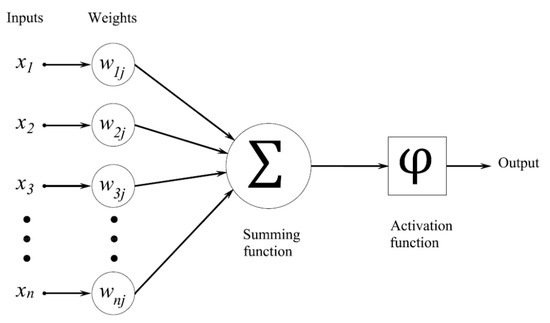
Figure 4.
An artificial neural network model.
As shown in Figure 4, the input information received by the neurons is multiplied by certain weights and summed to obtain the net inputs. The obtained net inputs are evaluated with an activation function to produce the output. The correct selection of the activation function is important for the performance of the network. Some of the activation functions frequently used in artificial neural networks are shown in Table 1.

Table 1.
Activation functions.
Sigmoid/LogSigmoid activation function: It is a nonlinear ANN activation function that produces values in the range of (−∞, +∞) and [0, 1] [48]. A logistic sigmoid function is an activation function that produces outputs in the range of (−∞, +0).
Hyperbolic tangent function (tanh): It is a function that is defined in the range of (−∞, +∞) and can take values in the range of [−1, +1], similar to the sigmoid function. The output for this function takes values that accept zero as the center, and it stands out compared to the sigmoid function with its effect of facilitating optimization, but it has the disadvantage of losing the slope over time [49].
Rectified linear unit function (ReLU): ReLU is a linear activation function that produces output values defined in the range of (0, +∞). It is frequently preferred in deep learning studies. It is stated that it shows better training performance compared to logistic sigmoid and hyperbolic tangent functions [48,50,51]. Mish activation function is a self-organizing activation function that offers a new perspective compared to other functions [52].
Leaky rectified linear unit function (Leaky ReLU): It is a function that can take values greater than 0, and it takes an output value of 0 for every number in the negative definition range. This prevents the activation of units in the layers by negative values in the layers [49]. To correct this, the Leaky ReLU activation function was developed. The function performs a slope addition process to correct the zero value that the neuron receives in the negative region.
Exponential linear unit (ELU): It is an activation function similar to ReLU functions with advanced learning capabilities that provide fast learning [53].
2.6. Neural Architecture Search and HyperNetExplorer
HyperNetExplorer is a web-based hyperparameter optimization tool that uses the neural network architecture search (NAS) method. In optimization, it uses the algorithms in the MealPy [54] package. It deals with the hyperparameter optimization of artificial neural network (ANN) parameters using the algorithms in the MealPy package based on artificial neural networks. The neural network framework is developed using Python 3.12 and Pytorch 2.7.1 [55] and Streamlit as the graphical user interface (GUI) (The GUI will be made available upon request). The parameters targeted to be optimized and the range values in which they are optimized are shown in Table 2.

Table 2.
Parameters to be optimized and their ranges.
In the HyperNetExplorer tool, learning rate, number of epochs, optimization algorithm, and loss function selection are made for optimization. In this study, a number of epochs of 200, a learning rate of 0.001, an optimization algorithm, the harmony search algorithm, and cross-entropy loss were used as the loss function since a classification problem was considered. In the data loading section, an ANN is created in each iteration with the FindBestNet command using the GUI, and each ANN is verified with the 10-fold cross-validation method. The mean values of 10 folds are taken, and outputs are obtained in line with the objective function. Each output obtained is evaluated by HyperNetExplorer, and the same processes are repeated by changing the hyperparameters. In the optimization tool, 1050 neural network architectures are created in each run with 20 epochs and 50 population numbers. Classification metrics are calculated for each ANN architecture produced and stored in the server as a table and can be downloaded when the training is completed.
Hyperparameter Optimization Algorithms
HyperNetExplorer uses metaheuristic algorithms to optimize ANN hyperparameters. Metaheuristic algorithms are algorithms that are based on various natural events and instinctive behaviors of living beings and are obtained by converting these behaviors or events into mathematical expressions. In the study, ANN parameters were optimized using the harmony search algorithm (HS). The harmony search algorithm is a metaheuristic algorithm inspired by the process of searching for the best harmony, developed by Geem et al. [31]. The harmony Search algorithm was used in the optimum production process of data to be used in the study and the optimization of ANN parameters, and information about the algorithm is explained in detail in Section 2.1.
2.7. Machine Learning
Machine learning is the process of imparting various abilities specific to the human brain, such as comprehension, inference, and problem-solving, to machines through various software. By learning from a given amount of data, the machine can make successful predictions with high precision. Depending on the type of data and the purpose of the problem, the desired outputs can be classified or numerically estimated at a good level with machine learning algorithms. In cases where the desired output value represents a class, group, or community, the problem is considered a classification problem, and in cases where it represents a numerical output, the problem is considered a regression problem. Within the scope of this study, design features were evaluated as a classification problem using beam and column examples, and the results were compared with the prediction models produced from artificial neural networks, where the best hyperparameters were obtained with the NAS tool. The algorithms used to evaluate machine learning models are briefly defined as follows.
K-nearest neighbors: It is an algorithm that estimates the desired outputs for the data by taking the mean of k observation data around a selected sample cluster in a data set or by calculating the frequency of these observation data. The output class is decided according to the similarity of k neighboring observation data around the selected sample [56]. The selection of the k value indicates the number of observations; it is aimed at establishing a balance by considering overfitting or underfitting [57,58].
Logistic regression: It is an algorithm that gives effective results, especially in classification problems involving two classes and seeks a logical relationship between two attributes. It is based on the least squares algorithm for the outputs to be estimated [59,60].
Linear discriminant analysis: It is an algorithm that aims to establish a linear relationship between the classes by determining the distinguishing features between them in data [61]. It serves to reduce dimensionality with the operation it performs.
Decision tree: It is an artificial intelligence algorithm that creates a structure consisting of roots, branches, and leaves, similar to a tree, in predicting a dependent variable based on independent variables in data. It was introduced by Breiman et al. [62,63]. Each feature in the data constitutes a node of the tree. The branches of the decision tree represent the combination of features used in the classification, and the leaves represent the classes [64]. New branches are produced until the defined adequacy criterion is met to stop, and the best predictions are obtained.
Adaboost: It is a prediction algorithm that aims to classify the dependent variables in data by bringing together weak learners that are classified incorrectly, adjusting their weights, and aiming for the most accurate classification. The working principle of the model is to change the weights that are initially defined equally for the trained data samples according to the case of incorrect classification and to strengthen them by creating a community of weak classifiers. In the examples taken from the data, the weights of those that produce incorrect predictions are increased, and those that are classified correctly are decreased [65].
Catboost: Developed as a gradient boosting algorithm, it is a machine learning algorithm that successfully uses categorical features [66,67]. It provides boosting of categorical features according to their effect on the prediction in the estimation of dependent variables in the data. It is suitable for classification and regression problems.
Bagging: Developed by Breiman [68], it is a learning algorithm in which the final prediction is obtained by evaluating the prediction results of more than one estimator. If the variable to be predicted specifies a numerical value, the mean of the prediction results is taken. When the variable targeted to be predicted represents a class or group, a vote is made on the prediction results, and the most accurate class is determined according to the majority.
Random forest: It is an ensemble algorithm created by combining decision trees, which stands out for its classification ability [69]. It is suitable for use in classification and regression problems. It concludes by combining the decisions of multiple decision trees.
2.8. Model Metrics
Determining the class or group specific to a problem based on the attributes in the data is defined as the classification process. When classification is performed with artificial intelligence methods, various model metrics are used to evaluate the performance of the created classifiers. These metrics are terms that express the level of model prediction accuracy. The error matrix is formed by how much of the predicted class is predicted correctly and how much is predicted incorrectly. These values are then used to calculate other model metrics. Table 3 shows the error matrix created for a 4-class classification study. In the table, the indices indicate class numbers, TP values indicate the correct predictions of the model, and FP values indicate the incorrect predictions of the model. While TP11 indicates the number of samples in which class 1 is predicted as class 1, FP13 indicates the number of samples in which class 1 is predicted incorrectly as class 3.

Table 3.
Confusion matrix example for 4 classes.
In classification-type machine learning applications, metrics such as accuracy, recall, precision, and f1-score are used. The explanation of these metrics is briefly presented below.
Accuracy: A metric that shows the model’s prediction success in the classification of data as a percentage. It expresses the level of accuracy of the classification.
Recall: A metric that indicates how much of the class is predicted correctly by the model and how much is predicted incorrectly when compared to the actual class. In the calculation of this value, the value at which the positive class is correctly predicted and the values at which the negative class is incorrectly predicted for two-class data with positive and negative classes are used. The recall metric calculation is shown in Equation (11).
In Equation (11), correctly predicted positives are expressed as and incorrectly predicted negatives as .
Precision: It represents the success of the model in predicting positive classes. In the calculation of this metric, incorrectly predicted positives are used, as well as correctly predicted positives. The calculation of precision is shown in Equation (12).
In Equation (12), false positives are shown as .
F1-score: It is a harmonic mean value calculated by taking into account the precision and recall values. By considering the class inequality in the data, it ensures that the class imbalance does not negatively affect the mean, and the best possible accuracy is obtained. Equation (13) shows the f1-score calculation equation.
2.9. Model Evaluation
Various validation methods are used as an indicator of the extent to which artificial intelligence models can explain their predictions. The k-fold cross-validation method is one of the model validation methods suggested by Geisser and Eddy [70]. In this method, the data are divided into k pieces, and one piece is used to test the model, and k-1 pieces are used to train the model. Then, the random data are divided into k pieces, and k performances are obtained by calculating the performance for each fold. As a result, the final accuracy value is reached by taking the mean of k performances. The 10-fold cross-validation method was used to validate machine learning models and the ANN models obtained with the HyperNetExplorer tool. Ten different folds were created, and the main performance value was obtained by taking the mean of the performance scores of each fold. Figure 5 shows a diagram showing the working principle of the 10-fold cross-validation method.
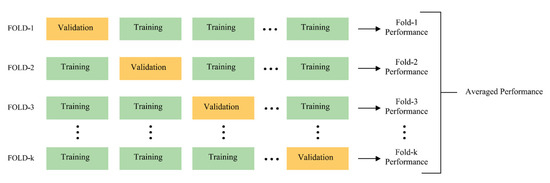
Figure 5.
Tenfold cross-validation method.
2.10. Reliability Analysis
The method used in this study is based on the search process for the best artificial neural network (ANN) architecture. This method aims to determine the most successful ANN architecture by testing parameters specific to the ANN, such as the number of hidden layers and the activation function. During the search process, evaluating the probability of random generation of the hyperparameter optimization or the resulting model is essential for the success of the method. The Mann–Whitney U test was applied to evaluate the values obtained from the neural architecture search (NAS) method implemented with the HyperNet Explorer optimization tool. To compare the results obtained with the NAS method and to provide reliability analysis, the results generated with the harmony search (HS) algorithm were reproduced by running them a second time. Comparisons were made by running the application examples twice more with a different heuristic algorithm, the genetic algorithm (GA). The reliability analysis aims to prove that the results are consistent and reproducible. The Mann–Whitney U test examines whether there is a difference between two data sets and checks the consistency of the results obtained when the same algorithm is run a second time. This test provides a reliability test that does not require a normal distribution in the data. In the Mann–Whitney U test, two groups are selected. This test is used to check whether two groups (such as a and b) come from the same population. The underlying hypothesis assumes that the two groups are subsets of population p [71]. First, the groups are ranked starting from 1 to the largest number in the population, N. When the two groups are combined and ranked from the smallest to the largest, they each receive an ordinal number. Then, the ordinal numbers of the elements in each group are added to obtain the Ta and Tb scores. The number of observations in the groups is expressed as na and nb. The U-statistic value is calculated to measure the difference between the two groups. Equation (14) shows the U-statistic value calculation [71].
3. Numerical Examples
In this study, a classification process was applied in which optimum section properties were estimated on a class basis for various load, strain, and size combinations by taking I-section beam and tubular column samples. A harmony search algorithm was used to obtain optimum section properties. Then, the NAS method, defined as the process of searching for the best neural network architecture with the HyperNetExplorer optimization tool, was used by training the machine with data containing optimum section properties, and the classification was performed. To compare the performance of the NAS method, the effectiveness of the method was investigated with machine learning models produced using various algorithms. Details and results regarding application examples are provided below.
3.1. I-Section Beam Example
In the example of an I-section beam, the flange and web thicknesses, which are effective parameters in resisting deflection using optimum section properties of a steel beam in different load combinations, were classified. In the creation of data to be used in education, the beam flange width and height were taken into account for various loads using the harmony search algorithm, and the beam web thickness and the flange thickness were optimized. The optimization aimed to prevent the beam from deflection under vertical and horizontal loads. The parameters used in the optimization for data generation, the ranges for loads, and various beam parameters are shown in Table 4.

Table 4.
Design features and optimization parameters for the I-section beam example.
In the data generated after optimization, the beam web and flange thicknesses were named “thin” for the range of 0.9–2.2 and “thick” for the range of 2.2–5. A few rows of the data set obtained from optimization are given in Table 5. In the table, the objective function column, calculated based on the moment of inertia and beam sections, is shown with Fx.

Table 5.
Ten rows of the I-section beam data set.
Of the beam web thicknesses (tw), 4917 were determined as thin and 596 as thick, and of the beam flange thicknesses (tf), 3931 were determined as thin and 1582 as thick. Before converting the web and flange thicknesses into classes, the correlation between the data attributes was examined. The correlation between the data attributes for the beam application is shown in Table 6, and the correlation matrix graph is shown in Figure 6.

Table 6.
The correlation matrix for the beam data set.
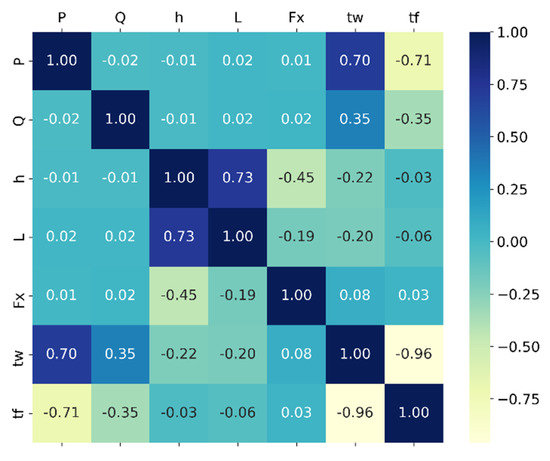
Figure 6.
The correlation matrix graph for the I-section beam example.
With the HyperNetExplorer optimization tool, in the neural network search architecture (NAS) method developed for the search for the best artificial neural network (ANN), prediction models for classification and regression problems can be created. In this method, the last column in the data is targeted as the desired output to be obtained by the machine. In the optimization, 1050 neural networks were created by testing ANN hyperparameters, such as 20 epochs and 50 population numbers with different hidden layer numbers and different activation functions using the harmony search algorithm, and the ANN model that best predicted the tw and tf values was searched. For the beam example, the beam web thickness and beam flange thicknesses were classified separately. The best 10 performance results of the ANN models classifying the beam tw and tf values as a result of the application of the NAS method are shown in Figure 7 and Figure 8, respectively.
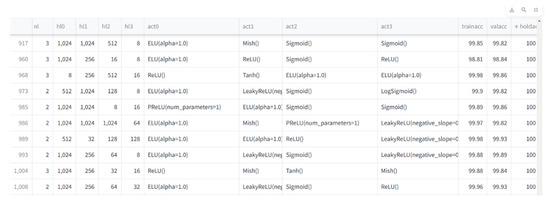
Figure 7.
ANN model performance results obtained with the NAS method for beam web thickness (tw).
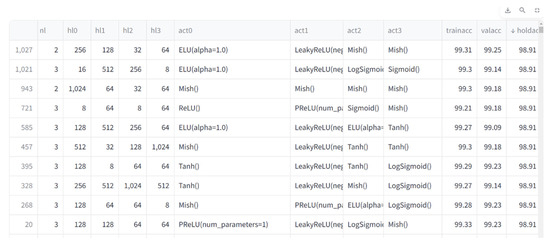
Figure 8.
ANN model performance results obtained with the NAS method for beam flange thickness (tf).
Confusion matrices used in the classification of the best ANN models produced with NAS were calculated. This matrix contains the correct and incorrect prediction numbers of the tested data classes. The confusion matrices calculated for the ANN model with the highest accuracy for the tw and tf values from the beam sections are shown in Figure 9 and Figure 10, respectively.
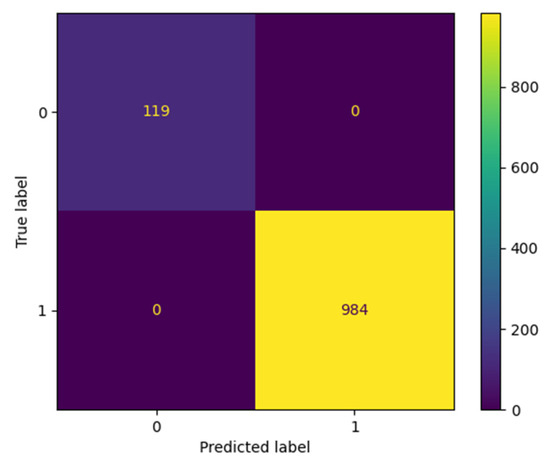
Figure 9.
The confusion matrix of the best ANN model generated with NAS for tw prediction.
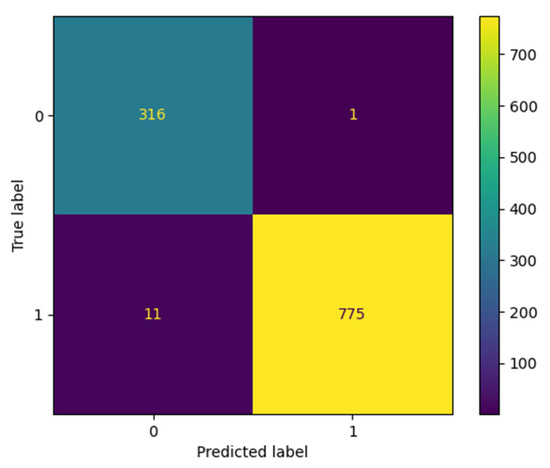
Figure 10.
The confusion matrix of the best ANN model generated with NAS for tf prediction.
To evaluate the performance of the best neural network architecture search (NAS) method, learning models were created by trying various machine learning algorithms. Following the study conducted with the hyperNetexplorer tool for machine learning, the tw and tf values were classified separately. In the classification, 10-fold cross-validation technique and k-nearest neighbors, linear discriminant analysis, logistic regression, decision tree, random forest, catboost, adaboost, and bagging algorithms were used. Accuracy, precision, recall, and f1-scores obtained from the classification models were calculated by taking the means of 10 folds. The imbalance of data distribution within the classes of the estimated tw and tf values was observed. Considering this situation, the classification metrics were calculated using macro-averaged values. The performance results of the learning models for predicting the beam web (tw) and flange (tf) thickness are presented in Table 7 and Table 8, respectively.

Table 7.
Performance results of the classification models obtained for beam web thickness (tw) using machine learning algorithms.

Table 8.
Performance results of the classification models obtained for beam flange thickness (tf) using machine learning algorithms.
3.2. Tubular Column Example
In this application, a classification model was produced by taking a tubular column subjected to axial compression load as an example and estimating the optimum column center diameter and section thickness parameters. Column sections were optimized with the harmony search algorithm for different loads, strains, and column lengths under axial load and buckling constraints. The goal of optimization is to obtain the safest and lowest-cost section properties for design. The obtained optimum section properties were organized and converted into a data set. The design parameters and design constraints used for the optimization process are given in Table 9.

Table 9.
Design features and optimization parameters for the tubular column example.
The optimum column center diameter (d) and column section thickness (t) values were converted to classes to reduce labor costs and obtain standard products. The column section thickness (t) was divided into 7 different classes (A, B, C, D, E, F, G) for values in the range of 0.2–0.9 cm with 0.1 cm intervals, and the column center diameter (d) was divided into 6 classes (H, J, K, L, M, N) for values in the range of 2–14 cm with 2 cm intervals. The 10 rows of the obtained data set are given in Table 10. The distribution of the classes for column center diameter (d) and column section thickness (t) is shown in Table 11.

Table 10.
Ten rows of a tubular column data set.

Table 11.
Class distribution of the tubular column data set.
The correlation values of the optimum data set obtained by optimizing the tubular column sample are shown in Table 12, and the visual graph of the correlation matrix is shown in Figure 11.

Table 12.
Correlation matrix for column data set.
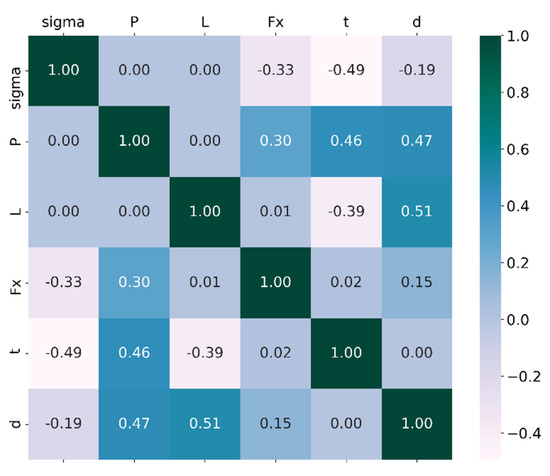
Figure 11.
The correlation matrix graph for the tubular column example.
In the tubular column application, the HyperNetExplorer optimization tool was used for the neural network search (NAS) method, which aims to find the best artificial neural network (ANN) architecture for estimating column sections. The column section d and t values were classified separately by optimizing the HyperNetExplorer tool’s ANN hyperparameters. In the optimization, the harmony search algorithm was used, and the most successful neural network architecture in estimating d and t values was determined. The best 10 ANN architectures and performance results created for column section thicknesses and column center diameters with the NAS method are shown in Figure 12 and Figure 13, respectively.
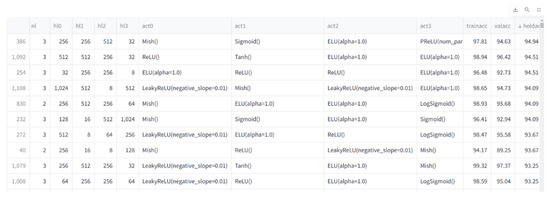
Figure 12.
ANN model performance results obtained with the NAS method for column section thickness (t).
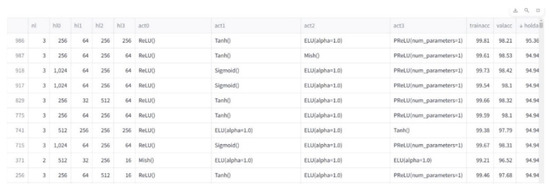
Figure 13.
ANN model performance results obtained with the NAS method for column center diameter (d).
Confusion matrices calculated for the ANN model with the highest accuracy produced with NAS are given in Figure 14 and Figure 15 for the t and d column sections, respectively.
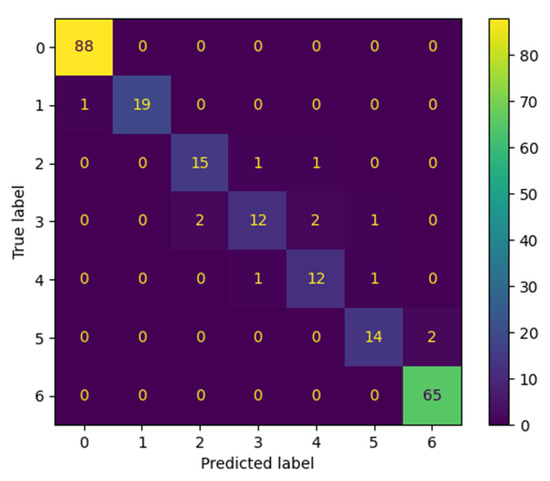
Figure 14.
Confusion matrix of the best ANN model generated with NAS for t prediction.
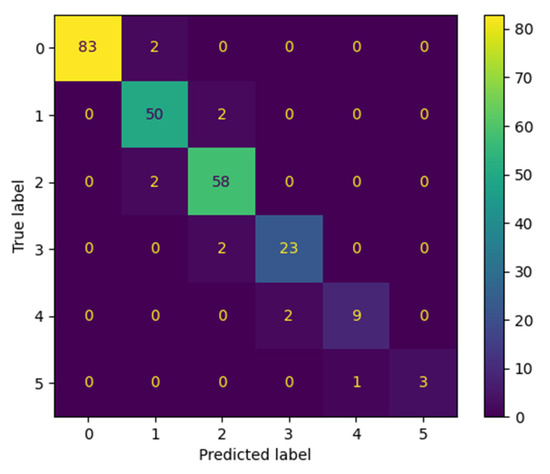
Figure 15.
Confusion matrix of the best ANN model generated with NAS for d prediction.
To compare the ANN prediction performance obtained with the NAS method, various machine learning models that predict d and t values were produced. The data were divided into 10 parts with the 10-fold cross-validation method, and the classification metrics for each fold were calculated. Finally, the accuracy, precision, recall, and f1 score evaluation metrics of the 10 folds were calculated as a mean. In the class distributions made for t in the data set, a maximum of 438 and a minimum of 72 data fell into a class, and a maximum of 424 and a minimum of 19 data fell into a class for d. Considering the imbalance in the number of data in the classes in the data set, macro-averaging was used in the calculation of the metrics. The performance results of the machine learning classification models developed for the estimation of the column section thickness are shown in Table 13, and the prediction performances of the models developed for the column center diameter are shown in Table 14.

Table 13.
Performance results of the classification models obtained for column section thickness (t) using machine learning algorithms.

Table 14.
Performance results of the classification models obtained for column center diameter (d) using machine learning algorithms.
3.3. NAS Algorithm Comparison
The results of the analysis on the comparison of NAS algorithms used in HyperNet Explorer indicate that the impact of the NAS algorithm on the discovery of the most efficient model is either minor, minimal, or negligible. We elaborate on the results below.
To evaluate the reliability of the NAS method used, the HyperNetExplorer tool was run a second time with the harmony search (HS) algorithm to produce new results, and it was run twice more with the genetic algorithm (GA). Table 15 shows the statistical values obtained from running the NAS method, HS, and GA algorithms once for the tubular column d parameter.

Table 15.
The comparison of holdout accuracy (dependent var: d).
GA1D indicates the first run of the tool to discover the ANN architecture that provides the most accurate estimation of the dependent variable d using the genetic algorithm. HS1D indicates the first run of the tool to discover the ANN architecture that provides the most accurate estimation of the dependent variable d using the harmony search algorithm.
The mean accuracy achieved with HS1D exceeded that of GA1D by a margin of 0.06. A Mann–Whitney U test indicates that there is no significant difference between the results of the two algorithms, and the effect sizes are small. A Cohen’s d value of approximately 0.03 supports the conclusion that the difference in effect size between the two groups is very small. This small difference indicates a negligible difference for both HS1D and GA1D results.
Table 16 shows the statistical values obtained by running the NAS method, HS, and GA algorithms once for the t parameter of the tubular column. GA1T indicates the first run of the tool to discover the ANN architecture that provides the most accurate estimation of the dependent variable t using the genetic algorithm. HS1T indicates the first run of the tool to discover the ANN architecture that provides the most accurate estimation of the dependent variable t using the harmony search algorithm.

Table 16.
The comparison of holdout accuracy (dependent var: t).
The GA1T group’s mean accuracy was 0.89, and its standard deviation was 0.35 higher than that of the HS1T. Neither data sets were normally distributed, and their variances were unequal. A Cohen’s d of 0.35 indicates a moderate difference between the GA1T and HS1T results, but there was still some overlap between the data. Consequently, the effect size is concluded to be small.
Table 17 shows the statistical values obtained by running the NAS method, HS, and GA algorithms once for the tf parameter of the I-section beam. GA1TF indicates the first run of the tool to discover the ANN architecture that provides the most accurate estimation of the dependent variable tf using the genetic algorithm. HS1TF indicates the first run of the tool to discover the ANN architecture that provides the most accurate estimation of the dependent variable tf using the harmony search algorithm.

Table 17.
The comparison of holdout accuracy (dependent var: tf).
The mean accuracy of HS1TF is slightly higher than that of GA1TF, with a difference of only 0.028. This difference is statistically insignificant. The Mann–Whitney p-value is approximately 0.14. This confirms that the difference between the two algorithms is due to chance. In other words, there is no significant difference between the two groups, and the small difference that exists is due to chance. Cohen’s d value was calculated as 0.046. This result supports the notion that the difference between the algorithm results is insignificant. The results overlap, and d indicates that there is no real difference between the two algorithm results.
Table 18 shows the statistical values obtained by running the NAS method, HS, and GA algorithms once for the tw parameter of the I-section beam. GA1TW indicates the first run of the tool to discover the ANN architecture that provides the most accurate estimation of the dependent variable tw using the genetic algorithm. HS1TW indicates the first run of the tool to discover the ANN architecture that provides the most accurate estimation of the dependent variable tw using the harmony search algorithm.

Table 18.
The comparison of holdout accuracy (dependent var: tw).
The median values for the GA1TW and HS1TW algorithms are the same, and the difference between their mean accuracy values is 0.046. Cohen’s d is approximately 0.12, indicating a very small effect size and no significant difference between the two groups. The score distributions for both algorithms largely overlap, indicating that the performance of the algorithms is largely similar.
3.4. Reliability of the Tool: HyperNet Explorer
The results of the analysis on the comparison of NAS algorithms used in HyperNet Explorer indicate that the impact of the different runs of the tool is either minor or negligible, and it can be concluded that the HyperNet Explorer provides reliable results in different runs. We elaborate on the results below.
Table 19 shows the statistical values obtained by running the HS algorithm of the NAS method twice for the d parameter of the tubular column example. HS1D indicates the first run of the tool to discover the ANN architecture that provides the most accurate estimation of the dependent variable d using the harmony search algorithm. HS2D indicates the second run of the tool to discover the ANN architecture that provides the most accurate estimation of the dependent variable d using the harmony search algorithm.

Table 19.
The comparison of holdout accuracy between runs with the HS algorithm for parameter d.
The median of the mean accuracies obtained from the first and second runs of the HS algorithm is the same. The mean accuracy of the HS1D is 0.371 higher than that of the HS2D. The p-value obtained from the Mann–Whitney U test is less than 0.001. This means that when the HS algorithm was run twice, new results were obtained that were significantly different from the first run, and the difference is unlikely to have occurred by chance. Cohen’s d was approximately 0.17. This value indicates that similar results were obtained with the HS algorithm run twice, and the effect size is small. Cohen’s d indicates that the difference between the two results is insignificant.
Table 20 shows the statistical values obtained by running the HS algorithm of the NAS method twice for the t parameter of the tubular column example. HS1T indicates the first run of the tool to discover the ANN architecture that provides the most accurate estimation of the dependent variable t using the harmony search algorithm. HS2T indicates the second run of the tool to discover the ANN architecture that provides the most accurate estimation of the dependent variable t using the harmony search algorithm.

Table 20.
The comparison of holdout accuracy between runs with the HS algorithm for parameter t.
HS2T, obtained from the second run of the HS algorithm, has a slightly higher, by 0.179, mean accuracy than HS1. There is no statistically significant difference. The p-value obtained from the Mann–Whitney U test is approximately 0.059, and the Cohen’s d value is approximately 0.07. This p-value is borderline significant. Furthermore, Cohen’s d value indicates that the values obtained from the two runs overlap and that the results obtained from the second run of the algorithm are not significantly different.
Table 21 shows the statistical values obtained by running the GA algorithm of the NAS method twice for the d parameter of the tubular column example. GA1D indicates the first run of the tool to discover the ANN architecture that provides the most accurate estimation of the dependent variable d using the genetic algorithm. GA2D indicates the second run of the tool to discover the ANN architecture that provides the most accurate estimation of the dependent variable d using the genetic algorithm.

Table 21.
The comparison of holdout accuracy between runs with the GA algorithm for parameter d.
GA2D has a mean accuracy and a common median of 0.091 higher than GA1D. The variances obtained from two runs of the genetic algorithm for variable d were equal. A Mann–Whitney U test result of p-value 0.033 indicates a statistically significant difference between the results of the two runs. A Cohen’s d value of approximately 0.06 indicates that the effect size is very small and that the results of the two runs overlap significantly. This indicates that the difference between the results of the two runs of the GA is negligible.
Table 22 shows the statistical values obtained by running the GA algorithm of the NAS method twice for the t parameter of the tubular column example. GA1T indicates the first run of the tool to discover the ANN architecture that provides the most accurate estimation of the dependent variable t using the genetic algorithm. GA2T indicates the second run of the tool to discover the ANN architecture that provides the most accurate estimation of the dependent variable t using the genetic algorithm.

Table 22.
The comparison of holdout accuracy between runs with the GA algorithm for parameter t.
According to the results of the genetic algorithm run twice for the t parameter, the mean accuracy of GA1T is 0.013 units higher than GA2T. According to the Mann–Whitney U test, the p-value is approximately 0.094. This p-value indicates that this difference was obtained by chance and is not statistically significant. Cohen’s d is approximately 0.005. Accordingly, the results of the two runs almost completely overlap, and the performance of GA1 and GA2 is similar.
4. Discussion
In this study, the harmony search algorithm, which is a metaheuristic algorithm, was used to optimize the section properties of I-section beam and tubular column samples under different load and stress combinations. A data set was created based on the design properties with the optimum column and beam parameters obtained from the optimization, and artificial neural network (ANN) models were produced that predicted the section properties of column and beam samples separately. For this purpose, the best neural network architecture (NAS) search method was applied with the optimization of ANN hyperparameters using the HyperNetExplorer optimization tool. In the I-section beam sample, prediction models were produced that classified separately for beam web thickness (tw) and beam flange thickness (tf), and for the tubular column sample, column center diameter (d) and column section thickness (t). Machine learning models were also tested to compare the performance of the NAS method. The accuracy values obtained from the NAS method and machine learning models for the beam sections tw and tf are shown in Figure 16.
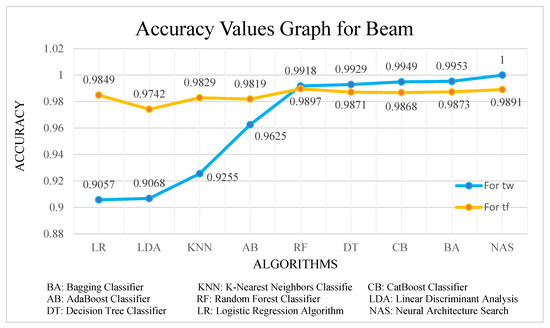
Figure 16.
The accuracy values graph obtained from the NAS method and machine learning models for tw and tf section estimation in the I-section beam.
When Figure 16 is examined, it is seen that the model that best predicts the tw and tf values is the ANN model obtained with the NAS method. A prediction success of over 90% was achieved with the models obtained with both methods. The ANN produced with NAS showed a more effective performance in estimating the tw and tf values from the beam data set. In particular, the ANN model produced for the prediction of the tw value achieved 100% success and made all predictions correctly. In the tubular column example, the best ANN model and machine learning models were produced with NAS for the column section thickness (t) and column center diameter (d) values. The accuracy values of the produced ANN and learning models are presented graphically in Figure 17.
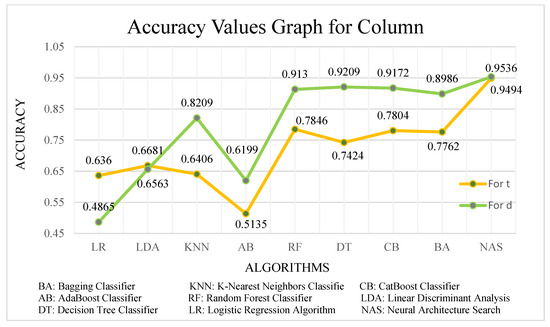
Figure 17.
Accuracy values graph obtained from the NAS method and machine learning models for t and d section estimation in the tubular column.
When Figure 17 is examined, it is seen that the ANN model produced using the NAS method provides the highest accuracy for t and d estimates. Machine learning models fell behind the ANN model with a maximum prediction success of 78%.
5. Conclusions
In this study, optimization was performed for I-section beam and tubular column samples to create the safest, most economical, and standard production for design under various load and stress conditions. A data set was created for beam and column samples using the optimum section properties obtained from the optimization. It aimed to develop an artificial neural network (ANN) that estimates optimum beam and column sections based on the obtained data. The best neural network architecture search method, called the NAS method, was applied. ANN hyperparameters were optimized with the HyperNetExplorer optimization tool, and the best neural network model was obtained. In addition, various machine learning models were created to evaluate the success of the NAS method, and the performance results of the models were compared. The ANN model obtained using the NAS method was the model with the highest accuracy in both application examples. In addition, it was able to estimate all of the beam web thicknesses correctly in the beam example. An estimation value such as 100% may suggest the possibility of overfitting for machine learning models. However, this value was calculated as holdout accuracy in the NAS method. In the NAS method application, the data section allocated to the machine as a holdout has not been shown before. This indicates that the holdout accuracy value in an ANN model produced with NAS cannot be memorized by the machine since it has not been seen before and is a possible estimation value. If the same situation occurs for the data allocated for training, a data leakage or overfitting situation can be considered. Although there are algorithms that show good estimation success for the beam in the models obtained with machine learning, the mean accuracy value of 10 folds remained at 78% in the tubular column example. Against this value, the ANN model produced with NAS achieved good estimation success with an estimation performance of approximately 95%. As a result of the findings obtained from the column and beam applications, it can be said that the NAS method shows a very impressive performance compared to classical machine learning applications, is an effective method in searching for the best ANN architecture, and has a promising future. The study is successful in terms of the accuracy performance of the method used compared to the prediction models obtained with classical artificial intelligence algorithms. The structural optimization problem used in the study is considered a common problem, but the prediction method used, NAS, is innovative in terms of its prediction performance, application functioning, and logic. In future studies, it is planned to predict different geometric shapes and support conditions with machine learning, to diversify the data, and to address more complex problems. The analysis results regarding the comparison of NAS algorithms used in HyperNet Explorer show that the effect of the NAS algorithm on discovering the most efficient model and the effect of different runs of the tool are minimal or negligible, and it can be concluded that HyperNet Explorer provides reliable results in different runs.
Author Contributions
A.O., G.B. and U.I. contributed to the conceptualization and methodology of the study. A.O., G.B., S.M.N. and U.I. developed the analysis code. A.O. and G.B. conducted formal analysis and investigation. S.M.N. and A.O. were responsible for data curation. The original draft of the manuscript was written by S.M.N., G.B., and A.O., while G.B. and Z.W.G. reviewed and edited the manuscript. The figures and visual materials were prepared by S.M.N., G.B. and A.O., G.B. and Z.W.G. supervised the research and provided project administration. Z.W.G. acquired the funding. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Data are available from the authors upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kaveh, A.; Izadifard, R.A.; Mottaghi, L. Optimal design of planar RC frames considering CO2 emissions using ECBO, EVPS, and PSO metaheuristic algorithms. J. Build. Eng. 2020, 28, 101014. [Google Scholar] [CrossRef]
- Tunca, O.; Carbas, S. Sustainable and cost-efficient design optimization of rectangular and circular-sectioned reinforced concrete columns considering slenderness and eccentricity. Structures 2024, 61, 105989. [Google Scholar] [CrossRef]
- Akhavan Kazemi, M.; Hoseini Vaez, S.R.; Fathali, M.A. An eco-friendly reliability-based design optimization of intermediate reinforced concrete moment frames. Eur. J. Environ. Civ. Eng. 2023, 27, 1876–1896. [Google Scholar] [CrossRef]
- Çoşut, M.; Bekdaş, G.; Niğdeli, S.M. Cost optimization and comparison of rectangular cross-section reinforced concrete beams using TS500, Eurocode 2, and ACI 318 code. In Proceedings of the 7th International Conference on Harmony Search, Soft Computing and Applications: ICHSA, Virtual, 2 September 2022; Springer Nature: Singapore, 2022; pp. 83–91. [Google Scholar]
- Kaveh, A.; Eslamlou, A.D.; Khodadadi, N. Dynamic water strider algorithm for optimal design of skeletal structures. Period. Polytech. Civ. Eng. 2020, 64, 904–916. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Russel, S.J.; Norvig, P. Artificial Intelligence: The gestation of artificial intelligence (1943–1956). In Artificial Intelligence: A Modern Approach; Prentice-Hall, Inc: Hoboken, NJ, USA, 1995; p. 16. ISBN 0-13-103805-2. [Google Scholar]
- Prasad, R.; Choudhary, P. State-of-the-Art of Artificial Intelligence. J. Mob. Multimed. 2021, 17, 427–454. [Google Scholar] [CrossRef]
- Ocak, A.; Bekdaş, G.; Nigdeli, S.M.; Işıkdağ, U. Machine Learning Applications in Structural Engineering. In New Advances in Soft Computing in Civil Engineering: AI-Based Optimization and Prediction; Springer Nature: Cham, Switzerland, 2024; pp. 47–76. [Google Scholar]
- Minsky, M. Neural Nets and the Brain-Model Problem. Ph.D. Dissertation, Princeton University, Princeton, NJ, USA, 1954. [Google Scholar]
- Poulton, M.M. A brief history. In Handbook of Geophysical Exploration: Seismic Exploration; Pergamon: New York, NY, USA, 2001; Volume 30, pp. 3–18. [Google Scholar]
- Trajkovic, S.; Todorovic, B.; Stankovic, M. Forecasting of reference evapotranspiration by artificial neural networks. J. Irrig. Drain. Eng. 2003, 129, 454–457. [Google Scholar] [CrossRef]
- Bougadis, J.; Adamowski, K.; Diduch, R. Short-term municipal water demand forecasting. Hydrol. Process. Int. J. 2005, 19, 137–148. [Google Scholar] [CrossRef]
- Kerh, T.; Huang, C.; Gunaratnam, D. Neural network approach for analyzing seismic data to identify potentially hazardous bridges. Math. Probl. Eng. 2011, 2011, 464353. [Google Scholar] [CrossRef]
- Sadowski, L. Non-destructive investigation of corrosion current density in steel reinforced concrete by artificial neural networks. Arch. Civ. Mech. Eng. 2013, 13, 104–111. [Google Scholar] [CrossRef]
- Kiran, S.; Lal, B. ANN-based prediction of shear strength of soil from their index properties. Int. J. Earth Sci. Eng 2015, 8, 2195–2202. [Google Scholar]
- Albuthbahak, O.M.; Alkhudery, H.H. Artificial neural network model for flexural design of concrete hydraulic structures. Int. J. Civil. Eng. Technol. 2018, 9, 265–274. [Google Scholar]
- Akpinar, P.; Uwanuakwa, I.D. Investigation of the parameters influencing the progress of concrete carbonation depth by using artificial neural networks. Mater. Constr. 2020, 70, e209. [Google Scholar] [CrossRef]
- Xiong, C.; Zheng, J.; Xu, L.; Cen, C.; Zheng, R.; Li, Y. Multiple-input convolutional neural network model for large-scale seismic damage assessment of reinforced concrete frame buildings. Appl. Sci. 2021, 11, 8258. [Google Scholar] [CrossRef]
- Ofrikhter, I.; Ponomaryov, A.; Zakharov, A.; Shenkman, R. Estimation of soil properties by an artificial neural network. Mag. Civ. Eng. 2022, 110, 11011. [Google Scholar]
- Sivasuriyan, A.; Vijayan, D.S. Prediction of displacement in reinforced concrete based on artificial neural networks using sensors. Meas. Sens. 2023, 27, 100764. [Google Scholar] [CrossRef]
- Saitoh, T.; Kato, T.; Hirose, S. Automatic detection of concrete surface defects using pre-trained CNN and laser ultrasonic visualization testing. Int. J. Progn. Health Manag. 2024. [Google Scholar] [CrossRef]
- Alibrahim, B.; Habib, A.; Habib, M. Developing a brain-inspired multilobar neural network architecture for rapidly and accurately estimating concrete compressive strength. Sci. Rep. 2025, 15, 1989. [Google Scholar] [CrossRef]
- Naderpour, H.; Poursaeidi, O.; Ahmadi, M. Shear resistance prediction of concrete beams reinforced by FRP bars using artificial neural networks. Measurement 2018, 126, 299–308. [Google Scholar] [CrossRef]
- Hashemi, S.S.; Sadeghi, K.; Fazeli, A.; Zarei, M. Predicting the weight of the steel moment-resisting frame structures using artificial neural networks. Int. J. Steel Struct. 2019, 19, 168–180. [Google Scholar] [CrossRef]
- Djerrad, A.; Fan, F.; Zhi, X.D.; Wu, Q.J. Artificial neural networks (ANN) based compressive strength prediction of afrp strengthened steel tube. Int. J. Steel Struct. 2020, 20, 156–174. [Google Scholar] [CrossRef]
- Hisham, M.; Hamdy, G.A.; El-Mahdy, O.O. Prediction of temperature variation in FRP-wrapped RC columns exposed to fire using artificial neural networks. Eng. Struct. 2021, 238, 112219. [Google Scholar] [CrossRef]
- Hong, W.K.; Nguyen, V.T.; Nguyen, M.C. Artificial intelligence-based novel design charts for doubly reinforced concrete beams. J. Asian Archit. Build. Eng. 2022, 21, 1497–1519. [Google Scholar] [CrossRef]
- Rabi, M.; Abarkan, I.; Shamass, R. Buckling resistance of hot-finished CHS beam-columns using FE modelling and machine learning. Steel Constr. 2024, 17, 93–103. [Google Scholar] [CrossRef]
- Peng, X.L.; Xu, B.X. Data-driven inverse design of composite triangular lattice structures. Int. J. Mech. Sci. 2024, 265, 108900. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Işıkdağ, Ü.; Bekdaş, G.; Aydın, Y.; Apak, S.; Hong, J.; Geem, Z.W. Adaptive Neural Architecture Search Using Meta-Heuristics: Discovering Fine-Tuned Predictive Models for Photocatalytic CO2 Reduction. Sustainability 2024, 16, 10756. [Google Scholar] [CrossRef]
- Karaboğa, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report-tr06; Computer Engineering Department, Engineering Faculty, Erciyes University: Kayseri, Turkey, 2005; Volume 200, pp. 1–10. [Google Scholar]
- Dorigo, M.; Maniezzo, V.; Colorni, A. The ant system: An autocatalytic optimizing process. IEEE Trans. Syst. Man. Cybern. B 1996, 26, 29–41. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-Learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Yang, X.S. A new metaheuristic bat-inspired algorithm. In Nature-Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Yang, X.S. Flower pollination algorithm for global optimization. In Proceedings of the Unconventional Computation and Natural Computation 11th International Conference, UCNC 2012, Orléans, France, 3–7 September 2012; Lecture Notes in Computer Science. Durand-Lose, J., Jonoska, N., Eds.; Springer: London, UK, 2012; Volume 7445, pp. 240–249. [Google Scholar]
- Holland, J. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Murty, K.G. Chapter 9: Heuristic Methods for Combinatorial Optimization Problems. In Optimization Models for Decision Making; University of Michigan: Ann Arbor, MI, USA, 2003. [Google Scholar]
- Yücel, M.; Kayabekir, A.E.; Bekdaş, G.; Nigdeli, S.M.; Kim, S.; Geem, Z.W. Adaptive-hybrid harmony search algorithm for multi-constrained optimum eco-design of reinforced concrete retaining walls. Sustainability 2021, 13, 1639. [Google Scholar] [CrossRef]
- Rao, S.S. Engineering Optimization Theory and Practice, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009; ISBN 978-0-470-18352-6. [Google Scholar]
- Bekdaş, G.; Nigdeli, S.M.; Yücel, M.; Kayabekir, A.E. Yapay Zeka Optimizasyon Algoritmaları ve Mühendislik Uygulamaları; Seçkin: Ankara, Turkey, 2021. [Google Scholar]
- Yang, X.S.; Bekdaş, G.; Niğdeli, S.M. Metaheuristic and Optimization in Civil Engineering; Springer: Cham, Switzerland, 2016; ISBN 9783319262451. [Google Scholar]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Fundamentals of artificial neural networks and deep learning. In Multivariate Statistical Machine Learning Methods for Genomic Prediction; Springer International Publishing: Cham, Switzerland, 2022; pp. 379–425. [Google Scholar]
- Wang, S.C. Artificial neural network. In Interdisciplinary Computing in Java Programming; Springer: Boston, MA, USA, 2003; pp. 81–100. [Google Scholar]
- Rasamoelina, A.D.; Adjailia, F.; Sinčák, P. A review of activation functions for artificial neural networks. In Proceedings of the 2020 IEEE 18th World Symposium on Applied Machine Intelligence and Informatics (SAMI), Herlany, Slovakia, 23–25 January 2020; pp. 281–286. [Google Scholar]
- Karlik, B.; Olgac, A.V. Performance analysis of various activation functions in generalized MLP architectures of neural networks. Int. J. Artif. Intell. Expert Syst. 2011, 1, 111–122. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Misra, D. Mish: A self-regulated non-monotonic activation function. arXiv 2019, arXiv:1908.08681. [Google Scholar]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and accurate deep network learning by exponential linear units (elus). arXiv 2015, arXiv:1511.07289. [Google Scholar]
- Mealpy. Available online: https://github.com/thieu1995/mealpy (accessed on 21 February 2025).
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32, 8026–8037. [Google Scholar]
- Ocak, A.; Işıkdağ, Ü.; Bekdaş, G.; Nigdeli, S.M. Prediction of Damping Capacity Demand in Seismic Base Isolators via Machine Learning. CMES-Comput. Model. Eng. Sci. 2024, 138. [Google Scholar] [CrossRef]
- Zhang, Z. Introduction to machine learning: K-nearest neighbors. Ann. Transl. Med. 2016, 4, 218. [Google Scholar] [CrossRef]
- Zhang, Z. Too many covariates in a multivariable model may cause the problem of overfitting. J. Thorac. Dis. 2014, 6, E196. [Google Scholar] [PubMed]
- Harrell, F.E. Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis; Springer: New York, NY, USA, 2001; Volume 608. [Google Scholar]
- Mellit, A.; Kalogirou, S. Artificial intelligence techniques: Machine learning and deep learning algorithms. In Handbook of Artificial Intelligence Techniques in Photovoltaic Systems; Academic Press: Cambridge, MA, USA, 2022; pp. 43–83. [Google Scholar]
- Subasi, A. Machine learning techniques. In Practical Machine Learning for Data Analysis Using Python; Academic Press: Cambridge, MA, USA, 2020; pp. 91–202. [Google Scholar]
- Nisbet, R.; Miner, G.; Yale, K. Chapter 9—Classification. In Handbook of Statistical Analysis and Data Mining Applications, 2nd ed.; Academic Press: Cambridge, MA, USA, 2018; pp. 169–186. [Google Scholar]
- Breiman, L.; Friedman, J.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Routledge: London, UK, 2017. [Google Scholar]
- Ye, J.; Dobson, S.; McKeever, S. Situation identification techniques in pervasive computing: A review. Pervasive Mob. Comput. 2012, 8, 36–66. [Google Scholar] [CrossRef]
- Li, X.; Wang, L.; Sung, E. A study of AdaBoost with SVM-based weak learners. In Proceedings of the Proceedings. 2005 IEEE International Joint Conference on Neural Networks, Montreal, QC, Canada, 31 July–4 August 2005; Volume 1, pp. 196–201. [Google Scholar]
- Dorogush, A.V.; Ershov, V.; Gulin, A. CatBoost: Gradient boosting with categorical features support. arXiv 2018, arXiv:1810.11363. [Google Scholar] [CrossRef]
- CatBoost Developers. Catboost Python Package. 2022. Available online: https://pypi.org/project/catboost/ (accessed on 21 February 2025).
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, S.; Qiu, Y. Optimization of random forest through the use of MVO, GWO, and MFO in evaluating the stability of underground entry-type excavations. Tunn. Undergr. Space Technol. 2022, 124, 104494. [Google Scholar] [CrossRef]
- Geisser, S.; Eddy, W.F. A predictive approach to model selection. J. Am. Stat. Assoc. 1979, 74, 153–160. [Google Scholar] [CrossRef]
- Mcknight, P.E.; Najab, J. Mann-Whitney U test. In The Corsini Encyclopedia of Psychology; Wiley: Hoboken, NJ, USA, 2010; p. 1. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).