Abstract
This paper introduces a conceptual mathematical framework for evaluating trustworthiness in AI-based big data analysis, emphasizing the critical role trust plays in the adoption and effectiveness of AI systems. The proposed model leverages the trustworthy AI-based big data management (TAI-BDM) reference model, focusing on three fundamental dimensions of trustworthiness: validity, capability, and reproducibility. It formalizes these dimensions mathematically, embedding them into a unified three-dimensional state space that enables the quantification of trustworthiness throughout AI-supported data exploration processes. It further defines update functions capturing the impact of individual data manipulation steps on overall system trustworthiness. Additionally, the paper proposes a scalar metric to integrate and evaluate these dimensions collectively, providing a practical measure of the overall trustworthiness of the system. The paper presents a starting point for modeling trustworthiness in TAI-BDM applications.
1. Introduction and Approach
Despite the current hype around artificial intelligence (AI) and machine learning (ML), their actual uptake and usefulness in industrial practice is arguably problematic: “If AI systems do not prove to be worthy of trust, their widespread acceptance and adoption will be hindered, and the potentially [...] economic benefits will not be fully realized” [1]. Large-scale projects, e.g., in the construction industry, “are characterized by carrying a high level of uncertainty and complexity” [2]. Risk identification is often based either on human experience or on statistical and quantitative analysis of individual past projects [3]. Correspondingly, the application of advanced or even fundamental big data analysis for a profound risk analysis is an widely unused option in that industry sector, even until today.
This research was motivated by [4,5] describing the AI-based data driven risk analysis (DARIA) approach (DARIA-A) in the following. It aims to identify financial risks in the execution phase of transportation infrastructure construction projects. DARIA-A encompasses experience-based financial risk identification processes. These processes could be organized and formalized as heuristics, but an IT-based automation support was still needed for scalability. Hence, a DARIA-A-based System (DARIA-S) was integrated into STRABAG’s productive IT-based risk controlling system and showed exceptional results. DARIA-S sometimes identified risky projects even when all other metrics within the other indicators of STRABAG were still not giving any indication of subpar performance [6].
The integration of its ML model (DARIA-AI) into the company’s existing processes took significantly longer than initially anticipated. The decisive issue was the inherent two-layered relationship between an AI-based system with its objective trustworthiness on the one hand and the subjective trust of its users towards the system on the other. Generally, users continuously and subconsciously try to ensure that their subjective level of trust placed in a system actually reflects its objective trustworthiness, resulting in so-called calibrated trust [7].
Trustworthiness, despite its recognized importance, plays a marginal role in practical implementation and is rarely a decisive factor in current industry deployments [8]. The EU’s approach to trustworthy AI, for example, emphasizes legal, ethical, and robustness principles and provides practical tools like the ALTAI assessment list, but these remain largely abstract and do not define mathematical models for trustworthiness [9]. The approach described below addresses the critical gap in mathematical models for software trustworthiness. While EU and NIST frameworks offer high-level principles, they lack systematic quantitative methods. We introduce a mathematical model defining trustworthiness through measurable metrics (e.g., transparency, robustness, fairness), enabling practical, actionable evaluation. These metrics integrate with tools like DARIA for automated assessments during development, contrasting with existing post hoc checklists and subjective approaches. While the TAI-BDM model provides a conceptual framework for integrating trustworthy AI into big data analysis workflows, it lacks formal mechanisms to measure or operationalize trustworthiness.
According to the empirical experience known as the AI pilot paradox, launching prototypes in organizations is deceptively easy but deploying them as pilots into production is notoriously challenging [10]. The calibrated trust of potential users depends on many factors that are difficult to describe technically. Thus, the users’ need for the trustworthiness of DARIA-AI had to be addressed by guarantees about its qualities, meaning validity, capability, and reproducibility (c.f. Figure 1). Finally, users developed such calibrated trust in DARIA-S sufficient for its roll-out [6].
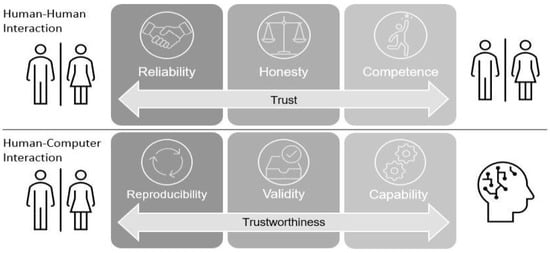
Figure 1.
Dimensions of trust and trustworthiness in the interaction between individuals as well as between individuals and systems, displaying the three basic concepts of trust in AI [11].
Consequently, DARIA-AI had to offer suitable indicators of its trustworthiness. This, in turn, required the introduction and evaluation of suitable metrics to qualify its trustworthiness (namely by its fundamental concepts validity, capability, and reproducibility). A first informal concept of trustworthiness could be introduced in DARIA-S only after and based on the human evaluation ratings, because of the lack of any suitable formalism. Although DARIA-S was based on TAI-BDM and therefore contains a trust bus, at least conceptually, its implementation was solely substituted by human evaluation.
In summary, the goal of this paper is the development of a conceptual mathematical model for the trustworthiness of an AI system, including the three basic concepts, validity, capability, and reproducibility. These were identified as relevant concepts for intelligent big data exploration systems by the TAI-BDM reference model, but have not yet been modeled rigorously.
More precisely, the problems to be addressed are the mathematical modeling of firstly each of the three basic concepts (validity, capability, and reproducibility) at any stage in a TAI-BDM-based data exploration session; secondly their dynamics related to subsequent TAI-BDM process steps; and thirdly the overall trustworthiness related to these components. Thus, the following research questions can be derived:
- RQ1.
- How can the three fundamental concepts validity, capability, and reproducibility of trustworthiness be mathematically modeled?
- RQ2.
- How can the relationship between the TAI-BDM-based data exploration process and the dynamics of these three concepts be integrated into that model?
- RQ3.
- How can the current overall trustworthiness of the AI-based data exploration system be integrated into that model?
This research on the trustworthiness of an AI system follows Nunamaker’s approach to system development [12] for the phases observation, theory building, implementation, and evaluation. Applying this re-iterative approach to designing a software model for trustworthy AI involves cyclical stages of conceptualization, development, evaluation, and refinement, integrating both technical and human-centric methodologies. In the observation phase, the TAI-BDM model of trustworthiness will be briefly reviewed in a selected relevant state-of-the-art Section 2.1 as a research objective. In the theory building phase, an initial sketch for a compound static mathematical model of the three concepts included in trustworthiness will first be presented. Next, this static model will become time dependent, reflecting each step of the TAI-BDM pipeline. Finally, and based on these findings, a scalar measure of trustworthiness will be defined. In summary, the need for the formulation of a conceptual mathematical model including a corresponding measure of trustworthiness has been motivated. Corresponding research objectives have been identified. In the next step, the selected state-of-the-art technology will be presented.
2. Selected State of the Art
An introduction to the reference model and a few necessary mathematical concepts are presented in the following.
2.1. The TAI-BDM Reference Model
The overall trustworthiness of a system depends on the trustworthiness of the outcome of an entire process [11]. Thus, the individual trustworthiness of every AI-supported step needs to be integrated into an overall trust building process. The trustworthy AI-based big data management (TAI-BDM) reference model integrates trustworthy AI into a complete big data analysis process and represents a data processing pipeline which was introduced in 2024 [11]. The TAI-BDM reference model is a conceptual framework designed to integrate trustworthiness into AI-driven big data analysis processes. By bridging the gap between AI theory and production, the TAI-BDM reference model aims to unlock AI’s societal and economic potential while maintaining trust. TAI-BDM’s definition of trustworthiness encompasses three features, namely capability, reproducibility, validity. These are aspects are denoted as “concepts” (see Figure 1). TAI-BDM is illustrated in Figure 2.
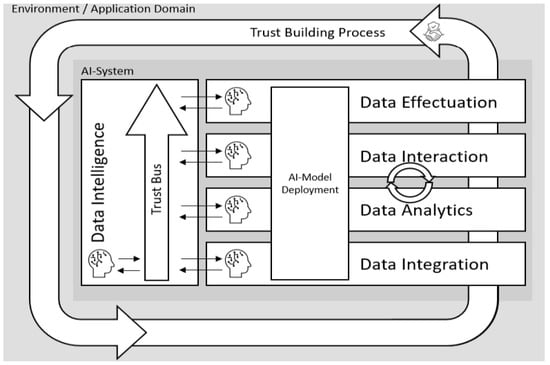
Figure 2.
Trustworthy AI-based big data management (TAI-BDM) reference model showing the trust-bus in relation to a data analytics pipeline [11].
Validation is “confirmation, through the provision of objective evidence, that the requirements for a specific intended use or application have been fulfilled” [13]. Validity can be determined by testing [14]. A number of validation techniques exist for AI systems [15], but their effectiveness depends on their alignment with the use-case.
AI capability is its performance toward its intended purpose, i.e., “the ability of an AI system to achieve its intended purpose” [16]. AI performance may be measured using goal-oriented metrics such as, e.g., “task completion time, financial cost and the practical implications of different types of errors” [17], or generic benchmarks like accuracy. Organizations also use key performance indicators (KPIs) to assess whether AI systems deliver on their intended purpose.
Reproducibility in AI means being able to consistently recreate a study’s results [18]. Reproducibility can be measured at different levels: repeatability, (in-)dependent reproducibility, and replicability, and the latter testing the generalizability of the method using a new implementation on new data.
Trust is based on the output of an individual or system [19]. Each layer of the conceptual TAI-BDM reference model (c.f. right side of Figure 2) produces its own output. Hence, each layer with AI support needs an individual trust component based on its output within the data intelligence layer. This part of the system represents the ability of the organization to acquire knowledge and skills in the context of big data management [20].
In order to gauge the trustworthiness of the AI-based big data analysis and to enable trustworthy AI [21], TAI-BDM stores partial information of trustworthiness for every layer, including information about previous interactions between individuals and the overall AI system. This constitutes “the emergent knowledge process” [20]. That process is symbolized by the outer loop of the conceptual reference model for trustworthiness in AI-based big data analysis (c.f. Figure 2).
Reis conceived AI2VIS4BigData as an adaption of IVIS4BigData, specifically designed for AI applications [22]. Based on that, the authors of this research introduced the concept of Abass’ trust bus as a reference architecture designed to enhance trustability analytics [11]. The “trust bus” is introduced as a reference architecture for trustability analytics, designed to be broadly applicable and to interact with all stages of AI2VIS4BigData analytics pipelines. Its main purpose is to synthesize and foster qualified trust between users (trustors) and AI systems (trustees), enabling self-assessment and user empowerment through transparency, explainability, and adaptability. TAI-BDM’s trust bus component facilitates this process of automatic trustworthiness assessment. This architecture aims to facilitate interactions within AI systems and between AI systems and users by synthesizing qualified trust through a rule-based expert system. The trust bus processes metadata to recommend analytics, preprocessing, and visualization methods that maximize user trust in different scenarios. Human domain experts can initially substitute such an expert system in early prototypes, which was the case in DARIA [5].
After choosing TAI-BDM as a model for trustworthiness in AI augmented data analytics pipelines, a suitable mathematical model of trustworthiness needs to be found, which will be explained in the following section.
2.2. Mathematical Foundations
A few mathematical tools are needed for a rigorous modeling of trustworthiness. These encompass topics from real-valued algebra, calculus, and geometry which can be found in foundational-level mathematical text books, e.g., [23]. Trust can be imagined as a point inside a unit cube, where each coordinate represents a different conceptual aspect of trust. The spot where the point lands shows how much of each aspect is present.
In mathematical terms, trustworthiness will be represented by vectors from the Euclidean vector space. These vectors will be denoted as “feature vectors”. Each vector specifies a point which is restricted to a certain compact subset of . These feature vectors and are represented by tuples of real scalars . The scalar values are denoted as “concept models” as they represent the trustworthiness concepts in a certain way. They serve as the “quality levels” of these concepts. Their numerical value determines the degree to which concepts are realized. Stakeholders may change with each step of an analytics pipeline, however. It is updated dynamically as data pass through the analytics pipeline. This dynamic process needs to be modeled mathematically: Updates of the state of trustworthiness are modeled by vector-valued functions. Hence, vectors are state vectors that model at a certain point in time. A real-valued measure function maps the state-vectors on a scalar value . Metrics are examples for those measures.
The concepts of validity, capability, and reproducibility are foundational to the trustworthiness of AI systems, but they are deeply interdependent rather than fully independent or “orthogonal” dimensions. This non-orthogonality introduces complexities analogous to those seen in physics when using non-orthogonal coordinate systems, though simplified representations are often adopted for practical modeling. Treating these concepts as orthogonal in an Euclidean vector space enables tractable models but ignores critical interactions. These relationships form a network of mutual reinforcement and constraint [24]. For example, efforts to improve reproducibility can uncover issues with validity (e.g., flawed experimental design), which in turn affect perceived capability.
3. Towards a Conceptual Modeling of Trustworthiness
As already introduced in Section 2.1, trustworthiness in a data exploration process based on the TAI-BDM reference model is determined by the three basic concepts, validity, capability, and reproducibility (c.f. Figure 1).
Initially tackling research question RQ1, each such concept will be formalized ad hoc as a corresponding mathematical concept model ( for capability, for reproducibility, and for validity). In general, these three concepts are not pairwise related in any systematic way, forcing the independence of these models. Each such incomplete and initial model aims to reflect the current quality of the relevant trustworthiness concept in a TAI-BDM-based data exploration process by a scalar value, which can then be interpreted by the semantics of the concept model. Therefore, handling scalars, these concept models can simply be embedded in three independent real-valued, one-dimensional subspaces .
For their further uniform analytical treatment including, for example, the modeling of correlations for use by the TAI-BDM trust bus (c.f. Figure 2), a comprehensive trustworthiness model , which integrates all three concept models, is needed. This model will be advanced in a follow-up paper. Each element of the current basic represents a state of trustworthiness completely characterized by the corresponding scalar quality levels of its integrated basic concept models (capability), (reproducibility), and (validity). As these are contained in three independent one-dimensional spaces , the trustworthiness state space can then be identified with a subset of by embedding each concept model in a different dimension: .
Any point can now be interpreted as a state s of trustworthiness, whose coordinate values directly reflect the related quality values of the three concept models , , and , respectively. For a precise distinction of the concept models and their discrete state values, the dimensions of , which embed the concept models, will be further denoted by uppercase letters and the coordinate values of concrete states by lowercase letters .
For the interpretability of their absolute values, each trustworthiness state coordinate should be restricted to a compact domain whose end points then denote zero or complete the satisfaction of the relevant basic concept, respectively. For simplicity and without loss of generality by appropriate normalization, all model concepts can be restricted to the unit range . Thus, finally, answering the research question RQ1, for the moment the compound trustworthiness state space of the concept models can be identified with the three-dimensional unit cube:
This is fundamentally a matter of normalization and practical application. It permits any value within the range from complete absence (0) to full expression (1) in each of the three conceptual dimensions of trustworthiness.
With a focus on research question RQ2, it must be noted, that each elementary data exploration step f in a TAI-BDM-based data analysis is characterized by the current AI2VIS4BigData [22] stage (e.g., “data integration” stage, “data analytics” stage etc.), the chosen data manipulation class (e.g., for “data integration”—the class of file import methods, for “data analytics”—the family of ML methods used), its selected parameters (e.g., for “data integration”—import specifications like file extension and delimiter, for “data analytics”—parameters of the chosen method) and all execution outputs (e.g., for “data integration”—imported data, for “data analytics”—method results). Summarizing all this manipulation step information in a multidimensional feature vector , its dynamic impact on the initial trustworthiness state can be modeled as an application of an appropriate update function in the model space :
must be determined for a specific algorithm and use-case in cooperation with domain experts, encoding the relevant features for trustworthiness. encompasses the meta-data flowing from the analytics pipeline in Figure 2 to the Trust Bus, needed, e.g., for reproducibility.
The environment variable is fixed throughout the whole process and reflects the general conditions of the data exploration session which are relevant for the trustworthiness of every state in the data exploration as, for example, the amount of expert knowledge needed available to the user or the quote of actually important but currently unreachable domain information. It should be estimated initially for each individual use-case with the help of domain experts.
Non-atomic data manipulation operations are performed by subsequently applying elementary operations with specified feature vectors. The related dynamics of the initial trustworthiness state can now be observed by the complex mapping built by the inversely concatenated corresponding basic update functions. However, since all single operations can also be interpreted as sequences of only one step, elementary or compound manipulation steps and simple or complex mappings, respectively, are no longer distinguished and simply be called manipulation steps f and their mappings .
The initial trustworthiness state at the very beginning of the data exploration process depends, of course, only on the global environment conditions, which are evaluated by the measure U. This starting point in the trustworthiness state space can then be simply modeled by the result of a corresponding, initially obligatory trustworthiness mapping .
In general, these trustworthiness mappings must at least meet the following dynamic conditions for consistency between the data exploration steps and the trustworthiness state trajectory built by the corresponding sequence of states:
- Commutativity. If in a data exploration situation for a manipulation step there exists an alternative algorithm leading to exactly the same output configuration as also the same produced insights and derived knowledge, their related trustworthiness state paths must end up at the same final point.
- Reversibility. If in an early TAI-BDM stage before any insight generation a data manipulation step can be fully reversed to exactly the initial data exploration configuration by an adapted redo operation, the corresponding compound trustworthiness mapping must act as the identity function.
Commutativity and reversibility are mainly of theoretical interest. In practice, different algorithms rarely produce identical results, and full reversibility in large-scale data processing can be impractical. However, these properties are important for understanding algorithmic principles.
Each use case has specific conditions for its trustworthiness modeling. These have to be described formally, leading to additional restrictions of the mapping functions. This may include, for example, the impossibility of complete trustworthiness. Finding heuristics for modeling mapping functions is left for future research and will be demonstrated in follow-up papers on a number of specific use cases.
Thus, initially answering the research question RQ2, changes in the concept models, which are introduced by a manipulation step f with parameters and global conditions U, can now be modeled by applying the corresponding mapping function to the related current state . The exact nature of these parameters will be scrutinized in future research.
Tackling research question RQ3 the three-dimensional states in need to be mapped to scalar measures of their overall trustworthiness. Therefore, an (overall) trustworthiness function has to evaluate the three coordinate values in an appropriate way, such that, comparing two points , their relationship can then be interpreted as being an overall more trustworthy state compared to its alternative .
For consistency, the trustworthiness norm must satisfy at least the monotony requirement; if two trustworthiness states are equal, except for one dimension with a value of less than or equal to that of , their overall trustworthiness values must satisfy the relationship .
For the meaningfulness of the absolute trustworthiness measure of a state , the norm should be bound by a compact domain. Without loss of generality, the trustworthiness function can be embedded in the unit interval as its unique minimal compact cover, implying the lower border condition of no trustworthiness at all. When a trajectory of trustworthiness states related to a sequence of data manipulation steps converges toward the ideal state , the minimality of the cover implies that its sequence of function values converges towards the upper bound value of one. In summary, the trustworthiness function is restricted to the domain .
As an example, every metric in immediately induces the trustworthiness norm that usually includes a balanced treatment, and therefore, the equal importance of the three dimensions. However, one could also implement a priority order of the concept models by building a transformed weighted sum of their coordinate values. A third use case variant could be the requirement of minimal concept model values for a positive overall trustworthiness. In that case, based on any metric , one could define using the cut function to implement the thresholds.
Thus, initially answering research question RQ3, the trustworthiness norm function provides a measure for the current overall trustworthiness for the TAI-BDM-based data exploration process. This measure fulfills the conditions but is ad hoc and needs to be evaluated in future research.
Imagine, for example, a scenario where the data effectuation phase is not suited to the intended end-user—for instance, because it employs an impractical data visualization approach. Doctors may misread outputs, delay treatments, and lose trust in the system despite its technical excellence. While validity and reproducibility remain unaffected, capability is severely compromised. As a result, the overall trustworthiness metric will drop significantly in such a case.
4. Conclusions and Future Work
This research discusses the development of a conceptual model for trustworthiness in AI-based big data analysis, focusing on the Trustworthy AI-based Big Data Management (TAI-BDM) reference model. The TAI-BDM model includes a trust bus component, which aims to enhance trustability through metadata processing and expert systems. However, the implementation of this trust bus was substituted by human evaluation in the DARIA project.
The research questions RQ1, RQ2, and RQ3 have been answered with the sketch of a mathematical model of trustworthiness as the main outcome. This sketch of a model integrates three fundamental concepts of trustworthiness; validity, capability, and reproducibility. The document highlights the challenges in achieving the widespread acceptance of AI systems due to issues of trust and proposes a mathematical framework to quantify these concepts and model their dynamics. It also introduces an overall trustworthiness measure.
A follow-up paper is planned that will apply the sketched mathematical model to a precise use case within DARIA’s context to demonstrate the model’s effectiveness, specifying the three concept models, appropriate mapping functions for each phase of the TAI-BDM reference model, and the overall trustworthiness measure.
For future research, several key areas are identified:
- Completing the model for learning trustworthiness: Developing a model that can learn and adapt trustworthiness based on acquired facts, potentially using, e.g., Bayesian methods, could enhance the dynamic nature of trust in AI systems. This model may also take dependencies between the concepts’ capability, validity, and reproducibility into consideration. The state space may be something different than the unit cube for advanced use cases, e.g., another convex subset of by giving the three concepts weights with .
- Implementing the trust bus architecture: In fact, coding and integrating the trust bus architecture into AI systems could significantly improve the user trust by providing a systematic framework for trust management. A new prototypical data analytics pipeline is currently being built according to TAI-BDM. It mimics the functionality of DARIA-S, but will be open source. A trust-bus component will be integrated. This prototype leverages existing workflow management systems (WMSs). One challenge is to replace the rather heavy Airflow in our prototypical AI2VIS4BigData analytics pipeline with a simpler modular system such as Luigi [25] or Prefect [26]. These should reduce maintenance overhead compared to Airflow.
- Evaluating the model of trustworthiness: Conducting thorough evaluations of the proposed trustworthiness model is crucial to ensure its effectiveness and applicability across different AI-based big data analysis scenarios. This involves assessing how well the model captures the dynamics of trust and its impact on user acceptance and system performance. This should also take the impact of dependencies between the concepts into consideration. A dual-phase validation approach stands to reason: Controlled scenario testing using synthetic datasets with engineered validity-capability-reproducibility profiles across the state space enabling the systematic analysis of trustworthiness trajectories through sequential manipulation steps . Secondly, empirical validation leveraging pseudonymized or masked longitudinal data from DARIA’s operational deployment. Structured expert interviews should be conducted in parallel as a complementary evaluation method.
Author Contributions
Conceptualization, S.B. and A.K.; methodology, M.L.H.; software, S.B. and A.K.; validation, S.B., A.K. and M.X.B.; formal analysis, S.B. and A.K.; investigation, S.B.; writing—original draft preparation, S.B. and A.K.; writing—review and editing, S.B., A.K., T.R. and M.X.B.; visualization, M.X.B.; supervision, M.L.H. and M.X.B.; project administration, S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Glossary of Mathematical Notations
| Trustworthiness state vector | |
| : Capability component, | |
| : Reproducibility component, | |
| : Validity component | |
| Trustworthiness state space defined as | |
| State update function | |
| : Feature vector of manipulation step, | |
| : Current trustworthiness state, | |
| : Environmental conditions factor | |
| Trustworthiness norm function | |
| Maps state vector to scalar trustworthiness measure |
References
- KPMG AG Wirtschaftsprüfungsgesellschaft. In Trust in Artificial Intelligence: A Five Country Study; The University of Queensland: Brisbane, Australia, 2021. [CrossRef]
- Cui, Q.; Erfani, A. Automatic Detection of Construction Risks. In Proceedings of the ECPPM 2021—eWork and eBusiness in Architecture, Engineering, and Construction, Moscow, Russia, 15–17 September 2021; CRC Press: Boca Raton, FL, USA, 2021; pp. 184–189. [Google Scholar]
- De Marco, A.; Thaheem, J. Risk Analysis in Construction Projects: A Practical Selection Methodology. Am. J. Appl. Sci. 2014, 11, 74–84. [Google Scholar] [CrossRef]
- FFG—The Austrian Research Promotion Agency. Data-driven Risk Analysis in the Construction Industry. In General Programmes 2022, FFG Project Number: FO999897631, Proposal Acronym: DARIA; FFG—The Austrian Research Promotion Agency: Vienna, Austria, 2022. [Google Scholar]
- Ivanova, M.; Grims, M.; Karas, D.; Höfinger, G.; Bornschlegl, M.X.; Hemmje, M.L. An AI-Based Approach to Identify Financial Risks in Transportation Infrastructure Construction Projects. In Artificial Intelligence Applications and Innovations; Maglogiannis, I., Iliadis, L., Macintyre, J., Avlonitis, M., Papaleonidas, A., Eds.; Springer: Cham, Switzerland, 2024; pp. 158–173. [Google Scholar] [CrossRef]
- Grims, M.; Karas, D.; Ivanova, M.; Bruchhaus, S.; Höfinger, G.; Bornschlegl, M.X.; Hemmje, M.L. Implementation and Rollout of a Trusted AI-based Approach to Identify Financial Risks in Transportation Infrastructure Construction Projects. In Proceedings of the Innovate 2025: World AI, Automation and Technology Forum, Davos, Switzerland, 16–18 April 2025. [Google Scholar]
- Wischnewski, M.; Krämer, N.; Müller, E. Measuring and Understanding Trust Calibrations for Automated Systems: A Survey of the State-Of-The-Art and Future Directions. In CHI ’23: Proceedings of the 2023 CHI Conference on Human Factors in Computing Systems; ACM: New York, NY, USA, 2023; pp. 1–16. [Google Scholar] [CrossRef]
- Horvat, S.; Horvat, T. Artificial Intelligence, Neurodiversity, and Trust: An Exploratory Overview. Humanit. Soc. Sci. Commun. 2024, 11, 1568. [Google Scholar] [CrossRef]
- Kortum, H.; Rebstadt, J.; Böschen, T.; Meier, P.; Thomas, O. Towards the Operationalization of Trustworthy AI: Integrating the EU Assessment List into a Procedure Model for the Development and Operation of AI-Systems. In Proceedings of the INFORMATIK 2023: 53rd Annual Conference of the Gesellschaft für Informatik e.V. (GI), Berlin, Germany, 26–29 September 2023; Gesellschaft für Informatik e.V.: Bonn, Germany, 2023; pp. 289–300. [Google Scholar] [CrossRef]
- Dekate, C. Gartner Predicts the Future of AI Technologies. 2020. Available online: https://www.cdotrends.com/story/14686/gartner-predicts-future-ai-technologies (accessed on 1 May 2025).
- Bornschlegl, M.X. Towards Trustworthiness in AI-Based Big Data Analysis; Research Report; FernUniversität: Hagen, Germany, 2024. [Google Scholar] [CrossRef]
- Nunamaker, J.F.; Chen, M.; Purdin, T.D. Systems Development in Information Systems Research. J. Manag. Inf. Syst. 1990, 7, 89–106. [Google Scholar] [CrossRef]
- ISO 9001:2015; Quality Management Systems—Requirements. International Organization for Standardization: Geneva, Switzerland, 2015.
- Zhang, J.M.; Harman, M.; Ma, L.; Liu, Y. Machine Learning Testing: Survey, Landscapes and Horizons. IEEE Trans. Softw. Eng. 2022, 48, 1–36. [Google Scholar] [CrossRef]
- Myllyaho, L.; Raatikainen, M.; Männistö, T.; Mikkonen, T.; Nurminen, J.K. Systematic literature review of validation methods for AI systems. J. Syst. Softw. 2021, 181, 111050. [Google Scholar] [CrossRef]
- European Parliament. Proposal for a Regulation of the European Parliament and of the Council Laying Down Harmonised Rules on Artificial Intelligence (Artificial Intelligence Act) and Amending Certain Union Legislative Acts; European Parliament: Strasbourg, France, 2024. [Google Scholar]
- Vaccaro, M.; Almaatouq, A.; Malone, T. When combinations of humans and AI are useful: A systematic review and meta-analysis. Nat. Hum. Behav. 2024, 8, 2293–2303. [Google Scholar] [CrossRef] [PubMed]
- Desai, A.; Abdelhamid, M.; Padalkar, N.R. What is reproducibility in artificial intelligence and machine learning research? AI Mag. 2025, 46, e70004. [Google Scholar] [CrossRef]
- Easton, D. A Re-Assessment of the Concept of Political Support. Br. J. Political Sci. 1975, 5, 435–457. [Google Scholar] [CrossRef]
- Kaufmann, M. Towards a Reference Model for Big Data Management; FernUniversität: Hagen, Germany, 2016. [Google Scholar]
- Abbass, H.A.; Leu, G.; Merrick, K. A Review of Theoretical and Practical Challenges of Trusted Autonomy in Big Data. IEEE Access 2016, 4, 2808–2830. [Google Scholar] [CrossRef]
- Reis, T.; Bornschlegl, M.X.; Hemmje, M.L. AI2VIS4BigData: A Reference Model for AI-Based Big Data Analysis and Visualization. In Advanced Visual Interfaces. Supporting Artificial Intelligence and Big Data Applications; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2021; Volume 12585, pp. 1–18. [Google Scholar] [CrossRef]
- Royden, H.L.; Fitzpatrick, P. Real Analysis, 4th ed.; Prentice Hall: Hoboken, NJ, USA, 2010. [Google Scholar]
- Manziuk, E.; Barmak, O.; Radiuk, P.; Kuznetsov, V.; Krak, I. Representation of Trustworthiness Components in AI Systems: A Formalized Approach Considering Interconnections and Overlap. In Proceedings of the ProfIT AI 2024: 4th International Workshop of IT-professionals on Artificial Intelligence (ProfIT AI 2024), Cambridge, MA, USA, 25–27 September 2024. [Google Scholar]
- Spotify. Luigi Documentation, Version 3.6.0; Spotify: Stockholm, Sweden, 2024. [Google Scholar]
- Prefect Technologies, Inc. Prefect: Pythonic, Modern Workflow Orchestration For Resilient Data Pipelines. 2024. Available online: https://www.prefect.io (accessed on 1 May 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).