Dynamic Algorithm for Mining Relevant Association Rules via Meta-Patterns and Refinement-Based Measures

Abstract

The mining of relevant association rules from transactional databases is a fundamental process in data mining. Traditional algorithms, however, will typically be based on fixed thresholds and general rule generation, with the result being large and redundant outcomes. This paper presents DERAR (Dynamic Extracting of Relevant Association Rules), a dynamic approach integrating structure pattern mining and dynamic multi-criteria filtering. The process begins with the generation of frequent meta-patterns. Each entity is given a stability score for its consistency across various data projections, then sorted by mutual information in order to preserve the most informative dimensions. The resulting association rules from these models are filtered through a dynamic confidence threshold that is adjusted according to the statistical distribution of the dataset. A final semantic filtering phase identifies rules with high coherence between antecedent and consequent. Experimental results show that DERAR reduces rules by up to 85%, improving interpretability and coherence. It outperforms Apriori, FP-Growth, and H-Apriori in rule quality and computational efficiency. DERAR consistently achieves lower execution times and memory use, especially on large or sparse datasets. These results confirm the benefits of adaptive, semantically guided rule mining for generating concise, high-quality, and actionable knowledge.

1. Introduction

Data mining is the process of discovering meaningful patterns from large datasets for effective decision-making. One of its techniques, association rule mining, discovers frequent co-occurrences in transactional data based on measures such as support and confidence [1,2]. The technique has extensive applications in various fields, such as business, healthcare, and finance. Support is an estimate of the frequency of an itemset occurring in the database, and confidence is an estimate of the probability that one item occurs together with another item [3]. An itemset is classified as frequent if its support exceeds or meets the user-defined threshold value. Association rule mining [2] generally comprises two distinct steps. Frequent itemsets are identified first based on the support threshold, and association rules are constructed in the second step, with rules with confidence values lower than a user-defined minimum threshold being eliminated to ensure their significance [4]. These techniques assist in removing non-significant relations and keeping just those with real analytical importance. An association rule is derived from an itemset I = {i₁, i₂, i₃, …, i_n}, where I is a set of distinct items. A transactional database DB = {T₁, T₂, T₃, …, T_m} contains a set of transactions, and each transaction is a subset of items in I. An association rule is represented as X → Y, where X and Y are subsets of I, satisfying the condition X ∩ Y = ∅, i.e., X and Y have distinct elements. Here, X is the antecedent (the preceding items), and Y is the consequent (the items related to X).

Various algorithms have been suggested to mine these kinds of rules, e.g., Apriori [3], Apriori-TID [3], and FP-Growth [4]. The Apriori algorithm adopts an iterative approach to discover frequent itemsets through the utilization of the anti-monotonicity property of patterns. Its greatest drawback, nonetheless, is the need for multiple scans of the database which significantly increases computational costs. A more efficient version, Apriori-TID, minimizes these scans by organizing transactions into preprocessed sets, thereby conserving memory. The FP-Growth algorithm, on the other hand, presents the tree-based data structure called the FP-Tree to make frequent pattern mining possible in a memory-efficient way without generating candidates. The algorithm is inefficient, however, when there are a very large number of distinct items, and trees become memory-intensive to handle. The Eclat algorithm [5] enhances the itemset mining via iterative intersections, and the High Utility Itemset Mining (HUIM) approach [6,7] takes into account the frequency and value of the items. One significant contribution to association rule mining is the H-Apriori [8] algorithm, which introduces a heuristic optimization of the standard Apriori method via the use of a support–leverage matrix. The matrix simultaneously examines both the frequency of occurrence of itemsets (support) and how much they diverge from statistical independence (leverage), thus enabling a more detailed assessment of rule significance. As compared to the traditional Apriori algorithm, which takes more than one database scan, H-Apriori attempts to operate in one pass by attributing weights to transactions in proportion to their relative significance in extracting useful patterns. Not only does this minimize processing time and space needs, but it also enhances the quality of rules generated.

Further studies have highlighted the necessity for taking special measures over specific fields in order to avoid the production of misleading or irrelevant rules. Additionally, they propose a multi-dimensional methodology for a more insightful analysis of associations, i.e., lift, conviction, leverage, and correlation [9], to further enhance the ranking or filtering of rules. Other advancements involve constraint-based mining [3], which incorporates user-specified knowledge to constrain the search space. More recently, information-theory-based approaches (e.g., mutual information) [10] have been applied to quantify the interdependence between itemsets. These approaches are designed to minimize output size but emphasize the most significant rules. There is also increasing acknowledgment in the literature that not all frequent co-occurrences are of equal relevance or usefulness. Additional studies [11] suggest that the selection of measures is extremely application-dependent, and there is no single measure that works well across all situations. The authors support a combined approach involving both quantitative measures and qualitative observations to enhance the quality and usefulness of the resulting models. Some researchers argue for the importance of semantic relevance and specificity in choosing rules—favoring rules that exhibit strong directional orientation or interpretability, instead of mere statistical correlation [12,13,14,15]. Nonetheless, this perspective remains inadequately explored in traditional association rule mining processes, which tend to favor quantity over clarity [11]. The current study concentrated on the meticulous refinement of association rule mining algorithms. Mudumba and Kabir [16] suggest a hybrid approach of various association rule mining techniques with a focus on how performance measures like memory and execution time influence data mining performance. Pinheiro et al. [17] present the use of association rule mining for enterprise architecture analysis, emphasizing the role of evaluation measures in determining interesting relationships in organizational databases. In a different work, Antonello et al. [18] present a novel measure for determining the effectiveness of association rules for discovering functional dependencies, which overcomes the drawbacks of conventional measures such as lift and suggests an improved way of quantifying relationships between items. Alhindawi [19] provides an exhaustive comparison of association rule mining with classification methods, detailing the impact of various measures (support, confidence, specificity) on the usefulness and accuracy of the induced rules. He et al. [20] proposed a GAN-based approach to multivariate time series temporal association rule mining. With generative adversarial networks, their approach learns complex temporal dependencies and enables the extraction of meaningful rules over time-aligned sequences. Although they primarily deal with the modeling of temporal dynamics in continuous data streams, this study tackles structural and semantic issues for static transactional data through the use of adaptive filtering and multi-level refinement approaches. Berteloot et al. [21] presented a new approach to association rule mining through the use of auto-encoders. Their approach leverages deep learning in order to learn compressed data representations, thereby facilitating the discovery of meaningful rules in high-dimensional settings. This method is more scalable and handles sparse or noisy data more effectively than conventional algorithms. Li et al. [22] optimized the Apriori algorithm by integrating web log mining techniques, thereby extending its usefulness in analyzing sports data. Their optimization is to minimize redundant computations and speed up the process of generating frequent itemsets, making the method more appropriate for large and dynamic settings. Dehghani and Yazdanparast [23] applied the Apriori algorithm to discover frequent patterns of symptoms in recovered and dead COVID-19 cases. The article illustrates the applicability of association rule mining to clinical data analysis, particularly for discovering significant combinations of symptoms in epidemiological research. Schoch et al. [24] utilized association rule mining for dynamic error classification in automobile manufacturing. Their approach enables the real-time detection of recurring fault patterns, improving industrial quality control process efficiency and reliability. The authors in [25] applied the Apriori algorithm to analyze the behavior of library users to discover patterns of borrowing behavior and service usage with a view to uncovering patterns of borrowing habits and service usage. Their study demonstrates how association rule mining can support data-driven decision-making in library service management and customization. The researchers in [17] tabulated and categorized novel association rule mining algorithms for application in enterprise architecture (EA) mining. The study maps 14 potential algorithms to categories like General Frequent Pattern Mining and High Utility Pattern Mining, providing a basis for EA model generation automation. Fister Jr. et al. [26] explored numerical association rule mining techniques for time series data in smart agriculture. The research suggested several algorithmic changes specifically designed to mine useful patterns from environmental and sensor data to facilitate informed decision-making in precision agriculture.

Despite substantial progress in association rule mining (ARM), the field continues to be afflicted by long-standing problems that limit the discovery of comprehensible, compact, and contextually meaningful sets of rules. Conventional algorithms such as Apriori and FP-Growth, while efficient for most applications, rely on global support and confidence thresholds that may not be inherently appropriate for the structure or variability of actual data. Low thresholds produce a profusion of meaningless or irrelevant rules, while too strict thresholds will prune out valuable patterns occurring with lower frequency. In addition, these methods provide purely frequency-based metrics, with no regard for important aspects such as semantic consistency, redundancy management, and logical correctness. In addition to this, they are afflicted with enormous computational burdens imposed by candidate generation and memory consumption, particularly for big or sparse data sets. Alternatives like H-Apriori attempt to mitigate some of these limitations through the use of heuristic techniques and support–leverage pruning but do not use adaptive or multi-dimensional rule evaluation.

In parallel, recent research in discovering relaxed or approximate functional dependencies (FDs) and association rules has increasingly turned to heuristic and metaheuristic techniques to handle the complexity of large and noisy datasets. These approaches are designed to find dependencies or rules that can withstand a specified amount of variation, thereby rendering them apt for noisy data environments encountered in reality. Specifically, evolutionary algorithms such as genetic algorithms have been effectively used to evolve candidate dependencies through iterative processes involving crossover, mutation, and fitness evaluation [27,28]. Similarly, metaheuristic optimization strategies have shown promise in navigating high-dimensional search spaces to uncover relaxed FDs with strong explanatory power [29]. Though effective, these approaches usually incur high computational costs since they are based on population-based search methods. Moreover, while these methods are conceptually related to association rule mining, most are intended for schema-level analysis and data quality applications, and not specifically tailored towards producing semantically meaningful rules for end-users.

This paper fills these gaps by presenting a multi-level, dynamic association rule mining algorithm called DERAR (Dynamic Extracting of Relevant Association Rules), which integrates structural compression through meta-patterns, statistical significance assessment using mutual information, and semantic filtering using a novel measure called the Target Concentration Measure (TCM). As shown in Figure 1, the process starts with a transactional dataset and undergoes a series of steps: meta-pattern extraction, mutual information assessment, adaptive filtering governed by the λ parameter, rule generation, and further semantic enrichment. In contrast to approximate functional dependency mining, DERAR does not enforce strict attribute determinism; rather, it is concerned with the extraction of rules that provide both statistical significance and semantic interpretability. Moreover, DERAR’s adaptive filtering is also conceptually related to heuristic optimization techniques used in FD discovery, in particular for reducing search space complexity and preferring high-quality patterns. By combining structural, statistical, and semantic constraints, DERAR strengthens traditional association rule mining and dependency mining approaches, hence offering an interpretable and flexible solution for large and varied data environments.

The central aims of this study are described as follows:

• To formulate a scalable multi-step rule mining process that incorporates statistical, structural, and semantic constraints.
• To introduce adaptive thresholding mechanisms based on mutual information and dataset-specific variability.
• To define and validate a novel semantic Target Concentration Measure (TCM) that calculates the concentration of rule consequents.
• To empirically compare the proposed algorithm with standard and new methods on different datasets, determining its performance in terms of rule quality, interpretability, and computational efficiency.

The DERAR method introduced in this paper offers a comprehensive solution that tackles the key issues in association rule mining, including redundancy, interpretability, and the capacity to deal with different data attributes. Engineered to work optimally on a wide range of datasets, it is geared towards producing rule sets that are not just concise but also contextually relevant, making it particularly well-adapted for applications for which scalability and semantic accuracy are critical.

The remainder of this paper is structured as follows: Section 2 introduces the methods of the proposed algorithm. Section 3 outlines the results obtained. Section 4 provides a discussion of the results and presents future research directions. Finally, Section 5 concludes the paper.

2. Methods

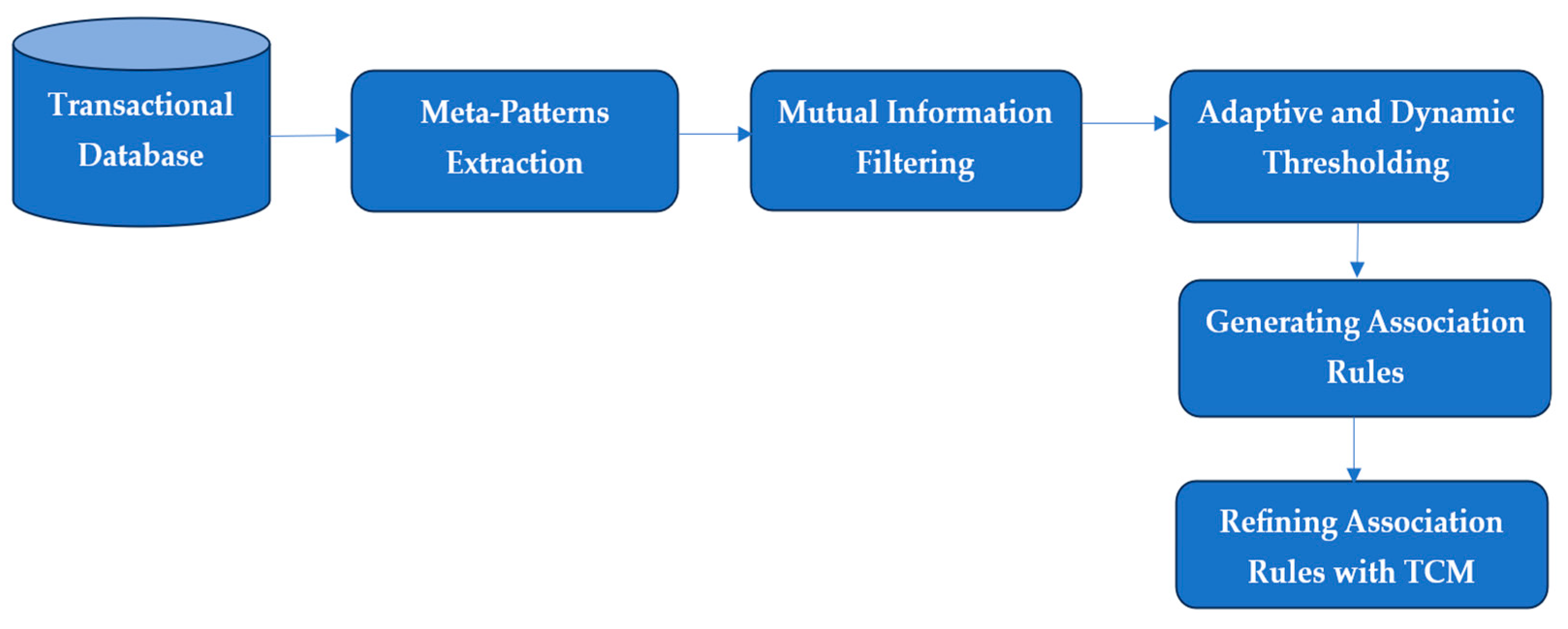
In this section, we provide our algorithm, DERAR (Dynamic Extracting of Relevant Association Rules), an adaptive rule filtering, statistical assessment integrating structural pattern optimization with statistical validation. DERAR presents a dynamic and intelligent filtering mechanism impacting selection criteria in terms of dataset features. Our algorithm is described by five prominent phases:

• Phase 1—Extraction of meta-patterns from a hierarchical transaction structure to group strongly co-occurring items and calculate stability score.
• Phase 2—Mutual information filtering, replacing purely frequency-based rating by finding statistically significant item associations.
• Phase 3—Adaptive and Dynamic Thresholding, where the decision criterion adapts to the distribution of mutual information, enhancing robustness.
• Phase 4—Generating Association Rules from validated meta-patterns, with confidence-based selection to retain the most valuable associations.
• Phase 5—Refining Association Rules through semantic coherence analysis among antecedents, ensuring clarity and reducing redundancy.

We discuss each phase in detail by providing a detailed explanation of the mathematical principles supporting our approach.

2.1. Extraction of Meta-Patterns

The DERAR (Dynamic Extracting of Relevant Association Rules) algorithm is based on the meta-pattern extraction. This stage is designed to effectively organize the dataset, optimize the identification of frequent itemsets, and reduce computational cost by establishing an efficient structure. DERAR uses hierarchical structuring to combine regularly co-occurring items into meta-patterns, unlike conventional techniques such as Apriori and FP-Growth, which produce an extensive number of itemset candidates and need numerous scans of the dataset. Association rule mining is more scalable since this method reduces duplication and enhances computing performance.

Building a meta-pattern tree initially permits the condensing and orderly arranging of the dataset. Item frequency determines each transaction’s sorting; frequent prefixes are combined into a hierarchical tree. Like the FP-Tree structure [4], this structuring method drastically lowers redundancy while frequently occurring patterns are grouped rather than handled individually for each occurrence. Using this tree-based compression assists the technique in improving processing performance by minimizing the number of database scans and memory usage.

DERAR generates candidate meta-patterns by finding itemsets that appear frequently in the structured representation once the meta-pattern tree is built. DERAR uses a more selective strategy, concentrating on patterns showing great co-occurrence and stability, instead of considering all possible subsets as possibilities. Closed itemset mining [30], where only maximal frequent patterns are retained to decrease redundancy, influenced this technique. This ensures that only significant item combinations are taken into account for additional processing, therefore preventing the exponential expansion of candidates, a typical difficulty in frequent pattern mining.

Promoted by the research of Agrawal et al. [2] and Han et al. [4], and to refine the selection of meta-patterns, we employ a score that compares the support of a pattern to its least strong sub-patterns. This score enables the selection of models without structural coherence in the dataset, but which may may be frequent. The stability score is computed by Equation (1):

$${\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}}(\mathrm{X})={\displaystyle \frac{\mathrm{S}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}\left(\mathrm{X}\right)}{\mathrm{m}\mathrm{i}\mathrm{n}\left(\mathrm{S}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}\left(\mathrm{s}\mathrm{u}\mathrm{b}-\mathrm{p}\mathrm{a}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{n}\right)\right)}}$$

(1)

where Support(X) represents the frequency of a set of elements X in the dataset, and min (Support (Sub-patterns)) corresponds to the lowest support among all subsets of X. The selection criterion is based on a threshold: if the stability score is greater than or equal to 80%, the meta-pattern is retained; otherwise, it is rejected. This choice of an 80% threshold is supported by empirical studies and recommendations from the literature [11,31,32] to eliminate insufficiently robust patterns while maintaining optimal coverage. This filtering mechanism confirms that only stable, recurrent, and representative patterns are maintained for the next phase of the algorithm. This concept corresponds with the measures of interest applied in data mining [9], where filtering based on the stability and coherence of patterns boosts the quality of the extracted rules.

Figure 2 shows an example of the DERAR meta-pattern extraction procedure. This figure provides a step-by-step illustration of the DERAR methodology with an example.

For instance, Figure 2a clearly shows that it is a transactional database involving six transactions of items {A, B, C, D, E}. This is used as the basis for pattern mining. Figure 2b demarcates the frequencies of individual items based on occurrence counts. The items are arranged in decreasing order based on their frequency. This ranking determines the item insertion order inside the meta-patterns tree to enable compression. In Figure 2c, we build a prefix-based meta-patterns tree to classify common item prefixes. The structure facilitates quick pattern generalization and meta-pattern mining. Item counts in each node represent the number of transactions sharing the same prefix path. Figure 2 provides a detailed analysis of the obtained patterns and their stability. It presents the different types of meta-patterns, classified into pairs (itemsets of size 2), triplets (size 3), and quadruplets (size 4), thus allowing for the observation of their evolution. For each meta-pattern, the table displays its support, which is related to the number of transactions in which it appears, and additionally, the minimum support of its sub-patterns, used to calculate the stability score. A meta-pattern is retained as stable and strong if its stability score is more than or equal to 80%. Conversely, it is deleted if its score falls below this level since it is considered too unstable or negligible for association rule extraction.

The meta-pattern extraction phase provides an organized, fast, and scalable technique for detecting frequent itemsets. The structured patterns acquired from this stage operate as a foundation for the mutual information-based filtering phase, which further benefits the quality of the extracted associations.

2.2. Mutual Information-Based Filtering

Following the stability score (≥80%), we first extract and filter the most stable meta-patterns; then, we proceed to the next phase: mutual information-based filtering. This stage requires improving the selection of patterns by removing those frequently associated but statistically independent and maintaining just the most significant associations between items. Widely employed in data mining and machine learning [9], mutual information (MI) is a basic measure in information theory [33], allowing the evaluation of statistical dependency between two items in a transaction. Unlike classical techniques based on support and confidence, which are constrained to the frequency of item occurrence, MI permits assessing the real strength of the relationship between items, surpassing simple frequency. It measures the degree of information one itemset offers about another, that is, how significantly the existence of a single element in a transaction affects the presence of another related item.

Cover and Thomas [33] present the mutual information for a pattern of N items {X₁, X₂, X₃, …, X_n}, as Equation (2):

$$\mathrm{I} ({\mathrm{X}}_1,{\mathrm{X}}_2,\dots ,{\mathrm{X}}_{\mathrm{N}})={\mathrm{P}({\mathrm{X}}_1,{\mathrm{X}}_2,\dots ,{\mathrm{X}}_{\mathrm{N}})\mathrm{l}\mathrm{o}\mathrm{g}}_2\left({\displaystyle \frac{\mathrm{P}({\mathrm{X}}_1,{\mathrm{X}}_2,\dots ,{\mathrm{X}}_{\mathrm{N}})}{\mathrm{P}\left({\mathrm{X}}_1\right)\mathrm{P}\left({\mathrm{X}}_2\right)\dots \mathrm{P}\left({\mathrm{X}}_{\mathrm{N}}\right)}}\right)$$

(2)

where P (${\mathrm{X}}_1,{\mathrm{X}}_2,\dots ,{\mathrm{X}}_{\mathrm{N}}$) is the probability of joint occurrence of the N items (Support(X)/Total Transactions) and P(${\mathrm{X}}_{\mathrm{i}}$) denotes the individual probability of each item ${\mathrm{X}}_{\mathrm{i}}$ (Support (${\mathrm{X}}_{\mathrm{i}}$)/Total Transactions).

The value of $\mathrm{I} ({\mathrm{X}}_1,{\mathrm{X}}_2,\dots ,{\mathrm{X}}_{\mathrm{N}})$ reflects the level of dependence among the items within the group.

• When $\mathrm{I} ({\mathrm{X}}_1,{\mathrm{X}}_2,\dots ,{\mathrm{X}}_{\mathrm{N}})$ > 0, the items tend to appear together more frequently than would be expected under statistical independence, indicating a meaningful dependency.
• When $\mathrm{I} ({\mathrm{X}}_1,{\mathrm{X}}_2,\dots ,{\mathrm{X}}_{\mathrm{N}})$ ≈ 0, the items are essentially independent, regardless of how often they individually occur.
• When $\mathrm{I} ({\mathrm{X}}_1,{\mathrm{X}}_2,\dots ,{\mathrm{X}}_{\mathrm{N}})$ < 0, their joint presence is less likely than predicted by their individual frequencies—a case that is typically not exploited in association rule mining.

Several papers have examined the application of MI in the context of data mining, especially for the selection of important and pertinent patterns [9]. It especially supports avoiding false positives in association rules, which are typical when only support and confidence are applied. Geng and Hamilton [11] indeed showed that by maintaining just those having a real statistical link, the use of MI enhances the quality of the obtained patterns. Commonly used in feature selection, this method facilitates the removal of irrelevant variables in machine learning [34]. Our method uses MI applied to meta-patterns following the phase of stability filtering. Retaining only the patterns with a strong statistical correlation provides confidence that the derived rules are based on meaningful association relations rather than on just frequent co-occurrences. Filtering by mutual information aims to assess the real strength of the relationships among meta-pattern items. Unlike classical approaches based just on support, MI enables statistical reliance between items to be measured and random associations not significant to be eliminated.

2.3. Adaptive and Dynamic Thresholding

Applying a fixed MI threshold can be limiting when the distribution of values varies across datasets. We apply a dynamic thresholding method based on MI dispersion, inspired by adaptive statistical techniques in data mining [10]. We evaluate the central tendency and MI value dispersion in the dataset by calculating the average (μ) and the standard deviation (σ). Particularly for data distribution analysis and population parameter estimation, the average is a frequently employed measure in probability theory and statistics [35]. Within the context of mutual information-based filtering, the average permits assessing the general degree of statistical dependency among the obtained items. It is defined as Equation (3):

$$\mu ={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N(A_i, B_i)$$

(3)

The MI value for each pattern is denoted by I ($A_i, B_i$), and N is the total number of meta-patterns that were considered. While μ reflects the central tendency, the standard deviation (σ) captures variability in association strength. The standard deviation is defined by Equation (4):

$$\sigma =\sqrt{{\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{(\left(A_i, B_i\right)-\mu )}^2 }$$

(4)

where a small value of σ denotes homogeneity and proximity to the average, a large value signifies important dispersion among the produced associations.

We establish a function that is dependent on the variance of the MI values; this allows for automatic threshold change according to the dataset structure, enabling dynamic filtering threshold adjustment. Several works in data mining and machine learning have investigated the concept of an adaptive threshold based on variance, especially for selecting optimal thresholds in classification and clustering techniques [9] and optimizing interest measurements of association rules [11]. Our method computes the dynamic threshold based on the following rules by Equation (5):

$${\mathrm{T}\mathrm{h}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{d}}_{dynamic}=\left\{\begin{array}{l}0.5 \mathrm{if} \sigma <0.1\times \mathsf{\mu } (\mathrm{small} \mathrm{dispersion}) \\ 0.3 \mathrm{if} 0.1\times \mathsf{\mu }\le \sigma <0.4\times \mathsf{\mu } \left(\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e} \mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\right)\\ 0.1 \mathrm{if} \sigma \ge 0.4\times \mathsf{\mu } \left(\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{g} \mathrm{d}\mathrm{i}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\right) \end{array}\right.$$

(5)

Inspired by data mining and machine learning, statistical and empirical approaches [8,10] guide the selection of thresholds 0.5, 0.3, and 0.1 for the dynamic adaptation of filtering based on mutual knowledge. These thresholds aim to modify the degree of pattern filtering depending on the dispersion of MI values in the dataset, providing an ideal balance between precision and recall of the produced patterns. When the standard deviation σ is small (σ < 0.1 × μ), it is reasonable to employ a strict criterion (0.5) because the MI values are similar and around the average in this case. A small dispersion suggests that the recovered associations have a rather homogeneous dependence, which facilitates more exact filtering to maintain just the most significant associations [9]. Low variance indicates the stability of the derived associations in dynamic threshold approaches in classification and data analysis; hence, this kind of strategy is frequently utilized where a stricter selection criterion is needed [11]. The threshold is set at 0.3 to permit certain flexibility of the filtering while maintaining adequate selectivity when the variance is moderate (0.1 × μ ≤ ϼ < 0.4 × μ). In this scenario, the dispersion is sufficient to show a diversity of dependencies between the elements. This method is compatible with the concepts applied in machine learning, where threshold regularization based on variance minimizes the filtering of possibly relevant patterns too extensively [36]. The MI values are greatly distributed when the variance is substantial (σ ≥ 0.4 × μ), indicating that some patterns have extremely high values and others very low. In this case, a 0.1 threshold is used to ensure the most relevant patterns possible while removing extremely low associations. This method minimizes data loss when the distribution of values shows great variability by using the concepts of adaptive threshold optimization [11].

Table 1. Obtained meta-patterns by threshold dynamic on MI.

Meta-Patterns	Support(X)	Mutual Information	Threshold Dynamic	Obtained?
{B, C}	4	−0.039	0.1	No
{B, E}	4	0.175	0.1	Yes
{A, C}	3	0.131	0.1	Yes
{B, C, E}	3	0.292	0.1	Yes
{C, E, A}	1	0	0.1	No
{B, C, E, A}	1	−0.078	0.1	No

presents the application of filtering based on MI in our example to the meta-patterns extracted following the stability phase, therefore enabling just the most relevant patterns to be retained for association rule extraction.

Table 1 includes highly supported meta-patterns with MI below the threshold due to insufficient statistical dependence, even though these patterns have high support. Patterns like {B, C} and {C, E, A} are rejected despite high support, due to low or null MI values indicating no statistical dependence. For instance, {B, E} shows non-randomly occurring together through sporting a MI value of (0.175). Additionally, {A, C} is preserved with a valid association identified by a MI of (0.131). The high mutual information (0.292) of the pattern {B, C, E} indicates a significant association between the three elements. This implies that the simultaneous presence of B and C significantly influences that of E, so validating their choice for the future stages of the process. The decision to retain or remove {B, C, E, A} is also based on its final MI value. If it is higher than the dynamic threshold, it will be adopted; otherwise, it will be removed.

This mutual information-based filtering facilitates identifying only meaningful patterns, therefore removing random or non-significant correlations. This method can assure a more consistent and interpretable rule extraction.

2.4. Association Rule Generation

After the discovery of robust meta-patterns, the subsequent task is the generation of significant association rules and the employment of a dynamic refining process for retaining only the rules with highly informative content. The aim of such an approach is to ensure that the rules chosen are not merely distinguished on the basis of frequency, but also effectively detect true dependence patterns between the items.

Association rules are derived from the meaningful patterns that were discovered previously. Each meta-pattern can be decomposed into several structured rules in the form of X→Y, where X is a subset of the model, and Y includes the other elements. For example, from the meta-pattern {B, E}, rule extraction produces the relations B→E and E→B. The aim is to mine the rules with a high level of reliability, as quantified using the following measures:

• Support [2]: Estimates the frequency of occurrence of the rule within the set of transactions as in Equation (6).

$$\mathrm{Support} (\mathrm{X}\to \mathrm{Y})={\displaystyle \frac{\mathrm{S}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t} (\mathrm{X}\cup \mathrm{Y})}{\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l} \mathrm{T}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s}}}$$

(6)

• Confidence [2]: Estimates the probability that Y will be visible when X is present by Equation (7).

$$\mathrm{Confidence} (\mathrm{X}\to \mathrm{Y})={\displaystyle \frac{\mathrm{S}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t} (\mathrm{X}\cup \mathrm{Y})}{\mathrm{S}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t} \left(\mathrm{X}\right)}}$$

(7)

After the association rules have been generated, it is crucial to use a last filtering step that retains only those with a high value of information. The standard techniques for selecting association rules are based on a predetermined threshold (e.g., confidence ≥ 50%), which is ineffective when the distribution of the measures is very different from one dataset to another [9]. Indeed, low variance in confidence values indicates that the majority of the rules have comparable values and hence can be subjected to a strict threshold. Conversely, high variance implies that too stringent a threshold will exclude potentially beneficial rules. To address dataset-specific variability, thresholds are dynamically adjusted using the average and standard deviation of confidence values. This method follows the principles of adaptive statistical techniques applied in data mining and machine learning [10].

We present an approach that adapts the thresholds based on observed confidence average (${\mu }_{conf}$) and standard deviation (${\mathsf{\sigma }}_{conf}$) values. The aim is to select only the most significant rules, but also consider the distribution of confidence values and not reject potentially useful rules just because of a fixed arbitrarily set threshold.

The average (${\mu }_{conf}$) is a measure of central tendency used to estimate the average value of the confidence levels observed in the generated association rules [37]. It is defined as Equation (8):

$${\mu }_{conf}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{f}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e} (X_i\to Y_i)$$

(8)

where N is the total number of rules generated. The standard deviation (σ), however, provides the range of values from the average. It is obtained from the formula [37] as Equation (9):

$${\mathsf{\sigma }}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{f}}=\sqrt{{\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{(\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{f}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e} (X_i\to Y_i)-{\mu }_{conf})}^2 }$$

(9)

The utilization of the range allows for dynamic adjustment of the thresholds according to variability in the confidence values, avoiding the arbitrary choice of excessively strict or loose thresholds. In particular, thresholds are varied as a function of the ratio ${\mathsf{\sigma }}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{f}}$/${\mu }_{conf}$, which is a measure of variability in rules produced. The filtration levels are as Equation (10):

$${\mathrm{T}\mathrm{h}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{d}}_{dynamiconf}=\left\{\begin{array}{l}0.7, \mathrm{if} {\mathsf{\sigma }}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{f}}<0.1\times {\mu }_{conf} \\ 0.5, \mathrm{if} 0.1\times {\mu }_{conf}\le {\mathsf{\sigma }}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{f}}<0.4\times {\mu }_{conf} \\ 0.3, \mathrm{if} {\mathsf{\sigma }}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{f}}\ge 0.4\times {\mu }_{conf} \end{array}\right.$$

(10)

This choice is well-grounded in the areas of statistical analysis and machine learning. When the variance is reduced (${\mathsf{\sigma }}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{f}}$ < 0.1 × ${\mu }_{conf}$), it averages that confidences are homogenous, which allows us to use a strict threshold (≥0.7) to retain only the most robust rules. Conversely, if the variance is modest (0.1 × ${\mu }_{conf}$ ≤ ${\mathsf{\sigma }}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{f}}$ < 0.4 × ${\mu }_{conf}$), there are strong disparities among a few rules, which call for an intermediate threshold (≥0). Lastly, with high variance (${\mathsf{\sigma }}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{f}}$ ≥ 0.4 × ${\mu }_{conf}$), there are rules with low confidence values and others with high confidence values. In this case, a less stringent threshold (≥0.3) is established to prevent excluding rules that may be relevant despite having slightly below-average confidence.

Previous work in data mining and machine learning thus influences the thresholds 0.7, 0.5, and 0.3 chosen. While Agrawal and Srikant [3] recommend a minimum threshold of 50% in traditional association rule extraction methods, the investigations by Tan et al. [8] reveal that typically considered accurate association rules when their confidence surpasses 70%. Moreover, Geng and Hamilton [11] suggest the need for a flexible threshold depending on data variance to prevent too strict or too flexible rule choosing. Our method thus depends on these concepts by suggesting an adaptive mechanism able to change the threshold depending on the particular properties of the investigated dataset.

Applying this method permits a flexible selection of association rules, ensuring that only those with real value for knowledge are retained. The suggested strategy assures optimal filtering, unlike fixed methods, which can be useless for datasets with a heterogeneous distribution of confidence values.

We applied our dynamic filtering approach to the subsets of meta-patterns retained from Table 1 {B, E}, {A, C}, {B, C, E} and identified five retained rules that satisfy the criteria of statistical significance and analytical relevance, after producing the association rules and using our computed dynamic threshold (0.5). Rules below this value and redundancies were discarded to ensure relevance and avoid overlap.

The selected rules are: B→E (Confidence: 0.659), E→B (Confidence: 0.604), C→A (Confidence: 0.706), A→C (Confidence: 0.564), B→E, C (Confidence: 0.535).

This approach balances statistical rigor with flexibility, ensuring that only the most relevant and non-redundant rules are retained for interpretation.

2.5. Refining Association Rules

The application of support and confidence measures in our algorithm is not enough to assess association rules; they both suffer from major drawbacks in the detailed examination of the logical consistency of these rules. Even though support identifies frequent rules, it does not provide a basis for determining the accuracy or specificity of the rule: a rule that is employed frequently may be insignificant or redundant. Confidence, however, calculates the probability that the consequent is present when the antecedent is known, but it fails to consider the variety of outcomes that a single antecedent can produce. A high level of confidence does not, however, ensure that the antecedent is uniquely associated with the considered consequent. If a rule has a confidence of 0.8 and is associated with multiple other consequences with the same confidence, it indicates that confidence alone cannot discover logical dispersion.

To overcome this limitation, we introduce the Target Concentration Measure (TCM) as an auxiliary measure. TCM gives a way to quantify the degree to which X is particularly concentrated around Y. In this case, the TCM supplements support and confidence with a structural and comparative component that assists in establishing well-defined rules, which are logically more powerful. The combined application of all three measures provides a finer-grained and more comprehensive assessment of the induced rules.

Formal Definition and Intuition of the Target Concentration Measure (TCM)

Let D be a transactional dataset, and let X⇒${\mathrm{Y}}_{\mathrm{i}}$ denote association rules where X ⊆ I is a fixed antecedent and ${\mathrm{Y}}_{\mathrm{i}}$ ∈ ${\mathrm{Y}}_{\mathrm{x}}$ = {${\mathrm{Y}}_1$, ${\mathrm{Y}}_2$,…, ${\mathrm{Y}}_{\mathrm{k}}$} is the set of consequents co-occurring with X. We define the Target Concentration Measure (TCM) for each rule X⇒${\mathrm{Y}}_{\mathrm{j}}$ as Equation (11):

$$\mathrm{TCM} (\mathrm{X}\to {\mathrm{Y}}_{\mathrm{j}})={\displaystyle \frac{\mathrm{S}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}(\mathrm{X}\cup {\mathrm{Y}}_{\mathrm{j}})}{\sum _{\mathrm{i}=1}^{\mathrm{k}}\mathrm{S}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}(\mathrm{X}\cup {\mathrm{Y}}_{\mathrm{i}})}}$$

(11)

• The numerator Support(X ∪ ${\mathrm{Y}}_{\mathrm{j}}$) measures the simultaneous frequency of the sets X and ${\mathrm{Y}}_{\mathrm{j}}$.
• The denominator $\sum _{\mathrm{i}=1}^{\mathrm{k}}\mathrm{S}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}(\mathrm{X}\cup {\mathrm{Y}}_{\mathrm{i}})$ represents the total frequency of X occurring with all its potential outcomes.

This measure quantifies the degree of semantic focus of the antecedent X on a particular consequent ${\mathrm{Y}}_{\mathrm{j}}$, normalized across all observed consequents of X. It functions as a probabilistic-like measure that strengthens the concept of confidence through the emphasis on logical exclusivity and specificity. To establish this measure, we show its inherent mathematical properties (normalization, boundedness, and interpretability) in Appendix A.

The perspective offered by TCM is especially useful in situations where an antecedent is implicated in numerous unrelated rules. An individual rule can exhibit high confidence; however, if X is also associated with several other results, the rule X⇒Y is logically uncertain and ambiguous. In that instance, only TCM enables the determination of the degree to which Y is favored compared to other consequences and hence makes it possible to identify the most precise or deterministic rules.

To effectively filter the most potential association rules with the Target Concentration Measure (TCM), we apply a dynamic filtering scheme, where the selection threshold is dynamically determined according to the statistical distribution of the scores. The dynamic threshold is formulated as Equation (12):

Θ = μ + λ⋅σ

(12)

where μ represents the average of the TCM scores, σ their standard deviation, and λ is a selectivity parameter. It is an important parameter as it provides the possibility to modulate filtering stringency according to analytical context and data variability. The choice of range λ ∈ [0.5, 1.5] is based on solid statistical grounds derived from the empirical rule distribution associated with the normal distribution [38,39]. The value of λ is selected according to the stringency level that the selection of the rules requires, combined with the extent of the variability discovered within the data. In fact:

When λ = 0.5, the threshold is set at μ + 0.5σ, and it retains approximately 30 to 35% of the most interesting rules. This flexible filtering procedure is especially appropriate at exploratory stages, or in high-variance situations where one would like to retain varied candidate rules.

For λ = 1.0, the threshold equals μ + σ, retaining approximately 16% of the most promising rules. This default value offers a trade-off between coverage and strictness, appropriate for semi-supervised, decision-making, or explanatory tasks.

Lastly, setting λ = 1.5 involves placing the threshold at μ + 1.5σ, which represents a statistical area encompassing just 6–7% of the densest rules. This level of stringent filtering is warranted in situations demanding absolute precision, e.g., personalized recommendation, medical diagnosis, or sensitive analysis.

The interval λ ∈ [0.5, 1.5] gives a systematic degree of flexibility regarding the threshold selection, supported on a robust statistical basis. It permits the varying strength of the filter to meet specific requirements of use (ranging from exploration, explanation, or recommendation) without compromising the mathematical integrity of the process. This approach eliminates the use of arbitrary thresholds by adhering to the actual score distribution, therefore providing a consistent probabilistic meaning. This method gives the user or the algorithm a degree of control over the density of rules retained, based on the goal of the analysis. The suggested approach is characterized by its generality, statistical validity, and straightforward integration with intelligent rule extraction procedures.

The Target Concentration Measure (TCM), based on dynamic filtering, adds structural and logical information to enable the discrimination of the most consistent rules, enhancing the semantic quality of the associations discovered. TCM is not intended to substitute traditional measures like support and confidence, but tries to supplement them. Whereas support is the general frequency of a given rule within the database, and confidence calculates the probability of Y given X, TCM clarifies another crucial aspect: the specificity of antecedent X concerning a singular consequent Y. In this way, a rule with both high confidence and high TCM is both probabilistically and precisely defined and therefore has greater explanatory power. On the contrary, a rule having high confidence and low TCM indicates a dispersion of the logical relation, i.e., X tends to have various consequences and therefore renders the rule less informative. The TCM offers a novel perspective of choice founded on discrimination of consequences and consequently is an effective tool for the purposes of explanation for decision-making.

The following

Table 2. Comparative overview of methods employed.

Measure	Advantages	Limits	What TCM Adds Additionally
Support	- Easy to calculate - Reflects the actual frequency - Robust to small datasets	- Favors frequent trivial rules - Ignores the distribution of consequences	TCM distinguishes whether this frequency is focused or dispersed
Confidence	- Intuitive probabilistic measure - Frequently used in practice	- Insensitive to the competition among several consequences - Can be high even if X is ambiguous	TCM completes the confidence by revealing the specificity of X→Y
TCM	- Evaluates the logical concentration of X - Normalized - Permits comparison between rules	- Depends on the availability of the rules X⇒Y - Not as well-known	Provides a structured, comparative, and standardized view on the consequences of X

summarizes the added value of TCM relative to traditional measures.

The pseudocode of our DERAR (Dynamic Extracting of Relevant Association Rules) approach is shown in Algorithm 1.

DERAR combines hierarchical pattern structuring, adaptive filtering based on mutual information and confidence, and semantic refinement via TCM. This ensures relevant, interpretable rules, even in large-scale datasets.

Algorithm 1: DERAR (Dynamic Extracting of Relevant Association Rules).

Input:    • DB: Transaction Database    • ${\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathrm{s}\mathrm{u}\mathrm{p}}$: Minimum support threshold    • ${\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathrm{M}\mathrm{I}}$: Initial minimum mutual information threshold    • ${\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{f}}$: Minimum confidence threshold to validate rules    • λ ∈ [0.5, 1.5]: Selectivity parameter for dynamic threshold for TCM Output:    • ${\mathrm{R}}_{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{d}}$: Final set of valid and relevant association rules    1. Construction of Meta-Patterns: 1.1 Initialize a Meta-pattern tree T. 1.2 For each transaction t in DB:        Insert into T by merging similar items. 1.3 Extract frequent meta-patterns X with support ≥ ${\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathrm{s}\mathrm{u}\mathrm{p}}$. 1.4 For each meta-pattern X:    • Calculate ${\mathrm{S}\mathrm{t}\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}}_{\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}$ (X) = Support(X)/${\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathrm{s}\mathrm{u}\mathrm{p}}$ (Sub-patterns).    • If ${\mathrm{S}\mathrm{t}\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}}_{\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}$ (X) ≥ 80%, retain X.    2. Filtering meta-patterns by mutual information with Dynamic Threshold: 2.1 For each meta-pattern X = {A, B, C, …}:    • Calculate MI, I (A, B, C) = P (A, B, C) × log (P (A, B, C) / (P(A) × P(B) × P(C))).    • If I (A, B, C) ≥ ${\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathrm{M}\mathrm{I}}$, retain X. 2.2 Calculate the average μ and standard deviation σ of MI values for meta-patterns X. 2.3 Calculate a Dynamic Adaptive Threshold for each meta-pattern X:    • If σ < 0.1 $\times$ μ, then ${\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathrm{M}\mathrm{I}}$ = 0.5 (Strict threshold).    • If 0.1 $\times$ μ ≤ σ < 0.4 $\times$ μ, then ${\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathrm{M}\mathrm{I}}$ = 0.3 (Moderate threshold).    • If σ ≥ 0.4 $\times$ μ, then ${\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathrm{M}\mathrm{I}}$ = 0.1 (Strong threshold). Retain X.    3. Generation of Association Rules: 3.1 Initialize R (set of association rules of the form X ⇒ Y). 3.2 For each meta-pattern X:    • Decompose X into possible subsets (A) → (B).    • Calculate Confidence (A → B) = Support (A, B) / Support (A).    • If Confidence (A → B) ≥ ${\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{f}}$, add A → B to R.    4. Dynamic Adjustment of Rule Filtering Threshold: 4.1 Calculate the average ${\mu }_{conf}$ and standard deviation ${\mathsf{\sigma }}_{conf}$ of mutual information values for generated rules. 4.2 Define a Dynamic Adaptive Threshold to filter rules:    • If ${\sigma }_{conf}<0.1\times {\mu }_{conf}$, then ${\mathrm{T}\mathrm{h}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{d}}_{dynamiconf}$ = 0.7 (Strict filtering).    • If $0.1\times {\mu }_{conf}\le {\mathsf{\sigma }}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{f}}<0.4\times {\mu }_{conf}$, then ${\mathrm{T}\mathrm{h}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{d}}_{dynamiconf}$ = 0.5 (Moderate filtering).    • If ${\sigma }_{conf}$ ≥ 0.4 × ${\mu }_{conf}$, then ${\mathrm{T}\mathrm{h}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{d}}_{dynamiconf}$ = 0.3 (Strong filtering). 4.3 Apply this threshold to dynamically filter generated association rules R.    5. Computing TCM and Filtering Association Rules: 5.1 Group all generated association rules R by their antecedent X 5.2 For each group ${\mathrm{G}}_{\mathrm{X}}$ of rules with the same antecedent X:    • Let ${\mathrm{Y}}_1$, ${\mathrm{Y}}_2$, …, ${\mathrm{Y}}_{\mathrm{k}}$ be all consequents such that for each I ∈ {1, …, k}, the rule X ⇒ ${\mathrm{Y}}_{\mathrm{i}}$ ∈ ${\mathrm{G}}_{\mathrm{X}}$    • For each rule X→${\mathrm{Y}}_{\mathrm{i}}$: ${\hspace{1em} \mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}}_{\mathrm{i}}$ = Support (X ∪ ${\mathrm{Y}}_{\mathrm{i}}$)    • ${\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{e}}_{\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}}$ = Sum of ${\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}}_{\mathrm{i}}$ over all ${\mathrm{Y}}_{\mathrm{i}}$    • For each rule X ⇒ ${\mathrm{Y}}_{\mathrm{i}}$:    TCM (X→${\mathrm{Y}}_{\mathrm{i}}$) = ${\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}}_{\mathrm{i}}$/${\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{e}}_{\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}}$ 5.3 Build the list ${\mathrm{T}\mathrm{C}\mathrm{M}}_{\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{s}}$ = {TCM(r) for all r ∈ R} 5.4 Compute μ = Average (${\mathrm{T}\mathrm{C}\mathrm{M}}_{\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{s}}$) and Compute σ =Deviation (${\mathrm{T}\mathrm{C}\mathrm{M}}_{\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{s}}$). 5.5 Compute dynamic threshold θ = μ + λ × σ 5.6 ${\mathrm{R}}_{\mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{d}}$ = {r ∈ R | TCM(r) ≥ θ} Return $R_{filtered }$

3. Results

In this section, we present the results obtained from applying our Dynamic Extracting of Relevant Association Rules (DERAR). We compare the results with those of conventional algorithms such as Apriori, FP-Growth, and H-Apriori based on several performance measures. We have taken into account five crucial factors in the analysis of results:

• Quantitative analysis of the resulting rules.
• Qualitative analysis of the resulting rules.
• Effect of TCM measurement on the logical integrity of rules.
• Computational efficiency: Execution time and memory consumption compared to other methods.
• Quantitative evaluation of λ-controlled dynamic Filtering: Impact analysis via precision, recall, and ROC metrics.

The experiments were conducted on a Windows 11 machine with an Intel^® Core™ i7-10875H processor clocked at 2.80 GHz, 16 GB RAM, and running Windows 11. The algorithms were implemented in Java with the NetBeans IDE.

3.1. Dataset Overview

Three datasets were selected from the UCI Machine Learning Repository [40]:

• Mushroom Dataset: The dense dataset contains descriptions of ~8124 mushroom samples, and ~119 various items. Categorical attributes were converted into transactions, and each feature is considered an item.
• Adult Dataset: Also called the “Census Income” dataset, this dense dataset contains ~48,842 instances with ~95 attributes and aims to predict whether a person’s annual income is above USD 50,000. The numerical attributes were discretized into discrete classes and then translated into transactions.
• Online Retail II Dataset: The sparse dataset includes all the transactions carried out between 1 December 2009, and 9 December 2011, by a United Kingdom-based online retailer. It has ~53,628 records with ~5305 attributes. It is typically used for sales pattern detection, customer segmentation, and market basket analysis.
• Retail Dataset: This sparse dataset, available at the SPMF website [41], contains ~88,162 retail transactions, widely used in frequent pattern mining and association rule mining, and ~16,470 items.

3.2. Analysis of Results

3.2.1. Quantitative Analysis of the Resulting Rules

One of the primary challenges in association rule mining concerns controlling the size of the rule set without sacrificing the identification of significant and useful patterns. Too many rules being generated may confuse the analyst and hide interpretations, particularly if a high proportion are redundant or have weak correlations. We present a quantitative comparison of the DERAR method with Apriori, FP-Growth, and H-Apriori in terms of the total number of rules generated on four benchmark datasets. We also investigate the impact of the λ parameter on the rule number and compare the scalability of all approaches.

Table 3. Number of rules generated by dataset and algorithm.

Dataset	DERAR (λ = 0.5)	DERAR (λ = 1.0)	DERAR (λ = 1.5)	H-Apriori	FP-Growth	Apriori
Mushroom	2140	1102	615	3120	4550	4690
Adult	3810	2230	1 072	4025	6324	6401
Retail	1965	982	410	1685	3723	3941
Online Retail	2540	1195	526	2090	5030	5197

gives a detailed summary of the number of definitive rules generated for various values of λ, compared to the traditional Apriori, FP-Growth, and H-Apriori approaches, on four different datasets.

Analysis by dataset:

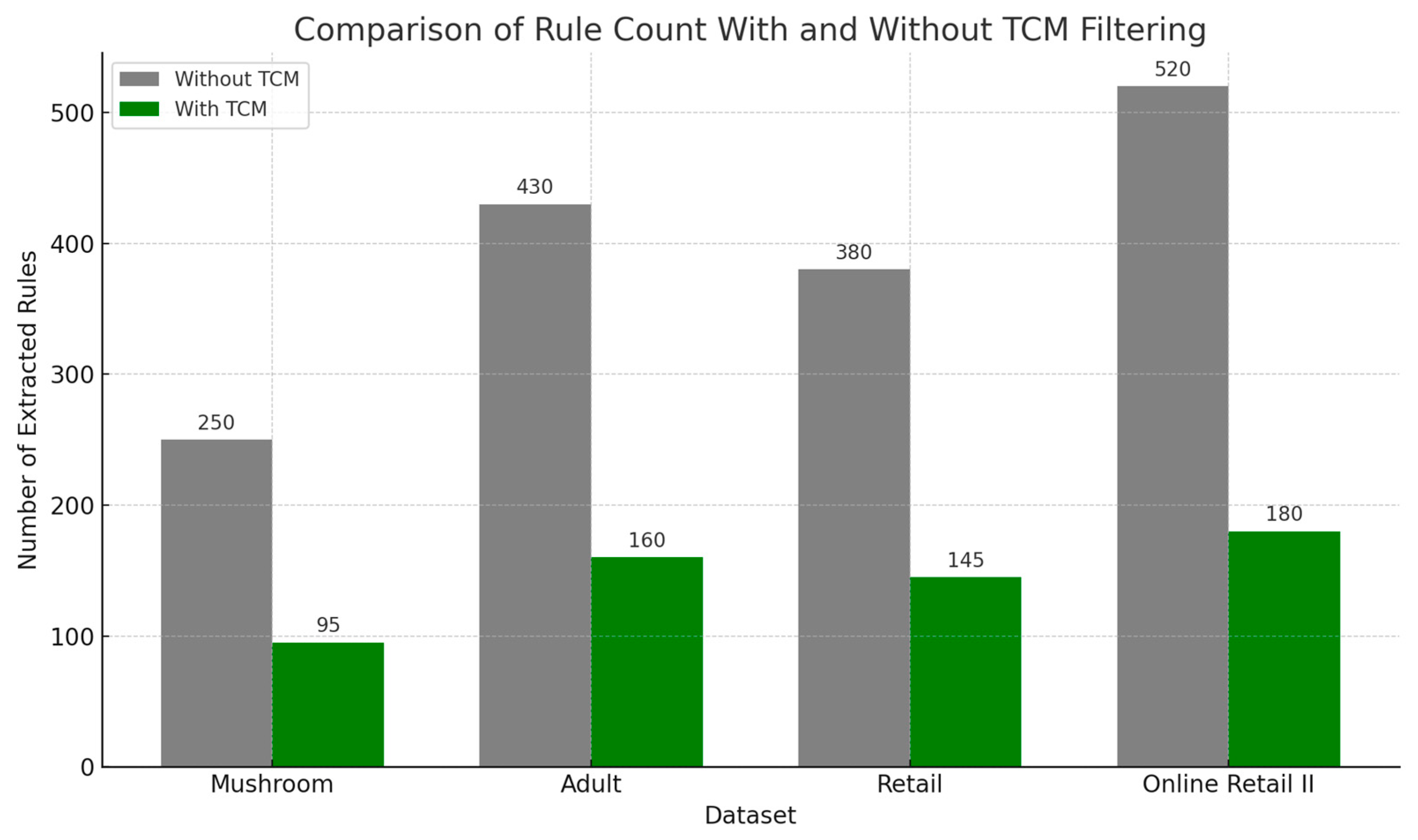
• Mushroom Dataset: consisting of structured and categorical data, normally generates a huge number of associations in classical algorithms. Apriori and FP-Growth both yield more than 4500 rules, whereas H-Apriori reduces this to 3120. In contrast, DERAR’s filtering mechanisms significantly minimize this quantity: from 2140 rules at λ = 0.5 to just 615 at λ = 1.5. This underscores the capacity of DERAR to remove redundant or weak statistical patterns while retaining important associations.
• Adult Dataset: with its socio-economic features and medium complexity, produces the largest rule counts of the datasets tested. Apriori and FP-Growth mine over 6300 rules. H-Apriori reduces this modestly to 4025. DERAR outperforms the three by a large margin by reducing the rule set to 2230 rules at λ = 1.0 and only 1072 rules at λ = 1.5. This result highlights the importance of both semantic and adaptive filtering for reducing cognitive overload in complex rule settings.
• Retail Dataset: This real-world dataset leads to over 3900 rules under Apriori and over 3700 with FP-Growth. H-Apriori improves output compactness to 1685. Yet DERAR offers even greater control: at λ = 1.5, only 410 rules remain, while still maintaining a high level of interpretability as previously demonstrated. This validates DERAR’s suitability for market basket analysis, where rule explosion is a common problem.
• Online Retail Dataset: Online Retail is the most sparse and high-dimensional dataset in this study. Classical algorithms suffer from a rule explosion, generating more than 5000 associations. H-Apriori cuts this by more than half (2090), but DERAR performs best with 1195 rules at λ = 1.0 and only 526 at λ = 1.5. These results show that DERAR handles data sparsity and dimensionality effectively by using dynamic thresholds and semantic structure to limit rule proliferation.

The quantitative findings in Table 3 clearly illustrate a definite and consistent decline in the number of rules generated with the increasing value of the λ parameter under the DERAR model. At λ = 0.5, DERAR manages to reduce the output by half that of Apriori and FP-Growth, with a volume close to that of H-Apriori. At λ = 1.0, there is approximately a 65–70% reduction in the number of rules, which is much less than that of H-Apriori. At the highest setting, λ = 1.5, merely 10–15% of the initial regulations are retained, substantiating DERAR’s superior capacity to outperform traditional and heuristic benchmarks in redundancy elimination. This finding attests to the efficacy of DERAR’s multi-level filtering algorithm, which consolidates structural compression and semantic prioritization. Notably, the λ parameter acts in a controlled and scalable manner—each increment yields a corresponding reduction without precipitous declines or undue loss of information. Consequently, it is an effective tuning mechanism that trades off coverage for conciseness and thereby tailors rule generation to varied application settings. In general, DERAR generates more compact and readable rule sets with high relevance, which makes it particularly well-suited for large-scale, noise-sensitive, or decision-critical settings.

3.2.2. Qualitative Analysis of the Resulting Rules

To complement the quantitative assessment of the rules generated by the different algorithms, we conducted a qualitative evaluation that addressed the interpretability of the rules produced.

Table 4. Comparative interpretability scores by datasets and algorithms.

Dataset	DERAR (λ = 0.5)	DERAR (λ = 1.0)	DERAR (λ = 1.5)	H-Apriori	FP-Growth	Apriori
Mushroom	66.67%	83.78%	96.00%	81.50%	69.80%	65.00%
Adult	57.95%	81.16%	95.83%	83.60%	71.30%	66.40%
Retail	48.20%	83.17%	95.83%	76.50%	68.20%	62.30%
Online Retail	46.40%	82.42%	93.85%	74.20%	65.00%	59.10%

presents the proportion of interpretable rules—that is, rules that were meaningful, specific, and not redundant on four datasets. Interpretability scores shown in Table 4 are derived from a qualitative assessment process with four main criteria: semantic clarity, low redundancy, domain relevance, and specificity. These criteria are often cited in the literature as standards for measuring the usefulness of association rules [9,11].

Semantic Clarity: This dimension refers to the degree to which a rule is comprehensible in its representation of a logical relationship between the consequent and the antecedent. Rules such as odor = foul → edibility = poisonous in the Mushroom dataset are comprehensible and readily interpretable. Rules such as sex = male → capital-gain > 0 (characteristic of baseline algorithms) are excessively general or vague. For interpretability testing, only rules that bore clear and direct causal or correlational importance were considered, thereby weighing the final scores heavily. Algorithms such as DERAR, when tuned to higher λ levels, encourage this level of clarity through semantic filtering naturally.

Low Redundancy: Rules were evaluated for redundancy—i.e., the degree to which they repeat similar logic using slightly different items or thresholds. For example, in approaches like FP-Growth and Apriori, it is common to find multiple very similar rules that differ in only one item (e.g., same antecedent resulting in multiple slightly different consequents). DERAR addresses this problem by systematically reducing and removing similar or overlapping rules. Interpretability penalties punish algorithms that generate too many complex, redundant rules, as this redundancy lowers the semantic value of the output.

Domain Alignment: Rules were judged based on their consistency with known or expected domain behaviors. For example, in the Adult dataset, education = masters → income > 50 K is domain-aligned, while marital status = divorced → income > 50 K may lack general validity. The closer a rule aligns with well-established patterns in the data domain, the more interpretable it is deemed. The use of mutual information and semantic emphasis by DERAR, as demonstrated via TCM, normally promotes such patterns, thereby enhancing its interpretability scores.

Specificity: Finally, rules were compared on whether their consequences were meaningful and focused. Rules like itemA → itemB (from Apriori) are statistically accurate, but not focused when itemA also predicts 10 other items. Specificity is best when the rule strongly concentrates its predictive capability on a single meaningful consequence. DERAR explicitly incorporates this by design through the λ-controlled filtering and concentration scoring mechanisms, which explain its superior performance in this measure.

The comparison includes several configurations of the suggested DERAR algorithm and three baseline benchmarks on the following datasets:

The Mushroom dataset, composed of categorical and well-structured attributes, shows robust results across all algorithms. Nevertheless, DERAR (λ = 1.5) achieves 96.00% interpretability, greatly surpassing H-Apriori (81.50%), FP-Growth (69.80%), and Apriori (65.00%). Even DERAR at λ = 1.0 provides 83.78%, indicating that the algorithm sustains high semantic precision under balanced filtering. This dataset illustrates that in highly structured settings, DERAR improves rule quality consistently.

The Adult dataset, having mixed socio-economic features with partial interdependencies, is a tougher terrain. Classical algorithms fare moderately: Apriori and FP-Growth are below 72%, while H-Apriori gives a little better interpretability of 83.60%. By comparison, DERAR (λ = 1.5) does 95.83%, whereas λ = 1.0 provides 81.16%, validating DERAR’s stability for moderately structured data. The low mark of λ = 0.5 (57.95%) further reinforces that a lenient filtering threshold preserves a lot of noisy or overlapping patterns.

The Online Retail II Dataset: This high-dimensional, sparse dataset is particularly prone to noise and redundancy. Interpretability is poor under Apriori (59.10%) and FP-Growth (65.00%). Even H-Apriori only reaches 74.20%. DERAR, however, excels in this context: at λ = 1.5, it reaches 93.85%, and even at λ = 1.0, the score is already high (82.42%). These findings prove that DERAR’s semantic and adaptive filtering capabilities are effective in the elimination of weak or spurious associations within complex transaction data.

The Retail dataset, a real-world market basket dataset with medium sparsity, demonstrates a similar trend. Conventional algorithms yield rules with reduced interpretability (ranging from 62.30% to 76.50%), whereas DERAR (λ = 1.5) attains 95.83%, and λ = 1.0 reaches 83.17%. The λ = 0.5 variant again performs worse (48.20%), emphasizing the effect of poor filtering. This validates the usefulness of semantic prioritization when rule sets are large and possibly overlapping.

The relative evaluation of interpretability on different datasets and algorithms highlights the continuing excellence of the proposed DERAR framework, particularly for λ values 1.0 and 1.5. Through its multi-dimensional evaluation based on semantic understandability, elimination of redundancy, conformity to domain relevance, and specificity, DERAR is successful in extracting rules that are not merely statistically strong but also logically consistent and semantically meaningful.

DERAR outperforms conventional algorithms such as Apriori and FP-Growth, which have the propensity to generate huge, redundant, and semantically diffuse rule sets, on all benchmark datasets. While heuristic approaches such as H-Apriori yield marginal gains, they remain bereft of adaptive, information-based filtering that enables DERAR to yield more concise and interpretable outputs.

This qualitative assessment validates that the inclusion of dynamic thresholds and semantic scoring greatly improves the relevance and utility of the ensuing rules. DERAR’s capacity to trade off rule quantity, simplicity, and domain consistency positions it as a viable contender for knowledge discovery tasks in the real world, where interpretability is paramount.

3.2.3. Impact of the TCM Measure on the Logical Quality of the Rules

Target Concentration Measure (TCM) was developed to overcome the inherent drawback of conventional approaches: the inability to quantify the logical consistency of a rule beyond frequency or statistical validity. In contrast to popular measures like support and confidence, which consider only the general associations between the antecedent and consequent, TCM concentrates on the capacity of the antecedent to effectively identify one prevailing consequent.

Figure 3 demonstrates the efficiency of Target Concentration Measure (TCM) in decreasing the rule set size considerably, showcasing its filtering capability. A comparison is shown regarding the number of rules extracted from four datasets (Mushroom, Adult, Retail, and Online Retail II) with and without TCM filtering. The gray bars show the total number of rules extracted without semantic filtering, whereas the green bars show the trimmed number of rules after TCM filtering is applied.

The examination of the figure discloses the uniform and remarkable decrease in the number of rules extracted following TCM filtering in each dataset. For the Mushroom dataset, the number of rules decreases from 250 to 95, denoting a decrease of more than 60%. For Adult, the count drops from 430 down to 160, whereas Retail drops from 380 to 145, and Online Retail II from 520 to 180. These outcomes show that TCM is able to filter out over half of the rules generated initially, only preserving those with a higher logical focus. This remarkable reduction not only reduces the overall output complexity but also increases the relevance and practical applicability of the resulting rules. TCM’s performance is accounted for by the fact that it manages to preserve just those rules that have an extremely high degree of logical coherence, with the antecedent considering primarily a dominant consequent. Through the elimination of redundant, general, or poorly discriminative rules, TCM assists in the production of a smaller, more accurate, and operational rule set. This fact is always realized in datasets of different sizes and levels of sparsity. Hence, the figure not only reveals the ability of TCM to decrease informational noise but also demonstrates its role in the overall quality of the induced rules, enhancing their interpretability and usefulness in decision-making contexts.

To further illustrate the practical importance of the Target Concentration Measure (TCM), we then show a selection of representative rules extracted from the Adult and Online Retail II datasets, categorized by their respective TCM scores.

Example 1: Adult dataset

• High-TCM Rule: education = Bachelors → income = High. (Support: 4.2%, Confidence: 72%, TCM: 0.94). Interpretation: The rule identifies a strong correlation between the possession of a bachelor’s degree and achieving high-income levels. The high TCM value reveals a high level of correspondence between the antecedent and a particular consequence, thus being very useful for the prediction of income or classification of the workforce.
• Low-TCM Rule: age = Middle → income = {Low, Medium, High}. (Support: 15.1%, Confidence: 56%, TCM: 0.34). Interpretation: Though frequent, this rule has a very dispersed set of consequences. The low TCM shows the lack of semantic concentration. Hence, it is not very useful for decision-making.

Example 2: Online Retail II Dataset

• High-TCM Rule: product_category = Stationery → country = United Kingdom. (Support: 3.8%, Confidence: 83%, TCM: 0.91). Use case: Helps to establish core markets for product-specific demand, guiding location-based inventory deployment.
• Low-TCM Rule: basket_size = Small → country = {UK, Germany, Netherlands, Others}. (Support: 10.5%, Confidence: 41%, TCM: 0.29). Use case: The widespread use of the consequent reduces the interpretability for supply chain optimization or targeted marketing.

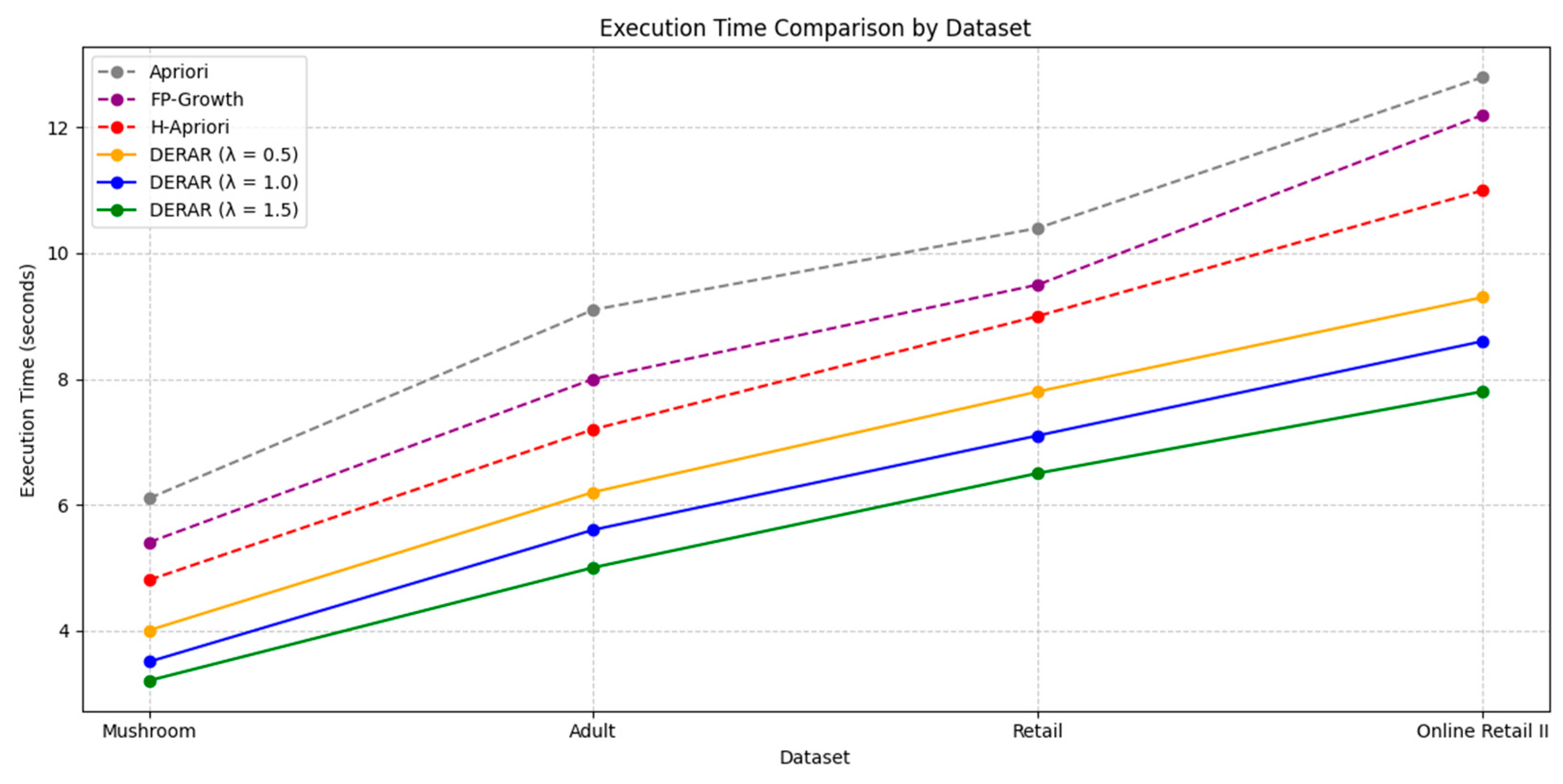
3.2.4. Execution Time

We compare the runtime performance of DERAR with Apriori, FP-Growth, and H-Apriori across four benchmark datasets. Execution time varies by dataset complexity and the value of the λ parameter. Figure 4 illustrates the execution times (in seconds) of the DERAR algorithm on four benchmark datasets—Mushroom, Adult, Retail, and Online Retail II—for various values of the dynamic selectivity parameter λ ∈ {0.5, 1.0, 1.5}, confirming the effectiveness of its adaptive rule generation strategy. The results are contrasted with the output obtained from the traditional Apriori, FP-Growth, and H-Apriori algorithms, which are commonly employed in association mining.

Mushroom Dataset: this small and structured dataset allows DERAR to outperform all the baselines at λ = 0.5. Higher values of λ boost efficiency as they enable the pruning of redundant meta-patterns early with minimal overhead because of the natural regularity of the data.

Adult Dataset: with partial correlations and medium dimensionality generates a rule explosion in Apriori and FP-Growth. H-Apriori is comparatively better at using heuristics. DERAR is more efficient across all λ levels, especially at λ = 1.0 and 1.5, where a majority of noisy associations are pruned.

Retail Dataset: The sparsity of the data set causes a combinatorial explosion under conventional methods. Though H-Apriori alleviates the problem to some extent, DERAR is more efficient for all values of λ. Filtering at λ = 1.0 and higher significantly reduces the rule space, thereby ensuring shorter runtimes.

Online Retail II Dataset: Both high-dimensional and extremely sparse, this dataset is the most computationally demanding. DERAR handles it best: λ = 1.0 skips most combinatorial overload, while λ = 1.5 runs the fastest by pruning low-value patterns aggressively.

Overall, the running time of DERAR is improved by its modular filter technique. As λ increases, the algorithm applies stricter semantic constraints, and fewer rules are evaluated. This control enables DERAR to adapt to different datasets and outperform Apriori, FP-Growth, and H-Apriori under all circumstances. Apriori and FP-Growth are not scalable due to full candidate generation. H-Apriori improves runtime via heuristics but remains limited by its frequency-based nature. DERAR, in contrast, combines meta-pattern compression, statistical analysis, and semantic filtering to sidestep low-informative candidate spaces at an early stage. This makes DERAR robust, efficient, and resilient to varying data complexities, especially for large-scale or high-dimensional scenarios.

Figure 5 presents a graphical comparison of the memory usage of Apriori, FP-Growth, H-Apriori, and DERAR algorithms on various datasets.

Across all datasets, DERAR has the lowest and most stable memory consumption, ranging from 92 to 116 MB across various λ values. FP-Growth has higher memory consumption, with a range of 158 to 160 MB, whereas Apriori has the highest memory consumption, with the highest being 235 MB for the densest dataset. H-Apriori has a modest reduction, with memory consumption ranging from 110 to 150 MB. These results confirm that DERAR, especially at large λ, is much more memory-efficient than both heuristic and traditional methods.

The memory analysis demonstrates dramatic variation among the various algorithms compared. As anticipated, DERAR consumes much less memory compared to the standard Apriori, FP-Growth and H-Apriori algorithms, independent of the dataset examined. This is attributable to the multi-level filtering approach of DERAR, which recursively decreases the volume of candidate rules stored in memory through the utilization of a combination of meta-patterns, mutual information, and the Target Concentration Measure (TCM).

The influence of the selectivity parameter λ is as follows: at λ = 1.5, the filtering process is stricter, and less specific rules can be eliminated quickly. This, in turn, results in a reduction in memory usage, even for large databases. With a less strict parameter (λ = 0.5), on the contrary, it results in more rule retention and, consequently, in higher memory usage. This adaptive control is a significant benefit of DERAR, as it permits flexible tuning of memory load based on analytic demands.

Among the conventional techniques, the Apriori algorithm is notable for its very high resource consumption, particularly in the Retail and Online Retail II datasets. This excessive overhead is inherent in its mechanism of work, involving candidate itemset generation and testing, which demands the utilization of multiple intermediate structures in memory. While more advanced, the FP-Growth technique also features a high resource demand, as it produces all frequent rules without any allowance for prior reduction or logical organization. H-Apriori introduces improvements through heuristic pruning, reducing memory usage compared to Apriori and FP-Growth. However, it still relies on frequency-based exploration and does not employ semantic reduction strategies, limiting its scalability in very large datasets. Generally, the curve shows how DERAR achieves precise memory control with integrity preserved on the derived rules. The fact that it can adjust to data sizes and complexities makes it a particularly suitable option for settings characterized by small resources or high volume.

3.2.5. Quantitative Evaluation of λ-Controlled Dynamic Filtering

In order to assess the influence of the λ parameter on the quality of rule selection, a comparison study was conducted on four benchmark datasets: Mushroom, Adult, Online Retail II, and Retail. Figure 6 presents a precision–recall analysis conducted with three λ values (0.5, 1.0, and 1.5), and each curve represents the performance metrics of a respective dataset. These ROC-type curves show the trade-off between recall, or the capacity to retain informative rules, and precision, or the density of semantically rich associations.

At λ = 0.5, the system applies permissive filtering, which achieves high recall rates (e.g., 91% for Mushroom), but the strategy is accompanied by low precision since it maintains a higher number of weaker or marginal rules. This discovery mode is beneficial when analysts wish to maximize coverage and avoid the elimination of potentially useful rules too soon.

As λ rises to 1.0, the algorithm is balanced between strictness and inclusiveness. In this setting, we observe a robust equilibrium between recall and precision, with consistently high F1-scores for all datasets. For example, on the Adult and Retail datasets, λ = 1.0 has more than 79% recall and 76–79% precision, indicating that it is highly suitable for applications demanding both rule relevance and representative coverage.

At λ = 1.5, filtering is more selective, reflected in a significant gain in precision (up to 91% on Mushroom and 88% on Retail), at the cost of a significant decrease in recall. Such a strict mode is ideal when the objective is to extract only the most concentrated and semantically consistent rules, practical in tasks like explainable AI or expert system design.

The building and differentiation of curves across λ values ensure that the DERAR model enables adaptive control of rule quality. The more heterogeneous datasets, such as Online Retail II, are more sensitive to λ changes and therefore display a more distinct differentiation between over-selection and under-selection. The Mushroom dataset, which is regular and structured, continues to be stable regardless of the variations in filtering strengths. Overall, this precision-recall characterization establishes that λ is an effective control lever, enabling analysts to tailor rule mining objectives to the needs of a specific domain, whether the emphasis is on breadth of discovery, interpretability, or decision relevance.

The experimental results point to several inherent limitations of traditional and heuristic-based approaches to association rule mining. Traditional algorithms, i.e., Apriori and FP-Growth, produce large sets of rules, most of which are expected to be redundant, trivial, or semantically insignificant. Their dependence on pre-defined support and confidence thresholds exposes them to data distribution shifts, typically leading to either excessively large rule sets or excessive pruning. While newer developments, such as H-Apriori, use heuristic approaches to reduce computational cost and rule quantity, they remain constrained by frequency-based assessment and do not address interpretability or semantic coherence issues in their entirety.

Furthermore, none of these methods provides dynamic, data-adaptive filtering operations with the capacity to modulate the level of selectivity based on contextual or application-dependent requirements. This shortcoming compromises their utility in large or heterogeneous datasets, where the capability to focus on meaningful and compact patterns is crucial. As a substitute, the proposed DERAR algorithm achieves general performance gains in rule relevance and resource consumption through its statistical, structural, and semantic filtering. These results highlight the need for more versatile and semantically aware solutions in the field of association rule mining.

3.3. Computational Complexity of the DERAR Algorithm

To ensure the theoretical soundness of our approach, we provide a phase-by-phase complexity analysis of the DERAR algorithm. While the O-notation disregards constant factors, it provides a consistent basis for judging the relative scalability of our method compared to baseline algorithms. The analysis shows that all essential parts of DERAR operate in polynomial time, with no exponential overhead, which is essential to process large-scale data sets. The complexity remains tractable even in the presence of semantic scoring and dynamic filtering thanks to early pruning methods that reduce the set of candidate rules and patterns.

• Meta-Pattern Extraction: this stage verifies all N transactions, with approximately I item per transaction, in order to categorize them into standardized pattern forms. The items of each transaction are set for uniform prefix alignment with a cost of O (I log I). Since this operation is performed for each transaction, the total cost becomes O (N × I × log I). This process is similar to preprocessing in FP-Growth and maintains scalability, even when run in parallel.
• Mutual Information-Based Filtering: Once meta-patterns are mined (P total), each is filtered based on mutual information to quantify the statistical dependence between items. Calculating MI is linear per pattern, and sorting the P values for ranking adds a log P term. Thus, the total cost is O (P × log P). This step eliminates noisy or weakly informative patterns prior to rule generation.
• Adaptive and Dynamic Thresholding of MI: Dynamic thresholding is applied to discard patterns with MI scores below an adaptive threshold. This threshold is determined from the distribution (average μ and standard deviation σ) of MI scores. As this process requires just one pass over the P-ranked patterns, this entails a linear complexity O(P). This process has minimal overhead but boosts selectivity.
• Association Rule Generation with Dynamic Filtering: The rule generation is performed only from the subset of selected meta-patterns, leading to a candidate set of R rules. Dynamic filtering of the rules is performed according to the λ parameter, which may involve sorting or indexing operations on support or confidence levels. The complexity is hence termed O (R × log R). This approach guarantees that the resulting rules are both targeted and computationally efficient.
• Semantic Refinement with TCM: Target Concentration Measure (TCM) is used to evaluate the logical focus of each rule. Since the TCM for each rule is computed separately from that rule’s support values, this step involves a single linear scan over all R rules. The complexity involved is therefore O(R). No sorting or recomputation is necessary at this stage.

Overall, DERAR has a complexity from quasi-linear to log-linear in its different stages, thus making it suitable for large-scale applications. The early filtering steps significantly reduce the number of patterns and rules, further reducing the computational cost in the later stages. This layered architecture makes DERAR distinct from conventional algorithms like Apriori, which is plagued by an exponential explosion in candidate generation and improves its efficiency for high-dimensional, sparse, or dense datasets.

3.4. Comparison with Related Algorithm

A comparison between the performance, flexibility, and quality of output of the DERAR, FP-Growth, and Apriori algorithms reveals significant differences in their respective characteristics.

• Execution time: DERAR outperforms Apriori and FP-Growth on each dataset. Despite heuristic pruning in H-Apriori, it continues to calculate huge candidate spaces. DERAR employs early structural and semantic pruning via the λ parameter, thus leading to faster convergence and fewer rule sets for increasing λ.
• Scalability: DERAR is scalable to large and sparse data such as Retail and Online Retail II. It is scalable because it prunes low-value candidates early. Apriori and FP-Growth are not scalable due to their exhaustive pattern enumeration. H-Apriori performs better than them, but is still limited by its frequency-based heuristic.
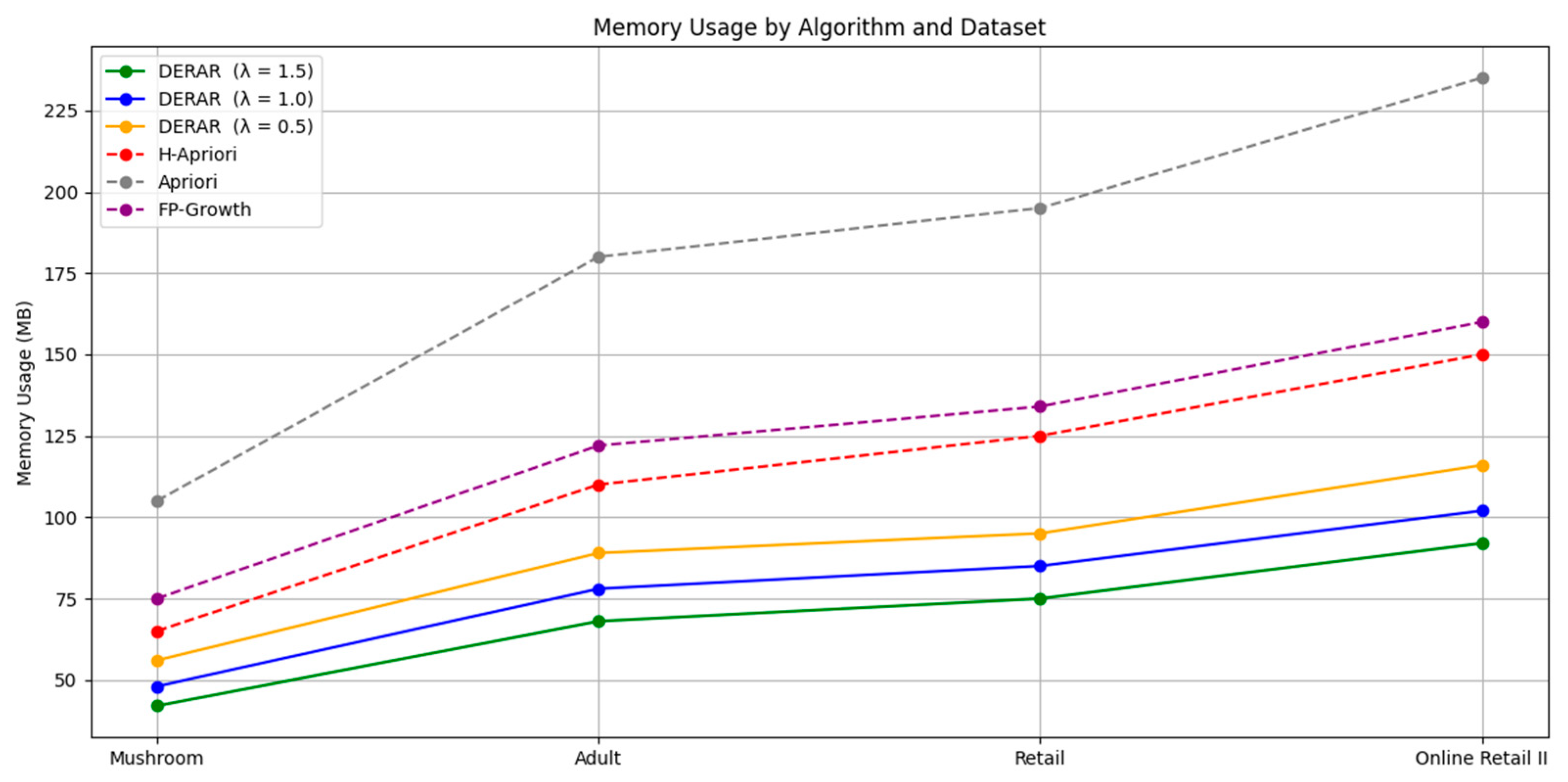
• Memory and Complexity: FP-Growth has linear memory growth with pattern frequencies, but Apriori’s exponential complexity limits its application. H-Apriori offers partial optimizations but no semantic filtering. DERAR’s meta-pattern compact structure and multi-layered filtering reduce memory usage and computational overhead.
• Logical quality of extracted rules: One significant benefit of DERAR is that it can generate rules of high logical quality. Through the use of the TCM measure, DERAR tends to support rules that link a single antecedent to a single consequent. This makes it possible to minimize broad rules and ambiguity. Apriori, FP-Growth, and H-Apriori, in contrast, due to the lack of semantic filtering, tend to generate numerous non-discriminative rules.
• Integrated semantic filtering: DERAR particularly incorporates an advanced filtering strategy in which the evaluation of rules is performed according to their structural form (meta-patterns), mutual information, contextual confidence, and logical density computed by TCM. Apriori, FP-Growth, and even H-Apriori only consider frequency thresholds alone and disregard the semantic context.
• Reduction of redundancy: Redundancy occurs frequently under the use of low thresholds in conventional algorithms. Although H-Apriori minimizes some redundancy through the utilization of heuristics, DERAR utilizes adaptive filtering combined with stability-based pattern selection to minimize redundancy greatly without compromising rule coverage.
• User control (dynamic λ): The introduction of the parameter λ in DERAR provides the user with a convenient way to dynamically adjust the level of selectivity. It is an effective method to manage the compromise between the number of rules and the targeted level of quality, an operation that is not possible with conventional techniques.

In summary, DERAR excels over traditional methods in all the important dimensions: speed, scalability, qualitative assessment, and flexibility. It is a solid and adaptive solution for association rule mining in applications where the quality and relevance of the knowledge gained are paramount.

4. Discussion

General interpretation of DERAR’s performance: A detailed comparison of the efficiency of the DERAR algorithm demonstrates that experimental results achieve notable enhancements in computational efficiency and logical consistency of extracted rules, as opposed to current techniques such as Apriori, FP-Growth, and H-Apriori. In terms of execution time, DERAR excels by effectively lowering the processing expenses, specifically for processing very large datasets (Retail, Online Retail II). This relies on multi-stage filtering at the high level: the initial discovery of meta-patterns, structuring through mutual information (MI) with dynamic thresholding, and ultimately selection through the Target Concentration Measure (TCM). This incremental architecture facilitates the removal of redundant or uninformative rules upstream, thus preventing the computational burden found in traditional methods.

Memory consumption follows a similar trend: DERAR consistently requires less memory than Apriori, FP-Growth, and H-Apriori. This is evidence of the structural and semantic reductionism built into the algorithm not only saving time but also hardware resources, a precious commodity when dealing with online or distributed analysis situations.

The semantic value of rules and semantic superiority: Along with efficiency, DERAR produces interpretable, high-quality rules. By leveraging the Target Concentration Measure (TCM), it promotes specific, logically coherent associations, reducing uncertainty common in confidence rule sets. The semantic orientation of DERAR enhances its usefulness in fields of application such as healthcare, marketing, and recommendation systems, where applicability and clarity are essential.

Scalability: Theoretically, DERAR scales both in time and space as the size of the dataset grows. The most time-consuming stage—meta-pattern extraction—scales linearly with the number of transactions N, moderated by a logarithmic factor because of item sorting within transactions. Subsequent phases, such as mutual information filtering and rule derivation, benefit from the reduced candidate space, especially since λ-controlled semantic filtering eliminates redundant computation. Space-wise, DERAR avoids huge intermediate data structures such as full FP-trees or candidate queues, uses compact meta-pattern representations, and thus memory usage grows sub-linearly with the number of item combinations available. Theoretical scalability is verified by empirical results across a variety of datasets, demonstrating that DERAR performs stably despite large increases in data size and item dimensionality.

Contextualization in terms of the existing literature: Several earlier efforts have suggested only algorithmic enhancements or new measures aimed at enhancing association rule mining [4,42]. Yet, none of these efforts attempt the multi-level strategy incorporating structure, information, and logic, which DERAR accomplishes. Additionally, the concept of a dynamic threshold governed by a selectivity parameter λ has not been thoroughly analyzed in earlier academic literature, although there is awareness that adaptive methods are advantageous in a range of contexts [11,43]. The novelty of DERAR is essentially that it can integrate statistical features (MI), structural features (meta-patterns), and semantic features (TCM), thereby improving simultaneously the accuracy and robustness of the generated rules.

Limits and constraints of the approach: Despite its promising performance, the DERAR method has some limitations. Firstly, the success of the rules partially depends on the quality of the mined meta-patterns in the first place; if they are too general or too specific, the process suffers from a lack of flexibility. Secondly, the selection of the parameter λ, while statistically grounded, can greatly influence the outcome and might need more accurate contextual adjustment. Furthermore, the DERAR algorithm exhibits sensitivity to extreme levels of sparsity, which may result in the premature exclusion of certain significant patterns. Lastly, while the dynamic strategy enhances relevance, it simultaneously adds a degree of tuning complexity for users lacking expertise.

Research perspectives: Numerous extensions can be considered as a follow-up to this study. First, the implementation of DERAR in a distributed setting (using Spark or MapReduce) would enable real-time processing of large-scale datasets. In addition, the introduction of dynamic meta-patterns that are responsive to individual profiles or domains would serve to further personalize the mining process. It would also be applicable to examine the integration of TCM with other measures (e.g., causality, stability, business cost) within a multi-criteria scoring system. Lastly, a promising direction for research would be the integration of DERAR with user feedback mechanisms, allowing automatic calibration of thresholds or filters according to the estimated utility of the rules produced.

5. Conclusions

We have introduced in this paper DERAR (Dynamic Extracting of Relevant Association Rules), a novel algorithm for the extraction of interesting association rules, grounded on a hierarchical combination of structural, informational, and semantic filtering processes. Through progressive incorporation of meta-patterns, mutual information with dynamic thresholding, and Target Concentration Measure (TCM), DERAR is able to extract rules that are characterized by conciseness, specificity, and interpretability.

The experimental results confirm that DERAR outperforms traditional and state-of-the-art algorithms in many significant aspects. It provides a significant reduction in rule number (up to 85% in comparison with Apriori), preserves high semantic density, and obtains lower execution time and memory consumption for a variety of datasets. These gains confirm that DERAR successfully trades off rule interpretability and computational efficiency. The introduction of the control parameter λ, allowing dynamic and adaptive filtering, offers a further mechanism to tailor completeness versus accuracy to the analytical objectives of the user. This flexibility positions DERAR especially favorably in contemporary data mining settings, where scalability and rule intelligibility have emerged as significant issues.

In future work, we aim to investigate the incorporation of DERAR within distributed or parallel architectures in order to achieve scalability for massive data streams. Furthermore, we aim to generalize the concept of semantic filtering to more intricate types of knowledge patterns like sequential, temporal, or graph-based rules. These proposed directions are designed to advance the applicability of DERAR in dynamic and heterogeneous data contexts and, consequently, improve its usefulness in decision-support systems.