A Process Tree-Based Incomplete Event Log Repair Approach
Abstract
1. Introduction
2. Related Work
2.1. Process-Model-Based Approach
2.2. Interpolation-Based Approach
2.3. Neural-Network-Based Approach
2.4. Trace-Clustering-Based Approach
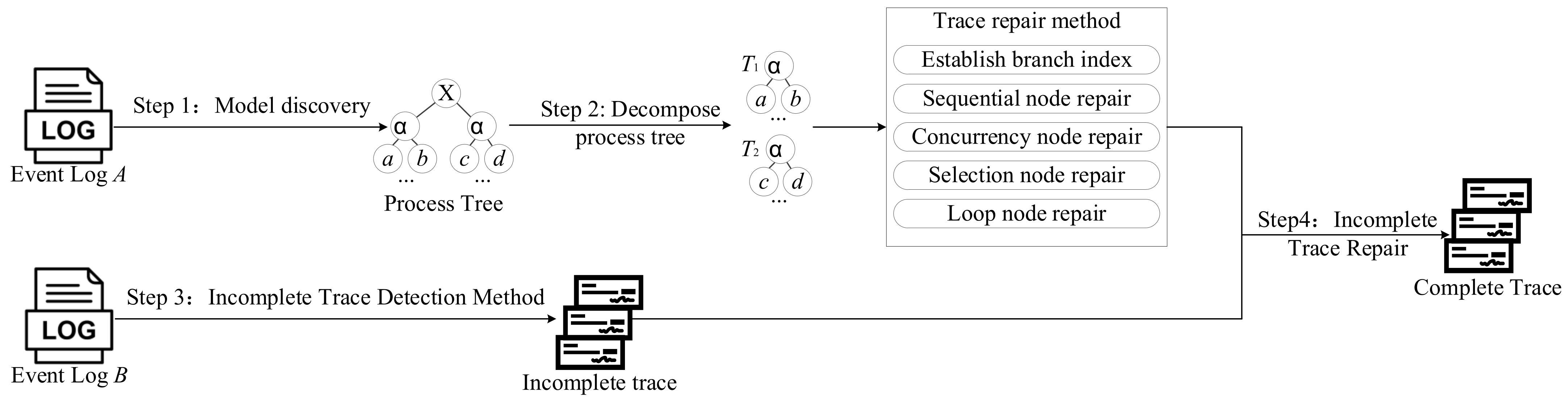
3. Incomplete Event Log Trace Repair Approach
3.1. An Approach Overview
3.2. Model Discovery
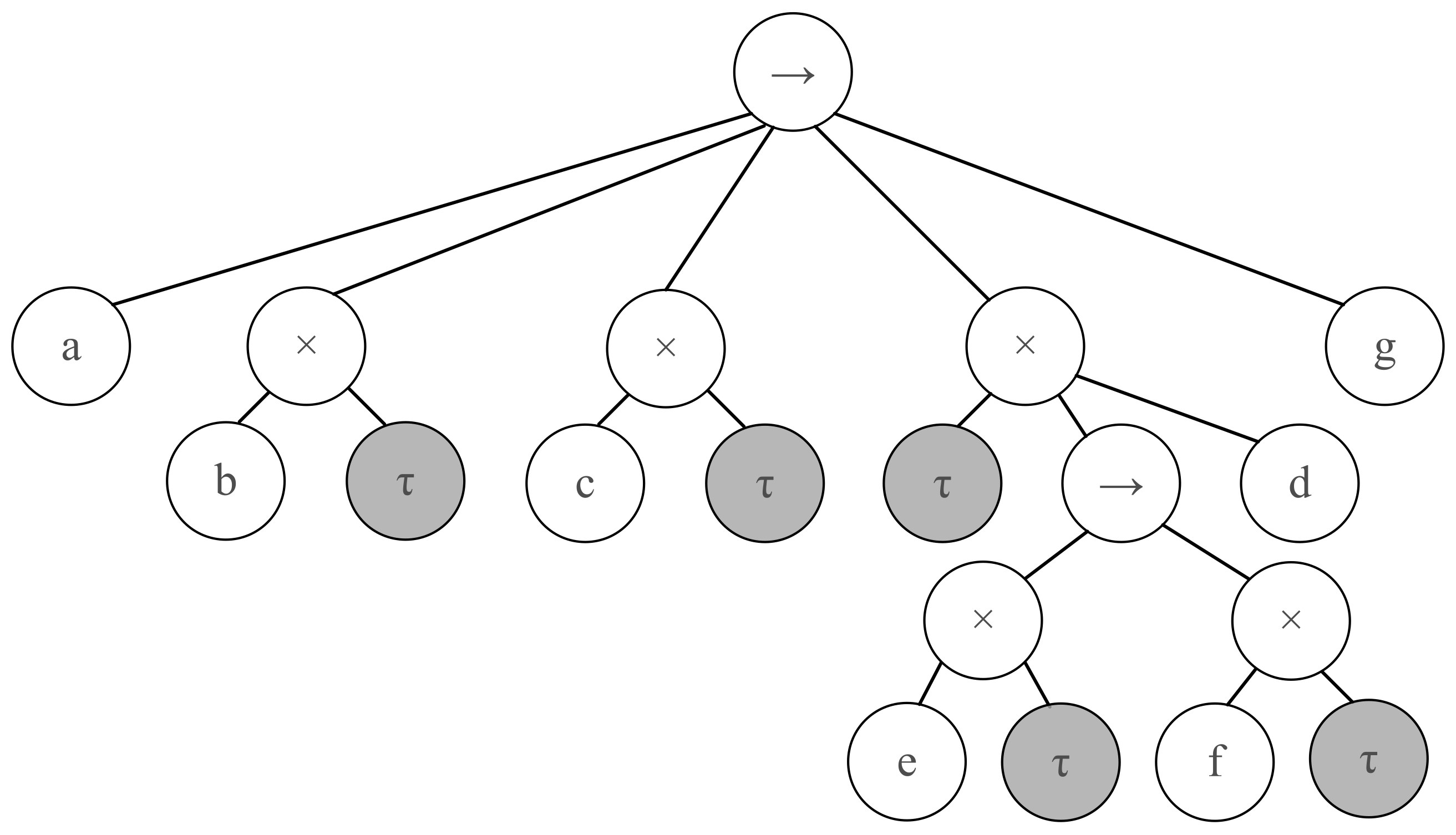
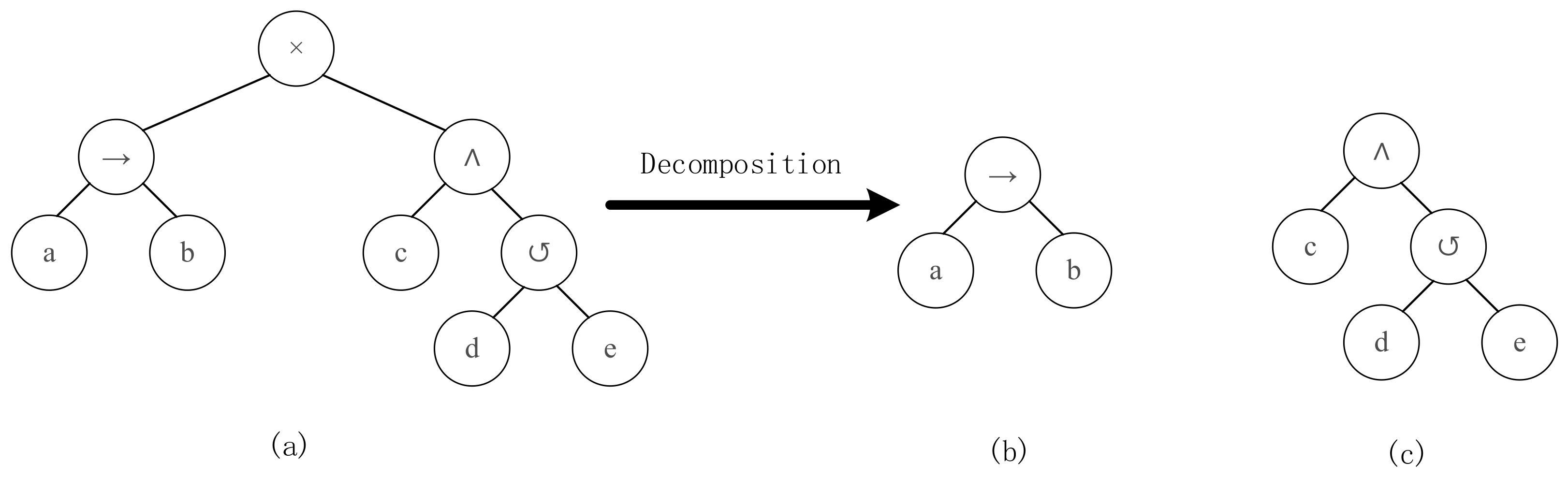
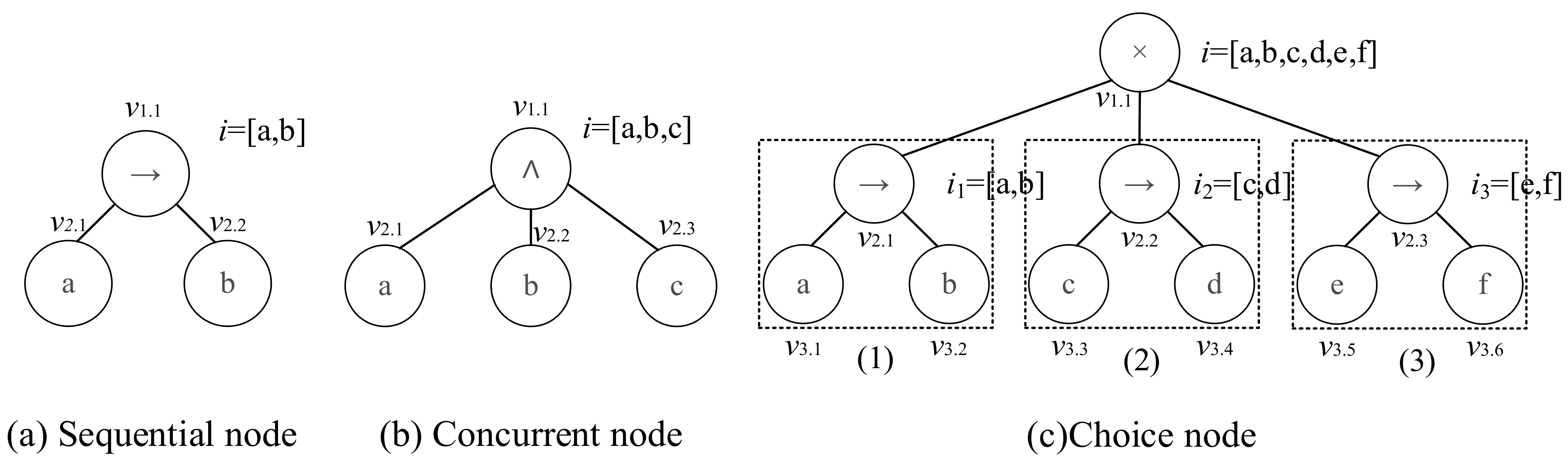
3.3. Process Tree Decomposition
3.4. Incomplete Trace Repair
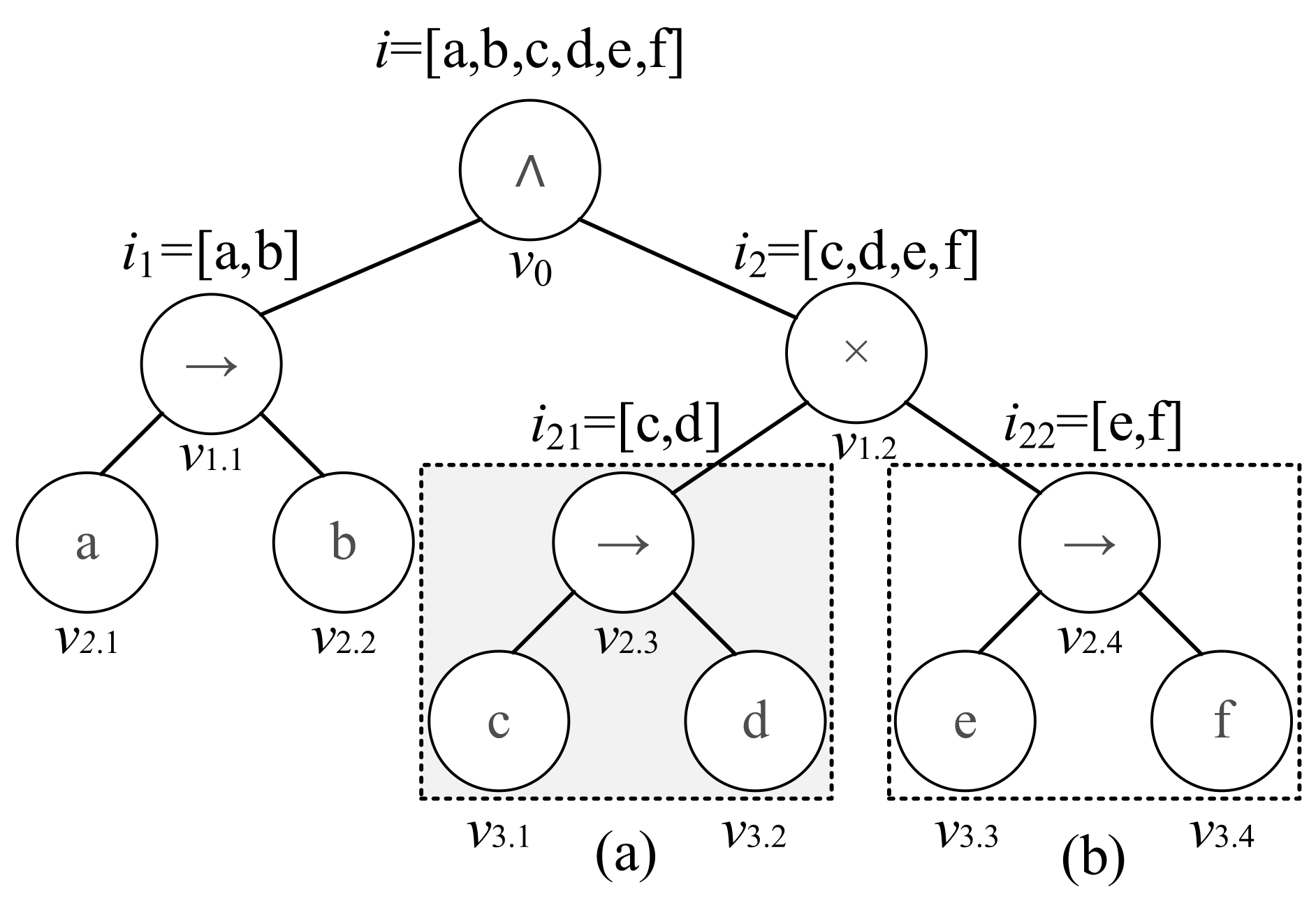
3.4.1. Branch Index Construction
3.4.2. Operation Node Repair
- Sequential Node
- 2.
- Concurrent Node
- 3.
- Choice Node
- 4.
- Loop Node
| Algorithm 1: Loop iteration determination |
| Input: loop node Loop, trace t Output: current loop node iteration count num 1. initial loop_count_list, num, loop_count = 0 2. while child in Loop.children do 3. if child.operator == Operator.XOR then 4. while xor_child in child do 5. if xor_child.label ! = None then 6. xor_join = intersection_of_lists(t, child.label) 7. loop_count_xor += max_occurrences(xor_join, t) 8. end if 9. if xor_child.operator! = None then 10. loop_count_xor += JudgeLoopCount(xor_join, xor_child) 11. end if 12. end while 13. loop_count = loop_count_xor 14. end if 15. if child.operator == Operator.PARALLEL or Operator.SEQUENCE then 16. while child_para_seq in child do 17. if child_para_seq != None then 18. loop_count_para_seq = max_occurrences(child_para_seq.label, t) 19. loop_count_para_seq_list.add(loop_count_para_seq) 20. end if 21. if child_para_seq.operator != None then 22. loop_count_para_seq = JudgeLoopCount(child_para_seq.label, t) 23. loop_count_para_seq_list.add(loop_count_para_seq) 24. end if 25. end while 26. loop_count = max(loop_count_para_seq_list) 27. end if 28. if child.operator == Operator.Loop then 29. if Intersection_of_lists(child.label, t) then 30. loop_count_loop = 1 31. end if 32. end if 33. end while 34. return loop_count |
4. Experimental Evaluation
4.1. Benchmark Approaches
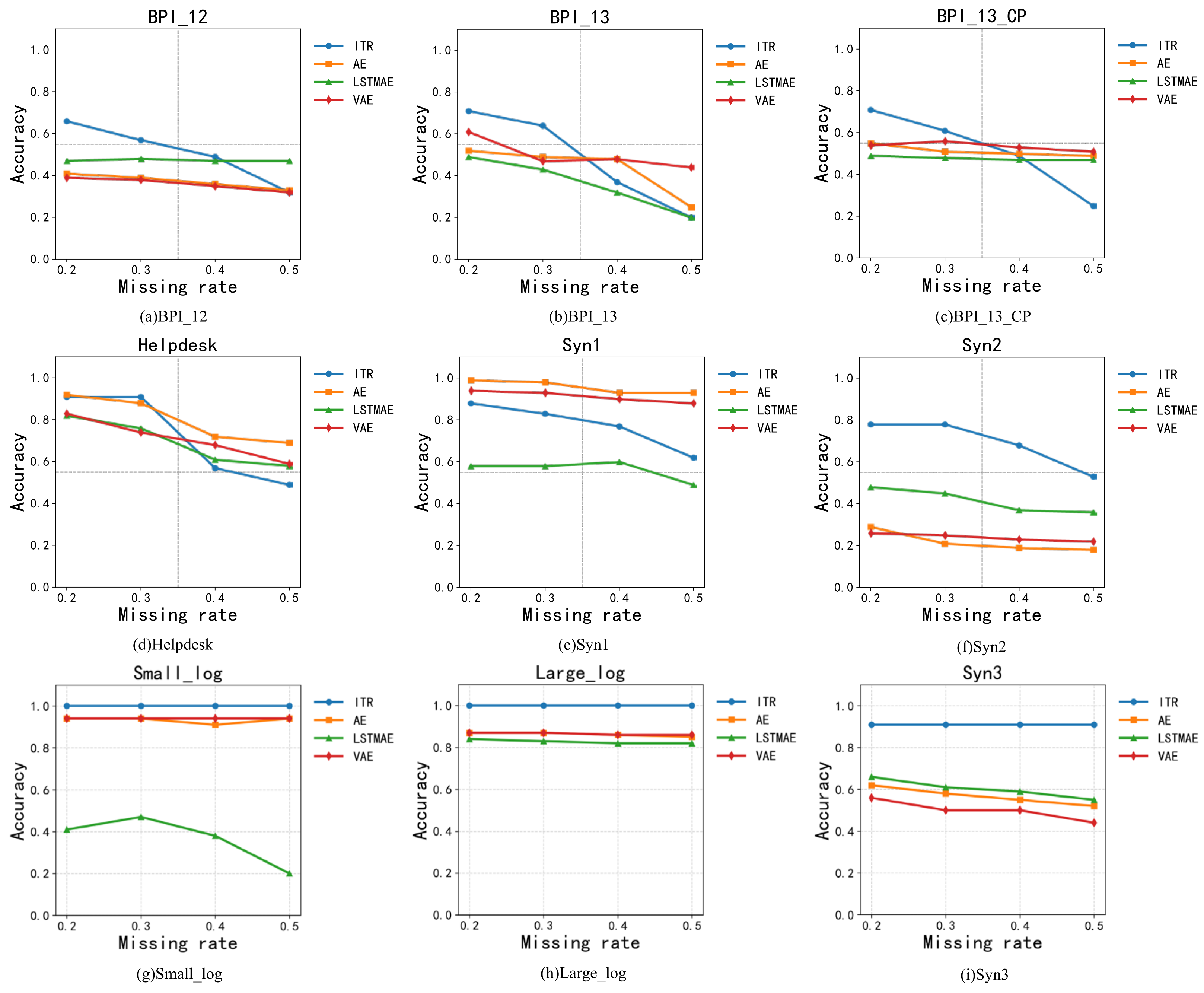
4.2. Accuracy Results of Incomplete Trace Repair
4.3. Time Performance of Incomplete Trace Repair
5. Discussion
5.1. Comparison with Existing Approaches
5.2. Experimental Results and Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, W.; Liu, C.; Wang, L.; Wen, L.; Zeng, Q. The token replay-based object-centric process conformance checking method. Comput. Integr. Manuf. Syst. 2025, 1–20. [Google Scholar] [CrossRef]
- Na, G.; Liu, C.; Li, C.; Ouyang, C.; Ni, W.; Zeng, Q. Causal inference-based root cause analysis method for business process time anomalies. Comput. Integr. Manuf. Syst. 2024, 1–17. [Google Scholar] [CrossRef]
- Ding, L.; Chen, S.; Rundensteiner, E.A.; Tatemura, J.; Hsiung, W.P.; Candan, K.S. Runtime semantic query optimization for event stream processing. In Proceedings of the 2008 IEEE 24th International Conference on Data Engineering, Cancun, Mexico, 7–12 April 2008. [Google Scholar]
- Bezerra, F.; Wainer, J. Algorithms for anomaly detection of traces in logs of process aware information systems. Inf. Syst. 2013, 38, 33–44. [Google Scholar] [CrossRef]
- Sun, P.; Liu, Z.; Davidson, S.B.; Chen, Y. Detecting and resolving unsound workflow views for correct provenance analysis. In Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data, Providence, RI, USA, 29 June–2 July 2009. [Google Scholar]
- Wang, J.; Song, S.; Zhu, X.; Lin, X. Efficient recovery of missing events. Proc. VLDB Endow. 2013, 6, 841–852. [Google Scholar] [CrossRef]
- Li, H.; Liu, C.; Zhang, Z.; Shen, X.; Mo, Q.; Zeng, Q. Cross-organizational business process conformance checking and anomaly behavior diagnosis Approach. Comput. Integr. Manuf. Syst. 2024, 1–17. [Google Scholar] [CrossRef]
- Li, T.; Liu, C.; Xu, X.; Zhang, S.; Wen, L.; Lin, L.; Zeng, Q. The quality evaluation framework for business process concept drift detection algorithms. Comput. Integr. Manuf. Syst. 2024, 30, 2722–2734. [Google Scholar]
- Song, S.; Zhang, A. IoT data quality. In Proceedings of the 29th ACM International Conference on Information & Knowledge Management, Seattle, WA, USA, 6–11 August 2020. [Google Scholar]
- Song, W.; Xia, X.; Jacobsen, H.A.; Zhang, P.; Hu, H. Efficient alignment between event logs and process models. IEEE Trans. Serv. Comput. 2016, 10, 136–149. [Google Scholar] [CrossRef]
- Song, W.; Xia, X.; Jacobsen, H.A.; Zhang, P.; Hu, H. Heuristic recovery of missing events in process logs. In Proceedings of the 2015 IEEE International Conference on Web Services, New York, NY, USA, 27 June–2 July 2015. [Google Scholar]
- Song, W.; Jacobsen, H.A.; Zhang, P. Self-healing event logs. IEEE Trans. Knowl. Data Eng. 2019, 33, 2750–2763. [Google Scholar] [CrossRef]
- Rogge-Solti, A.; Mans, R.S.; van der Aalst, W.M.; Weske, M. Improving documentation by repairing event logs. In Proceedings of the The Practice of Enterprise Modeling: 6th IFIP WG 8.1 Working Conference, Riga, Latvia, 6–7 November 2013. [Google Scholar]
- Sim, S.; Bae, H.; Choi, Y. Likelihood-based multiple imputation by event chain methodology for repair of imperfect event logs with missing data. In Proceedings of the 2019 International Conference on Process Mining, Aachen, Germany, 24–26 June 2019. [Google Scholar]
- Sim, S.; Bae, H.; Liu, L. Bagging recurrent event imputation for repair of imperfect event log with missing categorical events. IEEE Trans. Serv. Comput. 2021, 16, 108–121. [Google Scholar] [CrossRef]
- Nguyen, H.T.C.; Lee, S.; Kim, J.; Ko, J.; Comuzzi, M. Autoencoders for improving quality of process event logs. Expert Syst. Appl. 2019, 131, 132–147. [Google Scholar] [CrossRef]
- Nguyen, H.T.C.; Comuzzi, M. Event log reconstruction using autoencoders. In Proceedings of the Service-Oriented Computing–ICSOC 2018 Workshops, Hangzhou, China, 12–15 November 2018. [Google Scholar]
- Lu, Y.; Chen, Q.; Poon, S.K. A deep learning approach for repairing missing activity labels in event logs for process mining. Information 2022, 13, 234. [Google Scholar] [CrossRef]
- Fang, H.; Li, B. A Multi-Perspective and Interpretable Log Repairing Method Based on Two-Level Attention and Weak Behavioral Profiles. 2024. Available online: https://ssrn.com/abstract=4798515 (accessed on 2 May 2025).
- Wu, P.; Fang, X.; Fang, H.; Gong, Z.; Kan, D. An Event Log Repair Method Based on Masked Transformer Model. Appl. Artif. Intell. 2024, 38, 2346059. [Google Scholar] [CrossRef]
- Liu, J.; Xu, J.; Zhang, R.; Reiff-Marganiec, S. A repairing missing activities approach with succession relation for event logs. Knowl. Inf. Syst. 2021, 63, 477–495. [Google Scholar] [CrossRef]
- Fani Sani, M.; van Zelst, S.J.; van der Aalst, W.M. Repairing outlier behaviour in event logs. In Proceedings of the Business Information Systems: 21st International Conference, Berlin, Germany, 18–20 July 2018. [Google Scholar]
- Xu, J.; Liu, J. A profile clustering based event logs repairing approach for process mining. IEEE Access 2019, 7, 17872–17881. [Google Scholar] [CrossRef]
- Fang, H.; Su, W. Log Clustering-based Method for Repairing Missing Traces with Context Probability Information. Int. J. Adv. Comput. Sci. Appl. 2024, 15, 1445–1452. [Google Scholar] [CrossRef]
- Van der Aalst, W.; Weijters, T.; Maruster, L. Workflow mining: Discovering process models from event logs. IEEE Trans. Knowl. Data Eng. 2004, 16, 1128–1142. [Google Scholar] [CrossRef]
- Weijters, A.J.M.M.; Ribeiro, J.T.S. Flexible heuristics miner (FHM). In Proceedings of the 2011 IEEE Symposium on Computational Intelligence and Data Mining, Paris, France, 11–15 April 2011. [Google Scholar]
- Ghionna, L.; Greco, G.; Guzzo, A.; Pontieri, L. Outlier detection techniques for process mining applications. In Proceedings of the Foundations of Intelligent Systems: 17th International Symposium, Toronto, ON, Canada, 20–23 May 2008. [Google Scholar]
- Suriadi, S.; Andrews, R.; ter Hofstede, A.H.; Wynn, M.T. Event log imperfection patterns for process mining: Towards a systematic approach to cleaning event logs. Inf. Syst. 2017, 64, 132–150. [Google Scholar] [CrossRef]
- Bernard, G.; Andritsos, P. Truncated trace classifier. removal of incomplete traces from event logs. In Proceedings of the Enterprise, Business-Process and Information Systems Modeling: 21st International Conference, Grenoble, France, 8–9 June 2020. [Google Scholar]
- Leemans, S.J.; Fahland, D.; Van Der Aalst, W.M. Discovering block-structured process models from event logs-a constructive approach. In Proceedings of the International Conference on Applications and Theory of Petri Nets and Concurrency, Milan, Italy, 24–28 June 2013. [Google Scholar]
- Yan, J.; Liu, C.; Su, X.; Wen, L.; Cao, J.; Zeng, Q. Inductive model mining method based on local process structure optimization. Comput. Integr. Manuf. Syst. 2025, 1–17. [Google Scholar] [CrossRef]
- Shen, X.; Liu, C.; Li, H.; Zheng, K.; Cheng, L.; Zeng, Q. Distributed compliance checking method based on process model decomposition. Comput. Integr. Manuf. Syst. 2024, 30, 2884–2896. [Google Scholar]
- Bohannon, P.; Fan, W.; Flaster, M.; Rastogi, R. A cost-based model and effective heuristic for repairing constraints by value modification. In Proceedings of the 2005 ACM SIGMOD International Conference on Management of Data, New York, NY, USA, 14–16 June 2005. [Google Scholar]
- Song, S.; Cheng, H.; Yu, J.X.; Chen, L. Repairing vertex labels under neighborhood constraints. Proc. VLDB Endow. 2014, 7, 987–998. [Google Scholar] [CrossRef]
- Schafer, J.L.; Graham, J.W. Missing data: Our view of the state of the art. Psychol. Methods 2002, 7, 147. [Google Scholar] [CrossRef]
- Ehrhardt, J.; Wilms, M. Autoencoders and variational autoencoders in medical image analysis. In Biomedical Image Synthesis and Simulation; Academic Press: Cambridge, MA, USA, 2022; pp. 129–162. [Google Scholar]
- Pinheiro Cinelli, L.; Araújo Marins, M.; Barros da Silva, E.A.; Lima Netto, S. Variational autoencoder. In Variational Methods for Machine Learning with Applications to Deep Networks; Springer International Publishing: Cham, Switzerland, 2021; pp. 111–149. [Google Scholar]
- Pu, Y.; Gan, Z.; Henao, R.; Yuan, X.; Li, C.; Stevens, A.; Carin, L. Variational autoencoder for deep learning of images, labels and captions. Adv. Neural Inf. Process. Syst. 2016, 29, 35. [Google Scholar]


| Datasets | Traces | Events | Activities | Maximum | Minimum |
|---|---|---|---|---|---|
| BPIC_12 | 13,087 | 164,506 | 23 | 96 | 3 |
| BPIC_13 | 7554 | 65,533 | 13 | 123 | 1 |
| BPIC_13_CP | 1487 | 6660 | 7 | 35 | 1 |
| Helpdesk | 3804 | 13,730 | 9 | 14 | 1 |
| Syn1 | 10,505 | 294,140 | 16 | 28 | 28 |
| Syn2 | 200 | 5778 | 20 | 253 | 5 |
| Syn3 | 1000 | 7365 | 18 | 10 | 5 |
| Small_log | 2000 | 28,000 | 14 | 14 | 14 |
| Large_log | 15,000 | 120,000 | 10 | 8 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Zhang, L.; Cao, R.; Guo, N.; Zhang, H.; Liu, C. A Process Tree-Based Incomplete Event Log Repair Approach. Information 2025, 16, 390. https://doi.org/10.3390/info16050390
Wang Q, Zhang L, Cao R, Guo N, Zhang H, Liu C. A Process Tree-Based Incomplete Event Log Repair Approach. Information. 2025; 16(5):390. https://doi.org/10.3390/info16050390
Chicago/Turabian StyleWang, Qiushi, Liye Zhang, Rui Cao, Na Guo, Haijun Zhang, and Cong Liu. 2025. "A Process Tree-Based Incomplete Event Log Repair Approach" Information 16, no. 5: 390. https://doi.org/10.3390/info16050390
APA StyleWang, Q., Zhang, L., Cao, R., Guo, N., Zhang, H., & Liu, C. (2025). A Process Tree-Based Incomplete Event Log Repair Approach. Information, 16(5), 390. https://doi.org/10.3390/info16050390







