Application of a KAN-LSTM Fusion Model for Stress Prediction in Large-Diameter Pipelines
Abstract
1. Introduction
2. Methodology
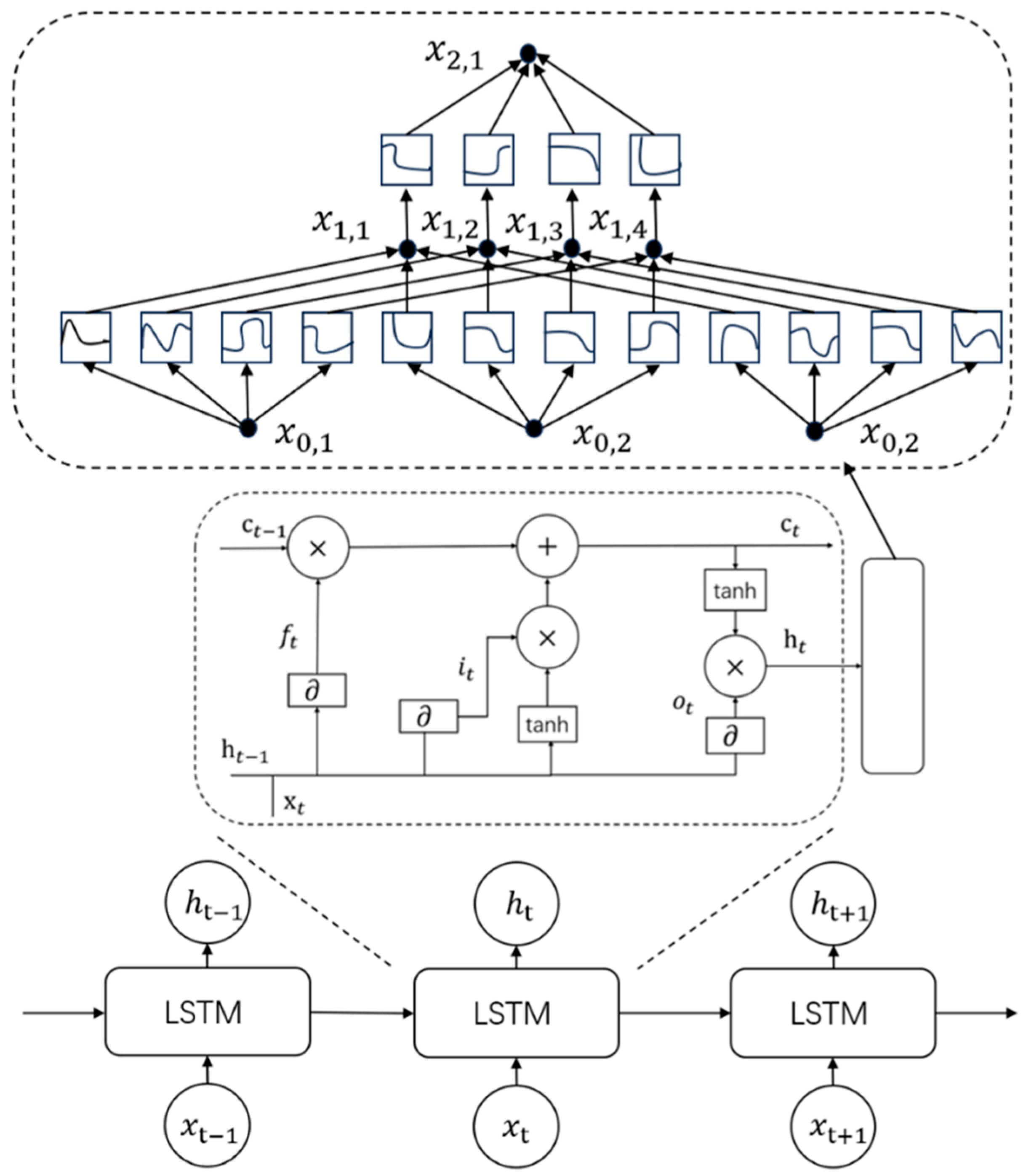
2.1. Principles of the Long Short-Term Memory (LSTM) Network Algorithm
- Forget Gate: Determines the extent to which information from the previous cell state should be discarded.Here is the forget gate, denotes the sigmoid function, is the weight matrix for the forget gate, is the bias term, and represents the concatenation of the previous hidden state and the current input .
- Input Gate: Determines the amount of the current input that should be stored in the cell state.Input Gate Activation:Candidate Cell State:In these equations, is the input gate, is the candidate cell state, represents the hyperbolic tangent function, and are weight matrices and and are bias terms.
- Output Gate: Determines the amount of information from the cell state to be output to the hidden state.Here, is the output gate, is the weight matrix for the output gate, and is its bias term.
- Cell State: Preserves long-term information and propagates it along the sequence.LSTM Output:In these equations, is the cell state at the current time, is the cell state at the previous time, and the symbol denotes element-wise multiplication.
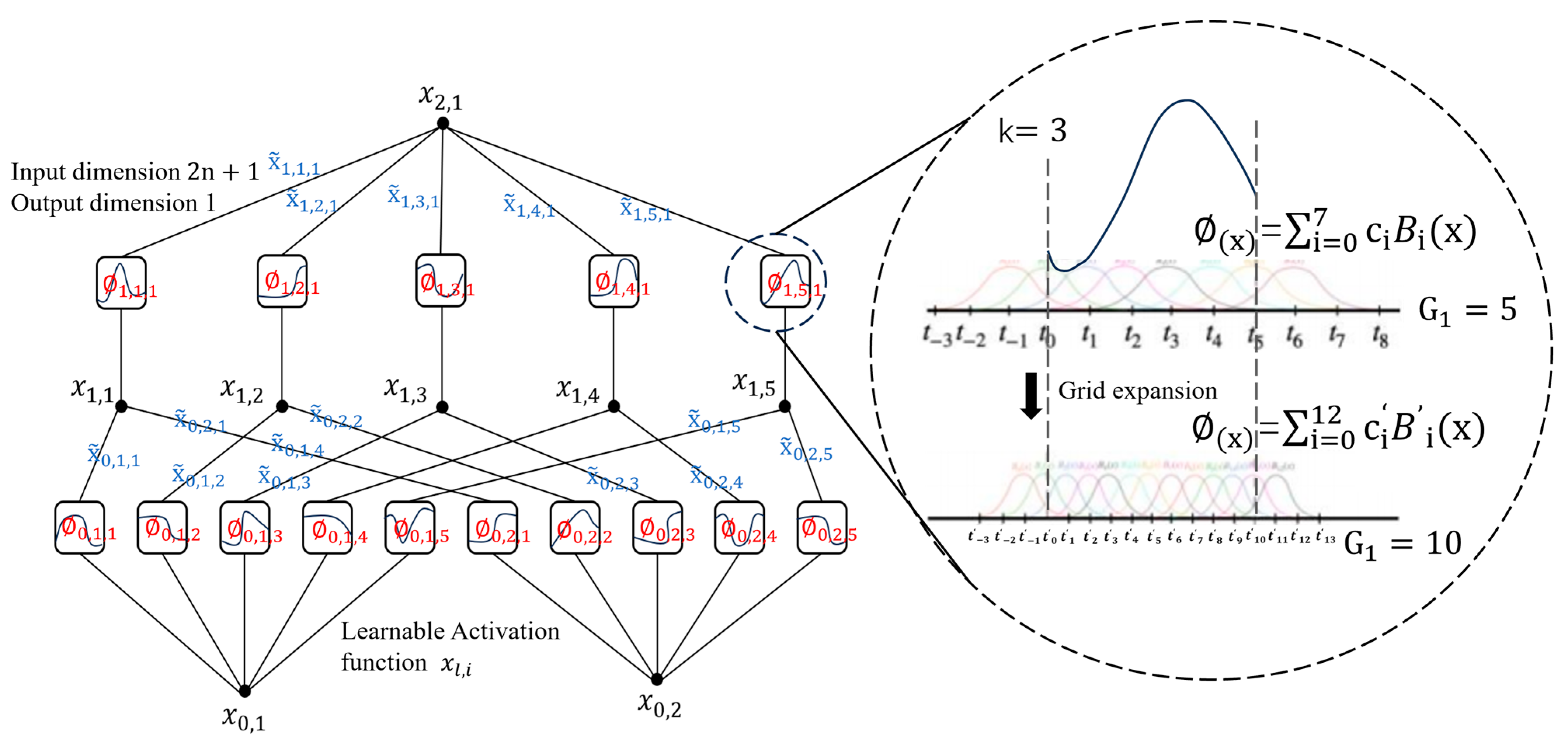
2.2. Principles of the Kolmogorov-Arnold Networks (KAN) Network Algorithm
2.3. LSTM-KAN Stress Prediction Model
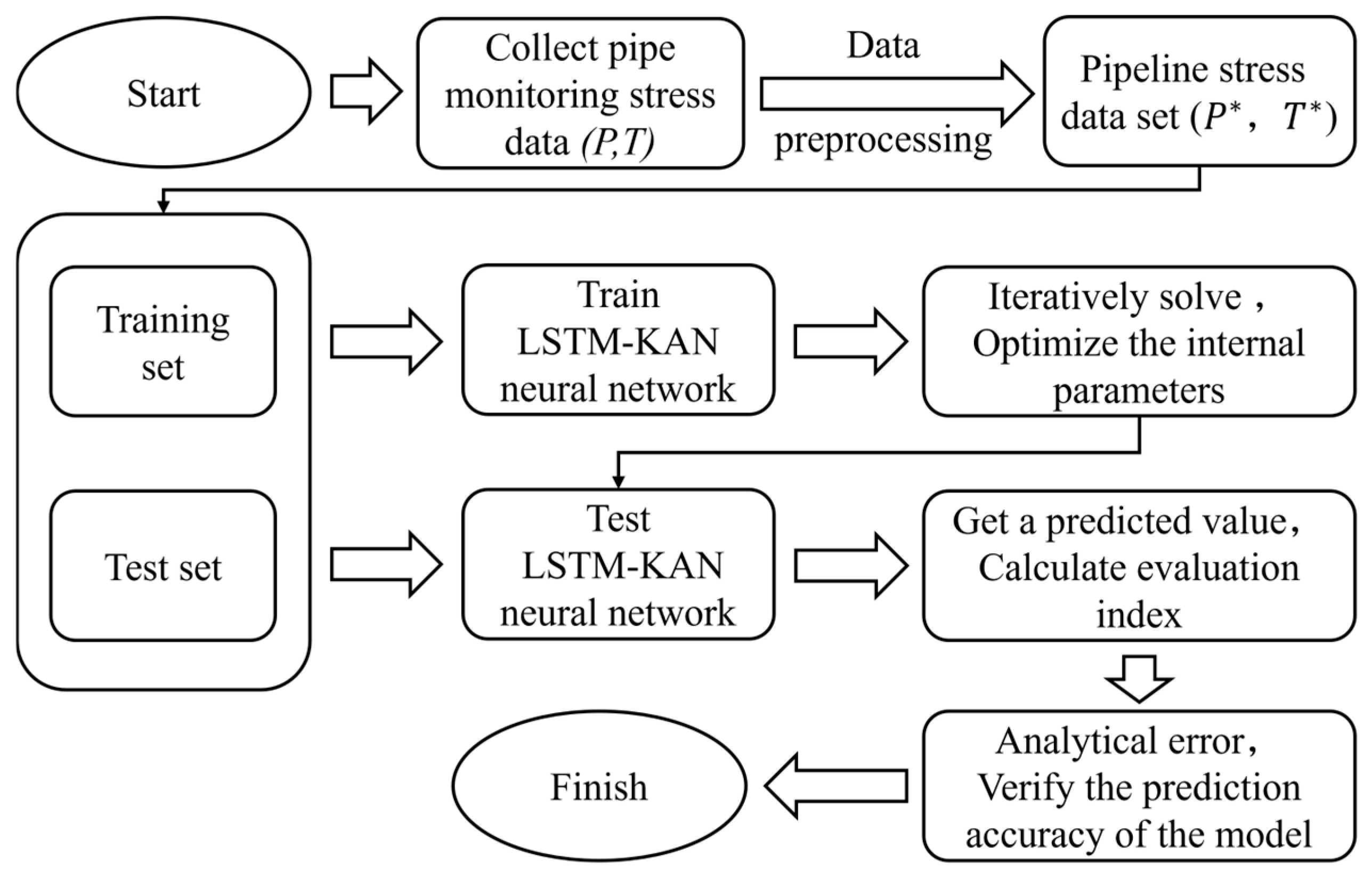
3. Research Applications
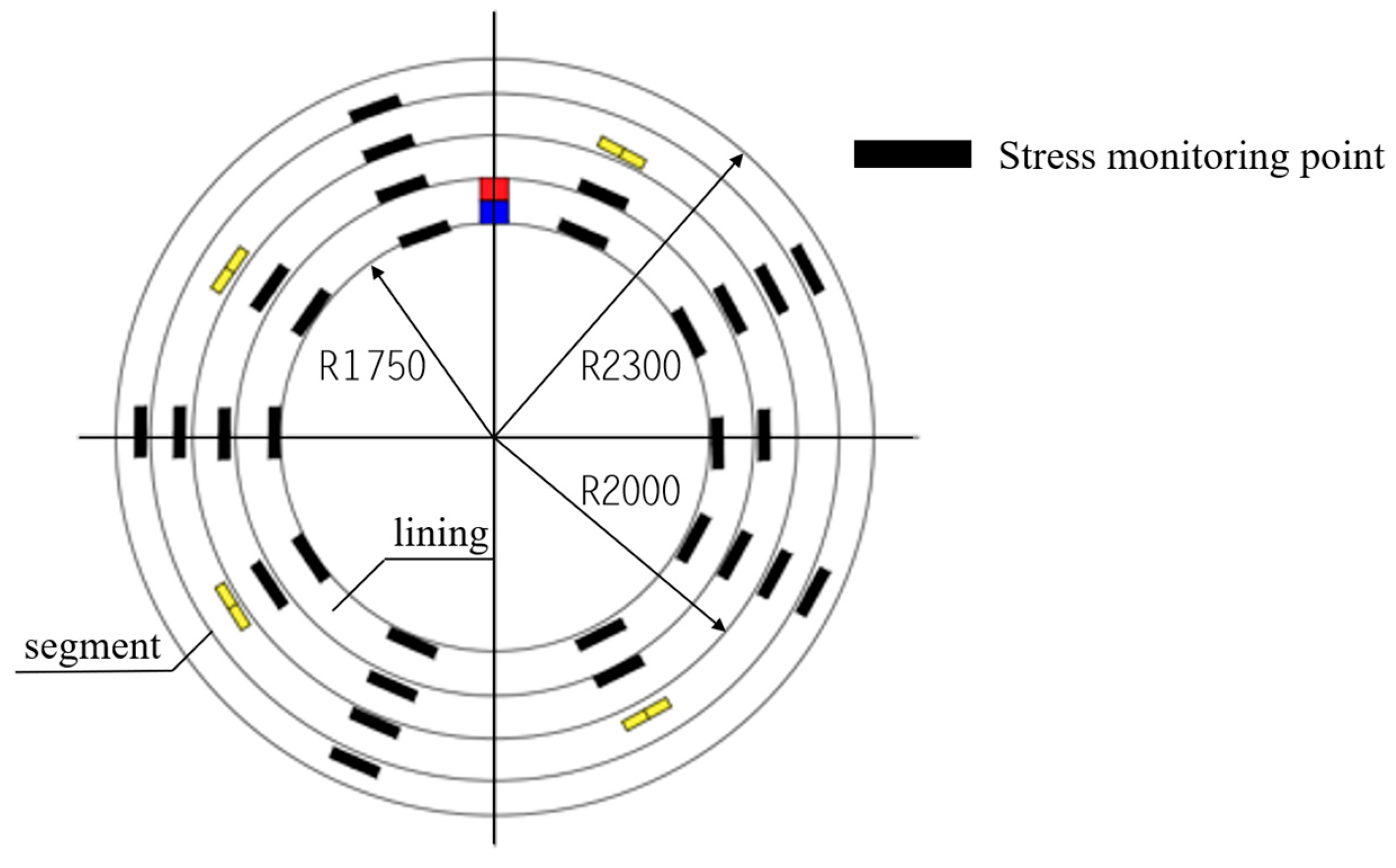
3.1. Project Background
3.2. Data Preprocessing and Model Parameter Settings
- is the updated state estimate,
- is the predicted state estimate,
- is the measurement at time i+1
- is the Kalman gain, which weights the predicted estimate and the new measurement.
- is the predicted error covariance (a measure of uncertainty in the predicted state),
- is the process noise covariance (representing uncertainty in the system dynamics), and
- is the measurement noise covariance (representing uncertainty in the measurement process).
- is the normalized pipeline stress, and is the actual pipeline stress.
3.3. Model Parameter Settings
4. Results and Discussion
5. Conclusions
- Compared with traditional fully connected layers, the KAN layer achieves higher prediction accuracy using fewer parameters and less training time, underscoring its potential not only for pipeline stress prediction but also for a broad range of forecasting applications. Moreover, the modular nature of the LSTM-KAN architecture enables it to be scaled for deeper and larger-scale tasks. By optimizing the structure and parameters of the KAN layer, both the prediction quality and computational efficiency can be further enhanced, which is an essential feature for real-time monitoring in large infrastructures.
- By combining the long-term memory capabilities of LSTM with the nonlinear representation power of KAN, the hybrid model effectively addresses the challenges posed by time-series data and the nonlinear complexities encountered in practical scenarios. Adjustments in the grid size and selection of appropriate activation functions allow for fine-tuning of the model’s flexibility and customizability, ensuring reliable performance across diverse data distributions and operational conditions.
- Future research should systematically investigate the model performance under varied parameter settings, including the impact of different depths and complexities of the KAN layer on both prediction accuracy and computational efficiency. Additionally, integrating supplementary data sources—such as environmental factors or historical maintenance records—may further enhance the model’s predictive power; investigating the applicability of this model for predicting stresses in sewage pipes with diverse functions and materials—such as prefabricated plastics (e.g., PVC or HDPE)—constitutes a promising direction for future research.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Das, S.; Saha, P. Structural health monitoring techniques implemented on IASC–ASCE benchmark problem: A review. J. Civ. Struct. Health Monit. 2018, 8, 689–718. [Google Scholar] [CrossRef]
- Rauch, W.; Bertrand-Krajewski, J.-L.; Krebs, P.; Mark, O.; Schilling, W.; Schütze, M.; Vanrolleghem, P. Deterministic modelling of integrated urban drainage systems. Water Sci. Technol. 2002, 45, 81–94. [Google Scholar] [CrossRef] [PubMed]
- Xu, C. Research on Non-invasive Detection Method of Pipeline Pressure Based on Fiber Bragg Grating. Master’s Thesis, China University of Petroleum, Beijing, China, 2018. [Google Scholar]
- Hu, B.; Zhou, M.; Li, Y. Real-time Stress Acquisition Method of In-service Pipe Based on Vibration Measurement. Agric. Equip. Veh. Eng. 2017, 55, 47–48+55. [Google Scholar]
- Zhang, H. Study on Stress Analysis and Monitoring Technology of Pipeline Landslide. Master’s Thesis, China University of Petroleum, Beijing, China, 2019. [Google Scholar]
- He, Y. Research on Long-Distance Pipeline Distributed Stress Monitoring and Health Diagnosis Method. Master’s Thesis, Wuhan Institute of Technology, Wuhan, China, 2015. [Google Scholar]
- El-Abbasy, M.S.; Senouci, A.; Zayed, T.; Mirahadi, F.; Parvizsedghy, L. Artificial neural network models for predicting condition of offshore oil and gas pipelines. Autom. Constr. 2014, 45, 50–65. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, Z.; Tong, L. Early Warning Model of Pipeline Stress State Based on Axial Stress Monitoring Data. China Pet. Mach. 2018, 46, 105–109. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, UK, 2016. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Graves, A. Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Leng, J.; Qian, W.; Zhou, L. Experimental Study on Safety Warning of Oil and Gas Pipeline Based on Stress Monitoring. China Pet. Mach. 2021, 49, 139–144. [Google Scholar]
- Liu, X. Research on pipeline stress prediction and early warning technology based on ARIMA-LSTM. Pet. Eng. Constr. 2022, 48, 38–43. [Google Scholar]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. Kan: Kolmogorov-Arnold networks. arXiv 2024, arXiv:2404.19756. [Google Scholar]
- Chen, S.; Ge, L. Exploring the attention mechanism in LSTM-based Hong Kong stock price movement prediction. Quant. Financ. 2019, 19, 1507–1515. [Google Scholar] [CrossRef]
- Liu, W.; Lu, H.; Fu, H.; Cao, Z. Learning to Upsample by Learning to Sample. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023. [Google Scholar]
- Zhou, L.; Leng, J.; Wei, L. Early Warning Technology of Oil and Gas Pipeline Based on Monitoring Data. Press. Vessel Technol. 2019, 36, 55–60. [Google Scholar]
- Bian, X.; Cheng, Y.; Bai, X. HW-CSC Stress-strain Model and Its Application in Strength Prediction. Chin. J. Undergr. Space Eng. 2021, 17, 1782–1788. [Google Scholar]
- Yang, B.; Yin, K.; Lacasse, S.; Liu, Z. Time series analysis and long short-term memory neural network to predict landslide displacement. Landslides 2019, 16, 677–694. [Google Scholar] [CrossRef]
- Huang, H.; Guo, P.; Yan, J.; Zhang, B.; Mao, Z. Impact of uncertainty in the physics-informed neural network on pressure prediction for water hammer in pressurized pipelines. J. Phys. Conf. Ser. 2024, 2707, 012095. [Google Scholar] [CrossRef]
- Soomro, A.A.; Mokhtar, A.A.; Hussin, H.B.; Lashari, N.; Oladosu, T.L.; Jameel, S.M.; Inayat, M. Analysis of machine learning models and data sources to forecast burst pressure of petroleum corroded pipelines: A comprehensive review. Eng. Fail. Anal. 2024, 155, 107747. [Google Scholar] [CrossRef]
- Seenuan, P.; Noraphaiphipaksa, N.; Kanchanomai, C. Stress Intensity Factors for Pressurized Pipes with an Internal Crack: The Prediction Model Based on an Artificial Neural Network. Appl. Sci. 2023, 13, 11446. [Google Scholar] [CrossRef]
- Guo, W.; Li, Z.; Gao, C.; Yang, Y. Stock price forecasting based on improved time convolution network. Comput. Intell. 2022, 38, 1474–1491. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Z. Design of financial big data audit model based on artificial neural network. Int. J. Syst. Assur. Eng. Manag. 2021, 1–10. [Google Scholar] [CrossRef]
- Zhu, X.; Xiong, Y.; Wu, M.; Nie, G.; Zhang, B.; Yang, Z. Weather2k: A multivariate spatio-temporal benchmark dataset for meteorological forecasting based on real-time observation data from ground weather stations. arXiv 2023, arXiv:2302.10493. [Google Scholar]
- Li, X.; Jing, H.; Liu, X.; Chen, G.; Han, L. The prediction analysis of failure pressure of pipelines with axial double corrosion defects in cold regions based on the BP neural network. Int. J. Press. Vessel Pip. 2023, 202, 104907. [Google Scholar] [CrossRef]
- Mehtab, S.; Sen, J. Analysis and forecasting of financial time seriesusing cnn and lstm-based deep learning models. In Advances in Distributed Computing and Machine Learning: Proceedings of ICADCML 2021; Springer: Berlin/Heidelberg, Germany, 2022; pp. 405–423. [Google Scholar]


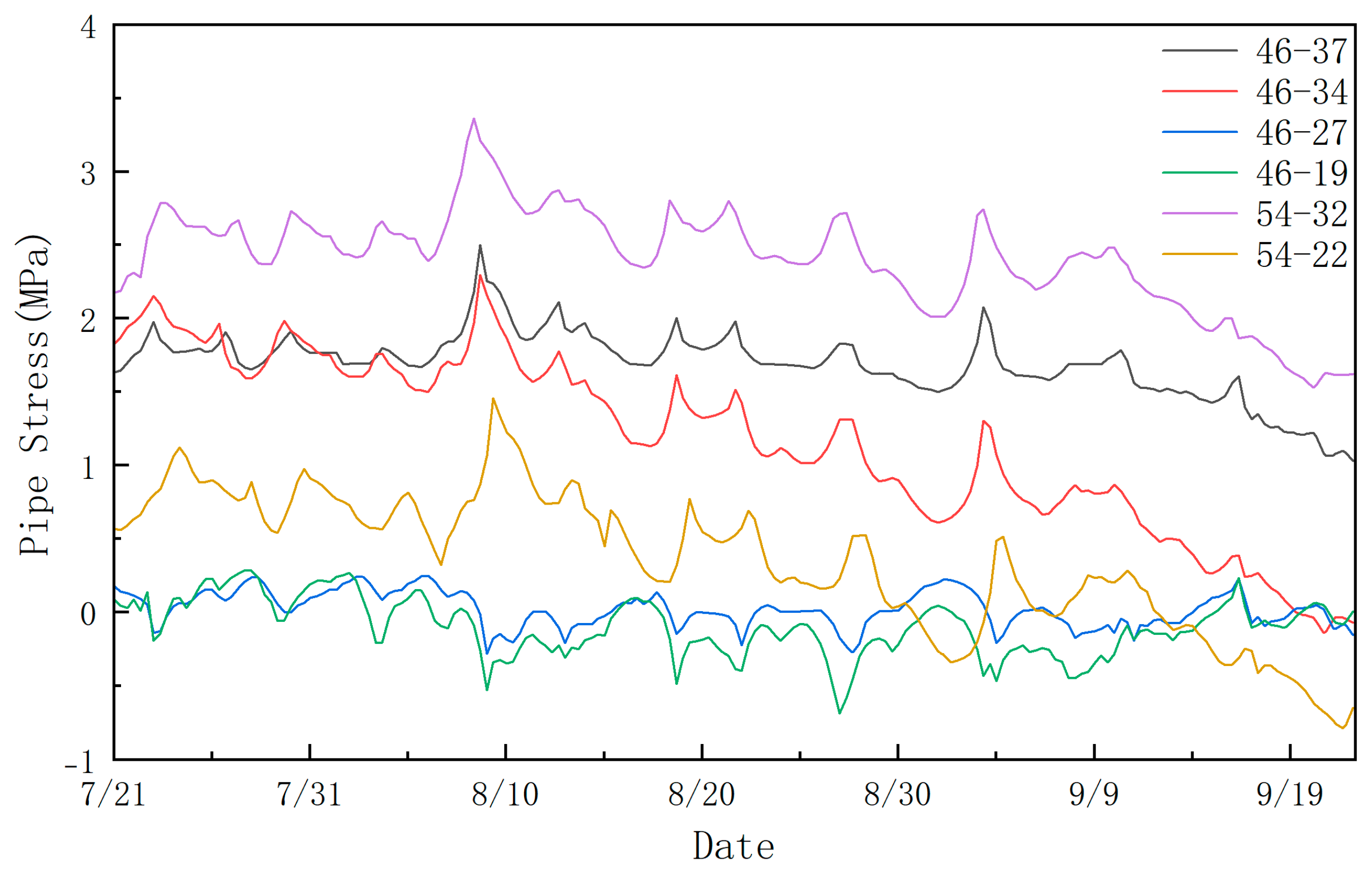
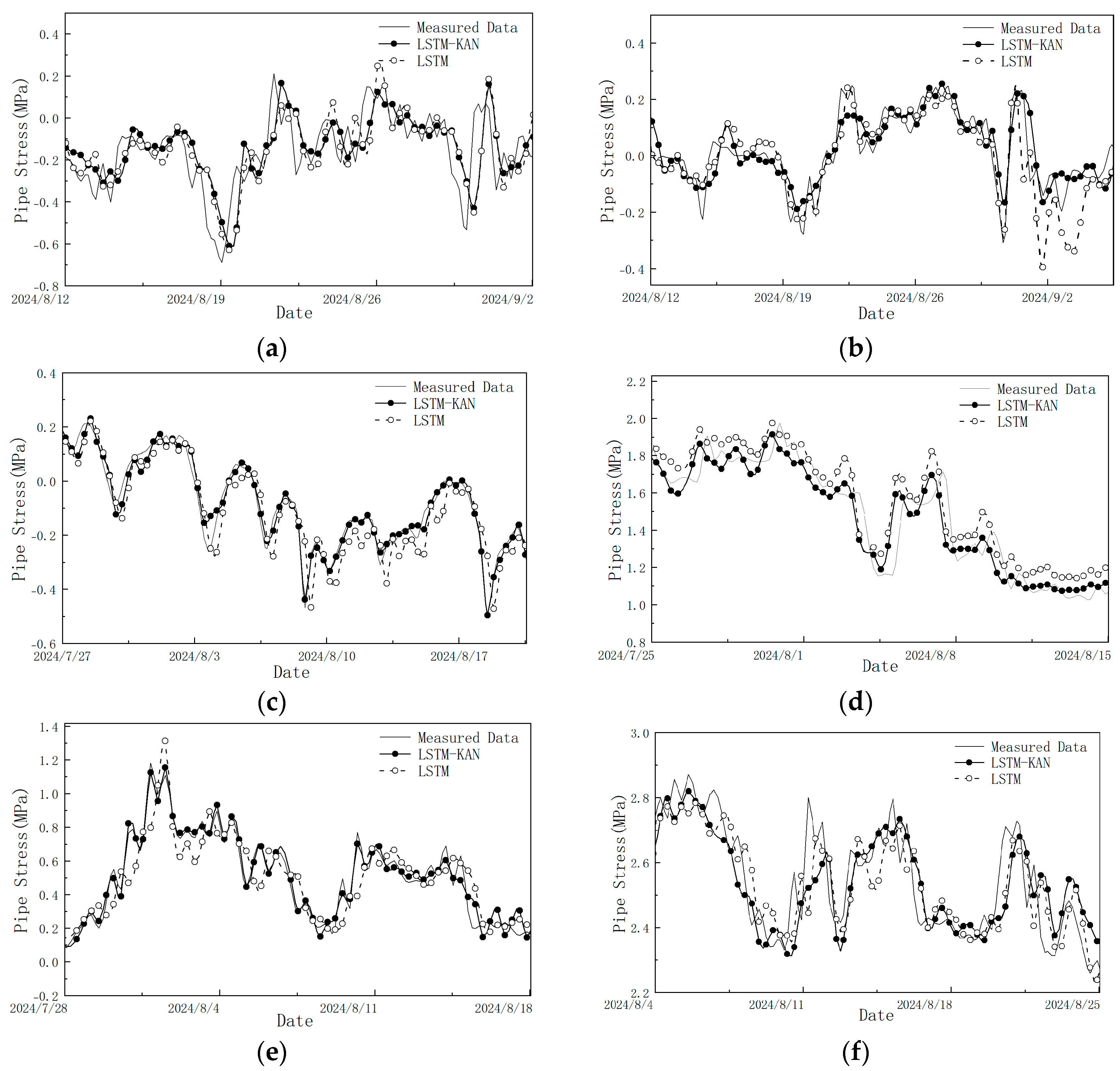

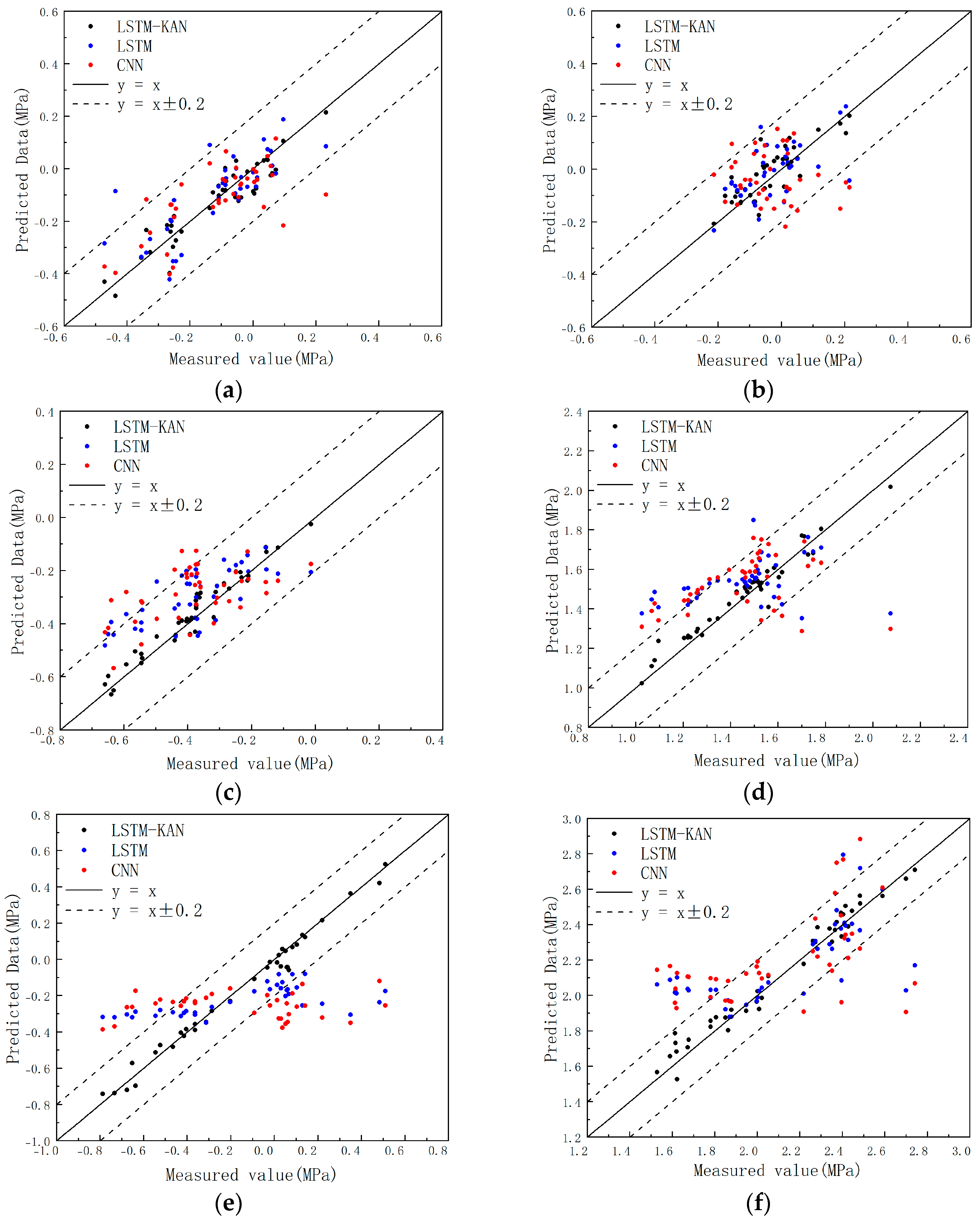
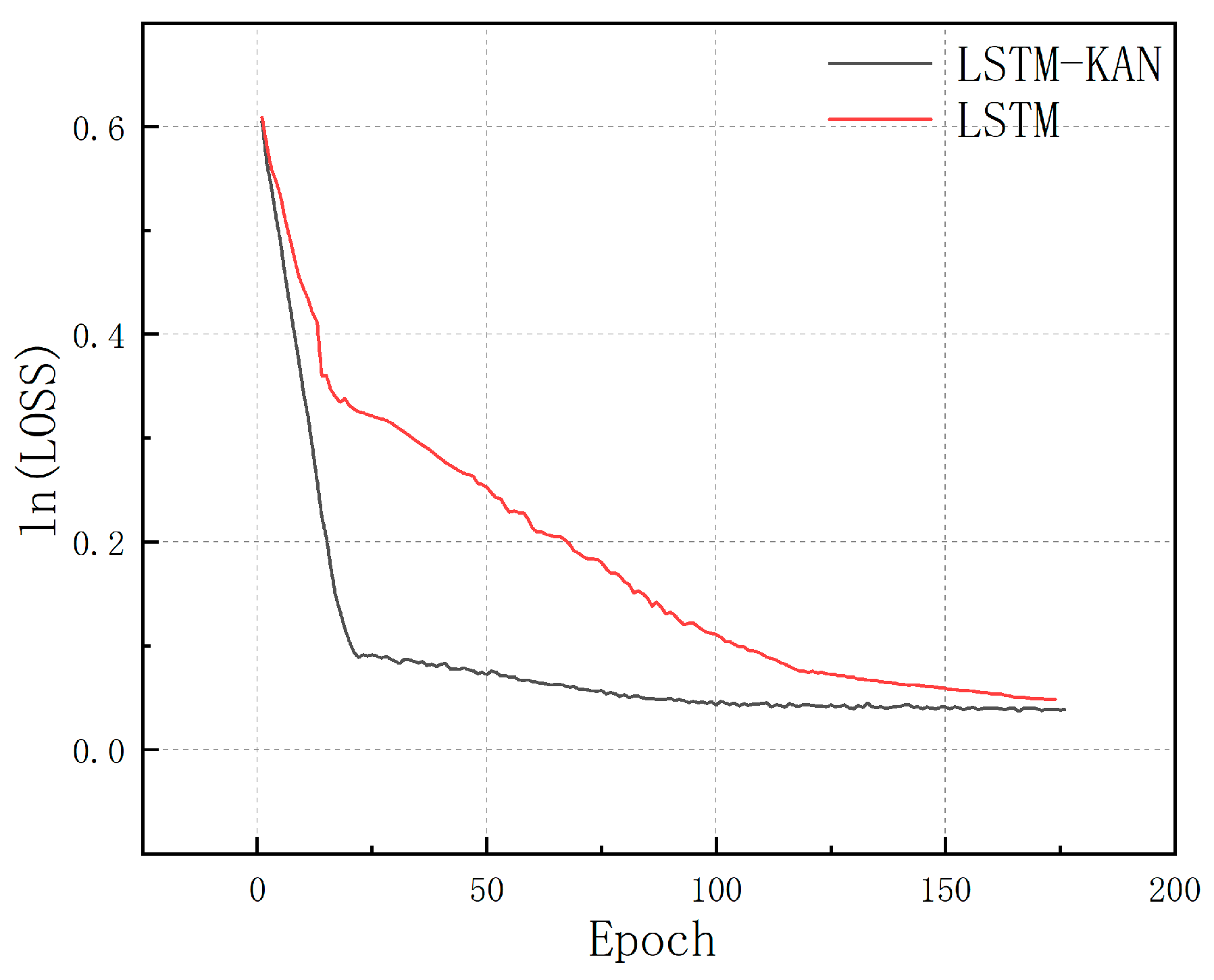

| 46–19 | 46–27 | 46–34 | 46–37 | 54–22 | 54–32 | |
|---|---|---|---|---|---|---|
| MAE | 0.034 | 0.033 | 0.032 | 0.032 | 0.033 | 0.032 |
| RMSE | 0.039 | 0.036 | 0.036 | 0.034 | 0.035 | 0.034 |
| R2 | 0.921 | 0.933 | 0.935 | 0.917 | 0.932 | 0.931 |
| MAE | RMSE | R2 | |
|---|---|---|---|
| CNN | 0.10 | 0.11 | 0.51 |
| LSTM | 0.09 | 0.10 | 0.57 |
| LSTM-KAN | 0.033 | 0.035 | 0.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Qin, S. Application of a KAN-LSTM Fusion Model for Stress Prediction in Large-Diameter Pipelines. Information 2025, 16, 347. https://doi.org/10.3390/info16050347
Li Z, Qin S. Application of a KAN-LSTM Fusion Model for Stress Prediction in Large-Diameter Pipelines. Information. 2025; 16(5):347. https://doi.org/10.3390/info16050347
Chicago/Turabian StyleLi, Zechao, and Shiwei Qin. 2025. "Application of a KAN-LSTM Fusion Model for Stress Prediction in Large-Diameter Pipelines" Information 16, no. 5: 347. https://doi.org/10.3390/info16050347
APA StyleLi, Z., & Qin, S. (2025). Application of a KAN-LSTM Fusion Model for Stress Prediction in Large-Diameter Pipelines. Information, 16(5), 347. https://doi.org/10.3390/info16050347





