Study on Radiation Protection Educational Tool Using Real-Time Scattering Radiation Distribution Calculation Method with Ray Tracing Technology
Abstract
1. Introduction
2. Materials and Methods
2.1. Reproduction of the X-Ray Examination Room and Calculation of Scattered Radiation Distribution Information
2.2. Building a Real-Time Calculation Model Using Ray Tracing Technology
2.3. Comparison of Ray Tracing and Monte Carlo Calculations
3. Results
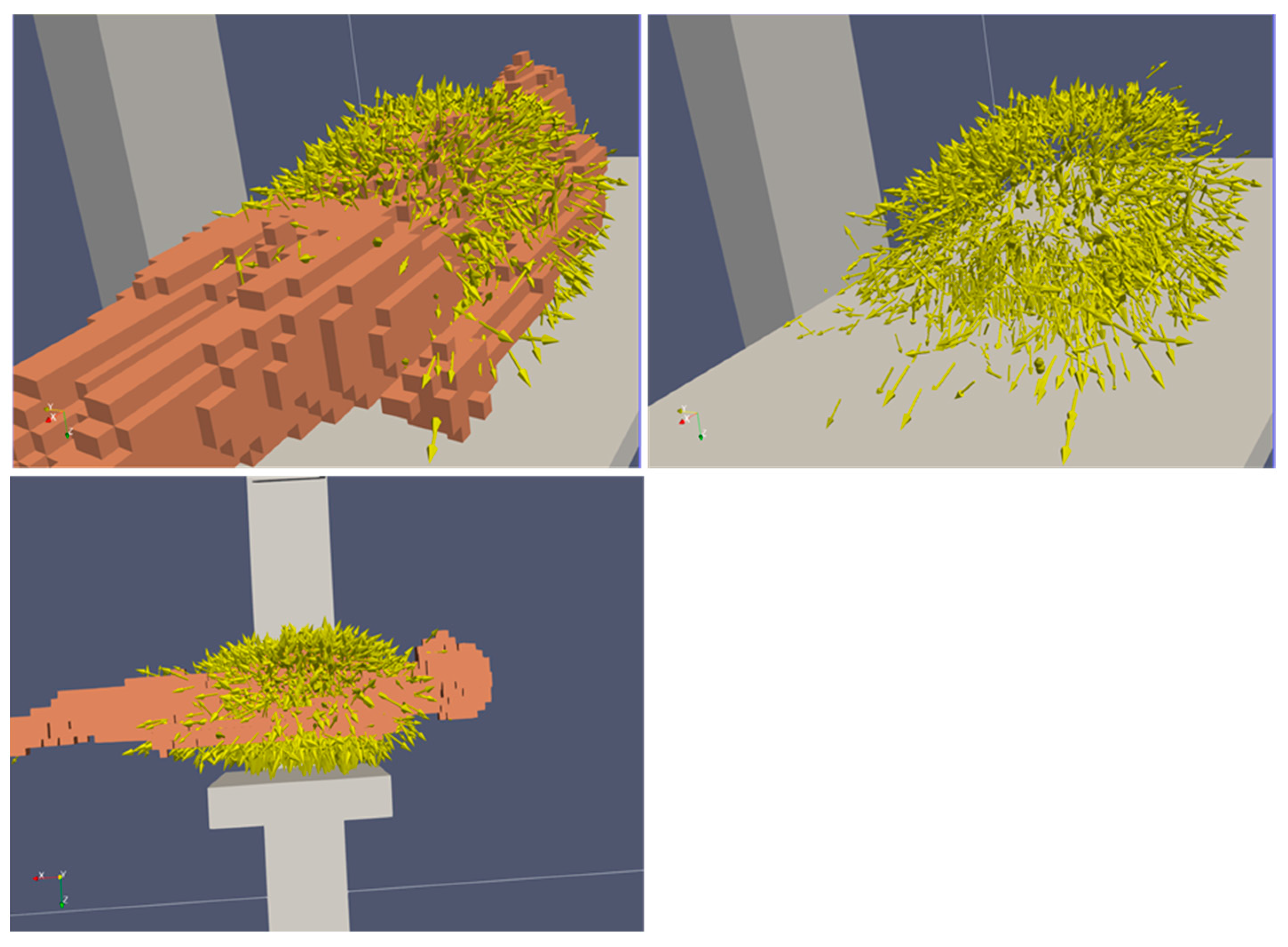
3.1. Scattered Ray Direction Vectors from the Patient
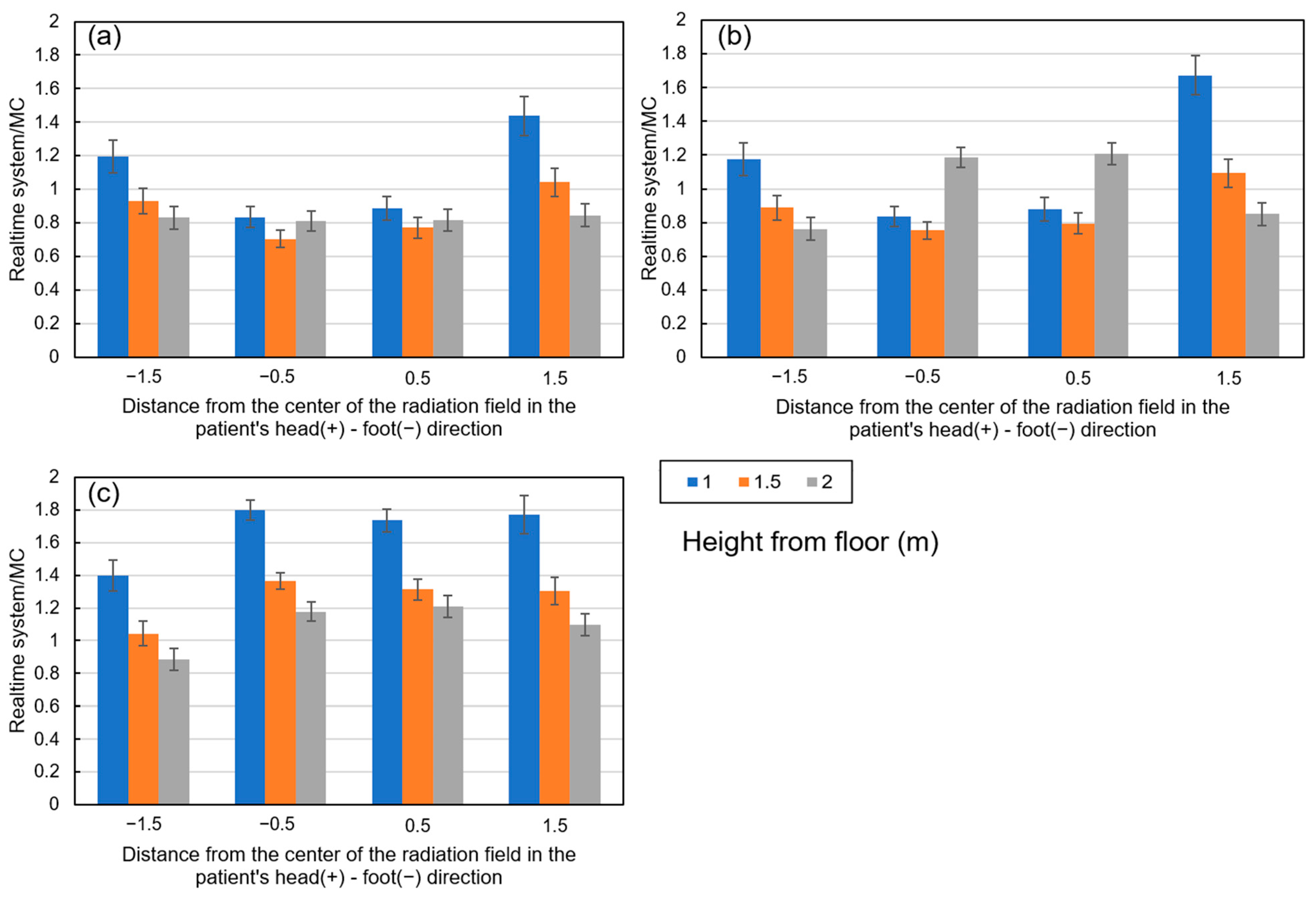
3.2. Simulation Results Using This System
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, K.P.; Miller, D.L. Minimising radiation exposure to physicians performing fluoroscopically guided cardiac catheterisation procedures: A review. Radiat. Prot. Dosim. 2009, 133, 227–233. [Google Scholar] [CrossRef] [PubMed]
- Quinn, C.M.; Cosette, M.S.; Michael, P.A.; Thomas, B.K.; Isabel, G.N. Radiation Protection for the Fluoroscopy Operator and Staff. Am. J. Roentgenol. 2016, 207, 745–754. [Google Scholar] [CrossRef]
- International Commission on Radiological Protection (ICRP). Avoidance of Radiation Injuries from Medical Interventional Procedures; ICRP Publication 85; Pergamon: Oxford, UK, 2000; Volume 30. [Google Scholar]
- Dauer, L.T.; Thornton, R.H.; Solomon, S.B.; St Germain, J. Unprotected operator eye lens doses in oncologic interventional radiology are clinically significant: Estimation from patient kerma-area-product data. J. Vasc. Interv. Radiol. 2010, 21, 1859–1861. [Google Scholar] [CrossRef] [PubMed]
- Vano, E.; Gonzalez, L.; Fernandez, J.M.; Haskal, Z.J. Eye lens exposure to radiation in interventional suites: Caution is warranted. Radiology 2008, 248, 945–953. [Google Scholar] [CrossRef] [PubMed]
- Mao, L.; Liu, T.; Caracappa, P.F.; Lin, H.; Gao, Y.; Dauer, L.T.; Xu, X.G. Influences of operator head posture and protective eyewear on eye lens doses in interventional radiology: A Monte Carlo Study. Med. Phys. 2019, 46, 2744–2751. [Google Scholar] [CrossRef] [PubMed]
- Schueler, B.A.; Fetterly, K.A. Eye protection in interventional procedures. Br. J. Radiol. 2021, 94, 20210436. [Google Scholar] [CrossRef] [PubMed]
- Akahane, M.; Yoshioka, N.; Kiryu, S. Radiation Protection of the Eye Lens in Fluoroscopy-guided Interventional Procedures. Interv. Radiol. 2022, 7, 44–48. [Google Scholar] [CrossRef] [PubMed]
- Galster, M.; Guhl, C.; Uder, M.; Adamus, R. Exposition der Augenlinse des Untersuchers und Effizienz der Strahlenschutzmittel bei fluoroskopischen Interventionen. RoFo 2013, 185, 474–481. [Google Scholar] [CrossRef] [PubMed]
- Jonathan, T.; Stephen, R.; Daniel, R.B. A prototype software system for intra-procedural staff dose monitoring and virtual reality training for fluoroscopically guided interventional procedures. J. Digit. Imaging 2023, 36, 1091–1109. [Google Scholar] [CrossRef]
- Troville, J.; Rudin, S.; Bednarek, D.R. Estimating Compton scatter distributions with a regressional neural network for use in a real-time staff dose management system for fluoroscopic procedures. In Proceedings of the SPIE International Society for Optical Engineering, Online, 27 June–1 July 2021; Volume 11595. [Google Scholar] [CrossRef]
- Fujibuchi, T.; Nakashima, M.; Arakawa, H.; Miyazaki, H.; Anam, C. Evaluation of radiation protection effectivity in a cardiac angiography room using visualized scattered radiation distribution. J. Radiol. Prot. 2024, 44, 031510. [Google Scholar] [CrossRef] [PubMed]
- Abdelrahman, M.; Lombardo, P.; Camp, A.; Duch, M.A.; Phillips, C.; Seret, A.; Vanhavere, F. A parametric study of occupational radiation dose in interventional radiology by Monte-Carlo simulations. Phys. Med. 2020, 78, 58–70. [Google Scholar] [CrossRef] [PubMed]
- Hizukuri, K.; Fujibuchi, T.; Han, D.; Arakawa, H.; Furuta, T. Directional vector-based quick evaluation method for protective plate effects in X-ray fluoroscopy (DQPEX). Radiol. Phys. Technol. 2024, 18, 196–208. [Google Scholar] [CrossRef] [PubMed]
- Bontempi, M.; Andreani, L.; Rossi, P.L.; Visani, A. Monte Carlo simulator of realistic x-ray beam for diagnostic applications. Med. Phys. 2010, 37, 4201–4209. [Google Scholar] [CrossRef] [PubMed]
- Alnewaini, Z.; Langer, E.; Schaber, P.; David, M.; Kretz, D.; Steil, V.; Hesser, J. Real-time, ray casting-based scatter dose estimation for c-arm x-ray system. J. Appl. Clin. Med. Phys. 2017, 18, 144–1153. [Google Scholar] [CrossRef] [PubMed]
- Sato, T.; Iwamoto, Y.; Hashimoto, S.; Ogawa, T.; Furuta, T.; Abe, S.I.; Kai, T.; Matsuya, Y.; Matsuda, N.; Hirata, Y.; et al. Recent improvements of the Particle and Heavy Ion Transport code System—PHITS version 3.33. J. Nucl. Sci. Technol. 2024, 61, 127–135. [Google Scholar] [CrossRef]
- Hirayama, H.; Namito, Y.; Bielajew, A.F.; Wilderman, S.J.; Nelson, W.R. The EGS5 code system SLAC-R-730 and KEK Report 2005–8. Stanford (California) and Tsukuba: SLAC and KEK; 2005. Available online: https://rcwww.kek.jp/research/egs/egs5_manual/slac730-150228.pdf (accessed on 10 March 2025).
- ICRP. Adult Reference Computational Phantoms. ICRP Publication 110. Ann. ICRP 2009, 39, 1–164. [Google Scholar] [CrossRef]
- Sakai, M.; Fujibuchi, T.; Lee, H.; Han, D. Imaging of scattered radiation sources in X-ray radiography using a semiconductor radiation visualization camera. Radiol. Phys. Technol. 2024, 18, 308–315. [Google Scholar] [CrossRef] [PubMed]






| Specifications | Models |
|---|---|
| Operation system | Windows 10 64-bit Education |
| Central processing unit (CPU) | Intel Core i9-9980 |
| Memory | 32 GB |
| Graphical processing unit (GPU) | GeForce RTX 2080 Ti |
| GPU m | 11 GB |
| Software | Unity 2020.3.30.f1 Unity DOTS |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fujibuchi, T. Study on Radiation Protection Educational Tool Using Real-Time Scattering Radiation Distribution Calculation Method with Ray Tracing Technology. Information 2025, 16, 266. https://doi.org/10.3390/info16040266
Fujibuchi T. Study on Radiation Protection Educational Tool Using Real-Time Scattering Radiation Distribution Calculation Method with Ray Tracing Technology. Information. 2025; 16(4):266. https://doi.org/10.3390/info16040266
Chicago/Turabian StyleFujibuchi, Toshioh. 2025. "Study on Radiation Protection Educational Tool Using Real-Time Scattering Radiation Distribution Calculation Method with Ray Tracing Technology" Information 16, no. 4: 266. https://doi.org/10.3390/info16040266
APA StyleFujibuchi, T. (2025). Study on Radiation Protection Educational Tool Using Real-Time Scattering Radiation Distribution Calculation Method with Ray Tracing Technology. Information, 16(4), 266. https://doi.org/10.3390/info16040266






