DLF: A Deep Active Ensemble Learning Framework for Test Case Generation

Abstract

High-quality test cases are vital for ensuring software reliability and security. However, existing symbolic execution tools generally rely on single-path search strategies, have limited feature extraction capability, and exhibit unstable model predictions. These limitations make them prone to local optima in complex or cross-scenario tasks and hinder their ability to balance testing quality with execution efficiency. To address these challenges, this paper proposes a Deep Active Ensemble Learning Framework for symbolic execution path exploration. During training, the framework integrates active learning with ensemble learning to reduce annotation costs and improve model robustness, while constructing a heterogeneous model pool to leverage complementary model strengths. In the testing stage, a dynamic ensemble mechanism based on sample similarity adaptively selects the optimal predictive model to guide symbolic path exploration. In addition, a gated graph neural network is employed to extract structural and semantic features from the control flow graph, improving program behavior understanding. To balance efficiency and coverage, a dynamic sliding window mechanism based on branch density enables real-time window adjustment under path complexity awareness. Experimental results on multiple real-world benchmark programs show that the proposed framework detects up to 16 vulnerabilities and achieves a cumulative 27.5% increase in discovered execution paths in hybrid fuzzing. Furthermore, the dynamic sliding window mechanism raises the F1 score to 93%.

1. Introduction

With the continuous growth in the scale and complexity of software systems, quality and security issues have become critical factors constraining system reliability. As a key stage in the software development lifecycle, testing plays a vital role in ensuring software quality, and its efficiency and effectiveness directly affect the reliability and maintainability of the system. High-quality test cases can uncover more potential defects under limited resources, thereby enhancing system robustness [1]. However, traditional manual testing methods, which rely heavily on human expertise, are not only inefficient and limited in coverage but also difficult to adapt to the rapid iteration and high complexity of modern software systems. Consequently, automated test case generation has emerged as a major research focus.

Symbolic execution [2,3,4], as an important branch of automated testing, enables systematic analysis of program paths and automatic generation of input data, theoretically achieving high test coverage. Nevertheless, in practical applications, symbolic execution suffers from critical bottlenecks such as path explosion [5] and the high complexity of constraint solving [6]. As the number of program branches increases exponentially, the path space rapidly expands, leading to a sharp decline in testing efficiency. How to improve path exploration efficiency and vulnerability detection accuracy while maintaining sufficient test coverage has become a central challenge in automated testing research.

In recent years, researchers have extensively explored performance optimization and intelligent enhancement of symbolic execution. Although traditional symbolic execution can systematically traverse program paths, it still struggles with path explosion and inefficient constraint solving in complex systems. To mitigate these issues, many studies have focused on optimizing path search strategies and constraint-solving mechanisms. With the rise of deep learning [7,8], intelligent models have been increasingly integrated into symbolic execution to guide path prediction and test generation. Approaches based on RNNs [9] and CNNs [10] learn sequential and structural features of program execution to identify high-value paths, while graph neural network (GNN)-based methods capture semantic dependencies within control flow [11], improving the model’s global comprehension capability. Meanwhile, active learning [12] has been introduced into the testing process, where uncertainty- or diversity-based sampling strategies are used to select representative samples, reduce redundant data, and enhance generalization performance.

In summary, although existing automated testing approaches have achieved notable progress in path exploration and vulnerability detection, they still suffer from the following three major limitations:

(1)

Path explosion and omission of critical paths. Under complex branching structures, symbolic execution tends to cause exponential growth in execution paths—known as the path explosion problem. Conventional pruning or heuristic strategies, while mitigating this issue, may inadvertently omit deep or cross-module critical paths, thereby compromising testing completeness.

(2)

Insufficient model generalization and stability. Most existing methods rely on a single predictive model or a fixed ensemble strategy, making it difficult to adapt to structural diversity across different programs. Consequently, they are prone to overfitting or performance fluctuations, lacking adaptability and robustness.

(3)

Low sample utilization and high annotation cost. Passive or random sampling leads to under-representative training samples that fail to efficiently capture key semantic features. Meanwhile, model training often depends on extensive manual labeling, limiting scalability and efficiency.

Therefore, there is an urgent need for a unified framework that combines active learning with a dynamic ensemble mechanism to balance path exploration depth, model generalization, and sample utilization efficiency. Existing studies tend to address these limitations separately and have yet to develop an integrated solution that can simultaneously improve generalization, reduce annotation costs, and adapt to diverse program structures during symbolic execution. The Deep Active Ensemble Learning Framework (DLF) proposed in this work is designed in response to these needs, providing a more coherent and effective way to address these challenges and compensating for the shortcomings of existing approaches.

To this end, this paper proposes a Deep Active Ensemble Learning Framework (DLF) for automated test case generation. DLF is driven by active learning principles: it employs a dual-criteria sampling strategy that combines uncertainty-based and diversity-based sampling to select the most informative symbolic state samples, while introducing an adaptive dynamic ensemble mechanism to enhance model robustness and generalization.

The DLF-based symbolic execution process consists of two stages:

Training phase: Guided by active learning, DLF performs uncertainty-driven sampling and similarity-constrained data selection to dynamically update the training set, thereby improving model learning efficiency.

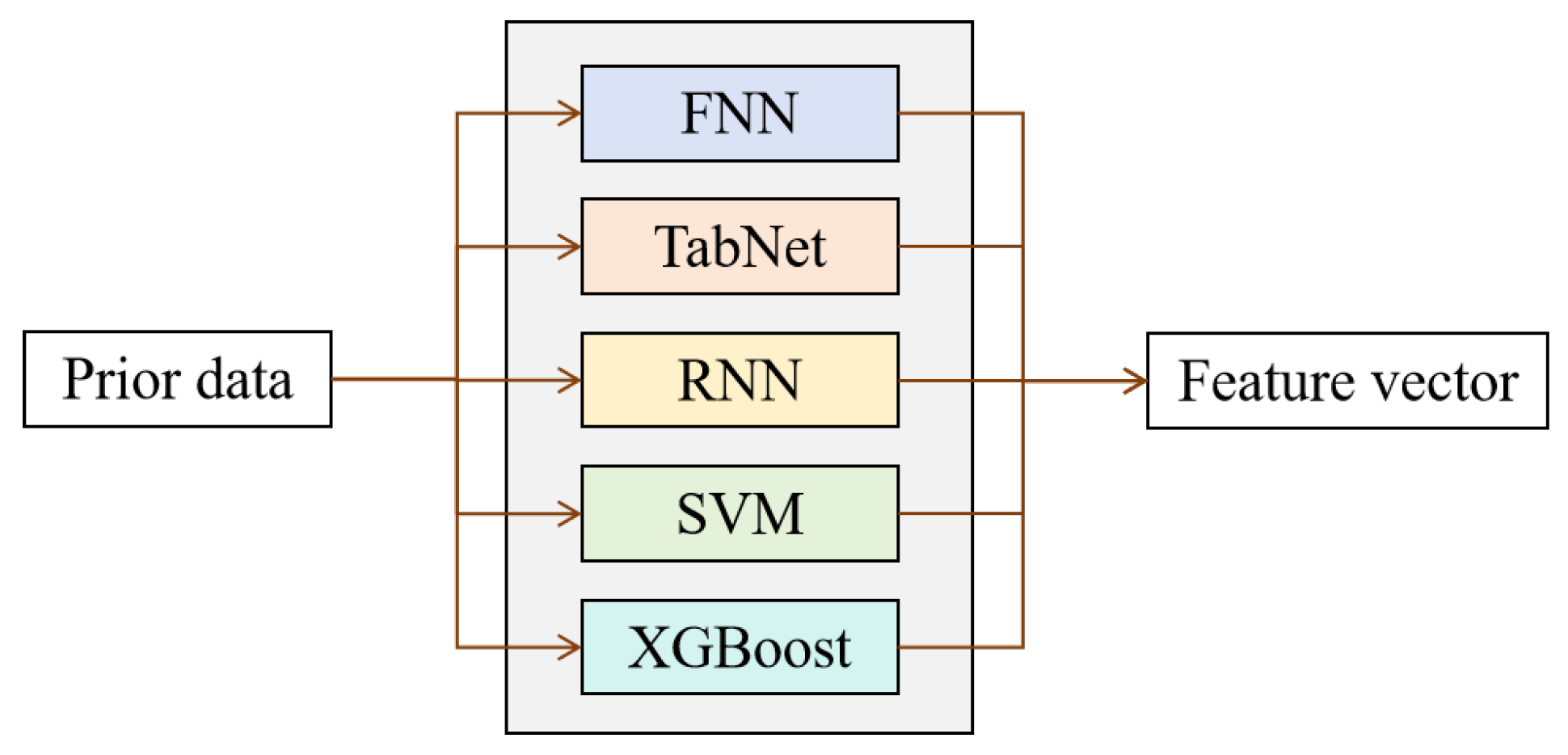
Testing phase: Within a heterogeneous model pool—comprising Feedforward Neural Networks (FNN), TabNet, Recurrent Neural Networks (RNN), Support Vector Machines (SVM), and XGBoost—DLF adaptively selects the optimal model combination according to sample-level feature similarity to perform path prediction and test case generation.

In addition, DLF incorporates a Gated Graph Neural Network (GGNN) [13] architecture to extract multidimensional features from the Control Flow Graph (CFG) [14], strengthening its understanding of program-level dependencies and semantic structures. Furthermore, a branch-density-based dynamic sliding-window mechanism is designed to adaptively adjust the search scope according to path complexity, achieving a dynamic balance between exploration depth and computational efficiency and effectively alleviating the path explosion problem.

The main innovations of the proposed approach are summarized as follows:

(1)

Vulnerability-probability-driven active guidance mechanism. DLF predicts the vulnerability probability of symbolic states based on source-code features and prioritizes the exploration of states with higher vulnerability likelihood. By integrating active learning with ensemble learning, DLF iteratively refines its classifier, thereby improving test-case quality while reducing labeling costs.

(2)

Dynamic ensemble strategy with a heterogeneous model pool. During the testing phase, DLF constructs a heterogeneous model pool composed of Feedforward Neural Networks (FNN) [15], TabNet [16], Recurrent Neural Networks (RNN) [9], Support Vector Machines (SVM) [17], and XGBoost [18]. It dynamically selects and adaptively weights the optimal model combination according to sample similarity, fully leveraging the complementary strengths of different models to enhance prediction accuracy and robustness.

(3)

Dynamic sliding-window and graph-feature modeling mechanism. A branch-density-based dynamic sliding window is designed to adaptively regulate exploration depth, while a Gated Graph Neural Network (GGNN) is employed to extract structural features from the Control Flow Graph (CFG), strengthening semantic understanding of program dependencies and alleviating the path-explosion problem.

(4)

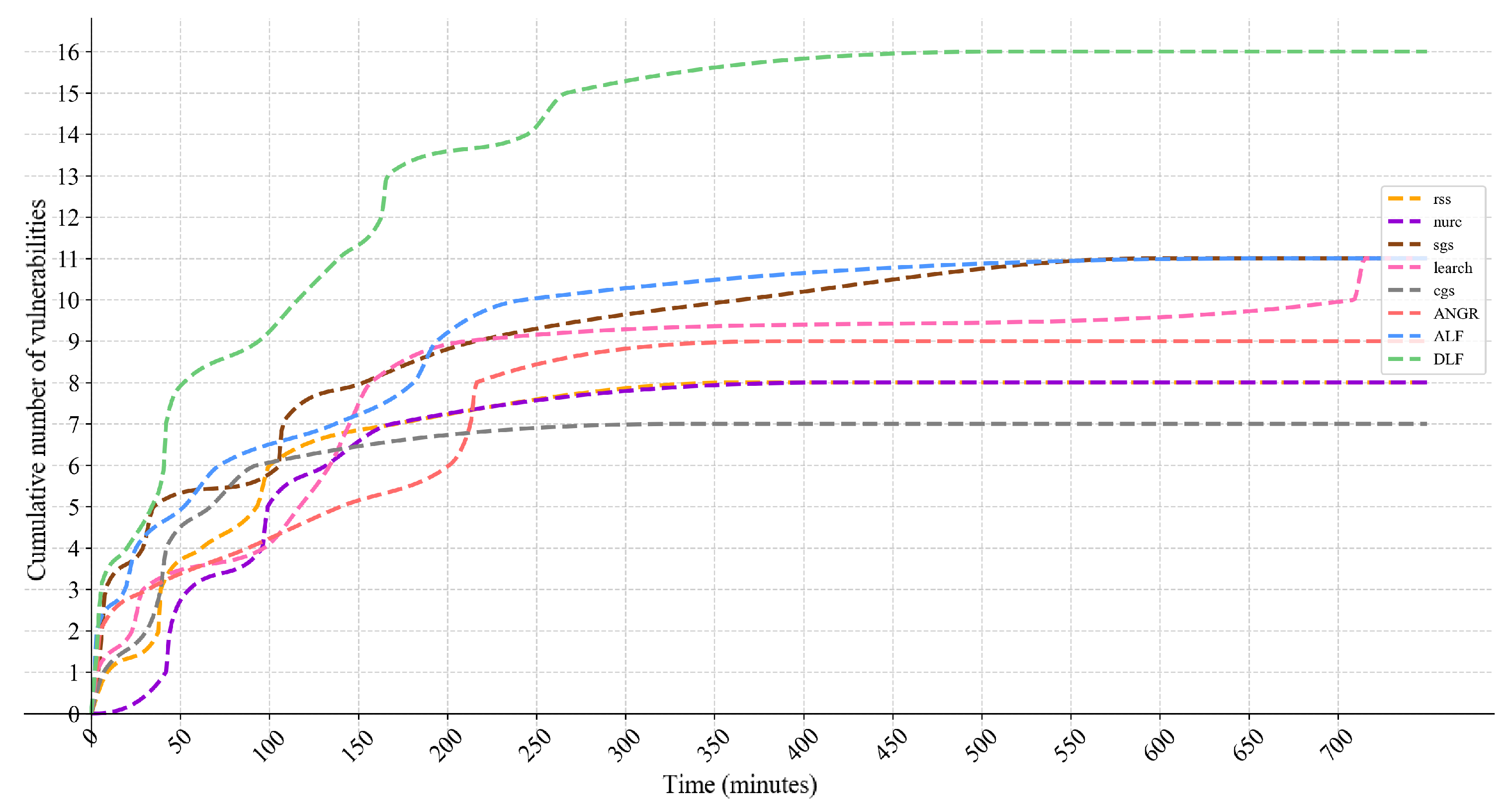
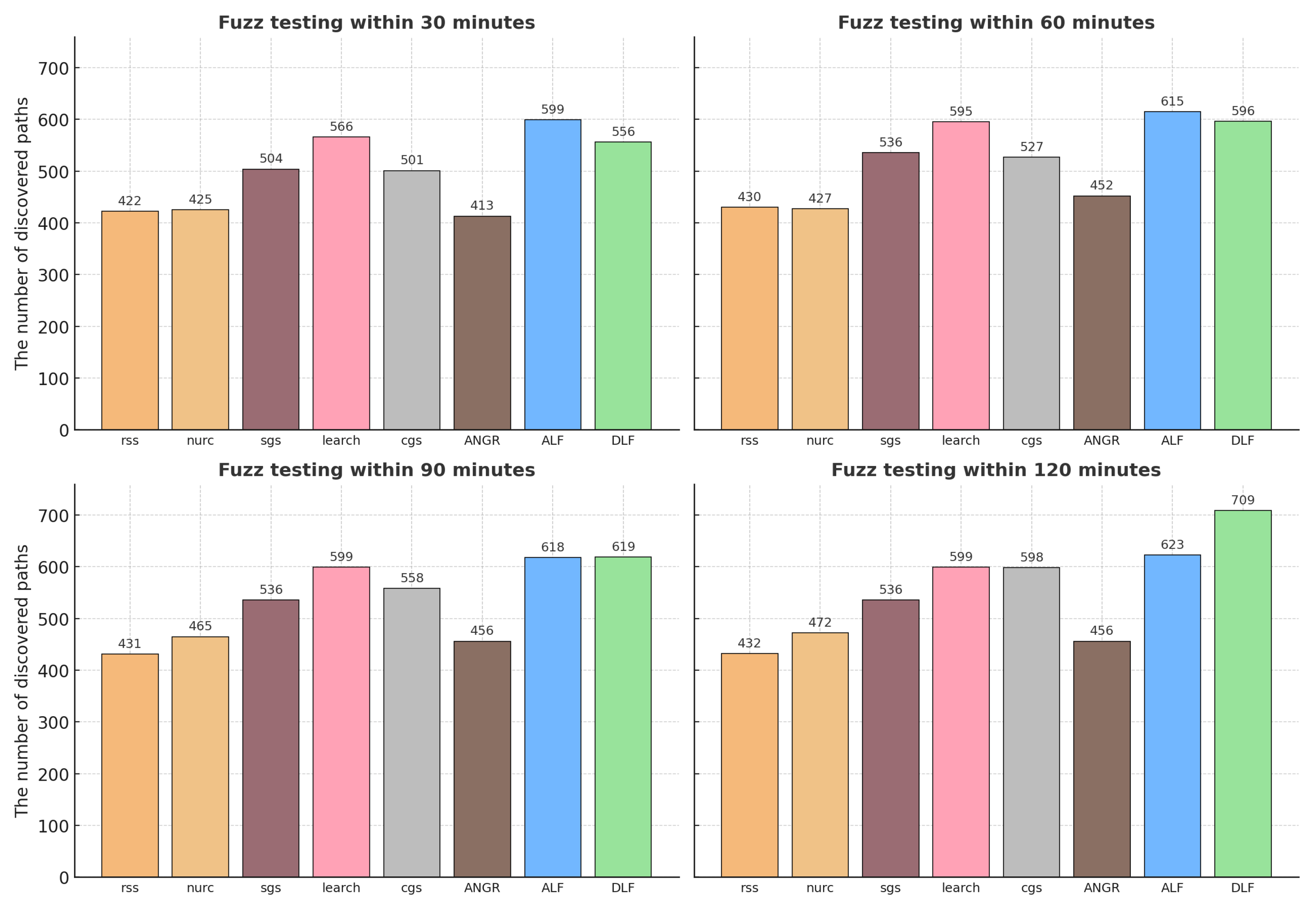
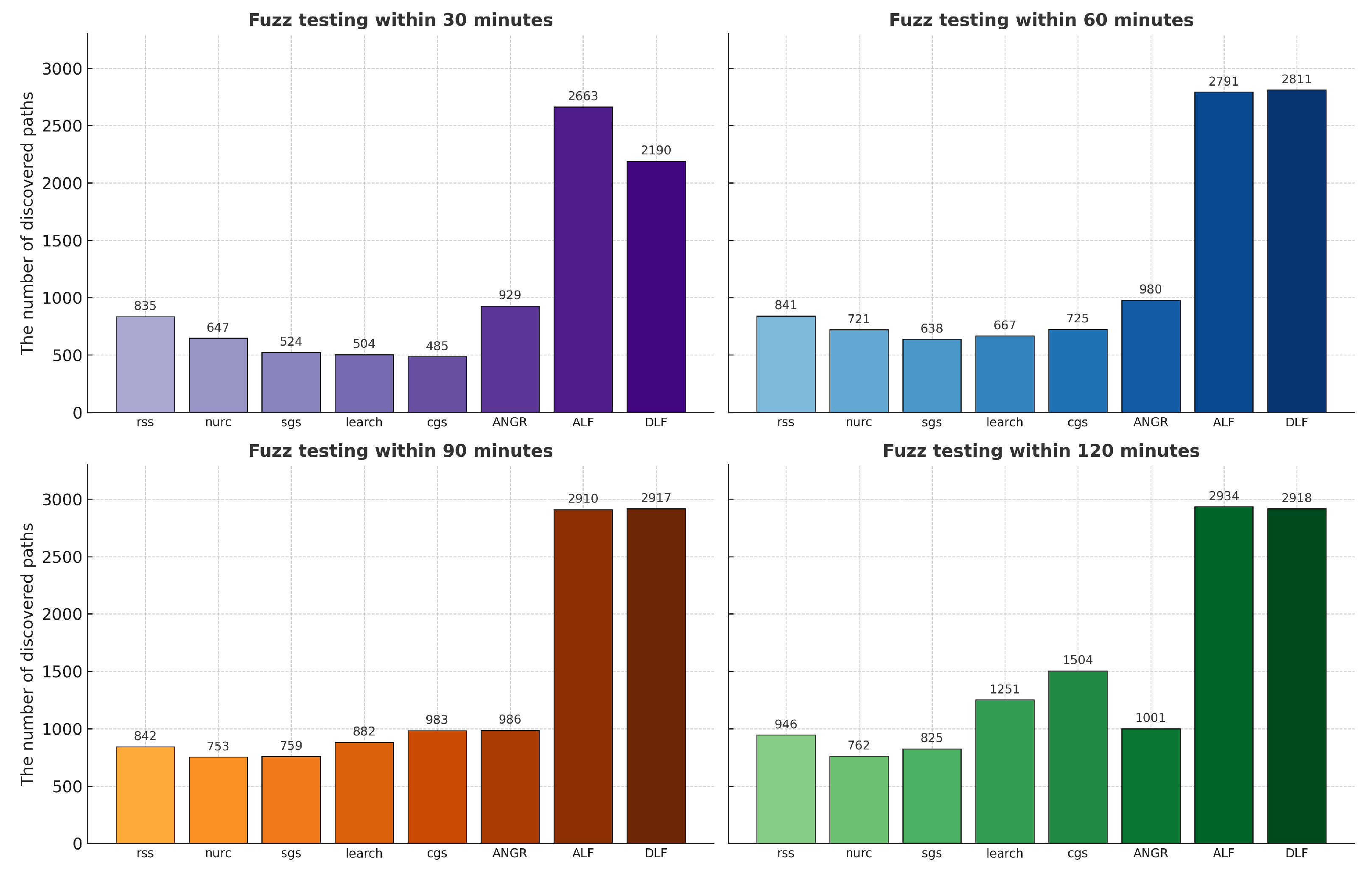
Extensive empirical validation on multiple datasets. The effectiveness of DLF is evaluated on several real-world benchmark datasets. Experimental results demonstrate that DLF consistently outperforms existing methods in terms of vulnerability detection rate, path coverage, and execution efficiency.

The remainder of this paper is organized as follows: Section 2 reviews related work; Section 3 presents the overall design and key techniques of DLF; Section 4 reports the experimental setup and results; Section 5 concludes the paper; and Section 6 outlines future work and suggestions.

2. Related Work

In recent years, automated test case generation and its intelligent optimization have become significant research directions in software engineering and security testing. To clarify the research foundation and innovation positioning of the proposed DLF framework, this section provides a comprehensive review and analysis of related work from four perspectives: automated test case generation methods, symbolic execution techniques, deep learning applications, and the integration of active learning with ensemble learning.

2.1. Automated Test Case Generation Method

Automated testing is a critical component of software quality assurance, aiming to generate high-coverage test cases under limited human and time resources to uncover potential defects. Early studies primarily focused on random testing and search-based testing methods. Random testing generates input data probabilistically, offering implementation simplicity but lacking targeting capability and coverage control. Search-based methods (e.g., genetic algorithms, simulated annealing) define coverage objectives and iteratively optimize test inputs, thereby improving testing effectiveness to some extent, albeit at the cost of higher computational overhead.

As program structural complexity increased, research attention gradually shifted toward constraint-driven test generation. Symbolic execution emerged as a key approach to automated testing—it replaces concrete inputs with symbolic variables and automatically generates test cases that satisfy specific path constraints through constraint solving, enabling systematic path exploration. Compared with traditional black-box testing [19], symbolic execution can precisely characterize program behavior and achieve higher test coverage. However, it faces significant bottlenecks in complex systems: the number of execution paths grows exponentially with branching depth (the so-called path explosion problem), and constraint solving becomes computationally expensive. These challenges have motivated researchers to combine symbolic execution with other intelligent techniques to balance efficiency and coverage.

In recent years, intelligent test generation has become a prevailing trend. By integrating machine learning models, researchers have sought to learn the distribution of input features from program execution data, control-flow structures, or historical testing results, enabling the prediction of high-value paths and the automatic generation of diverse test inputs. This learning-driven approach provides a new optimization direction for traditional symbolic execution, effectively bridging the gap between theoretical exhaustiveness and practical scalability.

2.2. Symbolic Execution

Symbolic execution is a white-box testing technique whose core idea is to model program inputs as symbolic variables, record path constraints during execution, and use constraint solvers to generate concrete inputs that satisfy these constraints, thereby guiding the program to execute along specific paths. Since its introduction in the mid-1970s, symbolic execution has undergone multiple stages of development and evolution, giving rise to various forms such as Dynamic Symbolic Execution (DSE) [20] and Selective Symbolic Execution (SSE) [21]. Theoretically, this method enables full path coverage and has been widely applied in program analysis, security testing, and vulnerability detection [22,23,24].

Early studies mainly focused on improving the scalability and path exploration capability of symbolic execution. Frameworks such as DART [25] and CUTE [26] pioneered the concept of combining concrete execution with symbolic execution—known as concolic execution—which effectively mitigated the path explosion problem and enabled automated input generation. Subsequently, tools such as EXE [27] and KLEE [28] introduced systematic optimizations in constraint solving and state merging, making symbolic execution applicable to large-scale program analysis. In addition, SAGE [29] integrated symbolic execution with white-box fuzzing, significantly improving the coverage of industrial-scale software vulnerability detection and successfully discovering multiple security flaws in Windows systems.

The major optimization directions in this line of research include:

(1)

Path search optimization—employing heuristic strategies (e.g., coverage-guided or goal-oriented search) to improve exploration efficiency;

(2)

Constraint-solving optimization—leveraging techniques such as caching, pruning, and incremental solving to reduce redundant computation;

(3)

State merging and scheduling optimization—applying path merging and state prioritization to reduce the complexity of the state space.

Although these methods alleviate the path explosion problem to some extent, they do not fundamentally solve the scalability bottleneck. Traditional symbolic execution still heavily relies on manually designed heuristic rules and lacks intelligent adaptivity, making it inadequate for handling deep logical paths and complex semantic dependencies. In recent years, researchers have begun to introduce data-driven and machine-learning-based approaches to enhance symbolic execution by extracting feature representations from symbolic states and constructing predictive models to assist path search and constraint solving [30,31]. This emerging trend provides the theoretical and methodological foundation for the DLF framework proposed in this paper.

2.3. Applications of Deep Learning

In recent years, the rise of deep learning (DL) techniques has brought new opportunities to program analysis and test case generation. By mapping program statements, control-flow structures, or input–output sequences into high-dimensional feature representations, deep models can automatically learn the structural and semantic characteristics of programs, providing intelligent decision support for test generation.

Recent studies have shown that deep learning can effectively encode rich program semantics across diverse analysis tasks, forming an essential foundation for enhancing symbolic execution. For example, John Philipose Villoth et al. [32] proposed a two-stage defect prediction framework that integrates CNNs with multi-class ensemble learning and employs an improved firefly algorithm for hyperparameter optimization, achieving notable gains on both traditional software metrics and NLP-based code representations. Similarly, Niloofar Khoshniat et al. [33] developed a hybrid graph neural network that fuses code semantic embeddings, corpus-level representations, and contextual features, where hierarchical attention enhances cross-layer interactions and significantly improves defect prediction accuracy. Beyond defect prediction, Lei Bu et al. [5] introduced the MLBSE framework, which incorporates machine-learning-driven derivative-free optimization into symbolic execution, transforming complex path-constraint solving into a sampling-and-learning search process and substantially improving the handling of nonlinear constraints and black-box library functions. Furthermore, Kevin Lano et al. [4] proposed a symbolic machine-learning approach over software abstract syntax trees that automatically learns tree-to-tree transformations from examples, effectively reducing the manual effort of building code generators and improving transformation quality.

Researchers have further approached automated test case generation from several DL-based perspectives:

(1)

Path feature modeling and prediction. Convolutional Neural Networks (CNNs) and Recurrent Neural Networks (RNNs) are employed to extract features from path sequences and predict high-risk or high-coverage paths.

(2)

Program structure and semantic modeling. Graph Neural Networks (GNNs) are introduced to model Control Flow Graphs (CFGs) and Data Flow Graphs (DFGs) [34], capturing dependencies among program nodes to achieve structured feature representation.

(3)

Test input generation. Deep generative models such as Variational Autoencoders (VAEs) [35] and Generative Adversarial Networks (GANs) [36] are utilized to learn input distributions from historical samples, thereby generating diverse and representative test data.

These methods have achieved remarkable progress in improving the intelligence of testing and the accuracy of path prediction. However, several challenges remain: insufficient training samples, limited model generalization capability, and poor interpretability. Moreover, deep models often rely on large-scale labeled datasets, whereas data generated by symbolic execution typically contain noise and bias, further constraining model practicality. Consequently, how to integrate active learning and ensemble strategies to enhance training efficiency and model stability has become an important direction for future research.

2.4. Applications of Active Learning and Ensemble Learning

The concept of active learning (AL) can be traced back to the 1980s, when Angluin et al. [37] proposed the query learning model in 1988, laying the theoretical foundation for active learning. The core idea of active learning is to select the most informative samples for labeling to improve model performance under limited annotation cost. In the field of automated testing, active learning has been applied to the selection of symbolic states or path samples. By employing uncertainty-based or diversity-based sampling strategies, it prioritizes high-value samples for model training. For example, uncertainty sampling—based on metrics such as entropy, confidence intervals, or margin distance—can effectively improve model precision in critical regions, while diversity sampling ensures broader representativeness of test data. Some studies have further integrated active learning with fuzz testing to achieve adaptive input expansion.

Ensemble learning (EL), on the other hand, enhances overall prediction accuracy and robustness by combining the outputs of multiple base learners. Common approaches include Bagging [38], Boosting [39], and Stacking [40]. Ensemble models distribute errors among different learners, thereby improving system stability. In automated testing, ensemble learning has been applied to path prediction, defect classification, and input generation tasks, where multi-model fusion effectively mitigates overfitting issues inherent to single-model architectures. However, most existing research adopts a static ensemble approach with fixed model weights, lacking the ability to adjust dynamically according to testing feedback, which limits its applicability in complex symbolic state spaces.

With their respective strengths in reducing labeling cost and achieving robust model fusion, active learning and ensemble learning offer new perspectives for improving symbolic execution. Active learning enables more targeted annotation by selecting the most valuable unlabeled samples, thus significantly lowering labeling overhead. Ensemble learning, meanwhile, combines the complementary strengths of multiple models to enhance robustness and generalization. Both paradigms have demonstrated substantial success in other domains, inspiring their integration into symbolic execution tools to overcome the inherent limitations of traditional approaches. Accordingly, we integrate AL with a dynamic EL scheme to address the aforementioned issues in SE.

3. Methods

3.1. DLF Framework Description

After analyzing the limitations of existing symbolic execution tools—particularly their insufficient detection accuracy and single-path exploration strategies in high-risk vulnerability detection—this paper proposes a Deep Active Ensemble Learning Framework (DLF) for symbolic execution path exploration. The framework aims to enhance both the path exploration capability and vulnerability detection accuracy of symbolic execution. It has been instantiated on the mainstream symbolic execution engine ANGR [41], forming a novel symbolic execution tool named Desbuild, which achieves high efficiency and robustness in path exploration.

During the training phase, DLF integrates self-ensemble learning and active learning mechanisms. By accumulating historical model weights, it stabilizes prediction results while actively introducing high-confidence pseudo-labeled samples for incremental self-training, in parallel with uncertainty-driven active selection, thereby forming an efficient and adaptive optimization loop. This approach reduces dependence on large-scale manually labeled data and enhances model generalization capability.

During the testing phase, DLF constructs a heterogeneous model pool consisting of a Feedforward Neural Network (FNN), TabNet (Attentive Interpretable Tabular Learning), Recurrent Neural Network (RNN), Support Vector Machine (SVM), and Extreme Gradient Boosting (XGBoost). The system dynamically selects and adaptively weights the optimal model combination based on the feature similarity between testing samples and training data. This allows DLF to fully exploit the complementary strengths of different models, thereby improving the accuracy and stability of path selection.

In addition, DLF introduces a dynamic sliding-window mechanism that adaptively adjusts the window size according to path complexity. This design effectively controls computational overhead while maintaining execution efficiency. Meanwhile, a Gated Graph Neural Network (GGNN) is incorporated to perform multidimensional feature extraction and semantic fusion from the Control Flow Graph (CFG), enhancing the model’s awareness of global program dependencies.

The proposed DLF framework strives to achieve efficient and accurate symbolic execution under limited labeling conditions. By embedding a closed-loop updating mechanism and dynamic window adjustment strategy into the symbolic execution workflow—and optimizing prediction outcomes through multi-model ensemble learning—DLF overcomes the traditional limitations of path exploration and feature extraction. This work not only provides a novel perspective for the design of symbolic execution tools but also introduces new momentum for research in software testing and vulnerability detection. The overall testing workflow of the DLF framework is illustrated in Figure 1.

The implementation of the core testing components in the DLF framework primarily consists of the following steps:

(1)

Initialization of the training set. Given an initial set of $N_0$ training programs, the Tracer technique is employed to backtrace the execution paths of known crashing inputs. At each symbolic state, a feature vector set F is extracted, along with its corresponding state label (TAKEN or NON-TAKEN), thereby forming the supervised dataset T.

(2)

Construction of multiple classifiers via self-ensemble learning. Based on the supervised dataset T, multiple classifiers are trained iteratively and continuously updated, thereby guiding the generation of high-quality test cases. The labeled training program set $L_R$ is initialized as an empty set $\varphi$, while the remaining $N_1$ program files are reserved for iterative model updating during the active learning phase.

(3)

Model training and iterative updating. The supervised dataset T is iteratively updated as new symbolic state samples are incorporated. The latest training results are continuously fed back to the learning models to refine and update the predictive model through incremental learning.

(4)

Symbolic state prediction. For each iteration, one program from the $N_1$ set is selected for symbolic execution. The trained predictive model is applied to perform vulnerability probability estimation for each symbolic state encountered during execution.

(5)

Model evaluation and convergence. When the number of active learning iterations ($als$) reaches the threshold n, and the number of model training epochs reaches the threshold N, the final predictive model is generated. This finalized model is then applied to the remaining test programs for evaluation. Otherwise, the process returns to Step (2) for the next training iteration.

(6)

Similarity-based model selection during testing. In the actual testing phase, dynamic model matching is performed based on the similarity between the target sample and the training set. The system adaptively integrates the most relevant models for symbolic execution, ensuring that the test cases generated are both targeted and of high quality.

3.2. Components of the DLF Framework

The DLF framework integrates multiple technologies and methodologies. From the perspective of its innovative mechanisms, this section provides a detailed description of each constituent component. By analyzing the key modules in depth, we elucidate their specific functions in path exploration and vulnerability detection, as well as their synergistic interactions. This comprehensive exposition aims to present a clear understanding of the concrete implementation process of the DLF framework.

3.2.1. Feature Design

The feature system designed in this study extends the original feature representations of active learning and ensemble learning by incorporating a multidimensional fusion of static, dynamic, and structural features. The objective is to construct an enhanced feature set oriented toward complex path awareness—systematically optimizing both code coverage and vulnerability detection capability—thereby improving the exploration efficiency and detection precision of symbolic execution.

Specifically, the feature configuration employs dynamic feedback indicators (e.g., coverage) to adjust the exploration direction in real time, maximizing code coverage. In parallel, it integrates structural and semantic features to identify high-risk code patterns, thereby enhancing the specificity of vulnerability detection.

A subset of critical structural features is extracted via a Gated Graph Neural Network (GGNN), which performs in-depth analysis of the Control Flow Graph (CFG) to capture characteristics such as node centrality, data-dependency edge ratio, and other topological metrics. These structural representations supplement DLF’s capability for deep semantic understanding of program behavior, enabling the model to more effectively grasp the overall control and execution flow of the program. Given a CFG with $\left|V\right|$ basic blocks and $\left|E\right|$ edges, one forward pass of the GGNN requires $O\left(T\right(\left|V\right|+\left|E\right|\left)\right)$ time and $O\left(\right|V\left|d\right)$ memory, where T is the number of propagation steps and d is the hidden dimension, so the structural feature extraction overhead grows linearly with the graph size.

Through the synergistic interaction among static, dynamic, and structural indicators, the feature system provides precise decision support for symbolic path selection while maintaining high test coverage and vulnerability discovery rates across diverse program environments. The features discussed in this section are summarized in

Table 1. Summary of features.

Feature Name	Description
memory_read_write	Number of memory read and write operations.
connectivity	Number of connected states within the control flow graph (CFG).
function_complexity	Loop and structural complexity of the current function.
num_calls	Number of function calls appearing within a branch.
registers_read_write	Number of register read/write operations, measuring program–environment interaction.
coverage	Number of newly covered branches and instructions achieved by the current state and exploration process.
depth	Number of branch levels executed along the current path.
subpath	Number of times the current path segment has been revisited.
instsincecovnew	Number of instructions executed since the last new coverage event.
centrality	Structural importance (centrality) of the basic block within the control flow graph.
data_edge_ratio	Ratio of data-dependency edges to control-dependency edges within a basic block.
loop_depth	Depth of loop nesting for the current node.
inter_module_density	Degree of interconnection between the current function and external modules.

.

3.2.2. Active Ensemble Learning Method

Traditional active learning methods typically rely on multiple iterative rounds to select high-value samples for manual annotation. However, this approach suffers from two major limitations: the high cost of human labeling, and the instability of sample selection caused by fluctuations in model performance during training, which ultimately degrades overall learning effectiveness. To address these issues, we propose a model training approach that couples self-ensemble learning with active learning. The self-ensemble results of the model are incorporated into the active-learning-based sample selection process to maximize prediction accuracy and multi-model efficiency under limited labeling cost conditions.

Specifically, self-ensemble learning aggregates the outputs of the network across multiple training epochs to suppress noise and improve prediction stability. The core idea of self-ensemble learning is to maintain a historical record of predictions using the Exponential Moving Average (EMA) mechanism. Equation (1) defines the computation of EMA, where $\alpha$ denotes the momentum factor (ranging from $[0,1]$; in this study $\alpha =0.6$, with larger values assigning higher weight to the current epoch), P represents the accumulated historical predictions on unlabeled data, p denotes the current prediction at training epoch t, and t is the index of the current epoch. Equation (2) provides a bias-correction adjustment for the accumulated prediction values, where the correction factor n is set to 2 in this work.

$$P_t=\alpha p_t+(1-\alpha )·P_{t-1}$$

(1)

$${\widehat{P}}_t={\displaystyle \frac{P_t}{1-{\alpha }^t}}$$

(2)

At the end of each training epoch, the model computes a consistency loss based on the discrepancy between the historical predictions and the current epoch’s predictions. This operation acts as a form of temporal regularization applied to the network, mitigating abrupt fluctuations during training and improving model stability. Specifically, the mean squared error (MSE) between the historical prediction P of unlabeled data and the current prediction p is computed and added as a regularization term to the loss function in each training epoch, guiding the model’s parameter updates.

Equation (3) defines how the mean squared difference between the current and historical predictions is integrated into the overall loss function as a regularization component. Here, $\omega \left(t\right)$ denotes a time-dependent variable (initialized as 0); when $\omega \left(t\right)<5$, its value equals the current epoch index t, otherwise it is fixed at 5. The index i represents the sample within a mini-batch.

$$L_{\mathrm{consistency}}={\displaystyle \frac{\omega \left(t\right)}{N}}\sum _{i=1}^N{\left(p_t^{\left(i\right)}-P_t^{\left(i\right)}\right)}^2$$

(3)

For a mini-batch containing N unlabeled symbolic states, the EMA update in Equations (1) and (2) and the consistency loss in Equation (3) can be computed in $O\left(N\right)$ time with $O\left(N\right)$ additional memory to store the historical predictions, so the self-ensemble overhead grows linearly with the number of actively tracked samples.

Through this self-ensemble mechanism, the model can leverage historical information to smooth its predictive outputs and select high-quality samples more efficiently during the active learning process, thereby enhancing prediction performance. The loss function returned by the training model consists of two main components: (1) a supervised loss term, which measures the model’s fitting capability on labeled data; and (2) an unsupervised regularization term, which reflects the smoothness and temporal consistency of the model’s predictions.

To further optimize the process of actively selecting high-quality samples for subsequent training rounds, this work couples self-ensemble learning with active learning by using the relative deviation between the historical prediction P and the current prediction p as the criterion for sample selection. Specifically, samples with a low relative deviation indicate stable model predictions and can be pseudo-labeled directly using the model’s output. In contrast, samples with a high relative deviation suggest unstable or uncertain predictions, and such samples are prioritized for manual annotation to ensure the accuracy of the training data. Equation (4) defines the computation of this relative deviation, which quantitatively measures the discrepancy between the historical and current predictions. This metric provides an objective and data-driven basis for sample selection during the active learning phase. Here, $p_t$ denotes the current forecast value, $P_{t-1}$ represents the historical forecast value, and $\epsilon$ is a constant used to prevent the denominator from becoming zero.

$$di{f}_t={\displaystyle \frac{\left|p_t-P_{t-1}\right|}{\left|P_{t-1}\right|+\epsilon }}$$

(4)

The historical prediction $P_{t-1}\left(x\right)$ is updated by the EMA rule in Equations (1) and (2). Based on the relative deviation in Equation (4), Algorithm 1 selects stable samples for pseudo-labeling and highly uncertain samples for manual annotation.

Algorithm 1 Active Sample Selection with EMA-Based Self-Ensemble

Input: Unlabeled set U; model $f_{\theta }$; historical predictions $\left\{P_{t-1}\left(x\right)\right\}$; thresholds ${\tau }_{\mathrm{low}}$, ${\tau }_{\mathrm{high}}$; constant $\epsilon$

Output: $S_{\mathrm{pseudo}}$, $S_{\mathrm{query}}$

1: $S_{\mathrm{pseudo}}\leftarrow \varnothing$; $S_{\mathrm{query}}\leftarrow \varnothing$   2: for each $x\in U$ do   3:     $p_t\left(x\right)\leftarrow f_{\theta }\left(x\right)$   4:     ${\mathrm{dif}}_t\left(x\right)\leftarrow {\displaystyle \frac{|p_t\left(x\right)-P_{t-1}\left(x\right)|}{\left|P_{t-1}\left(x\right)\right|+\epsilon }}$, Equation (4)   5:     if ${\mathrm{dif}}_t\left(x\right)\le {\tau }_{\mathrm{low}}$ then   6:         $\widehat{y}\left(x\right)\leftarrow \mathrm{LabelFromPrediction}\left(p_t\left(x\right)\right)$   7:         $S_{\mathrm{pseudo}}\leftarrow S_{\mathrm{pseudo}}\cup \left\{(x,\widehat{y}\left(x\right))\right\}$   8:     $\mathbf{else\; if} {\mathrm{dif}}_t\left(x\right)\ge {\tau }_{\mathrm{high}} \mathbf{then}$   9:         $S_{\mathrm{query}}\leftarrow S_{\mathrm{query}}\cup \left\{x\right\}$ 10:     end if 11: end for 12: return$S_{\mathrm{pseudo}},S_{\mathrm{query}}$

By introducing a deterministic–uncertain hybrid sampling mechanism in the active learning phase, DLF achieves adaptive optimization across different testing objectives. In code coverage optimization, deterministic sampling efficiently identifies paths that yield significant coverage gains. In vulnerability detection tasks, the hybrid sampling strategy balances the exploitation of high-risk paths with the exploration of anomalous states, thereby enhancing both detection accuracy and comprehensiveness. This mechanism demonstrates, both theoretically and empirically, the effectiveness of DLF’s active learning strategy in symbolic execution path exploration and provides valuable insights for the design of future intelligent testing strategies.

3.2.3. Model Pool Construction

During the testing phase, to enhance the adaptability of the symbolic execution system across diverse scenarios, this study constructs a heterogeneous model pool and introduces a dynamic scenario adaptation mechanism. The model pool consists of five distinct models: a Feedforward Neural Network (FNN), TabNet, a Recurrent Neural Network (RNN), a Support Vector Machine (SVM), and XGBoost. By integrating these models, Desbuild can dynamically select the optimal model combination under varying conditions, enabling accurate capture and efficient prediction of diverse data characteristics encountered during symbolic execution. The heterogeneous model pool is shown in Figure 2.

The Feedforward Neural Network (FNN) serves as the foundational component of the model pool and is primarily used for processing structured data. By constructing deep hierarchical feature representations through multiple fully connected layers, FNN exhibits strong nonlinear mapping and generalization capabilities. Within symbolic execution, it captures the global correlations among program variables and effectively learns the global interactions among various static features during program execution. This enables FNN to provide a solid foundation for subsequent path selection and state prediction tasks.

TabNet is a deep learning model designed for tabular data, and its primary advantage lies in its ability to automatically identify and learn feature importance. By introducing an attention mechanism, TabNet performs stepwise feature selection and weighting, allowing the model to capture key information even when dealing with high-dimensional or sparse program data. Given the large volume of intermediate state data generated during symbolic execution, TabNet’s adaptive feature learning capability makes it an important tool for improving the accuracy of generated test cases.

The Recurrent Neural Network (RNN) possesses inherent advantages in processing sequential data, making it suitable for capturing temporal dependencies and dynamic variations. During symbolic execution, program states and execution paths often exhibit temporal correlations and interdependencies. RNNs leverage their memory mechanisms to track and predict these dynamic changes, providing temporal context to the overall prediction process within the model pool. Moreover, RNN variants such as Long Short-Term Memory (LSTM) [42] networks and Gated Recurrent Units (GRU) [43] can mitigate gradient vanishing issues in long-sequence training, thereby enhancing model stability.

The Support Vector Machine (SVM) is renowned for its ability to construct optimal hyperplanes in high-dimensional spaces and particularly excels in small-sample learning scenarios. In symbolic execution testing, where high-quality labeled data are often scarce, SVMs demonstrate clear advantages in achieving high-precision classification and regression with limited samples. By incorporating SVMs into the model pool, Desbuild can maintain strong predictive accuracy even under limited data conditions, providing a robust supplement to the overall ensemble.

XGBoost is an efficient algorithm based on gradient boosting decision trees and is widely recognized for its strong predictive performance and robustness to outliers. In the context of symbolic execution, XGBoost integrates multiple weak learners to evaluate program execution paths from multiple perspectives and achieve precise prediction of complex state transitions. Its efficient training and inference capabilities also make it well suited for large-scale testing data processing.

By integrating these diverse models into a heterogeneous model pool and coupling them with a dynamic scenario adaptation mechanism, Desbuild can automatically select the optimal model combination—or employ a full-model ensemble strategy—based on the characteristics of the current input data during testing. This flexible model selection mechanism not only leverages the strengths of each individual model but also enhances overall prediction accuracy and robustness, providing a more refined and efficient test case generation methodology for symbolic execution.

3.2.4. Dynamic Model Integration

To maximize the adaptability of the model’s predictions to the target program under test, this study proposes a dynamic similarity–based prediction consistency mechanism. The core idea is to exploit information from historical training data to dynamically select the model most compatible with the current sample, thereby achieving more accurate and context-aware predictions. The detailed procedure is as follows:

(1)

Feature Extraction. Feature vectors are extracted from the sample to be predicted, while the corresponding feature vectors of the training data are obtained from the model–feature adaptation matrix.

(2)

Similarity Measurement. Cosine similarity is employed to compute the similarity score between the feature vector of the test sample and those of the training samples.

(3)

Model Selection. Based on the similarity scores, the predictive model corresponding to the training sample most similar to the current test sample is selected for inference.

Specifically, each model in the framework is trained independently, and its accuracy on the training set is denoted as $Ac{c}_i(i\in \{1,2,\dots ,5\})$. Meanwhile, the model’s performance under different feature data distributions is recorded to construct a model–feature adaptation matrix M. During each prediction phase, the system dynamically selects the most suitable model by evaluating the feature similarity between the test sample and the training samples. The similarity measurement adopts cosine similarity as the evaluation criterion, as defined in Equation (5). Here, X represents the set of all feature vectors of the test samples, $D_{train}$ denotes the feature column vectors within the adaptation matrix M, $x_i$ refers to the feature vector of the current test sample, and $x_j$ denotes the feature vector of a historical training sample. The cosine similarity, denoted as $Sim(X,D_{train})$, quantifies the degree of alignment between the two feature vectors.

$$Sim(X,D_{\mathrm{train}})=\underset{x_i\in X,x_j\in D_{\mathrm{train}}}{max}{\displaystyle \frac{x_i^T·x_j}{\parallel x_i\parallel \parallel x_j\parallel }}$$

(5)

When $Sim(X,D_{\mathrm{train}})\ge \theta ;(\theta =0.7)$, the framework selects the top two models from the adaptation matrix M that correspond to the most similar scenarios for prediction. The weight assigned to each selected model is determined by its respective training accuracy, while the threshold parameter $\theta$ is derived empirically through experimental validation. Otherwise, when this condition is not satisfied, the framework activates a full-model weighted ensemble to compute the vulnerability probability of symbolic states. The weighting method for each model in the ensemble is defined in Equation (6).

$${\omega }_i={\displaystyle \frac{Ac{c}_i}{{\sum }_{j=1}^{5}Ac{c}_j}}$$

(6)

The weight allocation strategy of the dynamic model similarity method ensures that high-accuracy models dominate the prediction results, while the use of cosine similarity fully leverages the knowledge embedded in historical training data. During the testing phase, targeted prediction is achieved through feature-similarity-based model selection and performance-weighted ensemble fusion, thereby enhancing overall predictive accuracy and effectiveness. Based on the above design, and to illustrate how models are selected and combined during testing, we outline the dynamic integration process in Algorithm 2. For a test feature vector of dimension d compared against N historical scenarios stored in the adaptation matrix M, the similarity-based selection in Algorithm 2 runs in $O\left(Nd\right)$ time and requires $O\left(Nd\right)$ memory for maintaining M. The additional cost of computing performance weights and aggregating up to K model outputs is $O\left(K\right)$; thus, the dynamic integration overhead scales linearly with the number of recorded scenarios and models.

3.2.5. Sliding Window Mechanism

To balance path exploration depth and computational efficiency during symbolic execution, this paper proposes an adaptive sliding-window strategy based on path complexity. The strategy dynamically adjusts the range of contextual information captured, thereby maintaining an optimal trade-off between computational overhead and exploration granularity.

In practice, when the execution encounters regions with high path complexity—areas characterized by high branch density—the system expands the sliding window to capture longer contextual dependencies, enabling deeper exploration of critical paths. Conversely, for regions with low path complexity, the window size is dynamically reduced to avoid unnecessary computation, thus improving overall execution efficiency. This adaptive adjustment mechanism effectively optimizes the symbolic execution process, ensuring comprehensive path coverage while efficiently utilizing computational resources.

Algorithm 2 Dynamic Model Integration

Input: Feature vector x of a test state; model pool ${\left\{f_i\right\}}_{i=1}^K$ with accuracies ${\left\{Ac{c}_i\right\}}_{i=1}^K$; adaptation matrix M; similarity threshold $\theta$

Output: Predicted vulnerability score $\widehat{p}$

1: $x_{\mathrm{feat}}\leftarrow \mathrm{ExtractFeatures}\left(x\right)$   2: $(Si{m}_{max},S)\leftarrow \mathrm{FindMostSimilarScenario}(x_{\mathrm{feat}},M)$   3: if$Si{m}_{max}<\theta$then   4:    $S\leftarrow \{1,2,\dots ,K\}$ {use full-model ensemble}   5: end if   6: $Z\leftarrow {\sum }_{i\in S}Ac{c}_i$   7: for each $i\in S$ do   8:    ${\omega }_i\leftarrow Ac{c}_i/Z$   9: end for 10: $\widehat{p}\leftarrow {\sum }_{i\in S}{\omega }_i·f_i\left(x_{\mathrm{feat}}\right)$ 11: return $\widehat{p}$

In this study, branch density is employed as the quantitative metric for path complexity. It is defined as the ratio of the number of branch instructions within a given window to the window size W, as shown in Equation (7), where W denotes the window size and $N_{branch}$ represents the number of branch instructions.

$$BD={\displaystyle \frac{N_{\mathrm{branch}}}{W}}$$

(7)

When the branch density (BD) exceeds the predefined threshold of 3, it indicates that the current window contains a large number of branch instructions. In such cases, a single small window may fail to adequately capture the inherent complexity of the path. Expanding the window allows the system to capture additional branch instructions and contextual information, enabling the model to more comprehensively assess the potential risk associated with the path. Accordingly, the system performs window expansion based on Equation (8) to capture richer contextual information and deepen path exploration. The window threshold parameters are determined empirically according to the results of ablation experiments.

$$W_{\mathrm{new}}=min(W_{\mathrm{old}}+2,W_{\max }=10)$$

(8)

When five consecutive nodes satisfy the condition that the branch density (BD) is less than or equal to 1, it indicates that the current path segment is relatively simple and stable. In this case, a smaller window is sufficient to provide adequate contextual information for symbolic execution, allowing computation to proceed more efficiently without unnecessary window expansion that could capture redundant data. Accordingly, the system performs window contraction based on Equation (9) to reduce computational overhead and improve execution efficiency. This adaptive shrinking mechanism effectively mitigates the path explosion problem during symbolic execution by dynamically controlling the exploration scope.

$$W_{\mathrm{new}}=max(W_{\mathrm{old}}-1,W_{\min }=2)$$

(9)

This adaptive sliding-window strategy based on path complexity dynamically adjusts the window size to achieve an optimal balance between depth and efficiency in symbolic execution, enabling deeper exploration of complex paths while reducing unnecessary computation on simpler paths. Given a symbolic execution trace with L nodes, the branch-density computation in Equation (7) and the window updates in Equations (8) and (9) can be implemented with a single pass over the trace, incurring $O\left(L\right)$ time and $O\left(W_{max}\right)$ memory overhead, where $W_{max}$ is the upper bound of the window size; thus, the adaptive sliding-window mechanism introduces only linear overhead with respect to the explored path length. To illustrate the operational logic of the window adjustment strategy, the adaptive update process of the sliding window is organized into Algorithm 3.

Algorithm 3 Adaptive Sliding Window Update

Input: Current window size W; branch density $BD$; counter c for consecutive simple nodes; thresholds $B{D}_{\mathrm{high}}=3$, $B{D}_{\mathrm{low}}=1$; $W_{min}=2$, $W_{max}=10$

Output: Updated window size W, updated counter c

1: if$BD>B{D}_{\mathrm{high}}$then   2:     $W\leftarrow min(W+2,W_{max})$   3:     $c\leftarrow 0$   4: else if $BD\le B{D}_{\mathrm{low}}$ then   5:     $c\leftarrow c+1$   6:     if $c\ge 5$ then   7:        $W\leftarrow max(W-1,W_{min})$   8:        $c\leftarrow 0$   9:     end if 10: else 11:    $c\leftarrow 0$ 12: end if 13: return $W,c$

From a theoretical point of view, the core parts of DLF can each be linked to a known stability mechanism. The EMA-based self-ensemble is closely related to consistency regularization: by smoothing predictions across epochs, it damps the small oscillations introduced by noisy gradients and gradually stabilizes the learning target. The deviation-based pseudo-labeling and query rule acts as a confidence-driven active-learning strategy: high-confidence samples are used for pseudo-labeling to avoid propagating label noise, while highly uncertain samples are sent for manual annotation, which helps reduce generalization error under a fixed labeling budget. The dynamic model integration mechanism is also inherently constrained. Because it operates over a fixed model pool and applies normalized weights, the final prediction stays within a bounded hypothesis space, and the influence of any unstable base model cannot grow without control. The same kind of boundedness appears in the sliding-window component: explicit upper and lower limits, together with small update steps, keep the window size from exploding or collapsing and make the scheduling process easier to control in practice. Viewed together, these design choices provide a reasonable theoretical basis for the convergence behaviour and robustness of the DLF framework in both training and testing.

4. Experimental Process and Result Analysis

This subsection primarily presents the experimental validation of the proposed DLF framework, including the datasets used, the experimental design, and the final results obtained.

4.1. Dataset

To evaluate the effectiveness of the proposed method, this study adopts the Cyber Grand Challenge (CGC) dataset, initiated by the Defense Advanced Research Projects Agency (DARPA), as both the training and testing set. The CGC dataset is specifically designed for research on automated vulnerability discovery and exploitation, containing a large number of binary programs with realistic attack surfaces as well as their corresponding crashing inputs [44]. These programs cover a wide range of application domains—including content management systems, network services, and mini-games—and are characterized by semantic complexity, diverse input structures, and expansive symbolic state spaces, making them highly challenging for analysis. The experimental platform constructed on the basis of the CGC dataset not only preserves the structural consistency and controllability of a standardized benchmark but also reflects the uncertainty and diversity inherent in complex software environments. This provides a rigorous and comprehensive foundation for evaluating the performance of symbolic execution path exploration strategies.

4.2. Experimental Design

In this study, seven baseline methods were selected for comparative evaluation. Most of these baselines represent heuristic strategies inherent to mainstream symbolic execution tools. Specifically, the selected methods include the random-state (rss) strategy, the nurs:cpicnt (nurc) strategy, the sgs hybrid strategy (integrated in this work), the learch strategy [5], and the cgs strategy [45], as well as two representative symbolic execution frameworks—ANGR and the Active Learning–based Framework (ALF). Since the symbolic execution engine, path scheduling strategy, and dynamic model integration all follow deterministic decision rules, the variance across repeated runs is extremely small. Therefore, reporting the mean over five independent runs provides a stable and representative estimate of performance.

The sgs hybrid strategy comprises three variants—sgs:1, sgs:2, and sgs:4—which differ in the granularity of symbolic state selection. The learch strategy employs machine learning techniques to replace heuristic-based decision-making during path exploration, while the cgs strategy focuses on constraint-guided path exploration using concrete branch constraints. Each of these strategies selects symbolic states according to different feature attributes, offering distinct advantages in specific testing scenarios.

ANGR is a comprehensive Python 3.10-based binary analysis framework first introduced by Shoshitaishvili et al. in 2016 [46]. It is designed for deep analysis of binary programs in the absence of source code. The core idea of ANGR is to convert binary code into an intermediate representation, systematically generate path constraints, and use constraint solvers to evaluate the feasibility of execution paths. This enables automated analysis of complex program behaviors, facilitating vulnerability discovery, behavioral verification, and exploit development.

ALF is a symbolic execution path exploration framework based on active ensemble learning. The framework first employs a reward-value prediction mechanism to filter symbolic states, automatically labeling high-value states and feeding them back to the predictive model for iterative optimization of path selection decisions. Moreover, ALF trains multiple sub-models in successive iterations and enables them to collaborate during path exploration, leveraging the complementary strengths of multiple models to improve the quality of generated test cases.

The experimental environment is deployed within a Docker container running on an Intel(R) Xeon(R) Gold 6130 CPU @ 2.10 GHz with 128 GB RAM, using Ubuntu 18.04 as the operating system. To comprehensively validate the effectiveness of the proposed DLF framework, three groups of experiments were designed, systematically evaluating its performance from three distinct perspectives:

(1)

Validation of vulnerability detection and performance effectiveness. This experiment aims to assess the capability and efficiency of the DLF framework in vulnerability detection. Specifically, through comparative analysis, it evaluates whether DLF can more accurately predict and prioritize symbolic states with higher vulnerability probabilities under the same limited amount of labeled data, thereby generating more targeted, high-quality test cases and improving detection efficiency. The experiments focus on several common software vulnerabilities, including stack buffer overflow, heap buffer overflow, out-of-bounds write, out-of-bounds read, and integer overflow. To ensure comprehensive and representative evaluation, several typical CGC programs are selected as test targets. The performance of different methods is compared in terms of their detection capability and efficiency across the aforementioned vulnerability types, providing an integrated assessment of DLF’s real-world performance.

(2)

Validation of test-case effectiveness in fuzz testing. To further evaluate the quality of the test cases generated by DLF, this experiment selects two representative programs—CROMU_00021 and NRFIN_00021—from the CGC dataset as test subjects. The test cases produced by different methods are used as the initial seed sets for the fuzzing tool AFL, and the number of execution paths triggered under identical test conditions is recorded. By comparing the path coverage achieved by different seed sets, this experiment analyzes the effectiveness of each method in improving fuzzing efficiency and coverage. The results further demonstrate the practical value and advantages of the DLF framework in real-world fuzz testing scenarios.

(3)

Ablation study. To investigate the practical contribution of key components within the DLF framework, this experiment focuses on validating the active self-ensemble mechanism. Representative vulnerability types—including type confusion, untrusted pointer dereference, and format string vulnerabilities—are selected as test targets. Four methods are compared under identical experimental conditions: baseline ANGR, ANGR + Active Learning, ANGR + Self-Ensemble Learning, and ANGR + Active Self-Ensemble Learning (i.e., the complete DLF framework). The results are used to evaluate the effectiveness of the proposed active self-ensemble mechanism in improving the efficiency of symbolic execution path selection. In addition, to further examine the impact of the sliding-window mechanism on model performance, experiments are conducted using different window sizes. The comparative analysis of detection results across varying configurations provides a comprehensive understanding of how this mechanism regulates model performance and stability during the testing phase.

4.3. Experimental Results

The experiments in this section comprehensively evaluate the effectiveness of the DLF framework from three perspectives through multiple rounds of multidimensional comparative testing. All baseline methods were executed under identical experimental environments to ensure fairness and consistency. Across the five independent runs, all performance trends remained consistent, and DLF exhibited stable improvements over all baselines under every configuration. Specifically, the DLF framework was instantiated as a novel symbolic execution tool named Desbuild, and thus the execution results of Desbuild directly reflect the experimental performance of the DLF framework.

4.3.1. Validation of Vulnerability Detection Effectiveness

This experiment aims to evaluate the effectiveness of the DLF framework in terms of both vulnerability detection capability and execution performance. The tests target several representative software vulnerabilities, including stack buffer overflow, heap buffer overflow, out-of-bounds write, out-of-bounds read, and integer overflow, assessing the detection performance of different methods within a 15-h time window. All experimental results are reported as the average of five independent runs to ensure statistical stability and reliability. In addition, the evolution curves of the number of detected vulnerabilities over time are plotted for each method, providing an intuitive comparison of their detection efficiency and temporal progression.

The results for stack buffer overflow detection are presented in

Table 2. Comparison of Detection Results for Stack Buffer Overflow.

Binary Program Name	rss	nurc	sgs	Learch	cgs	ANGR	ALF	DLF
CADET_00001	38 min	×	4 min	3 min	×	3 min	–	2 min
CADET_00003	×	96 min	8 min	29 min	7 min	×	3 min	5 min
CROMU_00019	×	×	216 min	×	×	×	137 min	94 min
EAGLE_00005	×	×	×	×	×	×	×	163 min
NRFIN_00016	93 min	107 min	211 min	67 min	88 min	72 min	–	52 min
NRFIN_00023	×	99 min	365 min	117 min	×	×	181 min	166 min
YAN01_00001	100 min	×	×	97 min	39 min	201 min	×	20 min
YAN01_0016	9 min	55 min	6 min	×	×	5 min	2 min	4 min
Total count	4	3	6	5	3	4	5	8
Average execution time	60 min	83 min	118 min	99 min	38 min	74 min	79 min	63 min

× indicates that the tool was unable to complete this detection task.

, where min denotes minutes. A total of eight binary programs containing stack buffer overflow vulnerabilities were selected as test subjects. The experiment compares the detection capability and efficiency of various path exploration methods. From the perspective of overall detection count, DLF successfully identified all vulnerabilities across the eight samples, outperforming all other baseline methods and demonstrating a clear advantage in detection capability.

In terms of detection efficiency, the average detection time was calculated based on successfully analyzed samples. The average detection time of DLF was 63 min, outperforming the second-best method, sgs, which required 118 min on average. This result indicates that DLF not only identifies more vulnerabilities but also achieves higher detection efficiency. For complex programs such as YAN01_00001 and CROMU_00019, DLF required significantly less time than other methods, while some baseline approaches failed to complete detection—further confirming the advantages of the DLF framework in both path selection and test sample generation. Overall, the results demonstrate that DLF exhibits superior comprehensiveness and stability in detecting stack buffer overflow vulnerabilities.

The detection results for other common vulnerabilities—heap buffer overflow (HBO), out-of-bounds write (OBW), out-of-bounds read (OBR), and integer overflow (IOF)—are summarized in

Table 3. Comparison of detection results for other bugs.

Binary Program Name	Vulnerability Type	rss	nurc	sgs	Learch	cgs	ANGR	ALF	DLF
CROMU_00006	HBO	171 min	×	153 min	134 min	×	140 min	–	116 min
CROMU_00014	HBO	×	169 min	×	145 min	93 min	213 min	25 min	×
KPRCA_00057	HBO	62 min	44 min	29 min	23 min	31 min	32 min	19 min	41 min
YAN01_00012	HBO	×	×	×	×	×	×	×	267 min
CROMU_00012	OBW	×	×	596 min	709 min	×	×	663 min	517 min
CROMU_00036	OBW	363 min	415 min	106 min	715 min	333 min	402 min	×	245 min
CROMU_00034	OBR	×	132 min	×	157 min	×	216 min	243 min	42 min
NRFIN_00052	IOF	39 min	42 min	35 min	×	42 min	×	52 min	34 min
KPRCA_00014	IOF	×	×	×	×	×	×	194 min	139 min
Total count	–	4	5	5	6	4	5	6	8
Average execution time	–	159 min	160 min	184 min	314 min	125 min	201 min	199 min	175 min

× indicates that the tool was unable to complete this detection task.

. From the perspective of overall detection capability, DLF successfully identified eight vulnerabilities across nine binary programs containing these types of defects, outperforming all baseline methods and demonstrating stronger vulnerability detection capacity. In terms of average detection time, calculated based on successfully analyzed programs, DLF required 175 min on average—slightly higher than the three other baseline methods. This increase is primarily attributed to the fact that, for complex samples such as YAN01_00012 and CROMU_00012, DLF successfully detected vulnerabilities but required longer path exploration time. Nevertheless, considering its substantially superior detection capability, this marginal increase in runtime remains within an acceptable and reasonable range.

The number of vulnerabilities detected over time by different methods is illustrated in Figure 3. It can be observed that the DLF framework consistently outperforms all baseline methods at most time points, achieving both a faster detection rate and a higher final vulnerability count. Specifically, DLF identified multiple vulnerabilities within the first 50 min of testing and continued to steadily increase its total number of detected vulnerabilities throughout the entire testing process, ultimately discovering 16 vulnerabilities in total. In contrast, although the other methods demonstrated a certain degree of detection capability, they lagged behind DLF in both coverage and growth rate. From the temporal distribution of detected vulnerabilities, it is evident that DLF not only covered most of the easily discoverable vulnerabilities at an early stage but also continued to uncover deeper and more complex defects in the later stages. This behavior highlights the accuracy and efficiency of DLF’s path selection strategy in guiding symbolic execution toward high-value exploration paths.

4.3.2. Validation of DLF Framework Effectiveness in Hybrid Testing

In this experiment, two structurally complex test programs were selected. Each program was first subjected to 10 min of symbolic execution using different methods. The test cases generated from symbolic execution were then used as initial seed inputs for the fuzzing tool AFL, enabling further fuzz testing. During the fuzzing process, the number of unique execution paths discovered over time was recorded and analyzed to evaluate both the quality of test cases generated by symbolic execution and their impact on fuzzing efficiency. All reported results represent the average of five independent experimental runs to ensure reliability.

The experimental results for the CROMU_00021 test program are shown in Figure 4. In this test, the DLF framework generated 556 execution paths within the first 30 min, significantly outperforming traditional methods such as ANGR and rss, while maintaining a performance gap of less than 7.7% compared to the current best-performing baseline, ALF. As testing progressed, DLF exhibited a distinct and sustained growth trend: the number of discovered paths increased to 596 at 60 min (a 7.2% improvement) and further to 709 at 120 min (a cumulative 27.5% increase), ultimately surpassing all baseline methods. In contrast, ANGR showed minimal growth throughout the process, with its path count increasing only from 413 to 456, an improvement of less than 10%, demonstrating its limited capability in path discovery and exploration depth.

Figure 5 presents the testing results for the NRFIN_00021 program. As shown, both DLF and ALF significantly outperform all baseline methods during the early stages of fuzz testing, demonstrating clear advantages in seed generation capability and path coverage efficiency. At the 30-min mark, ALF and DLF improved path discovery by approximately 187% and 136%, respectively, compared with ANGR. In subsequent testing phases, DLF maintained a steady upward trajectory, achieving nearly a 33% increase over its initial path count by 90 min, while ALF exhibited only marginal growth after the 30-min point.

Overall, both DLF and ALF substantially outperform ANGR, generating more diverse and guidance-effective initial seeds that significantly enhance fuzzing efficiency. The DLF framework excels in the early-stage rapid coverage of critical paths, whereas ALF demonstrates stronger stability during continuous exploration. In contrast, ANGR exhibits clear deficiencies in both seed generation and path coverage efficiency, making it difficult to meet the dual requirements of efficiency and coverage in hybrid testing scenarios.

4.3.3. Ablation Experiment

To verify the effectiveness of the individual components within the DLF framework, the experiments focus on evaluating whether the introduction of the active self-ensemble learning mechanism and the sliding-window mechanism can effectively enhance both vulnerability detection capability and execution efficiency. Each reported result represents the average of five independent experimental runs to ensure statistical robustness.

Table 4. Comparison of Detection Results for Different Methods.

Binary Program Name	Vulnerability Type	ANGR	ANGR + Active Learning	ANGR + Ensemble Learning	ANGR + Active + Ensemble Learning
KPRCA_00033	Type_Confusion	43 min	42 min	40 min	38 min
KPRCA_00015	Untrusted_Pointer_Dereference	×	3 min	×	3 min
CROMU_00043	Format_String	137 min	×	251 min	94 min
NRFIN_00023	Untrusted_Pointer_Dereference	×	2 min	×	4 min
Total count	–	2	3	2	4
Average execution time	–	90 min	15.67 min	145.5 min	34.75 min

summarizes the detection capability and efficiency of different methods across multiple vulnerability types. As shown in the table, the baseline ANGR method successfully detected only two vulnerabilities, with an average detection time of 90 min, indicating relatively low detection efficiency and capability. After incorporating the active learning mechanism, the number of detected vulnerabilities increased to three, and the average detection time decreased dramatically to 15.67 min. This result demonstrates that active learning enables rapid localization of potential vulnerability regions, thereby improving the utilization efficiency of testing resources while maintaining a high detection success rate. Although the ensemble learning method alone also detected two vulnerabilities, its average detection time increased to 145.5 min, as the multi-model fusion process introduces additional computational overhead. While ensemble learning improves detection stability, it does so at the cost of efficiency. In contrast, the active ensemble learning approach combines the strengths of both methods: it successfully detected all four test vulnerabilities, outperforming all other strategies in detection capability, while maintaining an average detection time of 34.75 min—only 38.6% of the baseline ANGR runtime and more than 76% faster than the single ensemble learning method. Furthermore, for the CROMU_00043 program featuring a complex format-string vulnerability, the detection time of the DLF framework was approximately 62.5% shorter than that of standalone ensemble learning. This further highlights the effectiveness of the active strategy in improving path guidance and seed diversity, leading to enhanced overall vulnerability detection performance. We also observe negligible variation across the five repetitions for all component combinations, highlighting the low-variance nature of the DLF pipeline and reinforcing the reliability of the ablation findings.

The experiment also evaluated the impact of the sliding-window mechanism on exploration efficiency and accuracy. Different initial window sizes were configured, and the comparative results are presented in

Table 5. Comparison of Testing Results for Different Sliding Window Sizes.

Sliding Window Size	0	2	5	10	20	Dynamic Window
Average Execution Time	0.02 s	0.25 s	0.41 s	0.58 s	0.79 s	0.81 s
F1 Score	88%	91%	89%	89%	85%	93%

. Each reported value represents the average of five independent experimental runs, where a window size of 0 indicates the absence of the sliding-window mechanism. As shown in Table 5, when the fixed sliding-window size increases, the average path exploration time also increases accordingly. This finding indicates that while the sliding-window mechanism enhances historical information utilization and improves sample diversity, it inevitably introduces additional scheduling complexity and path evaluation overhead.

However, this increase in computational overhead does not exhibit a linear relationship with prediction accuracy. As observed from the trend of F1 scores, when using fixed window sizes, the F1 score reached its highest value at a window size of 2, improving by approximately 4.5% compared with the no-window configuration (88%). This result indicates that a moderate sliding window effectively mitigates sample bias and enhances the accuracy of path evaluation. In contrast, when the window size was further enlarged to 20, the F1 score decreased to 85%, slightly lower than that of the no-window strategy. This finding suggests that while a properly sized window can significantly improve the model’s decision-making capability and the precision of vulnerability detection, an excessively large window may introduce redundant historical information, thereby reducing the model’s responsiveness to current inputs and negatively impacting overall detection performance. The dynamic sliding-window mechanism proposed in this paper addresses this trade-off by adjusting the window size adaptively based on branch density, maintaining it within the effective range of [2, 10]. This approach fully exploits both the effectiveness of windowing and the flexibility of dynamic adjustment, achieving the highest F1 score among all configurations. Therefore, the proposed branch-density-based dynamic sliding-window adjustment mechanism is proven to be effective in enhancing the performance of the DLF framework.

5. Conclusions

This paper addresses the inherent limitations of mainstream symbolic execution tools in path exploration and achieves a technical breakthrough from the perspective of vulnerability detection capability optimization. A novel symbolic execution framework, DLF, integrating active learning and ensemble learning, is proposed and implemented on top of the mainstream symbolic execution engine ANGR, forming the prototype tool Desbuild. The proposed framework enables efficient and stable model training under low labeling cost conditions, while constructing a flexible heterogeneous model pool. By incorporating dynamic scenario adaptation and self-adaptive mechanisms, the framework can accurately capture multidimensional program features, thereby significantly improving the accuracy and robustness of test case generation. In addition, by introducing graph neural networks (GNNs) to perform deep feature extraction from control flow graphs (CFGs) and integrating these structural features with traditional ones, DLF provides a new approach for comprehensive program behavior modeling. Extensive experiments conducted on the CGC corpus covering multiple real-world programs demonstrate that the proposed method not only achieves substantial improvements in test case generation quality and efficiency under limited annotation conditions but also achieves a notable breakthrough in code vulnerability detection. These results indicate that DLF offers a novel and effective technical pathway for advancing automated testing and vulnerability detection, carrying significant theoretical value and practical implications for the future development of symbolic execution and program analysis technologies.

6. Future Prospects and Suggestions

Although the proposed DLF framework has demonstrated promising results in vulnerability detection and automated test case generation, there remains room for further improvement. First, the optimization between code coverage and vulnerability detection has yet to achieve a tightly coupled synergy, and a more adaptive trade-off strategy is needed to balance the two objectives dynamically. Second, the sliding-window mechanism currently relies on predefined branch-density rules, which limits its adaptability to programs of varying complexity and execution phases. Finally, while the dynamic model integration mechanism exhibits strong predictive performance, its interpretability and generalization across heterogeneous program scenarios still require enhancement.

Future research can focus on the following three directions:

(1)

Joint optimization of coverage and vulnerability detection. Future work may formulate coverage maximization and high-risk path discovery as a unified multi-objective optimization problem. Adaptive weighting and feedback mechanisms can help the framework balance exploration breadth and detection precision throughout execution.

(2)

Intelligent self-adaptation of the sliding window. To overcome the static nature of branch-density–based adjustment, learning-based or reinforcement strategies can be introduced to tune window size online according to coverage gain, constraint-solving cost, or model uncertainty, improving exploration efficiency under limited resources.

(3)

Enhancement of dynamic model integration and interpretability. The current heterogeneous model pool can be extended with more robust similarity measures and explainable components—such as attention weights or feature-contribution analysis—to strengthen adaptability and transparency across diverse program domains.